Abstract
We consider a generalized Langevin equation with regularized Prabhakar derivative operator. We analyze the mean square displacement, time-dependent diffusion coefficient and velocity autocorrelation function. We further introduce the so-called tempered regularized Prabhakar derivative and analyze the corresponding generalized Langevin equation with friction term represented through the tempered derivative. Various diffusive behaviors are observed. We show the importance of the three parameter Mittag-Leffler function in the description of anomalous diffusion in complex media. We also give analytical results related to the generalized Langevin equation for a harmonic oscillator with generalized friction. The normalized displacement correlation function shows different behaviors, such as monotonic and non-monotonic decay without zero-crossings, oscillation-like behavior without zero-crossings, critical behavior, and oscillation-like behavior with zero-crossings. These various behaviors appear due to the friction of the complex environment represented by the Mittag-Leffler and tempered Mittag-Leffler memory kernels. Depending on the values of the friction parameters in the system, either diffusion or oscillations dominate.
1. Introduction
The Langevin equation for a Brownian particle with mass is represented by the following equaion [1,2,3]
where is the particle displacement, is the particle velocity, is the friction coefficient, and is a stationary random force with zero mean and correlation , where is the so-called spectral density. By calculation of the mean square displacement (MSD) it has been shown that such process shows normal diffusive behavior, i.e., linear dependence of the MSD on time, . The corresponding diffusion coefficient for the Brownian motion is given by , and the normalized velocity autocorrelation function (VACF) by [1,3].
In the work by Lutz [4], a fractional Langevin equation describing non-Markovian stochastic process is introduced,
where
is the Caputo fractional derivative of order [5], and is the generalized friction coefficient. This equation is a special case of the generalized Langevin equation (GLE) with the power-law memory kernel (see Section 3). Additionally, if the noise is internal, the second fluctuation-dissipation relation
holds true, where . It has been shown that the MSD for the fractional Langevin Equation (2) is represented in terms of the two parameter Mittag-Leffler (M-L) function [4] (see Section 2 for details),
which is a proof of existence of anomalous diffusion in the system. Since , it is a subdiffusive process [6].
In this paper we introduce the GLE with a friction term represented through the regularized Prabhakar derivative (see Section 2 for details), i.e.,
where , , , , is a time parameter, and is the generalized friction coefficient. This equation is a generalization of the fractional Langevin Equation (2) which is recovered by setting . We further introduce a GLE with a tempered regularized Prabhakar friction term and analyze the normalized displacement correlation function in case of harmonic potential. Tempered fractional equations nowadays attract more and more attention due to their application in different systems [7,8,9,10].
This paper is organized as follows. In Section 2 we give definitions for the Prabhakar derivatives and integral, and related three parameter Mittag-Leffler function. We also introduce a so-called tempered regularized Prabhakar derivative and derive its Laplace transform. GLE for a free particle is considered in Section 3. The MSD, time-dependent diffusion coefficient and VACF are obtained explicitly. In Section 4 we introduce a GLE with friction term represented via tempered regularized Prabhakar derivative. Normal diffusive behavior in the long time limit is obtained due to the exponential truncation in the memory kernel. The case of harmonic oscillator is considered in Section 5, and the normalized displacement correlation function, which is experimentally measured quantity, is obtained. Different diffusion regimes have been observed, therefore the considered equations are of importance for description of anomalous diffusion in complex media. A summary is provided in Section 6.
2. Prabhakar Derivatives
The Prabhakar integral is defined by [11]
where
with —the Pochhammer symbol, is the three parameter M-L function [11]. The Laplace transform, , of the three parameter M-L function is given by
The functions and are the two parameter and one parameter M-L function, respectively. For the Prabhakar integral becomes the Riemann-Liouville (R-L) fractional integral, defined by . Its Laplace transform is given by [5].
The regularized Prabhakar derivative is defined as follows [12]
where , , , . For one obtains the Caputo fractional derivative [5]. Here we note that the Prabhakar derivative in a form of R-L is given by [12,13] (see also [14]). For it becomes the R-L fractional derivative [5]. These derivatives are applicable in the fractional Poisson process [12], for description of dielectric relaxation phenomena [15,16], in the fractional Maxwell model in the linear viscoelasticity [17], in mathematical modeling of fractional differential filtration dynamics [18], in fractional dynamical systems [19], generalized reaction-diffusion equations [20], in generalized model of particle deposition in porous media [21], etc.
In our paper we are particularly interested in the case with , so one has
From here we conclude that the regularized Prabhakar derivative is a special case of the generalized derivative
which has been investigated in different contexts in [10,22,23], where
We note that the Prabhakar derivative in the R-L form for is a special case of the generalized derivative , which has been investigated in [10,22,23], where the memory kernel is given by .
The Laplace transform of regularized Prabhakar derivative, Equation (11), is given by [12]
where [12]. For , Prabhakar derivative corresponds to the Caputo fractional derivative of order with Laplace transform [5]
Here we note that the regularized Prabhakar derivative, Equation (11), is a special case of the Hilfer-Prabhakar derivative defined by [12]
for the case with . Its Laplace transform reads [12]
From this formula we see that the initial value term is given in an integral form. Only the case with yields the initial value in the natural form . Therefore, the regularized Prabhakar derivative (11) is suitable for application in the GLE model. The case with corresponds to the so-called Hilfer composite fractional derivative of order and type , which is given by [24]. This composite fractional derivative has been successfully applied in description of dielectric and viscoelastic phenomena [25,26].
Furthermore, in this paper we introduce the tempered regularized Prabhakar derivative in the following way
where
and . Other parameters are the same as in the regularized Prabhakar derivative (11). From the definition we see that this derivative is a special case of the generalized derivative (12) for
Therefore, for the Laplace transform of the tempered regularized Prabhakar derivative we find
We will use this derivative in the GLE and analyze the influence of the exponential truncation on the particle behavior.
On the other hand, one can introduce the so-called tempered Prabhakar derivative in the R-L form in a similar way, by introducing exponential truncation in the memory kernel, i.e., .
Here we note that different fractional equations have been used for modeling anomalous diffusion in various systems, including fractional reaction-diffusion equations [27,28] and their application [29], fractional relaxation and diffusion equations [5,6,9,10,24,25,26], fractional cable equation [30], etc.
3. Free Particle
We showed in Section 2 that the regularized Prabhakar derivative (11) is a special case of the generalized derivative (12), therefore we conclude that the Langevin Equation (6) can be written in a form of the generalized Langevin equation (see [31])
where
By using the asymptotic expansion of the three parameter M-L function , which follows from the formula [9] (for details of the three parameter M-L function see [32])
for and , one can show that the assumption [33] is satisfied since . Additionally to this equation, we assume that the second fluctuation-dissipation relation
holds true.
From the Laplace transform method one finds that
where and are the initial particle displacement and initial particle velocity, respectively,
are the average particle displacement and the average particle velocity, respectively, and the Laplace pairs of the relaxation functions , and are given through by
respectively. From the relaxation functions one can derive the MSD, time-dependent diffusion coefficient and VACF, for thermal initial conditions and , and under the assumption , as follows [33,34,35]
Therefore, for the MSD, and VACF we find
respectively. Such series in three parameter M-L functions are convergent [36,37,38].
From Equation (22), for the long time limit we find
where . Therefore, from the MSD we conclude that there exists subdiffusion with anomalous diffusion exponent , where .
Graphical representation of the MSD (30) is given in Figure 1. From the figure we see that the MSD shows oscillation-like behavior for intermediate times which can be explained as a result of the cage effect of the environment represented by the M-L memory kernel (see also Section 5).
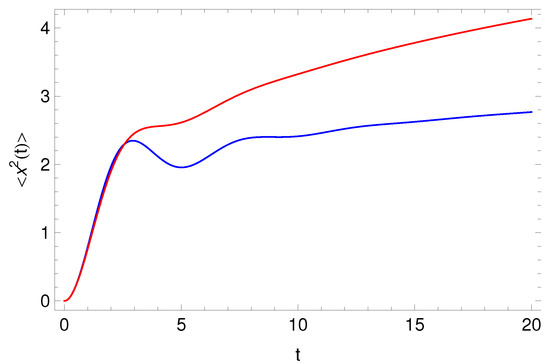
Figure 1.
Graphical representation of the MSD (30) for , , , , , and (blue line), (red line).
Remark 1.
The case with high viscous damping, i.e., Equation (20) with vanishing second derivative term , yields the following result
Since the anomalous diffusion exponent from μ for the short time limit turns to in the long time limit, we conclude that decelerating subdiffusion exists in the system.
4. Tempered Friction
We further consider the GLE with a friction term represented through the tempered regularized Prabhakar derivative. Therefore, we consider
where , and all the parameters are the same as in Equation (6). From definition (16) one may conclude that the memory kernel in GLE is given by
The second fluctuation-dissipation relation then reads
Following the same procedure as previous, for the MSD we find
where is the R-L fractional integral. In the case of no truncation (), from Equation (40), by using the formula [14], we recover the result (30) for the MSD.
Remark 2.
In the absence of the inertial term, in Equation (37), we find the following result for the MSD
The short time limit yields subdiffusion , and the long time limit normal diffusion . Therefore, there exists accelerating diffusion—from subdiffusion to normal diffusion. Such crossover from subdiffusion to normal diffusion has been observed, for example, in complex viscoelastic systems [39].
Graphical representation of the MSD (40) is given in Figure 2. From the figure one observes the influence of the truncation parameter b on the behavior of the MSD. The case with no truncation shows subdiffusive behavior (blue line), and the case with truncation (red and green lines) normal diffusion in the long time limit.
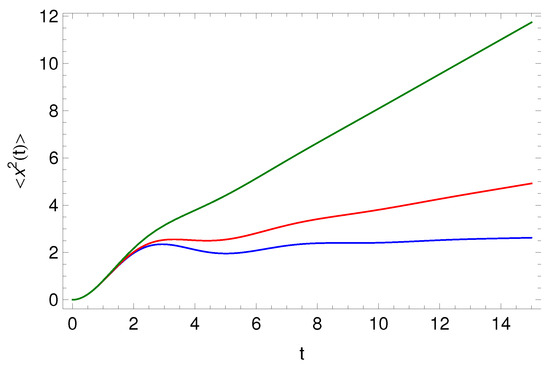
Figure 2.
Graphical representation of the MSD (40), for , , , , , , and (blue line), (red line) and (green line).
5. Harmonically Bounded Particle in Presence of Prabhakar Friction Term
At the end we consider GLE for a harmonic oscillator with tempered regularized Prabhakar friction, i.e.,
where is the frequency of the oscillator. By Laplace transform method we find exact result for the MSD. It is given by
where is the Prabhakar integral (7). For the free particle case , the Prabhakar integral corresponds to the R-L fractional integral, therefore, from Equation (43) one finds the previously obtained result for free particle, Equation (30).
Here we are particularly interested in the normalized displacement correlation function which is experimental measured quantity related to the GLE [40],
under the conditions , , and [41]. From here one concludes that , where . Therefore, it is given by
The case with no truncation yields
Graphical representation of the , Equations (46) and (45), is given in Figure 3 and Figure 4, respectively. From Figure 3 we see that different behaviors of appear, monotonic or non-monotonic decay without zero crossings (for ), critical behavior between the situations with and without zero crossings (at critical frequency ), and oscillation-like behavior with zero crossings (for ), which appear due to the cage effect of the environment [8,41]. The friction, depending on the memory kernel parameters, forces either diffusion or oscillations. In Figure 4 we see that with increasing of tempering, oscillation behavior with zero crossings appears. Therefore, in comparison to the standard harmonic oscillator (standard Langevin equation in presence of harmonic potential) where two types of motion are observed for the normalized displacement correlation function, either monotonic decay without zero crossings or oscillation-like behavior with zero crossings (that are separated at the critical frequency ), in case of the GLE with Prabhakar memory kernel more different complex behaviors of the are observed. Thus, the friction parameters contained in the tempered Prabhakar derivative, by their tuning, increase the versatility to fit complex experimental data.
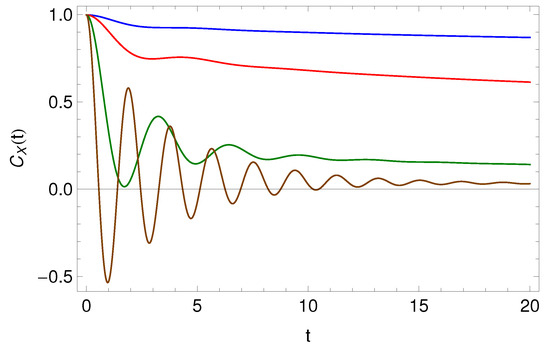
Figure 3.
Graphical representation of the normalized displacement correlation function, Equation (46), for , , , , and (blue line), (red line), (green line), (brown line).
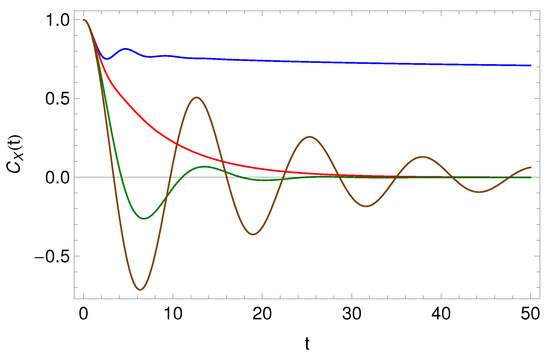
Figure 4.
Graphical representation of the normalized displacement correlation function, Equation (45), for , , , , and (blue line), (red line), (green line), (brown line).
6. Summary
We show that the generalized Langevin equation with a friction represented in terms of the regularized Prabhakar derivative generates decelerating subdiffusion. We also introduce a tempered regularized Prabhakar derivative in the friction term and we show that the system from subdiffusion switches to normal diffusion due to the exponential truncation in the memory kernel. Such model could be used in the description of diffusive processes in viscoelastic systems, where subdiffusion turns to normal diffusive behavior. We demonstrate the role of the three parameter Mittag-Leffler function and the Prabhakar integral in the anomalous dynamics theory. The obtained results are generalizations of those for the fractional Langevin equation. We also observe various behaviors of the normalized displacement correlation function in case of harmonic oscillator. The proposed models in this paper generate various anomalous diffusive realizations; therefore, by adjusting the memory kernel parameters one could better fit complex experimental data.
Acknowledgments
The author acknowledges funding from the Deutsche Forschungsgemeinschaft (DFG), project ME 1535/6-1 ”Random search processes, Lévy flights, and random walks on complex networks”.
Conflicts of Interest
The author declares no conflict of interest.
References
- Coffey, W.T.; Kalmykov, Yu.P.; Waldron, J.T. The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering; World Scientific: Singapore, 2012. [Google Scholar]
- Langevin, P. On the theory of Brownian motion. Comptes Rendus 1908, 146, 530–533. [Google Scholar]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Lutz, E. Fractional Langevin equation. Phys. Rev. E 2001, 64, 051106. [Google Scholar] [CrossRef] [PubMed]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelesticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]
- Metzler, R.; Jeon, J.-H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wang, X.; Deng, W. Localization and ballistic diffusion for the tempered fractional Brownian-Langevin motion. J. Stat. Phys. 2017, 169, 18–37. [Google Scholar] [CrossRef]
- Liemert, A.; Sandev, T.; Kantz, H. Generalized Langevin equation with tempered memory kernel. Physica A 2017, 466, 356–369. [Google Scholar] [CrossRef]
- Sandev, T.; Chechkin, A.; Kantz, H.; Metzler, R. Diffusion and Fokker-Planck-Smoluchowski equations with generalized memory kernel. Fract. Calc. Appl. Anal. 2015, 18, 1006–1038. [Google Scholar] [CrossRef]
- Sandev, T.; Sokolov, I.M.; Metzler, R.; Chechkin, A. Beyond monofractional kinetics. Chaos Solitons Fractals 2017, 102, 210–217. [Google Scholar] [CrossRef]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag-Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Garra, R.; Gorenflo, R.; Polito, F.; Tomovski, A. Hilfer-Prabhakar derivatives and some applications. Appl. Math. Comput. 2014, 242, 576–589. [Google Scholar] [CrossRef]
- Polito, F.; Tomovski, Z. Some properties of Prabhakar-type fractional calculus operators. Fract. Differ. Calc. 2016, 6, 73–94. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integral Transform. Spec. Funct. 2004, 15, 31–49. [Google Scholar] [CrossRef]
- Garrappa, R. Grünwald-Letnikov operators for fractional relaxation in Havriliak-Negami models. Commun. Nonlinear Sci. Numer. Simul. 2016, 38, 178–191. [Google Scholar] [CrossRef]
- Garrappa, R.; Mainardi, F.; Maione, G. Models of dielectric relaxation based on completely monotone functions. Fract. Calc. Appl. Anal. 2016, 19, 1105–1160. [Google Scholar] [CrossRef]
- Giusti, A.; Colombaro, I. Prabhakar-like fractional viscoelasticity. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 138–143. [Google Scholar] [CrossRef]
- Bulavatsky, V.M. Mathematical modeling of fractional differential filtration dynamics based on models with Hilfer–Prabhakar derivative. Cybern. Syst. Anal. 2017, 53, 204–216. [Google Scholar] [CrossRef]
- Darani, M.A.; Derakhshan, M.H.; Ansari, A.; Khoshsiar, R. On asymptotic stability of Prabhakar fractional differential systems. Comput. Methods Differ. Equ. 2016, 4, 276–284. [Google Scholar]
- Agarwal, R.; Jain, S.; Agarwal, R.P. Analytic solution of generalized space time fractional reaction diffusion equation. Fract. Differ. Calc. 2017, 7, 169–184. [Google Scholar] [CrossRef]
- Xu, J. Time-fractional particle deposition in porous media. J. Phys. A Math. Theor. 2017, 50, 195002. [Google Scholar] [CrossRef]
- Kochubei, A. General fractional calculus, evolution equations, and renewal processes. Integral Equ. Oper. Theory 2011, 71, 583–600. [Google Scholar] [CrossRef]
- Luchko, Y.; Yamamoto, M. General time fractional diffusion equation: Some uniqueness and existence results for the initial-boundary-value problems. Fract. Calc. Appl. Anal. 2016, 19, 676–695. [Google Scholar] [CrossRef]
- Hilfer, R. Application of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Hilfer, R. Experimental evidence for fractional time evolution in glass forming materials. Chem. Phys. 2002, 284, 399–408. [Google Scholar] [CrossRef]
- Sandev, T.; Metzler, R.; Tomovski, Z. Fractional diffusion equation with a generalized Riemann-Liouville time fractional derivative. J. Phys. A Math. Theor. 2011, 44, 255203. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Space-time fractional reaction-diffusion equations associated with a generalized Riemann-Liouville fractional derivative. Axioms 2014, 3, 320–334. [Google Scholar] [CrossRef]
- Saxena, R.K.; Mathai, A.M.; Haubold, H.J. Computational solutions of distributed order reaction-diffusion systems associated with Riemann-Liouville derivatives. Axioms 2015, 4, 120–133. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Analysis of solar neutrino data from Super-Kamiokande I and II. Entropy 2014, 16, 1414–1425. [Google Scholar] [CrossRef]
- Saxena, R.K.; Tomovski, Z.; Sandev, T. Analytical solution of generalized space-time fractional cable equation. Mathematics 2015, 3, 153–170. [Google Scholar] [CrossRef]
- Kubo, R. The Fluctuation-Dissipation Theorem. Rep. Prog. Phys. 1966, 29, 255–284. [Google Scholar] [CrossRef]
- Garra, R.; Garrappa, R. The Prabhakar or three parameter Mittag–Leffler function: Theory and application. Commun. Nonlinear Sci. Numer. Simul. 2018. [Google Scholar] [CrossRef]
- Despósito, M.A.; Viñales, A.D. Subdiffusive behavior in a trapping potential: Mean square displacement and velocity autocorrelation function. Phys. Rev. E 2009, 80, 021111. [Google Scholar] [CrossRef] [PubMed]
- Mainardi, F.; Pironi, P. The fractional Langevin equation: Brownian motion revisited. Extr. Math. 1996, 10, 140–154. [Google Scholar]
- Pottier, N. Aging properties of an anomalously diffusing particle. Physica A 2003, 317, 371–382. [Google Scholar] [CrossRef]
- Paneva-Konovska, J. Convergence of series in three parametric Mittag-Leffler functions. Math. Slovaca 2014, 64, 73–84. [Google Scholar] [CrossRef]
- Paneva-Konovska, J. From Bessel to Multi-Index Mittag-Leffler Functions: Enumerable Families, Series in Them and Convergence; World Scientific: Hackensack, NJ, USA, 2016. [Google Scholar]
- Sandev, T.; Tomovski, Z.; Dubbeldam, J.L.A. Generalized Langevin equation with a three parameter Mittag-Leffler noise. Physica A 2011, 390, 3627–3636. [Google Scholar] [CrossRef]
- Jeon, J.-H.; Monne, H.M.-S.; Javanainen, M.; Metzler, R. Anomalous diffusion of phospholipids and cholesterols in a lipid bilayer and its origins. Phys. Rev. Lett. 2012, 109, 188103. [Google Scholar] [CrossRef] [PubMed]
- Min, W.; Luo, G.; Cherayil, B.J.; Kou, S.C.; Xie, X.S. Observation of a power-law memory kernel for fluctuations within a single protein molecule. Phys. Rev. Lett. 2005, 94, 198302. [Google Scholar] [CrossRef] [PubMed]
- Burov, S.; Barkai, E. Fractional Langevin equation: Overdamped, underdamped, and critical behaviors. Phys. Rev. E 2008, 78, 031112. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).