Least-Squares Solution of Linear Differential Equations ^†

Abstract

This study shows how to obtain least-squares solutions to initial value problems (IVPs), boundary value problems (BVPs), and multi-value problems (MVPs) for nonhomogeneous linear differential equations (DEs) with nonconstant coefficients of any order. However, without loss of generality, the approach has been applied to second-order DEs. The proposed method has two steps. The first step consists of writing a constrained expression, that has the DE constraints embedded. These kind of expressions are given in terms of a new unknown function, $g\left(t\right)$, and they satisfy the constraints, no matter what $g\left(t\right)$ is. The second step consists of expressing $g\left(t\right)$ as a linear combination of m independent known basis functions. Specifically, orthogonal polynomials are adopted for the basis functions. This choice requires rewriting the DE and the constraints in terms of a new independent variable, $x\in [-1,+1]$. The procedure leads to a set of linear equations in terms of the unknown coefficients of the basis functions that are then computed by least-squares. Numerical examples are provided to quantify the solutions’ accuracy for IVPs, BVPs and MVPs. In all the examples provided, the least-squares solution is obtained with machine error accuracy.

1. Introduction

The purpose of this article is to provide a unified framework to obtain analytical, least-squares, approximated solutions of nonhomogeneous linear differential equations (DEs) of order $n\ge 1$ with nonconstant coefficients subject to a set of n constraints:

$${\displaystyle \sum _{k=0}^n{f}_k\left(t\right){\displaystyle \frac{{\mathrm{d}}^{k}y}{\mathrm{d}{t}^k}}=f\left(t\right)\mathrm{subject}\mathrm{to}:{\left.{\displaystyle \frac{{\mathrm{d}}^{i}y}{\mathrm{d}{t}^i}}\right|}_{t_j}=y_j^{\left(i\right)}}$$

(1)

where $f_k\left(t\right)$ and $f\left(t\right)$ can be any functions, continuous and nonsingular, within the range of integration, and $y_j^{\left(i\right)}$ indicates the ith derivative specified at time $t_j$. The proposed method unifies how to solve initial value problems (IVPs), boundary value problems (BVPs), or multi-point value problems (MVPs).

While the proposed method works for linear DEs of any order, for brevity of exposition, the method is presented to solve second-order DEs:

$$f_2\left(t\right){\displaystyle \frac{{\mathrm{d}}^{2}y}{\mathrm{d}{t}^2}}+f_1\left(t\right){\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}+f_0\left(t\right)y=f\left(t\right)$$

(2)

This is because the proposed technique does not change if n increases, other than by adding additional terms.

1.1. Background on the Existing Approaches

Various techniques exist to provide numerical approximations of the DEs given in Equation (1). The most widely used approaches are the Runge–Kutta methods [1] for IVPs and shooting methods for BVPs. The shooting methods solve BVPs essentially by transforming BVPs into IVPs. These methods provide enough precision for most of the practical problems. However, the estimated solution is not analytic and is provided at discrete points, usually with an error growing along the range of integration. References [2,3] provide a collection of the most well-known methods for solving IVPs and BVPs. Other existing alternative integration approaches include, but are not limited to, the Gauss–Jackson method [4], collocation techniques [5], and the Modified Chebyshev–Picard Iteration [6] (a path-length integral approximation), which has recently been proven to be highly effective. All of these methods are based on low-order Taylor expansions, which limits the step size that can be used to propagate the solution. Higher-order Taylor methods have also been analyzed [7]. More contemporary approaches are the following:

• Collocation Techniques. In these techniques, the solution components are approximated by piecewise polynomials on a mesh. The coefficients of the polynomials form the unknowns to be computed. The approximation to the solution must satisfy the constraint conditions and the DEs at collocation points in each mesh subinterval. We note that the placement of the collocation points is not arbitrary. A modified Newton-type method, known as quasi-linearization, is then used to solve the nonlinear equations for the polynomial coefficients. The mesh is then refined by trying to equidistribute the estimated error over the whole interval. An initial estimate of the solution across the mesh is also required. However, a common weakness of all these collocation techniques (low-order Taylor expansion models) is that they are not effective in enforcing algebraic constraints. Enforcing the DE constraints is the strength of the proposed method, as the DE constraints are embedded in the searched solution expressions. This means that the analytical solution obtained, even if completely wrong, perfectly satisfies all the DE constraints.
• Spectral methods. Spectral methods are used to numerically solve DEs by writing the solution as a sum of certain “basis functions” (e.g., Fourier series) and then choosing the coefficients in the sum in order to satisfy the DEs as well as possible (e.g., by least-squares). Additionally, in spectral methods, the constraints must then be enforced. This is done by replacing one (or more) of the least-squares equations with the constraint conditions. The proposed method proceeds in the reverse sequence. It first builds a special function, called a “constrained expression”, that has the boundary conditions embedded, no matter what the final estimation is. Then, it uses this expression to minimize the DE residuals by expressing the free function of the constrained expression, $g\left(t\right)$, as a sum of some basis functions (e.g., orthogonal polynomials). The resulting estimation always perfectly satisfies the boundary conditions as long as they are linear. To provide an example, a linear constraint involving four times ($t_1$, $t_2$, $t_3$ and $t_4$) can be:

  $$\pi =7y\left(t_1\right)-e\dot{y}\left(t_1\right)-2y\left(t_2\right)-5\dot{y}\left(t_3\right)+\sqrt{3}\ddot{y}\left(t_3\right)-y\left(t_4\right)$$
  It is not clear how the spectral methods can enforce this kind of general linear constraint. Additionally, the spectral methods provide solutions approximating the constraints.

The solution of the proposed method is an analytical function fully complying with the DE constraints, and it approximates the DE by minimizing the residuals in a least-squares sense.

1.2. The Idea Behind the Proposed Method

The least-squares solution of Equation (2) is obtained using constrained expressions, which are introduced in [8] by the theory of connections, a methodology to provide general interpolation functions with an embedded set of n linear constraints. These expressions are found using the following general form:

$${\displaystyle y\left(t\right)=g\left(t\right)+\sum _{k=1}^n{\eta }_k{h}_k\left(t\right)=g\left(t\right)+{\mathbf{\eta }}^{\mathrm{T}}\mathit{h}\left(t\right))}$$

(3)

where $h_k\left(t\right)$ are n assigned functions and $g\left(t\right)$ is an unknown function, independent from the $\mathit{h}\left(t\right)$ functions; ${\eta }_k$ are n coefficients that are derived by imposing the n linear constraints on the $y\left(t\right)$ function. The linear constraints considered in the theory of connections [8] are any linear combination of the function and/or its derivatives evaluated at specified values of the independent variable, t. For an assigned set of n independent functions, $h_k\left(t\right)$, the n constraints of the DE allow us to derive the unknown vector of coefficients, $\mathbf{\eta }$. By substituting this expression into Equation (3), we obtain an equation satisfying all the constraints, no matter what $g\left(t\right)$ is. The problem of solving the DE is, therefore, to find the function $g\left(t\right)$. Because the DE is linear in $y\left(t\right)$ and $y\left(t\right)$ is linear in $g\left(t\right)$, then, by substituting Equation (3) into the DE, we obtain a new DE, linear in $g\left(t\right)$. In this paper, the solution, $g\left(t\right)$, is then expressed as a linear combination of orthogonal polynomials. The coefficients of this linear combination constitute the solution of the problem.

Orthogonal polynomials are excellent basis sets to describe the $g\left(t\right)$ free function appearing in Equation (3). However, most of these orthogonal polynomials, such as Chebyshev or Legendre orthogonal polynomials, are defined in some specific defined range, $x\in [x_0,x_f]$. (Specifically, Chebyshev and Legendre orthogonal polynomials are defined in $x\in [-1,+1]$.) Therefore, in order to adopt them, the DE must be rewritten in terms of the new variable, x, linearly related to $t\in [t_0,t_f]$ as:

$$x={\displaystyle \frac{x_f-x_0}{t_f-t_0}}(t-t_0)+x_0⟷t={\displaystyle \frac{t_f-t_0}{x_f-x_0}}(x-x_0)+t_0$$

and by introducing the integration range ratio, $c={\displaystyle \frac{x_f-x_0}{t_f-t_0}}$, these relationships become:

$$x=c(t-t_0)+x_0⟷t={\displaystyle \frac{x-x_0}{c}}+t_0$$

where $t_f$ is specified in BVPs while in IVPs it is the integration upper limit. This change of variable also affects the derivatives. Using the notation $\dot{y}$ for the derivative with respect to t and $y^{\prime }$ for the derivative with respect to x, we obtain:

$$\dot{y}={\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}}·{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}=c{y}^{\prime }\mathrm{and}\ddot{y}=c^2{y}^{″}$$

(4)

By changing the integration variable, particular attention must be given to the constraints specified in terms of derivatives. In fact, the constraints provided in terms of the first and/or second derivatives also need to comply with the rules given in Equation (4), meaning that the constraints on the derivatives in terms of the new x variable depend on the integration time range, through the integration range ratio, c.

Functions $f_2\left(t\right)$, $f_1\left(t\right)$, $f_0\left(t\right)$ and $f\left(t\right)$ are also rewritten in terms of x, where, for instance, $f_0\left(t\right)=f_0\left[t_0+(x+1)/c\right]$, which can be indicated by $f_0\left(x\right)$. This means that, using the new variable, we can write $f_2\left(t\right)=f_2\left(x\right)$, $f_1\left(t\right)=f_1\left(x\right)$, $f_0\left(t\right)=f_0\left(x\right)$, and $f\left(t\right)=f\left(x\right)$. Therefore, Equation (2) can be rewritten as:

$$c^2{f}_2\left(x\right)y^{″}\left(x\right)+c{f}_1\left(x\right)y^{\prime }\left(x\right)+f_0\left(x\right)y\left(x\right)=f\left(x\right)$$

(5)

2. Least-Squares Solution of IVPs

A second-order DE has two constraints. Therefore, once the DE is written as in Equation (5), the constrained expression is searched, having the form:

$$y\left(x\right)=g\left(x\right)+{\eta }_{1}p\left(x\right)+{\eta }_{2}q\left(x\right)$$

(6)

For IVPs, with constraints,

$$y\left(t_0\right)=y(-1)=y_0\mathrm{and}\dot{y}\left(t_0\right)={\dot{y}}_0=c{y}^{\prime }(-1)=c{y}_0^{\prime }$$

The values of ${\eta }_1$ and ${\eta }_2$ are:

$$\left\{\begin{array}{c}{\eta }_1\\ {\eta }_2\end{array}\right\}={\left[\begin{array}{cc}{p}_0& q_0\\ p_0^{\prime }& q_0^{\prime }\end{array}\right]}^{-1}\left\{\begin{array}{c}{y}_0-g_0\\ y_0^{\prime }-g_0^{\prime }\end{array}\right\}=\left\{\begin{array}{c}{Y}_0\\ Y_0^{\prime }\end{array}\right\}-\left\{\begin{array}{c}{h}_{11}{g}_0+h_{12}{g}_0^{\prime }\\ h_{21}{g}_0+h_{22}{g}_0^{\prime }\end{array}\right\}$$

Substituting into Equation (6),

$$y\left(x\right)=g\left(x\right)+(Y_0-h_{11}{g}_0-h_{12}{g}_0^{\prime })p\left(x\right)+(Y_0^{\prime }-h_{21}{g}_0-h_{22}{g}_0^{\prime })q\left(x\right)$$

and setting $\alpha \left(x\right)=h_{11}p\left(x\right)+h_{21}q\left(x\right)$ and $\beta \left(x\right)=h_{12}p\left(x\right)+h_{22}q\left(x\right)$, we obtain:

$$y\left(x\right)=g\left(x\right)-\alpha \left(x\right)g_0-\beta \left(x\right)g_0^{\prime }+Y_{0}p\left(x\right)+Y_0^{\prime }q\left(x\right)$$

Then, substituting into Equation (6),

$$\begin{array}{c}c{c}^2{f}_2[g^{″}-{\alpha }^{″}{g}_0-{\beta }^{″}{g}_0^{\prime }]+c{f}_1[g^{\prime }-{\alpha }^{\prime }{g}_0-{\beta }^{\prime }{g}_0^{\prime }]+f_0[g-\alpha g_0-\beta g_0^{\prime }]\hfill \\ =f-c^2{f}_2[Y_0{p}^{″}+Y_0^{\prime }{q}^{″}]-c{f}_1[Y_0{p}^{\prime }+Y_0^{\prime }{q}^{\prime }]-f_0[Y_{0}p+Y_0^{\prime }q]\hfill \end{array},$$

The DE, written in terms of $g\left(x\right)$, becomes:

$$c^2{f}_2\left(x\right)g^{″}\left(x\right)+c{f}_1\left(x\right)g^{\prime }\left(x\right)+f_0\left(x\right)g\left(x\right)-m_1\left(x\right)g_0-m_2\left(x\right)g_0^{\prime }=b\left(x\right)$$

(7)

where:

$$\left\{\begin{array}{cc}\hfill m_1\left(x\right)=& c^2{f}_2\left(x\right){\alpha }^{″}\left(x\right)+c{f}_1\left(x\right){\alpha }^{\prime }\left(x\right)+f_0\left(x\right)\alpha \left(x\right)\hfill \\ \hfill m_2\left(x\right)=& c^2{f}_2\left(x\right){\beta }^{″}\left(x\right)+c{f}_1\left(x\right){\beta }^{\prime }\left(x\right)+f_0\left(x\right)\beta \left(x\right)\hfill \\ \hfill b\left(x\right)=& f\left(x\right)-c^2{f}_2\left(x\right)[Y_0{p}^{″}+Y_0^{\prime }{q}^{″}]-c{f}_1\left(x\right)[Y_0{p}^{\prime }+Y_0^{\prime }{q}^{\prime }]-f_0\left(x\right)[Y_{0}p+Y_0^{\prime }q]\hfill \end{array}\right.$$

(8)

The function $g\left(x\right)$ can be set as a linear combination of m basis functions, $g\left(x\right)={\mathbf{\xi }}^{\mathrm{T}}\mathit{h}\left(x\right)$, where $\mathit{h}\left(x\right)$ is the vector of m basis functions, and $\mathbf{\xi }$ is a vector of m unknown coefficients. Therefore, Equation (7) becomes:

$${\left[c^2{f}_2{\mathit{h}}^{″}+c{f}_1{\mathit{h}}^{\prime }+f_0\mathit{h}-m_1{\mathit{h}}_0-m_2{\mathit{h}}_0^{\prime }\right]}^{\mathrm{T}}\mathbf{\xi }={\mathit{a}}^{\mathrm{T}}\left(x\right)\mathbf{\xi }=b\left(x\right)$$

(9)

Equation (9), for any value of x, is linear in terms of the unknown coefficients ($\mathbf{\xi }$). Therefore, this equation can be specified for a set of N values of x ranging from the initial value, $x=x_0$, to the final value, $x=x_f$. This can be done, for instance, by a uniform $\Delta x$ step. This set of N equations in m unknowns (usually, $N\gg m$) can be set in the matrix form:

$$\mathbb{A}\mathbf{\xi }=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1m}\\ a_{21}& a_{22}& \cdots & a_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ a_{N1}& a_{N2}& \cdots & a_{Nm}\end{array}\right]\left\{\begin{array}{c}{\xi }_1\\ {\xi }_2\\ ⋮\\ {\xi }_m\end{array}\right\}=\left\{\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_N\end{array}\right\}=\mathit{b}$$

(10)

where:

$$a_{ij}=c^2{f}_2\left(x_i\right)h_j^{″}\left(x_i\right)+c{f}_1\left(x_i\right)h_j^{\prime }\left(x_i\right)+f_0\left(x_i\right)h_j\left(x_i\right)-m_1\left(x_i\right)h_0-m_2\left(x_i\right)h_0^{\prime }$$

The linear system of Equation (10) allows us to compute the solution (coefficient vector $\mathbf{\xi }$) by least-squares.

The simplest way to write a constrained expression subject to $y\left(x_0\right)=y_0$ and $y^{\prime }\left(x_0\right)=y_0^{\prime }={\dot{y}}_0/c$ is to select $p\left(x\right)=1$ and $q\left(x\right)=x$. This provides the values of ${\eta }_1$ and ${\eta }_2$ by inverting a $2\times 2$ matrix with its determinant equal to 1. For the variety of constraints considered in this paper, this property can be obtained by selecting the functions $p\left(x\right)$ and $q\left(x\right)$ to be those provided in

Table 1. Simplest selection of $p\left(x\right)$ and $q\left(x\right)$ for various initial value problem and boundary value problem constraints.

Differential Equation Constraints	$\mathit{p}\left(\mathit{x}\right)$	$\mathit{q}\left(\mathit{x}\right)$
$[y_0,y_0^{\prime }]$ or $[y_0,y_f]$ or $[y_0,y_f^{\prime }]$ or $[y_0^{\prime },y_f]$	1	x
$[y_0,y_0^{″}]$ or $[y_0,y_f^{″}]$ or $[y_0^{″},y_f]$	1	$x^2/2$
$[y_0^{\prime },y_0^{″}]$ or $[y_0^{\prime },y_f^{\prime }]$ or $[y_0^{\prime },y_f^{″}]$ or $[y_0^{″},y_f^{\prime }]$	x	$x^2/2$
$[y_0^{″},y_f^{″}]$	$x^2/2$	$x^3/3$

.

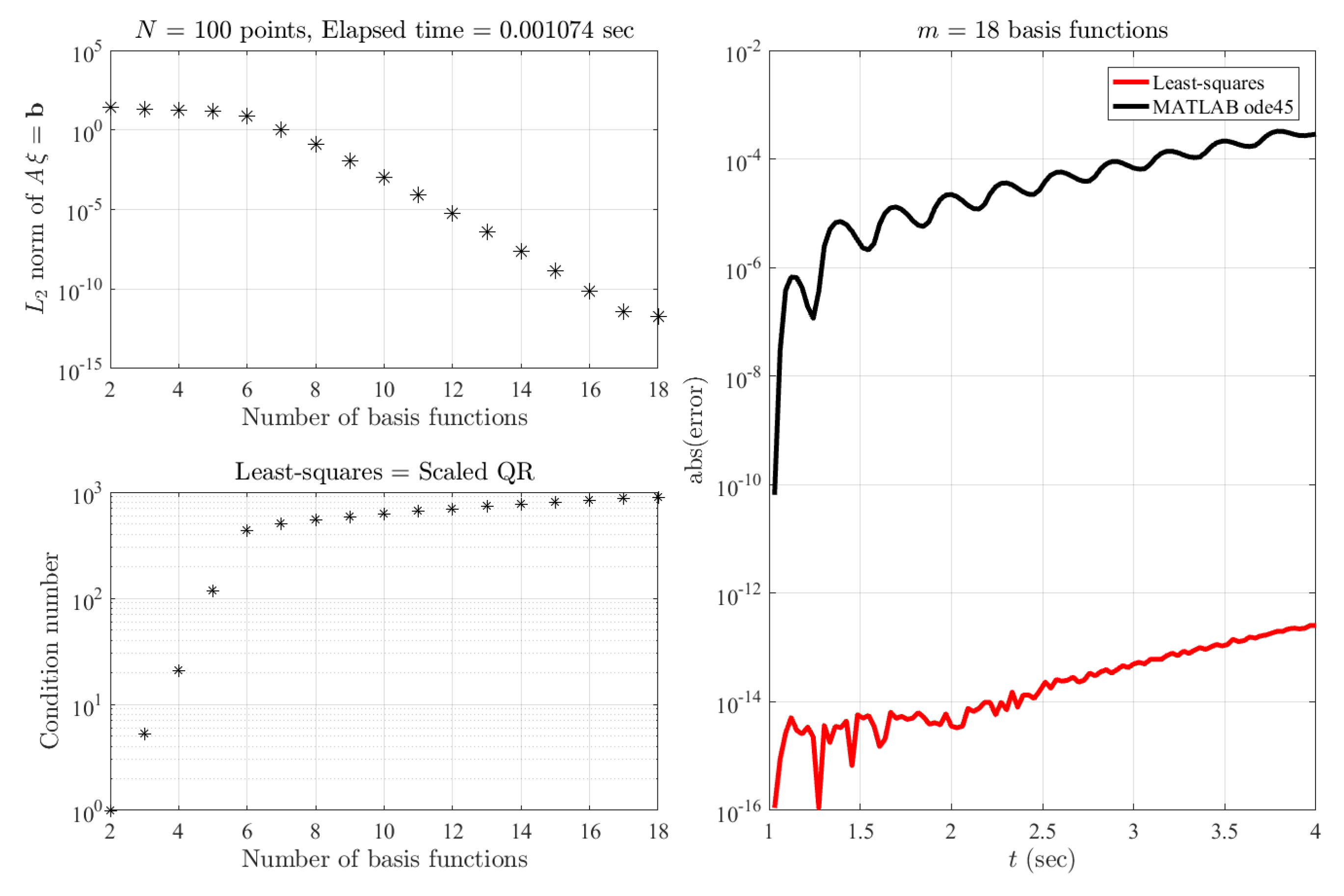
2.1. Accuracy Tests

We consider integrating the following IVP from $t_0=1$ to $t_f=4$:

$$t^2\ddot{y}-t(t+2)\dot{y}+(t+2)y=0\mathrm{subject}\mathrm{to}:\left\{\begin{array}{c}y\left(1\right)=y_0=1\hfill \\ \dot{y}\left(1\right)={\dot{y}}_0=0\hfill \end{array}\right.$$

(11)

whose general solution is $y\left(t\right)=\left(2-e^{t-1}\right)t$. We consider solving this IVP using Chebyshev orthogonal polynomials. This implies that, in terms of the new variable, the constraint derivative becomes $y_0^{\prime }={\displaystyle \frac{3}{2}}{\dot{y}}_0=0$. Equation (11) has been solved using the proposed least-squares approach with $m=18$ basis functions and a discretization made of $N=100$ points, and it has been integrated using the MATLAB function ode45 (The numerical comparisons made in this paper are limited to ode45 because it is the most widely used method in commercial applications.), implementing a Runge–Kutta variable-step integrator formula [1].

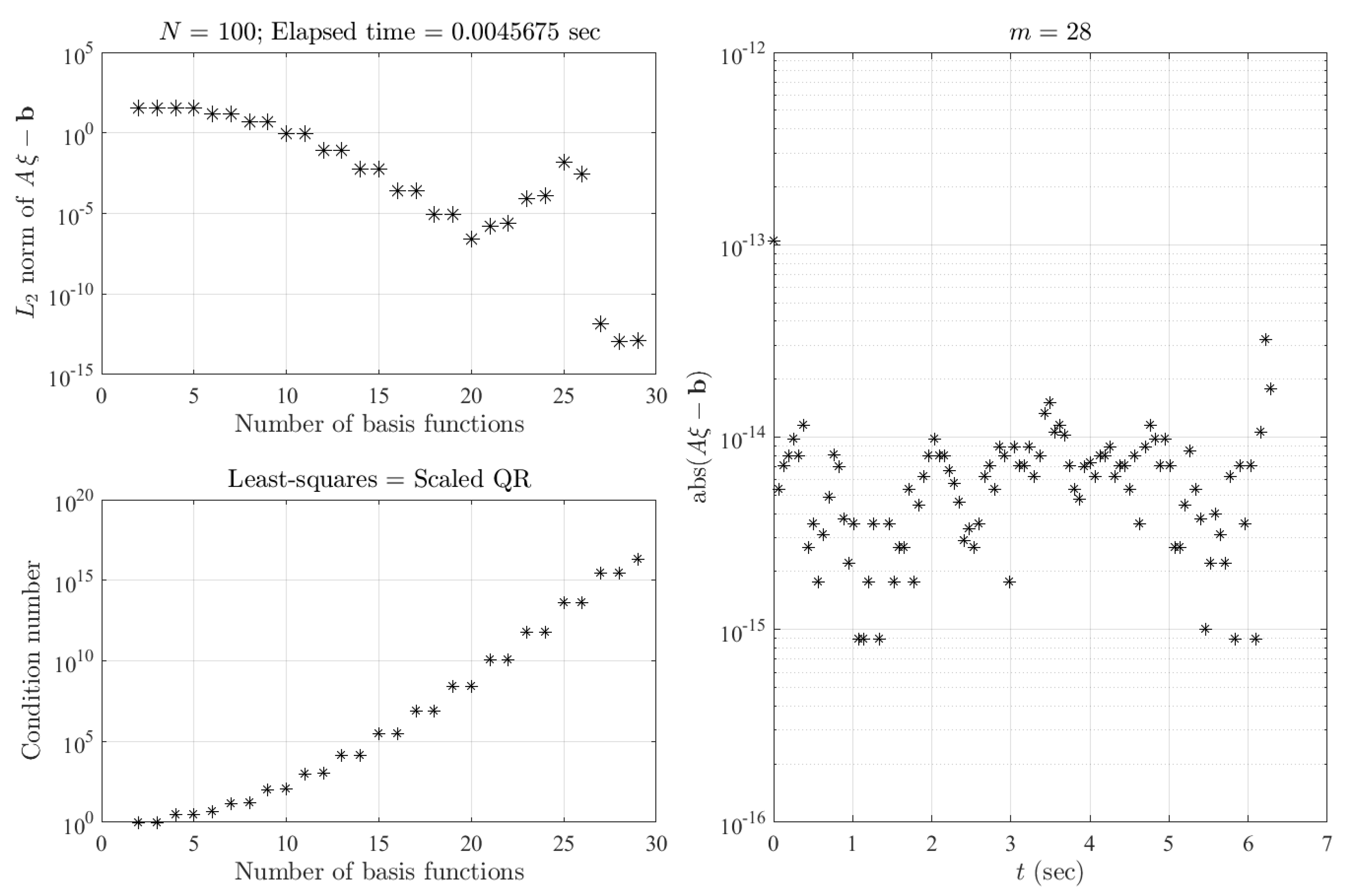
The results obtained are shown in Figure 1. In the top-left plot, the $L_2$ norm of $(\mathbb{A}\mathbf{\xi }-\mathit{b})$ is shown as a function of the number of basis functions, while the bottom-left plot provides the condition number to solve the least-squares. If the solution requires just $m=9$ basis functions and $m=18$ is used, then the coefficients from $m\in [10,18]$ are all zeros. The values of the $L_2$ norm of the least-squares residuals identify the minimum number of basis functions. The accuracies obtained using MATLAB’s ode45 [1] integrator and using the least-squares solution (The least-squares problem has been solved by QR decomposition of a scaled $\mathbb{A}$ matrix.) with $m=18$ basis functions and $N=100$ points are shown in the right plot. The least-squares solution shows about 9 orders of magnitude of accuracy gain.

In the following subsections, the constrained expressions for two other kinds of IVP—known-function and first-derivative and known first- and second-derivative—are provided.

2.2. Second-Order DE Subject to $y\left(t_0\right)=y_0$ and $\ddot{y}\left(t_0\right)={\ddot{y}}_0$

In terms of the new x variable, the initial conditions are $y_0$ and $y_0^{″}={\ddot{y}}_0/c^2$, while a constrained expression is:

$$y\left(x\right)=g\left(x\right)-x(y_0-g_0)+{\displaystyle \frac{x^2+x}{2}}(y_0^{″}-g_0^{″})$$

Then Equation (5) becomes:

$$\begin{array}{c}{c}^2{f}_2(g^{″}-g_0^{″})+c{f}_1\left(g^{\prime }+g_0-g_0^{″}{\displaystyle \frac{2x+1}{2}}\right)+f_0\left(g+g_{0}x-g_0^{″}{\displaystyle \frac{x^2+x}{2}}\right)\hfill \\ =f-c^2{f}_2{y}_0^{″}-c{f}_1\left(-y_0+y_0^{″}{\displaystyle \frac{2x+1}{2}}\right)-f_0\left(-y_{0}x+y_0^{″}{\displaystyle \frac{x^2+x}{2}}\right)\hfill \end{array}$$

and the least-squares solutions follows the same steps provided in Equations (7)–(10).

We note that, if $y_0$ and $y_0^{″}$ are known, then $y_0^{\prime }$ can be derived using Equation (5) evaluated at $x_0$:

$$y_0^{\prime }={\displaystyle \frac{f\left(t_0\right)-c^2{f}_2{y}_0^{″}-f_0\left(t_0\right)y_0}{c{f}_1\left(t_0\right)}}$$

provided that $f_1\left(t_0\right)\ne 0$. Therefore, the least-squares solution of the DE given in Equation (5) with constraints $y_0$ and $y_0^{″}$ can be solved as in the previous section with constraints $y_0$ and $y_0^{\prime }$.

2.3. Second-Order DE Subject to $\dot{y}\left(t_0\right)={\dot{y}}_0$ and $\ddot{y}\left(t_0\right)={\ddot{y}}_0$

In terms of the new variable, the initial conditions are $y_0^{\prime }={\dot{y}}_0/c$ and $y_0^{″}={\ddot{y}}_0/c^2$. In this case, a constrained expression is:

$$y\left(x\right)=g\left(x\right)+x(y_0^{\prime }-g_0^{\prime })+\left({\displaystyle \frac{x^2}{2}}+x\right)(y_0^{″}-g_0^{″})$$

Equation (5) becomes:

$$\begin{array}{c}{c}^2{f}_2\left(g^{″}-g_0^{″}\right)+c{f}_1\left[g^{\prime }-g_0^{\prime }-g_0^{″}(x+1)\right]+f_0\left[g-g_0^{\prime }x-g_0^{″}\left({\displaystyle \frac{x^2}{2}}+x\right)\right]\hfill \\ =f-c^2{f}_2{y}_0^{″}-c{f}_1\left[y_0^{\prime }+y_0^{″}(x+1)\right]-f_0\left[y_0^{\prime }x+y_0^{″}\left({\displaystyle \frac{x^2}{2}}+x\right)\right]\hfill \end{array}$$

and the least-squares solution follows the same steps provided in Equations (7)–(10).

Again, if $y_0^{\prime }$ and $y_0^{″}$ are known, then $y_0$ can also be computed by specializing Equation (5) at $x_0$:

$$y_0={\displaystyle \frac{f\left(t_0\right)-c^2{f}_2{y}_0^{″}-c{f}_1\left(t_0\right)y_0^{\prime }}{f_0\left(t_0\right)}}\mathrm{where}{f}_0\left(t_0\right)\ne 0$$

Therefore, the solution of the DE given in Equation (5) with constraints $y_0^{\prime }$ and $y_0^{″}$ can also be solved as in the previous section with constraints $y_0$ and $y_0^{\prime }$.

3. Least-Squares Solutions of BVPs

A two-point BVP, already written in terms of the new variable and subject to the constraints $y\left(x_0\right)=y_0$ and $y\left(x_f\right)=y_f$, has a constrained expression that can be obtained using Equation (6), where the values of ${\eta }_1$ and ${\eta }_2$ are:

$$\left\{\begin{array}{c}{\eta }_1\\ {\eta }_2\end{array}\right\}={\left[\begin{array}{cc}{p}_0& q_0\\ p_f& q_f\end{array}\right]}^{-1}\left\{\begin{array}{c}{y}_0-g_0\\ y_f-g_f\end{array}\right\}=\left\{\begin{array}{c}{Y}_0\\ Y_f\end{array}\right\}-\left\{\begin{array}{c}{h}_{11}{g}_0+h_{12}{g}_f\\ h_{21}{g}_0+h_{22}{g}_f\end{array}\right\}$$

Substituting into Equation (6),

$$y\left(x\right)=g\left(x\right)+(Y_0-h_{11}{g}_0-h_{12}{g}_f)p\left(x\right)+(Y_f-h_{21}{g}_0-h_{22}{g}_f)q\left(x\right)$$

that is,

$$y\left(x\right)=g\left(x\right)-[p\left(x\right)h_{11}+q\left(x\right)h_{21}]g_0-[p\left(x\right)h_{12}+q\left(x\right)h_{22}]g_f+Y_{0}p\left(x\right)+Y_{f}q\left(x\right)$$

which is an equation that can be written as:

$$y\left(x\right)=g\left(x\right)-\alpha \left(x\right)g_0-\beta \left(x\right)g_f+Y_{0}p\left(x\right)+Y_{f}q\left(x\right)$$

Substituting this expression into the DE,

$$c^2{f}_2\left(x\right)y^{″}\left(x\right)+c{f}_1\left(x\right)y^{\prime }\left(x\right)+f_0\left(x\right)y\left(x\right)=f\left(x\right)$$

and we obtain:

$$c^2{f}_2\left(x\right)g^{″}\left(x\right)+c{f}_1\left(x\right)\dot{g}\left(x\right)+f_0\left(x\right)g\left(x\right)-m_1\left(x\right)g_0-m_2\left(x\right)g_f=b\left(x\right)$$

(12)

where:

$$\left\{\begin{array}{cc}\hfill m_1\left(x\right)=& c^2{f}_2\left(x\right){\alpha }^{″}\left(x\right)+c{f}_1\left(x\right){\alpha }^{\prime }+f_0\left(x\right)\alpha \left(x\right)\hfill \\ \hfill m_2\left(x\right)=& c^2{f}_2\left(x\right){\beta }^{″}\left(x\right)+c{f}_1\dot{\beta }\left(x\right)+f_0\left(x\right)\beta \left(x\right)\hfill \\ \hfill b\left(x\right)=& f\left(x\right)-c^2{f}_2\left(x\right)[Y_0{p}^{″}+Y_f{q}^{″}]-c{f}_1[Y_0{p}^{\prime }+Y_f{q}^{\prime }]-f_0[Y_{0}p+Y_{f}q]\hfill \end{array}\right.$$

(13)

Therefore, the procedures to solve IVPs and BVPs have little differences. In fact, for BVPs, we obtain the linear equation:

$${\mathit{a}}^{\mathrm{T}}\left(x\right)\mathbf{\xi }={\left[c^2{f}_2\left(x\right){\mathit{h}}^{″}\left(x\right)+c{f}_1\left(x\right)\mathit{h}\left(x\right)+f_0\left(x\right)\mathit{h}\left(x\right)-m_1\left(x\right){\mathit{h}}_0-m_2\left(x\right){\mathit{h}}_f\right]}^{\mathrm{T}}\mathbf{\xi }=b\left(x\right)$$

(14)

Once the least-squares has been solved and, therefore, the coefficients vector $\mathbf{\xi }$ has been computed, then the solution is:

$$\left\{\begin{array}{cc}\hfill y\left(x\right)=& {\mathbf{\xi }}^{\mathrm{T}}\mathit{h}\left(x\right)+{\eta }_{1}p\left(x\right)+{\eta }_{2}q\left(x\right)\hfill \\ \hfill y^{\prime }\left(x\right)=& {\mathbf{\xi }}^{\mathrm{T}}{\mathit{h}}^{\prime }\left(x\right)+{\eta }_1{p}^{\prime }\left(x\right)+{\eta }_2{q}^{\prime }\left(x\right)\hfill \\ \hfill y^{″}\left(x\right)=& {\mathbf{\xi }}^{\mathrm{T}}{\mathit{h}}^{″}\left(x\right)+{\eta }_1{p}^{″}\left(x\right)+{\eta }_2{q}^{″}\left(x\right)\hfill \end{array}\right.$$

(15)

Numerical integrations of IVPs provide subsequent estimates based on previous estimates. This implies that the error, in general, increases along the integration range. On the contrary, as shown by the next numerical tests, the accuracy provided by the least-squares solution is “uniformly” distributed along the integration range. In addition, if greater accuracy is desired for some specific regions, then by increasing the number of points in those regions, accuracy increase is obtained where desired. Alternatively, by adopting weighted least-squares, the weight’s value gives us an additional option to control the accuracy distribution.

In the following subsections, the proposed least-squares approach is tested, for the four cases of BVPs with known, unknown, no, and infinite solutions.

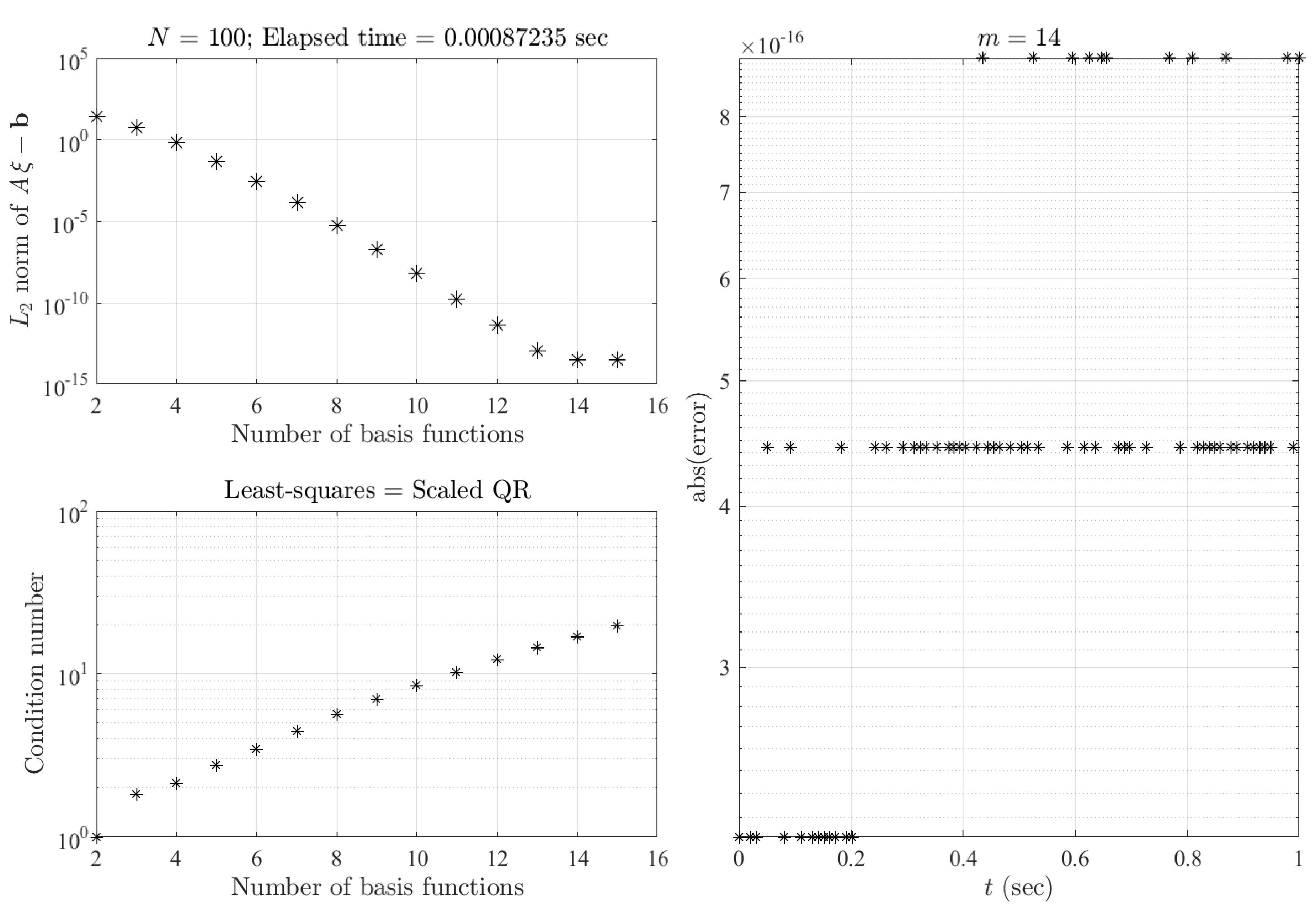
3.1. Numerical Accuracy Tests for a BVP with Known Solution

We consider the following BVP:

$$\ddot{y}+2\dot{y}+y=0\mathrm{subject}\mathrm{to}:\left\{\begin{array}{c}y\left(0\right)=1\hfill \\ y\left(1\right)=3\hfill \end{array}\right.$$

(16)

whose solution is $y\left(t\right)=e^{-t}+(3e-1)t{e}^{-t}$, with derivatives $\dot{y}\left(t\right)=-e^{-t}(3et-t-3e+2)$ and $\ddot{y}\left(t\right)=e^{-t}(3et-t-6e+3)$.

Figure 2 shows the least-squares-approach results for this test in terms of the $L_2$ norm of $(\mathbb{A}\mathbf{\xi }-\mathit{b})$ residuals (top-left) and the condition number of matrix ${\mathbb{A}}^{\mathrm{T}}\mathbb{A}$ (bottom-left) as a function of the number of basis functions considered. The errors with respect to the true solution obtained with $m=14$ basis functions (Legendre orthogonal polynomials) and $N=100$ points (discretization) are provided in the right plot. These plots clearly show that the machine error precision is obtained with excellent numerical stability (low condition number).

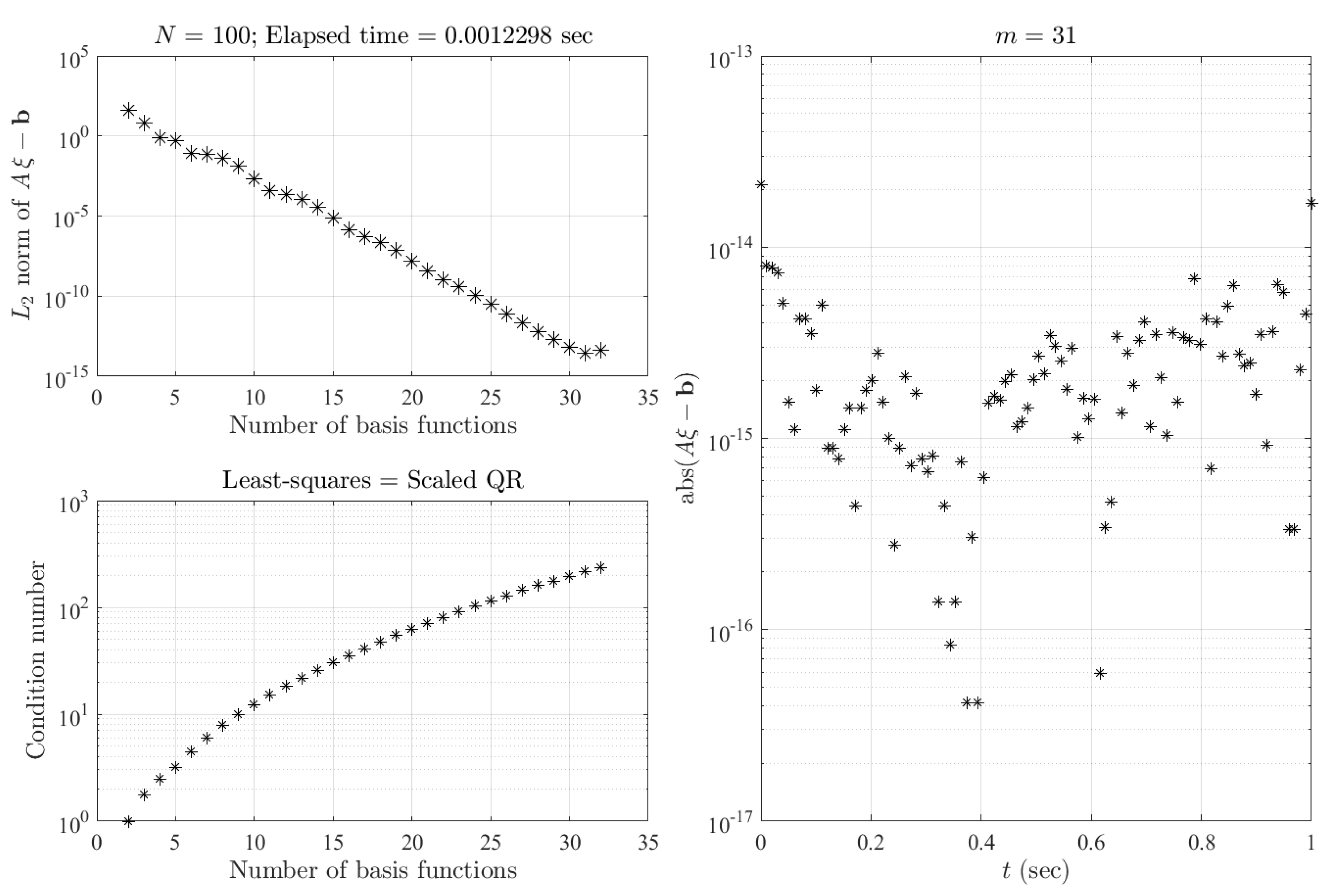
3.2. Numerical Accuracy Tests for a BVP with Unknown Solution

We consider the DE (completely invented) with an unknown analytical solution:

$$(1+2t)\ddot{y}+\left(cos{t}^2-3t+1\right)\dot{y}+\left(6sin{t}^2-e^{cos\left(3t\right)}\right)y={\displaystyle \frac{2[1-sin(3t\left)\right](3t-\pi )}{4-t}}$$

subject to $y\left(0\right)=2$ and $y\left(1\right)=2$. In this case, the least-squares-solution results are given in the plots of Figure 3 with the same explanation as for those provided in Figure 2. The $L_2$ norm of the residuals (top-left plot) decreases up to $m=31$-degree basis functions (Chebyshev orthogonal polynomials of the first kind) while the condition number remains at good values (bottom-left plot). The machine error values of the residuals, obtained for $m=31$-degree basis functions and $N=100$ points, are shown in the right plot.

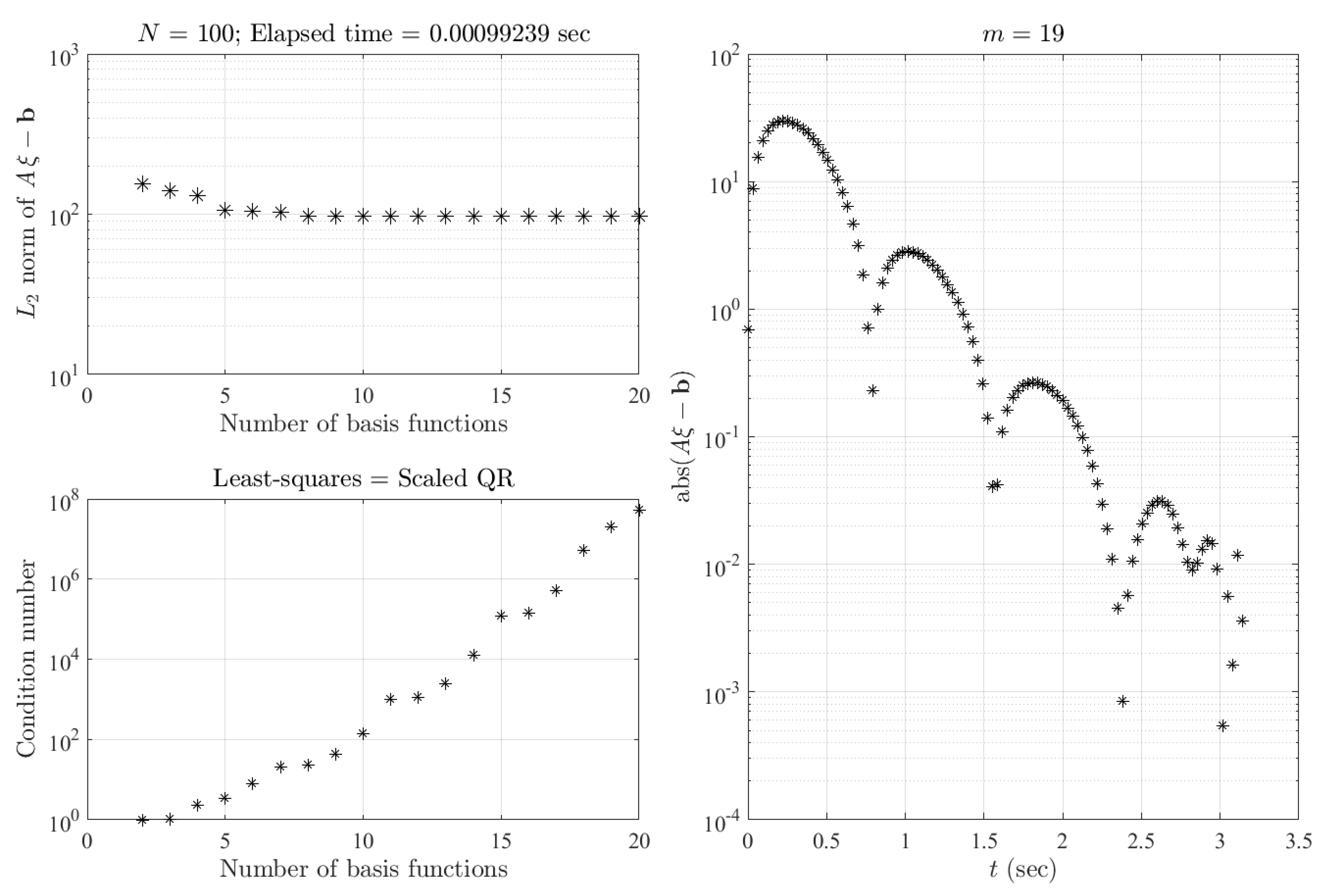
3.3. Numerical Accuracy Tests for a BVP with No Solution

We consider the following BVP with no solution:

$$\ddot{y}-6\dot{y}+25y=0\mathrm{subject}\mathrm{to}:\left\{\begin{array}{c}y\left(0\right)=1\hfill \\ y\left(\pi \right)=2\hfill \end{array}\right.$$

(17)

In fact, the general solution of Equation (17) is $y\left(t\right)=[acos\left(4t\right)+bsin\left(4t\right)]e^{3t}$, where the constraint $y\left(0\right)=1$ gives $a=1$, while the constraint $y\left(\pi \right)=2$ gives $2=e^{3\pi }$, a wrong identity.

Figure 4 shows the results when trying to solve, by least-squares, the problem given in Equation (17). For this example, the number of orthogonal polynomials has been increased up to that for which the condition number of the matrix ${\mathbb{A}}^{\mathrm{T}}\mathbb{A}$ becomes too large (numerical instability), at an upper bound of ${10}^8$. The number of basis functions has been increased up to $m=20$ by keeping the number of points to $N=100$. By increasing the number of basis functions, the $L_2$ norm of $(\mathbb{A}\mathbf{\xi }-\mathit{b})$ does not converge, and the condition number of ${\mathbb{A}}^{\mathrm{T}}\mathbb{A}$ becomes huge. These are two potential indicators that the problem has no solution. However, even in this no-solution case, the proposed least-squares approach provides a “solution” complying with the DE constraints.

3.4. Numerical Accuracy Tests for a BVP with Infinite Solutions

Finally, we consider the BVP with infinite solutions:

$$\ddot{y}+4y=0\mathrm{subject}\mathrm{to}:\left\{\begin{array}{c}y\left(0\right)=-2\hfill \\ y\left(2\pi \right)=-2\hfill \end{array}\right.$$

(18)

In fact, the general solution of Equation (18) is $y\left(t\right)=acos\left(2t\right)+bsin\left(2t\right)$, consisting of infinite solutions, as b can have any value. The results of the least-squares approach are given in Figure 5, showing the convergence, but not at machine-level accuracy.

Figure 5 shows the results obtained for this infinite-solutions case. The main difference with respect to the no-solution case is in the unstable convergence of the $L_2$ norm of $(\mathbb{A}\mathbf{\xi }-\mathit{b})$. In fact, by increasing the number of basis functions from $m=20$ to $m=25$, the $L_2$ norm actually increases. This unusual behavior is still under analysis, and no explanation is currently available. The instability may be explained by several (infinite) solutions being possible, and some of these may be “close” from a convergence numerical point of view. In this infinite-solutions case, as in the no-solution case, the value of the condition number increases to very high values. In this example, an upper bound has been defined for the number of basis functions ($m=30$), while there is no upper bound for the condition number value.

3.5. Constrained Expressions for BVP with Different Constraints

In this section, constrained expressions are provided for BVPs of a second-order DE subject to all (nine) possible constraints.

(1)

The first constraints considered are the function at the initial time, $y\left(t_0\right)=y_0$, and the first derivative at the final time, $\dot{y}\left(t_f\right)={\dot{y}}_f$. For this case, the final constraint in terms of the new variable, $x\in [-1,+1]$, becomes $y_f^{\prime }={\dot{y}}_f/c$, and the constrained expression:

$$y\left(x\right)=g\left(x\right)+(y_0-g_0)+(x+1)(y_f^{\prime }-g_f^{\prime })$$

can be used. Substituting this into Equation (5), we obtain:

$$c^2{f}_2{g}^{″}+c{f}_1(g^{\prime }-g_f^{\prime })+f_0[g-g_0-g_f^{\prime }(x+1)]=f-c{f}_1{y}_f^{\prime }-f_0[y_0+y_f^{\prime }(x+1)]$$

(19)

Then, the least-squares solution can be obtained using the procedure described by Equations (12)–(15). Equation (19) has been tested, providing excellent results, which are not included here for sake of brevity.

(2)

The second constraints are the function at the initial time, $y\left(t_0\right)=y_0$, and the second derivative at the final time, $\ddot{y}\left(t_f\right)={\ddot{y}}_f$. For this case, the final constraint in terms of the new variable is $y_f^{″}={\ddot{y}}_f/c^2$, and the constrained expression is:

$$y\left(x\right)=g\left(x\right)-x(y_0-g_0)+{\displaystyle \frac{x^2+x}{2}}(y_f^{″}-g_f^{″})$$

Substituting this into Equation (5), we obtain:

$$\begin{array}{c}{c}^2{f}_2(g^{″}-g_f^{″})+c{f}_1\left(g^{\prime }+g_0-g_f^{″}{\displaystyle \frac{2x+1}{2}}\right)+f_0\left(g+g_{0}x-g_f^{″}{\displaystyle \frac{x^2+x}{2}}\right)\hfill \\ =f-c^2{y}_f^{″}{f}_2-c{f}_1\left(-y_0+y_f^{″}{\displaystyle \frac{2x+1}{2}}\right)-f_0\left(-y_{0}x+y_f^{″}{\displaystyle \frac{x^2+x}{2}}\right)\hfill \end{array}$$

Then, it follows as in the first case.

(3)

The third constraints are the first derivative at the initial time, $\dot{y}\left(t_0\right)={\dot{y}}_0$, and the function at the final time, $y\left(t_f\right)=y_f$. For this case, the initial constraint in terms of the new variable is $y_0^{\prime }={\dot{y}}_0/c$, while the constrained equation:

$$y\left(x\right)=g\left(x\right)+(y_f-g_f)+(x-1)(y_0^{\prime }-g_0^{\prime })$$

can be used. Substituting this into Equation (5), we obtain:

$$c^2{f}_2{g}^{″}+c{f}_1(g^{\prime }-g_0^{\prime })+f_0[g-g_f-g_0^{\prime }(x-1)]=f-c{y}_0^{\prime }{f}_1-f_0[y_f+y_0^{\prime }(x-1)]$$

and the least-squares solution can be obtained using the procedure described by Equations (12)–(15).

(4)

The fourth constraints are the first derivative at the initial and final times, $\dot{y}\left(t_0\right)={\dot{y}}_0$ and $\dot{y}\left(t_f\right)={\dot{y}}_f$. This special equation is known as Mathieu’s DE [9,10]. For this case, the constraints in terms of the new variable are $y_0^{\prime }={\dot{y}}_0/c$ and $y_f^{\prime }={\dot{y}}_f/c$, while the constrained equation:

$$y\left(x\right)=g\left(x\right)+{\displaystyle \frac{x}{2}}\left(1-{\displaystyle \frac{x}{2}}\right)(y_0^{\prime }-g_0^{\prime })+{\displaystyle \frac{x}{2}}\left(1+{\displaystyle \frac{x}{2}}\right)(y_f^{\prime }-g_f^{\prime })$$

can be used. Substituting this into Equation (5), we obtain:

$$\begin{array}{c}{c}^2{f}_2\left(g^{″}+{\displaystyle \frac{g_0^{\prime }-g_f^{\prime }}{2}}\right)+c{f}_1\left[g^{\prime }-{\displaystyle \frac{(1-x)g_0^{\prime }+(x+1)g_f^{\prime }}{2}}\right]+f_0\left\{g-{\displaystyle \frac{x}{2}}\left[\left(1-{\displaystyle \frac{x}{2}}\right)g_0^{\prime }+\left({\displaystyle \frac{x}{2}}+1\right)g_f^{\prime }\right]\right\}\hfill \\ =f-{\displaystyle \frac{c^2}{2}}(y_f^{\prime }-y_0^{\prime })f_2-{\displaystyle \frac{c}{2}}{f}_1\left[(1-x)y_0^{\prime }+(x+1)y_f^{\prime }\right]-f_0{\displaystyle \frac{x}{2}}\left[\left(1-{\displaystyle \frac{x}{2}}\right)y_0^{\prime }+\left({\displaystyle \frac{x}{2}}+1\right)y_f^{\prime }\right]\hfill \end{array}$$

and the least-squares solution can be obtained using the procedure described by Equations (12)–(15).

(5)

The fifth constraints are the first derivative at the initial time, $\dot{y}\left(t_0\right)={\dot{y}}_0$, and the second derivative at the final time, $\ddot{y}\left(t_f\right)={\ddot{y}}_f$. For this case, the constraints in terms of the new variable are $y_0^{\prime }={\dot{y}}_0/c$ and $y_f^{″}={\ddot{y}}_f/c^2$, while the constrained equation:

$$y\left(x\right)=g\left(x\right)+x(y_0^{\prime }-g_0^{\prime })+x\left({\displaystyle \frac{x}{2}}+1\right)(y_f^{″}-g_f^{″})$$

can be used. Substituting this into Equation (5), we obtain:

$$\begin{array}{c}{c}^2{f}_2(g^{″}-g_f^{″})+c{f}_1[g^{\prime }-g_0^{\prime }-g_f^{″}(x+1)]+f_0\left[g-g_0^{\prime }x-g_f^{″}\left({\displaystyle \frac{x}{2}}+1\right)x\right]=\\ =f-c^2{y}_f^{″}{f}_2-c{f}_1[y_0^{\prime }+y_f^{″}(x+1)]-f_0\left[x{y}_0^{\prime }+\left({\displaystyle \frac{x}{2}}+1\right)x{y}_f^{″}\right]\end{array}$$

and the least-squares solution can be obtained using the procedure described by Equations (12)–(15).

(6)

The sixth constraints are the second derivative at the initial time, $\ddot{y}\left(t_0\right)={\ddot{y}}_0$, and the function at the final time, $y\left(t_f\right)=y_f$. For this case, the first constraint in terms of the new variable is $y_0^{″}={\ddot{y}}_0/c^2$, while the constrained equation:

$$y\left(x\right)=g\left(x\right)+x(y_f-g_f)+{\displaystyle \frac{x}{2}}(x-1)(y_0^{″}-g_0^{″})$$

can be used. Substituting this into Equation (5), we obtain:

$$\begin{array}{c}{c}^2{f}_2(g^{″}-g_0^{″})+c{f}_1\left(g^{\prime }-g_f-g_0^{″}{\displaystyle \frac{2x-1}{2}}\right)+f_0\left(g-g_{f}x-g_0^{″}{\displaystyle \frac{x^2-x}{2}}\right)\\ =f-c^2{y}_0^{″}{f}_2-c{f}_1\left(y_f+y_0^{″}{\displaystyle \frac{2x-1}{2}}\right)-f_0\left(y_f+y_0^{″}{\displaystyle \frac{x^2-x}{2}}\right)\end{array}$$

and the least-squares solution can be obtained using the procedure described by Equations (12)–(15).

(7)

The seventh constraints are the second derivative at the initial time, $\ddot{y}\left(t_0\right)={\ddot{y}}_0$, and the first derivative at the final time, $\dot{y}\left(t_f\right)={\dot{y}}_f$. For this case, the constraints in terms of the new variable are $y_0^{″}={\ddot{y}}_0/c^2$ and $y_f^{\prime }={\dot{y}}_f/c$, while the constrained equation:

$$y\left(x\right)=g\left(x\right)+x(y_f^{\prime }-g_f^{\prime })+{\displaystyle \frac{x}{2}}(x-2)(y_0^{″}-g_0^{″})$$

can be used. Substituting this into Equation (5), we obtain:

$$\begin{array}{c}{c}^2{f}_2(g^{″}-g_0^{″})+c{f}_1[g^{\prime }-g_f^{\prime }-g_0^{″}(x-1)]+f_0\left[g-g_f^{\prime }x-g_0^{″}\left({\displaystyle \frac{x^2}{2}}-x\right)\right]=\\ =f-c^2{y}_0^{″}{f}_2-c{f}_1\left[y_f^{\prime }+y_0^{″}(x-1)\right]-f_0\left[y_f^{\prime }x+y_0^{″}\left({\displaystyle \frac{x^2}{2}}-x\right)\right]\end{array}$$

and the least-squares solution can be obtained using the procedure described by Equations (12)–(15).

(8)

The final (eighth) constraints are the second derivative at the initial and final times, $\ddot{y}\left(t_0\right)={\ddot{y}}_0$ and $\ddot{y}\left(t_f\right)={\ddot{y}}_f$. For this case, the constraints in terms of the new variable are $y_0^{″}={\ddot{y}}_0/c^2$ and $y_f^{″}={\ddot{y}}_f/c^2$, while the constrained equation:

$$y\left(x\right)=g\left(x\right)+{\displaystyle \frac{x^2}{12}}(3-x)(y_0^{″}-g_0^{″})+{\displaystyle \frac{x^2}{12}}(3+x)(y_f^{″}-g_f^{″})$$

can be used. Substituting this into Equation (5), we obtain:

$$\begin{array}{c}{c}^2{f}_2\left[g^{″}-{\displaystyle \frac{(1-x)g_0^{″}+(x+1)g_f^{″}}{2}}\right]+c{f}_1\left[g^{\prime }-{\displaystyle \frac{(2x-x^2)g_0^{″}+(x^2+2x)g_f^{″}}{4}}\right]\hfill \\ +f_0\left[g-{\displaystyle \frac{(3x^2-x^3)g_0^{″}+(x^3+3x^2)g_f^{″}}{12}}\right]\hfill \\ =f-{\displaystyle \frac{c^2}{2}}{f}_2[y_0^{″}(1-x)+y_f^{″}(x+1)]-c{f}_1{\displaystyle \frac{(2x-x^2)y_0^{″}+(x^2+2x)y_f^{″}}{4}}-f_0{\displaystyle \frac{(3x^2-x^3)y_0^{″}+(x^3+3x^2)y_f^{″}}{12}}\hfill \end{array}$$

and the least-squares solution can be obtained using the procedure described by Equations (12)–(15).

4. MVP Example

Finally, to show the potential of the proposed least-squares approach, we consider solving the following third order DE:

$$\stackrel{⃛}{y}+sint\ddot{y}+(1-t)\dot{y}+ty=f\left(t\right)$$

(20)

where:

$$f\left(t\right)=(t-1){sin}^{2}t+(2+2t-t^2-2cost)sint+t(t-1)cost$$

and is subject to the multi-point constraints:

$$y(t_1=1)=0,\dot{y}(t_2=\pi /2)=-1,\mathrm{and}y(t_3=\pi )=0,$$

whose analytical solution is $y\left(t\right)=(1-t)sint$. We consider integrating this DE from $t_0=0$ to $t_f=4$ (beyond the constraint bounds, $[1,\pi ]$) using Legendre orthogonal polynomials ($x\in [-1,+1]$). Therefore,

$$t=2(x+1)\leftrightarrow x={\displaystyle \frac{t}{2}}-1\to c={\displaystyle \frac{2}{t_f-t_0}}={\displaystyle \frac{1}{2}}$$

Equation (20) becomes:

$$c^3{y}^{‴}+c^{2}sint{y}^{″}+c(1-t)y^{\prime }+ty=f\left(t\right)$$

(21)

subject to:

$$y\left(x_1\right)=0,y^{\prime }\left(x_2\right)=-1/c=-2,\mathrm{and}y\left(x_3\right)=0$$

(22)

where $x_1=t_1/2-1=-1/2$, $x_2=t_f/2-1=\pi /4-1$, and $x_3=t_3/2-1=\pi /2-1$.

A constrained expression [8] satisfying Equation (22) can be found as:

$$y\left(x\right)=g\left(x\right)+{\eta }_1{h}_1\left(x\right)+{\eta }_2{h}_2\left(x\right)+{\eta }_3{h}_3\left(x\right)$$

(23)

where $h_1\left(x\right)=1$, $h_2\left(x\right)=x$, and $h_3\left(x\right)=x^2$ have been selected as the first three monomials. The three coefficients, ${\eta }_1$, ${\eta }_2$, and ${\eta }_3$, can be derived from the DE constraints:

$$\left\{\begin{array}{c}0-g\left(x_1\right)\\ -2-g^{\prime }\left(x_2\right)\\ 0-g\left(x_3\right)\end{array}\right\}=\left[\begin{array}{ccc}1& x_1& x_1^2\\ 0& 1& 2x_2\\ 1& x_3& x_3^2\end{array}\right]\left\{\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\end{array}\right\}$$

Now, setting $g_0=g\left(x_1\right)={\mathbf{\xi }}^{\mathrm{T}}{\mathit{h}}_1$, $g_f^{\prime }=g^{\prime }\left(x_2\right)={\mathbf{\xi }}^{\mathrm{T}}{\mathit{h}}_2^{\prime }$, and $g_3=g\left(x_3\right)={\mathbf{\xi }}^{\mathrm{T}}{\mathit{h}}_3$, the coefficients ${\eta }_1$, ${\eta }_2$ and ${\eta }_3$ are:

$$\left\{\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\end{array}\right\}={\mathcal{M}}^{-1}\left\{\begin{array}{c}0\\ -2\\ 0\end{array}\right\}-{\mathcal{M}}^{-1}{\left\{\begin{array}{c}{\mathit{h}}_1\\ {\mathit{h}}_2^{\prime }\\ {\mathit{h}}_3\end{array}\right\}}^{\mathrm{T}}\mathbf{\xi }=\left\{\begin{array}{c}{v}_1\\ v_2\\ v_3\end{array}\right\}-{\left\{\begin{array}{c}{m}_{11}{\mathit{h}}_1+m_{12}{\mathit{h}}_2^{\prime }+m_{13}{\mathit{h}}_3\\ m_{21}{\mathit{h}}_1+m_{22}{\mathit{h}}_2^{\prime }+m_{23}{\mathit{h}}_3\\ m_{31}{\mathit{h}}_1+m_{32}{\mathit{h}}_2^{\prime }+m_{33}{\mathit{h}}_3\end{array}\right\}}^{\mathrm{T}}\mathbf{\xi }$$

Then, substituting in the constrained expression, we obtain:

$$\begin{array}{cc}\hfill y\left(x\right)& ={\mathbf{\xi }}^{\mathrm{T}}\mathit{h}\left(x\right)+v_1+v_{2}x+v_3{x}^2-(m_{11}+m_{21}x+m_{31}{x}^2){\mathit{h}}_1^{\mathrm{T}}\mathbf{\xi }+\\ & -(m_{12}+m_{22}x+m_{32}{x}^2){{\mathit{h}}_2^{\prime }}^{\mathrm{T}}\mathbf{\xi }-(m_{13}+m_{23}x+m_{33}{x}^2){\mathit{h}}_3^{\mathrm{T}}\mathbf{\xi }\end{array}$$

whose derivatives are:

$$\begin{array}{ccc}\hfill y^{\prime }\left(x\right)& =& {\mathbf{\xi }}^{\mathrm{T}}{\mathit{h}}^{\prime }\left(x\right)+v_2+2v_{3}x-(m_{21}+2m_{31}x){\mathit{h}}_1^{\mathrm{T}}\mathbf{\xi }-(m_{22}+2m_{32}x){{\mathit{h}}_2^{\prime }}^{\mathrm{T}}\mathbf{\xi }-(m_{23}+2m_{33}x){\mathit{h}}_3^{\mathrm{T}}\mathbf{\xi }\hfill \\ \hfill y^{″}\left(x\right)& =& {\mathbf{\xi }}^{\mathrm{T}}{\mathit{h}}^{″}\left(x\right)+2v_3-2m_{31}{\mathit{h}}_1^{\mathrm{T}}\mathbf{\xi }-2m_{32}{{\mathit{h}}_2^{\prime }}^{\mathrm{T}}\mathbf{\xi }-2m_{33}{\mathit{h}}_3^{\mathrm{T}}\mathbf{\xi }\hfill \\ \hfill y^{‴}\left(x\right)& =& {\mathbf{\xi }}^{\mathrm{T}}{\mathit{h}}^{‴}\left(x\right)\hfill \end{array}$$

These expressions are then substituted back into Equation (21), and the linear equation provided by the least-squares approach is obtained. The numerical results of this procedure are given in Figure 6.

The top-left plot of Figure 6 shows the analytic true solution (black line) with the three constraints: two for the function (black markers) and one for the first derivative (red line). We note that the range of integration, $t\in [0,4]$, goes beyond the constraints’ coordinate range, $[1,\pi ]$. This is purposefully done to show that for the proposed least-squares approach, the range of integration, $t\in [0,4]$, is independent from the constraint range, $[1,\pi ]$.

The bottom-left plot shows that as the number of basis functions considered increases, the condition number to solve the least-squares problem has values that guarantee the numerical stability of the least-squares solution. The number of basis functions continues to increase until the $L_2$ norm of $(\mathbb{A}\mathbf{\xi }-\mathit{b})$ decreases, as shown in the top-right plot. The minimum is reached when $m=21$. However, the true number of basis functions adopted to describe $g\left(x\right)$ is 18 and not 21. The reason is that, to build the constrained expression appearing in Equation (23), the functions for $h_1\left(x\right)$, $h_2\left(x\right)$, and $h_3\left(x\right)$ are constant, linear, and quadratic, respectively. These three functions cannot be included to express $g\left(x\right)$, which is consequently expressed as:

$${\displaystyle g\left(x\right)=\sum _{k=3}^{21}{\xi }_k{h}_k\left(x\right)}$$

The bottom-right plot of Figure 6 shows the absolute error obtained when $m=21$ basis functions are used to express $y\left(x\right)$, while the number of Legendre polynomials used for $g\left(x\right)$ is $m=18$. This plot clearly shows that, using 18 basis functions for $g\left(x\right)$, the least-squares approach provides a machine error solution.

5. Conclusions

This study presents a new approach to provide least-squares solutions of linear nonhomogeneous DEs of any order with nonconstant coefficients, both continuous and nonsingular in the integration range. Without loss of generality and for the sake of brevity, the implementation of the proposed method has been applied to second-order DEs. This least-squares approach can be adopted to solve IVPs, BVPs, and MVPs with constraints given in terms of the function and/or derivatives.

The proposed method is based on imposing that the solution has a specific expression, called a constrained expression, which is a function with the DE constraints embedded. This expression is given in terms of a new unknown function, $g\left(t\right)$. The original DE is rewritten in terms of $g\left(t\right)$, thus obtaining a new DE for which the constraints are embedded in the DE itself. Then, the $g\left(t\right)$ function is expressed as a linear combination of basis functions, $\mathit{h}\left(t\right)$. The coefficients of this linear expansion are then computed by least-squares by specializing the new DE for a set of N different values of the independent variable. In this study, the Chebyshev and Legendre orthogonal polynomials have been selected as basis functions.

Numerical tests have been performed for IVPs with known and unknown solutions. A direct comparison has been made with the solution provided by the MATLAB function ode45, implementing a Runge–Kutta variable-step integrator [1]. In this test, the least-squares approach shows about 9 orders of magnitude of accuracy gain. Numerical tests have been performed for BVPs for the four cases of known, unknown, no, and infinite solutions. In particular, the condition number value and the $L_2$ norm of the residual can be used to discriminate between whether or not a BVP has a single solution.

Finally, a numerical test has been performed for a third-order MVP with constraints (two on functions and one on the first derivative) defined inside the integration range. In all our tests, the machine error precision has been reached with a limited number of basis functions and the discretization number. All the computations were performed on a laptop using MATLAB software. The elapsed times (in seconds) required to obtain all the solutions are specified in the figures for all the test cases considered.

The proposed method is not iterative, is easy to implement, and, as opposed to numerical approaches, is based on truncated Taylor series (such as Runge–Kutta methods); the solution error distribution does not increase along the integration, but it is approximately uniformly distributed in the integration range. In addition, the proposed technique unifies the way to solve IVPs, BVPs, and MVPs. The method can also be used to solve higher-order linear DEs, as long as the DE constraints are linear.

This study is not complete, as many investigations should be performed before setting this approach as a standard method to integrate linear DEs. In addition, many research areas are still open and under question. A few of these open research areas are the following:

(1)

Extension to weighted least-squares.

(2)

Error-bound estimates for the problems admitting solutions.

(3)

Nonuniform distribution of points and optimal distributions of points to increase accuracy in specific ranges of interest.

(4)

Comparisons between different function bases and identification of an optimal function base (if it exists).

(5)

Analysis using Fourier bases.

(6)

Accuracy analysis of number of basis functions versus points distribution.

(7)

Extension to nonlinear DEs.

(8)

Extension to partial DEs.

(9)

Extension to nonlinear constraints.