New Analytical Technique for Solving a System of Nonlinear Fractional Partial Differential Equations

Abstract

This paper introduces a new analytical technique (NAT) for solving a system of nonlinear fractional partial differential equations (NFPDEs) in full general set. Moreover, the convergence and error analysis of the proposed technique is shown. The approximate solutions for a system of NFPDEs are easily obtained by means of Caputo fractional partial derivatives based on the properties of fractional calculus. However, analytical and numerical traveling wave solutions for some systems of nonlinear wave equations are successfully obtained to confirm the accuracy and efficiency of the proposed technique. Several numerical results are presented in the format of tables and graphs to make a comparison with results previously obtained by other well-known methods.

1. Introduction

Over the last few decades, fractional partial differential equations (FPDEs) have been proposed and investigated in many research fields, such as fluid mechanics, the mechanics of materials, biology, plasma physics, finance, and chemistry, and they have played an important role in modeling the so-called anomalous transport phenomena as well as in theory of complex systems, see [1,2,3,4,5,6,7,8]. In study of FPDEs, one should note that finding an analytical or approximate solution is a challenging problem, therefore, accurate methods for finding the solutions of FPDEs are still under investigation. Several analytical and numerical methods for solving FPDEs exist in the literature, for example; the fractional complex transformation [9], homotopy perturbation method [10], a homotopy perturbation technique [11], variational iteration method [12], decomposition method [12], and so on. There are, however, a few solution methods for only traveling wave solutions, for example; the transformed rational function method [13], the multiple exp-function algorithm [14]), and some references cited therein.

The system of NFPDEs have been increasingly used to represent physical and control systems (see for instant, [15,16,17] and references cited therein). The systems of nonlinear wave equations play an important role in a variety of oceanographic phenomena, for example, in the change in mean sea level due to storm waves, the interaction of waves with steady currents, and the steepening of short gravity waves on the crests of longer waves (see for example, [18,19,20,21,22]). In this paper, two systems of nonlinear wave equations with a fractional order are studied; one is the nonlinear KdV system (see [23,24]) and another one is the system of dispersive long wave equations (see [24,25,26]).

Some numerical or analytical methods have been investigated for solving a system of NFPDEs, such as an iterative Laplace transform method [27], homotopy analysis method [28], and adaptive observer [29]. Moreover, very few algorithms for the analytical solution of a system of NFPDEs have been suggested, and some of these methods are essentially used for particular types of systems, often just linear ones or even smaller classes. Therefore, it should be noted that most of these methods cannot be generalized to nonlinear cases.

In the present work, we introduce a new analytical technique (NAT) to solve a full general system of NFPDEs of the following form:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{D}}_t^{q_i}{u}_i(\overline{x},t)& =f_i(\overline{x},t)+L_i\overline{u}+N_i\overline{u},m_i-1<q_i<m_i\in \mathbb{N},i=1,2,\dots ,n,\hfill \\ \hfill \frac{{\partial }^{k_i}{u}_i}{\partial t^{k_i}}(\overline{x},0)& =f_{i{k}_i}(\overline{x}),k_i=0,1,2,\dots ,m_i-1,i=1,2,\dots ,n,\hfill \end{array}\right.\end{array}$$

(1)

where $L_i$ and $N_i$ are linear and nonlinear operators, respectively, of $\overline{u}=\overline{u}(\overline{x},t)$ and its partial derivatives, which might include other fractional partial derivatives of orders less than $q_i$; $f_i(\overline{x},t)$ are known analytic functions; and ${\mathcal{D}}_t^{q_i}$ are the Caputo partial derivatives of fractional orders $q_i$, where we define $\overline{u}=\overline{u}(\overline{x},t)=(u_1(\overline{x},t),u_2(\overline{x},t),\dots ,u_n(\overline{x},t)),\overline{x}=(x_1,x_2,\dots ,x_n)\in {\mathbb{R}}^n$.

The goal of this paper is to demonstrate that a full general system of NFPDEs can be solved easily by using a NAT without any assumption and that it gives good results in analytical and numerical experiments. The rest of the paper is organized in as follows. In Section 2, we present basic definitions and preliminaries which are needed in the sequel. In Section 3, we introduce a NAT for solving a full general system of NFPDEs. Approximate analytical and numerical solutions for the systems of nonlinear wave equations are obtained in Section 4.

2. Basic Definitions and Preliminaries

There are various definitions and properties of fractional integrals and derivatives. In this section, we present modifications of some basic definitions and preliminaries of the fractional calculus theory, which are used in this paper and can be found in [10,30,31,32,33,34,35].

Definition 1.

A real function $u(x,t)$, $x,t\in \mathbb{R},t>0$, is said to be in the space $C_{\mu }$, $\mu \in \mathbb{R}$ if there exists a real number $p(>\mu )$, such that $u(x,t)=t^p{u}_1(x,t)$, where $u_1(x,t)\in C(\mathbb{R}\times [0,\infty ))$, and it is said to be in the space $C_{\mu }^m$ if and only if $\frac{{\partial }^{m}u(x,t)}{\partial t^m}\in C_{\mu },m\in \mathbb{N}$.

Definition 2.

Let $q\in \mathbb{R}\backslash \mathbb{N}$ and $q\ge 0$. The Riemann–Liouville fractional partial integral denoted by ${\mathcal{I}}_t^q$ of order q for a function $u(x,t)\in C_{\mu }$, $\mu >-1$ is defined as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{I}}_t^{q}u(x,t)& =\frac{1}{\mathsf{\Gamma }(q)}{\int }_0^t{(t-\tau )}^{q-1}u(x,\tau )d\tau ,q,t>0,\hfill \\ \hfill {\mathcal{I}}_t^{0}u(x,t)& =u(x,t),q=0,t>0,\hfill \end{array}\right.\end{array}$$

(2)

where Γ is the well-known Gamma function.

Theorem 1.

Let $q_1,q_2\in \mathbb{R}\backslash \mathbb{N},q_1,q_2\ge 0$ and $p>-1$. For a function $u(x,t)\in C_{\mu }$, $\mu >-1$, the operator ${\mathcal{I}}_t^q$ satisfies the following properties:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{I}}_t^{q_1}{\mathcal{I}}_t^{q_2}u(x,t)={\mathcal{I}}_t^{q_1+q_2}u(x,t)\hfill \\ {\mathcal{I}}_t^{q_1}{\mathcal{I}}_t^{q_2}u(x,t)={\mathcal{I}}_t^{q_2}{\mathcal{I}}_t^{q_1}u(x,t)\hfill \\ {\mathcal{I}}_t^q{t}^p=\frac{\mathsf{\Gamma }(p+1)}{\mathsf{\Gamma }(p+q+1)}{t}^{p+q}\hfill \end{array}\right.\end{array}$$

(3)

Definition 3.

Let $q,t\in \mathbb{R},t>0$ and $u(x,t)\in C_{\mu }^m$. Then

$$\begin{array}{c}\hfill \left\{\begin{array}{cccc}\hfill {\mathcal{D}}_t^{q}u(x,t)& ={\int }_a^t\frac{{(t-\tau )}^{m-q-1}}{\mathsf{\Gamma }(m-q)}\frac{{\partial }^{m}u(x,\tau )}{\partial {\tau }^m}d\tau ,\hfill & \hfill m-1<q<m& \in \mathbb{N},\hfill \\ \hfill {\mathcal{D}}_t^{q}u(x,t)& =\frac{{\partial }^{m}u(x,t)}{\partial t^m},\hfill & \hfill q=m& \in \mathbb{N},\hfill \end{array}\right.\end{array}$$

(4)

is called the Caputo fractional partial derivative of order q for a function $u(x,t)$.

Theorem 2.

Let $t,q\in \mathbb{R},t>0$ and $m-1<q<m\in \mathbb{N}$. Then

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{I}}_t^q{\mathcal{D}}_t^{q}u(x,t)& =u(x,t)-\sum _{k=0}^{m-1}\frac{t^k}{k!}\frac{{\partial }^{k}u(x,0^{+})}{\partial t^k},\hfill \\ \hfill {\mathcal{D}}_t^q{\mathcal{I}}_t^{q}u(x,t)& =u(x,t).\hfill \end{array}\right.\end{array}$$

(5)

3. NAT for Solving a System of NFPDEs

This section discusses a NAT to solve a system of NFPDEs. This NAT has much more computational power in obtaining piecewise analytical solutions.

To establish our technique, first we need to introduce the following results.

Lemma 1.

For $\overline{u}={\sum }_{k=0}^{\infty }{p}^k{\overline{u}}_k$, the linear operator $L_i\overline{u}$ satisfies the following property:

$$\begin{array}{cc}\hfill L_i\overline{u}=L_i\sum _{k=0}^{\infty }{p}^k{\overline{u}}_k& =\sum _{k=0}^{\infty }{p}^k{L}_i{\overline{u}}_k,i=1,2,\dots ,n.\hfill \end{array}$$

(6)

Theorem 3.

Let $\overline{u}(\overline{x},t)={\sum }_{k=0}^{\infty }{\overline{u}}_k(\overline{x},t)$, for the parameter λ, we define ${\overline{u}}_{\lambda }(\overline{x},t)={\sum }_{k=0}^{\infty }{\lambda }^k{\overline{u}}_k(\overline{x},t)$, then the nonlinear operator $N_i{\overline{u}}_{\lambda }$ satisfies the following property

$$\begin{array}{cc}\hfill N_i{\overline{u}}_{\lambda }=N_i\sum _{k=0}^{\infty }{\lambda }^k{\overline{u}}_k& =\sum _{n=0}^{\infty }\left[\frac{1}{n!}\frac{{\partial }^n}{\partial {\lambda }^n}{[N_i\sum _{k=0}^n{\lambda }^k{\overline{u}}_k]}_{\lambda =0}\right]{\lambda }^n,i=1,2,\dots ,n.\hfill \end{array}$$

(7)

Proof. 

According to the Maclaurin expansion of $N_i{\sum }_{k=0}^{\infty }{\lambda }^k{\overline{u}}_k$ with respect to $\lambda$, we have

$$\begin{array}{cc}\hfill N_i{\overline{u}}_{\lambda }& =N_i\sum _{k=0}^{\infty }{\lambda }^k{\overline{u}}_k={[N_i\sum _{k=0}^{\infty }{\lambda }^k{\overline{u}}_k]}_{\lambda =0}+[\frac{\partial }{\partial \lambda }{[N_i\sum _{k=0}^{\infty }{\lambda }^k{\overline{u}}_k]}_{\lambda =0}]\lambda \hfill \\ & +[\frac{1}{2!}\frac{{\partial }^2}{\partial {\lambda }^2}{[N_i\sum _{k=0}^{\infty }{\lambda }^k{\overline{u}}_k]}_{\lambda =0}]{\lambda }^2+\cdots \hfill \\ & =\sum _{n=0}^{\infty }[\frac{1}{n!}\frac{{\partial }^n}{\partial {\lambda }^n}{[N_i\sum _{k=0}^{\infty }{\lambda }^k{\overline{u}}_k]}_{\lambda =0}]{\lambda }^n\hfill \\ & =\sum _{n=0}^{\infty }\left[\frac{1}{n!}\frac{{\partial }^n}{\partial {\lambda }^n}{[N_i(\sum _{k=0}^n{\lambda }^k{\overline{u}}_k+\sum _{k=n+1}^{\infty }{\lambda }^k{\overline{u}}_k)]}_{\lambda =0}\right]{\lambda }^n\hfill \\ & =\sum _{n=0}^{\infty }\left[\frac{1}{n!}\frac{{\partial }^n}{\partial {\lambda }^n}{[N_i\sum _{k=0}^n{\lambda }^k{\overline{u}}_k]}_{\lambda =0}\right]{\lambda }^n,i=1,2,\dots ,n.\hfill \end{array}$$

 ☐

Definition 4.

The polynomials $E_{in}(u_{i0},u_{i1},\dots ,u_{in})$, for $i=1,2,\dots n$, are defined as

$$\begin{array}{cc}\hfill E_{in}(u_{i0},u_{i1},\dots ,u_{in})& =\frac{1}{n!}\frac{{\partial }^n}{\partial {\lambda }^n}{\left[N_i\sum _{k=0}^n{\lambda }^k{\overline{u}}_k\right]}_{\lambda =0},i=1,2,\dots ,n.\hfill \end{array}$$

(8)

Remark 1.

Let $E_{in}=E_{in}(u_{i0},u_{i1},\dots ,u_{in})$, by using Theorem 3 and Definition 4, the nonlinear operators $N_i{\overline{u}}_{\lambda }$ can be expressed in terms of $E_{in}$ as

$$\begin{array}{c}\hfill N_i{\overline{u}}_{\lambda }=\sum _{n=0}^{\infty }{\lambda }^n{E}_{in},i=1,2,\dots ,n.\end{array}$$

(9)

3.1. Existence Theorem

Theorem 4.

Let $m_i-1<q_i<m_i\in \mathbb{N}$ for $i=1,2,\dots n$, and let $f_i(\overline{x},t),f_{i{k}_i}(\overline{x})$ to be as in (6), respectively. Then the system (1) admits at least a solution given by

$$\begin{array}{cc}\hfill u_i(\overline{x},t)& =\sum _{k_i=0}^{m_i-1}\frac{t^{k_i}}{k_i!}{f}_{i{k}_i}(\overline{x})+f_{it}^{(-q_i)}(\overline{x},t)+\sum _{k=1}^{\infty }\left[L_{it}^{(-q_i)}{\overline{u}}_{(k-1)}+E_{i(k-1)t}^{(-q_i)}\right],i=1,2,\dots n;\hfill \end{array}$$

(10)

where $L_{it}^{(-q_i)}{\overline{u}}_{(k-1)}$ and $E_{i(k-1)t}^{(-q_i)}$ denote the fractional partial integral of order $q_i$ for $L_{i(k-1)}$ and $E_{i(k-1)}$ respectively with respect to t.

Proof. 

Let the solution function $u_i(\overline{x},t)$ of the system (6) to be as in the following analytical expansion:

$$\begin{array}{c}\hfill u_i(\overline{x},t)=\sum _{k=0}^{\infty }{u}_{ik}(\overline{x},t),i=1,2,\dots ,n.\end{array}$$

(11)

To solve system (1), we consider

$$\begin{array}{c}\hfill {\mathcal{D}}_t^{q_i}{u}_{i\lambda }(\overline{x},t)=\lambda \left[f_i(\overline{x},t)+L_i{\overline{u}}_{\lambda }+N_i{\overline{u}}_{\lambda }\right],i=1,2,\dots ,n;\lambda \in [0,1].\end{array}$$

(12)

with initial conditions given by

$$\begin{array}{c}\hfill \frac{{\partial }^{k_i}{u}_{i\lambda }(\overline{x},0)}{\partial t^{k_i}}=g_{i{k}_i}(\overline{x}),k_i=0,1,2,\dots ,m_i-1.\end{array}$$

(13)

Next, we assume that, system (12) has a solution given by

$$\begin{array}{c}\hfill u_{i\lambda }(\overline{x},t)=\sum _{k=0}^{\infty }{\lambda }^k{u}_{ik}(\overline{x},t),i=1,2,\dots ,n.\end{array}$$

(14)

Performing Riemann-Liouville fractional partial integral of order $q_i$ with respect to t to both sides of system (12) and using Theorem 1, we obtain

$$\begin{array}{c}\hfill u_{i\lambda }(\overline{x},t)=\sum _{k_i=0}^{m_i-1}\frac{t^{k_i}}{k_i!}\frac{{\partial }^{k_i}{u}_{i\lambda }(\overline{x},0)}{\partial t^{k_i}}+\lambda {\mathcal{I}}_t^{q_i}\left[f_i(\overline{x},t)+L_i{\overline{u}}_{\lambda }+N_i{\overline{u}}_{\lambda }\right],\end{array}$$

(15)

for $i=1,2,\dots ,n$. By using the initial condition from the system (1), the system (15) can be rewritten as

$$\begin{array}{c}\hfill u_{i\lambda }(\overline{x},t)=\sum _{k_i=0}^{m_i-1}\frac{t^{k_i}}{k_i!}{g}_{i{k}_i}(\overline{x})+\lambda \left[f_{it}^{(-q_i)}(\overline{x},t)+{\mathcal{I}}_t^{q_i}[L_i{\overline{u}}_{\lambda }]+{\mathcal{I}}_t^{q_i}[N_i{\overline{u}}_{\lambda }]\right],\end{array}$$

(16)

for $i=1,2,\dots ,n$. Inserting (14) into (16), we obtain

$$\begin{array}{cc}\hfill \sum _{k=0}^{\infty }{\lambda }^k{u}_{ik}(\overline{x},t)& =\sum _{k_i=0}^{m_i-1}\frac{t^{k_i}}{k_i!}{g}_{i{k}_i}(\overline{x})+\lambda [f_{it}^{(-q_i)}(\overline{x},t)+{\mathcal{I}}_t^{q_i}[L_i\sum _{k=0}^{\infty }{\lambda }^k{\overline{u}}_k]\hfill \\ & +{\mathcal{I}}_t^{q_i}[N_i\sum _{k=0}^{\infty }{\lambda }^k{\overline{u}}_k]],i=1,2,\dots ,n.\hfill \end{array}$$

(17)

By using Lemma 1 and Theorem 3, the system (17) becomes

$$\begin{array}{cc}\hfill \sum _{k=0}^{\infty }{\lambda }^k{u}_{ik}(\overline{x},t)& =\sum _{k_i=0}^{m_i-1}\frac{t^{k_i}}{k_i!}{g}_{i{k}_i}(\overline{x})+\lambda f_{it}^{(-q_i)}(\overline{x},t)+{\mathcal{I}}_t^{q_i}\lambda \sum _{k=0}^{\infty }[L_i{\lambda }^k{\overline{u}}_k]\hfill \\ & +{\mathcal{I}}_t^{q_i}\lambda \sum _{n=0}^{\infty }\left[\frac{1}{n!}\frac{{\partial }^n}{\partial {\lambda }^n}{[N_i\sum _{k=0}^n{\lambda }^k{\overline{u}}_k]}_{\lambda =0}\right]{\lambda }^n,i=1,2,\dots ,n.\hfill \end{array}$$

(18)

Next, we use Definition 4 in the system (18), we obtain

$$\begin{array}{cc}\hfill \sum _{k=0}^{\infty }{\lambda }^k{u}_{ik}(\overline{x},t)& =\sum _{k_i=0}^{m_i-1}\frac{t^{k_i}}{k_i!}{g}_{i{k}_i}(\overline{x})+\lambda f_{it}^{(-q_i)}(\overline{x},t)+{\mathcal{I}}_t^{q_i}\lambda \sum _{k=0}^{\infty }[L_i{\lambda }^k{\overline{u}}_k]\hfill \\ & +{\mathcal{I}}_t^{q_i}\lambda \sum _{n=0}^{\infty }{E}_{in}{\lambda }^n,i=1,2,\dots ,n.\hfill \end{array}$$

(19)

By equating the terms in system (17) with identical powers of $\lambda$, we obtain a series of the following systems

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill u_{i0}(\overline{x},t)& =\sum _{k_i=0}^{m_i-1}\frac{t^{k_i}}{k_i!}{g}_{i{k}_i}(\overline{x}),\hfill \\ \hfill u_{i1}(\overline{x},t)& =f_{it}^{(-q_i)}(\overline{x},t)+L_{it}^{(-q_i)}{\overline{u}}_0+E_{i0t}^{(-q_i)},\hfill \\ \hfill u_{i2}(\overline{x},t)& =L_{it}^{(-q_i)}{\overline{u}}_1+E_{i1t}^{(-q_i)},\hfill \\ \hfill ⋮\\ \hfill u_{ik}(\overline{x},t)& =L_{it}^{(-q_i)}{\overline{u}}_{(k-1)}+E_{i(k-1)t}^{(-q_i)},k=2,3,\dots ,i=1,2,\dots ,n.\hfill \end{array}\right.\end{array}$$

(20)

Substituting the series (20) in the system (14) gives the solution of the system (12). Now, from the systems (11) and (14), we obtain

$$\begin{array}{cc}\hfill u_i(\overline{x},t)& =\underset{\lambda \to 1}{lim}{u}_{i\lambda }(\overline{x},t)=u_{i0}(\overline{x},t)+u_{i1}(\overline{x},t)+\sum _{k=2}^{\infty }{u}_{ik}(\overline{x},t),i=1,2,\dots ,n.\hfill \end{array}$$

(21)

By using the first equations of (21), we see that $\frac{{\partial }^{k_i}{u}_i(\overline{x},0)}{\partial t^{k_i}}={lim}_{\lambda \to 1}\frac{{\partial }^{k_i}{u}_{i\lambda }(\overline{x},0)}{\partial t^{k_i}},i=1,2,\dots ,n$, which implies that $g_{i{k}_i}(\overline{x})=f_{i{k}_i}(\overline{x}),i=1,2,\dots ,n$.

Inserting (20) into (21) completes the proof. ☐

3.2. Convergence and Error Analysis

Theorem 5.

Let B be a Banach space. Then the series solution of the system (20) converges to $S_i\in B$ for $i=1,2,\dots ,n,$ if there exists ${\gamma }_i,0\le {\gamma }_i<1$ such that, $\parallel u_{in}\parallel \le {\gamma }_i\parallel u_{i(n-1)}\parallel$ for $\forall n\in \mathbb{N}$.

Proof. 

Define the sequences $S_{in}$, $i=1,2,\dots ,n$ of partial sums of the series given by the system (20) as

$$\begin{array}{c}\left\{\begin{array}{cc}\hfill S_{i0}& =u_{i0}(\overline{x},t),\hfill \\ \hfill S_{i1}& =u_{i0}(\overline{x},t)+u_{i1}(\overline{x},t),\hfill \\ \hfill S_{i2}& =u_{i0}(\overline{x},t)+u_{i1}(\overline{x},t)+u_{i2}(\overline{x},t),\hfill \\ \hfill ⋮\\ \hfill S_{in}& =u_{i0}(\overline{x},t)+u_{i1}(\overline{x},t)+u_{i2}(\overline{x},t)+\cdots +u_{in}(\overline{x},t),i=1,2,\dots ,n,\hfill \end{array}\right.,\end{array}$$

(22)

and we need to show that $\left\{S_{in}\right\}$ are a Cauchy sequences in Banach space B. For this purpose, we consider

$$\begin{array}{cc}\hfill \parallel S_{i(n+1)}-S_{in}\parallel & =\parallel u_{i(n+1)}(\overline{x},t)\parallel \le {\gamma }_i\parallel u_{in}(\overline{x},t)\parallel \le {\gamma }_i^2\parallel u_{i(n-1)}(\overline{x},t)\parallel \le \cdots \hfill \\ & \le {\gamma }_i^{n+1}\parallel u_{i0}(\overline{x},t)\parallel ,i=1,2,\dots ,n.\hfill \end{array}$$

(23)

For every $n,m\in \mathbb{N},n\ge m$, by using the system (23) and triangle inequality successively, we have,

$$\begin{array}{cc}\hfill \parallel S_{in}-S_{im}\parallel & =\parallel S_{i(m+1)}-S_{im}+S_{i(m+2)}-S_{i(m+1)}+\cdots +S_{in}-S_{i(n-1)}\parallel \hfill \\ & \le \parallel S_{i(m+1)}-S_{im}\parallel +\parallel S_{i(m+2)}-S_{i(m+1)}\parallel +\cdots +\parallel S_{in}-S_{i(n-1)}\parallel \hfill \\ & \le {\gamma }_i^{m+1}\parallel u_{i0}(\overline{x},t)\parallel +{\gamma }_i^{m+2}\parallel u_{i0}(\overline{x},t)\parallel +\cdots +{\gamma }_i^n\parallel u_{i0}(\overline{x},t)\parallel \hfill \\ & ={\gamma }_i^{m+1}(1+{\gamma }_i+\cdots +{\gamma }_i^{n-m-1})\parallel u_{i0}(\overline{x},t)\parallel \hfill \\ & \le {\gamma }_i^{m+1}\left(\frac{1-{\gamma }^{n-m}}{1-{\gamma }_i}\right)\parallel u_{i0}(\overline{x},t)\parallel .\hfill \end{array}$$

(24)

Since $0<{\gamma }_i<1$, so $1-{\gamma }_i^{n-m}\le 1$ then

$$\begin{array}{c}\hfill \parallel S_{in}-S_{im}\parallel \le {\frac{{\gamma }_i^{m+1}}{1-\gamma }}_i\parallel u_{i0}(\overline{x},t)\parallel .\end{array}$$

(25)

Since $u_{i0}(\overline{x},t)$ is bounded, then

$$\underset{n,m\to \infty }{lim}\parallel S_{in}-S_{im}\parallel =0,i=1,2,\dots ,n.$$

(26)

Therefore, the sequences $\left\{S_{in}\right\}$ are Cauchy sequences in the Banach space B, so the series solution defined in the system (21) converges. This completes the proof. ☐

Theorem 6.

The maximum absolute truncation error of the series solution (11) of the nonlinear fractional partial differential system (1) is estimated to be

$$\begin{array}{c}\hfill \underset{(\overline{x},t)\in \mathsf{\Omega }}{sup}|u_i(\overline{x},t)-\sum _{k=0}^m{u}_{ik}(\overline{x},t)|\le \frac{{\gamma }_i^{m+1}}{1-{\gamma }_i}\underset{(\overline{x},t)\in \mathsf{\Omega }}{sup}|u_{i0}(\overline{x},t)|,i=1,2,\dots ,n,\end{array}$$

(27)

where the region $\mathsf{\Omega }\subset {\mathbb{R}}^{n+1}$.

Proof. 

From Theorem 5, we have

$$\begin{array}{c}\hfill \parallel S_{in}-S_{im}\parallel \le \frac{{\gamma }_i^{m+1}}{1-{\gamma }_i}\underset{(\overline{x},t)\in \mathsf{\Omega }}{sup}|u_{i0}(\overline{x},t)|,i=1,2,\dots ,n.\end{array}$$

(28)

But we assume that $S_{in}={\sum }_{k=0}^n{u}_{ik}(\overline{x},t)$ for $i=1,2,\dots ,n$, and since $n\to \infty$, we obtain $S_{in}\to u_i(\overline{x},t)$, so the system (28) can be rewritten as

$$\begin{array}{cc}\hfill \parallel u_i(\overline{x},t)-S_{im}\parallel & =\parallel u_i(\overline{x},t)-\sum _{k=0}^m{u}_{ik}(\overline{x},t)\parallel \hfill \\ & \le \frac{{\gamma }_i^{m+1}}{1-{\gamma }_i}\underset{(\overline{x},t)\in \mathsf{\Omega }}{sup}|u_{i0}(\overline{x},t)|,i=1,2,\dots ,n.\hfill \end{array}$$

(29)

So, the maximum absolute truncation error in the region $\mathsf{\Omega }$ is

$$\begin{array}{c}\hfill \underset{(\overline{x},t)\in \mathsf{\Omega }}{sup}|u_i(\overline{x},t)-\sum _{k=0}^m{u}_{ik}(\overline{x},t)|\le \frac{{\gamma }_i^{m+1}}{1-{\gamma }_i}\underset{(\overline{x},t)\in \mathsf{\Omega }}{sup}|u_{i0}(\overline{x},t)|,i=1,2,\dots ,n.\end{array}$$

(30)

and this completes the proof. ☐

4. Applications to the Systems of Nonlinear Wave Equations

In this section, we present examples of some systems of nonlinear wave equations. These examples are chosen because their closed form solutions are available, or they have been solved previously by some other well-known methods.

Example 1.

Consider the nonlinear KdV system of time-fractional order of the form [24]

$$\begin{array}{c}\hfill D_t^{q}u=-\alpha u_{xxx}-6\alpha u{u}_x+6v{v}_x,D_t^{q}v=-\alpha v_{xxx}-3\alpha u{v}_x,\end{array}$$

(31)

for $0<q<1$, subject to the initial conditions

$$\begin{array}{c}\hfill u(x,0)={\beta }^2{\mathit{sech}}^2(\frac{\gamma }{2}+\frac{\beta x}{2}),v(x,0)=\sqrt{\frac{\alpha }{2}}{\beta }^2{\mathit{sech}}^2(\frac{\gamma }{2}+\frac{\beta x}{2}).\end{array}$$

(32)

For $q=1$, the exact solitary wave solutions of the KdV system (31) is given by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill u(x,t)& ={\beta }^2{\mathit{sech}}^2(\frac{1}{2}[\gamma -\alpha {\beta }^{3}t+\beta x]),\hfill \\ \hfill v(x,t)& =\sqrt{\frac{\alpha }{2}}{\beta }^2{\mathit{sech}}^2(\frac{1}{2}[\gamma -\alpha {\beta }^{3}t+\beta x]),\hfill \end{array}\right.\end{array}$$

(33)

where the constant α is a wave velocity and $\beta ,\gamma$ are arbitrary constants.

To solve the system (31), we compare (31) with the system (1), we obtain

$$\begin{array}{c}\hfill D_t^{q}u=-\alpha u_{xxx}+N_1(u,v),D_t^{q}v=-\alpha v_{xxx}+N_2(u,v),\end{array}$$

(34)

where we assume $N_1(u,v)=6v{v}_x-6\alpha u{u}_x$ and $N_2(u,v)=-3\alpha u{v}_x$.

Next, we assume the system (31) has a solution given by

$$\begin{array}{c}\hfill u(x,t)=\sum _{k=0}^{\infty }{u}_k(x,t),v(x,t)=\sum _{k=0}^{\infty }{v}_k(x,t).\end{array}$$

(35)

To obtain the approximate solution of the system (31), we consider the following system.

$$\begin{array}{c}\hfill {\mathcal{D}}_t^q{u}_{\lambda }=\lambda \left[-\alpha u_{\lambda xxx}+N_1(u_{\lambda },v_{\lambda })\right],{\mathcal{D}}_t^q{v}_{\lambda }=\lambda \left[-\alpha v_{\lambda xxx}+N_2(u_{\lambda },v_{\lambda })\right],\end{array}$$

(36)

subject to the initial conditions given by

$$\begin{array}{c}\hfill u_{\lambda }(x,0)=g_1(x),v_{\lambda }(x,0)=g_2(x),\end{array}$$

(37)

and we assume that the system (36) has a solution of the form

$$\begin{array}{c}\hfill u_{\lambda }(x,t)=\sum _{k=0}^{\infty }{\lambda }^k{u}_k(x,t),v_{\lambda }(x,t)=\sum _{k=0}^{\infty }{\lambda }^k{v}_k(x,t).\end{array}$$

(38)

By operating Riemann-Liouville fractional partial integral of order q with respect to t for both sides of the system (36) and by using Theorem 2 and the system (37), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill u_{\lambda }& =g_1(x)+\lambda {\mathcal{I}}_t^q\left[-\alpha u_{\lambda xxx}+N_1(u_{\lambda },v_{\lambda })\right],\hfill \\ \hfill v_{\lambda }& =g_2(x)+\lambda {\mathcal{I}}_t^q\left[-\alpha v_{\lambda xxx}+N_2(u_{\lambda },v_{\lambda })\right]\hfill \end{array}\right.\end{array}$$

(39)

By using Remark 1 and system (38), in the system (39), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \sum _{k=0}^{\infty }{\lambda }^k{u}_k& =g_1(x)+\lambda {\mathcal{I}}_t^q[-\alpha \sum _{k=0}^{\infty }{\lambda }^k{u}_{kxxx}+\sum _{n=0}^{\infty }{\lambda }^n{E}_{1n}],\hfill \\ \hfill \sum _{k=0}^{\infty }{\lambda }^k{v}_k& =g_2(x)+\lambda {\mathcal{I}}_t^q[-\alpha \sum _{k=0}^{\infty }{\lambda }^k{v}_{kxxx}+\sum _{n=0}^{\infty }{\lambda }^n{E}_{2n}].\hfill \end{array}\right.\end{array}$$

(40)

By equating the terms in the system (40) with identical powers of $\lambda$, we obtain a series of the following systems.

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill u_0& =g_1(x),v_0=g_2(x),\hfill \\ \hfill u_1& ={\mathcal{I}}_t^q\left[-\alpha u_{0xxx}+E_{10}\right],v_1={\mathcal{I}}_t^q\left[-\alpha v_{0xxx}+E_{20}\right],\hfill \\ \hfill u_2& ={\mathcal{I}}_t^q\left[-\alpha u_{1xxx}+E_{11}\right],v_2={\mathcal{I}}_t^q\left[-\alpha v_{1xxx}+E_{21}\right],\hfill \\ \hfill ⋮\\ \hfill u_k& ={\mathcal{I}}_t^q\left[-\alpha u_{(k-1)xxx}+E_{1(k-1)}\right],v_k={\mathcal{I}}_t^q\left[-\alpha v_{(k-1)xxx}+E_{2(k-1)}\right],\hfill \end{array}\right.\end{array}$$

(41)

for $k=1,2,\dots$, where $E_{1(k-1)},E_{1(k-1)}$ can be obtain by using Definition 4.

By using the systems (35) and (38), we can set

$$\begin{array}{c}\hfill u(x,t)=\underset{\lambda \to 1}{lim}{u}_{\lambda }(x,t)=\sum _{k=0}^{\infty }{u}_k(x,t),v(x,t)=\underset{\lambda \to 1}{lim}{v}_{\lambda }(x,t)=\sum _{k=0}^{\infty }{v}_k(x,t).\end{array}$$

(42)

By using the first equations of (42), we have $u(x,0)={lim}_{\lambda \to 1}{u}_{\lambda }(x,0),v(x,0)={lim}_{\lambda \to 1}{v}_{\lambda }(x,0)$, which implies that $g_1(x)=u(x,0)$ and $g_2(x)=v(x,0)$. Consequently, by using (41) and Definition 4, with the help of Mathematica software, the first few components of the solution for the system (31) are derived as follows.

$$\begin{array}{cc}\hfill u_0(x,t)& ={\beta }^2{\mathrm{sech}}^2(\frac{\gamma }{2}+\frac{\beta x}{2}),v_0(x,t)=\sqrt{\frac{\alpha }{2}}{\beta }^2{\mathrm{sech}}^2(\frac{\gamma }{2}+\frac{\beta x}{2}),\hfill \\ \hfill u_1(x,t)& =\frac{\alpha {\beta }^5}{\mathsf{\Gamma }(q+1)}tanh(\frac{\gamma }{2}+\frac{\beta x}{2}){\mathrm{sech}}^2(\frac{\gamma }{2}+\frac{\beta x}{2})t^q,\hfill \\ \hfill v_1(x,t)& =\frac{{\alpha }^{3/2}{\beta }^5}{\sqrt{2}\mathsf{\Gamma }(q+1)}tanh(\gamma 2+\frac{\beta x}{2}){\mathrm{sech}}^2(\frac{\gamma }{2}+\frac{\beta x}{2})t^q,\hfill \\ \hfill u_2(x,t)& =\frac{{\alpha }^2{\beta }^8}{2\mathsf{\Gamma }(2q+1)}[cosh(\gamma +\beta x)-2]{\mathrm{sech}}^4(\frac{\gamma }{2}+\frac{\beta x}{2}))t^{2q},\hfill \\ \hfill v_2(x,t)& =\frac{{\alpha }^{5/2}{\beta }^8}{2\sqrt{2}\mathsf{\Gamma }(2q+1)}(cosh(\gamma +\beta x)-2){\mathrm{sech}}^4(\frac{\gamma }{2}+\frac{\beta x}{2})t^{2q},\hfill \\ \hfill u_3(x,t)& =\frac{{\alpha }^3{\beta }^{11}}{8\mathsf{\Gamma }{(q+1)}^2\mathsf{\Gamma }(3q+1)}[\mathsf{\Gamma }{(q+1)}^2[-32cosh(\gamma +\beta x)+cosh(2[\gamma +\beta x])\hfill \\ & +39]+12\mathsf{\Gamma }(2q+1)[cosh(\gamma +\beta x)-2]]tanh(\frac{\gamma }{2}+\frac{\beta x}{2}){\mathrm{sech}}^6(\frac{\gamma }{2}+\frac{\beta x}{2})t^{3q},\hfill \\ \hfill v_3(x,t)& =\frac{{\alpha }^{7/2}{\beta }^{11}}{8\sqrt{2}\mathsf{\Gamma }{(q+1)}^2\mathsf{\Gamma }(3q+1)}[\mathsf{\Gamma }{(q+1)}^2[-32cosh(\gamma +\beta x)+cosh(2(\gamma +\beta x))\hfill \\ & +39]+12\mathsf{\Gamma }(2q+1)[cosh(\gamma +\beta x)-2]]tanh(\frac{\gamma }{2}+\frac{\beta x}{2}){\mathrm{sech}}^6(\frac{\gamma }{2}+\frac{\beta x}{2})t^{3q},\hfill \\ \hfill ⋮& \end{array}$$

and so on.

Hence the third-order term approximate solution for the system (31) is given by

$$\begin{array}{cc}\hfill u(x,t)& ={\beta }^2{\mathrm{sech}}^2(\frac{\gamma }{2}+\frac{\beta x}{2})+\frac{\alpha {\beta }^5}{\mathsf{\Gamma }(q+1)}tanh(\frac{\gamma }{2}+\frac{\beta x}{2}){\mathrm{sech}}^2(\frac{\gamma }{2}+\frac{\beta x}{2})t^q\hfill \\ & +\frac{{\alpha }^2{\beta }^8}{2\mathsf{\Gamma }(2q+1)}[cosh(\gamma +\beta x)-2]{\mathrm{sech}}^4(\frac{\gamma }{2}+\frac{\beta x}{2}))t^{2q}\hfill \\ & +\frac{{\alpha }^3{\beta }^{11}}{8\mathsf{\Gamma }{(q+1)}^2\mathsf{\Gamma }(3q+1)}[\mathsf{\Gamma }{(q+1)}^2[-32cosh(\gamma +\beta x)+cosh(2[\gamma +\beta x])\hfill \\ & +39]+12\mathsf{\Gamma }(2q+1)[cosh(\gamma +\beta x)-2]]tanh(\frac{\gamma }{2}+\frac{\beta x}{2}){\mathrm{sech}}^6(\frac{\gamma }{2}+\frac{\beta x}{2})t^{3q},\hfill \\ \hfill v(x,t)& =\sqrt{\frac{\alpha }{2}}{\beta }^2{\mathrm{sech}}^2(\frac{\gamma }{2}+\frac{\beta x}{2})+\frac{{\alpha }^{3/2}{\beta }^5}{\sqrt{2}\mathsf{\Gamma }(q+1)}tanh(\gamma 2+\frac{\beta x}{2}){\mathrm{sech}}^2(\frac{\gamma }{2}+\frac{\beta x}{2})t^q\hfill \\ & +\frac{{\alpha }^{5/2}{\beta }^8}{2\sqrt{2}\mathsf{\Gamma }(2q+1)}(cosh(\gamma +\beta x)-2){\mathrm{sech}}^4(\frac{\gamma }{2}+\frac{\beta x}{2})t^{2q}\hfill \\ & +\frac{{\alpha }^{7/2}{\beta }^{11}}{8\sqrt{2}\mathsf{\Gamma }{(q+1)}^2\mathsf{\Gamma }(3q+1)}[\mathsf{\Gamma }{(q+1)}^2[-32cosh(\gamma +\beta x)+cosh(2(\gamma +\beta x))\hfill \\ & +39]+12\mathsf{\Gamma }(2q+1)[cosh(\gamma +\beta x)-2]]tanh(\frac{\gamma }{2}+\frac{\beta x}{2}){\mathrm{sech}}^6(\frac{\gamma }{2}+\frac{\beta x}{2})t^{3q}.\hfill \end{array}$$

In

Table 1. Numerical values when $q=0.5,1$ and $\alpha =\beta =0.5,\gamma =1$ for Example 1.

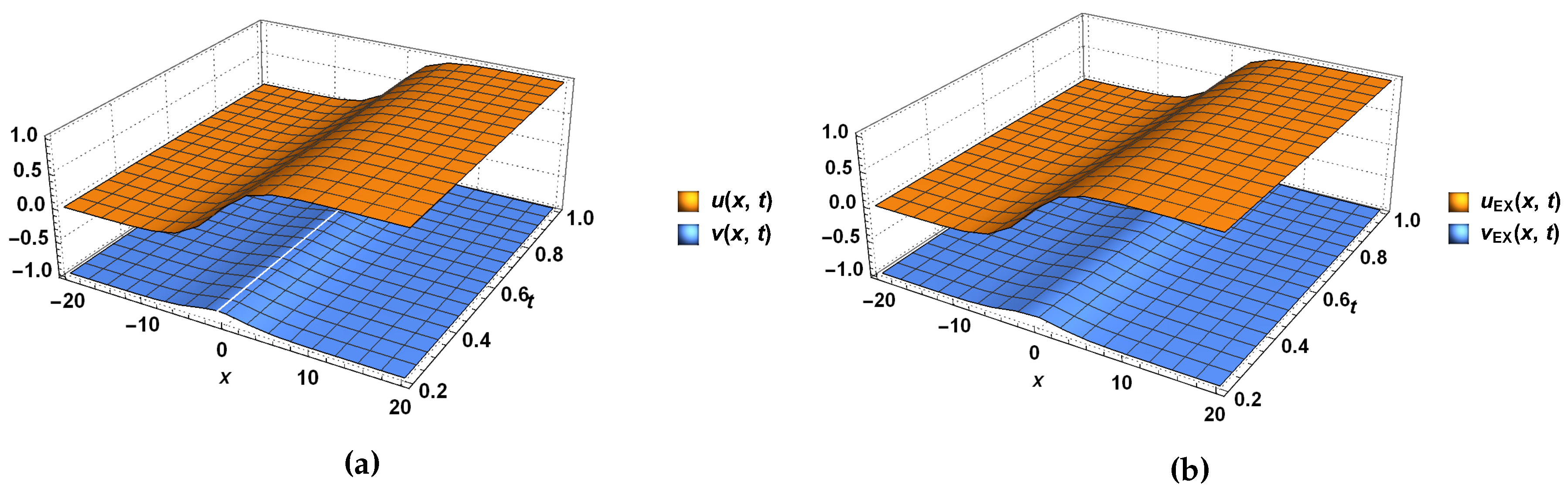
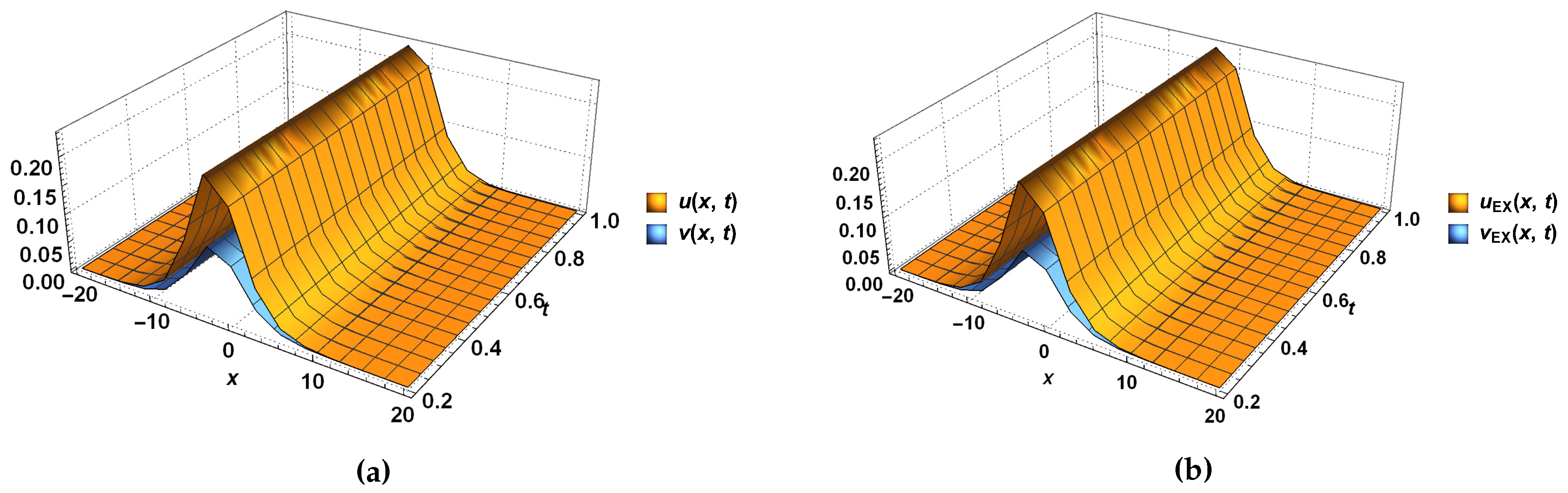
x	t	$\mathit{q}=0.5$		$\mathit{q}=1$		$\mathit{\alpha }=\mathit{\beta }=0.5$, $\mathit{\gamma }=1$		Absolute Error
		${\mathit{u}}_{\mathit{NAT}}$	${\mathit{v}}_{\mathit{NAT}}$	${\mathit{u}}_{\mathit{NAT}}$	${\mathit{v}}_{\mathit{NAT}}$	${\mathit{u}}_{\mathit{EX}}$	${\mathit{v}}_{\mathit{EX}}$	$|{\mathit{u}}_{\mathit{EX}}-{\mathit{u}}_{\mathit{NAT}}|$	$|{\mathit{v}}_{\mathit{EX}}-{\mathit{v}}_{\mathit{NAT}}|$
−10	0.20	0.0171378	0.0085689	0.0174511	0.0087256	0.0174511	0.0087256	9.11712 × ${10}^{-12}$	4.55856 × ${10}^{-12}$
	0.40	0.0169274	0.0084637	0.0172419	0.0086210	0.0172419	0.0086210	1.45834 × ${10}^{-10}$	7.29172 × ${10}^{-11}$
	0.60	0.0167686	0.0083843	0.0170352	0.0085176	0.0170352	0.0085176	7.38075 × ${10}^{-10}$	3.69037 × ${10}^{-10}$
0	0.20	0.1994480	0.0997242	0.1977450	0.0988724	0.1977450	0.0988724	5.11989 × ${10}^{-11}$	2.55994 × ${10}^{-11}$
	0.40	0.2006050	0.1003020	0.1988720	0.0994360	0.1988720	0.0994360	8.07505 × ${10}^{-10}$	4.03753 × ${10}^{-10}$
	0.60	0.20148400	0.1007420	0.1999930	0.0999966	0.1999930	0.0999966	4.02841 × ${10}^{-9}$	2.01421 × ${10}^{-9}$
20	0.20	0.0000172	8.62 × ${10}^{-6}$	0.0000169	8.46 × ${10}^{-6}$	0.0000169	8.46 × ${10}^{-6}$	1.70233 × ${10}^{-14}$	8.51164 × ${10}^{-15}$
	0.40	0.0000175	8.74 × ${10}^{-6}$	0.0000171	8.56 × ${10}^{-6}$	0.0000171	8.56 × ${10}^{-6}$	2.73056 × ${10}^{-13}$	1.36528 × ${10}^{-13}$
	0.60	0.0000177	8.83 × ${10}^{-6}$	0.0000173	8.67 × ${10}^{-6}$	0.0000173	8.67 × ${10}^{-6}$	1.38582 × ${10}^{-12}$	6.92909 × ${10}^{-13}$

, the numerical values of the approximate and exact solutions for Example 1 show the accuracy and efficiency of our technique at different values of $x,t$. The absolute error is listed for different values of $x,t$. In Figure 1a, we consider fixed values $\alpha =\beta =0.5,\gamma =1$ and fixed order $q=1$ for piecewise approximation values of $x,t$ in the domain $-20\le x\le 20$ and $0.20\le t\le 1$. In Figure 1b, we plot the exact solution with fixed values $\alpha =\beta =0.5$ and $\gamma =1$ in the domain $-20\le x\le 20$ and $0.20\le t\le 1$.

Example 2.

Consider the nonlinear dispersive long wave system of time fractional order [24,25,26]

$$\begin{array}{c}\hfill D_t^{q_1}u=-v_x-\frac{1}{2}{(u^2)}_x,D_t^{q_2}v=-{(u+u_{xx}+uv)}_x,\end{array}$$

(43)

for $0<q_1,q_1<1$, with initial condition given by

$$\begin{array}{c}\hfill u(x,0)=\alpha [tanh(\frac{1}{2}[\beta +\alpha x])+1],v(x,0)=-1+\frac{1}{2}{\alpha }^2{\mathit{sech}}^2(\frac{1}{2}[\beta +\alpha x]).\end{array}$$

(44)

For $q_1=q_2=1$, the system (43) has the following exact solitary wave solutions:

$$\begin{array}{c}\hfill u(x,t)=\alpha [tanh(\frac{1}{2}[\beta +\alpha x-{\alpha }^{2}t])+1],v(x,t)=-1+\frac{1}{2}{\alpha }^2{\mathit{sech}}^2(\frac{1}{2}[\beta +\alpha x-{\alpha }^{2}t]),\end{array}$$

(45)

where $\alpha ,\beta$ are arbitrary constants.

By comparing the system (43) with the system (1), the system (43) can be rewritten as

$$\begin{array}{c}\hfill D_t^{q_1}u=-v_x+N_1(u,v),D_t^{q_2}v=-u_x-u_{xxx}+N_2(u,v),\end{array}$$

(46)

where $N_1(u,v)=-u{u}_x$ and $N_2(u,v)=-(u{v}_x+v{u}_x)$. To solve the system (46) by NAT discussed in Section 3, we assume that the system (46) has a solution given by

$$\begin{array}{c}\hfill u(x,t)=\sum _{k=0}^{\infty }{u}_k(x,t),v(x,t)=\sum _{k=0}^{\infty }{v}_k(x,t).\end{array}$$

(47)

Forgetting the approximate solution of the system (43), we consider the following system.

$$\begin{array}{c}\hfill D_t^{q_1}{u}_{\lambda }=\lambda [-v_{x\lambda }+N_1(u_{\lambda },v_{\lambda })],D_t^{q_2}{v}_{\lambda }=\lambda [-u_{\lambda x}-u_{\lambda xxx}+N_2(u_{\lambda },v_{\lambda })],\end{array}$$

(48)

subject to the initial conditions given by

$$\begin{array}{c}\hfill u_{\lambda }(x,0)=g_1(x),v_{\lambda }(x,0)=g_2(x).\end{array}$$

(49)

Assume that the system (48) has a solution given by

$$\begin{array}{c}\hfill u_{\lambda }(x,t)=\sum _{k=0}^{\infty }{\lambda }^k{u}_k(x,t),v_{\lambda }(x,t)=\sum _{k=0}^{\infty }{\lambda }^k{v}_k(x,t).\end{array}$$

(50)

By using Theorem 2, we take Riemann-Liouville fractional partial integrals of order $q_1$ and $q_2$ with respect to t for both sides of the system (48) and using (47), we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill u_{\lambda }& =g_1(x)+\lambda {\mathcal{I}}_t^{q_1}\left[-v_{x\lambda }+N_1(u_{\lambda },v_{\lambda })\right],\hfill \\ \hfill v_{\lambda }& =g_2(x)+\lambda {\mathcal{I}}_t^{q_2}\left[-u_{x\lambda }-u_{xxx\lambda }+N_2(u_{\lambda },v_{\lambda })\right].\hfill \end{array}\right.\end{array}$$

(51)

Next, we use Theorem 1. The system (51) can be rewritten as

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \sum _{k=0}^{\infty }{\lambda }^k{u}_k& =g_1(x)+\lambda {\mathcal{I}}_t^{q_1}[-\sum _{k=0}^{\infty }{\lambda }^k{v}_{xk}+\sum _{n=0}^{\infty }{\lambda }^n{E}_{1n}],\hfill \\ \hfill \sum _{k=0}^{\infty }{\lambda }^k{v}_k& =g_2(x)+\lambda {\mathcal{I}}_t^{q_2}[-\sum _{k=0}^{\infty }{\lambda }^k{u}_{kx}-\sum _{k=0}^{\infty }{\lambda }^k{u}_{kxxx}+\sum _{n=0}^{\infty }{\lambda }^n{E}_{2n}].\hfill \end{array}\right.\end{array}$$

(52)

By equating the terms in the system (52) with identical powers of $\lambda$, we obtain a series of the following systems.

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill u_0& =g_1(x),v_0=g_2(x),\hfill \\ \hfill u_1& ={\mathcal{I}}_t^{q_1}\left[-v_{0x}+E_{10}\right],v_1={\mathcal{I}}_t^{q_2}\left[-u_{0x}-u_{0xxx}+E_{20}\right],\hfill \\ \hfill u_2& ={\mathcal{I}}_t^{q_1}\left[-v_{1x}+E_{11}\right],v_2={\mathcal{I}}_t^{q_2}\left[-u_{1x}-u_{1xxx}+E_{21}\right],\hfill \\ \hfill ⋮\\ \hfill u_k& ={\mathcal{I}}_t^{q_1}\left[-v_{(k-1)x}+E_{1(k-1)}\right],v_k={\mathcal{I}}_t^{q_2}\left[-u_{(k-1)x}-u_{(k-1)xxx}+E_{2(k-1)}\right],\hfill \end{array}\right.\end{array}$$

(53)

for $k=1,2,\dots$, where $E_{1(k-1)},E_{1(k-1)}$ can be obtain by using Theorem 4.

From the systems (47) and (50), we have

$$\begin{array}{c}\hfill u(x,t)=\underset{\lambda \to 1}{lim}{u}_{\lambda }(x,t)=\sum _{k=0}^{\infty }{u}_k(x,t),v(x,t)=\underset{\lambda \to 1}{lim}{v}_{\lambda }(x,t)=\sum _{k=0}^{\infty }{v}_k(x,t).\end{array}$$

(54)

By using the first equations of (54), we have $u(x,0)={lim}_{\lambda \to 1}{u}_{\lambda }(x,0),v(x,0)={lim}_{\lambda \to 1}{v}_{\lambda }(x,0)$, which implies that $g_1(x)=u(x,0)$ and $g_2(x)=v(x,0)$. Consequently, by using (53) and Definition 4 by the help of Mathematica software, the first few components of the solution for the system (43) are derived as follows.

$$\begin{array}{cc}\hfill u_0(x,t)& =\alpha [tanh(\frac{1}{2}[\beta +\alpha x])+1],v_0(x,t)=-1+\frac{1}{2}{\alpha }^2{\mathrm{sech}}^2(\frac{1}{2}[\beta +\alpha x]),\hfill \\ \hfill u_1(x,t)& =-\frac{{\alpha }^3}{2q_1\mathsf{\Gamma }\left(q_1\right)}{\mathrm{sech}}^2(\frac{1}{2}[\beta +\alpha x])t^{q_1},\hfill \\ \hfill v_1(x,t)& =\frac{4{\alpha }^4}{q_2\mathsf{\Gamma }\left(q_2\right)}{sinh}^4(\frac{1}{2}[\beta +\alpha x]){\mathrm{csch}}^3(\beta +\alpha x)t^{q_2},\hfill \\ \hfill u_2(x,t)& =\frac{1}{4}{\alpha }^5{\mathrm{sech}}^4(\frac{1}{2}[\beta +\alpha x])[\frac{[cosh(\beta +\alpha x)-2]t^{q_2}}{\mathsf{\Gamma }\left(q_1+q_2+1\right)}\hfill \\ & -\frac{[sinh(\beta +\alpha x)+cosh(\beta +\alpha x)-2]t^{q_1}}{\mathsf{\Gamma }\left(2q_1+1\right)}]t^{q_1},\hfill \\ \hfill v_2(x,t)& =\frac{{\alpha }^6{\mathrm{sech}}^5(\frac{1}{2}[\beta +\alpha x])}{8\mathsf{\Gamma }\left(q_1+q_2+1\right)\mathsf{\Gamma }\left(2q_2+1\right)}{t}^{q_2}[t^{q_1}\mathsf{\Gamma }\left(2q_2+1\right)[7sinh(\frac{1}{2}[\beta +\alpha x])\hfill \\ & -sinh(\frac{3}{2}[\beta +\alpha x])]-\mathsf{\Gamma }\left(q_1+q_2+1\right)[7sinh(\frac{1}{2}[\beta +\alpha x])\hfill \\ & -sinh(\frac{3}{2}[\beta +\alpha x])+3cosh(\frac{1}{2}[\beta +\alpha x])-cosh(32[\beta +\alpha x])]t^{q_2}],\hfill \\ \hfill u_3(x,t)& =\frac{1}{16}{\alpha }^7{t}^{q_1}\left[\frac{64t^{2q_1}{e}^{2(\beta +\alpha x)}}{\mathsf{\Gamma }\left(3q_1+1\right){\left(e^{\beta +\alpha x}+1\right)}^6}\right[\frac{4^{q_1}\mathsf{\Gamma }\left[q_1+\frac{1}{2}\right]\left[e^{2(\beta +\alpha x)}-1\right]}{\sqrt{\pi }\mathsf{\Gamma }\left(q_1+1\right)}\hfill \\ & -2e^{\beta +\alpha x}\left[e^{\beta +\alpha x}[e^{\beta +\alpha x}-8]+6\right]]+t^{q_2}{\mathrm{sech}}^6(\frac{1}{2}[\beta +\alpha x])\hfill \\ & \times [\frac{t^{q_2}{e}^{\alpha (-x)-\beta }\left[e^{\beta +\alpha x}[e^{\beta +\alpha x}[e^{\beta +\alpha x}-14]+21]-4\right]}{\mathsf{\Gamma }\left(q_1+2q_2+1\right)}\hfill \\ & +\frac{t^{q_1}\left[-10sinh(\beta +\alpha x)+sinh(2[\beta +\alpha x])+4cosh(\beta +\alpha x)-6\right]}{\mathsf{\Gamma }\left(2q_1+q_2+1\right)}\left]\right],\hfill \\ \hfill v_3(x,t)& =\frac{2{\alpha }^8{t}^{q_2}{e}^{\beta +\alpha x}}{{\left[e^{\beta +\alpha x}+1\right]}^7}\left[t^{q_2}\right[\frac{4t^{q_2}{e}^{2(\beta +\alpha x)}\left[e^{\beta +\alpha x}\left(e^{\beta +\alpha x}-13\right)\left(e^{\beta +\alpha x}-2\right)-6\right]}{\mathsf{\Gamma }\left(3q_2+1\right)}\hfill \\ & +[-\frac{4\mathsf{\Gamma }\left(q_1+q_2+1\right)e^{\beta +\alpha x}\left[e^{\beta +\alpha x}+1\right]\left[e^{\beta +\alpha x}\left(e^{\beta +\alpha x}-3\right)+1\right]}{\mathsf{\Gamma }\left(q_1+1\right)\mathsf{\Gamma }\left(q_2+1\right)\mathsf{\Gamma }\left(q_1+2q_2+1\right)}\hfill \\ & +\frac{e^{\beta +\alpha x}\left[49-e^{\beta +\alpha x}\left[e^{\beta +\alpha x}\left[e^{\beta +\alpha x}\left(e^{\beta +\alpha x}+15\right)-172\right]+220\right]\right]}{\mathsf{\Gamma }\left(q_1+2q_2+1\right)}-1]t^{q_1}]\hfill \\ & -\frac{2t^{2q_1}{e}^{\beta +\alpha x}\left[e^{\beta +\alpha x}\left(e^{\beta +\alpha x}\left[e^{\beta +\alpha x}\left(e^{\beta +\alpha x}-37\right)+151\right]-119\right)+16\right]}{\mathsf{\Gamma }\left(2q_1+q_2+1\right)}],\hfill \\ \hfill ⋮& \end{array}$$

and so on.

Hence the third-order term approximate solution for the system (43) is given by

$$\begin{array}{cc}\hfill u(x,t)& =\alpha [tanh(\frac{1}{2}[\beta +\alpha x])+1]-\frac{{\alpha }^3}{2q_1\mathsf{\Gamma }\left(q_1\right)}{\mathrm{sech}}^2(\frac{1}{2}[\beta +\alpha x])t^{q_1}\hfill \\ & +\frac{1}{4}{\alpha }^5{\mathrm{sech}}^4(\frac{1}{2}[\beta +\alpha x])[\frac{[cosh(\beta +\alpha x)-2]t^{q_2}}{\mathsf{\Gamma }\left(q_1+q_2+1\right)}\hfill \\ & -\frac{[sinh(\beta +\alpha x)+cosh(\beta +\alpha x)-2]t^{q_1}}{\mathsf{\Gamma }\left(2q_1+1\right)}]t^{q_1}\hfill \\ & +\frac{1}{16}{\alpha }^7{t}^{q_1}\left[\frac{64t^{2q_1}{e}^{2(\beta +\alpha x)}}{\mathsf{\Gamma }\left(3q_1+1\right){\left(e^{\beta +\alpha x}+1\right)}^6}\right[\frac{4^{q_1}\mathsf{\Gamma }\left[q_1+\frac{1}{2}\right]\left[e^{2(\beta +\alpha x)}-1\right]}{\sqrt{\pi }\mathsf{\Gamma }\left(q_1+1\right)}\hfill \\ & -2e^{\beta +\alpha x}\left[e^{\beta +\alpha x}[e^{\beta +\alpha x}-8]+6\right]]+t^{q_2}{\mathrm{sech}}^6(\frac{1}{2}[\beta +\alpha x])\hfill \\ & \times [\frac{t^{q_2}{e}^{\alpha (-x)-\beta }\left[e^{\beta +\alpha x}[e^{\beta +\alpha x}[e^{\beta +\alpha x}-14]+21]-4\right]}{\mathsf{\Gamma }\left(q_1+2q_2+1\right)}\hfill \\ & +\frac{t^{q_1}(-10sinh(\beta +\alpha x)+sinh(2(\beta +\alpha x))+4cosh(\beta +\alpha x)-6)}{\mathsf{\Gamma }\left(2q_1+q_2+1\right)}\left]\right],\hfill \\ \hfill v(x,t)& =-1+\frac{1}{2}{\alpha }^2{\mathrm{sech}}^2(\frac{1}{2}[\beta +\alpha x])+\frac{4{\alpha }^4}{q_2\mathsf{\Gamma }\left(q_2\right)}{sinh}^4(\frac{1}{2}[\beta +\alpha x]){\mathrm{csch}}^3(\beta +\alpha x)t^{q_2}\hfill \\ & +\frac{{\alpha }^6{\mathrm{sech}}^5(\frac{1}{2}[\beta +\alpha x])}{8\mathsf{\Gamma }\left(q_1+q_2+1\right)\mathsf{\Gamma }\left(2q_2+1\right)}{t}^{q_2}[t^{q_1}\mathsf{\Gamma }\left(2q_2+1\right)[7sinh(\frac{1}{2}[\beta +\alpha x])\hfill \\ & -sinh(\frac{3}{2}[\beta +\alpha x])]-\mathsf{\Gamma }\left(q_1+q_2+1\right)[7sinh(\frac{1}{2}[\beta +\alpha x])\hfill \\ & -sinh(\frac{3}{2}[\beta +\alpha x])+3cosh(\frac{1}{2}[\beta +\alpha x])-cosh(32[\beta +\alpha x])]t^{q_2}]\hfill \\ & +\frac{2{\alpha }^8{t}^{q_2}{e}^{\beta +\alpha x}}{{[e^{\beta +\alpha x}+1]}^7}\left[t^{q_2}\right[\frac{4t^{q_2}{e}^{2(\beta +\alpha x)}\left[e^{\beta +\alpha x}[e^{\beta +\alpha x}-13][e^{\beta +\alpha x}-2]-6\right]}{\mathsf{\Gamma }\left(3q_2+1\right)}\hfill \\ & +[-\frac{4\mathsf{\Gamma }\left(q_1+q_2+1\right)e^{\beta +\alpha x}[e^{\beta +\alpha x}+1]\left[e^{\beta +\alpha x}[e^{\beta +\alpha x}-3]+1\right]}{\mathsf{\Gamma }\left(q_1+1\right)\mathsf{\Gamma }\left(q_2+1\right)\mathsf{\Gamma }\left(q_1+2q_2+1\right)}\hfill \\ & +\frac{e^{\beta +\alpha x}\left[49-e^{\beta +\alpha x}[e^{\beta +\alpha x}\left[e^{\beta +\alpha x}[e^{\beta +\alpha x}+15]-172\right]+220]\right]}{\mathsf{\Gamma }\left(q_1+2q_2+1\right)}-1\left]t^{q_1}\right]\hfill \\ & -\frac{2t^{2q_1}{e}^{\beta +\alpha x}\left[e^{\beta +\alpha x}\left[e^{\beta +\alpha x}\left[e^{\beta +\alpha x}[e^{\beta +\alpha x}-37]+151\right]-119\right]+16\right]}{\mathsf{\Gamma }\left(2q_1+q_2+1\right)}].\hfill \end{array}$$

In

Table 2. Numerical values when $q_1=q_2=0.5,1$ and $\alpha =\beta =0.5$ for Example 2.

x	t	${\mathit{q}}_1=0.5$	${\mathit{q}}_2=0.5$	${\mathit{q}}_1=1$	${\mathit{q}}_2=1$	$\mathit{\alpha }=0.5$	$\mathit{\beta }=0.5$	Absolute Error
		${\mathit{u}}_{\mathit{NAT}}$	${\mathit{v}}_{\mathit{NAT}}$	${\mathit{u}}_{\mathit{NAT}}$	${\mathit{v}}_{\mathit{NAT}}$	${\mathit{u}}_{\mathit{EX}}$	${\mathit{v}}_{\mathit{EX}}$	$|{\mathit{u}}_{\mathit{EX}}-{\mathit{u}}_{\mathit{NAT}}|$	$|{\mathit{v}}_{\mathit{EX}}-{\mathit{v}}_{\mathit{NAT}}|$
−10	0.20	0.0104859	−0.9952150	0.0104567	−0.9948260	0.0104567	−0.9948260	2.38731 × ${10}^{-9}$	9.68267 × ${10}^{-10}$
	0.40	0.0100181	−0.9954506	0.0099518	−0.9950740	0.0099518	−0.9950740	3.78897 × ${10}^{-8}$	1.54049 × ${10}^{-8}$
	0.60	0.0095700	−0.9956240	0.0094709	−0.9953090	0.0094710	−0.9953090	1.90276 × ${10}^{-8}$	7.75425 × ${10}^{-8}$
0	0.20	0.6103320	−0.8796460	0.6106390	−0.8811210	0.6106390	−0.8811210	2.69185 × ${10}^{-8}$	1.81638 × ${10}^{-8}$
	0.40	0.5979280	−0.8788030	0.5986870	−0.8798700	0.5986880	−0.8798700	4.24645 × ${10}^{-7}$	2.98579 × ${10}^{-7}$
	0.60	0.5853820	−0.8782520	0.5866150	−0.8787530	0.5866180	−0.8787510	2.11781 × ${10}^{-6}$	1.55116 × ${10}^{-6}$
20	0.20	0.9999710	−0.9999840	0.9999710	−0.9999860	0.9999710	−0.9999860	7.23998 × ${10}^{-12}$	3.61844 × ${10}^{-12}$
	0.40	0.9999700	−0.9999830	0.9999700	−0.9999850	0.9999000	−0.9999850	1.17016 × ${10}^{-10}$	5.84818 × ${10}^{-11}$
	0.60	0.9999680	−0.9999820	0.9999680	−0.9999840	0.9999680	−0.9999840	5.98445 × ${10}^{-10}$	2.99087 × ${10}^{-10}$

, we obtain similar approximation values as in the exact solution for Example 2 at different values of $x,t$. The absolute error is listed against different values of $x,t$. In Figure 2a, we plot the approximate solution at fixed values of the constants $\alpha =\beta =0.5$ and fixed order $q=1$. In Figure 2b, we plot the exact solution with fixed values of the constants $\alpha =\beta =0.5$. The graphs of the approximate and exact solutions are drawing in the domain $-20\le x\le 20$ and $0.20\le t\le 1$.

5. Discussion and Conclusions

In this paper, a nonlinear time-fractional partial differential system via NAT was studied. Moreover, the convergence and error analysis was also shown. From the computational point of view, the solutions obtained by our technique were in excellent agreement with those obtained via previous works and also conformed with the exact solution to confirm the effectiveness and accuracy of this technique. Moreover, approximate traveling wave solutions for some systems of nonlinear wave equations were successfully obtained. We used Mathematica software to obtain the approximate and numerical results as well as drawing the graphs.