1. Introduction
At present, fixed point theory is an immensely active area of research due to its applications in multiple fields. It addresses the results which state that, under certain conditions, a self map on a set admits a fixed point. Among all the results in fixed point theory, the “Banach Contraction Principle” in metric fixed point theory is the most celebrated one due to its simplicity and ease of application in major areas of mathematics. Following the Banach Contraction Principle, Boyd and Wong [
1] investigated the fixed point results in nonlinear contraction mappings. Subsequently, many authors extended and generalized this fixed point theorem in different directions.
Study of fixed point results in partially ordered sets has been a very well motivated research area because of its ease of compatibility in modelling various problems and in finding new convergence schemes. The first attempt in this direction was carried out by Ran and Reurings [
2] who combined the Banach contraction principle and the Knaster–Tarski fixed point theorem. Ran and Reurings considered a class of mappings
, with
as a complete metric space and a partial order ≤. The mappings they considered were continuous and monotone with respect to the partial order ≤. Those mappings also satisfy a Banach contraction inequality for every pair
such that
. When for some
, the inequality
is satisfied, they proved that the Picard sequence
would converge to a fixed point of
f. Ran and Reurings also combined this interesting result with the Schauder fixed point theorem and applied it to obtain some existence and uniqueness results to nonlinear matrix equations.
Neito and Rodríguez-López ([
3,
4]) extended the results of Ran and Reurings to the functions which were not necessarily continuous. The authors also applied their results to obtain a theorem on the existence of a unique solution for periodic boundary problems relative to ordinary differential equations.
Some very important works in this direction that deserve attention are [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18].
Nadler [
19] and Assad and Kirk [
20] established some very important fixed point results for set valued and multivalued contraction mappings. Meanwhile, Espinola and Kirk [
21] combined the concepts of fixed point theory and graph theory to prove some interesting fixed point theorems in
R-trees. In 2008, Jachymski [
22] introduced an interesting idea of using the language of graph theory in the study of fixed point results. He was interested in establishing results that would eventually generalize the existing results and also in applying the results to the theory of linear operators. So, he studied the class of generalized Banach contractions on a metric space with a directed graph. The advantage of using graph theoretical concepts was that it helped him to describe the results in a unified way and also weaken some conditions significantly. Such works were further extended by Bojor [
23,
24] in a significant way.
Very recently, some fixed point results on subgraphs of directed graphs were established by Aleomraninejad, Rezapour and Shahzad [
6,
25]. They showed that the Caristi fixed point theorem and a version of the Knaster–Tarski fixed point theorem are special cases of their results. Inspired by their work, in the present paper, we prove some fixed point theorems in the case of set valued mappings in the setting of a metric space with a graph by defining a new notion called start point of a directed graph.
Let
be a complete metric space and
be the class of all nonempty closed and bounded subsets of
X. For
, let:
where
. Then
is a metric space and
D is said to be a Hausdorff metric induced by
d.
Let be a metric space and denote the diagonal of the Cartesian product . Consider a directed graph G such that the set of its vertices coincides with X (i.e., ) and the set of its edges is such that , i.e., G contains all the loops. We assume G has no parallel edges and thus we identify G with the pair .
If , then a path in G from x to y is a sequence of vertices such that , and for .
In this article, we assume that a path may be finite or infinite and a cycle may be considered as a finite path. Also, we assume that G has no isolated vertex.
2. Main Results
Now we are ready to discuss our main results. The following definitions will be useful in this context.
Definition 1. Let be the class of all nonempty closed and bounded subsets of X. For each , the notation denotes a class of nonempty closed and bounded subsets of G such that : there exists a path from u to x for some }.
Definition 2. We say that the set valued map is a self-path map, whenever, for each , there is a path from u to x for some , we denote this by .
When , by the notation we mean that there is a path from x to for some .
Also, we define as .
Furthermore, the point is said to be a fixed point of the set valued map if .
The next example motivates the study of multivalued mappings by showing that control problems may be translated in terms of multivalued maps, and hence, study of their fixed points could provide new solution schemes to such problems.
Example 1. Suppose that the following control problem is to be solved:which is controlled by parameters (called the controls), where . To solve the above problem, we define a multivalued map as follows: Then solutions of the above problem are solutions of the following differential inclusions: Definition 3. Let be a subgraph of the directed graph G. We say that is a lower bound for whenever for all . Also, we say that is an infimum of whenever for all lower bounds c.
Definition 4. Let G be a directed graph and . We say that u is a start point whenever there is no such that and .
Definition 5. Let H be a subgraph of the directed graph G. A vertex is said to be a start point of H if there is no such that and .
Definition 6. Let be a metric space and a map. Suppose that G is the directed graph defined by and . We say that ϕ is upper semicontinuous whenever for all sequences in X such that converges to x.
Our first result uses the concept of a minimal path. If Y denotes the set of all paths in a directed graph G, then is a partially ordered set. Also, since it is trivially true that every partially ordered set has a minimal element, we can conclude that G has a minimal path.
Theorem 1. Let G be a directed graph such that every path in G has a lower bound within itself. Then, there exists a path in G, considered as a subgraph of G, which has a start point or a cycle.
Proof. We assume that G has no cycle. Let M be a minimal path in G and be a lower bound of M. If l is not a start point, then there exists such that and . Then, is a path in G and . This contradicts the fact that M is a minimal path. Hence, l must be a start point of M. ☐
Below, we give an example to verify Theorem 1.
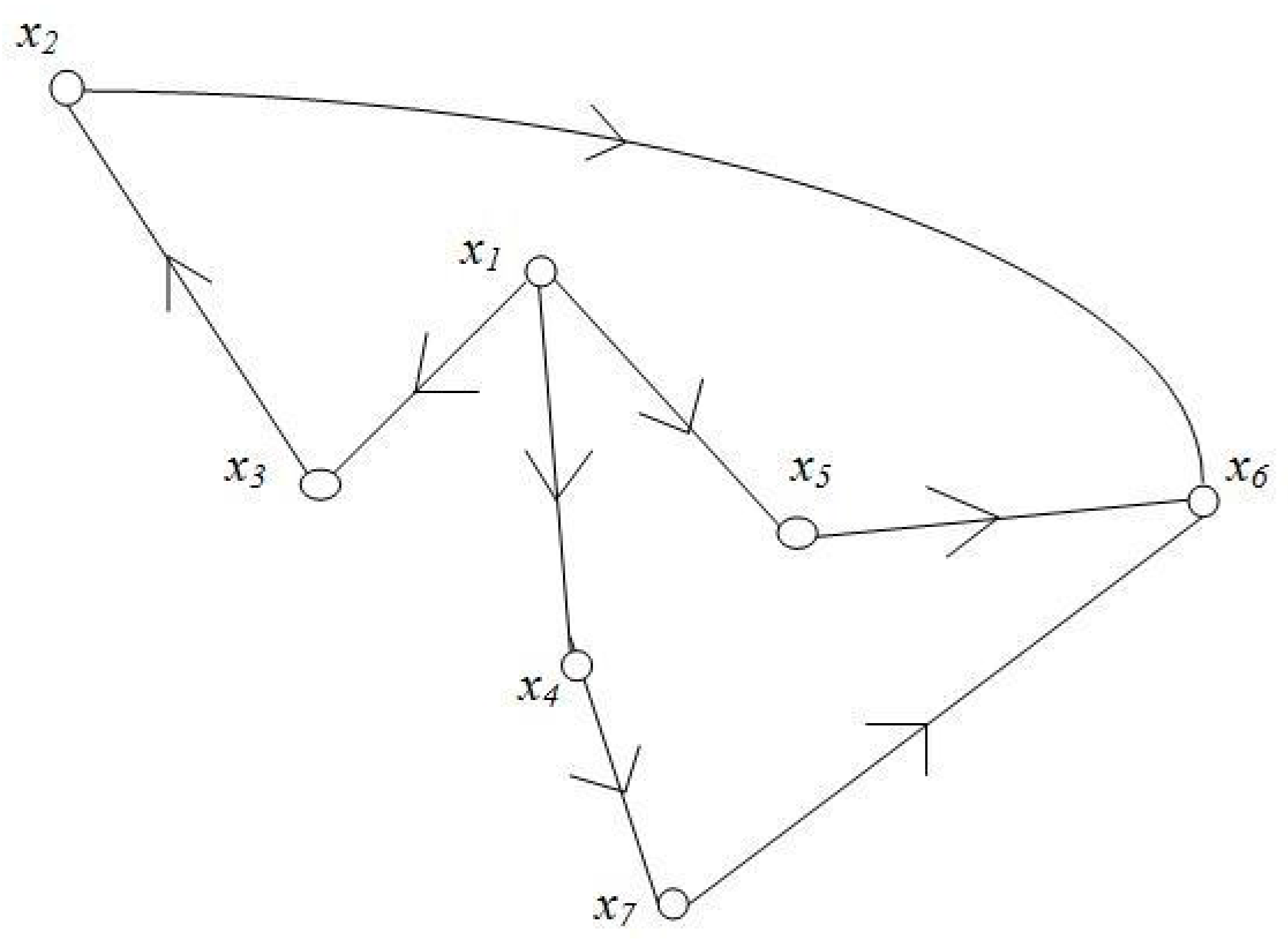
Example 2. Let and G be a directed graph with vertices . Suppose H is a subgraph of G with vertices and the edges (Figure 1). Then, it is easy to see that H has no cycle and every path in H has a lower bound within itself. Here, is a minimal path, which has a start point .
Theorem 2. Let G be a directed graph. Then, G has a start point if and only if each self path map on G has a fixed point.
Proof. Let G be a graph with a start point s and T be a self path map on G. We claim that s is a fixed point of T. Since , there is a path (finite or infinite) from u to s for some . However, since s is a start point, this is not possible for any s unless . Thus, we must have , i.e., s is a fixed point of T.
Again, suppose G is a directed graph and each self path map on G has a fixed point. If possible, assume that G has no start point. Then, for each , there exists such that and . Now, considering every such pair , we can define a map such that for each , . It is easy to see that T is a self path map because , but T has no fixed point as for any . This contradicts our hypothesis and thus G has a start point. ☐
Our next example shows that, indeed, if a directed graph has no start point, then a self-path map may be defined which has no fixed point.
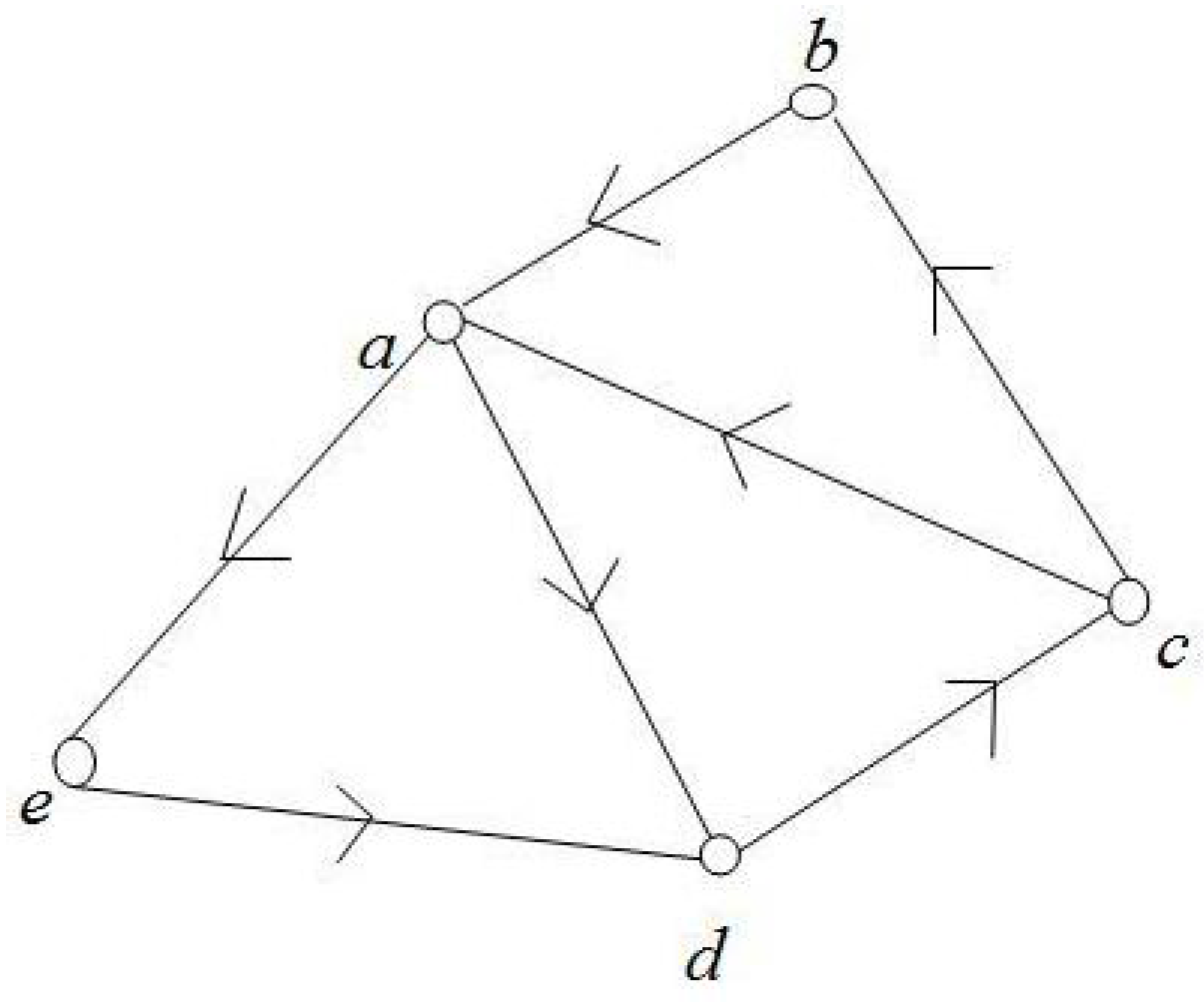
Example 3. Let G be a directed graph with vertices and the edges (Figure 2). Define the map such that . Then, it is easy to see that T is a self path map but G has no fixed point and no start point either.
Theorem 3. Let G be a directed graph such that every path in G has an infimum within itself and let be a self-path map. Also, let and has no cycle. Then, T has a fixed point in .
Proof. Let B be a path in and be its infimum (greatest lower bound). Therefore, from the definition of self path map, we have , which implies that . Also, is a subgraph of G. Now, using Theorem 1, has a start point. Again, since T may be considered as a self-path map on , using Theorem 2 we can conclude that T has a fixed point in . ☐
Below, we show that using Theorem 3, a version of the Knaster–Tarski fixed point theorem can be established.
Theorem 4. Let be a partially ordered set such that each chain in X has an infimum within itself and let be a monotone self-path map. Then, T has a fixed point.
Proof. We define the graph G as and . Then, for all . Let . Then, is a subgraph of G and it has no cycle. Thus, by using Theorem 3, we can conclude that T has a fixed point in . ☐
Lemma 1. Let X be a complete metric space and let be a map bounded from above. Suppose that G is the directed graph defined by and . If ϕ is upper semicontinuous, then G has a start point.
Proof. First, we prove that G has no cycle. If G has a cycle, then there exists a finite path in G such that (for, in a cycle, initial and terminal vertices are same).
Now, , and also, . However, this is possible only when , i.e., . This implies that , which is a contradiction. Thus, G cannot have any cycle.
Next, we show that each path in G has a lower bound. Let be a path in G. Then, is an increasing net of real numbers. As is bounded from above, we can obtain a decreasing sequence such that .
Therefore, we have that is a Cauchy sequence. Since X is complete, must converge to some . As is upper semicontinuous, we now have i.e.,
Thus, . So, x is a lower bound for . Now, we show that x is a lower bound for . If there exists such that , then which implies that . Since , from the definition of upper semicontinuous map, we have . This implies that (for ). Hence, . We claim that . In fact, if there is such that then , and so, . Since is a path in G, if the previous case is not true, then for each , there exists such that .
Again, we have . This implies that . Thus, x is a lower bound for . Now, using Theorem 1, we can say that G has a start point. ☐
Theorem 5. Let be a complete metric space, a map bounded from above and upper semicontinuous and a self path map satisfying the condition and . Then, T has a fixed point.
Proof. Suppose that G is the directed graph via the vertices and the edges . Using Lemma 1, we can conclude that G has a start point. Again, using Theorem 2, it is routine to check that T has a fixed point. ☐
The following example verifies Theorem 5.
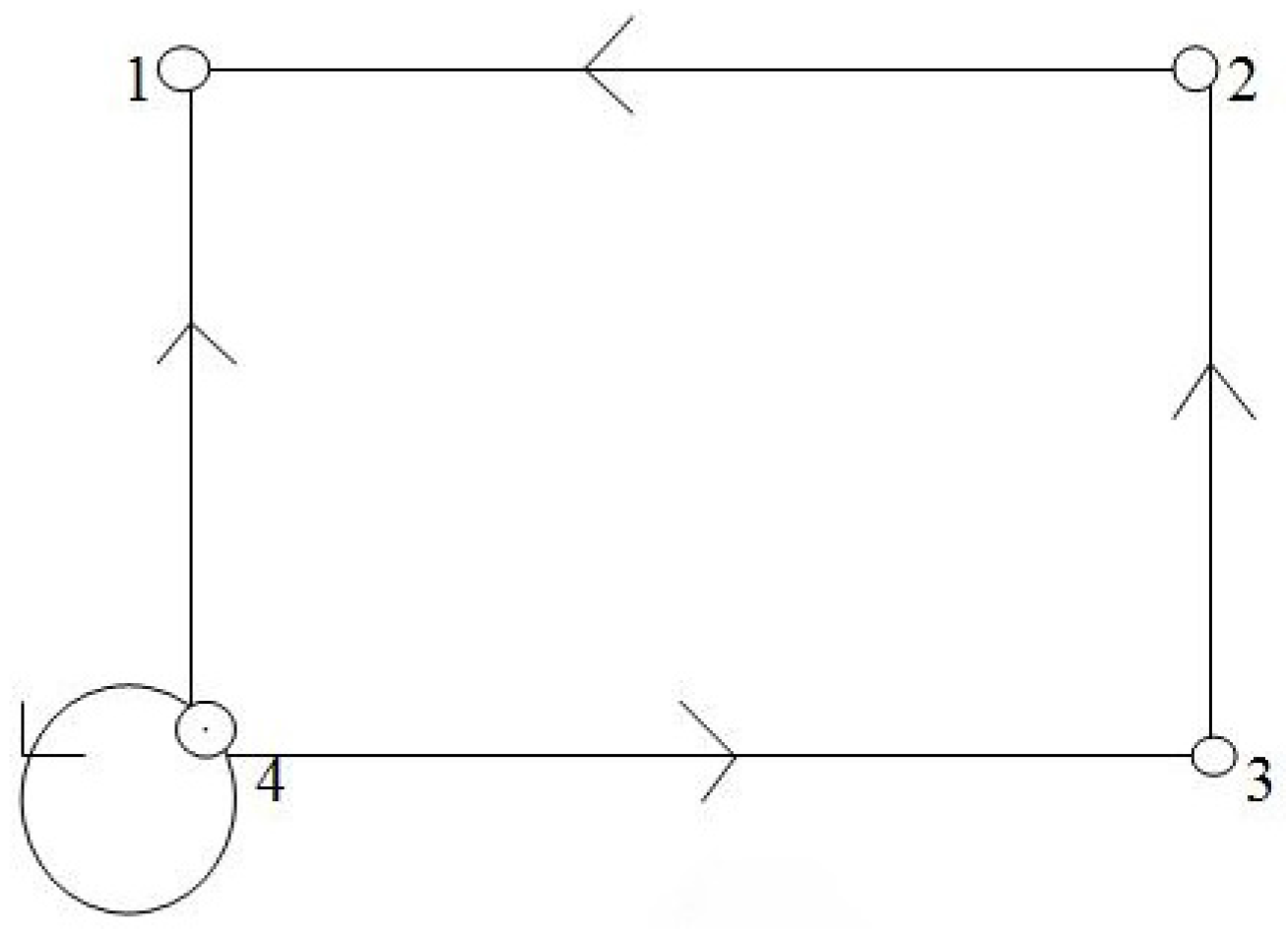
Example 4. Let and (Figure 3). Consider the closed and bounded subsets of X as and .
Define as follows: It is easy to verify that T is a self path map. Let be endowed with metric by , for all . Define by . Then, the conditions of Theorem 5 are satisfied. Thus, T has a fixed point 4.