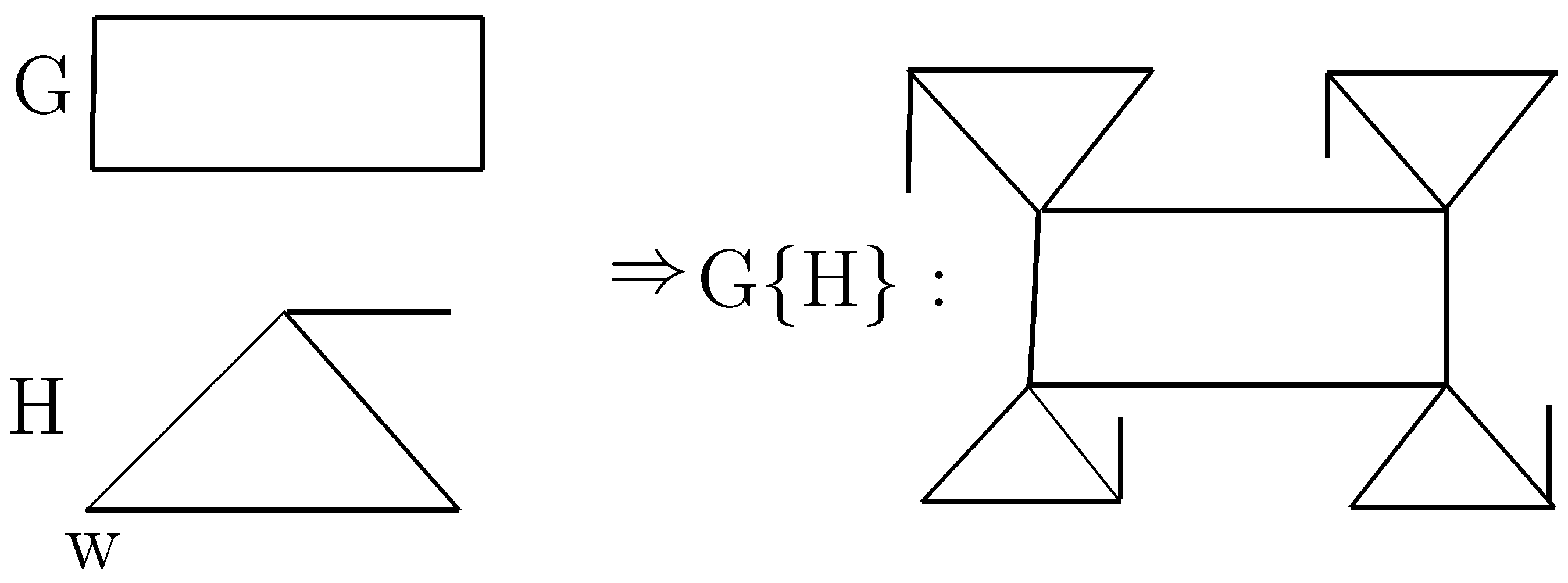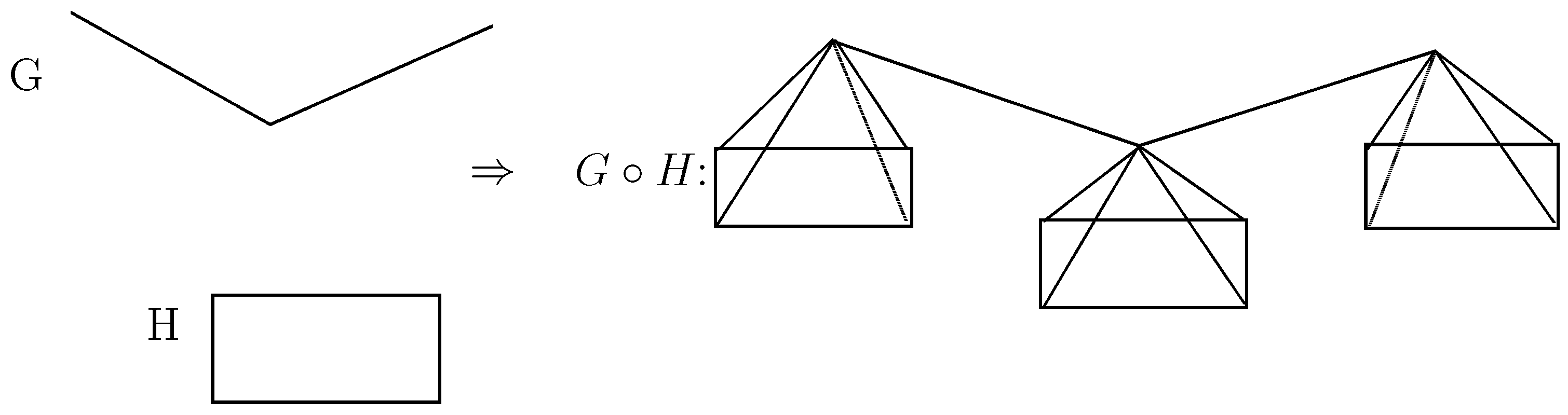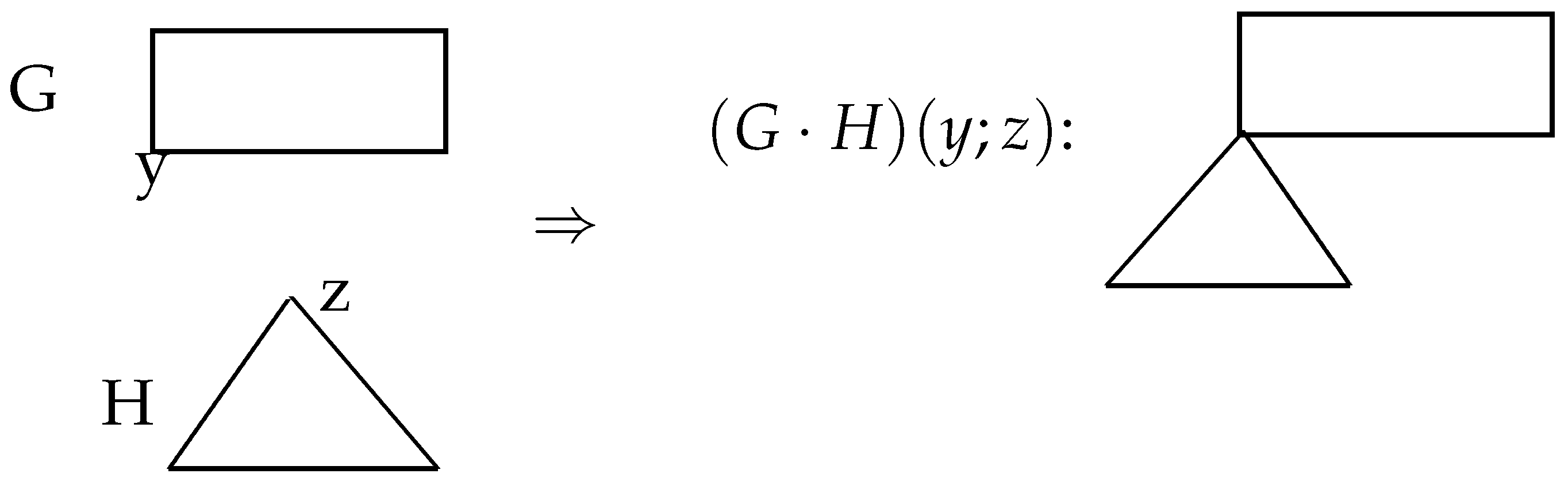On the Additively Weighted Harary Index of Some Composite Graphs

Abstract

The Harary index is defined as the sum of reciprocals of distances between all pairs of vertices of a connected graph. The additively weighted Harary index $H_A\left(G\right)$ is a modification of the Harary index in which the contributions of vertex pairs are weighted by the sum of their degrees. This new invariant was introduced in (Alizadeh, Iranmanesh and Došlić. Additively weighted Harary index of some composite graphs, Discrete Math, 2013) and they posed the following question: What is the behavior of $H_A\left(G\right)$ when G is a composite graph resulting for example by: splice, link, corona and rooted product? We investigate the additively weighted Harary index for these standard graph products. Then we obtain lower and upper bounds for some of them.

1. Introduction

A topological index is a real number derived from the structure of a graph in a way that does not depend on the labeling of the vertices. Hence, isomorphic graphs have the same values of topological indices. Chemical graph theory is a branch of mathematical chemistry that is mostly concerned with finding topological indices of chemical graphs that correlate well with certain physico-chemical properties of the corresponding molecules. The basic idea behind this approach is that the physico-chemical properties are governed by the mechanism depending mostly on the valences of atoms and on their relative positions within the molecule. Since both concepts are well described in graph-theoretical terms, there are reasons to believe that chemical graphs capture enough information about real molecules to make them useful as their models.

Hundreds of different topological indices have been investigated so far and have been employed in QSAR (Quantitative Structure Activity Relationship)/QSPR (Quantitative Structure Property Relationship) studies, with various degrees of success. Most of the more useful invariants belong to one of two broad classes: they are either distance based, or bond additive. The first class contains the indices that are defined in terms of distances between pairs of vertices; the second class contains the indices defined as the sums of contributions over all edges. Typical representants of the first type are the Wiener index and its various modifications; characteristic for the second type are the Randić index [1] and the two Zagreb indices.

Another distance-based topological index of the graph G is the Harary index. The Harary index of a graph G, denoted by $H\left(G\right)$, was introduced independently by Plavšić et al. [2] and by Ivanciuc et al. [3] in 1993. The Harary index is defined as follows:

$$H\left(G\right)=\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{1}{d_G(u,v)},$$

where the summation goes over all pairs of vertices of G and $d_G(u,v)$ denotes the distance of the two vertices u and v in the graph G. For a list of new results about the Harary index see [4,5,6,7].

The additively weighted version of the Harary index was introduced by Alizadeh et al. [8] in 2013. For a given graph G, its additively weighted Harary index $H_A\left(G\right)$ is defined as:

$$H_A\left(G\right)=\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_G\left(v\right)}{d_G(u,v)},$$

where ${\delta }_G\left(u\right)$ denotes the degree of vertex u in G. It is obvious that, if G is a k-regular graph, then $H_A\left(G\right)=2kH\left(G\right)$.

Also, in the paper [8], they posed the following question: What is the behavior of $H_A\left(G\right)$ when G is a composite graph resulting for example by: splice, link, corona and rooted product?

In this paper we investigate the behavior of $H_A\left(G\right)$ under these four operations which are useful in chemistry. Also, we try to obtain upper and lower bounds for $H_A\left(G\right)$ of these operations.

2. Preliminary Results

All graphs considered in this paper are finite, simple and connected. For a given graph G we denote by $V\left(G\right)$ its vertex set, and by $E\left(G\right)$ its edge set. The cardinalities of these two sets are denoted by n and e, respectively. The degree of a vertex $u\in V\left(G\right)$ is denoted by ${\delta }_G\left(u\right)$ and the distance $d_G(u,v)$ between vertices u and v in G is the length of any shortest path in G connecting u and v. The diameter of the graph G, denoted by $D\left(G\right)$, is $max\left\{d_G(u,v)\right|u,v\in V\left(G\right)\}$. We denote by $K_n$ and $P_n$ the complete graph and the path graph with n vertices, respectively.

A regular graph is a graph where each vertex has the same number of neighbors. A regular graph with vertices of degree k is called a k-regular graph or regular graph of degree k.

The first and the second Zagreb indices of a graph G are defined as follows:

$$M_1\left(G\right)=\sum _{uv\in E\left(G\right)}({\delta }_G\left(u\right)+{\delta }_G\left(v\right)),M_2\left(G\right)=\sum _{uv\in E\left(G\right)}{\delta }_G\left(u\right){\delta }_G\left(v\right).$$

These topological indices were conceived in the 1970s [9,10]. In 2008, in [11] the first and the second Zagreb coindices of a graph G are defined as follows:

$${\overline{M}}_1\left(G\right)=\sum _{uv\notin E\left(G\right)}({\delta }_G\left(u\right)+{\delta }_G\left(v\right)),{\overline{M}}_2\left(G\right)=\sum _{uv\notin E\left(G\right)}{\delta }_G\left(u\right){\delta }_G\left(v\right).$$

Also, the first and the second Zagreb coindices of graph G with n vertices and e edges are equal to ${\overline{M}}_1\left(G\right)=2e(n-1)-M_1\left(G\right)$ and ${\overline{M}}_2\left(G\right)=2e^2-M_2\left(G\right)-\frac{1}{2}{M}_1\left(G\right)$, respectively. For the proof of these facts, we refer the readers to [12]. We will use Zagreb indices and Zagreb coindices to formulate our results in a more compact way.

For a graph G with $u\in V\left(G\right)$, we define $P\left(G\right)={\sum }_{u,v\in V\left(G\right)}\frac{1}{d_G(u,v)+1}$ and $P_G\left(v\right)={\sum }_{u\in V\left(G\right)}\frac{1}{d_G(u,v)+1}$. Also we define $H_G\left(v\right)={\sum }_{u\in V\left(G\right)\setminus \left\{v\right\}}\frac{1}{d_G(u,v)}$.

In the rest of the paper any sum ${\sum }_{\{u,v\}\subseteq V\left(G\right)}h(u,v)$ denotes the sum ${\sum }_{u\in V\left(G\right)}h(u,u)+2{\sum }_{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}h(u,v)$, where $h(u,v)$ is the contribution of pair $u,v$ to the sum.

In the sequel of this paper we denote by $n_G$, $e_G$ for the number of vertices and the number of edges of G and we denote by $n_H$, $e_H$ for the same quantities for H.

3. Main Results

In this section we introduce the standard graph products resulting in composite graphs and then we present explicit formulas for the values of additively weighted Harary indices of them.

3.1. Rooted Product

Definition 1.

The rooted product $G\left\{H\right\}$ is obtained by taking one copy of G and $\left|V\right(G\left)\right|$ copies of a rooted graph H, and by identifying the root of the i-th copy of H with the i-th vertex of G, $i=1,2,...,\left|V\right(G\left)\right|$.

For the rooted product $G\left\{H\right\}$ we have:

$$\left|V\right(G\left\{H\right\}\left)\right|=\left|V\right(G\left)\right|\left|V\right(H\left)\right|,\left|E\right(G\left\{H\right\}\left)\right|=\left|E\right(G\left)\right|+\left|V\right(G\left)\right|\left|E\right(H\left)\right|.$$

As an example for rooted product see Figure 1.

Lemma 1.

Let G be a simple graph and H be a rooted graph with w as its root. Then for a vertex u of $G\left\{H\right\}$ such that $u\in V\left(G\right)$, we have ${\delta }_{G\left\{H\right\}}\left(u\right)={\delta }_G\left(u\right)+{\delta }_H\left(w\right)$, and for a vertex v of $G\left\{H\right\}$ such that $v\notin V\left(G\right)$ we have ${\delta }_{G\left\{H\right\}}\left(v\right)={\delta }_H\left(v_0\right)$, where $v_0$ is the corresponding vertex in H as v of $H_i$. Also:

(1) 

if $u,v\in V\left(G\right)$, then $d_{G\left\{H\right\}}(u,v)=d_G(u,v),$

(2) 

if $u\in V\left(G\right),v\in V\left(H_i\right)$, where $i=1,2,...,\left|V\right(G\left)\right|$, then $d_{G\left\{H\right\}}(u,v)=d_G(u,w_i)+d_{H_i}(w_i,v)=d_G(u,w_i)+d_H(w,v_0)$, where $w_i$ is the root of $H_i$ and $v_0$ is the corresponding vertex in H as v of $H_i$,

(3) 

if $u,v\in V\left(H_i\right)$, where $i=1,2,...,\left|V\right(G\left)\right|$, then $d_{G\left\{H\right\}}(u,v)=d_H(u_0,v_0)$, where $u_0$ and $v_0$ are the corresponding vertices in H as u and v of $H_i$,

(4) 

if $u\in V\left(H_i\right),v\in V\left(H_j\right)$ and $1⩽i<j⩽\left|V\right(G\left)\right|$, then $d_{G\left\{H\right\}}(u,v)=d_{H_i}(u,w_i)+d_{H_j}(v,w_j)+d_G(w_i,w_j)=d_H(u_0,w)+d_H(v_0,w)+d_G(w_i,w_j)$, where $w_i$ is the root of $H_i$ and $w_j$ is the root of $H_j$. Also, $u_0$ and $v_0$ are the corresponding vertices in H as u of $H_i$ and v of $H_j$, respectively.

Proof. 

The proof is straightforward. ☐

Theorem 1.

Let G be a simple graph and H be a rooted graph with w as its root. Then:

$$\begin{array}{cc}\hfill H_A\left(G\left\{H\right\}\right)& =H_A\left(G\right)+2{\delta }_H\left(w\right)H\left(G\right)+n_G{H}_A\left(H\right)+2e_G{H}_H\left(w\right)\hfill \\ & +2\sum _{\begin{array}{c}\{u,t\}\subseteq V\left(G\right)\\ u\ne t\end{array}}\sum _{v\in V\left(H\right)\setminus \left\{w\right\}}\frac{{\delta }_G\left(u\right)+{\delta }_H\left(v\right)+{\delta }_H\left(w\right)}{d_G(u,t)+d_H(v,w)}\hfill \\ & +\sum _{\begin{array}{c}\{t,l\}\subseteq V\left(G\right)\\ t\ne l\end{array}}\sum _{\{u,v\}\subseteq V\left(H\right)\setminus \left\{w\right\}}\frac{{\delta }_H\left(u\right)+{\delta }_H\left(v\right)}{d_H(u,w)+d_H(v,w)+d_G(t,l)}.\hfill \end{array}$$

Proof. 

From the definition we have:

$$H_A\left(G\left\{H\right\}\right)=\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right\{H\left\}\right)\\ u\ne v\end{array}}\frac{{\delta }_{G\left\{H\right\}}\left(u\right)+{\delta }_{G\left\{H\right\}}\left(v\right)}{d_{G\left\{H\right\}}(u,v)}.$$

By Lemma 1, we partition the sum into four sums $S_i$, $i=$ 1, 2, 3, 4, where:

$$\begin{array}{cc}\hfill S_1& =\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{{\delta }_{G\left\{H\right\}}\left(u\right)+{\delta }_{G\left\{H\right\}}\left(v\right)}{d_{G\left\{H\right\}}(u,v)}=\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_G\left(v\right)+2{\delta }_H\left(w\right)}{d_G(u,v)}\hfill \\ & =H_A\left(G\right)+2{\delta }_H\left(w\right)H\left(G\right),\hfill \\ \hfill S_2& =\sum _{i=1}^{n_G}\sum _{\begin{array}{c}u\in V\left(G\right)\\ v\in V\left(H_i\right)\setminus \left\{w_i\right\}\end{array}}\frac{{\delta }_{G\left\{H\right\}}\left(u\right)+{\delta }_{G\left\{H\right\}}\left(v\right)}{d_{G\left\{H\right\}}(u,v)}=\sum _{\begin{array}{c}\{u,t\}\subseteq V\left(G\right)\\ v\in V\left(H\right)\setminus \left\{w\right\}\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_H\left(w\right)+{\delta }_H\left(v\right)}{d_G(u,t)+d_H(v,w)},\hfill \\ \hfill S_3& =\sum _{i=1}^{n_G}\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(H_i\right)\setminus \left\{w_i\right\}\\ u\ne v\end{array}}\frac{{\delta }_{G\left\{H\right\}}\left(u\right)+{\delta }_{G\left\{H\right\}}\left(v\right)}{d_{G\left\{H\right\}}(u,v)}=n_G\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(H\right)\setminus \left\{w\right\}\\ u\ne v\end{array}}\frac{{\delta }_H\left(u\right)+{\delta }_H\left(v\right)}{d_H(u,v)},\hfill \\ \hfill S_4& =\sum _{1⩽i<j⩽n_G}\sum _{\begin{array}{c}u\in V\left(H_i\right)\setminus \left\{w_i\right\}\\ v\in V\left(H_j\right)\setminus \left\{w_j\right\}\end{array}}\frac{{\delta }_{G\left\{H\right\}}\left(u\right)+{\delta }_{G\left\{H\right\}}\left(v\right)}{d_{G\left\{H\right\}}(u,v)}\hfill \\ & =\sum _{\begin{array}{c}\{t,l\}\subseteq V\left(G\right)\\ t\ne l\end{array}}\sum _{\{u,v\}\subseteq V\left(H\right)\setminus \left\{w\right\}}\frac{{\delta }_H\left(u\right)+{\delta }_H\left(v\right)}{d_H(u,w)+d_H(v,w)+d_G(t,l)}.\hfill \end{array}$$

Hence:

$$\begin{array}{cc}\hfill H_A\left(G\left\{H\right\}\right)& =H_A\left(G\right)+2{\delta }_H\left(w\right)H\left(G\right)+2\sum _{v\in V\left(H\right)\setminus \left\{w\right\}}\sum _{\begin{array}{c}\{u,t\}\subseteq V\left(G\right)\\ u\ne t\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_H\left(w\right)+{\delta }_H\left(v\right)}{d_G(u,t)+d_H(v,w)}\hfill \\ & +\sum _{\begin{array}{c}u\in V\left(G\right)\\ v\in V\left(H\right)\setminus \left\{w\right\}\end{array}}\frac{{\delta }_G\left(u\right)}{d_H(v,w)}+n_G\sum _{\begin{array}{c}\{w,v\}\subseteq V\left(H\right)\\ w\ne v\end{array}}\frac{{\delta }_H\left(w\right)+{\delta }_H\left(v\right)}{d_H(v,w)}\hfill \\ & +\sum _{\begin{array}{c}\{t,l\}\subseteq V\left(G\right)\\ t\ne l\end{array}}\sum _{\{u,v\}\subseteq V\left(H\right)\setminus \left\{w\right\}}\frac{{\delta }_H\left(u\right)+{\delta }_H\left(v\right)}{d_H(u,w)+d_H(v,w)+d_G(t,l)}.\hfill \end{array}$$

Thus we complete the proof of this theorem. ☐

Example 1.

We have:

$$H_A\left(P_2\left\{K_3\right\}\right)=\frac{148}{3},H_A\left(P_3\left\{K_3\right\}\right)=\frac{313}{3}.$$

Based on Theorem 1, we obtain the next corollary immediately.

Corollary 1.

Let G be a r-regular graph and H be a k-regular rooted graph with w as its root. Then:

$$\begin{array}{cc}\hfill H_A\left(G\left\{H\right\}\right)& =2(r+k)H\left(G\right)+2k{n}_{G}H\left(H\right)+n_{G}r{H}_H\left(w\right)\hfill \\ & +2(r+2k)\sum _{\begin{array}{c}\{u,t\}\subseteq V\left(G\right)\\ u\ne t\end{array}}\sum _{v\in V\left(H\right)\setminus \left\{w\right\}}\frac{1}{d_G(u,t)+d_H(v,w)}\hfill \\ & +2k\sum _{\begin{array}{c}\{t,l\}\subseteq V\left(G\right)\\ t\ne l\end{array}}\sum _{\{u,v\}\subseteq V\left(H\right)\setminus \left\{w\right\}}\frac{1}{d_H(u,w)+d_H(v,w)+d_G(t,l)}.\hfill \end{array}$$

We can determine a lower and an upper bound for $H_A\left(G\left\{H\right\}\right)$, where G is a r-regular graph and H is a k-regular rooted graph.

We know that $1⩽d_G(u,v)⩽D\left(G\right)$, where $\{u,v\}\subseteq V\left(G\right)$, $u\ne v$ and $D\left(G\right)$ is the diameter of G. Similarly, we have $1⩽d_H(u,v)⩽D\left(H\right)$, where $\{u,v\}\subseteq V\left(H\right)$, $u\ne v$ and $D\left(H\right)$ is the diameter of H. Hence, we have:

$$\begin{array}{cc}\hfill H_A\left(G\left\{H\right\}\right)& \ge 2(r+k)H\left(G\right)+2k{n}_{G}H\left(H\right)+n_{G}r{H}_H\left(w\right)\hfill \\ & +n_G(n_G-1)(n_H-1)[\frac{r+2k}{D\left(H\right)+D\left(G\right)}+\frac{k(n_H-1)}{2D\left(H\right)+D\left(G\right)}],\hfill \\ \hfill H_A\left(G\left\{H\right\}\right)& \le 2(r+k)H\left(G\right)+2k{n}_{G}H\left(H\right)+n_{G}r{H}_H\left(w\right)\hfill \\ & +n_G(n_G-1)(n_H-1)[\frac{r+2k}{2}+\frac{k(n_H-1)}{3}].\hfill \end{array}$$

3.2. Corona

Definition 2.

Let G and H be two graphs. The corona product $G\circ H$ is obtained by taking one copy of G and $\left|V\right(G\left)\right|$ copies of H; and by joining each vertex of the i-th copy of H to the i-th vertex of G, $i=$ 1, 2, ..., $\left|V\right(G\left)\right|$.

For the corona product $G\circ H$, we have:

$$\left|V\right(G\circ H\left)\right|=\left|V\right(G\left)\right|(1+|V\left(H\right)\left|\right),\left|E\right(G\circ H\left)\right|=\left|E\right(G\left)\right|+\left|V\right(G\left)\right|\left(\right|V\left(H\right)|+|E\left(H\right)\left|\right).$$

As an example for the corona product see Figure 2.

Lemma 2.

Let G and H be two simple connected graphs. For a vertex u of $G\circ H$ such that $u\in V\left(G\right)$, we have ${\delta }_{G\circ H}\left(u\right)={\delta }_G\left(u\right)+\left|V\left(H\right)\right|$, and for a vertex v of $G\circ H$ such that $v\in V\left(H\right)$, we have ${\delta }_{G\circ H}\left(v\right)={\delta }_H\left(v\right)+1$. Also:

(1) 

if $u,v\in V\left(G\right)$, then $d_{G\circ H}(u,v)=d_G(u,v),$

(2) 

if $u\in V\left(G\right),v\in V\left(H_i\right)$, where $i=1,2,...,\left|V\right(G\left)\right|$, then $d_{G\circ H}(u,v)=d_G(u,w_i)+1$, where $w_i$ is the i-th vertex in G,

(3) 

if $u,v\in V\left(H_i\right)$, where $i=1,2,...,\left|V\right(G\left)\right|$, then:

$$d_{G\circ H}(u,v)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}uv\in E\left(H_i\right)\hfill \\ 2\hfill & \mathrm{if}uv\notin E\left(H_i\right)\hfill \end{array}\right.$$

(4) 

if $u\in V\left(H_i\right),v\in V\left(H_j\right)$ and $1⩽i<j⩽\left|V\right(G\left)\right|$, then $d_{G\circ H}(u,v)=d_G(w_i,w_j)+2$, where $w_i$ is the i-th and $w_j$ is the j-th vertices in G.

Proof. 

The proof is obvious. ☐

Lemma 3.

Let G be a simple graph and $K_2$ be the complete graph of order 2. Then:

$$H\left(G\left\{K_2\right\}\right)=H\left(G\right)+P\left(G\right)+\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{1}{d_G(u,v)+2}.$$

Proof. 

By definition:

$$H\left(G\left\{K_2\right\}\right)=\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\left\{K_2\right\}\right)\\ u\ne v\end{array}}\frac{1}{d_{G\left\{K_2\right\}}(u,v)}.$$

We partition the sum in the formula of $H\left(G\left\{K_2\right\}\right)$ into three sums $S_i$ such that $S_i$ is over $A_i$ for $i=$ 1, 2, 3, where:

• $A_1=\left\{(u,v)\right|u,v\in V\left(G\right)\}$,
• $A_2=\left\{(u,v)\right|u\in V\left(G\right),v\in V\left({\left(K_2\right)}_i\right)\setminus \left\{w_i\right\},1⩽i⩽|V\left(G\right)\left|\right\}$,
• $A_3=\left\{(u,v)\right|u\in V\left({\left(K_2\right)}_i\right)\setminus \left\{w_i\right\},v\in V\left({\left(K_2\right)}_j\right)\setminus \left\{w_j\right\},1⩽i<j⩽|V\left(G\right)\left|\right\}$,

where ${\left(K_2\right)}_i$ is the i-th copy of $K_2$ and ${\left(K_2\right)}_j$ is the j-th copy of $K_2$ in $G\left\{K_2\right\}$.

So we have:

$$\begin{array}{cc}\hfill H\left(G\left\{K_2\right\}\right)& =S_1+S_2+S_3\hfill \\ & =\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{1}{d_{G\left\{K_2\right\}}(u,v)}+\sum _{i=1}^{n_G}\sum _{\begin{array}{c}u\in V\left(G\right)\\ v\in V\left({\left(K_2\right)}_i\right)\setminus \left\{w_i\right\}\end{array}}\frac{1}{d_{G\left\{K_2\right\}}(u,v)}\hfill \\ & +\sum _{1⩽i<j⩽n_G}\sum _{\begin{array}{c}u\in V\left({\left(K_2\right)}_i\right)\setminus \left\{w_i\right\}\\ v\in V\left({\left(K_2\right)}_j\right)\setminus \left\{w_j\right\}\end{array}}\frac{1}{d_{G\left\{K_2\right\}}(u,v)}\hfill \\ & =\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{1}{d_G(u,v)}+\sum _{i=1}^{n_G}\sum _{u\in V\left(G\right)}\frac{1}{d_G(u,w_i)+1}+\sum _{1⩽i<j⩽n_G}\frac{1}{d_G(w_i,w_j)+2}\hfill \\ & =H\left(G\right)+P\left(G\right)+\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{1}{d_G(u,v)+2}.\hfill \end{array}$$

 ☐

Theorem 2.

Let G and H be simple graphs. Then:

$$\begin{array}{cc}\hfill H_A(G\circ H)& =H_A\left(G\right)+2n_H(1-2e_H-n_H)H\left(G\right)+2n_H(2e_H+n_H)H\left(G\left\{K_2\right\}\right)\hfill \\ & +\frac{n_G}{2}{M}_1\left(H\right)+[2e_H(1-2n_H)-n_H^2+n_H]P\left(G\right)\hfill \\ & +n_G{n}_H(e_H+\frac{n_H-1}{2})+n_H\sum _{\{u,v\}\subseteq V\left(G\right)}\frac{{\delta }_G\left(u\right)}{d_G(u,v)+1}.\hfill \end{array}$$

Proof. 

By definition we have:

$$H_A(G\circ H)=\sum _{\begin{array}{c}\{u,v\}\subseteq V(G\circ H)\\ u\ne v\end{array}}\frac{{\delta }_{G\circ H}\left(u\right)+{\delta }_{G\circ H}\left(v\right)}{d_{G\circ H}(u,v)}.$$

By Lemma 2, we partition the sum into four sums $S_i$, $i=1,2,3,4$. We consider four sums $S_1,S_2,S_3,S_4$ as follows:

$$\begin{array}{cc}\hfill S_1& =\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{{\delta }_{G\circ H}\left(u\right)+{\delta }_{G\circ H}\left(v\right)}{d_{G\circ H}(u,v)}=\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_G\left(v\right)+2\left|V\left(H\right)\right|}{d_G(u,v)}\hfill \\ & =H_A\left(G\right)+2n_{H}H\left(G\right)\hfill \\ \hfill S_2& =\sum _{i=1}^{\left|V\right(G\left)\right|}\sum _{\begin{array}{c}u\in V\left(G\right)\\ v\in V\left(H_i\right)\end{array}}\frac{{\delta }_{G\circ H}\left(u\right)+{\delta }_{G\circ H}\left(v\right)}{d_{G\circ H}(u,v)}=\sum _{i=1}^{n_G}\sum _{\begin{array}{c}u\in V\left(G\right)\\ v\in V\left(H_i\right)\end{array}}\frac{{\delta }_G\left(u\right)+\left|V\left(H\right)\right|+{\delta }_H\left(v\right)+1}{d_G(u,w_i)+1}\hfill \end{array}$$

Now we consider the following relation:

$$\begin{array}{cc}\hfill \sum _{\begin{array}{c}u\in V\left(G\right)\\ v\in V\left(H_i\right)\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_H\left(v\right)+n_H+1}{d_G(u,w_i)+1}& =\sum _{u\in V\left(G\right)}\frac{n_H{\delta }_G\left(u\right)+2e_H}{d_G(u,w_i)+1}+(n_H+1)n_H\sum _{u\in V\left(G\right)}\frac{1}{d_G(u,w_i)+1}\hfill \\ & =n_H\sum _{u\in V\left(G\right)}\frac{{\delta }_G\left(u\right)}{d_G(u,w_i)+1}+(2e_H+n_H^2+n_H)\sum _{u\in V\left(G\right)}\frac{1}{d_G(u,w_i)+1}\hfill \\ & =n_H\sum _{u\in V\left(G\right)}\frac{{\delta }_G\left(u\right)}{d_G(u,w_i)+1}+(2e_H+n_H^2+n_H)P_G\left(w_i\right).\hfill \end{array}$$

Hence, we have:

$$\begin{array}{cc}\hfill S_2& =\sum _{i=1}^{n_G}[n_H\sum _{u\in V\left(G\right)}\frac{{\delta }_G\left(u\right)}{d_G(u,w_i)+1}+(2e_H+n_H^2+n_H)P_G\left(w_i\right)]\hfill \\ & =n_H\sum _{\{u,v\}\subseteq V\left(G\right)}\frac{{\delta }_G\left(u\right)}{d_G(u,v)+1}+(2e_H+n_H^2+n_H)P\left(G\right)\hfill \\ \hfill S_3& =\sum _{i=1}^{\left|V\right(G\left)\right|}\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(H_i\right)\\ u\ne v\end{array}}\frac{{\delta }_{G\circ H}\left(u\right)+{\delta }_{G\circ H}\left(v\right)}{d_{G\circ H}(u,v)}=\sum _{i=1}^{n_G}\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(H_i\right)\\ u\ne v\end{array}}\frac{{\delta }_H\left(u\right)+{\delta }_H\left(v\right)+2}{d_{G\circ H}(u,v)}.\hfill \end{array}$$

Now we consider the following relation:

$$\begin{array}{cc}\hfill \sum _{\begin{array}{c}\{u,v\}\subseteq V\left(H\right)\\ u\ne v\end{array}}\frac{{\delta }_H\left(u\right)+{\delta }_H\left(v\right)+2}{d_{G\circ H}(u,v)}& =\sum _{uv\in E\left(H\right)}({\delta }_H\left(u\right)+{\delta }_H\left(v\right)+2)+\sum _{uv\notin E\left(H\right)}\frac{{\delta }_H\left(u\right)+{\delta }_H\left(v\right)+2}{2}\hfill \\ & =M_1\left(H\right)+\frac{1}{2}{\overline{M}}_1\left(H\right)+2\left|E\left(H\right)\right|+[\left(\genfrac{}{}{0pt}{}{\left|V\right(H\left)\right|}{2}\right)-\left|E\left(H\right)\right|]\hfill \\ & =\frac{1}{2}{M}_1\left(H\right)+n_H(e_H+\frac{n_H-1}{2}).\hfill \end{array}$$

Note that the last equality holds in view of the fact that ${\overline{M}}_1\left(H\right)=2e_H(n_H-1)-M_1\left(H\right)$. So:

$$\begin{array}{cc}\hfill S_3& =\sum _{i=1}^{n_G}[\frac{1}{2}{M}_1\left(H\right)+n_H(e_H+\frac{n_H-1}{2})]=n_G[\frac{1}{2}{M}_1\left(H\right)+n_H(e_H+\frac{n_H-1}{2})]\hfill \\ \hfill S_4& =\sum _{1⩽i<j⩽n_G}\sum _{\begin{array}{c}u\in V\left(H_i\right)\\ v\in V\left(H_j\right)\end{array}}\frac{{\delta }_{G\circ H}\left(u\right)+{\delta }_{G\circ H}\left(v\right)}{d_{G\circ H}(u,v)}=\sum _{1⩽i<j⩽n_G}\sum _{\begin{array}{c}u\in V\left(H_i\right)\\ v\in V\left(H_j\right)\end{array}}\frac{{\delta }_H\left(u\right)+{\delta }_H\left(v\right)+2}{d_G(w_i,w_j)+2}\hfill \end{array}$$

Now we consider the following relation, where $1⩽i<j⩽n_G$

$$\begin{array}{cc}\hfill \sum _{\begin{array}{c}u\in V\left(H_i\right)\\ v\in V\left(H_j\right)\end{array}}\frac{{\delta }_H\left(u\right)+{\delta }_H\left(v\right)+2}{d_G(w_i,w_j)+2}& =\frac{1}{d_G(w_i,w_j)+2}[\sum _{\begin{array}{c}u\in V\left(H_i\right)\\ v\in V\left(H_j\right)\end{array}}({\delta }_H\left(u\right)+{\delta }_H\left(v\right))+2n_H^2]=\frac{2n_H(2e_H+n_H)}{d_G(w_i,w_j)+2}\hfill \end{array}$$

By using Lemma 3 we have:

$$\begin{array}{cc}\hfill S_4& =2n_H(2e_H+n_H)\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{1}{d_G(u,v)+2}=2n_H(2e_H+n_H)[H\left(G\left\{K_2\right\}\right)-H\left(G\right)-P\left(G\right)].\hfill \end{array}$$

The result now follows by adding the four contributions and simplifying the expression. ☐

Example 2.

$$H_A(P_2\circ K_2)=\frac{148}{3},$$

$$H_A(P_3\circ K_2)=\frac{313}{3}.$$

We note that $P_2\circ K_2=P_2\left\{K_3\right\}$ and $P_3\circ K_2=P_3\left\{K_3\right\}$ and the result is similar to Example 1.

Corollary 2.

Let G be a r-regular graph and H be a simple graph. Then:

$$\begin{array}{cc}\hfill H_A(G\circ H)& =2[n_H(1-2e_H-n_H)+r]H\left(G\right)+[2e_H(1-2n_H)-n_H^2+n_H(r+1)]P\left(G\right)\hfill \\ & +\frac{n_G}{2}{M}_1\left(H\right)+2n_H(2e_H+n_H)H\left(G\left\{K_2\right\}\right)+n_G{n}_H(e_H+\frac{n_H-1}{2}).\hfill \end{array}$$

3.3. Splice

Definition 3.

For given vertices $y\in V\left(G\right)$ and $z\in V\left(H\right)$ the splice of G and H by vertices y and z, which is denoted by $(G·H)(y;z)$, is defined by identifying the vertices y and z in the union of G and H.

As an example for the splice of G and H see Figure 3.

Then for the splice of G and H by vertices y and z we have:

$$|V\left((G·H)(y;z)\right)|=|V\left(G\right)|+|V\left(H\right)|-1,|E\left((G·H)(y;z)\right)|=|E\left(G\right)|+|E\left(H\right)|.$$

Lemma 4.

Let G and H be simple graphs with disjoint vertex sets. For given vertices $y\in V\left(G\right)$ and $z\in V\left(H\right)$ suppose that the splice of G and H by vertices y and z is denoted by $G·H$ for convenience. Then for a vertex u of $G·H$ such that $u\in V\left(G\right)\setminus \left\{y\right\}$ we have ${\delta }_{G·H}\left(u\right)={\delta }_G\left(u\right)$ and for a vertex v of $G·H$ such that $v\in V\left(H\right)\setminus \left\{z\right\}$ we have ${\delta }_{G·H}\left(v\right)={\delta }_H\left(v\right)$ and ${\delta }_{G·H}\left(y\right)={\delta }_G\left(y\right)+{\delta }_H\left(z\right)={\delta }_{G·H}\left(z\right).$ Also:

(1) 

if $u,v\in V\left(G\right)$, then $d_{G·H}(u,v)=d_G(u,v),$

(2) 

if $u,v\in V\left(H\right)$, then $d_{G·H}(u,v)=d_H(u,v),$

(3) 

if $u\in V\left(G\right),v\in V\left(H\right)$, then $d_{G·H}(u,v)=d_G(u,y)+d_H(z,v).$

Proof. 

The proof is obvious. ☐

Theorem 3.

Let G and H be two simple graphs. For vertices $y\in V\left(G\right)$ and $z\in V\left(H\right)$, consider $(G·H)(y;z)$. Then:

$$\begin{array}{cc}\hfill H_A\left((G·H)(y;z)\right)& =H_A\left(G\right)+H_A\left(H\right)+{\delta }_H\left(z\right)H_G\left(y\right)\hfill \\ & +{\delta }_G\left(y\right)H_H\left(z\right)+\sum _{\begin{array}{c}u\in V\left(G\right)\setminus \left\{y\right\}\\ v\in V\left(H\right)\setminus \left\{z\right\}\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_H\left(v\right)}{d_G(u,y)+d_H(v,z)}.\hfill \end{array}$$

Proof. 

For convenience we denote $(G·H)(y;z)$ by $G·H$. By definition we have:

$$H_A(G·H)=\sum _{\begin{array}{c}\{u,v\}\subseteq V(G·H)\\ u\ne v\end{array}}\frac{{\delta }_{G·H}\left(u\right)+{\delta }_{G·H}\left(v\right)}{d_{G·H}(u,v)}.$$

We partition the sum into three sums $S_i$ such that $S_i$ is over $A_i$ for $i=1,2,3$, where $A_1=\left\{(u,v)\right|u,v\in V\left(G\right)\}$, $A_2=\left\{(u,v)\right|u,v\in V\left(H\right)\}$, $A_3=\left\{(u,v)\right|u\in V\left(G\right)\setminus \left\{y\right\},v\in V\left(H\right)\setminus \left\{z\right\}\}.$

So we have:

$$\begin{array}{cc}\hfill S_1& =\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{{\delta }_{G·H}\left(u\right)+{\delta }_{G·H}\left(v\right)}{d_{G·H}(u,v)}\hfill \\ & =\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\setminus \left\{y\right\}\\ u\ne v\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_G\left(v\right)}{d_G(u,v)}+\sum _{v\in V\left(G\right)\setminus \left\{y\right\}}\frac{{\delta }_G\left(y\right)+{\delta }_H\left(z\right)+{\delta }_G\left(v\right)}{d_G(y,v)}\hfill \\ & =H_A\left(G\right)+{\delta }_H\left(z\right)H_G\left(y\right).\hfill \end{array}$$

Similarly, we have $S_2=H_A\left(H\right)+{\delta }_G\left(y\right)H_H\left(z\right)$. Also:

$$\begin{array}{cc}\hfill S_3& =\sum _{\begin{array}{c}u\in V\left(G\right)\setminus \left\{y\right\}\\ v\in V\left(H\right)\setminus \left\{z\right\}\end{array}}\frac{{\delta }_{G·H}\left(u\right)+{\delta }_{G·H}\left(v\right)}{d_{G·H}(u,v)}=\sum _{\begin{array}{c}u\in V\left(G\right)\setminus \left\{y\right\}\\ v\in V\left(H\right)\setminus \left\{z\right\}\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_H\left(v\right)}{d_G(u,y)+d_H(v,z)}\hfill \end{array}$$

The result now follows by adding the three sums $S_i$, $i=1,2,3$. ☐

Corollary 3.

Let G be a r-regular graph and H be a k-regular graph. For vertices $y\in V\left(G\right)$ and $z\in V\left(H\right)$, consider $(G·H)(y;z)$. Then:

$$\begin{array}{cc}\hfill H_A\left((G·H)(y;z)\right)& =2rH\left(G\right)+2kH\left(H\right)+k{H}_G\left(y\right)\hfill \\ & +r{H}_H\left(z\right)+(r+k)\sum _{\begin{array}{c}u\in V\left(G\right)\setminus \left\{y\right\}\\ v\in V\left(H\right)\setminus \left\{z\right\}\end{array}}\frac{1}{d_G(u,y)+d_H(v,z)}.\hfill \end{array}$$

We can determine a lower and an upper bound for $H_A\left((G·H)(y;z)\right)$, where G and H are r-regular and k-regular graphs, respectively.

We know that $1⩽d_G(u,y)⩽D\left(G\right)$, where $u\in V\left(G\right)\setminus \left\{y\right\}$ and $D\left(G\right)$ is the diameter of G. Similarly, we have $1⩽d_H(v,z)⩽D\left(H\right)$, where $v\in V\left(H\right)\setminus \left\{z\right\}$ and $D\left(H\right)$ is the diameter of H. Hence, we have:

$$H_A\left((G·H)(y;z)\right)\ge 2rH\left(G\right)+2kH\left(H\right)+k{H}_G\left(y\right)+r{H}_H\left(z\right)+\frac{(r+k)(n_G-1)(n_H-1)}{D\left(G\right)+D\left(H\right)},$$

$$H_A\left((G·H)(y;z)\right)\le 2rH\left(G\right)+2kH\left(H\right)+k{H}_G\left(y\right)+r{H}_H\left(z\right)+\frac{(r+k)(n_G-1)(n_H-1)}{2}.$$

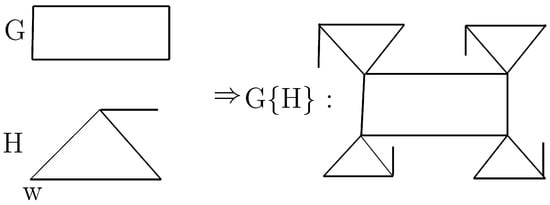
3.4. Link

Definition 4.

A link of G and H by vertices y and z, which is denoted by $(G\sim H)(y;z)$, is defined as the graph obtained by joining y and z by an edge in the union of these graphs.

As an example of the link of two graphs see Figure 4.

For a link of G and H by vertices y and z we have:

$$|V\left((G\sim H)(y;z)\right)|=|V\left(G\right)|+|V\left(H\right)|,|E\left((G\sim H)(y;z)\right)|=|E\left(G\right)|+|E\left(H\right)|+1.$$

Lemma 5.

Let G and H be two simple graphs with disjoint vertex sets. For given vertices $y\in V\left(G\right)$ and $z\in V\left(H\right)$ suppose a link of G and H by vertices y and z is denoted by $G\sim H$ for convenience. Then for a vertex u of $G\sim H$ such that $u\in V\left(G\right)\setminus \left\{y\right\}$ we have ${\delta }_{G\sim H}\left(u\right)={\delta }_G\left(u\right)$ and for a vertex v of $G\sim H$ such that $v\in V\left(H\right)\setminus \left\{z\right\}$ we have ${\delta }_{G\sim H}\left(v\right)={\delta }_H\left(v\right)$ and ${\delta }_{G\sim H}\left(y\right)={\delta }_G\left(y\right)+1,{\delta }_{G\sim H}\left(z\right)={\delta }_H\left(z\right)+1$. Also:

(1) 

if $u,v\in V\left(G\right)$, then $d_{G\sim H}(u,v)=d_G(u,v)$,

(2) 

if $u,v\in V\left(H\right)$, then $d_{G\sim H}(u,v)=d_H(u,v)$,

(3) 

if $u\in V\left(G\right),v\in V\left(H\right)$, then $d_{G\sim H}(u,v)=d_G(u,y)+d_H(z,v)+1.$

Proof. 

The proof is straightforward. ☐

Theorem 4.

Let G and H be two simple graphs. For vertices $y\in V\left(G\right)$ and $z\in V\left(H\right)$, consider $(G\sim H)(y;z)$. Then:

$$\begin{array}{cc}\hfill H_A\left((G\sim H)(y;z)\right)& =H_A\left(G\right)+H_A\left(H\right)+H_G\left(y\right)+H_H\left(z\right)\hfill \\ & +({\delta }_H\left(z\right)+1)(P_G\left(y\right)-1)+({\delta }_G\left(y\right)+1)(P_H\left(z\right)-1)\hfill \\ & +{\delta }_G\left(y\right)+{\delta }_H\left(z\right)+2+\sum _{\begin{array}{c}u\in V\left(G\right)\setminus \left\{y\right\}\\ v\in V\left(H\right)\setminus \left\{z\right\}\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_H\left(v\right)}{d_G(u,y)+d_H(v,z)+1}\hfill \\ & +\sum _{u\in V\left(G\right)\setminus \left\{y\right\}}\frac{{\delta }_G\left(u\right)}{d_G(u,y)+1}+\sum _{v\in V\left(H\right)\setminus \left\{z\right\}}\frac{{\delta }_H\left(v\right)}{d_H(v,z)+1}.\hfill \end{array}$$

Proof. 

For convenience we denote $(G\sim H)(y;z)$ by $G\sim H$. By definition we have:

$$H_A(G\sim H)=\sum _{\begin{array}{c}\{u,v\}\subseteq V(G\sim H)\\ u\ne v\end{array}}\frac{{\delta }_{G\sim H}\left(u\right)+{\delta }_{G\sim H}\left(v\right)}{d_{G\sim H}(u,v)}.$$

Similarly to the proof of Theorem 3, we partition the sum into three sums $S_i$ such that $S_i$ is over $A_i$ for $i=1,2,3$, where:

• $A_1=\left\{(u,v)\right|u,v\in V\left(G\right)\}$,
• $A_2=\left\{(u,v)\right|u,v\in V\left(H\right)\}$,
• $A_3=\left\{(u,v)\right|u\in V\left(G\right),v\in V\left(H\right)\}.$

We consider three sums $S_1$, $S_2$, $S_3$ as follows:

$$\begin{array}{cc}\hfill S_1& =\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\\ u\ne v\end{array}}\frac{{\delta }_{G\sim H}\left(u\right)+{\delta }_{G\sim H}\left(v\right)}{d_{G\sim H}(u,v)}\hfill \\ & =\sum _{\begin{array}{c}\{u,v\}\subseteq V\left(G\right)\setminus \left\{y\right\}\\ u\ne v\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_G\left(v\right)}{d_G(u,v)}+\sum _{u\in V\left(G\right)\setminus \left\{y\right\}}\frac{{\delta }_G\left(u\right)+{\delta }_G\left(y\right)+1}{d_G(u,y)}\hfill \\ & =H_A\left(G\right)+H_G\left(y\right).\hfill \end{array}$$

Similarly, we have $S_2=H_A\left(H\right)+H_H\left(z\right)$. Also:

$$\begin{array}{cc}\hfill S_3& =\sum _{\begin{array}{c}u\in V\left(G\right)\\ v\in V\left(H\right)\end{array}}\frac{{\delta }_{G\sim H}\left(u\right)+{\delta }_{G\sim H}\left(v\right)}{d_{G\sim H}(u,v)}\hfill \\ & =\sum _{\begin{array}{c}u\in V\left(G\right)\setminus \left\{y\right\}\\ v\in V\left(H\right)\setminus \left\{z\right\}\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_H\left(v\right)}{d_G(u,y)+d_H(v,z)+1}+\sum _{u\in V\left(G\right)\setminus \left\{y\right\}}\frac{{\delta }_G\left(u\right)+{\delta }_H\left(z\right)+1}{d_G(u,y)+1}\hfill \\ & +\sum _{v\in V\left(H\right)\setminus \left\{z\right\}}(\frac{{\delta }_G\left(y\right)+{\delta }_H\left(v\right)+1}{d_H(v,z)+1})+{\delta }_G\left(y\right)+{\delta }_H\left(z\right)+2\hfill \\ & =\sum _{\begin{array}{c}u\in V\left(G\right)\setminus \left\{y\right\}\\ v\in V\left(H\right)\setminus \left\{z\right\}\end{array}}\frac{{\delta }_G\left(u\right)+{\delta }_H\left(v\right)}{d_G(u,y)+d_H(v,z)+1}+{\delta }_G\left(y\right)+{\delta }_H\left(z\right)+2\hfill \\ & +\sum _{u\in V\left(G\right)\setminus \left\{y\right\}}\frac{{\delta }_G\left(u\right)}{d_G(u,y)+1}+({\delta }_H\left(z\right)+1)(P_G\left(y\right)-1)\hfill \\ & +\sum _{v\in V\left(H\right)\setminus \left\{z\right\}}\frac{{\delta }_H\left(v\right)}{d_H(v,z)+1}+({\delta }_G\left(y\right)+1)(P_H\left(z\right)-1).\hfill \end{array}$$

We obtain the result by adding the three sums $S_i$, $i=1,2,3$. ☐

Corollary 4.

Let G be a r-regular graph and H be a k-regular graph. For vertices $y\in V\left(G\right)$ and $z\in V\left(H\right)$, consider $(G\sim H)(y;z)$. Then:

$$\begin{array}{cc}\hfill H_A\left((G\sim H)(y;z)\right)& =2rH\left(G\right)+2kH\left(H\right)+H_G\left(y\right)+H_H\left(z\right)\hfill \\ & +(k+r+1)[P_G\left(y\right)+P_H\left(z\right)-1]+1\hfill \\ & +(k+r)\sum _{\begin{array}{c}u\in V\left(G\right)\setminus \left\{y\right\}\\ v\in V\left(H\right)\setminus \left\{z\right\}\end{array}}\frac{1}{d_G(u,y)+d_H(v,z)+1}.\hfill \end{array}$$

Similarly, we can determine a lower and an upper bound for $H_A\left((G\sim H)(y;z)\right)$, where G and H are r-regular and k-regular graphs, respectively.

We know that $1⩽d_G(u,y)⩽D\left(G\right)$, where $u\in V\left(G\right)\setminus \left\{y\right\}$ and $D\left(G\right)$ is the diameter of G. Similarly, we have $1⩽d_H(v,z)⩽D\left(H\right)$, where $v\in V\left(H\right)\setminus \left\{z\right\}$ and $D\left(H\right)$ is the diameter of H. So we have:

$$\begin{array}{cc}\hfill H_A\left((G\sim H)(y;z)\right)& \ge 2rH\left(G\right)+2kH\left(H\right)+H_G\left(y\right)+H_H\left(z\right)\hfill \\ & +(r+k+1)[P_G\left(y\right)+P_H\left(z\right)-1]+1+\frac{(r+k)(n_G-1)(n_H-1)}{D\left(G\right)+D\left(H\right)+1},\hfill \\ \hfill H_A\left((G\sim H)(y;z)\right)& \le 2rH\left(G\right)+2kH\left(H\right)+H_G\left(y\right)+H_H\left(z\right)\hfill \\ & +(r+k+1)[P_G\left(y\right)+P_H\left(z\right)-1]+1+\frac{(r+k)(n_G-1)(n_H-1)}{3}.\hfill \end{array}$$

Remark 1.

From the definition of $H\left(G\right)$ and $P\left(G\right)$, it is obvious that the complete graph has the largest $H\left(G\right)$ and $P\left(G\right)$ among all graphs on the same number of vertices. So, for any graph G on n vertices we have $H\left(G\right)\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)$ and $P\left(G\right)\le \left(\genfrac{}{}{0pt}{}{n}{2}\right)+n$. Also, from the fact that adding an edge to G will increase its additively weighted Harary index, it immediately follows that the complete graph has the largest $H_A\left(G\right)$ among all graph on the same number of vertices. Hence, for any graph G on n vertices we have $H_A\left(G\right)\le n{(n-1)}^2$.

From the above remark, we obtain the next corollaries immediately.

Corollary 5.

Let G be a r-regular graph and H be a k-regular rooted graph. Then:

$$\begin{array}{cc}\hfill H_A\left(G\left\{H\right\}\right)& \le (r+1)[r(r+k)+k^2(k+1)]\hfill \\ & +rk(r+1)[1+\frac{r+2k}{2}+\frac{k^2}{3}].\hfill \end{array}$$

Corollary 6.

Let G be a r-regular graph and H be a k-regular graph. Then:

$$\begin{array}{cc}\hfill H_A\left((G·H)(y;z)\right)& \le (r+1)r^2+(k+1)k^2+rk[2+\frac{r+k}{2}],\hfill \\ \hfill H_A\left((G\sim H)(y;z)\right)& \le (r+1)r^2+(k+1)k^2+\frac{1}{3}rk(r+k)\hfill \\ & +\frac{1}{2}(r+k+1)[(r+1)(r+2)+(k+1)(k+2)].\hfill \end{array}$$

4. Conclusions

In this paper we have investigated the additively weighted Harary index for some graph products such as splice, link, corona and rooted product. Also we have determined lower and upper bounds for some of them.