Abstract
The main objective of this paper is to generalize the Extended Irreversible Thermodynamics in order to include the anomalous transport in systems in non-equilibrium conditions. Considering the generalized entropy, the corresponding flux and entropy production, and using the time fractional derivative, we have derived a space-time generalized telegrapher’s equation with a fractional nested hierarchy which can be used in separate developments for the mass transport, for the heat conduction and for the flux of ions. We have obtained a new formalism which includes the contribution of fast of higher-order fluxes in the mesoscopic and inhomogeneous media. The results take the form of continued fraction expansions. The balance equations are used in a scheme of continued fractions, and they appear as a closure condition. In this way the transport equation and its corresponding wave number-frequency relation are obtained, both of them in the mathematical structure of the continued fraction scheme. Numerical examples are included to show the dispersive nature of the solutions, and the generalized fractional transport equation in the same mathematical form, which can be applied to the mass transport, the heat conduction and the flux of ions.
Keywords:
transport phenomena; anomalous transport; continued fraction; Extended Irreversible Thermodynamics PACS:
05.60.Cd; 05.70.Ln; 47.10.A; 44.10.+i
1. Introduction
The constitutive equations in the Linear Irreversible Thermodynamic (LIT) framework valid under macroscopic conditions are the basic relations ruling the transport of chemical species by diffusion, ion transport, and heat flux. They are the so-called Fick, Nernst-Planck and Fourier equations, respectively, that relate linearly the fluxes and the driving forces in non-equilibrium systems [1].
The Maxwell-Cattaneo (MC) equation generalizes the constitutive relations of LIT, considering a relaxation process with a perturbation with finite velocity of propagation. The MC equation, considers fast phenomena in which the relaxation effect takes into account the time derivative of the flux in the constitutive equation. This generalization leads to a hyperbolic transport equation instead of the parabolic one [2]. As an example, the non-local time constitutive equations for the heat flux and phonon hydrodynamics in nanosytems have been presented by Cimmelli, Sellitto and Jou [3].
A further advance was introduced by the Extended Irreversible Thermodynamics (EIT) considering the coupling between forces and fluxes of different tensorial order (beyond the Curie principle). So far, two generalizations were proposed in the EIT [4], each one supported by a different scheme: one is the delayed flux-force relation (MC), and the second is the introduction of nonlocal transport theory with higher-order fluxes as variables. The former includes the evolution of the new variables introduced in the physical description to include properties of phenomena related to both, the long-time and the short-time regimes. In the long-time limit, we recover the mean-square displacement of particle diffusion, which is a characteristic of the normal hydrodynamics as expected. In the short-time behavior case the formalism is comparable to the generalized hydrodynamics, which leads to non-local diffusion equations. On the other hand, the introduction of the higher-order fluxes as variables includes deviation as it was reported at a mesoscopic scale phenomena description. As is well known, this approach can be expressed as the continued fraction formalism to account the nonlocal contributions [5].
Fractional diffusion equations have been worked out by several authors as Wyss [6], Schneider and Wyss [7], Fujita [8,9]. After this, fractional diffusion equations with random initial conditions have been analyzed in the paper of Anh and Leonenko [10]. The study of fractional diffusion equations has been motivated by the analysis of thermal diffusion in fractal media by Saichev and Zaslavsky [11].
Regarding the formulation of fractional transport addressed within the continuous time random walk (CTRW) formalism [12], it introduces correlated steps in the diffusive limit, and in the absence of any external field driving the walker [13]. Klafter and Sokolov have remarked that many anomalous phenomena described by the fractional dynamics are usually experimentally observed [14]. Viscoelastic relaxation [15], transient photocurrent [13] and dielectric relaxation [16] in amorphous materials show anomalous transport properties ruled by an anomalous dispersion of the transit-time.
One attempt to give physical grounds for the time-fractional transport equation was the work of Compte and Metzler [17]. Notably, Metzler et al. [18] had presented the underlined mathematical of fractional dynamic equation, assuming that the long waiting times are the central key in the description of anomalous relaxation and transport processes.
During the last decade, a number of works have appeared in the mathematics literature, particularly those of Orshinger and collaborators, analyzing mathematical and other formal properties of the fractional transport equation. The fundamental solutions of the fractional telegraph equation were considered by Orsingher and Zhao [19], and Orsingher and Beghin [20], in particular the Brownian motion modification for the derivative ½-order. Masoliver generalize the telegrapher´s equation from the formalism of the persistent random walk in continuous time [21]. Khamzin, Popov, and Nigmatullin [22], have done the fractal correction for the ion conductivity transport theory.
Anomalous diffusion models have been described as non-stationarity, non-ergodic and ageing using a fractional dynamics [23]. A foundation on microscopic dynamics within the Langevin picture sheds some light on the coming into existence of fractional dynamics as is shown in the paper of Metzler and Klafter. They pointed out that anomalous diffusion is intimately connected with the breakdown of the central limit theorem caused by either broad distribution or long-range correlation [24].
Furthermore, it has been discussed that the fractional equations set in an ad hoc fashion by replacing the ordinary derivatives that appear in the heat transport by fractional derivatives, describe anomalous transport equations, as it is obtained by using the formalism of the persistent random walk in continuous time [25].
In the case of forced diffusion of transport of chemical species in a porous media considering the basic relation ruling in the Darcy equation, it has been shown that the mass transport of fluid particles across a porous media is related to the description with fractional time derivatives [26,27]. This is, in turn, an example of a hierarchical dynamic property, which may be applied at several different scales, including large scales, as shown in the thermodynamically constrained averaging [28,29].
One of the aims of this work is to show that transport phenomena of mass, heat and ions can be described with the same formalism. With this objective, we consider the EIT framework is its broadest form, in which temporal delay in the fluxes and higher-order coupling fluxes are involved, in a simplified form that has been used with good results and referred as the asymptotic approximation.
Another of the aims of this paper is to show that Brownian processes are governed by time-fractional telegraph equations, and to obtain their Fourier-Laplace transformed solutions. In fact, we have generalized such equation to account the anomalous transport in three dimensions. From here, we were able to obtain transport coefficients in terms of continued fractions, and also we were able to explicitly obtain the relation for , which drive the underlying dynamics in systems that show anomalous behavior, and where we have obtained analytic expressions and plots for transport coefficients. Finally, we can mention that this kind of results are not usually reported in the literature.
2. Methods
In this section, we propose a methodology consisting in including an infinite number of fluxes a priori in the description, which is necessary in the mesoscopic scale. Additionally, most of these extra variables are then eliminated by introducing an asymptotic assumption with an effective relaxation time, which takes into account their contribution in a statistical sense. Such a reduction in the number of variables is finally needed, as we wish to compare with experimental results, usually described by a limited number of variables.
As a starting point, we consider the balance law for the specific internal energy, with no velocity fields. So far, we have taken as non-equilibrium variables and their fluxes as the heat flux, electrical conduction and the mass diffusion transport [30], see Table 1.

Table 1.
The elements of the theory, such as the fluxes, the variables and the balance equations are summarized. u is the internal energy, ρ is the density, Cp the specific heat capacity, μ is the chemical potential, and μk is the electrical chemical potential.
The general form of the internal energy balance equation can be written as,
where could be any of the following fluxes , and ρ is the density.
The balance law for the entropy is:
where the entropy production is .
In the non-equilibrium extended thermodynamic, there have been selected as the extra variables the heat flux, the mass flux and the electric current. However, there exists no restriction on extending the space of variables by including a whole hierarchy of new quantities obeying linear laws, and considering different time derivatives into the linear evolution equations. Then, it is sufficient to base a mesoscopic description exclusively on the conserved variables, plus the usual dissipative fluxes.
Now, from the material derivative of the Gibbs equation (up to the nth-order moment in the fluxes) we have,
Also, we express the entropy flux in terms of the nth-order moment of the fluxes,
In this way, we can obtain an expression for the entropy production from Equation (2) as follow,
Substituting Equation (1) in the previous one, and after rearranging in a sum, we obtain [4]
From the entropy production, we can write down a set of evolution equations for the fluxes,
In order that the entropy production is positive, then we consider . Defining we can recast the set of equations as,
with . Furthermore, in Equation (9) represents any of the three transport coefficients: thermal conductivity, diffusion coefficient or the electric conductivity and .
In the next section, we will apply the fractional derivative to the set of equations for the fluxes in order to find a result in terms of continued fractions.
3. Results
So far, we have found a hierarchy of differential equations describing the transient flows with contributions from higher-order derivatives, in order to include the molecular dynamics of unconventional contributions from rapid processes.
We consider the Fourier transform for fractional derivatives [31,32,33],
We now apply Equation (11), to the next system of equation for the fluxes,
where is the flux of . Note that relaxation times have changed consistently with the change introduced by the fractional time derivative. Therefore, the time scale has been affected by the modification in the exponent . Also, note that the constant term in Equation (11), is taken to be zero, since it is considered that there is no variation of the fluxes at initial time. The Fourier transform is not convergent when the tends to steady , and the fluxes would tend to constants [34]. It is noteworthy that the initial condition , the condition gas relaxed and when the initiation happens at , the Fourier transform explicitly involves initial values.
Now we apply the Fourier transform, and calculate some terms explicitly,
From Equation (17),
By substituting Equation (18) on Equation (16), we obtain,
Now, substituting Equation (19) on Equation (15)
and finally, substituting Equation (20) on Equation (14)
We can define , and taking
with the generalized transport coefficient. Finally, we can obtain
Now, introducing the asymptotic assumption, this allows including an infinite number of higher-order fluxes in the following way. Let us define by
Then the recurrent form for is introduced in such a way that it is renormalized into , as we state in the following equation:
in which we introduce the asymptotic approximations and , that are the limits of the characteristic relaxation time and characteristic length respectively.
Solving for the renormalized expression, it results in
And writing for
In Figure 1 we plot the generalized transport coefficient in Equation (27), considering the wave number k as a constant.
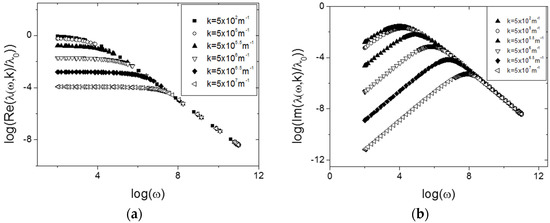
Figure 1.
Variation of the generalization of the transport coefficient from Equation (27) with several constant values of the wave number k: (a) Real part of ; (b) Imaginary part of . The parameters values are: , in the units which correspond to the considered flux, m, and s.
In order to plot the Equation (27) for a general case, we first have to obtain the diffusion relation, what we will do in the next subsection.
The Relation
In the asymptotic limit, we finally obtain an expression for the diffusion relationship
And using Equation (30), the relation becomes,
From this expression, the wavenumber in terms of the frequency and the model parameters are obtained. In this way, the real and imaginary parts of the wave number are plotted and showed in the Figure 2.
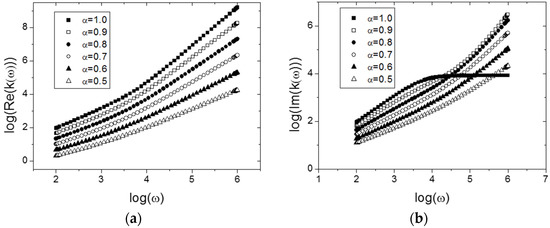
Figure 2.
Plot of the wave number relation obtained from Equation (31) for several values of : (a) Real part of ; (b) Imaginary part of . The parameter values are: in the units which correspond to the considered flux, m, and s.
As we can see in Figure 2b, we have a limit behavior of the imaginary part of the relation. In order to clarify such characteristic in Figure 3 we plot Equation (31) for several values of the -parameter, from 0.96 to 1.0.
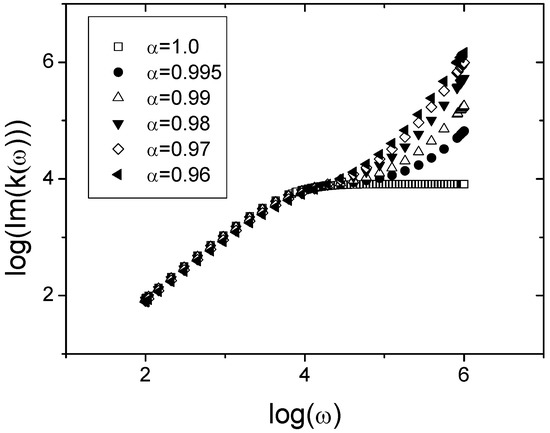
Figure 3.
Plot of the limit behavior of the imaginary part of from Equation (31), for values of near to 1.0. The parameter values are: in the units which correspond to the considered flux, m, and s.
In Figure 4, we present the plots of the generalization of the transport coefficient in Equation (27) and using the relation from Equation (31).
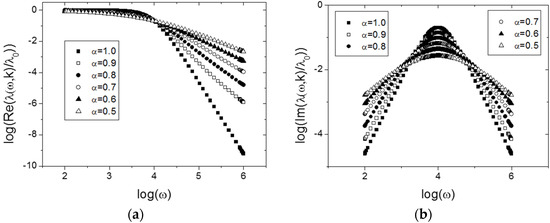
Figure 4.
Variation of the generalization of the transport coefficient from Equation (27) for several values of , and with the relation in Equation (31): (a) real part of ; (b) imaginary part of . The parameters are the same as in Figure 2.
We devote the next section to a discussion of the presented results.
4. Discussion
We have shown that mass diffusion in mesoscopic media, ion conduction in complex media, porous media systems and thermal energy transfer in amorphous solids at nano-scales are similar phenomena, while they are treated with the same formalism. This formalism can be used for larger scales and with multiphase systems [35].
So, they are properly modeled for high and low frequencies as a suitable extension of linear and Extended Irreversible Thermodynamics for transport equation in terms of fractional derivatives. Such extension relies on the long-tail properties of the time delay of the constitutive equation in the relation of forces and their fluxes, including the higher-order contributions in a coupled hierarchy of non-local thermodynamics to describe the spatial and temporal evolution of anomalous phenomena, observed at the mesoscale on complex heterogeneous materials.
The results for the dynamical hierarchy are given in Equations (12) and (13), and their Laplace-Fourier transformation are given in Equation (23). This expression is simplified by renormalized the continued fraction expansion making an assumption through the asymptotic approximation, which leads to our main result in a closed form in Equation (27), giving the generalized properties for the thermal conductivity, the diffusion coefficient and the ion conductivity, in terms of the frequency and the wave number. Note that this Equation (27) is accompanied by another result that expresses the relation, whereby the model is finally completed.
In this paper, we included a numerical estimation of the obtained results. In fact, the real and imaginary parts of the generalized transport coefficient are shown graphically in Figure 1, for several values of the wave number. In Figure 2, the real and imaginary parts of the wave number are observed for six different values of the -parameter (Equation (11)). An interesting result for the imaginary part for the wave number when -parameter is near to one is described in Figure 3. Finally, the complete results for the generalized transport coefficient are shown in the Figure 4.
5. Conclusions
We have obtained a hierarchy of differential equations with fractional derivatives to describe transient anomalous effects on flows, considering contributions of the dynamics of rapid effects present at the mesoscopic scale.
We considered the asymptotic approximation of the values of the relaxation times for the different relaxation processes, by obtaining a closed transport coefficient expression for thermal conductivity, for diffusion coefficient and for electrical conductivity.
Finally, we obtained the wave number-frequency relation and it was graphically expressed in terms of fractional exponents.
Acknowledgments
We thank UNAM-DGAPA-PAPIIT project IG 100315. SIH is grateful to UNAM-DGAPA-PAPIIT project IN113415 and project IN116617, and to DGTIC-UNAM project SC16-1-IR-113.
Author Contributions
All authors contributed equally on writing this paper. All authors have read and have approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; North-Holland Publishing Company: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Dedeurwaerdere, T.; Casas-Vázquez, J.; Jou, D.; Lebon, G. Foundation and application of a mesoscopic thermodynamic theory of fast phenomenon. Phys. Rev. E 1996, 53, 498–506. [Google Scholar] [CrossRef]
- Cimmelli, V.A.; Sellitto, A.; Jou, D. Nonequilibrium temperatures, heat waves, and nonlinear heat transport equations. Phys. Rev. B 2010, 81, 054301. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 4th ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Boon, J.P.; Yip, S. Molecular Hydrodynamics; Dover Publications: New York, NY, USA, 1991. [Google Scholar]
- Wyss, W. Fractional diffusion equation. J. Math. Phys. 1986, 27, 2782–2785. [Google Scholar] [CrossRef]
- Schneider, W.R.; Wyss, W. Fractional diffusion and wave equations. J. Math. Phys. 1989, 30, 134–144. [Google Scholar] [CrossRef]
- Fujita, Y. Integrodifferential equation which interpolates the heat equation and the wave equation (I). Osaka J. Math. 1990, 27, 309–321. [Google Scholar]
- Fujita, Y. Integrodifferential equation which interpolates the heat equation and the wave equation (II). Osaka J. Math. 1990, 27, 797–804. [Google Scholar]
- Anh, V.V.; Leonenko, N.N. Scaling laws for fractional diffusion-wave equation with singular data. Stat. Probab. Lett. 2000, 48, 239–252. [Google Scholar] [CrossRef]
- Saichev, A.I.; Zaslavsky, G.M. Fractional kinetic equations: solutions and applications. Chaos 1997, 7, 753–764. [Google Scholar] [CrossRef] [PubMed]
- Montroll, E.W.; Scher, H. Random walks on lattices. IV. Continuous-time walks and influence of absorbing boundaries. J. Stat. Phys. 1973, 9, 101. [Google Scholar] [CrossRef]
- Scher, H.; Montroll, E.W. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 1975, 12, 2455. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. Anomalous diffusion spreads its wings. Phys. World 2005, 18, 29–32. [Google Scholar] [CrossRef]
- Lazopoulos, K. Non-local continuum mechanics and fractional calculus. Mech. Res. Commun. 2006, 33, 753–757. [Google Scholar] [CrossRef]
- Khamzin, A.A.; Nigmatullin, R.R.; Popov, I.I. Description of the anomalous dielectric relaxation in disordered systems in the frame of the Mori-Zwanzig formalism. J. Phys. Conf. Ser. 2012, 394, 012013. [Google Scholar] [CrossRef]
- Metzler, R.; Compte, A. Stochastic foundation of normal and anomalous Cattaneo-type transport. Phys. A 1999, 268, 454. [Google Scholar] [CrossRef]
- Metzler, R.; Nonnenmacher, T.F. Fractional diffusion, waiting-time distributions, and Cattaneo-type equations. Phys. Rev. E 1998, 57, 6409. [Google Scholar] [CrossRef]
- Orsingher, E.; Zhao, X. The space-fractional telegraph equation and the related fractional telegraph process. Chin. Ann. Math. 2003, 24, 1. [Google Scholar] [CrossRef]
- Orsingher, E.; Beghin, L. Time-fractional telegraph equations and telegraph processes with Brownian time. Probab. Theor. Relat. Fields 2004, 128, 141. [Google Scholar]
- Masoliver, J. Fractional telegrapher’s equation from fractional persistent random walks. Phys. Rev. E 2016, 93, 052107. [Google Scholar] [CrossRef] [PubMed]
- Khamzin, A.A.; Popov, I.I.; Nigmatullin, R.R. Correction of the power law of ac conductivity in ion-conducting materials due to the electrode polarization effect. Phys. Rev. E 2014, 89, 032303. [Google Scholar] [CrossRef] [PubMed]
- Meztler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Zingales, M. Fractional-order theory of heat transport in rigid bodies. Commun. Nonlinear Sci. Numer. Simulat. 2014, 19, 3938–3953. [Google Scholar] [CrossRef]
- Deseri, L.; Zingales, Z. A mechanical picture of fractional-order Darcy equation. Commun. Nonlinear Sci. Numer. Simulat. 2015, 20, 940–949. [Google Scholar] [CrossRef]
- Ochoa-Tapia, J.A.; Valdés-Parada, F.J.; Alvarez-Ramirez, J. A fractional-order Darcy’s law. Phys. A 2007, 374, 1–14. [Google Scholar] [CrossRef]
- Gray, W.G.; Miller, C.T. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 1. Motivation and overview. Adv. Water Resour. 2005, 28, 161–180. [Google Scholar] [CrossRef]
- Gray, W.G.; Miller, C.T. Introduction to the Thermodynamically Constrained Averaging Theory for Porous Medium Systems; Springer: New York, NY, USA, 2014. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- García-Bernabé, A.; Sanchis, M.J.; Díaz-Calleja, R.; del Castillo, L.F. Fractional Fokker-Planck equation approach for the interconversion between dielectric and mechanical measurements. J. Appl. Phys. 2009, 106, 014912. [Google Scholar] [CrossRef]
- Garcia-Bernabé, A.; Lidón-Roger, J.V.; Sanchis, M.J.; Díaz-Calleja, R.; del Castillo, L.F. Interconversion algorithm between mechanical and dielectric relaxation measurements for acetate of cis- and trans-2-phenyl-5-hydroxymethyl-1,3-dioxane. Phys. Rev. E 2015, 92, 042307–042315. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Grosso, C.; Moroni, S.; Pastore-Parravicini, G. The ordinary and matrix continued fractions in the theoretical analysis of Hermitian and relaxation operators. Appl. Num. Math. 1988, 4, 273–295. [Google Scholar] [CrossRef]
- Li, S.; Cao, B. Generalized variational principles for heat conduction models based on Laplace transforms. Int. J. Heat Mass Transfer. 2016, 103, 1176–1180. [Google Scholar]
- Jackson, A.S.; Rybak, I.; Helmig, R.; Gray, W.G.; Miller, C.T. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 9. Transition region models. Adv. Water Resour. 2012, 42, 71–90. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).