Analysis of Dynamics in Multiphysics Modelling of Active Faults
Abstract
:1. Introduction
2. Materials and Methods
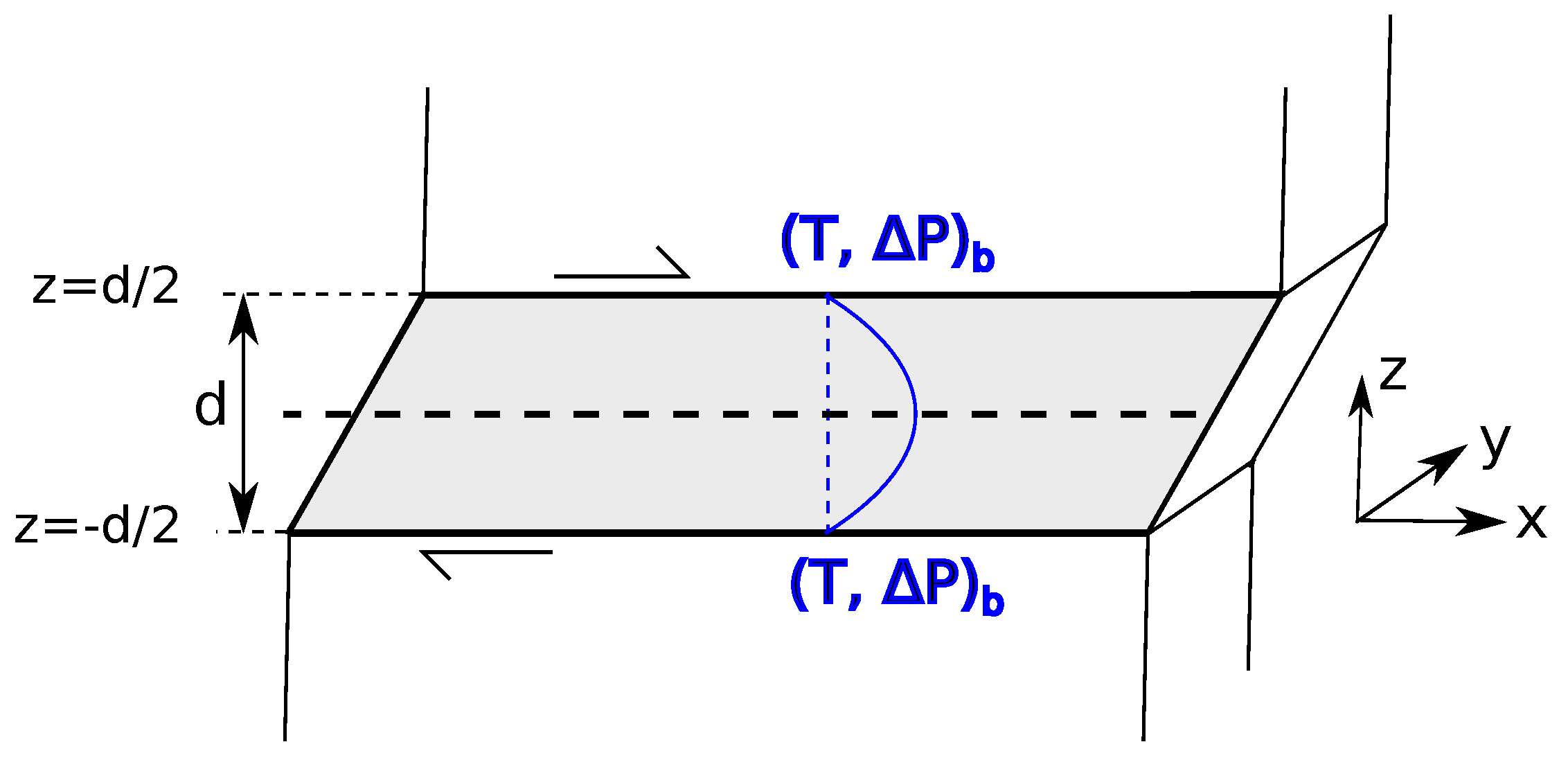
2.1. Problem Formulation—Previous Work
2.2. Method
3. Results
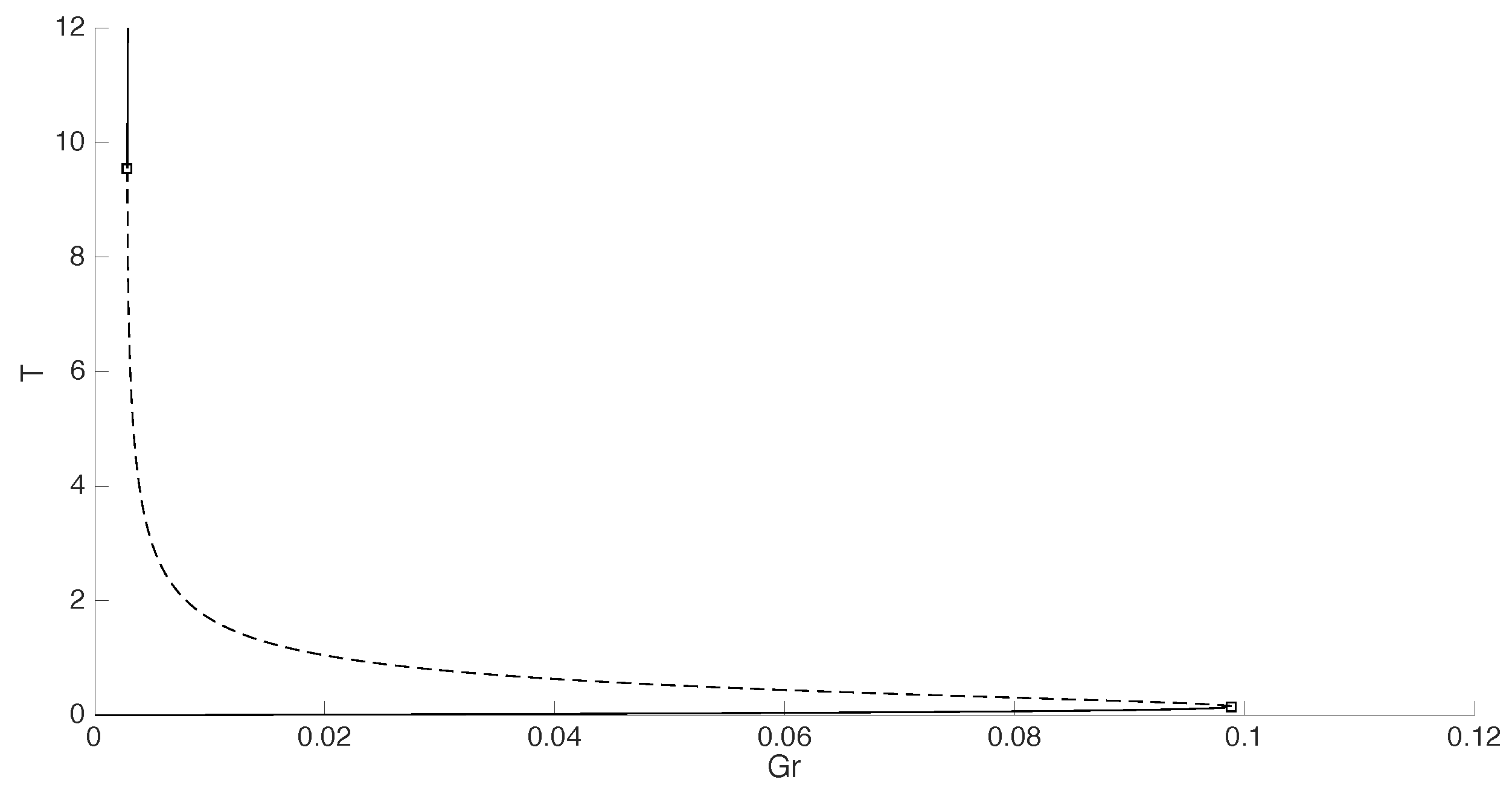
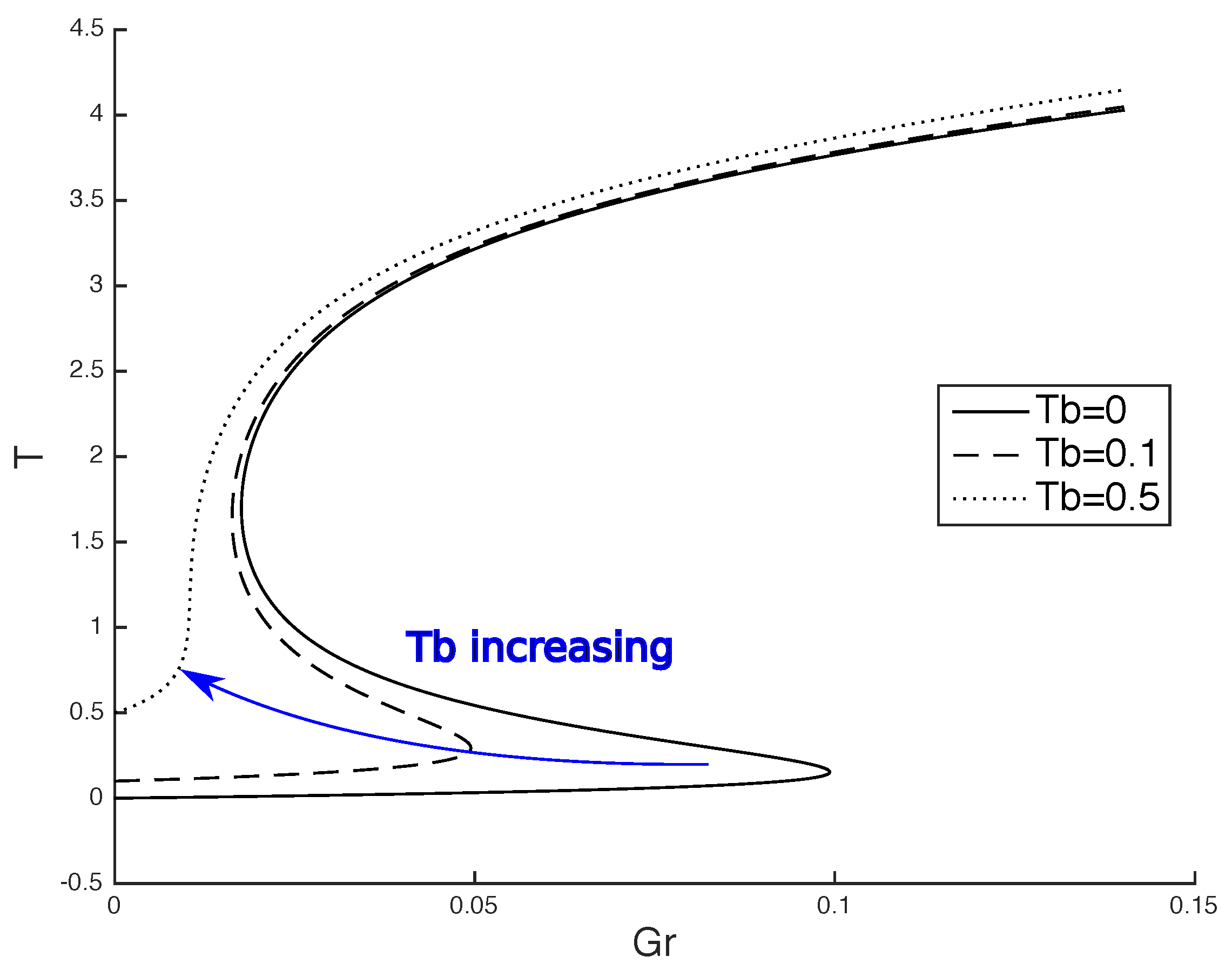
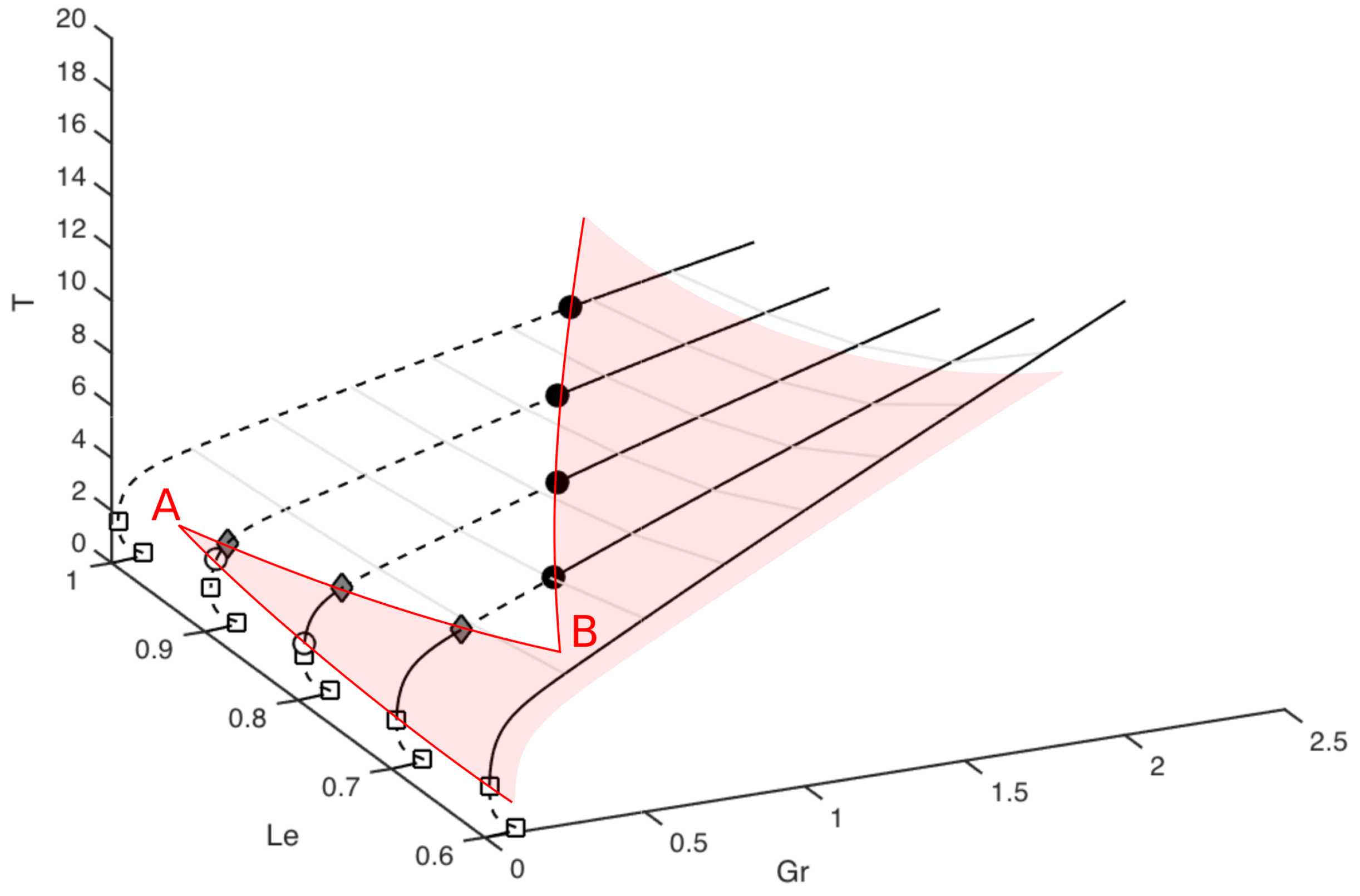
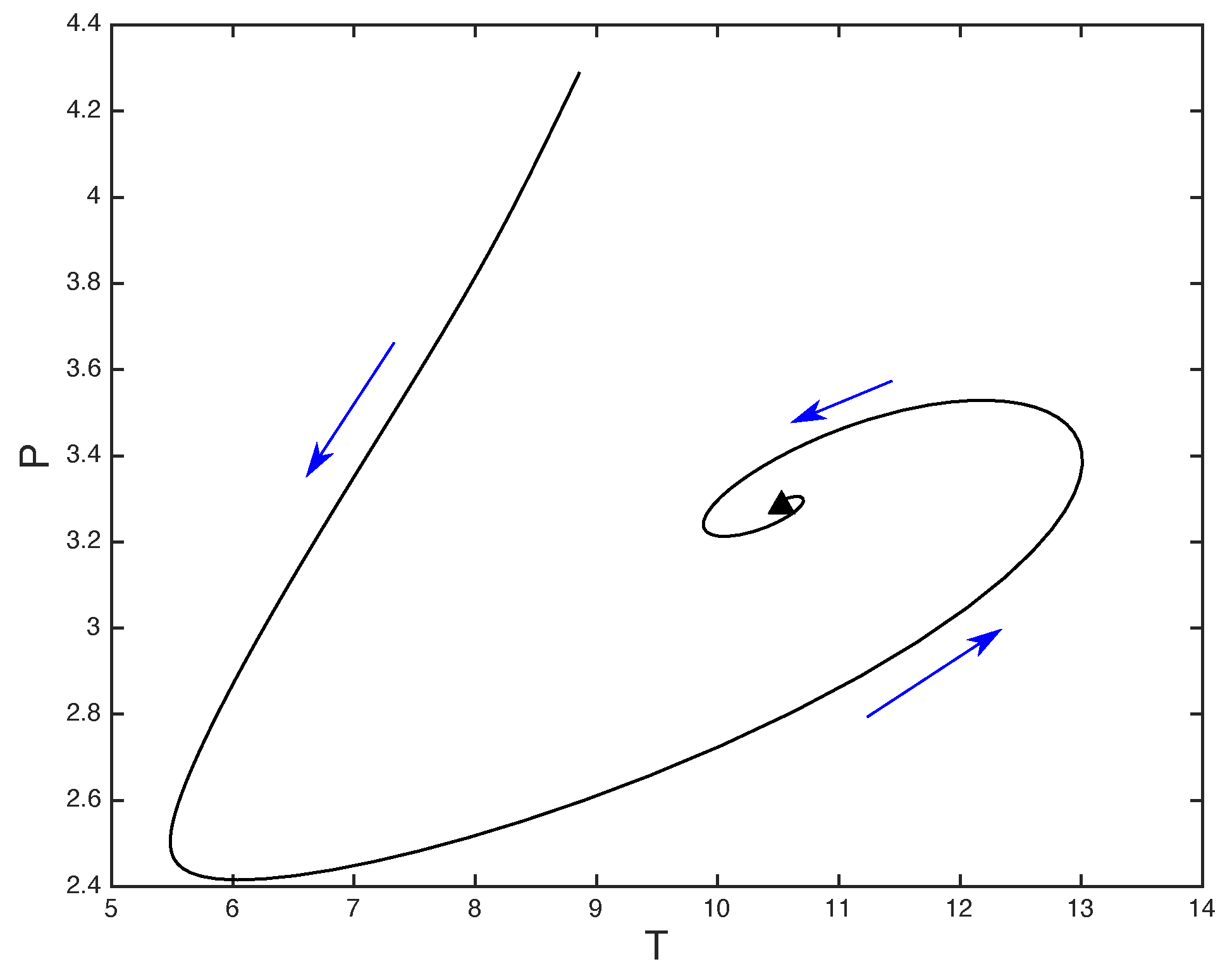
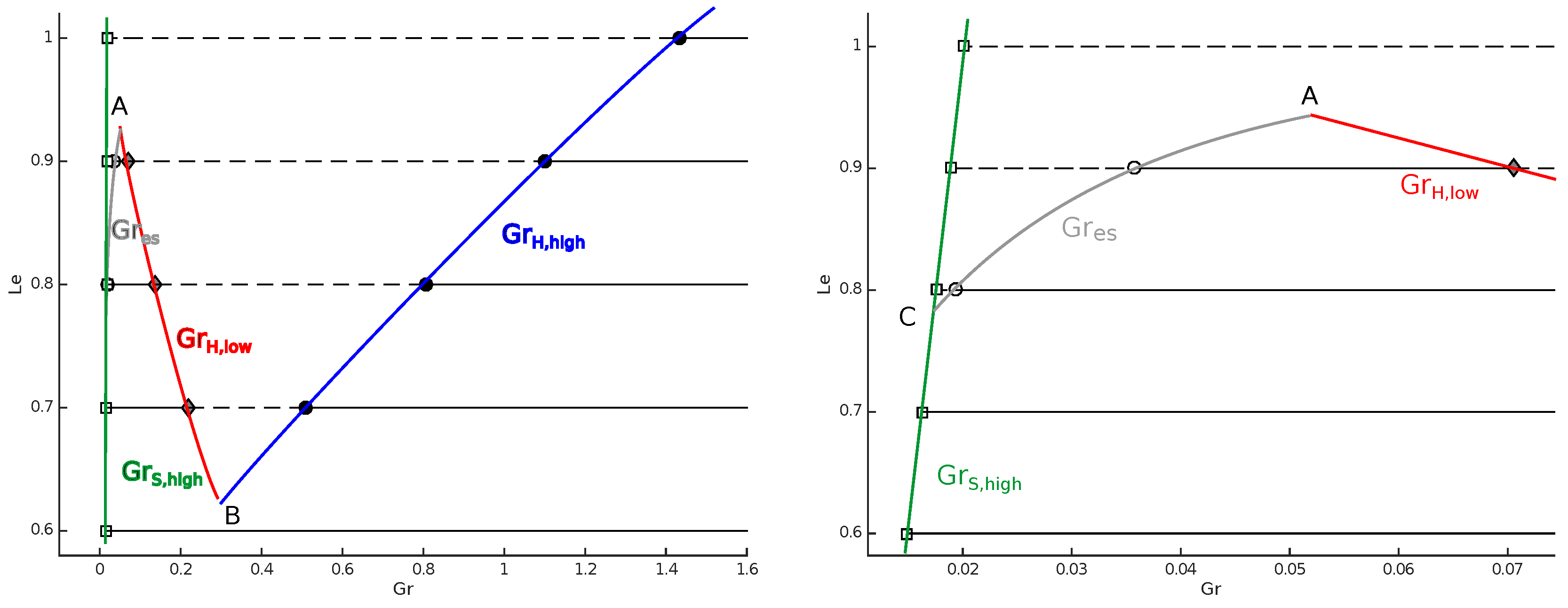
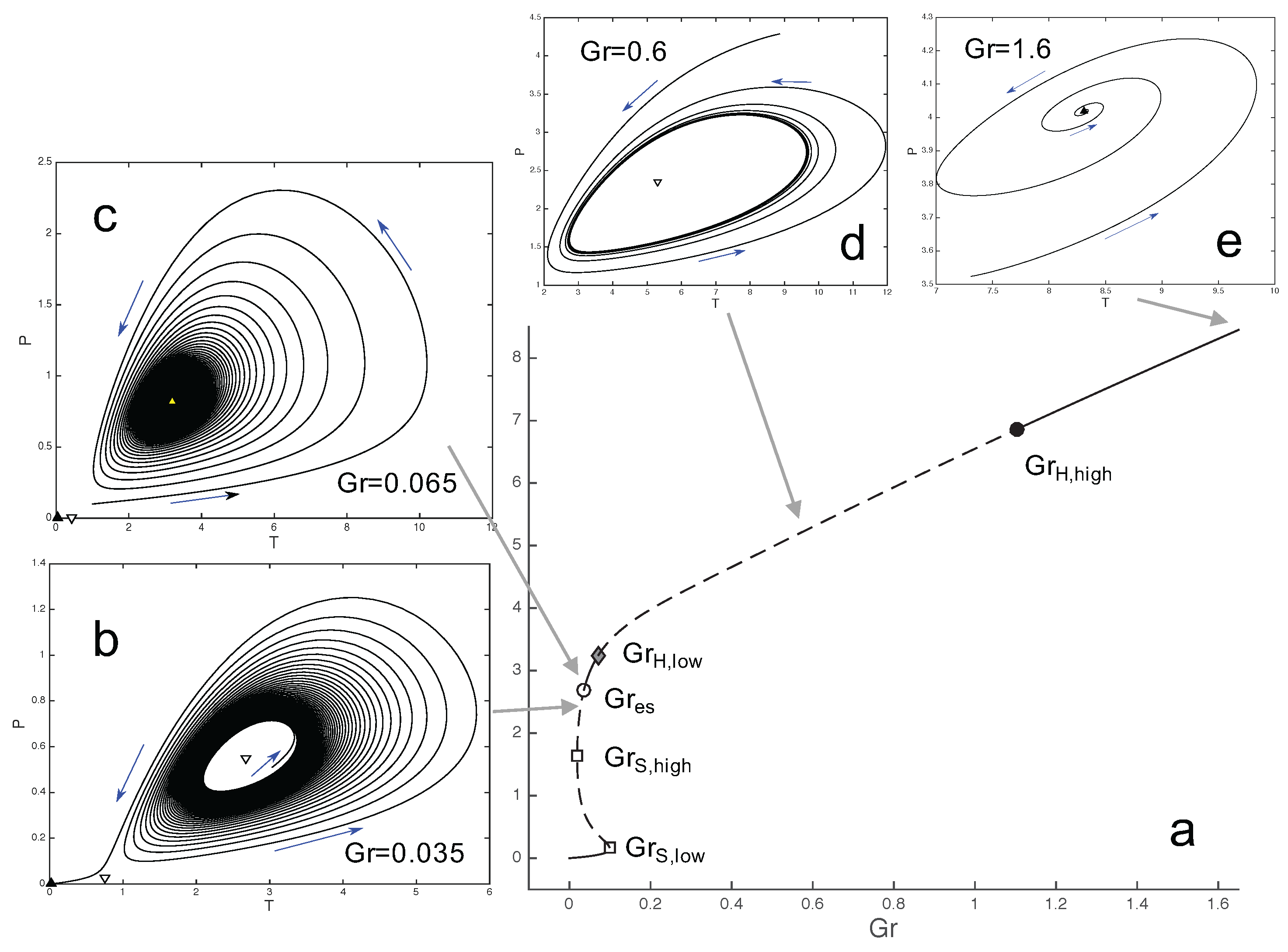
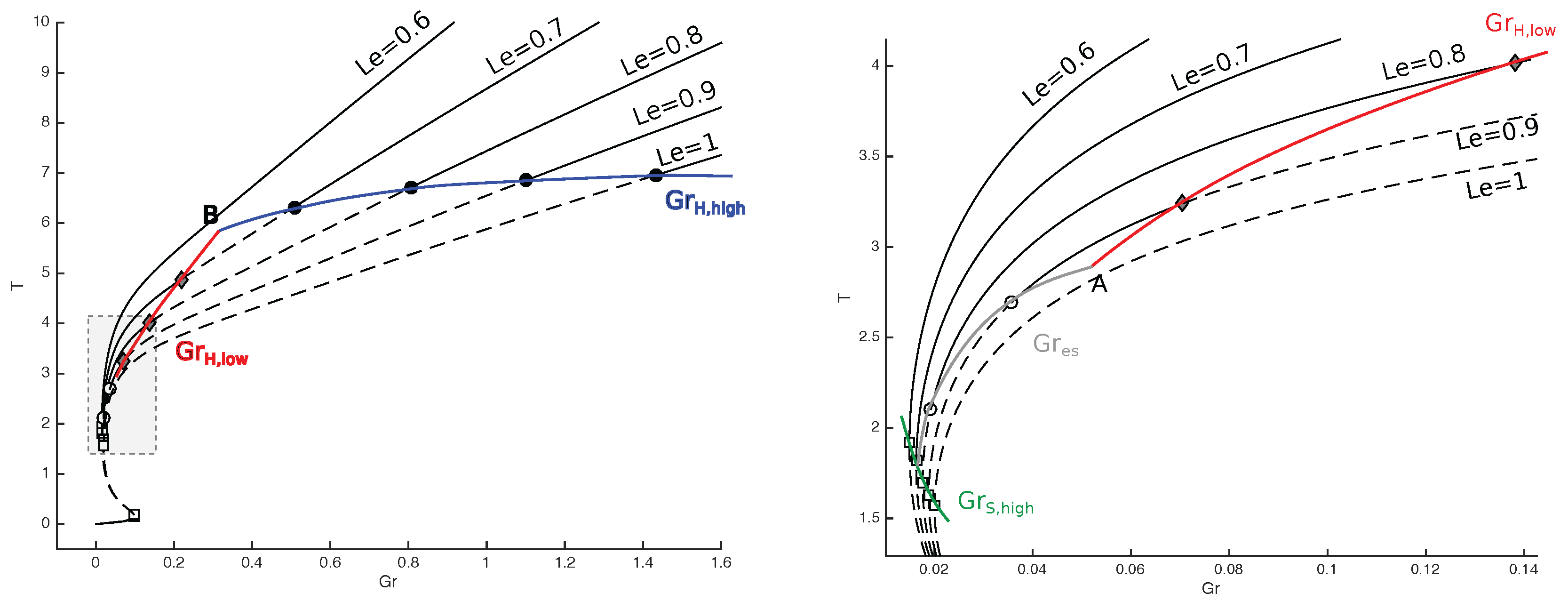
3.1. Gruntfest and Damköhler Numbers
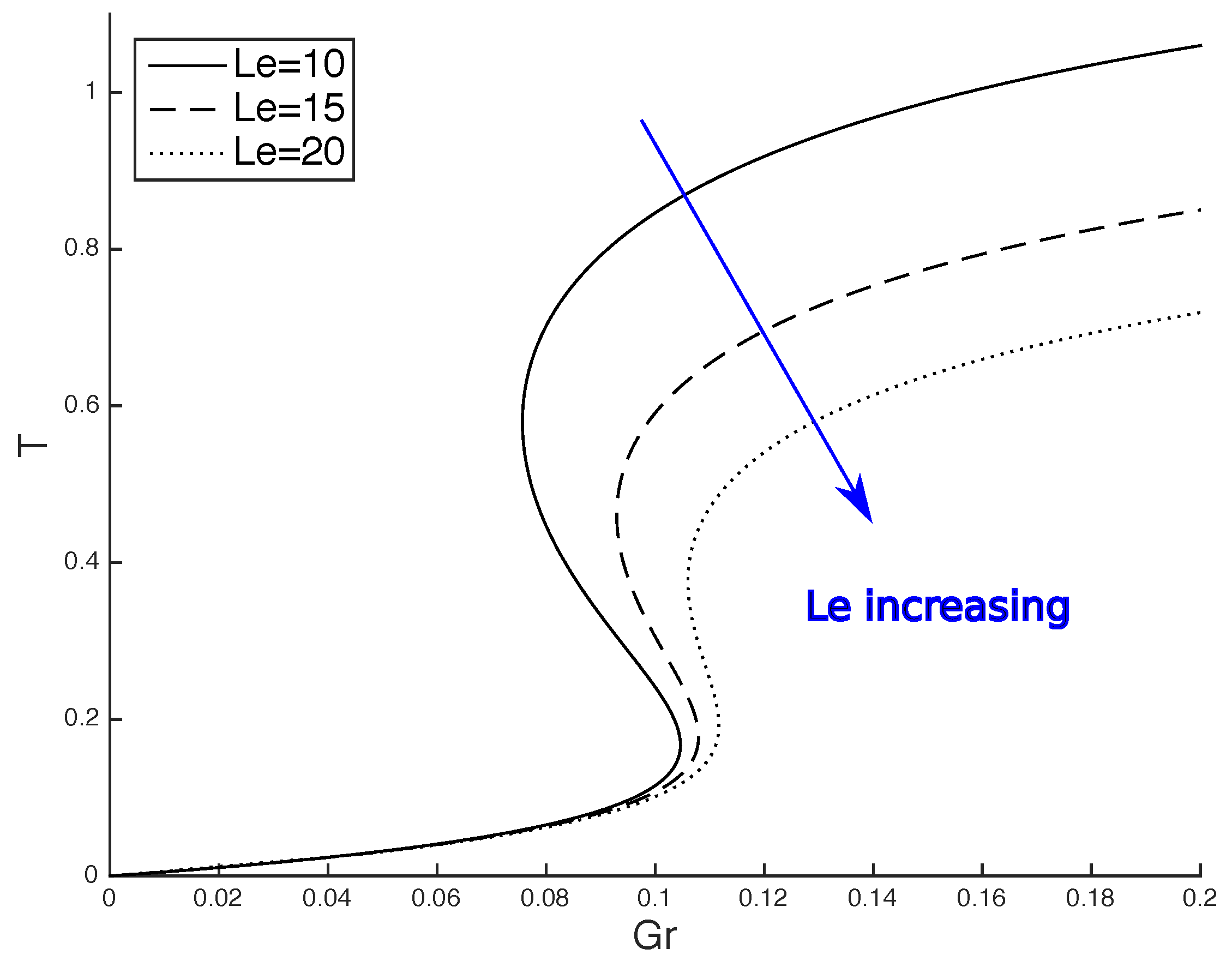
3.2. Lewis Number
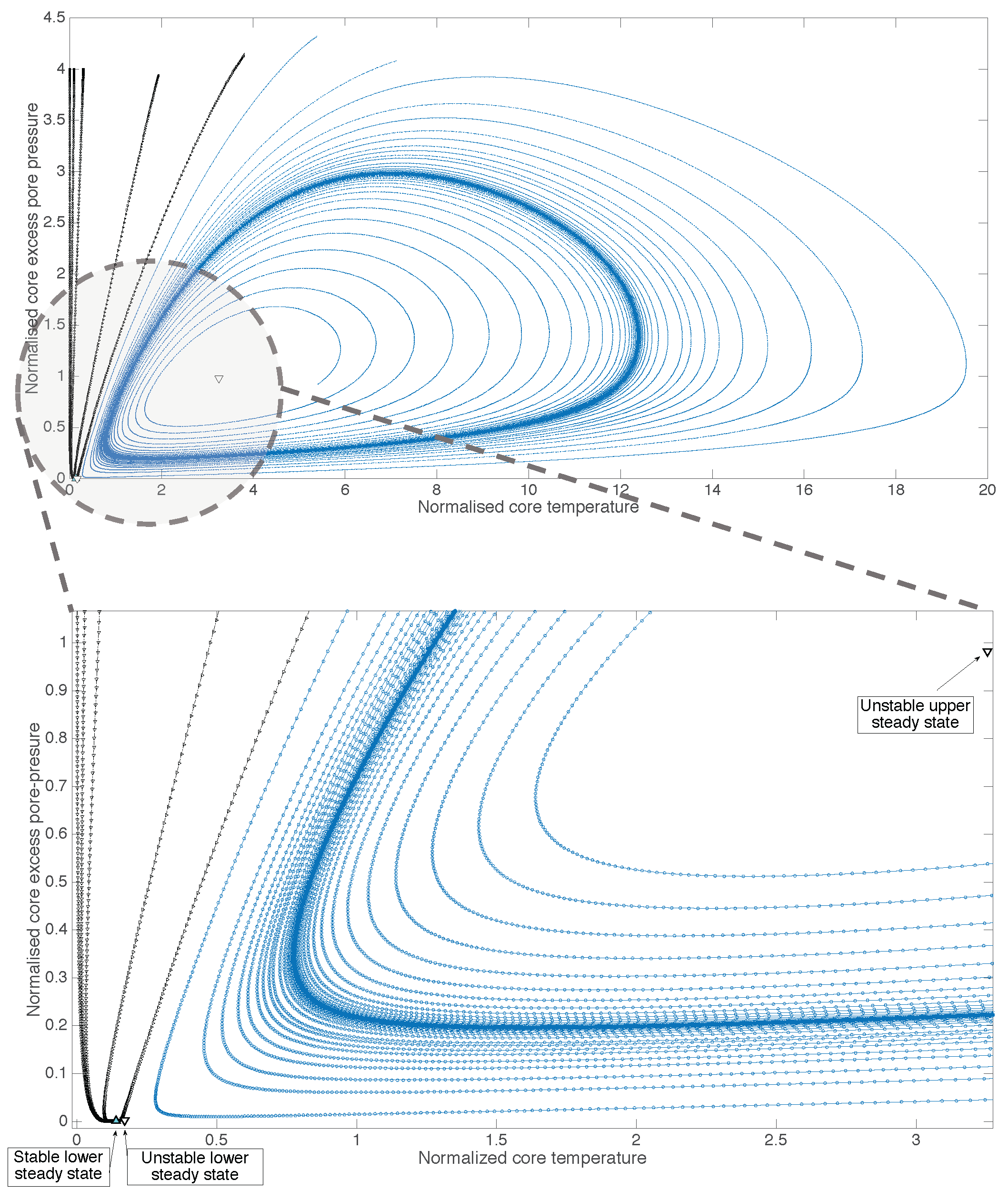
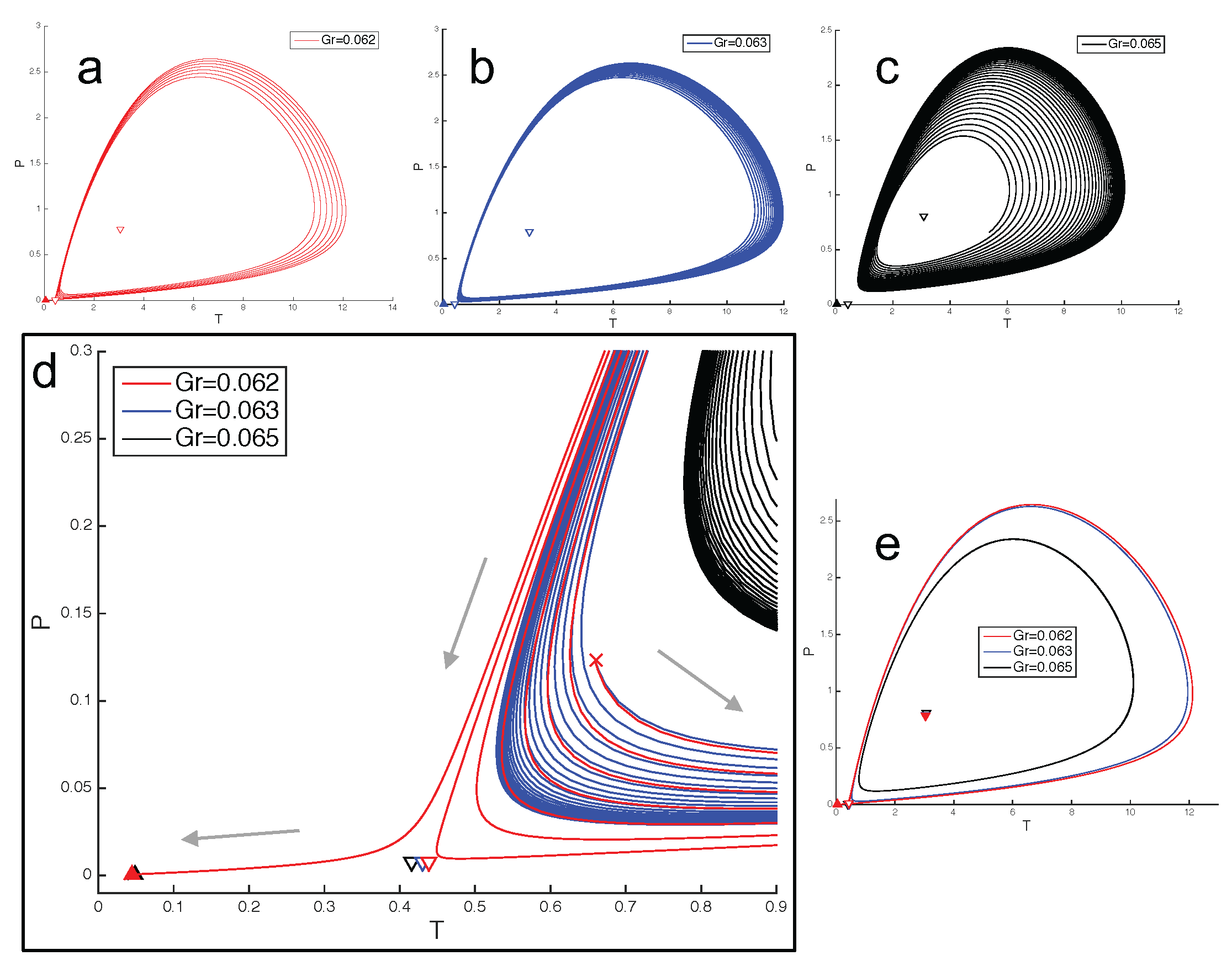
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kostić, S.; Vasović, N.; Perc, M.; Toljić, M.; Nikolić, D. Stochastic nature of earthquake ground motion. Phys. A Stat. Mech. Its Appl. 2013, 392, 4134–4145. [Google Scholar] [CrossRef]
- Kostić, S.; Franović, I.; Perc, M.; Vasović, N.; Todorović, K. Triggered dynamics in a model of different fault creep regimes. Sci. Rep. 2014, 4, 5401. [Google Scholar] [CrossRef] [PubMed]
- Kostić, S.; Vasović, N.; Perc, M. Temporal distribution of recorded magnitudes in Serbia earthquake catalog. Appl. Math. Comp. 2014, 244, 917–924. [Google Scholar] [CrossRef]
- Dieterich, J. Time-dependent friction in rocks. J. Geophys. Res. 1972, 377, 3690–3697. [Google Scholar] [CrossRef]
- Ruina, A. Slip instability and state variable friction laws. J. Geophys. Res. 1983, 88, 10359–10370. [Google Scholar] [CrossRef]
- Gu, J.; Rice, J.R.; Ruina, A.L.; Tse, S.T. Slip Motion and Stability of a Single Degree of Freedom Elastic System with Rate and State Dependent Friction. J. Mech. Phys. Solids 1984, 32, 167–196. [Google Scholar] [CrossRef]
- Rundle, P.B.; Rundle, J.B.; Tiampo, K.F.; Martins, J.S.S.; McGinnis, S.; Klein, W. Nonlinear network dynamics on earthquake fault systems. Phys. Rev. Lett. 2001, 8714, 148501. [Google Scholar] [CrossRef] [PubMed]
- Alevizos, S.; Veveakis, M.; Poulet, T. Thermo-Poro-Mechanics of chemically active creeping faults: 1. Steady State. J. Geophys. Res. Solis Earth 2014, 119, 4558–4582. [Google Scholar] [CrossRef]
- Veveakis, E.; Poulet, T.; Alevizos, S. Thermo-Poro-Mechanics of chemically active creeping faults: 2. Transient considerations. J. Geophys. Res. Solis Earth 2014, 119, 4583–4605. [Google Scholar] [CrossRef]
- Poulet, T.; Veveakis, E.; Regenauer-Lieb, K.; Yuen, D. Thermo-Poro-Mechanics of chemically active creeping faults: 3. The role of serpentinite in episodic tremor and slip sequences, and transition to chaos. J. Geophys. Res. Solis Earth 2014, 119, 4606–4625. [Google Scholar] [CrossRef]
- Veveakis, E.; Alevizos, S.; Vardoulakis, I. Chemical reaction capping of thermal instabilities during shear of frictional faults. J. Mech. Phys. Solids 2010, 58, 1175–1194. [Google Scholar] [CrossRef]
- Sulem, J.; Famin, V. Thermal decomposition of carbonates in fault zones: Slip-weakening and temperature-limiting effects. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Poulet, T.; Veveakis, M. A viscoplastic approach for pore collapse in saturated soft rocks using REDBACK: An open-source parallel simulator for Rock mEchanics with Dissipative feedBACKs. Comput. Geotech. 2016, 74, 211–221. [Google Scholar] [CrossRef]
- Poulet, T.; Paesold, M.; Veveakis, M. Multi-Physics Modelling of Fault Mechanics Using REDBACK: A Parallel Open-Source Simulator for Tightly Coupled Problems. Rock Mech. Rock Eng. 2016. [Google Scholar] [CrossRef]
- Law, C. Combustion Physics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Fowler, A. Mathematical Models in the Applied Sciences, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kelemen, P.; Hirth, G. A periodic shear-heating mechanism for intermediate-depth earthquakes in the mantle. Nature 2007, 446, 787–790. [Google Scholar] [CrossRef] [PubMed]
- Alevizos, S.; Poulet, T.; Sari, M.; Lesueur, M.; Regenauer-Lieb, K.; Veveakis, E. A framework for fracture network formation in overpressurized impermeable shale: Deformability vs diagenesis. Rock Mech. Rock Eng. 2016, in press. [Google Scholar] [CrossRef]
- Gottlieb, D.; Orszag, S. Numerical Analysis of Spectral Methods: Theory and Applications. In CBMS-NSF Regional Conference Series in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1987. [Google Scholar]
- Trefethen, L.N. Spectral Methods in MatLab; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Chan, T.; Keller, H. Arc-length Continuation and Multi-grid Techniques for Nonlinear Elliptic Eigenvalue Problems. SIAM J. Sci. Stat. Comput. 1991, 3, 173–194. [Google Scholar] [CrossRef]
- Gruntfest, I. Thermal feedback in liquid flow: Plane shear at constant stress. Trans. Soc. Rheol. 1963, 7, 95–207. [Google Scholar] [CrossRef]
- Poulet, T.; Veveakis, M.; Herwegh, M.; Buckingham, T.; Regenauer-Lieb, K. Modeling episodic fluid-release events in the ductile carbonates of the Glarus thrust. Geophys. Res. Lett. 2014, 41, 7121–7128. [Google Scholar] [CrossRef]
- Abarbanel, H.D.I.; Brown, R.; Sidorowich, J.J.; Tsimring, L.S. The analysis of observed chaotic data in physical systems. Rev. Mod. Phys. 1993, 65, 1331–1392. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| 20 | |
| 10 | |
| α | 4 |
| 10−4 | |
| 3 × 10−3 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alevizos, S.; Poulet, T.; Veveakis, M.; Regenauer-Lieb, K. Analysis of Dynamics in Multiphysics Modelling of Active Faults. Mathematics 2016, 4, 57. https://doi.org/10.3390/math4040057
Alevizos S, Poulet T, Veveakis M, Regenauer-Lieb K. Analysis of Dynamics in Multiphysics Modelling of Active Faults. Mathematics. 2016; 4(4):57. https://doi.org/10.3390/math4040057
Chicago/Turabian StyleAlevizos, Sotiris, Thomas Poulet, Manolis Veveakis, and Klaus Regenauer-Lieb. 2016. "Analysis of Dynamics in Multiphysics Modelling of Active Faults" Mathematics 4, no. 4: 57. https://doi.org/10.3390/math4040057
APA StyleAlevizos, S., Poulet, T., Veveakis, M., & Regenauer-Lieb, K. (2016). Analysis of Dynamics in Multiphysics Modelling of Active Faults. Mathematics, 4(4), 57. https://doi.org/10.3390/math4040057





