Solution for Rational Systems of Difference Equations of Order Three

Abstract

In this paper, we consider the solution and periodicity of the following systems of difference equations: $x_{n+1}={\displaystyle \frac{y_{n-2}}{-1+y_{n-2}{x}_{n-1}{y}_n}}$, $y_{n+1}={\displaystyle \frac{x_{n-2}}{\pm 1\pm x_{n-2}{y}_{n-1}{x}_n}}$, with initial conditions $x_{-2},x_{-1},x_0,y_{-2},y_{-1},$and$y_0$are nonzero real numbers.

1. Introduction

This paper is devoted to study the form of the solution and periodicity of the following third order systems of rational difference equations

$$x_{n+1}={\displaystyle \frac{y_{n-2}}{-1+y_{n-2}{x}_{n-1}{y}_n}},y_{n+1}={\displaystyle \frac{x_{n-2}}{\pm 1\pm x_{n-2}{y}_{n-1}{x}_n}}$$

with initial conditions $x_{-2},x_{-1},x_0,y_{-2},y_{-1},$and$y_0$ are nonzero real numbers.

Recently, there has been great interest in studying difference equation systems. One of the reasons for this is the necessity for some techniques that can be used in the investigation of equations arising in mathematical models describing real life situations in population biology, economics, probability theory, genetics, psychology, etc. There are many papers related to difference equations systems; for example, The global asymptotic behavior of the positive solutions of the rational difference system

$$x_{n+1}=1+{\displaystyle \frac{x_n}{y_{n-m}}},y_{n+1}=1+{\displaystyle \frac{y_n}{x_{n-m}}}$$

has been studied by Camouzis et al. in [1].

The periodicity of the positive solutions of the rational difference equations systems

$$x_{n+1}={\displaystyle \frac{1}{y_n}},y_{n+1}={\displaystyle \frac{y_n}{x_{n-1}{y}_{n-1}}}$$

has been obtained by Cinar in [2].

Elabbasy et al. [3] studied the solutions of particular cases of the following general system of difference equations:

$$x_{n+1}=\frac{a_1+a_2{y}_n}{a_3{z}_n+a_4{x}_{n-1}{z}_n},y_{n+1}=\frac{b_1{z}_{n-1}+b_2{z}_n}{b_3{x}_n{y}_n+b_4{x}_n{y}_{n-1}},z_{n+1}=\frac{c_1{z}_{n-1}+c_2{z}_n}{c_3{x}_{n-1}{y}_{n-1}+c_4{x}_{n-1}{y}_n+c_5{x}_n{y}_n}$$

Elsayed [4] obtained the solutions of the following system of the difference equations:

$$x_{n+1}={\displaystyle \frac{1}{y_{n-k}}},y_{n+1}={\displaystyle \frac{y_{n-k}}{x_n{y}_n}}$$

Grove et al. [5] studied existence and behavior of solutions of the rational system

$$x_{n+1}={\displaystyle \frac{a}{x_n}}+{\displaystyle \frac{b}{y_n}},y_{n+1}={\displaystyle \frac{c}{x_n}}+{\displaystyle \frac{d}{y_n}}$$

The behavior of positive solutions of the system,

$$x_{n+1}={\displaystyle \frac{x_{n-1}}{1+x_{n-1}{y}_n}},y_{n+1}={\displaystyle \frac{y_{n-1}}{1+y_{n-1}{x}_n}}$$

has been studied by Kurbanli et al. [6].

In addition, Kurbanli [7] investigated the behavior of the solutions of the difference equation system,

$$x_{n+1}={\displaystyle \frac{x_{n-1}}{x_{n-1}{y}_n-1}},y_{n+1}={\displaystyle \frac{y_{n-1}}{y_{n-1}{x}_n-1}},z_{n+1}={\displaystyle \frac{1}{z_n{y}_n}}$$

In [8], Ozban studied the positive solutions of the system of rational difference equations

$$x_{n+1}=\frac{a}{y_{n-3}},y_{n+1}=\frac{b{y}_{n-3}}{x_{n-q}{y}_{n-q}}$$

In [9], Papaschinopoulos and Schinas studied the oscillatory behavior, the boundedness of the solutions, and the global asymptotic stability of the positive equilibrium of the system of nonlinear difference equations

$$x_{n+1}=A+\frac{y_n}{x_{n-p}},y_{n+1}=A+\frac{x_n}{y_{n-q}}$$

Schinas [10] studied some invariants for difference equations and systems of difference equations of rational form.

El-Dessoky et al. [11] obtained the solution of the following system of difference equations

$$x_{n+1}=\frac{x_n{y}_{n-1}}{\pm x_n\pm y_{n-2}},y_{n+1}=\frac{x_{n-1}{y}_n}{\pm y_n\pm x_{n-2}}$$

Touafek et al. [12] investigated the periodic nature and gave the form of the solutions of the following systems of rational difference equations

$$x_{n+1}={\displaystyle \frac{x_{n-3}}{\pm 1\pm x_{n-3}{y}_{n-1}}},y_{n+1}={\displaystyle \frac{y_{n-3}}{\pm 1\pm y_{n-3}{x}_{n-1}}}$$

In [13,14], Zhang et al. studied the boundedness, the persistence, and the global asymptotic stability of the positive solutions of the systems of difference equations:

$$x_n=A+{\displaystyle \frac{1}{y_{n-p}}},y_n=A+{\displaystyle \frac{y_{n-1}}{x_{n-r}{y}_{n-s}}}$$

and

$$x_{n+}=A+{\displaystyle \frac{y_{n-m}}{x_n}},y_{n+1}=A+{\displaystyle \frac{x_{n-m}}{y_n}}$$

In [15], El-Dessoky obtained the form of the solutions and the periodicity character of some systems of rational difference equations:

$$x_{n+1}=\frac{z_{n-3}}{a_1+b_1{z}_n{y}_{n-1}{x}_{n-2}{z}_{n-3}},y_{n+1}=\frac{x_{n-3}}{a_2+b_2{x}_n{z}_{n-1}{y}_{n-2}{x}_{n-3}},z_{n+1}=\frac{y_{n-3}}{a_3+b_3{y}_n{x}_{n-1}{z}_{n-2}{y}_{n-3}}$$

Alzahrani et al. [16] obtained the form of the solution and the qualitative properties of the a rational difference equations of order two:

$$x_{n+1}={\displaystyle \frac{y_n{y}_{n-1}}{x_n\left(\pm 1\pm y_n{y}_{n-1}\right)}},y_{n+1}={\displaystyle \frac{x_n{x}_{n-1}}{y_n\left(\pm 1\pm x_n{x}_{n-1}\right)}}$$

For similar work to the difference equations and nonlinear systems of rational difference equations investigated herein, see references [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43].

2. The System: ${\mathit{x}}_{\mathit{n}+\mathbf{1}}=\frac{{\mathit{y}}_{\mathit{n}-\mathbf{2}}}{-\mathbf{1}+{\mathit{y}}_{\mathit{n}-\mathbf{2}}{\mathit{x}}_{\mathit{n}-\mathbf{1}}{\mathit{y}}_{\mathit{n}}},{\mathit{y}}_{\mathit{n}+\mathbf{1}}=\frac{{\mathit{x}}_{\mathit{n}-\mathbf{2}}}{\mathbf{1}+{\mathit{x}}_{\mathit{n}-\mathbf{2}}{\mathit{y}}_{\mathit{n}-\mathbf{1}}{\mathit{x}}_{\mathit{n}}}$

In this section, we investigate the solutions of the system of two difference equations

$$x_{n+1}={\displaystyle \frac{y_{n-2}}{-1+y_{n-2}{x}_{n-1}{y}_n}},y_{n+1}={\displaystyle \frac{x_{n-2}}{1+x_{n-2}{y}_{n-1}{x}_n}}$$

(1)

where $n\in {\mathbb{N}}_0$, and the initial conditions are arbitrary nonzero real numbers with $y_{-2}{x}_{-1}{y}_0\ne 1,\ne \frac{1}{2}$ and $x_{-2}{y}_{-1}{x}_0\ne \pm 1$.

The following theorem is devoted to the form of the solutions of system (1).

Theorem 1. 

Assume that $\{x_n,y_n\}$ are solutions of system (1). Then, for $n=0,1,2,...,$ we see that all solutions of system (1) are periodic with period twelve and

$$\begin{array}{ccc}\hfill x_{12n-2}& =& x_{-2},x_{12n-1}=x_{-1},x_{12n}=x_0,x_{12n+1}=\frac{y_{-2}}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{12n+2}& =& -y_{-1}(1+x_{-2}{y}_{-1}{x}_0),x_{12n+3}=\frac{-y_0(-1+2y_{-2}{x}_{-1}{y}_0)}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{12n+4}& =& \frac{-x_{-2}(1-x_{-2}{y}_{-1}{x}_0)}{(1+x_{-2}{y}_{-1}{x}_0)},x_{12n+5}=\frac{x_{-1}}{(-1+2y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{12n+6}& =& \frac{-x_0(1+x_{-2}{y}_{-1}{x}_0)}{(1-x_{-2}{y}_{-1}{x}_0)},x_{12n+7}=\frac{y_{-2}(-1+2y_{-2}{x}_{-1}{y}_0)}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{12n+8}& =& y_{-1}(1-x_{-2}{y}_{-1}{x}_0),x_{12n+9}=\frac{-y_0}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill y_{12n-2}& =& y_{-2},y_{12n-1}=y_{-1},y_{12n}=y_0,y_{12n+1}=\frac{x_{-2}}{(1+x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{12n+2}& =& \frac{x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{(-1+2y_{-2}{x}_{-1}{y}_0)},y_{12n+3}=\frac{x_0}{(1-x_{-2}{y}_{-1}{x}_0)},y_{12n+4}=-y_{-2},\hfill \\ \hfill y_{12n+5}& =& -y_{-1},y_{12n+6}=-y_0,y_{12n+7}=\frac{-x_{-2}}{(1+x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{12n+8}& =& \frac{-x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{(-1+2y_{-2}{x}_{-1}{y}_0)},y_{12n+9}=\frac{-x_0}{(1-x_{-2}{y}_{-1}{x}_0)}.\hfill \end{array}$$

Proof. 

For $n=0$, the result holds. Now suppose that $n>0$ and that our assumption holds for $n-1$. That is,

$$\begin{array}{ccc}\hfill x_{12n-14}& =& x_{-2},x_{12n-13}=x_{-1},x_{12n-12}=x_0,x_{12n-11}=\frac{y_{-2}}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{12n-10}& =& -y_{-1}(1+x_{-2}{y}_{-1}{x}_0),x_{12n-9}=\frac{-y_0(-1+2y_{-2}{x}_{-1}{y}_0)}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill {}_{12n-8}& =& \frac{-x_{-2}(1-x_{-2}{y}_{-1}{x}_0)}{(1+x_{-2}{y}_{-1}{x}_0)},x_{12n-7}=\frac{x_{-1}}{(-1+2y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{12n-6}& =& \frac{-x_0(1+x_{-2}{y}_{-1}{x}_0)}{(1-x_{-2}{y}_{-1}{x}_0)},x_{12n-5}=\frac{y_{-2}(-1+2y_{-2}{x}_{-1}{y}_0)}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{12n-4}& =& y_{-1}(1-x_{-2}{y}_{-1}{x}_0),x_{12n-3}=\frac{-y_0}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill y_{12n-14}& =& y_{-2},y_{12n-13}=y_{-1},y_{12n-12}=y_0,y_{12n-11}=\frac{x_{-2}}{(1+x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{12n-10}& =& \frac{x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{(-1+2y_{-2}{x}_{-1}{y}_0)},y_{12n-9}=\frac{x_0}{(1-x_{-2}{y}_{-1}{x}_0)},y_{12n-8}=-y_{-2},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill y_{12n-7}& =& -y_{-1},y_{12n-6}=-y_0,y_{12n-5}=\frac{-x_{-2}}{(1+x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{12n-4}& =& \frac{-x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{(-1+2y_{-2}{x}_{-1}{y}_0)},y_{12n-3}=\frac{-x_0}{(1-x_{-2}{y}_{-1}{x}_0)}.\hfill \end{array}$$

Now it follows from Equation (1) that

$$\begin{array}{ccc}\hfill x_{12n-2}& =& \frac{y_{12n-5}}{-1+y_{12n-5}{x}_{12n-4}{y}_{12n-3}}\hfill \\ & =& \frac{\frac{-x_{-2}}{(1+x_{-2}{y}_{-1}{x}_0)}}{\left(-1+\frac{-x_{-2}}{(1+x_{-2}{y}_{-1}{x}_0)}{y}_{-1}(1-x_{-2}{y}_{-1}{x}_0)\frac{-x_0}{(1-x_{-2}{y}_{-1}{x}_0)}\right)}\hfill \\ & =& \frac{\frac{-x_{-2}}{(1+x_{-2}{y}_{-1}{x}_0)}}{-1+\frac{x_{-2}{y}_{-1}{x}_0}{(1+x_{-2}{y}_{-1}{x}_0)}}=x_{-2},\hfill \\ \hfill y_{12n-2}& =& \frac{x_{12n-5}}{1+x_{12n-5}{y}_{12n-4}{x}_{12n-3}}\hfill \\ & =& \frac{\frac{y_{-2}(-1+2y_{-2}{x}_{-1}{y}_0)}{(-1+y_{-2}{x}_{-1}{y}_0)}}{\left(1+\frac{y_{-2}(-1+2y_{-2}{x}_{-1}{y}_0)}{(-1+y_{-2}{x}_{-1}{y}_0)}\frac{-x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{(-1+2y_{-2}{x}_{-1}{y}_0)}\frac{-y_0}{(-1+y_{-2}{x}_{-1}{y}_0)}\right)}\hfill \\ & =& \frac{\frac{y_{-2}(-1+2y_{-2}{x}_{-1}{y}_0)}{(-1+y_{-2}{x}_{-1}{y}_0)}}{\left(1+\frac{y_{-2}{x}_{-1}{y}_0}{(-1+y_{-2}{x}_{-1}{y}_0)}\right)}=\frac{y_{-2}(-1+2y_{-2}{x}_{-1}{y}_0)}{(-1+y_{-2}{x}_{-1}{y}_0)\left(1+\frac{y_{-2}{x}_{-1}{y}_0}{(-1+y_{-2}{x}_{-1}{y}_0)}\right)}\hfill \\ & =& \frac{y_{-2}(-1+2y_{-2}{x}_{-1}{y}_0)}{\left(-1+y_{-2}{x}_{-1}{y}_0+y_{-2}{x}_{-1}{y}_0\right)}=y_{-2},\hfill \end{array}$$

We also see that

$$\begin{array}{ccc}\hfill x_{12n-1}& =& \frac{y_{12n-4}}{-1+y_{12n-4}{x}_{12n-3}{y}_{12n-2}}\hfill \\ & =& \frac{\frac{-x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{(-1+2y_{-2}{x}_{-1}{y}_0)}}{\left(-1+\frac{-x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{(-1+2y_{-2}{x}_{-1}{y}_0)}\frac{-y_0}{(-1+y_{-2}{x}_{-1}{y}_0)}{y}_{-2}\right)}\hfill \\ & =& \frac{-x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{(-1+2y_{-2}{x}_{-1}{y}_0)\left(-1+\frac{y_{-2}{x}_{-1}{y}_0}{(-1+2y_{-2}{x}_{-1}{y}_0)}\right)}\hfill \\ & =& \frac{-x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{\left(1-2y_{-2}{x}_{-1}{y}_0+y_{-2}{x}_{-1}{y}_0\right)}=x_{-1},\hfill \\ \hfill y_{12n-1}& =& \frac{x_{12n-4}}{1+x_{12n-4}{y}_{12n-3}{x}_{12n-2}}\hfill \\ & =& \frac{y_{-1}(1-x_{-2}{y}_{-1}{x}_0)}{\left(1+y_{-1}(1-x_{-2}{y}_{-1}{x}_0)\frac{-x_0}{(1-x_{-2}{y}_{-1}{x}_0)}{x}_{-2}\right)}\hfill \\ & =& \frac{y_{-1}(1-x_{-2}{y}_{-1}{x}_0)}{\left(1-x_{-2}{y}_{-1}{x}_0\right)}=y_{-1}.\hfill \end{array}$$

We can also prove the other relation. The proof is complete. ☐

Example 1. 

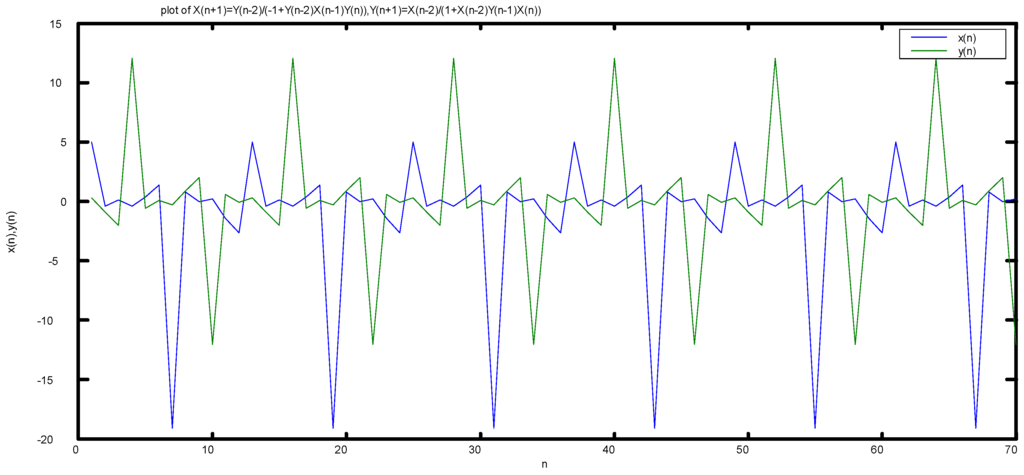
See Figure 1 when we put the initial conditions $x_{-2}=5,x_{-1}=-0.4,x_0=0.13,$ $y_{-2}=0.3$, $y_{-1}=-0.9$, and $y_0=-2$ for the difference system (1).

Figure 1. Plot of system $x_{n+1}=\frac{y_{n-2}}{-1+y_{n-2}{x}_{n-1}{y}_n}$, $y_{n+1}=\frac{x_{n-2}}{1+x_{n-2}{y}_{n-1}{x}_n}$.

3. The System: ${\mathit{x}}_{\mathit{n}+\mathbf{1}}=\frac{{\mathit{y}}_{\mathit{n}-\mathbf{2}}}{-\mathbf{1}+{\mathit{y}}_{\mathit{n}-\mathbf{2}}{\mathit{x}}_{\mathit{n}-\mathbf{1}}{\mathit{y}}_{\mathit{n}}},{\mathit{y}}_{\mathit{n}+\mathbf{1}}=\frac{{\mathit{x}}_{\mathit{n}-\mathbf{2}}}{\mathbf{1}-{\mathit{x}}_{\mathit{n}-\mathbf{2}}{\mathit{y}}_{\mathit{n}-\mathbf{1}}{\mathit{x}}_{\mathit{n}}}$

In this section, we obtain the form of the solutions of the system of two difference equations

$$x_{n+1}={\displaystyle \frac{y_{n-2}}{-1+y_{n-2}{x}_{n-1}{y}_n}},y_{n+1}={\displaystyle \frac{x_{n-2}}{1-x_{n-2}{y}_{n-1}{x}_n}}$$

(2)

where $n\in {\mathbb{N}}_0$ and the initial conditions are arbitrary non zero real numbers with $y_{-2}{x}_{-1}{y}_0\ne \pm 1$ and $x_{-2}{y}_{-1}{x}_0\ne 1,\ne \frac{1}{2}.$

The following theorem is devoted to the expression of the form of the solutions of System (2).

Theorem 2. 

Suppose that ${\left\{x_n,y_n\right\}}_{n=-2}^{+\infty }$ are solutions of System (2). Then, ${\{x_n\}}_{n=-2}^{+\infty }$ and ${\left\{y_n\right\}}_{n=-2}^{+\infty }$ and are periodic with period twelve and for $n=0,1,2,...,$

$$\begin{array}{ccc}\hfill x_{12n-2}& =& x_{-2},x_{12n-1}=x_{-1},x_{12n}=x_0,x_{12n+1}=\frac{y_{-2}}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{12n+2}& =& \frac{y_{-1}(1-x_{-2}{y}_{-1}{x}_0)}{(-1+2x_{-2}{y}_{-1}{x}_0)},x_{12n+3}=\frac{-y_0}{(1+y_{-2}{x}_{-1}{y}_0)},x_{12n+4}=-x_{-2},\hfill \\ \hfill x_{12n+5}& =& -x_{-1},x_{12n+6}=-x_0,x_{12n+7}=\frac{-y_{-2}}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{12n+8}& =& \frac{-y_{-1}(1-x_{-2}{y}_{-1}{x}_0)}{(-1+2x_{-2}{y}_{-1}{x}_0)},x_{12n+9}=\frac{y_0}{(1+y_{-2}{x}_{-1}{y}_0)},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill y_{12n-2}& =& y_{-2},y_{12n-1}=y_{-1},y_{12n}=y_0,y_{12n+1}=\frac{x_{-2}}{(1-x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{12n+2}& =& -x_{-1}(-1+y_{-2}{x}_{-1}{y}_0),y_{12n+3}=\frac{x_0(-1+2x_{-2}{y}_{-1}{x}_0)}{(-1+x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{12n+4}& =& \frac{y_{-2}(1+y_{-2}{x}_{-1}{y}_0)}{(-1+y_{-2}{x}_{-1}{y}_0)},y_{12n+5}=\frac{y_{-1}}{(-1+2x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{12n+6}& =& \frac{y_0(-1+y_{-2}{x}_{-1}{y}_0)}{(1+y_{-2}{x}_{-1}{y}_0)},y_{12n+7}=\frac{-x_{-2}(-1+2x_{-2}{y}_{-1}{x}_0)}{(-1+x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{12n+8}& =& -x_{-1}(1+y_{-2}{x}_{-1}{y}_0),y_{12n+9}=\frac{-x_0}{(1-x_{-2}{y}_{-1}{x}_0)}.\hfill \end{array}$$

Or, equivalently,

$${\{x_n\}}_{n=-2}^{+\infty }=\left\{\begin{array}{c}{x}_{-2},x_{-1},x_0,\frac{y_{-2}}{(-1+y_{-2}{x}_{-1}{y}_0)},\frac{y_{-1}(1-x_{-2}{y}_{-1}{x}_0)}{(-1+2x_{-2}{y}_{-1}{x}_0)},\frac{-y_0}{(1+y_{-2}{x}_{-1}{y}_0)},-x_{-2},-x_{-1},\\ -x_0,\frac{-y_{-2}}{(-1+y_{-2}{x}_{-1}{y}_0)},\frac{-y_{-1}(1-x_{-2}{y}_{-1}{x}_0)}{(-1+2x_{-2}{y}_{-1}{x}_0)},\frac{y_0}{(1+y_{-2}{x}_{-1}{y}_0)},x_{-2},x_{-1},x_0,...\end{array}\right\},$$

and

$${\{y_n\}}_{n=-2}^{+\infty }=\left\{\begin{array}{c}{y}_{-2},y_{-1},y_0,\frac{x_{-2}}{(1-x_{-2}{y}_{-1}{x}_0)},-x_{-1}(-1+y_{-2}{x}_{-1}{y}_0),\frac{x_0(-1+2x_{-2}{y}_{-1}{x}_0)}{(-1+x_{-2}{y}_{-1}{x}_0)},\\ \frac{y_{-2}(1+y_{-2}{x}_{-1}{y}_0)}{(-1+y_{-2}{x}_{-1}{y}_0)},\frac{y_{-1}}{(-1+2x_{-2}{y}_{-1}{x}_0)},\frac{y_0(-1+y_{-2}{x}_{-1}{y}_0)}{(1+y_{-2}{x}_{-1}{y}_0)},\frac{-x_{-2}(-1+2x_{-2}{y}_{-1}{x}_0)}{(-1+x_{-2}{y}_{-1}{x}_0)},\\ -x_{-1}(1+y_{-2}{x}_{-1}{y}_0),\frac{-x_0}{(1-x_{-2}{y}_{-1}{x}_0)},y_{-2},y_{-1},y_0,...\end{array}\right\}.$$

Proof. 

The proof follows the form of the proof of Theorem 1, and so will be omitted. ☐

Example 2. 

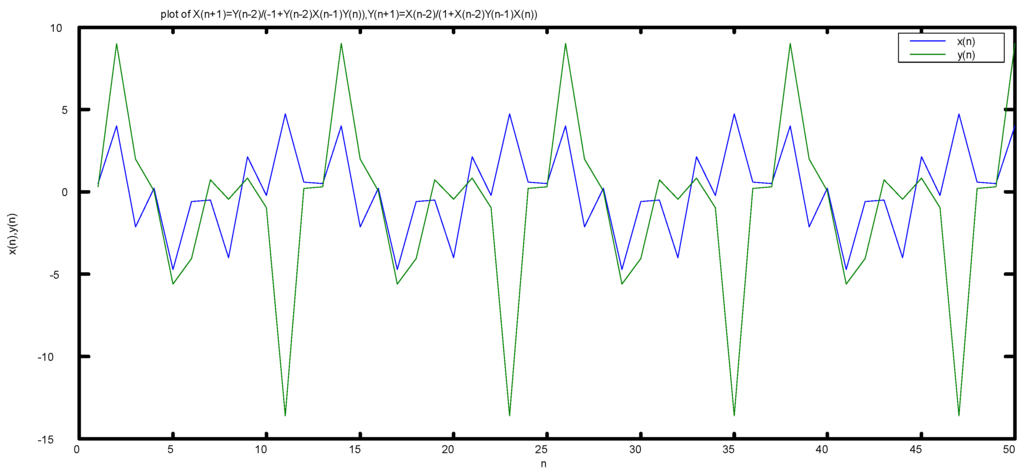
We assume the initial conditions $x_{-2}=0.5,x_{-1}=4,x_0=-2.13,y_{-2}=0.3,y_{-1}=9$, and $y_0=2$ for difference system (2); see Figure 2.

Figure 2. Plot of system $x_{n+1}=\frac{y_{n-2}}{-1+y_{n-2}{x}_{n-1}{y}_n}$, $y_{n+1}=\frac{x_{n-2}}{1-x_{n-2}{y}_{n-1}{x}_n}.$

4. The System: ${\mathit{x}}_{\mathit{n}+\mathbf{1}}=\frac{{\mathit{y}}_{\mathit{n}-\mathbf{2}}}{-\mathbf{1}+{\mathit{y}}_{\mathit{n}-\mathbf{2}}{\mathit{x}}_{\mathit{n}-\mathbf{1}}{\mathit{y}}_{\mathit{n}}},{\mathit{y}}_{\mathit{n}+\mathbf{1}}=\frac{{\mathit{x}}_{\mathit{n}-\mathbf{2}}}{-\mathbf{1}+{\mathit{x}}_{\mathit{n}-\mathbf{2}}{\mathit{y}}_{\mathit{n}-\mathbf{1}}{\mathit{x}}_{\mathit{n}}}$

In this section, we get the solutions of the system of the difference equations

$$x_{n+1}={\displaystyle \frac{y_{n-2}}{-1+y_{n-2}{x}_{n-1}{y}_n}},y_{n+1}={\displaystyle \frac{x_{n-2}}{-1+x_{n-2}{y}_{n-1}{x}_n}}$$

(3)

where $n\in {\mathbb{N}}_0$, and the initial conditions are arbitrary nonzero real numbers such that $x_{-2}{y}_{-1}{x}_0\ne 1$ and $y_{-2}{x}_{-1}{y}_0\ne 1.$

Theorem 3. 

If $\{x_n,y_n\}$ are solutions of difference equation system (3), then every solution of system (3) is periodic with period six, and takes the form for $n=0,1,2,...,$

$$\begin{array}{ccc}\hfill x_{6n-2}& =& x_{-2},x_{6n-1}=x_{-1},x_{6n}=x_0,x_{6n+1}=\frac{y_{-2}}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{6n+2}& =& y_{-1}(-1+x_{-2}{y}_{-1}{x}_0),x_{6n+3}=\frac{y_0}{(-1+y_{-2}{x}_{-1}{y}_0)},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill y_{6n-2}& =& y_{-2},y_{6n-1}=y_{-1},y_{6n}=y_0,y_{6n+1}=\frac{x_{-2}}{(-1+x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{6n+2}& =& x_{-1}(-1+y_{-2}{x}_{-1}{y}_0),y_{6n+3}=\frac{x_0}{(-1+x_{-2}{y}_{-1}{x}_0)}.\hfill \end{array}$$

Proof. 

The proof follows the form of the proof of Theorem 1, and so will be omitted. ☐

Example 3. 

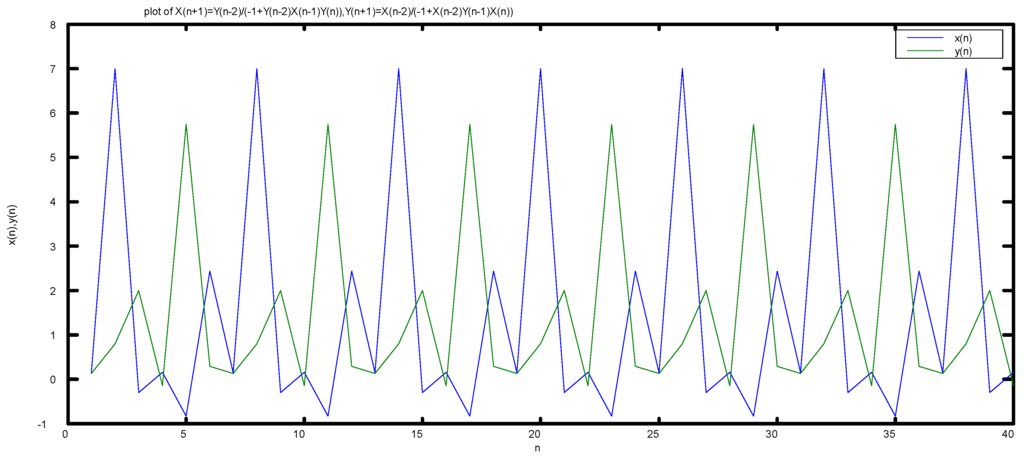
We consider an interesting numerical example for difference system (3) with the initial conditions $x_{-2}=0.15,x_{-1}=7,x_0=-0.3,y_{-2}=0.13,y_{-1}=0.8$, and $y_0=2$; see Figure 3.

Figure 3. Plot of system $x_{n+1}=\frac{y_{n-2}}{-1+y_{n-2}{x}_{n-1}{y}_n}$, $y_{n+1}=\frac{x_{n-2}}{-1+x_{n-2}{y}_{n-1}{x}_n}.$

5. The System: ${\mathit{x}}_{\mathit{n}+\mathbf{1}}=\frac{{\mathit{y}}_{\mathit{n}-\mathbf{2}}}{-\mathbf{1}+{\mathit{y}}_{\mathit{n}-\mathbf{2}}{\mathit{x}}_{\mathit{n}-\mathbf{1}}{\mathit{y}}_{\mathit{n}}},{\mathit{y}}_{\mathit{n}+\mathbf{1}}=\frac{{\mathit{x}}_{\mathit{n}-\mathbf{2}}}{-\mathbf{1}-{\mathit{x}}_{\mathit{n}-\mathbf{2}}{\mathit{y}}_{\mathit{n}-\mathbf{1}}{\mathit{x}}_{\mathit{n}}}$

In this section, we study the solutions of the following system of difference equations

$$x_{n+1}={\displaystyle \frac{y_{n-2}}{-1+y_{n-2}{x}_{n-1}{y}_n}},y_{n+1}={\displaystyle \frac{x_{n-2}}{-1-x_{n-2}{y}_{n-1}{x}_n}}$$

(4)

where $n\in {\mathbb{N}}_0$, and the initial conditions are arbitrary non-zero real numbers.

Theorem 4. 

Assume that $\{x_n,y_n\}$ are solutions of System (4). Then, for $n=0,1,2,...,$

$$\begin{array}{ccc}\hfill x_{6n-2}& =& x_{-2}\prod _{i=0}^{n-1}\frac{(1+(6i)x_{-2}{y}_{-1}{x}_0)(1+(6i+3)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+1)x_{-2}{y}_{-1}{x}_0)(1+(6i+4)x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill x_{6n-1}& =& x_{-1}\prod _{i=0}^{n-1}\frac{(1-(6i+1)y_{-2}{x}_{-1}{y}_0)(1-(6i+4)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+2)y_{-2}{x}_{-1}{y}_0)(1-(6i+5)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{6n}& =& x_0\prod _{i=0}^{n-1}\frac{(1+(6i+2)x_{-2}{y}_{-1}{x}_0)(1+(6i+5)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill x_{6n+1}& =& \frac{y_{-2}}{(-1+y_{-2}{x}_{-1}{y}_0)}\prod _{i=0}^{n-1}\frac{(1-(6i+3)y_{-2}{x}_{-1}{y}_0)(1-(6i+6)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+4)y_{-2}{x}_{-1}{y}_0)(1-(6i+7)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{6n+2}& =& \frac{y_{-1}(-1-x_{-2}{y}_{-1}{x}_0)}{(1+2x_{-2}{y}_{-1}{x}_0)}\prod _{i=0}^{n-1}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill x_{6n+3}& =& \frac{y_0(1-2y_{-2}{x}_{-1}{y}_0)}{(-1+3y_{-2}{x}_{-1}{y}_0)}\prod _{i=0}^{n-1}\frac{(1-(6i+5)y_{-2}{x}_{-1}{y}_0)(1-(6i+8)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+6)y_{-2}{x}_{-1}{y}_0)(1-(6i+9)y_{-2}{x}_{-1}{y}_0)},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill y_{6n-2}& =& y_{-2}\prod _{i=0}^{n-1}\frac{(1-(6i)y_{-2}{x}_{-1}{y}_0)(1-(6i+3)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+1)y_{-2}{x}_{-1}{y}_0)(1-(6i+4)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill y_{6n-1}& =& y_{-1}\prod _{i=0}^{n-1}\frac{(1+(6i+1)x_{-2}{y}_{-1}{x}_0)(1+(6i+4)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+2)x_{-2}{y}_{-1}{x}_0)(1+(6i+5)x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{6n}& =& y_0\prod _{i=0}^{n-1}\frac{(1-(6i+2)y_{-2}{x}_{-1}{y}_0)(1-(6i+5)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+3)y_{-2}{x}_{-1}{y}_0)(1-(6i+6)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill y_{6n+1}& =& \frac{x_{-2}}{(-1-x_{-2}{y}_{-1}{x}_0)}\prod _{i=0}^{n-1}\frac{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{6n+2}& =& \frac{x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{(1-2y_{-2}{x}_{-1}{y}_0)}\prod _{i=0}^{n-1}\frac{(1-(6i+4)y_{-2}{x}_{-1}{y}_0)(1-(6i+7)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+5)y_{-2}{x}_{-1}{y}_0)(1-(6i+8)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill y_{6n+3}& =& \frac{x_0(1+2x_{-2}{y}_{-1}{x}_0)}{(-1-3x_{-2}{y}_{-1}{x}_0)}\prod _{i=0}^{n-1}\frac{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+6)x_{-2}{y}_{-1}{x}_0)(1+(6i+9)x_{-2}{y}_{-1}{x}_0)}.\hfill \end{array}$$

where ${\displaystyle \prod _{i=0}^{-1}}{A}_i=1.$

Proof. 

For $n=0$, the result holds. Now, suppose that $n>0$ and that our assumption holds for $n-1$. that is,

$$\begin{array}{ccc}\hfill x_{6n-8}& =& x_{-2}\prod _{i=0}^{n-2}\frac{(1+(6i)x_{-2}{y}_{-1}{x}_0)(1+(6i+3)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+1)x_{-2}{y}_{-1}{x}_0)(1+(6i+4)x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill x_{6n-7}& =& x_{-1}\prod _{i=0}^{n-2}\frac{(1-(6i+1)y_{-2}{x}_{-1}{y}_0)(1-(6i+4)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+2)y_{-2}{x}_{-1}{y}_0)(1-(6i+5)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{6n-6}& =& x_0\prod _{i=0}^{n-2}\frac{(1+(6i+2)x_{-2}{y}_{-1}{x}_0)(1+(6i+5)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill x_{6n-5}& =& \frac{y_{-2}}{(-1+y_{-2}{x}_{-1}{y}_0)}\prod _{i=0}^{n-2}\frac{(1-(6i+3)y_{-2}{x}_{-1}{y}_0)(1-(6i+6)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+4)y_{-2}{x}_{-1}{y}_0)(1-(6i+7)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill x_{6n-4}& =& \frac{y_{-1}(-1-x_{-2}{y}_{-1}{x}_0)}{(1+2x_{-2}{y}_{-1}{x}_0)}\prod _{i=0}^{n-2}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill x_{6n-3}& =& \frac{y_0(1-2y_{-2}{x}_{-1}{y}_0)}{(-1+3y_{-2}{x}_{-1}{y}_0)}\prod _{i=0}^{n-2}\frac{(1-(6i+5)y_{-2}{x}_{-1}{y}_0)(1-(6i+8)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+6)y_{-2}{x}_{-1}{y}_0)(1-(6i+9)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill y_{6n-8}& =& y_{-2}\prod _{i=0}^{n-2}\frac{(1-(6i)y_{-2}{x}_{-1}{y}_0)(1-(6i+3)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+1)y_{-2}{x}_{-1}{y}_0)(1-(6i+4)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill y_{6n-7}& =& y_{-1}\prod _{i=0}^{n-2}\frac{(1+(6i+1)x_{-2}{y}_{-1}{x}_0)(1+(6i+4)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+2)x_{-2}{y}_{-1}{x}_0)(1+(6i+5)x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{6n-6}& =& y_0\prod _{i=0}^{n-2}\frac{(1-(6i+2)y_{-2}{x}_{-1}{y}_0)(1-(6i+5)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+3)y_{-2}{x}_{-1}{y}_0)(1-(6i+6)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill y_{6n-5}& =& \frac{x_{-2}}{(-1-x_{-2}{y}_{-1}{x}_0)}\prod _{i=0}^{n-2}\frac{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)},\hfill \\ \hfill y_{6n-4}& =& \frac{x_{-1}(-1+y_{-2}{x}_{-1}{y}_0)}{(1-2y_{-2}{x}_{-1}{y}_0)}\prod _{i=0}^{n-2}\frac{(1-(6i+4)y_{-2}{x}_{-1}{y}_0)(1-(6i+7)y_{-2}{x}_{-1}{y}_0)}{(1-(6i+5)y_{-2}{x}_{-1}{y}_0)(1-(6i+8)y_{-2}{x}_{-1}{y}_0)},\hfill \\ \hfill y_{6n-3}& =& \frac{x_0(1+2x_{-2}{y}_{-1}{x}_0)}{(-1-3x_{-2}{y}_{-1}{x}_0)}\prod _{i=0}^{n-2}\frac{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+6)x_{-2}{y}_{-1}{x}_0)(1+(6i+9)x_{-2}{y}_{-1}{x}_0)}.\hfill \end{array}$$

It follows from Equation (4) that

$$\begin{array}{ccc}\hfill x_{6n-2}& =& {\displaystyle \frac{y_{6n-5}}{-1+y_{6n-5}{x}_{6n-4}{y}_{6n-3}}}\hfill \\ & =& {\displaystyle \frac{\frac{x_{-2}}{(-1-x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}}{\left(\begin{array}{c}-1+\frac{x_{-2}}{(-1-x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}\\ \frac{y_{-1}(-1-x_{-2}{y}_{-1}{x}_0)}{(1+2x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}\\ \frac{x_0(1+2x_{-2}{y}_{-1}{x}_0)}{(-1-3x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+6)x_{-2}{y}_{-1}{x}_0)(1+(6i+9)x_{-2}{y}_{-1}{x}_0)}\end{array}\right)}}\hfill \\ & =& \frac{\frac{x_{-2}}{(-1-x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}}{\left(-1+\frac{x_0{y}_{-1}{x}_{-2}}{(-1-3x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+9)x_{-2}{y}_{-1}{x}_0)}\right)}\hfill \\ & =& \frac{\frac{x_{-2}}{(-1-x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}}{\left(-1-\frac{x_{-2}{y}_{-1}{x}_0}{(1+(6n-3)x_{-2}{y}_{-1}{x}_0)}\right)}\hfill \\ & =& \frac{\frac{x_{-2}}{(-1-x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}}{\left(\frac{-1-(6n-3)x_{-2}{y}_{-1}{x}_0-x_{-2}{y}_{-1}{x}_0}{(1+(6n-3)x_{-2}{y}_{-1}{x}_0)}\right)}\hfill \\ & =& \frac{\frac{x_{-2}}{(1+x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}}{\left(\frac{1+(6n-2)x_{-2}{y}_{-1}{x}_0}{1+(6n-3)x_{-2}{y}_{-1}{x}_0}\right)}\hfill \\ & =& \frac{x_{-2}}{(1+x_{-2}{y}_{-1}{x}_0)}\prod _{i=0}^{n-2}\frac{(1+(6i+3)x_{-2}{y}_{-1}{x}_0)(1+(6i+6)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}\left(\frac{1+(6n-3)x_{-2}{y}_{-1}{x}_0}{1+(6n-2)x_{-2}{y}_{-1}{x}_0}\right)\hfill \\ & =& x_{-2}\prod _{i=0}^{n-1}\frac{(1+(6i)x_{-2}{y}_{-1}{x}_0)(1+(6i+3)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+1)x_{-2}{y}_{-1}{x}_0)(1+(6i+4)x_{-2}{y}_{-1}{x}_0)}.\hfill \end{array}$$

We also see from Equation (4) that

$$\begin{array}{ccc}\hfill y_{6n-1}& =& {\displaystyle \frac{x_{6n-4}}{-1-x_{6n-4}{y}_{6n-3}{x}_{6n-2}}}\hfill \\ & =& {\displaystyle \frac{\frac{y_{-1}(-1-x_{-2}{y}_{-1}{x}_0)}{(1+2x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}}{-1-\left(\begin{array}{c}\frac{y_{-1}(-1-x_{-2}{y}_{-1}{x}_0)}{(1+2x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}\\ \frac{x_0(1+2x_{-2}{y}_{-1}{x}_0)}{(-1-3x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+6)x_{-2}{y}_{-1}{x}_0)(1+(6i+9)x_{-2}{y}_{-1}{x}_0)}\\ x_{-2}{\displaystyle \prod _{i=0}^{n-1}}\frac{(1+(6i)x_{-2}{y}_{-1}{x}_0)(1+(6i+3)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+1)x_{-2}{y}_{-1}{x}_0)(1+(6i+4)x_{-2}{y}_{-1}{x}_0)}\end{array}\right)}}\hfill \\ & =& {\displaystyle \frac{\frac{y_{-1}(-1-x_{-2}{y}_{-1}{x}_0)}{(1+2x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}}{-1-\left(\begin{array}{c}\frac{x_{-2}{x}_0{y}_{-1}(1+x_{-2}{y}_{-1}{x}_0)}{(1+3x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+6)x_{-2}{y}_{-1}{x}_0)(1+(6i+9)x_{-2}{y}_{-1}{x}_0)}\\ {\displaystyle \prod _{i=0}^{n-1}}\frac{(1+(6i)x_{-2}{y}_{-1}{x}_0)(1+(6i+3)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+1)x_{-2}{y}_{-1}{x}_0)(1+(6i+4)x_{-2}{y}_{-1}{x}_0)}\end{array}\right)}}\hfill \end{array}$$

$$\begin{array}{ccc}& =& \frac{\frac{y_{-1}(1+x_{-2}{y}_{-1}{x}_0)}{(1+2x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}}{1+\left(x_{-2}{x}_0{y}_{-1}{\displaystyle \prod _{i=0}^{n-2}}(1+(6i+4)x_{-2}{y}_{-1}{x}_0){\displaystyle \prod _{i=0}^{n-1}}\frac{1}{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)}\right)}\hfill \\ & =& {\displaystyle \frac{\frac{y_{-1}(1+x_{-2}{y}_{-1}{x}_0)}{(1+2x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}}{1+\left(\frac{x_{-2}{x}_0{y}_{-1}}{1+(6n-2)x_{-2}{y}_{-1}{x}_0}\right)}}\hfill \\ & =& {\displaystyle \frac{\frac{y_{-1}(1+x_{-2}{y}_{-1}{x}_0)}{(1+2x_{-2}{y}_{-1}{x}_0)}{\displaystyle \prod _{i=0}^{n-2}}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}}{\left(\frac{1+(6n-2)x_{-2}{y}_{-1}{x}_0+x_{-2}{x}_0{y}_{-1}}{1+(6n-2)x_{-2}{y}_{-1}{x}_0}\right)}}\hfill \\ & =& \frac{y_{-1}(1+x_{-2}{y}_{-1}{x}_0)}{(1+2x_{-2}{y}_{-1}{x}_0)}\prod _{i=0}^{n-2}\frac{(1+(6i+4)x_{-2}{y}_{-1}{x}_0)(1+(6i+7)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+5)x_{-2}{y}_{-1}{x}_0)(1+(6i+8)x_{-2}{y}_{-1}{x}_0)}\left(\frac{1+(6n-2)x_{-2}{y}_{-1}{x}_0}{1+(6n-1)x_{-2}{y}_{-1}{x}_0}\right)\hfill \\ & =& y_{-1}\prod _{i=0}^{n-1}\frac{(1+(6i+1)x_{-2}{y}_{-1}{x}_0)(1+(6i+4)x_{-2}{y}_{-1}{x}_0)}{(1+(6i+2)x_{-2}{y}_{-1}{x}_0)(1+(6i+5)x_{-2}{y}_{-1}{x}_0)}.\hfill \end{array}$$

We can prove the other relations similarly. This completes the proof. ☐

Corollary 1. 

If $x_{-2},x_{-1},x_0,y_{-2},y_{-1}$, and $y_0$ are arbitrary real numbers and let $\{x_n,y_n\}$ are solutions of System (4), then the following statements are true:

(i) 

If $x_{-2}=0,y_{-1}\ne 0,x_0\ne 0,$then we have $x_{6n-2}=y_{6n+1}=0$ and $x_{6n}=x_0,$ $x_{6n+2}=-y_{-1},$ $y_{6n-1}=y_{-1},$ $y_{6n+3}=-x_0.$

(ii) 

If $x_{-1}=0,y_{-2}\ne 0,y_0\ne 0,$then we have $x_{6n-1}=y_{6n+2}=0$and$x_{6n+1}=-y_{-2},$ $x_{6n+3}=-y_0,$ $y_{6n-2}=y_{-2},$ $y_{6n}=y_0.$

(iii) 

If $x_0=0,y_{-1}\ne 0,x_{-2}\ne 0,$then we have $x_{6n}=y_{6n+3}=0$ and $x_{6n-2}=x_{-2},$ $x_{6n+2}=-y_{-1},$ $y_{6n-1}=y_{-1},$ $y_{6n+1}=-x_{-2}.$

(iv) 

If $y_{-2}=0,x_{-1}\ne 0,y_0\ne 0,$then we have $y_{6n-2}=x_{6n+1}=0$ and $x_{6n-1}=x_{-1},$ $x_{6n+3}=-y_0,$ $y_{6n}=y_0,$ $y_{6n+2}=-x_{-1}.$

(v) 

If $y_{-1}=0,x_0\ne 0,x_{-2}\ne 0,$then we have $y_{6n-1}=x_{6n+2}=0$ and $x_{6n-2}=x_{-2},$ $x_{6n}=x_0,$ $y_{6n+1}=-x_{-2},$ $y_{6n+3}=-x_0.$

(vi) 

If $y_0=0,y_{-2}\ne 0,x_{-1}\ne 0,$then we have $y_{6n}=x_{6n+3}=0$ and $x_{6n-1}=x_{-1},$ $x_{6n+1}=-y_{-2},$ $y_{6n-2}=y_{-2},$ $y_{6n+2}=-x_{-1}.$

Proof. 

The proof follows from the form of the solutions of System (4). ☐

Example 4. 

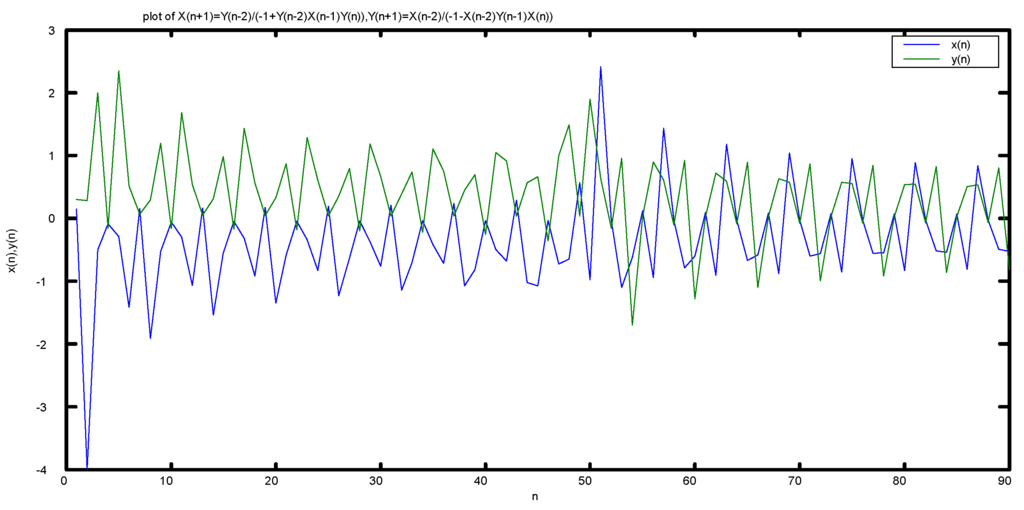
Figure 4 shows the behavior of the solution of the difference system (4) with the initial conditions $x_{-2}=0.15,x_{-1}=-4,x_0=-0.5,$ $y_{-2}=0.3$, $y_{-1}=0.28$, and $y_0=2$.

Figure 4. Plot of system $x_{n+1}=\frac{y_{n-2}}{-1+y_{n-2}{x}_{n-1}{y}_n}$, $y_{n+1}=\frac{x_{n-2}}{-1-x_{n-2}{y}_{n-1}{x}_n}.$