It is worth mentioning that Schulz method [
33] is another well-known iterative method for computing the inverse of a given matrix
A. From a given
, it produces the following iterates
, and so it needs two matrix–matrix products per iteration. Schulz method can be obtained applying Newton’s method to the related map
, and hence it possesses local
q-quadratic convergence; for recent variations and applications see [
34,
35,
36]. However, the
q-quadratic rate of convergence requires that the scheme is performed without dropping (see e.g., [
34]). As a consequence, Schulz method is not competitive with CauchyCos, CauchyFro, MinRes, and MinCos for large and sparse matrices (see
Section 2.5).
In
Table 1, we report the considered test matrices with their size, sparsity properties, and two-norm condition number
. Notice that the Wathen matrices have random entries so we cannot report their spectral properties. Moreover, Wathen (
N) is a sparse
matrix with
. In general, the inverse of all the considered matrices are dense, except the inverse of the Lehmer matrix which is tridiagonal.
3.1. Approximation to the Inverse with No Dropping Strategy
To add understanding to the properties of the new CauchyCos and MinCos Algorithms, we start by testing their behavior, as well as the behavior of CauchyFro and MinRes, without imposing sparsity. Since the goal is to compute an approximation to , it is not necessary to carry on the iterations up to a very small tolerance parameter ϵ, and we choose for our experiments. For all methods, we stop the iterations when .
Table 2 shows the number of required iterations by the four considered algorithms when applied to some of the test functions, and for different values of
n. No information in some of the entries of the table indicates that the corresponding method requires an excessive amount of iterations as compared with the MinRes and MinCos Algorithms. We can observe that CauchyFro and CauchyCos are not competitive with MinRes and MinCos, except for very few cases and for very small dimensions. Among the Cauchy-type methods, CauchyCos requires less iterations than CauchyFro, and in several cases the difference is significant. The MinCos and MinRes Algorithms were able to accomplish the required tolerance using a reasonable amount of iterations, except for the Lehmer(
n) and minij(
n) matrices for larger values of
n, which are the most difficult ones in our list of test matrices. The MinCos Algorithm clearly outperforms the MinRes Algorithm, except for the Poisson 2D (
n) and Poisson 3D (
n) for which both methods require the same number of iterations. For the more difficult matrices and especially for larger values of
n, MinCos reduces in the average the number of iterations with respect to MinRes by a factor of 4.
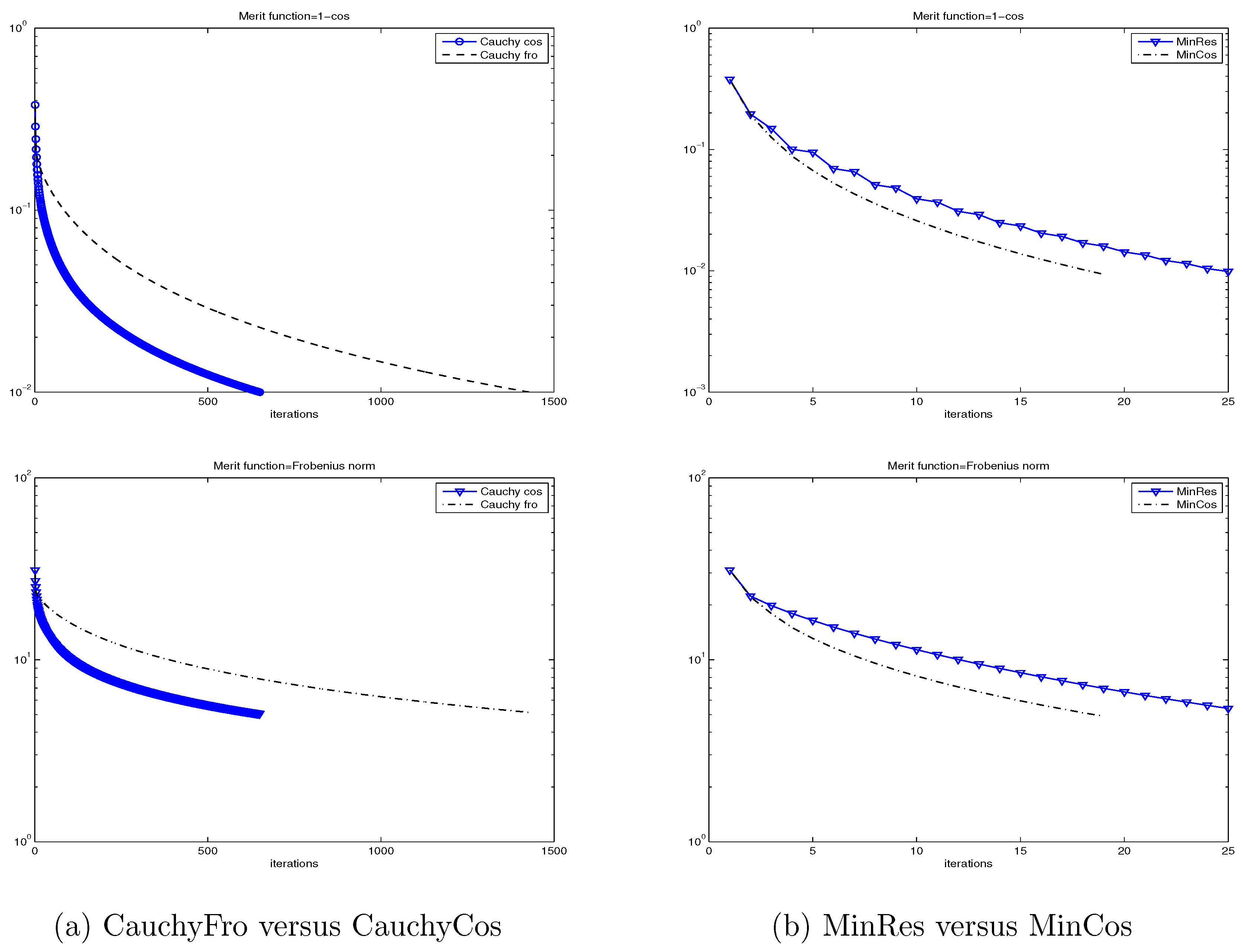
In
Figure 1, we show the (semilog) convergence history for the four considered methods and for both merit functions:
and
, when applied to the Wathen matrix for
and
. Once again, we can observe that CauchyFro and CauchyCos are not competitive with MinRes and MinCos, and that MinCos outperforms MinRes. Moreover, we observe in this case that the function
is a better merit function than
in the sense that it indicates with fewer iterations that a given iterate is sufficiently close to the inverse matrix. The same good behavior of the merit function
has been observed in all our experiments.
Based on these preliminary results, we will only report the behavior of MinRes and MinCos for the forthcoming numerical experiments.
3.2. Sparse Approximation to the Inverse
We now build sparse approximations by applying the dropping strategy, described in
Section 2.5, which is based on a threshold tolerance with a limited fill-in (
) on the matrix
, at each iteration, right before the scaling step to guarantee that the iterate
. We define
as the percentage of coefficients less than the maximum value of the modulus of all the coefficients in a column. To be precise, for each
i-th column, we select at most
off-diagonal coefficients among the ones that are larger in magnitude than
, where
represents the
i-th column of
. Once the sparsity has been imposed at each column and a sparse matrix is obtained, say
, we guarantee symmetry by setting
.
We have implemented the relatively simple dropping strategy, described above, for both MinRes and MinCos to make a first validation of the new method. Of course, we could use a more sophisticated dropping procedure for both methods as one can find in [
6]. The current numerical comparison is preliminary and indicates the potential of MinCos versus MinRes. We begin by comparing both methods when we apply the numerical described dropping strategy on the Matrix Market matrices.
Table 3 shows the performance of MinRes and MinCos when applied to the matrices nos1, nos2, nos5, and nos6, for
,
, and several values of
. We report the iteration
k (Iter) at which the method was stopped, the interval
of
, the quotient
/
, and the percentage of fill-in (% fill-in) at the final matrix
. We observe that, when imposing the dropping strategy to obtain sparsity, MinRes fails to produce an acceptable preconditioner. Indeed, as it has been already observed (see [
6,
15]) quite frequently that MinRes produces an indefinite approximation to the inverse of a sparse matrix in the
cone. We also observe that, in all cases, the MinCos method produces a sparse symmetric and positive definite preconditioner with relatively few iterations and a low level of fill-in. Moreover, with the exception of the matrix nos6, the MinCos method produces a preconditioned matrix
whose condition number is reduced by a factor of approximately 10 with respect to the condition number of
A. In some cases, MinRes was capable of producing a sparse symmetric and positive definite preconditioner, but in those cases, the MinCos produced a better preconditioner in the sense that it exhibits a better reduction of the condition number, and also a better eigenvalues distribution. Based on these results, for the remaining experiments, we only report the behavior of the MinCos Algorithm.
Table 4 shows the performance of the MinCos Algorithm when applied to the Wathen matrix for different values of
n and a maximum of 20 iterations. For this numerical experiment, we fix
,
, and
. For the particular case of the Wathen matrix when
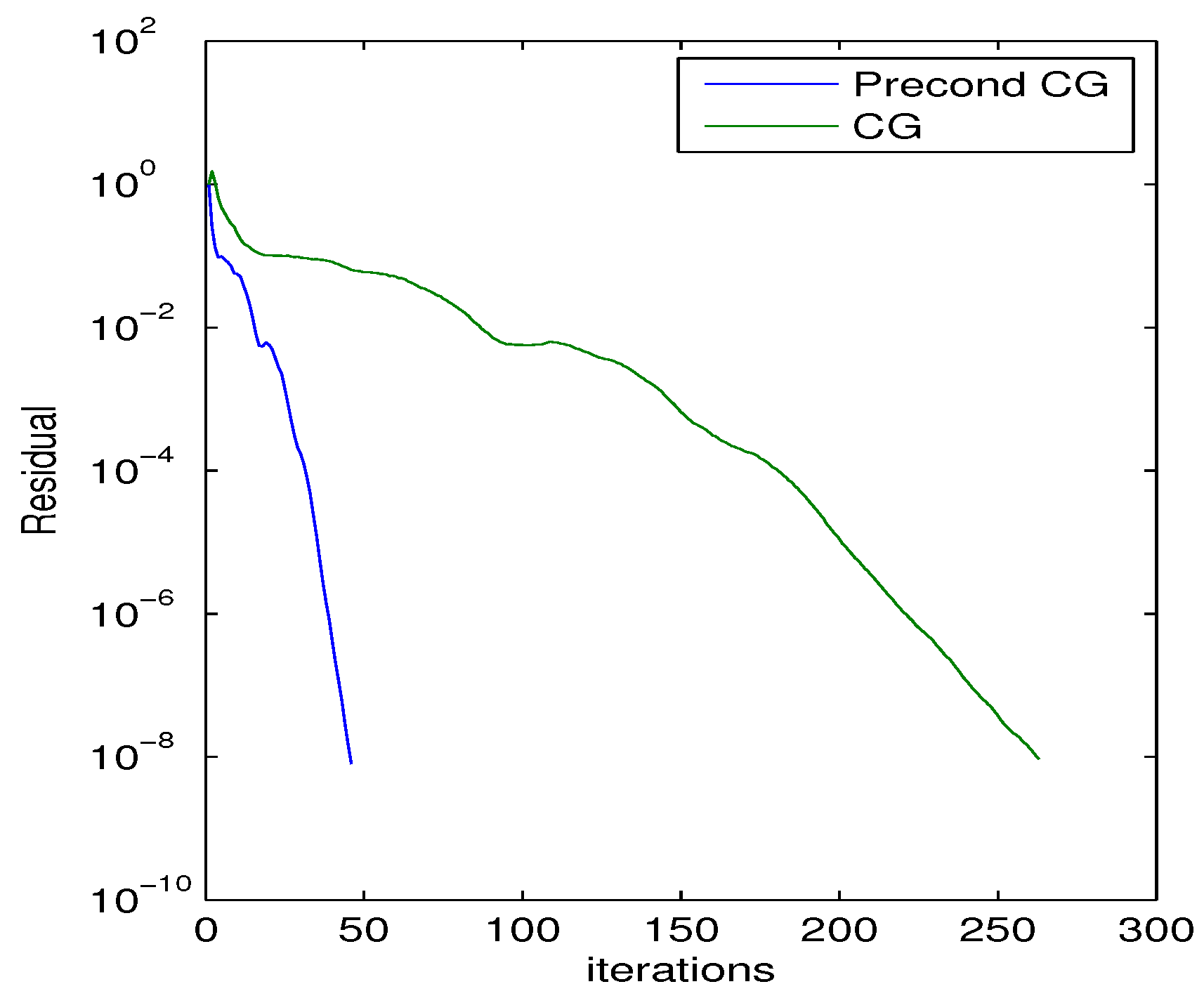
, we show in
Figure 2 that the (semilog) convergence history of the norm of the residual when solving a linear system with a random right-hand side vector, using the Conjugate Gradient (CG) method without preconditioning, and also using the preconditioner generated by the MinCos Algorithm after 20 iterations, fixing
,
, and
. We also report in
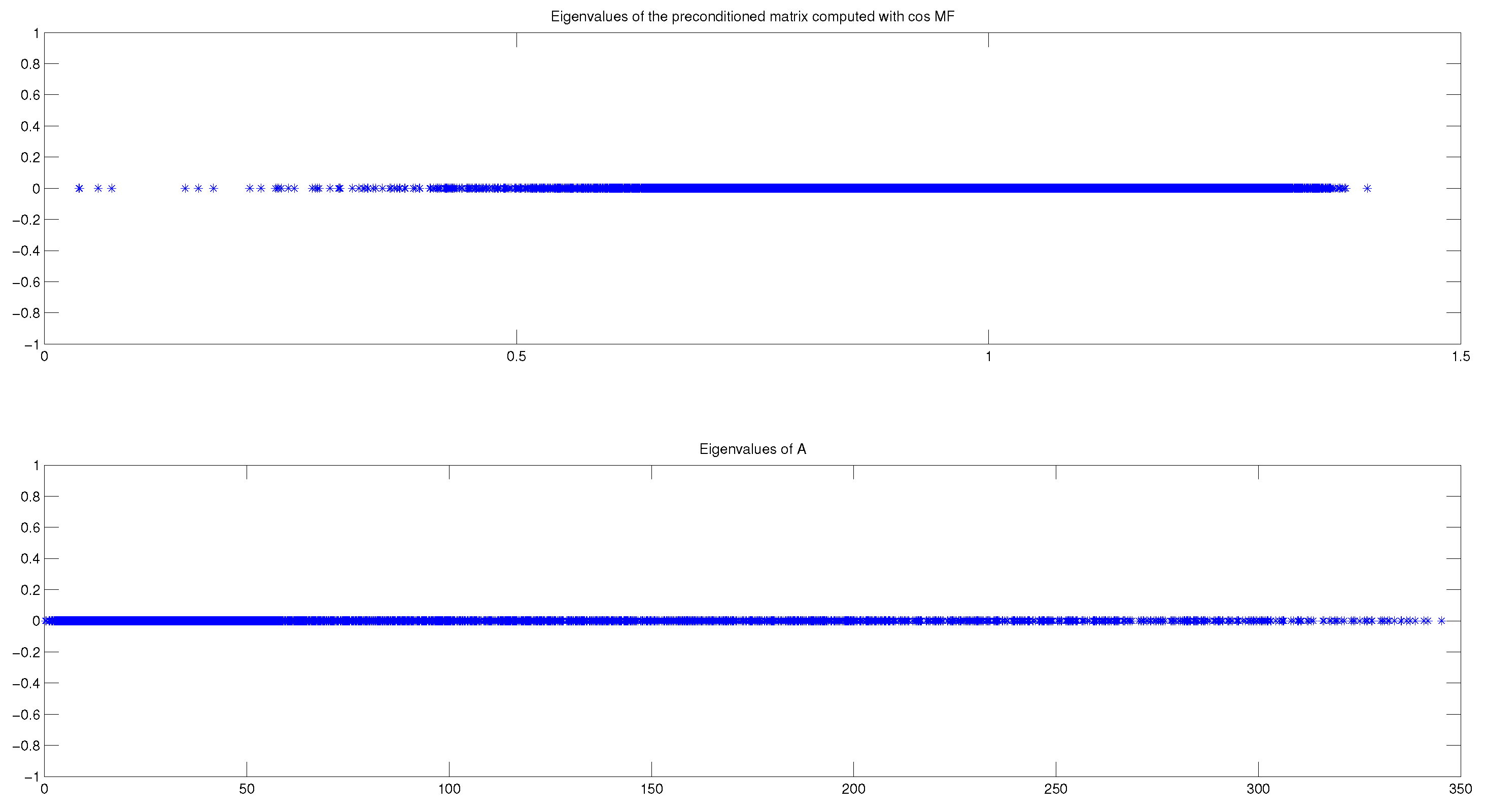
Figure 3 the eigenvalues distribution of
A and of
, at
, for the same experiment with the Wathen matrix and
. Notice that the eigenvalues of
A are distributed in the interval
, whereas the eigenvalues of
are located in the interval
(see
Table 4). Even better, we can observe that most of the eigenvalues are in the interval
, and very few of them are in the interval
, which clearly accounts for the good behavior of the preconditioned CG method (see
Figure 2).
Table 5,
Table 6 and
Table 7 show the performance of the MinCos Algorithm when applied to the Poisson 2D, the Poisson 3D, and the Lehmer matrices, respectively, for different values of
n, and different values of the maximum number of iterations,
ϵ,
, and
. We can observe that, for the Poisson 2D and 3D matrices, the MinCos Algorithm produces a sparse symmetric and positive definite preconditioner with very few iterations, a low level of fill-in, and a significant reduction of the condition number.
For the Lehmer matrix, which is one of the most difficult considered matrices, we observe in
Table 7 that the MinCos Algorithm produces a symmetric and positive definite preconditioner with a significant reduction of the condition number, but after 40 iterations and fixing
, for which the preconditioner accepts a high level of fill-in. If we impose a low level of fill-in, by reducing the value of
, MinCos still produces a symmetric and positive definite matrix, but the reduction of the condition number is not significant.
We close this section mentioning that both methods (MinCos and MinRes) produce sparse approximations to the inverse with comparable sparsity as shown in
Table 3 (last column). Notice also that MinCos produces a sequence
such that the eigenvalues of
are strictly positive at convergence, which, in turn, implies that the matrices
are invertible after a sufficiently large
k. This important property cannot be satisfied by MinRes.