Smoothness in Binomial Edge Ideals

Abstract

In this paper we study some geometric properties of the algebraic set associated to the binomial edge ideal of a graph. We study the singularity and smoothness of the algebraic set associated to the binomial edge ideal of a graph. Some of these algebraic sets are irreducible and some of them are reducible. If every irreducible component of the algebraic set is smooth we call the graph an edge smooth graph, otherwise it is called an edge singular graph. We show that complete graphs are edge smooth and introduce two conditions such that the graph G is edge singular if and only if it satisfies these conditions. Then, it is shown that cycles and most of trees are edge singular. In addition, it is proved that complete bipartite graphs are edge smooth.

1. Introduction

There are several natural ways to associate an ideal to a graph. Let K be a field and G a graph on the vertex set $\left[n\right]=\{1,2,\dots ,n\}$. The monomial edge ideal of G, ${\mathrm{I}}_G$, in $K[x_1,\dots ,x_n]$ is the ideal generated by the monomials $x_i{x}_j$, where $\{i,j\}$ is an edge of G. These ideals were first introduced by Villarreal in [1], where he studied the Cohen-Macaulay property of such graphs. Many authors have studied the algebraic properties of these ideals in terms of the underlying graphs, especially their Cohen-Macaulay property. In 2010, Binomial edge ideals were introduced by Herzog, Hibi, Hreinsdóttir, Kahle and Rauh in [2]. They appear independently, and at about the same time, also in the paper [3]. Let $S=K[x_1,\dots ,x_n,y_1,\dots ,y_n]$ be the polynomial ring in $2n$ variables. For each edge $e=\{i,j\}$ of G we associate to e a binomial $f_e$ defined by $f_e=f_{ij}=x_i{y}_j-x_j{y}_i$ with $i<j$. The ideal generated by the set of all $f_e$ with $e\in E\left(G\right)$ is called binomial edge ideal.

Observe that a binomial edge ideal can be viewed as an ideal generated by a set of 2-minors of the $2\times n$-matrix of indeterminates $x_1,\dots ,x_n,y_1,\dots ,y_n$. Indeed, the ideal of 2-minors of the $2\times n$-matrix may be interpreted as the binomial edge ideal of a complete graph on $\left[n\right]$. Algebraic properties of those ideals in terms of properties of the underlying graphs have been studied by many authors, and further studies are in progress. Related to binomial edge ideals are the ideals of adjacent minors considered by Hoşten and Sullivant [4]. In the case of a line graph the binomial edge ideal may be interpreted as an ideal of adjacent minors. This particular class of binomial edge ideals has also been considered by Diaconis, Eisenbud and Sturmfels in [5] where they compute the primary decomposition of this ideal.

It is said that a graph G on $\left[n\right]$ is closed with respect to the given labeling of vertices, if G satisfies condition (2) of the following theorem ([2], Theorem 1.1):

Theorem 1. 

Let G be a simple graph on the vertex set [n], and let < be the lexicographic order on $S=K[x_1,\dots ,x_n,y_1,\dots ,y_n]$ induced by $x_1>x_2>\cdots >x_n>y_1>y_2>\cdots >y_n$. Then the following conditions are equivalent:

1.

The generators $f_{ij}$ of $J_G$ form a quadratic Groebner basis;

2.

For all edges $\{i,j\}$ and $\{k,l\}$ with $i<j$ and $k<l$ one has $\{j,l\}\in E\left(G\right)$ if $i=k$, and $\{i,k\}\in E\left(G\right)$ if $j=l$.

Now let I be an ideal in $K[x_1,\dots ,x_n]$, where K is algebraically closed. By $\mathrm{Z}\left(\mathrm{I}\right)$ we mean, the algebraic set associated to I, the set of all points, $\mathbf{a}=(a_1,\dots ,a_n)$ in $K^n$ such that for each f in I, $f(a_1,\dots ,a_n)=0$. When I is a monomial ideal we can see I as intersection of some pure monomial ideals, i.e., the ideals generated by some of $x_i^{{\alpha }_i};i=1,\dots ,n$ and ${\alpha }_i\in IN$. The minimal associated primes of I are of the form $<x_{i_1},\dots ,x_{i_r}>$, with $\{i_1,\dots ,i_r\}\subset \left[n\right]$ and $\mathrm{Z}\left(\mathrm{I}\right)=\mathrm{Z}\left(\sqrt{\mathrm{I}}\right)={\bigcup }_{\mathrm{P}\in \mathrm{Min}\left(\mathrm{I}\right)}\mathrm{Z}\left(\mathrm{P}\right)$ where $\mathrm{Min}\left(\mathrm{I}\right)$ is the set of the minimal prime ideals of I. From the geometric point of view, $\mathrm{Z}\left(\mathrm{P}\right)=\mathrm{Z}({\mathrm{x}}_{{\mathrm{i}}_1},\dots ,{\mathrm{x}}_{{\mathrm{i}}_{\mathrm{r}}})={\bigcap }_{\mathrm{j}=1}^{\mathrm{r}}\mathrm{Z}\left({\mathrm{x}}_{{\mathrm{i}}_{\mathrm{j}}}\right)$ is the intersection of some Euclidean hyperplanes,

$$\{(a_1,\dots ,a_n)\in K^n;a_i=0forsomei\},$$

which have no complicated geometric structure. In contrast to monomial edge ideals, binomial edge ideals have many interesting geometric properties.

The purpose of this paper is a initial study of geometric properties of binomial edge ideals and the first geometric property of an algebraic set is the smoothness or the locus of singularity.

Let $\mathbf{Y}\subset K^n$ be an affine variety, and let $f_1,f_2,\dots ,f_t\in A=K[x_1,x_2,\dots ,x_n]$ be a set of generators for the ideal of $\mathbf{Y}$. $\mathbf{Y}$ is nonsingular at a point $\mathbf{p}\in \mathbf{Y}$ if the rank of the matrix $\parallel (\frac{\partial f_i}{\partial x_j})(\mathbf{p})\parallel$ is $n-r$, where r is the dimension of $\mathbf{Y}$. $\mathbf{Y}$ is nonsingular if it is nonsingular at every point. Otherwise, $\mathbf{Y}$ is called singular. Let I be an ideal in A and $\mathrm{Z}\left(\mathrm{I}\right)$ be the algebraic set associated to I. We have $\mathrm{Z}\left(\mathrm{I}\right)=\mathrm{Z}\left(\sqrt{\mathrm{I}}\right)={\bigcup }_{\mathrm{P}\in \mathrm{Min}\left(\mathrm{I}\right)}\mathrm{Z}\left(\mathrm{P}\right)$ where each $\mathrm{Z}\left(\mathrm{P}\right)$ is an affine variety. It is said $\mathbf{y}\in K^n$ is a singular point of $\mathrm{Z}\left(\mathrm{I}\right)$ when there exists $P\in \mathrm{Min}\left(\mathrm{I}\right)$ such that $\mathbf{y}$ is a singular point of $\mathrm{Z}\left(\mathrm{P}\right)$.

In this paper we prove that complete graphs are edge smooth and also introduce two conditions such that G is edge singular if and only if G satisfies these conditions.

2. Edge Singularity

Let G be a simple graph on $\left[n\right]$. For each subset $S\subset \left[n\right]$, a prime ideal, $P_S\left(G\right)$, is defined in [2]. Let $T=\left[n\right]\setminus S$, and let $G_1,\dots ,G_{c\left(S\right)}$ be the connected components of $G_T$. Here $G_T$ is the restriction of G to T whose edges are exactly those edges $\{i,j\}$ of G for which $i,j\in T$. For each $G_i$ we denote by ${\tilde{G}}_i$ the complete graph on the vertex set $V\left(G_i\right)$. Setting

$$P_S\left(G\right)=(\bigcup _{i\in S}\{x_i,y_i\},J_{{\tilde{G}}_1},\dots ,J_{{\tilde{G}}_{c\left(S\right)}}).$$

By corollary 3.9 [2] some of $P_S\left(G\right)$’s construct the set of minimal prime ideals of $J_G$. We define the graph G is edge smooth if the affine variety of the binomial edge ideal of G is nonsingular at every nonzero point. Otherwise G is called edge singular.

Theorem 2. 

Any complete graph G is edge smooth.

Proof. 

Let G be a simple complete graph on $\left[n\right]$. Put $\mathbf{Y}=\mathrm{V}\left({\mathrm{J}}_{\mathrm{G}}\right)$. By corollary 2.2 [2], $J_G$ is a radical ideal so $J_G=\mathrm{I}\left(\mathrm{V}\left({\mathrm{J}}_{\mathrm{G}}\right)\right)$. Since G is complete, by proposition 1.6 [2], $\frac{S}{J_G}$ is Cohen-Macaulay and hence by corollary 3.4 [2], we have $\dim \mathbf{Y}=\dim \frac{\mathrm{S}}{{\mathrm{J}}_{\mathrm{G}}}=\mathrm{n}+1$. We must show that for all $0\ne \mathbf{p}=(p_1,\dots ,p_n,q_1,\dots ,q_n)\in K^{2n}$, rank $\parallel \left(\frac{\partial f_i}{\partial t_j}\right)\left(\mathbf{p}\right)\parallel =2n-(n+1)=n-1$, where $1\le i\le \frac{n(n-1)}{2}$ and

$$t_j=\left\{\begin{array}{ccc}{x}_j\hfill & & 1\le j\le n\\ y_{j-n}\hfill & & n+1\le j\le 2n\end{array}\right.$$

It is enough to show that $\mathrm{rank}\parallel (\frac{\partial {\mathrm{f}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}})\left(\mathbf{p}\right)\parallel =\mathrm{n}-1$, for all $0\ne \mathbf{p}=(p_1,\dots ,p_n)\in K^n$. Without loss of generality assume $p_1\ne 0$. By setting suitable order on $f_{ij}$’s (that is $f_{12},f_{13},\dots ,f_{1n},f_{23},f_{24},\dots ,f_{n-1n}$), the first half of the Jacobian matrix is represented by the following matrix:

$$\left(\begin{array}{ccccc}{y}_2\hfill & -y_1& 0\cdots & 0& 0\\ y_3\hfill & 0& -y_1\cdots & 0& 0\\ ⋮\hfill \\ y_n\hfill & 0& 0\cdots & 0& -y_1\\ 0\hfill & y_3& -y_2\cdots & 0& 0\\ 0\hfill & y_4& 0\cdots & -y_2& 0\\ ⋮\hfill \\ 0\hfill & 0& 0\cdots & y_n& -y_{n-1}\end{array}\right)$$

Multiply the first row by $y_1^{-1}{y}_3$ and add it to the n’th row, and multiply the first row by $y_1^{-1}{y}_4$ then add it to the $n+1$’th row, and in the same way multiply the first row by $y_1^{-1}{y}_n$ and add the result to the $2n-3$’th row. Continuing this pattern for the second row to the $n-1$’th row. We observe that all rows become zero except the first $n-1$ rows, so $\mathrm{rank}\parallel (\frac{\partial {\mathrm{f}}_{\mathrm{i}}}{\partial {\mathrm{x}}_{\mathrm{j}}})\left(\mathbf{p}\right)\parallel =\mathrm{n}-1$. Since $\mathbf{p}$ is arbitrary, G is edge smooth. ☐

Example 1. 

Let $G=K_4$ and $S=K[x_1,\dots ,x_4,y_1,\dots ,y_4]$. We have:

$$J_G=<f_{12},f_{13},f_{14},f_{23},f_{24},f_{34}>$$

and

$$\dim \frac{\mathrm{S}}{{\mathrm{J}}_{\mathrm{G}}}=5.$$

By the appropriate order on $f_{ij}$’s we have:

$$\left(\begin{array}{cccc}{y}_2\hfill & -y_1& 0& 0\\ y_3\hfill & 0& -y_1& 0\\ y_4\hfill & 0& 0& -y_1\\ 0\hfill & y_3& -y_2& 0\\ 0\hfill & y_4& 0& -y_2\\ 0\hfill & 0& y_4& -y_3\end{array}\right)$$

By using the same way explained in the proof of Theorem 2, the rank of this matrix is 3 at any nonzero point of $K^4$. So G is a edge smooth graph.

The following theorem characterizes all edge singular graphs. Two conditions introduced in this theorem can be checked algorithmically. This theorem also shows that edge singularity is just a combinatorial property and does not depend on K.

Theorem 3. 

Let G be a simple connected graph on the vertex set $\left[n\right]$. The graph G is edge singular if and only if there exists $S\subset \left[n\right]$ which satisfies the following conditions:

1.

$S\ne \varnothing$ and for each $i\in S$ one has $c(S\setminus \{i\left\}\right)<c\left(S\right)$.

2.

$c\left(S\right)<n-\left|S\right|$.

Proof. 

Assume that there is some $S\subset \left[n\right]$ that satisfies conditions 1 and 2. By corollary 3.9 [2] the first condition implies that $P_S\left(G\right)\in \mathrm{Min}{\mathrm{J}}_{\mathrm{G}}$. Let $G_1,\dots ,G_{c\left(S\right)}$ be the connected components of $G_T$. Put the following labeling for the vertices of G;

• $v_1,\dots ,v_s$ are the vertices corresponded to S,
• $v_{s+1},\dots ,v_{t_1}$ are the vertices of $G_1$,
• $v_{t_1+1},\dots ,v_{t_2}$ are the vertices of $G_2$,

⋮

• $v_{t_{c\left(S\right)-1}+1},\dots ,v_n$ are the vertices of $G_{c\left(S\right)}$.

Now the Jacobian matrix of $P_S\left(G\right)$ has the following form;

$$\left(\begin{array}{cccccccccc}{A}_1\hfill & 0& 0& \cdots & 0& 0& 0& 0& \dots & 0\\ 0\hfill & 0& 0& \dots & 0& A_2& 0& 0& \dots & 0\\ 0\hfill & B_1& 0& \dots & 0& 0& D_1& 0& \dots & 0\\ 0\hfill & 0& B_2& \dots & 0& 0& 0& D_2& \dots & 0\\ ⋮\hfill & ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0\hfill & 0& 0& \dots & B_{c\left(S\right)}& 0& 0& 0& \dots & D_{c\left(S\right)}\end{array}\right)$$

where $A_1$ and $A_2$ are $\left|S\right|\times \left|S\right|$ identity matrices and $\left(B_1\right|D_1),\dots ,\left(B_{c\left(S\right)}\right|D_{c\left(S\right)})$ are the Jacobian matrices of $J_{{\tilde{G}}_1},\dots ,J_{{\tilde{G}}_{c\left(S\right)}}$ respectively.

By choosing $\mathbf{Q}=(Q_1,\dots ,Q_{2n})\in K^{2n}$ as the following

$$Q_i=\left\{\begin{array}{ccc}1\hfill & & i\in S\\ 0\hfill & & Otherwise\end{array}\right.$$

the rank of Jacobian matrix of $P_S\left(G\right)$ at $\mathbf{Q}$ is equal to $2\left|S\right|$. On the other hand we know that;

$$2n-\dim \mathrm{Z}\left({\mathrm{P}}_{\mathrm{S}}\left(\mathrm{G}\right)\right)=\mathrm{n}+\left|\mathrm{S}\right|-\mathrm{c}\left(\mathrm{S}\right).$$

Since

$$c\left(S\right)<\left|T\right|=n-\left|S\right|,$$

hence

$$2\left|S\right|<n+\left|S\right|-c\left(S\right).$$

So G is edge singular.

Now suppose that G is an edge singular graph. Then there is some $S\subset \left[n\right]$ that $P_S\left(G\right)\in \mathrm{Min}{\mathrm{J}}_{\mathrm{G}}$, and there exists nonzero $\mathbf{Q}$ in $K^{2n}$ such that the rank of the Jacobian matrix of $P_S\left(G\right)$ at $\mathbf{Q}$ is less than $n+\left|S\right|-c\left(S\right)$. If $c\left(S\right)=n-\left|S\right|$, then this rank is less than $2\left|S\right|$, but this is a contradiction since the rank of the Jacobian matrix of $P_S\left(G\right)$ is greater than or equal to $2\left|S\right|$. Hence we have $c\left(S\right)<n-\left|S\right|.$ Moreover, note that S is not empty since if S is empty then $P_S\left(G\right)$ is equal to the binomial edge ideal of the complete graph, but complete graphs are edge smooth by Theorem 2. ☐

Example 2. 

Let G be the following graph:

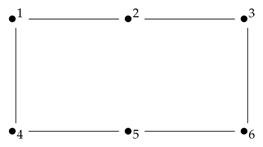We set $S=\{1,6\}$. This S satisfies the mentioned conditions in Theorem 3, then G is edge singular.

The following example illustrates Theorem 2 is not two sided that is any edge smooth graph is not necessarily complete. Also this shows any non complete graph is not necessarily edge singular.

Example 3. 

Let G be the following graph:

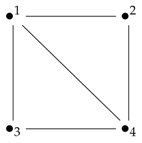There does not exist $S\subset \left[n\right]$ that satisfies the conditions of Theorem 3. Hence G is edge smooth.

Corollary 4. 

For all $n\ge 5$, $G=C_n$ is a singular graph.

Proof. 

Put $S=\{1,4\}$. $G_{\left[n\right]\setminus S}$ separates into two connected components (in case $C_5$, it separates into an edge and an isolated vertex). Also S satisfies the first condition of Theorem 3, so a cycle with n vertices, $n\ge 5$, is a singular graph. ☐

Corollary 5. 

A tree is a singular graph if the number of vertices which are not leaf, is at least 2.

Proof. 

Assume that the three of the non-leaf vertices are $k,k+1$. Put $S=\left\{k\right\}$. One can check easily that S satisfies the conditions of Theorem 3. ☐

Example 4. 

Let G be the following graph:

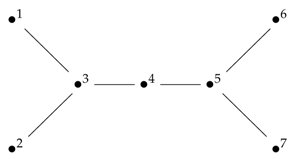Put $S=\left\{4\right\}$. S satisfies the conditions of Theorem 3.

Corollary 6. 

For all $n,m$, ${\mathcal{K}}_{n,m}$ is a smooth graph.

Proof. 

Let $S\subset [n+m]$. $G_{[n+m]\setminus S}$ is a connected graph unless either S contains n vertices of a part of G or m vertices of the other part. If S just contains the whole vertices of one part of G, then S does not satisfy the second condition of Theorem 3, and if S is the another subset of $[n+m]$, S does not satisfy the first condition of Theorem 3. So ${\mathcal{K}}_{n,m}$ is a smooth graph. ☐

Remark 1. 

With the same argument it is concluded that all complete multipartite graphs are edge singular.

3. Conclusions

Smoothness is a geometric property which could be studied by algebraic tools. In this paper smoothness of some varieties are studied by algebraic and combinatorial properties of corresponded combinatorial objects.