Abstract
In this paper, the interconnection between the cohomology of measured group actions and the cohomology of measured laminations is explored, the latter being a generalization of the former for the case of discrete group actions and cocycles evaluated on abelian groups. This relation gives a rich interplay between these concepts. Several results can be adapted to this setting—for instance, Zimmer’s reduction of the coefficient group of bounded cocycles or Fustenberg’s cohomological obstruction for extending the ergodicity of a -action to a skew product relative to an evaluated cocycle. Another way to think about foliated cocycles is also shown, and a particular application is the characterization of the existence of certain classes of invariant measures for smooth foliations in terms of the -cohomology class of the infinitesimal holonomy.
1. Introduction
One of the most important tools to study the dynamical properties of an ergodic group action is given by the cohomology of its measurable 1-cocycles. For instance, Furstenberg’s example (see [1]) of a minimal dynamical system on the torus which is minimal but non-Lebesgue strictly ergodic can be interpreted as an obstruction for some continuous 1-cocycles to be cohomologically trivial in the measurable cohomology. Zimmer’s results relative to semisimple Lie group ergodic actions and their lattices are stated in terms of the cohomology of their actions [2]. Again, 1-cocycles carry their own importance in terms of rigidity and amenability [3,4]. Zimmer pointed out the geometric interpretation of the cohomology of group actions as the cohomology of a measurable lamination in the 1980s , which led to a Mostow rigidity theorem for some kind of measured foliations [5]. Cocycles associated with pseudogroup actions or holonomy grupoids are the direct generalization of cocycles associated to group actions where the infinitesimal holonomy cocycle is the best example (see e.g., [6,7]).
The measurable cohomology of foliations can be traced back to the works of Connes [8,9] and Heitsch and Lazarov [10], and it was studied in full generality by Bermudez and Hector [11,12,13]. In [14], the author introduced the singular version of this cohomology which was a missing piece in order to apply the full power of algebraic topology to this setting. The author was initially motivated by the relation between the cup product of this cohomology and the tangential Lusternik–Schnirelmann category of measured foliations [15]. It is required to mention that, in this work, we deal with generalized measurable laminations in the sense that leaves could not be manifolds but only path connected and locally compact Polish spaces, for instance connected and locally compact graphs or CW-complexes (see e.g. [16] for formal definitions). We shall use the word lamination for such generic foliations and the word foliation if every leaf is a manifold.
The purpose of this paper is to extend another bridge between these concepts. It is important to note that only abelian groups are considered here as coefficient groups, whilst non-abelian coefficients can be considered for group actions or foliated cocycles (e.g., Γ-structures).
The paper is organized in five sections. The first section serves as an introduction to the definitions of singular and simplicial cohomology of measured laminations and the cohomology of group actions. It is shown that, for a given group action of a discrete group, there exists a measurable lamination where its first cohomology group is isomorphic to the cohomology of that action. In fact, it is possible to obtain a measurable foliation with this property.
The second section is devoted to prove an analogue of a Zimmer’s result (see [2]) for ergodic group actions: if an R-evaluated 1-cocycle satisfies that is precompact for every , then ω is cohomologous to a 1-cocycle evaluated in a compact subgroup of R. This result is extended to higher dimensional cohomology groups.
In the third section, some classical results due to Furstenberg (see [1]) are translated to our setting of measurable laminations. Furstenberg shows obstructions for a -action given by a skew product over a strictly ergodic process to be also strictly ergodic, the obstruction is measured by the triviality of some cohomological classes. This result is extended to the case of measurable cohomology of laminations. In this section, it is also introduced the first group of continuous cohomology—it is no surprise that the obstruction for a skew product to be minimal is given by the triviality of some cohomology classes in the continuous category.
The fourth section deals with the infinitesimal holonomy cocycle associated with a smooth foliation. This cocycle induces a closed -valued 1-cochain in an associated measurable lamination. Observe that the Lebesgue measure is always quasi-invariant for any (transversely) smooth foliation. For Lebesgue ergodic smooth foliations, the triviality of this cocycle in -cohomology is equivalent to the existence of invariant measures in the Lebesgue class with Radon-Nikodyn derivative, and it is also shown that this is equivalent to a boundedness condition on the infinitesimal holonomy.
The final section gives further comments and other possible generalizations of well-known results of cohomological dynamics, as the Livsic theorem, to the setting of leafwise cohomology.
2. Cohomology of Measured Laminations
The purpose of this section is to introduce the singular and simplicial cohomology of measurable laminations. It will be necessary to introduce a wider category of objects that are able to manage the dual character of measurable laminations (the measurable structure and the leaf topology). A measurable topological space, or MT-space, is a set X endowed with a σ-algebra and a topology. Usually, measure theoretic concepts will refer to the σ-algebra of X, and topological concepts will refer to its topology; in general, the σ-algebra is different from the Borel σ-algebra induced by the topology. An MT-map between MT-spaces is a measurable and continuous map. An MT-isomorphism is a map between MT-spaces, which is a measurable isomorphism and a homeomorphism.
Obvious examples are topological spaces with the Borel σ-algebra and measurable spaces with the discrete topology. Let X and Y be MT-spaces. Suppose that there exists a measurable embedding that maps measurable sets to measurable sets. Then, X is called an MT-subspace of Y. The product is also an MT-space with the product topology and σ-algebra.
Let “∼” be an equivalent relation on an MT-space X. The quotient is an MT-space with the quotient topology and the σ-algebra generated by the projections of measurable saturated sets of X.
A Polish space is a completely metrizable and separable topological space. A standard Borel space is a measurable space isomorphic to a Borel subset of a Polish space. Let S be a standard Borel space and let P be a Polish space and let us consider the Borel σ-algebra on P. will be endowed with the structure of MT-space defined by the product σ-algebra and the product of the discrete topology on S and the topology of P.
A measurable chart on an MT-space X is an MT-isomorphism , where U is open and measurable in X, S is a standard Borel space, and P is a locally compact, connected and locally path connected Polish space; let us remark that P and T depend on the chart. The sets are called plaques of φ, and the sets are called associated transversals of φ. A measurable atlas on X is a countable family of measurable charts whose domains cover X. A measurable lamination is an MT-space that admits a measurable atlas. Observe that we always consider countable atlases; therefore, the ambient space is also a standard space. The connected components of X are called leaves. An example of measurable lamination is a usual foliation with the ambient Borel σ-algebra and the leaf topology. The notation will be used to denote the collection of leaves and will denote the underlying MT-space. For every , the leaf of that contains x will be denoted by .
According to this definition, the leaves are second countable connected manifolds, but they may not be Hausdorff. Therefore, in what follows, it will be assumed that is Hausdorff, locally path connected and locally compact. Under these conditions, leaves are locally compact and path connected Polish spaces.
In the case where the plaques of each chart are homeomorphic to a Euclidean ball, we shall use the term measurable foliation. In the case where the leaves are graphs the term measurable graph will be used.
A measurable subset is called a transversal if its intersection with each leaf is countable [10]. Let be the family of transversals of X. This set is closed under countable unions and intersections, but it is not σ-algebra. A transversal meeting all leaves is called complete.
A measurable holonomy transformation is a measurable isomorphism , for , which maps each point to a point in the same leaf. A transverse invariant measure on X is a σ-additive map, , invariant by measurable holonomy transformations. The classical definition of transverse invariant measure in the context of foliated spaces is a measure on topological transversals invariant by holonomy transformations (see e.g., [6]). These two notions of transverse invariant measures agree for foliated spaces [8]. When the sets of null measure are invariant by holonomy transformations, the measure μ will be called quasi-invariant. A measured foliation is a pair where μ is a finite measure over some complete transversal and quasi-invariant for . Fix a complete transversal T of so that is a finite measure space. Given a set , let denote the set given by the union of all the leaves meeting A, this set will be called the saturation of A.
Definition 1.
The measured foliation will be called ergodic if for every measurable subset , the set (which is always measurable) has null or full measure. This is equivalent to say that every leafwise constant measurable map is almost everywhere constant.
Remark 1.
In the world of measured laminations, holonomy transformations can be still interpreted as the slice of a transversal following a leafwise path [14]. For this, it is always assumed that our atlas is regular, i.e., plaques are precompact spaces in the corresponding leaf, every intersecting pair of measurable charts of a given atlas is contained in another measurable chart (not necessarily in the given atlas), and any chart meets a finite number of other charts. However, the concept of germ of a measurable holonomy transformation makes no sense since transverse topology is needed, i.e., from a measurable point of view, the holonomy group of a leaf is trivial. In a measured lamination, the ergodic components play the role of minimal sets for foliations; therefore, ergodicity will be a natural hypothesis with which to work.
Example 1 (Measurable suspensions).
Let P be a locally compact, connected, locally path connected and semi-locally 1-connected Polish space, and let S be a standard space. Let denote the group of measurable transformations of S. Let
be a homomorphism. Let be the universal covering of P and consider the action of on the MT-space given by
The corresponding quotient MT-space, denoted as , will be called the MT-suspension of h. is a measurable lamination, is a complete transversal, and its leaves are covering spaces of P. See Figure 1 for a clarifying picture.
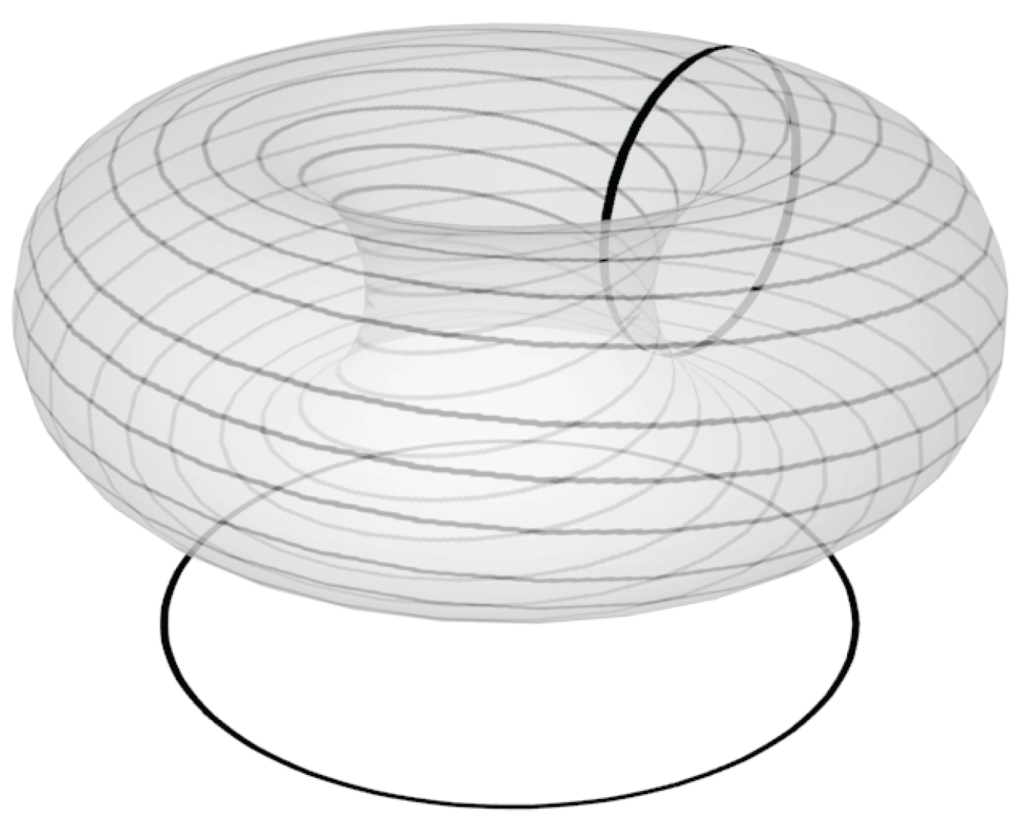
Figure 1.
The simplest suspension of a circle transformation over . Bold circles represent the fiber and base spaces.
The measurable cohomology of MT-spaces is the natural version of a cohomology theory, which takes into account the mixing of their topology and measurable structure. It is also supposed that the considered coefficient groups, which will be denoted by R, are standard abelian groups, i.e., an admissible coefficient group is an abelian group and a standard space where the product and the inverse maps are measurable. In the world of group actions, cocycles evaluated in non-abelian groups (e.g., or ) are of great importance, however the introduction of a non-commutative cohomology theory is beyond the purpose of this work.
Definition 2 (Measurable simplex).
A measurable simplex is the MT-space induced by the product where S is a standard space and is the canonical N-simplex. A measurable singular simplex on is an MT-map .
Let ω be a usual singular n-cochain over a coefficient group R, as usual, an inversion of orientation is translated to an inversion in R. It is said that ω is measurable if , , is measurable for all measurable singular n-simplices σ. The set of measurable cochains is a subcomplex of the complex of usual cochains since the coboundary operator δ preserves the measurability. This measurable subcomplex is denoted by , and the coboundary operator restricted to this complex is also denoted by δ.
The singular measurable cohomology is defined as usual by
Any MT-map defines a cochain map by . Since it commutes with the coboundary operator, it induces a homomorphism between measurable cohomology groups, .
The importance of the measurable singular cohomology is the fact that it has substantial theoretical advantages, which allows for adapting easily classical results from algebraic topology as excision, functoriality, homotopy invariance, Mayer–Vietoris or cup product in relative cohomology—another bonus is that it can be applied to every MT-space. This topic is treated deeply in [14]. However, for explicit calculus, simplicial cohomology is easier to be analyzed. They are fully described in [11,12,13] and, in [14], it is shown that simplicial and singular measurable versions are isomorphic, in particular, it does not depend on the (measurable) simplicial description of leaves.
Definition 3
(Measurable triangulation [11]). A measurable triangulation of a measurable lamination is the assocation of a structure of simplicial complex to each leaf of , it will be denoted by . Measurability must be understood in the following way. For each n, the set of barycenters of n-simplices, which will be denoted by , is a (measurable) transversal and the function , mapping a barycenter to the embedding given by the triangulation , is also measurable, where is the canonical n-simplex. The term measurable simplicial lamination will be also used for a measurable lamination endowed with a measurable triangulation.
Let b a barycenter of some n-simplex in , then will denote the simplex containing b, i.e., the map , will denote the set of faces of the canonical n-simplex and .
Remark 2.
A simplicial complex does not need to be a manifold. This is the case for measurable graphs.
A measurable simplicial lamination will be denoted by the pair . An n-cochain over a standard abelian group R is a measurable map
such that . The orientation refers to the orientation induced by the standard orientation of the canonical n-simplex in the domain of and to the inverse orientation. In order to relax the notation, we use only the notation b for signed barycenters and should denote the inverse orientation on the corresponding simplex. In this sense, we can define the set formed by the face barycenters of with a positive sign if the orientation agrees with the orientation in or negative otherwise. Analogously, we shall use the signed notation for oriented simplices, where will denote that simplex with the opposite orientation. Clearly, a measurable n-cochain is determined by the values on , in this sense n-cochains can be interpreted as measurable maps . This relaxed notation will be used only for the cases and . Let denote the set of simplicial n-cochains; this set is endowed with a group structure induced by R. We define the coboundary operator as usual by ,
Clearly, and we can define the cohomology groups as usual:
Remark 3.
In the case of a measured lamination , the above definitions can be applied in an almost everywhere sense (a.e. in what follows). This means that exact cocycles satisfy a.e., and this leads to the concept of a.e. cohomology or measured cohomology. The cohomology groups in this sense will be denoted by .
In a similar sense, when or , it can be introduced the cohomology, which we denote by , . For a locally compact R, the cohomology is obtained by considering cochains which are taking its values a.e. in a compact subset of R.
It is also obvious that the definition of simplicial cohomology can be extended to the case of polygonal subdivisions on the leaves, where simplices are replaced by compact linear regions of the Euclidean space.
3. Cohomology of Measurable Group Actions and Measurable Laminations
The cohomology of measured group actions was introduced to provide invariants useful to detect the wild dynamical behavior shown by non-amenable group actions [4]. For the amenable case, a measured group action is orbit equivalent to a -action [17] and measurable dynamics are not so interesting.
Let G be a locally compact separable group acting (on the right) by measurable isomorphisms on a measured standard Borel space , where μ is a quasi-invariant measure. Let R be a standard group (not necessarily conmutative). A 1-cocycle for the action is a map
such that for all and and it is said that ω and θ are cohomologous if there exists a measurable function such that a.e. and all , when R is abelian this is written as .
The right action will be denoted by , however, the notation will be ignored if it is clear in the context (). Let denote the set of 1-cocycles up to cohomology.
Recall that only abelian coefficient groups R and finitely generated G are considered in this work, the remaining cases (G a continuous group and R non-abelian) are of great importance ([2,18]) but they will not be treated in this work.
Assuming G finitely generated and R abelian, let be a minimal system of generators of G and let be the wedge union of n circles. Of course, with generators given by the loops of each circle component. Let us consider the homomorphism
which allows for defining the MT-suspension . Clearly, is a measurable simplicial lamination, and, moreover, a measurable graph where the 0-simplices correspond with , and the 1-simplices are provided by the lifts of the generators to each leaf, their barycenters are in a natural bijection with n copies of T. A positive orientation on the edges is provided by .
Now, we want to attach 2-cells to this measurable graph in the following way. Whenever we have a non trivial irreducible relation , a chain of 2-cells bounded by the respective edges in is attached. This is done by attaching a 2-cell to the loop given by the relation in a minimal set of relations. Let be the resulting measurable cellular lamination. To obtain a simplicial structure on leaves, we can add edges joining the barycenter of each added 2-cell to each vertex in its boundary. It is clear that these triangulations perform a structure of measurable triangulation on which will be denoted by .
Remark 4.
It is not important, for the definition of , the fact that the sets of generators and relations are minimal (whenever they perform a presentation of the given group). However, the space depends strongly on the choice of generators and relations (even minimal). This can be seen directly in the points where the isotropy group is trivial, the leaf of meeting s is homeomorphic to the Cayley graph of G associated to where every simple loop is bounded by at least one chain of 2-cells.
When the isotropy group is not trivial, interesting topology can appear. For instance, assume that some generator e satisfies the relation and for some s. Thus, in the construction of the leaf passing through s, we have to attach a 2-cell to the loop induced by e but in such a way that its boundary is a double covering of that loop. This produces a projective plane embedded in that leaf. It is clear that different relations can produce other embedded surfaces without any limitations.
The main point of this construction is the following observation: although the topology of the leaves can change wildly, the first cohomology group of leaves is invariant.
Proposition 4.
Let G be a finitely generated group acting by measurable isomorphisms on a standard measure space and let R be a standard abelian coefficient group. Then and are isomorphic.
Proof.
Let us consider the above CW-structure on the leaves of and identify the set of 1-barycenters of with . Therefore, a 1-cocycle ω induces a simplicial 1-cochain of via the restriction map. The cocycle condition implies that for all , hence is closed since the attached 2-cells occur in a minimal set of relations for the group. Remark that, since 2-cells were attached on a minimal set of relations, every relation (not necessarily irreducible) induces a 1-simplicial chain bounded by a chain of 2-cells.
Clearly, 0-cocycles are naturally identified since . If ω is exact then a.e. and by definition. Therefore, defines an injective map at the level of 1-cohomology groups.
Given a closed 1-cochain , it defines an R-value on any chain of 1-simplices just by summing over the values on each simplex of the chain. We have to show that it determines a 1-cocycle so that . Let us define
Observe that θ extends naturally to a map on the simplicial chains of , in fact, a complete definition of cochain is given as a homomorphism from the abelian group of simplicial chains to R, and the map θ is a way to give values for the generators of the group of simplicial chains. The above definition of ω is consistent with the value of θ in the simplicial chain given by a oriented path of edges with initial point in and determined by the sequences of generators . However, the above equation does not guarantee the cocycle condition for ω. For an arbitrary measurable cochain, two different words representing the same element in G can give different values in R. This is the point where we use the fact that ω is closed. Let , be words in representing the same element , then is a trivial relation for G, and therefore (considering )
since the edges provided by the word bound a chain of 2-cells. The above equality means that as desired. ☐
Example 2.
In the case where G is a free group (with the usual presentation), there are no relations and, therefore, .
Example 3.
The suspension of two circle rotations gives a well known foliation over with base . In this case, this foliation agrees with the space . This is not the case for a suspension of three circle rotations. In this case, three minimal relations appear (the commutators of each pair of generators of ) and can be given as a 2-skeleton on the suspension foliation in with base . Since the MT-spaces considered only differ by 3-cells, the first cohomology groups of and the suspension foliation on are isomorphic.
The above example suggests that under certain hypothesis we can replace by a measurable foliation, this happens when G is the fundamental group of a (closed) manifold such that the fundamental region in the universal covering space is an n-cell. This is the case for surfaces of genus . However, in general, the homomorphism is not a monomorphism, this means that non-trivial words in (or in G) can act trivially, which leads to a non-trivial (in cohomology) loop on every leaf, even when is a monomorphism it could happen that a non-trivial word induces an a.e. trivial map leading to a similar issue. This can be represented by a measurable 1-cochain (evaluating by a constant in these loops and 0 otherwise). Thus, non-trivial classes represent non-trivial dynamics whenever the action of is a.e. faithfull or essentially free, this depends on our meaning of “non-trivial dynamics”. In the a.e. faithful case, non-trivial classes with trivial dynamics can arise from a set of fixed points of positive measure, but interesting things can be happening outside of this set. In the essentially free case, a non-trivial cohomology class is always detecting dynamics, but this is a more restrictive condition. Observe that, for a.e. faithful (resp. essentially free), it is equivalent to say that fixed points in S have non-full (resp. null) measure for any element of G.
When G is finitely presented, then it is well known that there exists a smooth closed 4-manifold with fundamental group isomorphic to G. Although the fundamental region for this 4-manifold could not be diffeomorphic to a disk, this region must be simply connected and the previous argument is easily adapted. This can be summarized as follows:
Proposition 5.
Let G be a group with finite presentation acting by measurable isomorphisms in . Let R be a standard abelian group, then there exists a measured foliation of dimension 4 such that is isomorphic to . This foliation is given by the suspension process of the G-action over a closed 4-manifold with a fundamental group isomorphic to G.
4. Reduction of the Coefficient Group
Assume for this section that R is a topological abelian group which is a locally compact Polish space.
Definition 6.
A cocycle is said to be bounded if the set is precompact for all .
We want to adapt the following result of Zimmer.
Proposition 7
(Zimmer [2]). Let be a measured ergodic action on a standard measure space . If ω is a bounded cocycle then ω is cohomologous to a cocycle evaluated on a compact subgroup of R.
The next definition is introduced in order to adapt the notion of bounded cochain.
Definition 8.
Let be the set of (finite) simplicial paths formed by an ordered finite family of oriented edges of the 1-skeleton of with initial point in , so that the end point of an edge is the initial point of the next one (with the eventual exception of the last edge). A (measurable) cochain is called bounded if is a precompact set for all . It is said that ω is uniformly bounded if there exists a measurable set of full measure so that is a precompact set.
Remark 5.
In the above section, where the cohomology of group actions was translated to the language of the cohomology of measurable laminations, the role of the edges of the 1-skeleton is the analogue of the generators of the group. Thus, the 1-dimensional simplicial paths can be thought as an analogue of the elements of the group.
Proposition 9.
Let ω be a measurable 1-cochain of an ergodic simplicial lamination . If ω is a bounded cochain, then ω is cohomologous to a closed cochain evaluated on a compact subgroup of R.
Proof.
The proof is a direct application of Zimmer’s original argument [2]. Since R is Polish, the space of compact sets in R is a complete and separable metric space with the Hausdorff metric. Let , and let denote the initial and end points of the edge containing b with the induced orientation. Since is a measurable function, the map , is measurable. Clearly, . If and there exists a sequence with in , then, by compactness, there exists a subsequence converging to such that . Therefore, the orbits of under the natural R action are closed. As a consequence, the quotient space is Polish. Since , the sets represent the same equivalence class in .
We want to show that there exists an equivalence class with for almost every . Remark that is a complete transversal and is ergodic relative to the action of the measurable holonomy pseudogroup, the measurable map
is constant on each orbit (which is the intersection of each leaf with ) and thus it is a.e. constant by ergodicity. Let , , and let be a measurable section, i.e., for all , (and ). The function satisfies, for almost every :
Therefore, ω is cohomologous, via φ, to a cochain θ which takes values a.e. in the stabilizer of B, , which is compact since B is compact. By redefining θ in a negligible set by 0 the proof is complete. ☐
Corollary 10.
Let ω be a measurable 1-cochain of an ergodic simplicial lamination . If ω is a uniformly bounded cochain then ω is -cohomologous to a closed cochain evaluated on a compact subgroup of R.
Proof.
Observe that a uniformly bounded cochain is necessarily an element of . All the arguments in the above proof works verbatim, and it is only required to check that the 0-cochain is essentialy bounded. Since , it follows that the image of φ is contained in a.e. which is a compact set by hypothesis. ☐
Remark 6.
Observe that the cochains are not required to be closed which is the natural translation of cocycles. This comes from the fact that any measurable cochain satisfies for free a cocycle condition since they can be seen as a homomorphism on the group of 1-simplicial chains, and this is enough for the above argument to work. From another point of view, arbitrary cochains are closed cochains relative to the measurable lamination defined by the 1-skeleton of .
The above proposition has an analogue for higher dimensional cochains, and this will need the introduction of new technology.
Definition 11.
A k-simplicial path starting at is a finite and ordered family of pairs where are oriented k-simplices and are (signed) barycenters of -simplices for all i and for some , such that
- and the sign of is determined by the induced orientation.
- and represent different faces of for all .
Definition 12.
For , let the set of k-simplicial paths starting at b. A measurable 1-cochain is bounded if is precompact for all .
Definition 13.
A measured simplicial lamination is said to be k-coherent if, for a.e. leaf, any pair of different non-oriented -simplices in the same leaf is connected by a k simplicial path and a.e. leaf contains simplices of dimension k. Observe that this is the case for measured simplicial foliations. For , coherency is automatic since leaves are path connected by definition (whenever a.e. leaf is not a singleton).
Definition 14.
A measurable simplicial lamination is said to be k-evenly triangulated if there exists a measurable set so that for every , contains exactly one element of .
Remark 7.
A barycentric subdivision of any triangulation is always even in the above sense. This is provided by the fact that the barycentric subdivision of any old simplex can be seen as a subdivision by attached pairs of new k-simplices, the faces (with a choice of orientation) between these attached pairs perform the set . This is the reason to use the word “evenly” for this kind of triangulation.
Proposition 15.
Let ω be a measurable k-cochain, , of an ergodic, k-coherent and k-evenly triangulated measured lamination . If ω is a bounded cochain then ω is uniformly bounded and cohomologous to a k-cochain evaluated on a compact subgroup of R.
Proof.
As before, let denote the Polish space given by the compact sets of R with the Hausdorff metric. Let and set an enumeration of face barycenters with the induced orientations. It is easy to check the following equation
By a symmetric argument we get the following chain of equations:
Thus for all . This is only possible if for all . An intuitive way to see this relation is by observing that a simplicial path starting at induces another simplicial path starting at for pairwise different , observe that this is only true for since an intermediate third face, , is needed to perform . Now, consider the involution , . As before is Polish. Since , the map
is a.e. constant if the measurable simplicial lamination is k-coherent. By ergodicity, there exists B, a compact subset of R, such that for a.e. . Therefore, ω is uniformly bounded.
Now, a simple calculation shows that for a.e. , or depending on whether or . If b and c are barycenters of contiguous k-simplices with compatible orientations (they form a k-simplicial path), then and thus which is a compact subgroup of R. If is a k-simplicial path of length 3, then a similar argument shows for a.e. in these conditions. More generally, if are connected by a k-simplicial path then either or belong to according to the length of the path being even or odd. Moreover, by ergodicity, either or belong to for a.e. (not necessarily in the same leaf).
Assume that there exists a k simplicial loop of even length based on a k-simplex b (b counts twice for the length of that loop), therefore, and, as a consequence, , which is also a compact subgroup. Observe that any other k-simplex in that leaf admits a simplicial loop of even length, suppose that is an even simplicial loop starting on and ending at , then is another even simplicial loop starting at c where is a k-simplicial path joining and provided by coherency. Therefore, ω itself takes values in the compact subgroup . Observe that the measurable function , defined as iff b has a simplicial loop of even length, is leafwise constant. Therefore, if the set of these simplices is non-negligible, then ω itself takes its values a.e. in a compact subgroup of R by ergodicity.
Assume now that a.e. leaf does not admit simplicial loops of even length and is k-evenly triangulated by . Therefore, there exists a measurable set so that each simplex of dimension k has exactly one face barycenter (up to orientation) in . Since there are not even loops, the measurable map mapping to 1 if and if , is well defined whenever (in which case ω takes its values in ). This gives a partition of into two subsets: . The main point is that each element has exactly one face barycenter in . Let be the measurable set obtained from in order to match the induced orientations of , it agrees with up to orientation. Let us define the measurable cochain as iff and 0 otherwise. It follows that is evaluated in completing the proof. ☐
Remark 8.
Let us remark that the reduction of ω is given by a -cochain in . Therefore, the Proposition 15 holds for -cohomology.
Question 1.
It is unclear whether the above result holds for non k-evenly triangulated laminations. Observe that measured cohomology does not depend on the chosen triangulation [14]. Let us consider the k-skeleton, of , thus every k-cochain is closed. Barycentric subdivision provides a k-even triangulation of , and we can consider the isomorphism between the measured simplicial cohomology of and its barycentric subdivision. However, it is uncertain whether this isomorphism should respect bounded k-cochains (up to cohomology).
Observe that the above proof holds when a.e. leaf admits even k-simplicial loops (even in the non k-evenly triangulated case). In the case where a.e. k-simplicial loop is odd, Lusin–Novikov theorem on the existence of measurable sections (see Theorem 18.10 in [19]) might be enough to produce a measurable set with the properties of .
Example 4.
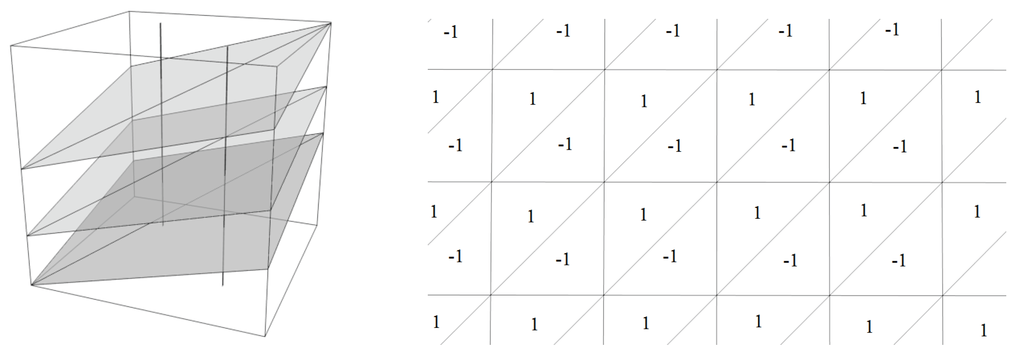
Let consider the suspension of two rationally independent circle rotations , , . The Lebesgue measure is an invariant and ergodic measure for . Leaves are planes, and we can consider the measurable triangulation given by the 2-simplices with vertices and , . Let ω be the evaluated measurable 2-cochain ω so that and relative to a compatible orientation of the foliation, see Figure 2.

Figure 2.
Minimal linear foliation on with a leafwise triangulation. Vertical segments represent, after quotient, the set of 1-barycenters . The bounded cochain given in Example 4 is represented in a generic leaf.
Clearly, ω is bounded (every simplicial path gives value , 0 or 1). Therefore it is cohomologous to a 0 evaluated cochain (0 is the unique compact subgroup of ), i.e., ω is exact. Observe that this triangulation is 2-even and can be given by the diagonal edges of the triangulation. An invariant element in is the class of or . This is a toy example where the steps of the proof of the Proposition 15 can be checked directly.
5. Furstenberg’s Criteria for Minimality and Ergodicity of Skew Products
In this section, we generalize some classical results due to Furstenberg for continuous -actions. In [1], a cohomological criterium for the strict ergodicity of a skew product over a strictly ergodic transformation is obtained. Observe that in this section we are working on topological laminations. A formal definition can be found in [6], essentially they are defined by changing in our introductory definitions of measurable laminations the word “standard” by “locally compact and Polish” and measurable by “continuous”. For topological foliations, the notation refers to the ambient space. Furstenberg gives also a criterium for the minimality in the setting of continuous cocycles, this allows to produce continuous transformations of the torus which are minimal but not Lebesgue ergodic.
Our aim is to define the necessary objects and show that Furstenberg’s proofs can be adapted wihout major issues. This is in fact a way to show that Furstenberg’s work holds for discrete actions and opens the door to higher dimensional analogues.
Furstenberg assumes that the measure μ is invariant instead of quasi-invariant. This is not restrictive for continuous flows: since leaves are homeomorphic to or , they satisfy the Fölner condition, the averaging process [20] on any orbit produces an invariant measure supported in the closure of that leaf. However, in general, the existence of invariant measures is a high restriction. In this section, all the considered measures will be quasi-invariant and Radon. As usual, will denote the circle as the set of unimodular complex numbers and m will denote the normalized Lebesgue measure on the circle. Although is abelian, we shall use the multiplicative notation for the operations in .
Now, the Furstenberg’s criterium is stated in a different way from the original. In this version, nothing is said about strict ergodicity, but this is a price to pay in order to allow the inclusion of quasi-invariant measures.
Proposition 16 (Furstenberg).
Let be a Borel transformation (which induces a -action) on a compact Polish space and let be a quasi-invariant measure which is ergodic for this action. Let be a Borel function and let , . Then is a ergodic measure for T if and only if is not trivial in measured cohomology for every integer , i.e., in where is the suspension of over the circle.
Proof.
We refer to the original proof in [1] for more details. It relies on the following two points:
- μ is always a quasi-invariant measure for T. This is provided by using Fubbini in the product measure μ, the quasi-invariance of and the fact that m is fiberwise invariant.
- Let so that , since μ is a product measure we can express f as a fiberwise Fourier seriesfor . By using the invariance under T, one can easily check that for every . The ergodicity of shows that some is non essentially zero for . Since the saturation of the non-zero set of is also non-zero, and thus has full measure. Therefore, trivializes g in measured cohomology. Conversely, if then the function is T invariant and is not a.e. constant, so T is not ergodic.
Before proceeding to adapt the above proposition, it is necessary to explain the meaning of a leafwise continuous triangulation of a topological lamination. A measurable triangulation of a topological lamination is said to be continuous if the union of the barycenters (of all simplices) is a closed space in the ambient topology and for every convergent sequence of barycenters, the corresponding simplices converge in the Hausdorff metric. Observe that simplices associated to and b could have different dimensions. In the case of foliations on a smooth manifold where the leaves are smooth manifolds, a leafwise triangulation can be obtained by choosing a triangulation of the ambient manifold in general position with the foliation (see Figure 3). This provides a polygonal subdivision on leaves which can be refined to simplicial after a barycentric subdivision. Most of the interesting examples of topological laminations arise from minimal sets of usual foliations, so the existence of a leafwise triangulation is not so strong as it seems at first glance.
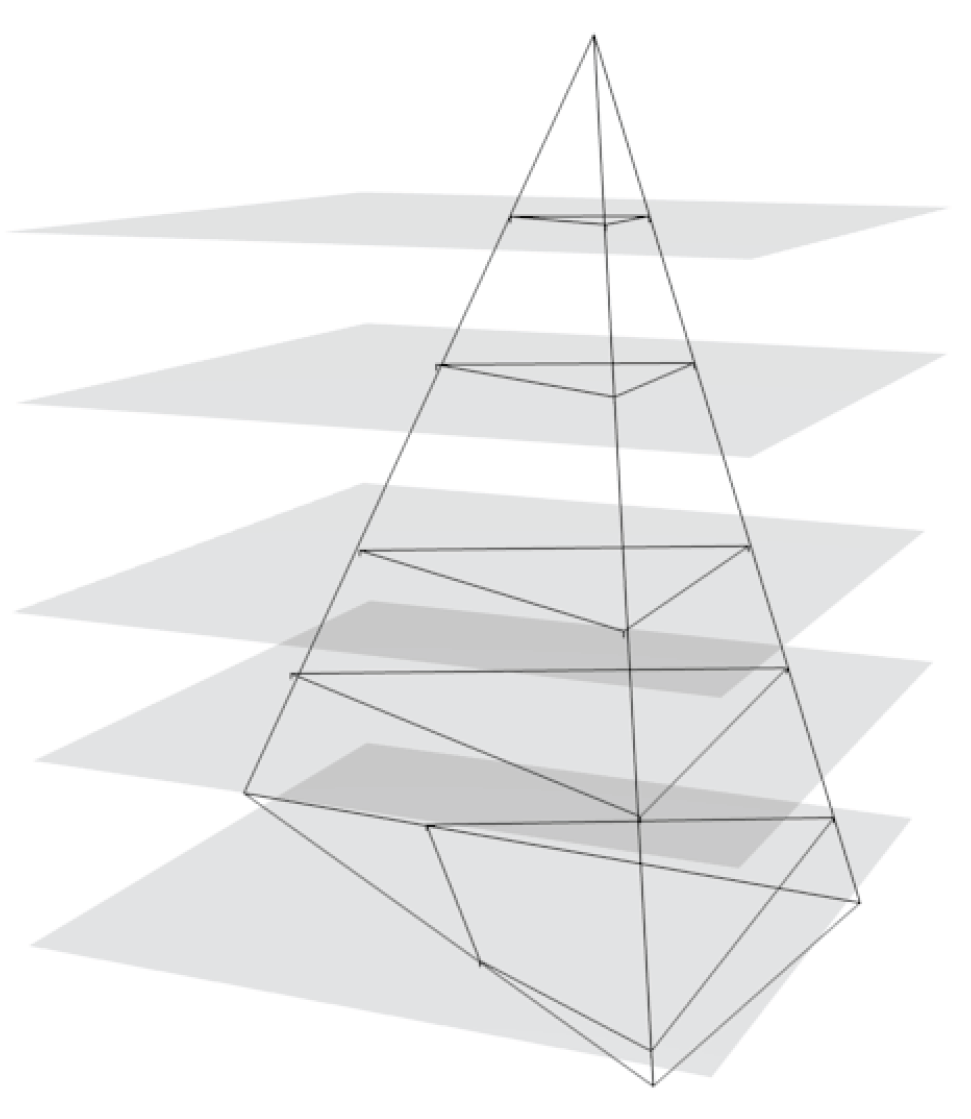
Figure 3.
Transverse intersection of a planar foliation with a 3-simplex in general position.
Now, it is time to translate the necessary objects and apply Furstenberg’s original proof. Of course, will be the set of 0-barycenters and must be now given by oriented edges. Whenever we consider the space , we can obtain a new topological foliation by translating each leaf of to each fiber , . This foliation can be seen as a “trivial skew product”. Its ambient space can fail to be a manifold in general (since is not a manifold in general), but we can at least perturb in the “direction” and ask what ergodic and topological properties of can be translated to the perturbed foliation.
When we deal with suspensions, the triangulation obtained by lifting a triangulation of the base manifold provides a leafwise continuous triangulation where each , , is homeomorphic to a disjoint union of closed sets homeomorphic to the fiber space. However, in the general case, can fail to be closed (check the Reeb component). In this case, it has accumulation points in .
Definition 17.
Let us consider , which is always a closed set. A continuous 1-cochain is a continuous map such that , i.e., g vanishes in its relative boundary.
Although is a complete transversal in the measurable sense it has, in general, singularities where bifurcations occur, this set of singularities agrees with . Recall that now the dynamics are generated by the holonomy maps associated to a 1-simplicial path of edges, we can assume that the domain and range are contained in whenever the initial point of the first edge and the end point of the last edge of the path are non-singular. If any of these points is singular, we can also assume that the domain and range are in but not as open subsets, this is done by considering the outer and inner transversal relative to a singular point and a 1-simplex defined below.
Definition 18.
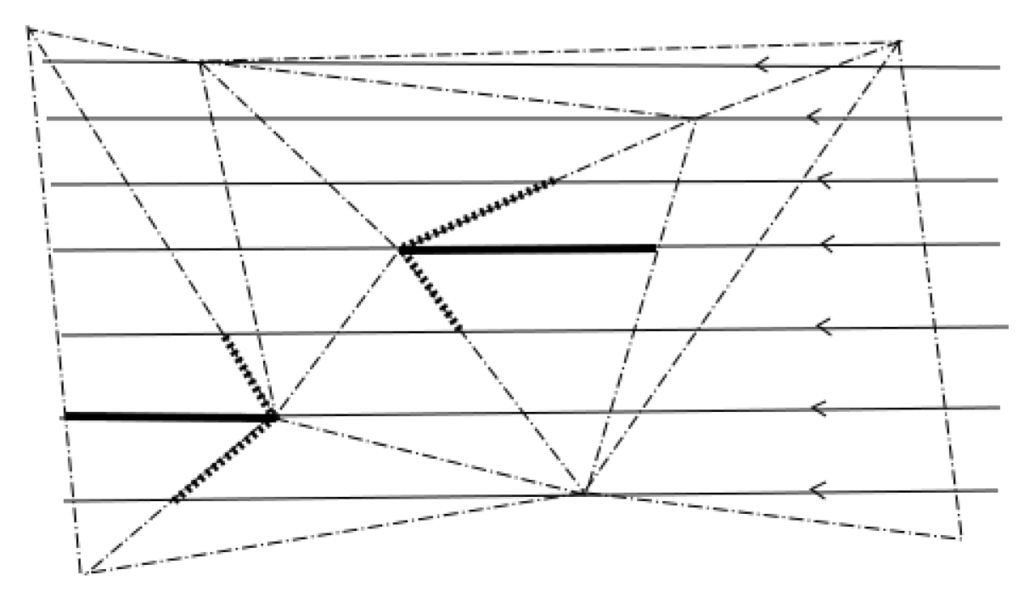
Let U be a foliated chart neighboring a singular point and let so that . Since simplices must be converging in the Hausdorff metric, it follows that for any plaque of U close to p, there exists a sequence of 1-simplices which are converging in the Hausdorff metric to . We define the outer transversal through p relative to b, denoted by , as the union of the initial points of all and p. This is a locally closed set which meets each plaque close to P in a single point, so it is a transversal in the topological sense where the holonomy is well defined. Analogously, the inner transversal, , is defined for a signed 1-barycenter b such that . See Figure 4.

Figure 4.
Outer and inner transversals associated to the extreme singular points of the bold 1-simplices. The leafwise triangulation is induced by a transverse triangulation.
Definition 19 (Leafwise skew product).
Let g be a continuous evaluated closed 1-cochain on the topological 1-dimensional foliation . For every , let such that . The leafwise skew product, is defined as the topological simplicial foliation in where the 0 simplices are identified with and each is joined with by an edge with this orientation. The fact that g is closed means that any 1-simplicial loop bounded by a 2-cell induces a family of 1-simplicial loops in the skew product and thus 2-cells (and higher dimensional cells) can be attached accordingly, this implies that . The fact that g vanishes in its relative boundary is necessary to make the holonomy of the leafwise skew product continuous.
Proposition 20.
Let be an ergodic oriented topological measured simplicial lamination. Let be a closed 1-cochain. Then is an ergodic measure for if and only if is not trivial in measured cohomology for every integer , i.e., in .
Proof.
We follow the method of proof of Proposition 16. First, we show that is quasi-invariant. Let us consider a holonomy transformation of , where are local transversals which can be considered as subsets of (see Definition 18) which are the domain and range of a holonomy transformation γ of associated to a 1-simplex, so . It is clear that such maps generate the holonomy pseudogroup of . Since μ is a Radon product measure, we can estimate the measure of a set Z of null measure by product functions. Let us consider a sequence of continuous and positive functions such that and
We only have to show that converges to zero. Since , we have
Since is quasi-invariant, μ is quasi-invariant for the transformation , therefore the latest expression converges to zero as desired.
In order to check whether is ergodic, let (with complex values) be a leafwise constant (but a.e. non-constant) function and let be the fiberwise Fourier series. At the level of the and for a given holonomy map γ of induced by an oriented 1-simplex, we obtain where denotes the 1-simplex joining w and . Of course is a.e. constant by ergodicity of and therefore some is not essentially zero for some . Now, by ergodicity of and the fact that , this is a.e. non-zero, and we can check that a.e. satisfies almost everywhere. Conversely, if some is trivial in cohomology then a.e. and a.e. gives a leafwise constant function in which is non a.e. constant. ☐
Example 5.
Let be a linear foliation on . Dealing with this foliation as a suspension with the polygonal structure given in Figure 2 by removing the diagonals, we obtain with no singularities. Let g be a 1-cochain with constant values on each copy of , it is clear that it is a closed 1-cochain. The foliation is nothing else than a 2-dimensional linear foliation on which can be seen as the suspension over of the following conmuting transformations on : and . It is well known that this foliation is not ergodic (or minimal) if and only if there exists integers so that and . We can check this directly, under this condition the function satisfies and , so . The converse is a little harder, but in this particular example it is easy to see that implies for all , since is irrational by hypothesis it follows, by a Fourier series argument, that f must be of the form for constants and some . Finally, the analysis of this example is finished by Furstenberg’s criterium.
The next step is to work in the continuous category and show that a similar proposition holds for the continuous cohomology.
Definition 21.
Let be a topological simplicial lamination as above and let be a leafwise continuous triangulation. The first R-evaluated continuous cohomology group for is defined as the quotient group of the continuous closed 1-cochains via the equivalence relation induced by the coboundary of continuous maps . It will be denoted by . Observe that vanishes in the relative boundary of .
Proposition 22.
Let be a minimal oriented 1-dimensional topological foliation with a regular leafwise triangulation . Let be a continuous closed 1-cochain. Then is minimal if and only if is not trivial in continuous cohomology for every integer , i.e., in .
Proof.
Recall that minimality can be checked by any of the following three equivalent definitions:
- There are no closed proper saturated sets,
- Every leaf is dense,
- Any continuous leafwise constant function , where H is any Frechet space, is constant.
We have a natural projection , by minimality of , any non-empty closed saturated set satisfies . Let be a leafwise constant (but non-constant) continuous function. As before, we can consider the fiberwise Fourier series where the Fourier coefficients belong to . Let γ be a holonomy transformation induced by an oriented 1-simplex, we have since the function is supposed to be leafwise constant. By minimality of , is a constant λ. If for all then f is constant which contradicts the choice of f. Assume that some is not constant zero for , then, since , the zero level set of is closed and saturated for and therefore it must be the emptyset. This means that is well defined and continuous and satisfies . Conversely for , the function is a continuous leafwise constant but non-constant. ☐
In fact, for the continuous cohomology we can adapt Zimmer’s result on the coefficient group. As a corollary, we obtain a well known characterization of exact or evaluated cocycles of -actions given by W. H. Gottschalk and G. A. Hedlund [21].
Proposition 23.
Let ω be a continuous 1-cochain of a minimal simplicial lamination evaluated in an abelian group R which is isomorphic to a discrete group, or . If ω is a bounded cochain then ω is cohomologous to a continuous cochain evaluated on a compact subgroup of R, in the particular case of or the bounded cochain is, in fact, null cohomologous.
Proof.
As in Proposition 9, denotes the Polish space of compact sets in R and the set of oriented 1-simplicial paths with initial point . Since is continuous and vanishes in its relative boundary the map , is also continuous. Clearly, . The quotient space is a Polish since the equivalence relation is closed. Since , the sets represent the same equivalence class in .
The map , is continuous and constant on each orbit (which is the intersection of each leaf with ) and thus it is constant by minimality of , call this constant class and assume without loss of generality that . Let , , the class is naturally identified with the coset . Now, we study each possibility in order to obtain a map which is a continuous section, i.e., for all , .
- If R is a discrete abelian group, then any section is also a continuous section because the quotient space is also discrete.
- If R is or , then because these spaces does not admit non-trivial compact subgroups, thus is bijective with continuous inverse. This is the desired section.
Let φ be the 0-cochain . As in Proposition 9 takes its values in . ☐
Corollary 24
(Gottschalk-Hedlund [21]). Let be a minimal homeomorphism on a compact Hausdorff space. A continuous function is null-cohomologous if and only if the functions , , are uniformly bounded for all .
Proof.
We are in the hypothesis of Proposition 23 by considering the suspension of h and the induced simplicial structure. In this corollary, . The fact that are uniformly bounded implies that f is a bounded cochain and so f is null cohomologous. Conversely, if f is null cohomologous, there exists continuous so that . Therefore, a telescopic argument shows that for and for . Thus for all concluding the proof. ☐
Remark 9.
Furstenberg uses this dual result to obtain a minimal but not strictly Lebesgue ergodic transformation on the torus , , just by obtaining a non-trivial class in the continuous cohomology which is trivial in the measurable cohomology. This work provides the technology to perform such examples in higher dimensional foliations. Another observation is that Furstenberg’s technique works in the world of discrete actions, and we are showing that in fact it works in the world of (simplicial) foliations. Another interesting option is to change the coefficient group by a compact Lie group and the Lebesgue measure by the Haar measure (although this is only interesting if non-abelian coefficient groups were allowed).
Observe also that our continuous simplicial cohomology of foliations is nothing else than the leafwise cohomology for usual foliations (via a leafwise de Rham theorem).
6. Foliated Cocycles and Invariant Measures
It is important to remark that all the dynamical information of a measurable lamination is encoded in the holonomy pseudogroup, and the holonomy pseudogroup is generated by the transverse coordinate changes of a regular foliated atlas. Given a locally finite foliated atlas , we can associate a measurable graph where each plaque in a foliated chart is identified with its barycenter and we perform an edge between barycenters associated to adjacent plaques.
Let so that . Let , , be plaques so that . They induce a 1-simplicial loop in the leaf which contains these plaques, these kind of loops will be called cocycle loops. We attach a 2-simplex on each cocycle loop, and we can perform these operation in a measurable way performing a new measurable lamination . This lamination induces the same holonomy pseudogroup in . In particular, they have the same invariant measures.
Definition 25.
(see e.g., [7]) An R-evaluated foliated cocycle relative to the atlas of the measurable lamination is a family of maps so that on any point of . Of course, we consider these maps only on non trivial intersections. When R is the germ of diffeomorphisms of at the origin, then the cocycle is called a Haefliger cocycle.
Of course, Haefliger cocycles are evaluated on a non-abelian group, and so they are out of our actual discussion. An interesting example to be considered is the infinitesimal holonomy cocycle associated to a usual foliation in a smooth manifold. For a point we define , where denotes the Jacobian matrix relative to the transverse change of coordinates. This evaluation does not depend on the points in the same plaque, and, therefore, we can define an -evaluated 1-cochain in by for any . This is a closed cochain in and, conversely, any closed 1-cochain in defines a foliated cocycle relative to which is constant on the plaques of the atlas.
The measurable cohomology class of ν is an obstruction to the existence of invariant measures in the measure class (i.e., with the same sets of null measure) of the Lebesgue measure of a smooth foliation. This is explictly done in [7,22].
Proposition 26.
Let be a smooth measured foliation on a smooth manifold M so that m is the Lebesgue measure in . Let be the measurable graph associated to a regular foliated atlas of . Then has an invariant measure in the same class of m if and only if the cohomology class is trivial.
Proof.
Let , we associate a holonomy transformaion . Of course, (resp. ) is identified with the projection of in an associated transversal of (resp. ). can be seen also as a map , where denotes the barycenter of the edge between t and with the orientation . We shall use the same notation for both maps.
Assume μ a measure in the Lebesgue class. Therefore, the Radon–Nikodyn formula provides a measurable map so that . The change of variable formula provides that (Lemma 7.1.21 in [7]). If μ is invariant, then a.e. and so . Conversely, let h so that a.e. then the above equation shows that the measure given by is invariant and, of course, it is in the Lebesgue class. ☐
The infinitesimal holonomy is one of the components of the Godbillon–Vey class of a foliation and Hurder shows in [22] that the existence of an invariant measure in the Lebesgue class forces the vanishing of the Godbillon–Vey class. The Godbillon–Vey class encodes interesting data of the transverse dynamics, for instance, a deep result of Duminy shows that, for codimension 1 foliations, a non-trivial Godbillon–Vey class implies the existence of a resilient leaf (a non-proper leaf which has a transverse self-accumulation point given by a holonomy contraction), see [7] for a proof. Then, even for smooth foliations, the measurable cohomology is interesting on its own. At this point, we can use our work in Section 4 and obtain the following corollary.
Corollary 27.
Let be a smooth Lebesgue ergodic foliation on a smooth manifold M. If ν is a bounded 1-cochain of (in the sense of Definition 8) then has an invariant measure in the Lebesgue class.
Remark 10.
When the Lebesgue measure is invariant, then it is clear that ν is trivial and in particular, bounded.
Recall that, in continuous cohomology, -valued bounded 1-cochains are exactly the cohomologically trivial 1-cochains (see Corollary 24). This suggests that Corollary 10 is close to be an equivalence. If M is a closed manifold, then ν defines an 1-cochain. Clearly, if for some then ν is uniformly bounded since for all . The converse is also true, and it was proved in Corollary 10. These data can be encoded in the following result.
Corollary 28.
Let be a smooth Lebesgue ergodic foliation on a smooth closed manifold M. Then ν is a uniformly bounded 1-cochain of (in the sense of Definition 8) if and only if there exists an invariant measure μ in the Lebesgue class so that for some .
7. Conclusions
What is lost in our approach is the possibility of having non-abelian coefficient groups. This is of extreme importance in many interesting problems where the coefficient groups can be , , a compact Lie group or the unitary group of a Hilbert space. For measurable graphs, the definition of the first cohomology set (in general fails to be a group) can be adapted with no further problems. However, higher dimensional cohomology seems to be much more difficult to properly define.
At this point, the reader would see that a lot of dynamical and topological results can be a target for being adapted in this framework. In this section, we state two of them.
Livsic’s theorem states that the Hölder cohomology classes of a transitive Anosov diffeomorphism are determined by their values on the periodic points. More precisely:
Theorem 29 (Livsic).
[18] Let be a transitive Anosov diffeomorphism. Let be an α-Hölder function so that implies , then there exists an α-Hölder function so that , i.e., f is null cohomologus in the α-Hölder cohomology.
It is well known that the Livsic theorem holds for transitive Anosov flows, and this suggests an adaptation to foliations: periodic points are interpreted as compact leaves, and the Anosov condition is translated to the notion of Anosov pseudogroups, which are analogous to Anosov flows.
On the other hand, the Mostow rigidity theorem says that the volume of hyperbolic manifolds of dimensions greater than 2 is determined by their fundamental group. Zimmer [5] adapted the Mostow rigidity for measurable laminations coming from ergodic measured locally free actions of certain Lie groups. Thus, the natural question is how to extend Zimmer’s result to a wider class of measurable laminations.
Acknowledgments
I have to express my gratitude to Steven Hurder who pointed out to me, back in 2012, that my treatment of cohomology of measurable laminations was linked in a natural way to Zimmer’s work and that it would be worthy of interest to explain this relation in more detail. This work was supported by CAPES (Brazil), postdoc program PNPV 2015.
Conflicts of Interest
The author declares no conflict of interest.
References
- Furstenberg, H. Strict ergodicity and transformation of the torus. Am. Math. J. 1961, 83, 573–601. [Google Scholar] [CrossRef]
- Zimmer, R.J. On the cohomology of ergodic group actions. Israel J. Math. 1980, 35, 289–300. [Google Scholar] [CrossRef]
- Gaboriau, D. Sur la (co-)homologie L2 des actions préservant une mesure. C. R. Acad. Sci. Paris Sér. I Math. 2000, 330, 365–370. [Google Scholar] [CrossRef]
- Zimmer, R.J. On the cohomology of ergodic actions of semisimple lie groups and discrete groups. Am. J. Math. 1981, 103, 937–950. [Google Scholar] [CrossRef]
- Zimmer, R.J. On the Mostow rigidity theorem and measurable foliations by hyperbolic space. Israel J. Math 1982, 43, 281–290. [Google Scholar] [CrossRef]
- Candel, A.; Conlon, L. Foliations I; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 1999; Volume 23. [Google Scholar]
- Candel, A.; Conlon, L. Foliations II; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 1999; Volume 60. [Google Scholar]
- Connes, A. A survey of foliations and operator algebras. Proc. Symp. Pure Math. 1982, 38, 520–628. [Google Scholar]
- Connes, A.; Fack, T. Morse inequalities for foliations. In C*-Algebras and Elliptic Theory; Trends in Mathematics; Birkhäuser Verlag: Basel, Switzerland, 2006; pp. 61–72. [Google Scholar]
- Heitsch, J.L.; Lazarov, C. Homotopy invariance of foliation Betti numbers. Invent. Math. 1991, 104, 321–347. [Google Scholar] [CrossRef]
- Bermúdez, M. La caratéristique d’Euler des feuilletages mesurés. J. Funct. Anal. 2006, 237, 150–175. [Google Scholar] [CrossRef]
- Bermúdez, M.; Hector, G. Laminations hyperfinies et revêtements. Ergod. Theory Dyn. Syst. 2006, 26, 305–339. [Google Scholar] [CrossRef]
- Bermúdez, M. Laminations Boréliennes. Ph.D. Thesis, Université Claude Bernard Lyon 1, Villeurbanne, France, 2002. [Google Scholar]
- Meniño, C. Cohomology of measurable laminations. Topol. Appl. 2013, 160, 692–702. [Google Scholar] [CrossRef]
- Meniño, C. Measurable versions of the LS category on laminations. Manuscr. Math. 2014, 144, 135–163. [Google Scholar] [CrossRef]
- Hatcher, A. Algebraic Topology; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Connes, A.; Feldman, J.; Weiss, B. An amenable equivalence relation is generated by a single transformation. Ergod. Theory Dyn. Syst. 1981, 1, 431–450. [Google Scholar] [CrossRef]
- Livsic, A. Certain properties of the homology of Y-systems. Mat. Zamet. 1971, 10, 555–564. [Google Scholar]
- Kechris, A.S. Classical Descriptive Set Theory; Graduate Texts in Mathematics; American Mathematical Society, Springer-Verlag: New York, NY, USA, 1994; Volume 156. [Google Scholar]
- Plante, J.F. Foliations with measure preserving holonomy. Ann. of Math. 1975, 102, 327–361. [Google Scholar] [CrossRef]
- Gottschalk, W.H.; Hedlund, G.A. Topological Dynamics; American Mathematical Society, Colloquium Publications: Providence, RI, USA, 1955; Volume 36. [Google Scholar]
- Hurder, H. The Godbillon measure of amenable foliations. J. Differ. Geom. 1986, 23, 347–365. [Google Scholar]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).