Modeling ITNs Usage: Optimal Promotion Programs Versus Pure Voluntary Adoptions
Abstract
:1. Introduction
2. Models Formulation
2.1. The Basic System
| Parameter | Description | Baseline Value |
|---|---|---|
| Immigration rate in humans | ||
| Immigration rate in mosquitoes | ||
| b | Proportion of ITN usage | varies in [0,1] |
| μ | Natural mortality rate in humans | |
| η | Natural mortality rate in mosquitoes | |
| Maximum ITN-induced death rate in mosquitoes | ||
| α | Disease–induced death rate in humans | |
| Prob. of disease transm. from mosquito to human | 1 | |
| Prob. of disease transm. from human to mosquito | 1 | |
| Maximum host–vector contact rate | 0.1 | |
| Minimum host–vector contact rate | 0 | |
| δ | Recovery rate of infectious humans to be susceptible | 1/4 |
- (i)
- ITNs usage reduces the human–mosquito contact rate and this is described by the relation:where and are the maximum and the minimum contact rate, respectively.
- (ii)
- ITNs usage increases the mosquito death rate η. This is modeled by:where is a non negative constant and represents the death rate due to insecticide on treated bed-nets.
2.2. Information Variable
- (a)
- the information on the status of the disease in the community where they live;
- (b)
- the information generated by an optimal health-promotion campaign aimed at encouraging people to use ITNs.
2.3. The Information Kernel
2.4. The Cases under Consideration
- Case I (Model M): Constant contact rate.
- Case II (Model V): Pure voluntary ITNs adoptions.
- Case III (Model P): ITNs promotion program.
3. Optimal ITNs Promotion Campaign
4. Numerical Simulations and Discussion
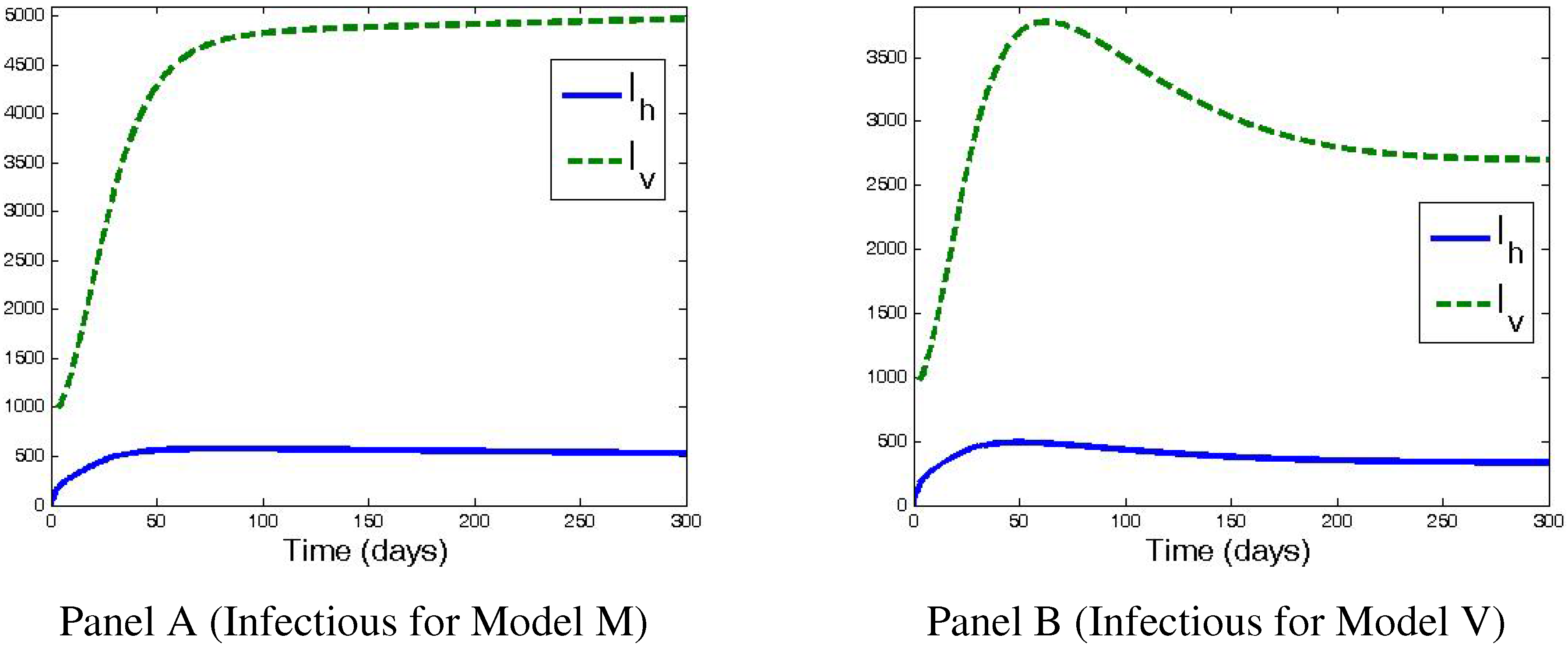
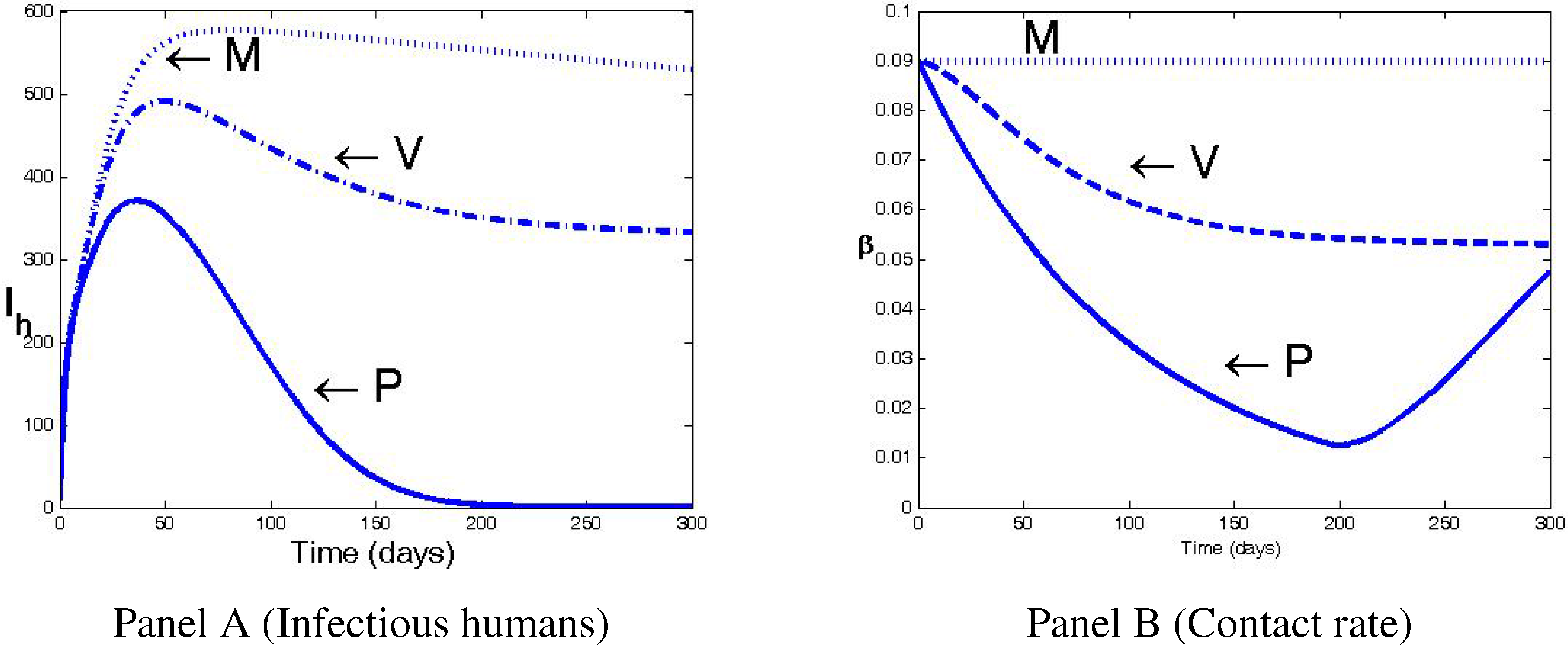
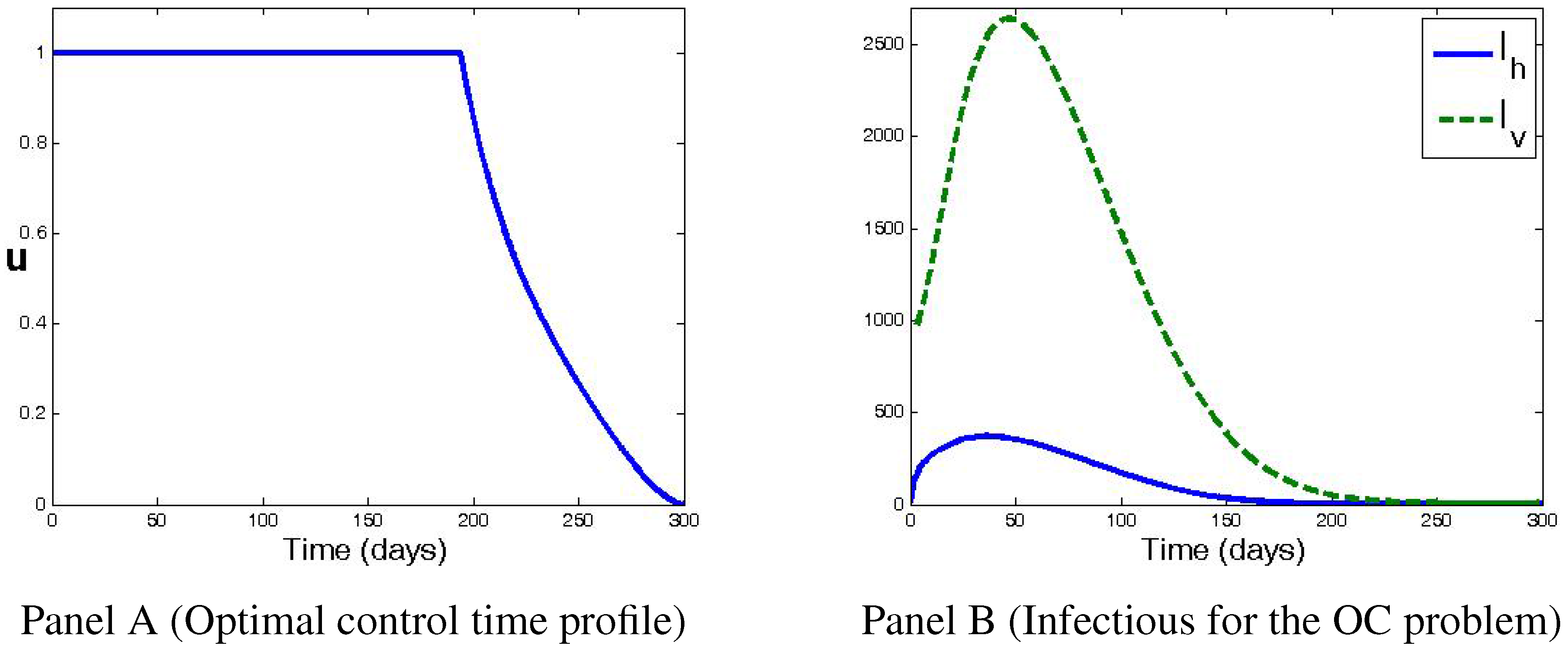
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix
Optimality System and Basic Properties of the Optimal Control
References
- Global Malaria Programme. World Malaria Report 2014; World Health Organization: Geneva, Switzerland, 2014. [Google Scholar]
- Wiwanitkit, V. Vaccination against mosquito borne viral infections: Current status. Iran J. Immunol. 2007, 4, 186–196. [Google Scholar] [PubMed]
- Ramsauer, K.; Schwameis, M.; Firbas, C.; Müllner, M.; Putnak, R.J.; Thomas, S.J.; Desprésd, P.; Tauber, E.; Jilma, B.; Tangy, F. Immunogenicity, safety, and tolerability of a recombinant measles-virus-based chikungunya vaccine: A randomised, double–blind, placebo–controlled, active–comparator, first–in–man trial. Lancet 2015, 15, 519–527. [Google Scholar] [CrossRef]
- World Health Organization. Malaria Vaccine Development. Available online: http://www.who.int/malaria/areas/vaccine/en/ (accessed on 1 September 2015).
- Halloran, M.E.; Struchiner, C.J. Modeling transmission dynamics of stage-specific malaria vaccines. Parasitol. Today 1992, 8, 77–85. [Google Scholar] [CrossRef]
- Prosper, O.; Ruktanonchai, N.; Martcheva, M. Optimal vaccination and bednet maintenance for the control of malaria in a region with naturally acquired immunity. J. Theor. Biol. 2014, 353, 142–156. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.; Muthuraman, K.; Lawley, M. An optimal control theory approach to non–pharmaceutical interventions. BMC Infect. Dis. 2010, 10, 32–45. [Google Scholar] [CrossRef] [PubMed]
- Briët, O.J.; Chitnis, N. Effects of changing mosquito host searching behaviour on the cost effectiveness of a mass distribution of long–lasting, insecticidal nets: A modelling study. Malaria J. 2013, 12, 215. [Google Scholar] [CrossRef] [PubMed]
- Centers for Disease Control and Prevention. Insecticide–Treated Bed Nets. Available online: http://www.cdc.gov/malaria/malaria_worldwide/reduction/itn.html (accessed on 1 September 2015).
- Lengeler, C. Insecticide–treated bed nets and curtains for preventing malaria. Cochane Database Syst. Rev. 2004. [Google Scholar] [CrossRef]
- Frey, C.; Traoré, C.; de Allegri, M.; Kouyaté, B.; Müller, O. Compliance of young children with ITN protection in rural Burkina Faso. Malaria J. 2006, 5, 70. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Modeling the Interplay Between Human Behavior and the Spread of Infectious Diseases; Manfredi, P.; d’Onofrio, A. (Eds.) Springer: Heidelberg, Germany, 2013.
- Agusto, F.B.; del Valle, S.Y.; Blayneh, K.W.; Ngonghala, C.N.; Goncalves, M.J.; Li, N.; Zhao, R.; Gong, H. The impact of bed-net use on malaria prevalence. J. Theor. Biol. 2013, 320, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Buonomo, B.; d’Onofrio, A.; Lacitignola, D. Global stability of an SIR epidemic model with information dependent vaccination. Math. Biosci. 2008, 216, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Buonomo, B.; d’Onofrio, A.; Lacitignola, D. Globally stable endemicity for infectious diseases with information-related changes in contact patterns. Appl. Math. Lett. 2012, 25, 1056–1060. [Google Scholar] [CrossRef]
- Buonomo, B.; d’Onofrio, A.; Lacitignola, D. Modeling of pseudo-rational exemption to vaccination for SEIR diseases. J. Math. Anal. Appl. 2013, 404, 385–398. [Google Scholar] [CrossRef]
- D’Onofrio, A.; Manfredi, P. Information-related changes in contact patterns may trigger oscillations in the endemic prevalence of infectious diseases. J. Theor. Biol. 2009, 256, 473–478. [Google Scholar] [CrossRef] [PubMed]
- D’Onofrio, A.; Manfredi, P.; Salinelli, E. Vaccinating behaviour, information, and the dynamics of SIR vaccine preventable diseases. Theor. Popul. Biol. 2007, 71, 301–317. [Google Scholar] [CrossRef] [PubMed]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Behncke, H. Optimal control of deterministic epidemics. Optim. Control Appl. Meth. 2000, 21, 269–285. [Google Scholar] [CrossRef]
- Smith, H. An Introduction to Delay Differential Equations with Applications to the Life Sciences; Springer: Heidelberg, Germany, 2011; Volume 57. [Google Scholar]
- Macdonald, G. The Epidemiology and Control of Malaria; Oxford University Press: London, UK, 1957. [Google Scholar]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman & Hall/CRC Mathematical and Computational Biology Series; Chapman & Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Isidori, A. Nonlinear Control Systems; Springer: Berlin, Germany, 1989. [Google Scholar]
- Sontag, E.D. Mathematical Control Theory, 2nd ed.; Springer: Berlin; Heidelberg, Germany, 1998. [Google Scholar]
- Nonlinear Controllability and Optimal Control; Sussmann, H.J. (Ed.) Dekker: New York, NY, USA, 1990.
- Anita, S.; Arnautu, V.; Capasso, V. An Introduction to Optimal Control Problems in Life Sciences and Economics; Birkhäuser: Boston, MA, USA, 2010. [Google Scholar]
- Buonomo, B. A simple analysis of vaccination strategies for rubella. Math. Biosci. Eng. 2011, 8, 677–687. [Google Scholar] [CrossRef] [PubMed]
- Buonomo, B. On the optimal vaccination strategies for horizontally and vertically transmitted infectious diseases. J. Biol. Sys. 2011, 19, 263–279. [Google Scholar] [CrossRef]
- Hocking, L.M. Optimal control. In An Introduction to the Theory with Applications; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Ozair, M.; Lashari, A.A.; Jung, I.H.; Okosun, K.O. Stability analysis and optimal control of a vector-borne disease with nonlinear incidence. Discrete Dyn. Nat. Soc. 2012. [Google Scholar] [CrossRef]
- Aldila, D.; Götz, T.; Soewono, E. An optimal control problem arising from a dengue disease transmission model. Math. Biosci. 2013, 242, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.; Qiu, Z.; Sang, Z.; Zou, Y. Optimal control of a vector-host epidemics model. Math. Control Rel. Fields 2011, 1, 493–508. [Google Scholar] [CrossRef]
- Agusto, F.B.; Marcus, N.; Okosun, K.O. Application of optimal control to the epidemiology of malaria. Electron. J. Diff. Eq. 2012, 2012, 1–22. [Google Scholar]
- Silva, C.J.; Torres, D.F.M. An optimal control approach to malaria prevention via insecticide-treated nets. Conf. Pap. Math. 2013. [Google Scholar] [CrossRef]
- McAsey, M.; Mou, L.; Han, W. Convergence of the forward-backward sweep method in optimal control. Comput. Opt. Appl. 2012, 53, 207–226. [Google Scholar] [CrossRef]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F.M. Optimal control and numerical software: An overview. In Systems Theory: Perspectives, Applications and Developments; Miranda, F., Ed.; Nova Science Publishers: New York, NY, USA, 2014. [Google Scholar]
- MATLAB Release 2010b; The MathWorks, Inc.: Natick, MA, USA, 2010.
- Chitnis, N.; Hardy, D.; Smith, T. A Periodically-forced mathematical model for the seasonal dynamics of malaria in mosquitoes. Bull. Math. Biol. 2012, 74, 1098–1124. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F.M. Seasonality effects on dengue: Basic reproduction number, sensitivity analysis and optimal control. Math. Meth. Appl. Sci. 2015, in press. [Google Scholar]
- Grass, D.; Caulkins, J.P.; Feichtinger, G.; Tragler, G.; Behrens, D.A. Optimal Control of Nonlinear Processes, with Applications in Drugs, Corruption, and Terror; Springer: Berlin, Germany, 2008. [Google Scholar]
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buonomo, B. Modeling ITNs Usage: Optimal Promotion Programs Versus Pure Voluntary Adoptions. Mathematics 2015, 3, 1241-1254. https://doi.org/10.3390/math3041241
Buonomo B. Modeling ITNs Usage: Optimal Promotion Programs Versus Pure Voluntary Adoptions. Mathematics. 2015; 3(4):1241-1254. https://doi.org/10.3390/math3041241
Chicago/Turabian StyleBuonomo, Bruno. 2015. "Modeling ITNs Usage: Optimal Promotion Programs Versus Pure Voluntary Adoptions" Mathematics 3, no. 4: 1241-1254. https://doi.org/10.3390/math3041241
APA StyleBuonomo, B. (2015). Modeling ITNs Usage: Optimal Promotion Programs Versus Pure Voluntary Adoptions. Mathematics, 3(4), 1241-1254. https://doi.org/10.3390/math3041241





