1.1. Preliminaries
Many quantum systems are defined by analytic solutions, which in turn compel us to generate them through (approximate) analytic methods. Although one is generally more interested in the hierarchical large-scale structure leading to quantization (
i.e., determining the discrete state energies and
convergent approximations to the wave function configurations), recovering the local structure is also important and the principal focus of this work. Our methods have the important advantage that they are essentially algebraic in nature, allowing for high precision calculations through multiple precision algorithms and symbolic calculations facilitated by computer algebraic systems, such as
Mathematica. Recent works also adopt a similar computational philosophy as developed in the context of supersymmetric quantum mechanics [
1,
2], group theory [
3] and Hermite distributed approximating functionals [
4]. These emphasize an algebra-based analysis for addressing the global (discrete state) structure of appropriate physical systems.
The emphasis on developing high precision, algebraic methods for addressing analytical problems is particularly important. What is desired are algebraic methods that originate from the analysis of purely algebraic quantum systems for which all discrete states are known in closed form. These are referred to as exactly-solvable (ES) systems. One can then attempt to extend the methods developed for ES systems to more general Hamiltonians, in a manner that preserves the basic algebraic structure of such methods in the numerical computation of physical properties. In this regard, supersymmetric and group theory formulations have played a prominent role [
1,
2,
3]. Two other approaches, of direct relevance to this work, are highlighted in the ensuing discussion: the Hill determinant (HD) method and the orthogonal polynomial projection quantization (OPPQ) method. The latter has important advantages over the former (
i.e.,
and pointwise convergence, greater numerical stability,
etc.) in facilitating our “global-local” quantization interests, as identified in
Subsection 1.2. Before discussing these, we define particular structures of importance to this work. Although our methods are applicable to multidimensional systems, for simplicity all of our analysis is developed for one-dimensional problems.
We are interested in the large and important class of problems for which the Schrödinger equation can be Fourier transformed into the momentum space representation, , and a power series analysis implemented therein, , generating a recursive, linear, finite difference equation for the power moments . This recursive relation will be referred to as a moment equation, of order (problem dependent). The recursion coefficients involve the energy variable. In reality, the generation of such moment equations is independent of the ability to perform a Fourier transform. Many Schrödinger systems, after a coordinate transformation if necessary, can be directly transformed into such moment equation representations.
We also assume that within the original configuration space representation, the physical discrete state solutions are analytic,
, and the power series coefficients can be generated through a linear, second order recursion relation involving energy-dependent coefficients. Directly coupling such local expansions to the asymptotic properties of the physical solutions is not straightforward. Numerically, the “shooting method” attempts to do this [
5]. This is also the objective of JWKBmethods, particularly in their analysis around turning points [
6]. Neither approach is algebraic or capable of high accuracy.
The Hill determinant (HD) method [
7], of relevance to this work, does define a quantization ansatz connecting the behavior of the
-coefficients for discrete states to the boundedness criteria for such states:
. It does so by representing the wavefunction as
, involving an appropriate (arbitrary) positive, analytic, exponentially-bounded reference function,
. It investigates the power series expansion coefficients generated through
; achieving quantization through the imposition of truncation relations corresponding to
(for second order differential systems) and taking
. Since these expressions involve energy-dependent coefficients, this leads to a
determinantal expression for the energy. The energy roots of this expression converge to the physical energies, when HD works.
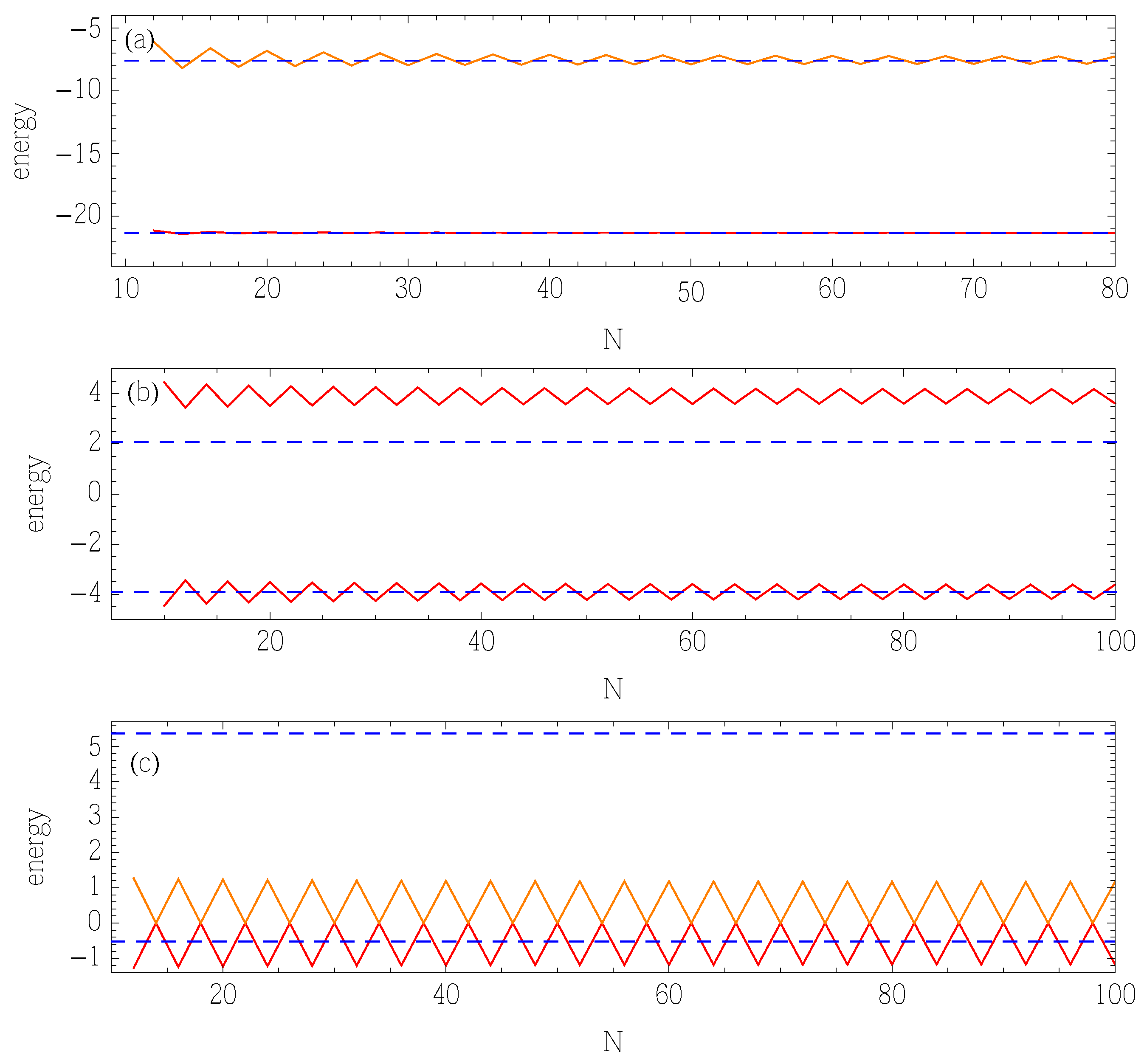
Despite its simplicity, and widespread popularity, it is well known that the HD method can lead to anomalous results yielding incorrect energies or becoming otherwise unstable. This was dramatized by Tater and Turbiner [
8] in their study of the double well sextic anharmonic oscillator. Since their work does not clearly reveal these difficulties, we have repeated the calculations as demonstrated in
Figure 1. These anomalous behaviors were anticipated by Hautot [
9], who proposed non-trivial strategies for circumventing these difficulties. If one can avoid these anomalous cases, HD can produce high precision results, since it is readily implementable, to unlimited precision, through Mathematica. However, the anomalous cases appear to correspond [
8,
9] to using reference functions that imitate the physical asymptotic form of the physical solution. Intuitively, one expects the best convergence when the reference function is allowed to assume this form. Indeed, this is one of the strengths of the alternative approach, OPPQ, to be discussed shortly. OPPQ allows one a wide choice of reference functions. When compared to HD, OPPQ manifests convergence at much higher rates, when the appropriate reference function is used. Furthermore, OPPQ has a stronger theoretical foundation than HD, for reasons given shortly. Despite all of these issues, HD was rediscovered by Tymczak
et al. [
10,
11], who also applied it in a new way within momentum space. It continues to be the subject of much interest, as amply demonstrated in the recent works by Killingbeck and Grosjean [
12].
The HD method does not define for us a rigorous, high precision, algebraic quantization method that is robust (numerically stable), efficient (producing rapidly converging results) and effective. The principal reason is that the underlying formalism does not readily impose on the
’s constraints due to the
boundedness criteria
. That is, there is no way to impose, or ensure, the latter condition on the behavior of the
’s. We believe that this is the primary reason for HD’s anomalous behaviors, particularly when the reference function assumes the asymptotic form of the physical states, as suggested by Tater and Turbiner’s investigations. As previously indicated, the results in
Figure 1 reveal the potential instability and slow convergence properties of HD, particularly when the reference function assumes the physical asymptotic form. In summary, we are interested in algebraic, arbitrary precision, quantization methods tied to representations that imitate, as much as possible, the true asymptotic form of the physical solutions. Despite all of its successful implementations, HD does not fall into this class of quantization schemes.
Figure 1.
Convergence of the Hill determinant calculation of the first two energy eigenvalues for anomalous cases of the sextic anharmonic oscillator . Parameter values are: (a) (m = −18, b = 0); (b) (m= −8, b = 0); and (c) (m = −4, b = 0). The dashed lines show the exact energy values. Case (a) show convergences to the correct values, although extremely slowly. Case (b) shows convergence for both energies, but only the ground state converges to the correct value, while the excited state converges to the wrong value. Case (c) shows complete lack of convergence for both energies.
Figure 1.
Convergence of the Hill determinant calculation of the first two energy eigenvalues for anomalous cases of the sextic anharmonic oscillator . Parameter values are: (a) (m = −18, b = 0); (b) (m= −8, b = 0); and (c) (m = −4, b = 0). The dashed lines show the exact energy values. Case (a) show convergences to the correct values, although extremely slowly. Case (b) shows convergence for both energies, but only the ground state converges to the correct value, while the excited state converges to the wrong value. Case (c) shows complete lack of convergence for both energies.
Despite the fact that the power moments are global, and therefore natural objects to study for determining the discrete states, until two years ago, with the discovery of the OPPQ method [
13,
14], of relevance to this work, there were very few, easily implementable moment methods for quantizing all of the discrete states of multidimensional physical systems. The only exception to this might be the momentum space application of HD, referred to as the multiscale reference function (MRF) method, as discussed in [
10,
11]. It does appear that MRF is (significantly) faster at converging than configuration space-HD, as demonstrated in [
13] (
Figure 1). However, it is not clear if the HD theoretical problems specified above also apply to the MRF case. The irony is that OPPQ, despite its basis formulation in configuration space, depends on the power moments for its generation. All of this is discussed below. Thus, OPPQ combines the best features of a configuration space analysis (
i.e., in easily identifying the physical asymptotic form for the required weight or reference function) with the effectiveness of moment representation quantization.
The earliest attempts in using moments for solving linear systems were by Blankenbeckler
et al. [
15] and Killinbgeck
et al. [
16]. Another work attempted the same for strongly-coupled, singular perturbation, nonlinear systems (“kink” solutions) [
17].
In 1984, Handy achieved a significant theoretical and computational advance by demonstrating that the classic moment problem theorems [
18] (
i.e., the moment-dependent positivity constraints required for nonnegative measures) could be used to constrain the moment equation solutions corresponding to positive wavefunction configurations; the most important of these being the multidimensional bosonic ground state,
. This led to a new spectral bounding method that could generate tight (converging) lower and upper bounds to the discrete state energies associated with positive configurations. This is referred to as the eigenvalue moment method (EMM). Handy’s original discovery was by way of the nesting property for Padé approximants generated from positive Stieltjes measures [
19]. This philosophy was further refined, making it more amenable to multidimensional systems, through the use of the well-known positivity Hankel Hadamard (nonlinear) determinantal inequality constraints [
20].
This seminal work by Handy and Bessis [
20] is one of the first to use semidefinite programming (SDP) analysis [
21,
22] to solve quantum operators. Since SDP algorithms were not available, Handy developed a cutting algorithm, within the context of a linear convex optimization analysis [
23], that allowed the extension of these methods to multidimensional systems. The most famous of these was the notoriously difficult, strong coupling, singular perturbation problem corresponding to determining the ground state binding energy of the quadratic Zeeman effect for super-strong magnetic fields (of the type encountered in neutron stars). Handy
et al. [
24,
25] were able to extend the EMM analysis to such problems confirming, through tight bounds, the results of Le Guillou and Zinn-Justin [
26] derived through more sophisticated, analytical methods.
The EMM analysis can also be used for bounding the excited discrete state energies of one-dimensional problems, since the probability density,
, for Sturm–Liouville problems with a real potential function, must satisfy a third order linear differential equation for which a moment equation can also be generated, for the types of systems considered here [
27,
28]. The same applies to Sturm–Liouville problems with complex potentials (
i.e., pseudo-Hermitian systems), since the Herglotz extension into the complex plane for the probability density
leads to a fourth order linear differential equation, for which a moment equation also ensues [
29,
30]. The application of EMM to the case
led to the generation of tight bounds for the real and imaginary parts of the discrete state complex eigenenergies. This led to the first computational prediction for the onset of spontaneous PT-symmetry breaking (predicting the
a-parameter regions where the discrete spectrum changed from being real to complex) for this important system [
30,
31], the subject of much current research.
1.3. OPPQ and HD: General Quantization Strategies Motivated by Exactly Solvable and Quasi-Exactly Solvable Quantum Systems
Exactly solvable (ES) systems are those for which the discrete states can be determined in closed form: energies and wavefunctions. In one dimension, they can be characterized as corresponding to wavefunctions of the form
, where
is an orthogonal polynomial of degree “j”, with respects to a particular positive weight
[
32]. The function factor
corresponds to a positive, exponentially-bounded configuration that embodies the controlling form of the asymptotic behavior of the physical solution.
It follows that if denotes the orthonormal polynomials of (i.e., where “n” is the degree), then we must have , for . This ensues from the orthogonality properties of the polynomials and the fact that the polynomial can be represented in terms of the first “”, polynomials (where ). These integral expressions depend on the power moments of the physical solution, . We can thus characterize ES systems as those for which the ’s truncate exactly.
The same applies to the case of quasi-exactly solvable (QES) systems [
33,
34,
35,
36,
37]. In this case, only a subset of the discrete states can be calculated in closed form. The corresponding wavefunctions take on the form
, where
is a polynomial of fixed degree,
(but with
j-dependent coefficients). In this case, we also have
, for
. That is, there is also exact truncation in the behavior of the
’s.
The OPPQ generalization of the above to arbitrary Hamiltonians (provided they admit a moment equation representation) assumes that the wavefunction can be represented as:
for an arbitrary, positive, exponentially-bounded (not necessarily analytic) weight
and its family of orthonormal polynomials,
.
The expansion coefficients project out exactly, , and involve all of the first power moments, which are assumed to be generated through their corresponding moment equation.
If we choose the weight to satisfy , then because , it follows that the projection coefficients must satisfy the asymptotic condition: . We can use this to define a truncation approximation quantization analysis involving , for , and . Here, we assume that denotes the order of the associated linear moment equation. To order N, these relations define a purely energy-dependent function (an determinant) whose zeroes converge (exponentially) to the physical energies.
One expects, as confirmed empirically, that the best convergence is when the weight mimics the asymptotic form of the physical states. The admissible weight can be arbitrary, provided , which allows for the weight to imitate the physical asymptotic form (assuming Ψ is also ).
In the Appendix (
Table A1), we reproduce the results communicated in [
13], for the quartic and sextic anharmonic oscillators. The reader will note that when the weight (reference function) imitates the physical, asymptotic form, improved convergence is obtained. We also show that slower convergence can be obtained even when the above condition is not satisfied (
i.e., the last entry for the quartic anharmonic oscillator). What is not shown is the impressive fact that the non-analytic reference function,
, also yields good converging results for the quartic case. Unlike the HD case, the OPPQ reference function does not have to be analytic, if one only wants to compute the energies.
The OPPQ wavefunction representation is usually referred to as a weighted polynomial expansions. It is well known that such expansions, particularly for Freudian weights,
,
, can exhibit pointwise convergence, in addition to
convergence [
38]. We stress that the expressions
represent a non-orthogonal basis, which is an essential component to the flexibility of the above representation as used here. Despite the extensive mathematical literature on the importance of weighted polynomial expansions, or orthogonal polynomial expansions (as referenced throughout this work), its relevance for quantizing physical systems (by incorporating the moment equation structure) had not been appreciated until its exploitation by Handy and Vrinceanu [
13,
14].
One example of the flexibility of the OPPQ representation is that one can take the weight to be as complicated as one wants, provided the corresponding orthonormal polynomials can be generated. Thus, instead of the non-analytic reference function , for the quartic anharmonic potential, one can consider working with the analytic counterpart . Regardless of what weight is chosen, the moment equations stay unchanged.
Another aspect of OPPQ’s flexibility is that one does not need the explicit functional form for the weight, in order to generate the discrete state energies. If one knows the moments for the weight, then its orthonormal polynomials can still be generated, leading to the generation of the discrete state energies. This is possible through the well-known three-term recursion relation for the monic orthogonal polynomials [
19]. An alternative approach (for multidimensional systems) is to use LUdecomposition methods on the (multidimensional) Hankel moment matrix (for the weight), in order to generate the same orthogonal polynomials [
39]. One interesting application of this is to use EMM [
20,
24,
25] to determine the power moments of the physical (positive) bosonic ground state (through tight bounds), for a given system. These can then be incorporated within OPPQ to generate the discrete state energies for all of the desired discrete states. The advantage of using EMM is that the generated moments will have automatically satisfied the necessary Hankel–Hadamard positivity constraints essential for ensuring that one is generating the orthonormal polynomials of a positive configuration (up to the order of the EMM analysis).
Returning to the previous ES/QES discussion, one can see that such states can also be characterized as corresponding to , where the analytic (polynomial) factor , truncates exactly: , if . One might consider this as a motivational factor for the development of the Hill determinant (HD) method, as previously discussed.
We have already noted that HD can manifest anomalous behavior (
i.e., convergence to the wrong energies, non-convergent or slow convergence behavior,
etc.), particularly when the reference function,
, assumes the physical asymptotic form (refer to
Figure 1); whereas OPPQ converges fastest precisely in such cases. To underscore the importance of this, we can consider the problem of varying the potential function parameters in order to determine the existence of ES/QES states. Within an HD framework, one cannot do this, reliably, since this type of variational analysis requires explicitly working with a weight, or reference function, that specifically incorporates the physical asymptotic form. Instead, by working with the OPPQ representation, where
incorporates the physical asymptotic form, one can reliably determine the parameter regimes corresponding to ES/QES states.
Consider the sextic anharmonic problem
. The ground state is of QES form for
, with lowest energy state
[
20,
36]. The HD analysis will recover the QES states; however, if we slightly perturb things,
, the resulting HD energies do not suggest the existence of QES states. This is summarized in the Appendix (
Table A2, extracted from a forthcoming article on ES and QES states). Whereas the OPPQ results appear to vary continuously for
, where
, the same is not true for the HD results. Besides the fact that HD yields erroneous, or slowly converging, results for all of the states (
i.e., with the exception of
for
) both in the QES regime (
) and non-QES regimes (
), HD does not appear to demonstrate continuity in its generated energies, for this case. Thus,
for
and then shoots to
for
. The same is true for the ground state energy. However, the true energies (obtained by OPPQ and confirmed through EMM) show a smooth variation in all of the energies for
.
Of greater importance to us is that the OPPQ representation is numerically stable and converges rapidly for the appropriate weight. Furthermore, the OPPQ representation is both and pointwise convergent, globally. The latter property allows us to implement the global-local quantization analysis identified at the outset. These properties cannot be easily claimed by HD.
1.4. Connecting the Power Moments to the Local Behavior of the Physical Solutions: Scaling Transform Reconstruction
There is another related result derived from the scaling transform formalism underlying continuous wavelet analysis [
40,
41]. It also couples the power moments to the local structure of the wave function.
Consider the scaling transform of the physical wave function, for some appropriate, exponentially-bounded, analytic scaling function,
, satisfying the normalization
:
Depending on the asymptotic decay of the scaling function relative to the physical solution, the scaling transform will be analytic (even entire) in the inverse scale variable,
, as generated from the power moments:
where
, involving a linear combination of the power moments for
.
Thus, the power moments control the large-scale structure of the scaling transform. Recovery of the local properties for the wavefunction then requires implementing an effective analytic continuation/re-summation strategy for Equation (2), combined with the small-scale asymptotic limits:
where
. That is, the analytic continuation, or re-summation, of Equation (2), combined with asymptotic matching at some intermediary scale, can be used to generate the
derivates at an arbitrary point
b.
For one-dimensional systems admitting a moment equation representation, we can generate an exact, closed set, of autonomous, coupled, first order differential equations (in the inverse scale variable) for scaling transform related expression. These can be integrated in order to generate an effective analytic continuation of Equation (1) into a sufficiently small-scale regime within which asymptotic matching with Equation (3) is used to recover the local properties of the physical solution at an arbitrary point
b. This approach works very well for the various examples considered in [
42,
43].
For two-dimensional systems, there are no such closed coupled differential equations; however, we believe that through OPPQ, one can generate a hierarchy of such autonomous differential equations, with increasing accuracy as the order of the hierarchy is increased. Alternatively, for appropriate scaling functions, for which Equation (2) defines a convergent series in , we can achieve the same, through appropriate re-summation methods, and then use asymptotic matching to recover the physical, configuration space, solution.
All of the above assumes that the (infinite scale) moments, , for each discrete state, are known. That is, knowledge of the physical power moments (derived through OPPQ, momentum space HD, EMM, etc.) coupled with the appropriate analytic continuation strategy, proves very effective in recovering the local solution. However, it proves to be difficult to use the above scaling transform relations to couple the power moments to the local structure (i.e., the local power series expansion of ), in order to determine the physical energies. It is this type of global-local analysis that we are trying to implement through the pointwise convergent properties of the OPPQ expansion.
As shown in this work, the OPPQ representation does allow for this type of “global-local” analysis.
The following sections provide the technical details for our global-local quantization analysis based on the OPPQ expansion. The energies will be determined by constraining the OPPQ expansion to generate the exact local structure of the wavefunction at a particular point b, based on the actual local configuration space power series expansion.
Section 2 gives the technical details for OPPQ. This includes generating the moment equation. We also motivate its
properties, as well as its global pointwise convergence to the configuration space function, along the real axis. Some of the earlier discussion is presented in greater detail.
Section 3 specifies the relations essential for our “global-local” quantization formalism. Two problems are considered: the general sextic anharmonic potential for parameter values where the HD method fails, or becomes ineffective, as depicted in
Figure 1; and a rational fraction potential problem with a ground state solution that is meromorphic. For the latter, we demonstrate the nonuniform, global, pointwise convergence (along an infinite strip in the complex-
x plane) for the OPPQ expansion of the solution, as determined by our “global-local” quantization analysis. We also provide numerical data on the error in the pointwise convergence.