Root Operators and “Evolution” Equations
Abstract
:1. Introduction
2. Examples of Evolution Equation: Heat, Schrödinger and Paraxial Wave Equations
2.1. General Treatment: Hamiltonian and Evolution Operators
2.2. Evolution Operator as Poisson and Fresnel Transforms
2.3. Polynomial Solutions and Symmetry Transformations
3. Evolution Operator and Fractional Partial Differential Equations
4. Dirac-like Factorization to Disentangle Root OperatorFunctions
4.1. Square Root Function
4.2. Estension of the Procedure to Higher-Degree Root Operator Functions
4.2.1. Cube Root
4.2.2. Quartic Root
4.2.3. m-th Roots
5. Possible Applications: Practical and Conceptual Issues
5.1. Square Root of Differential Operators
5.1.1. Solving Relativistic-like Free Evolution Equations
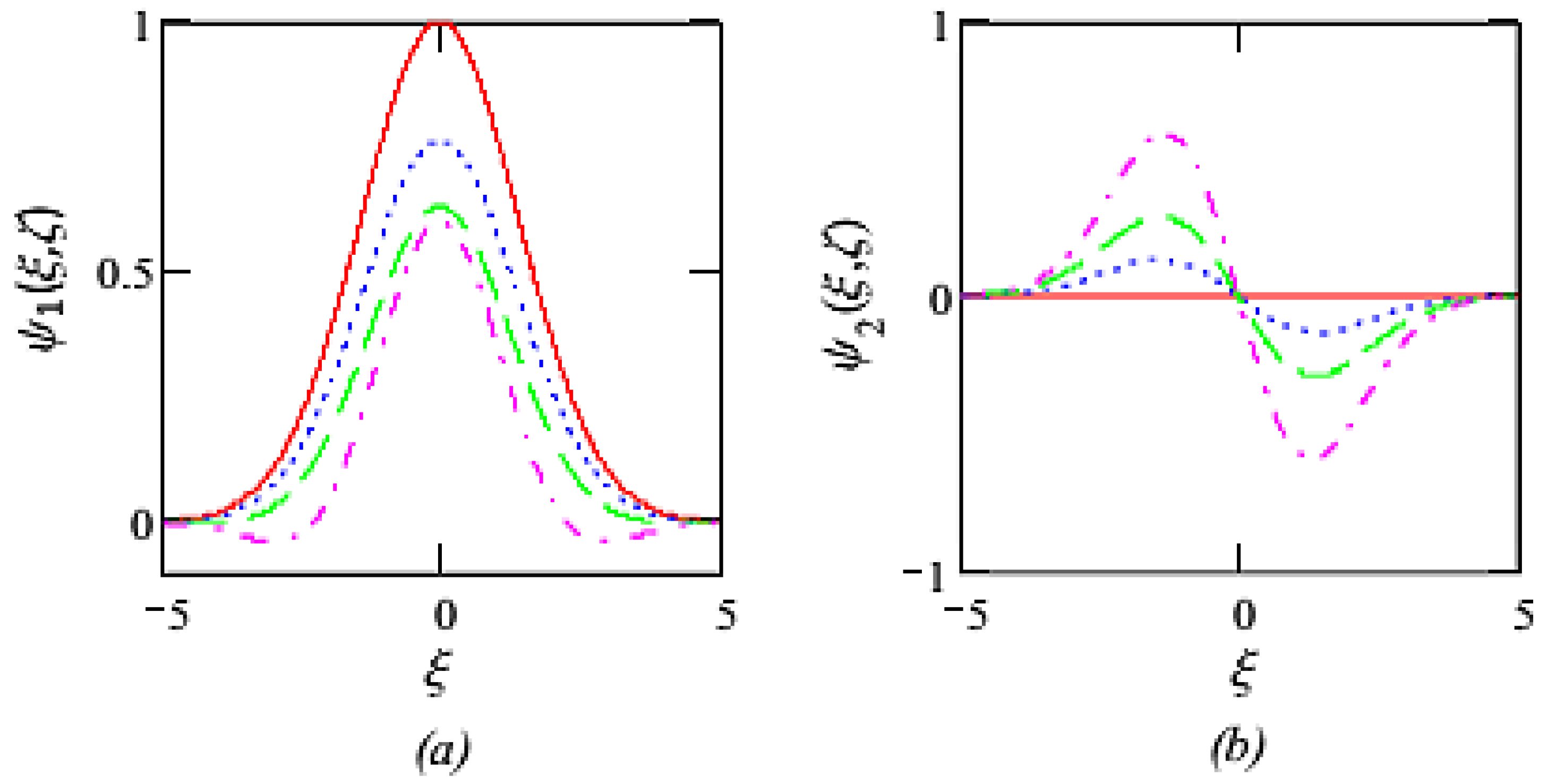

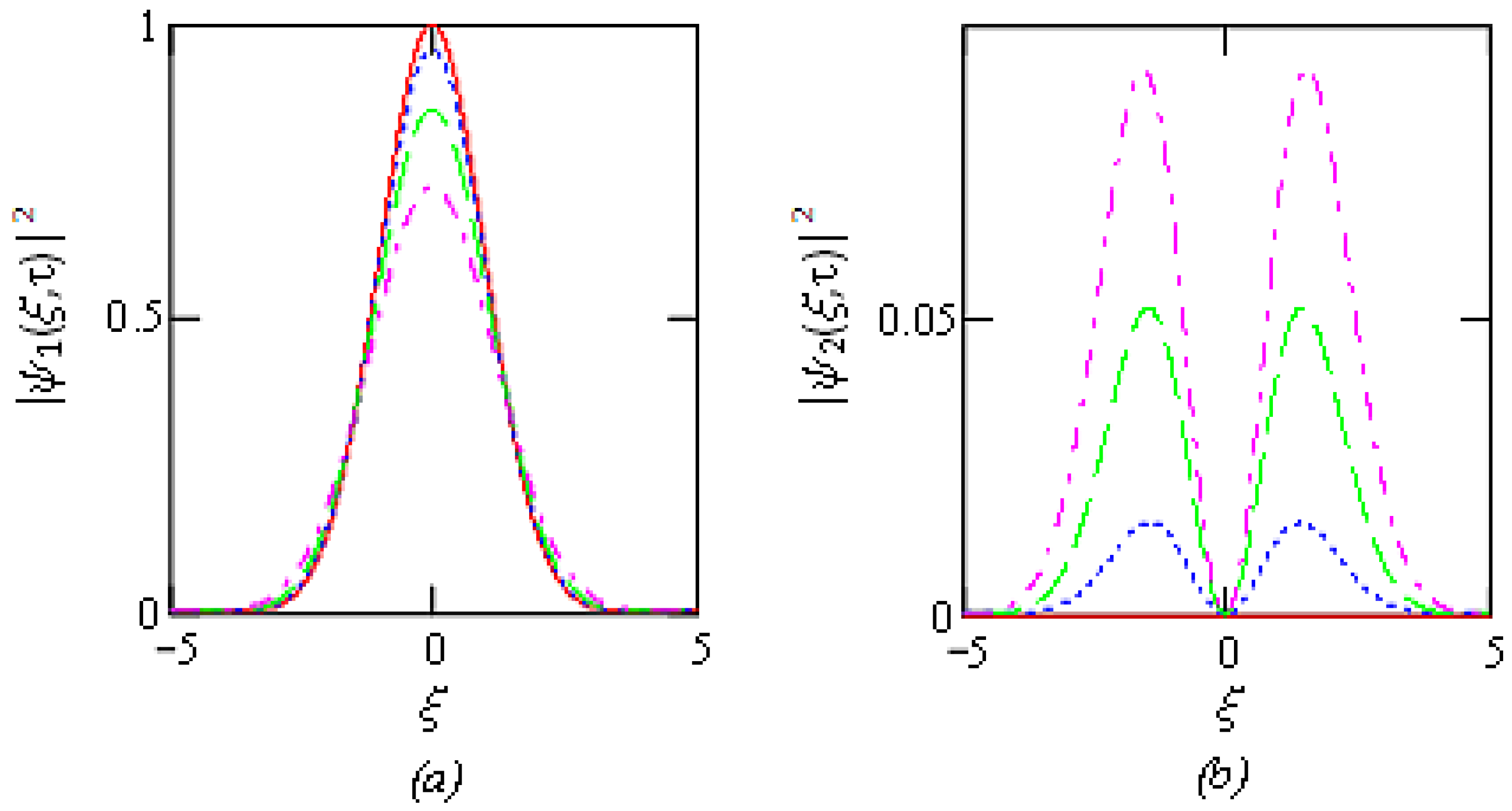
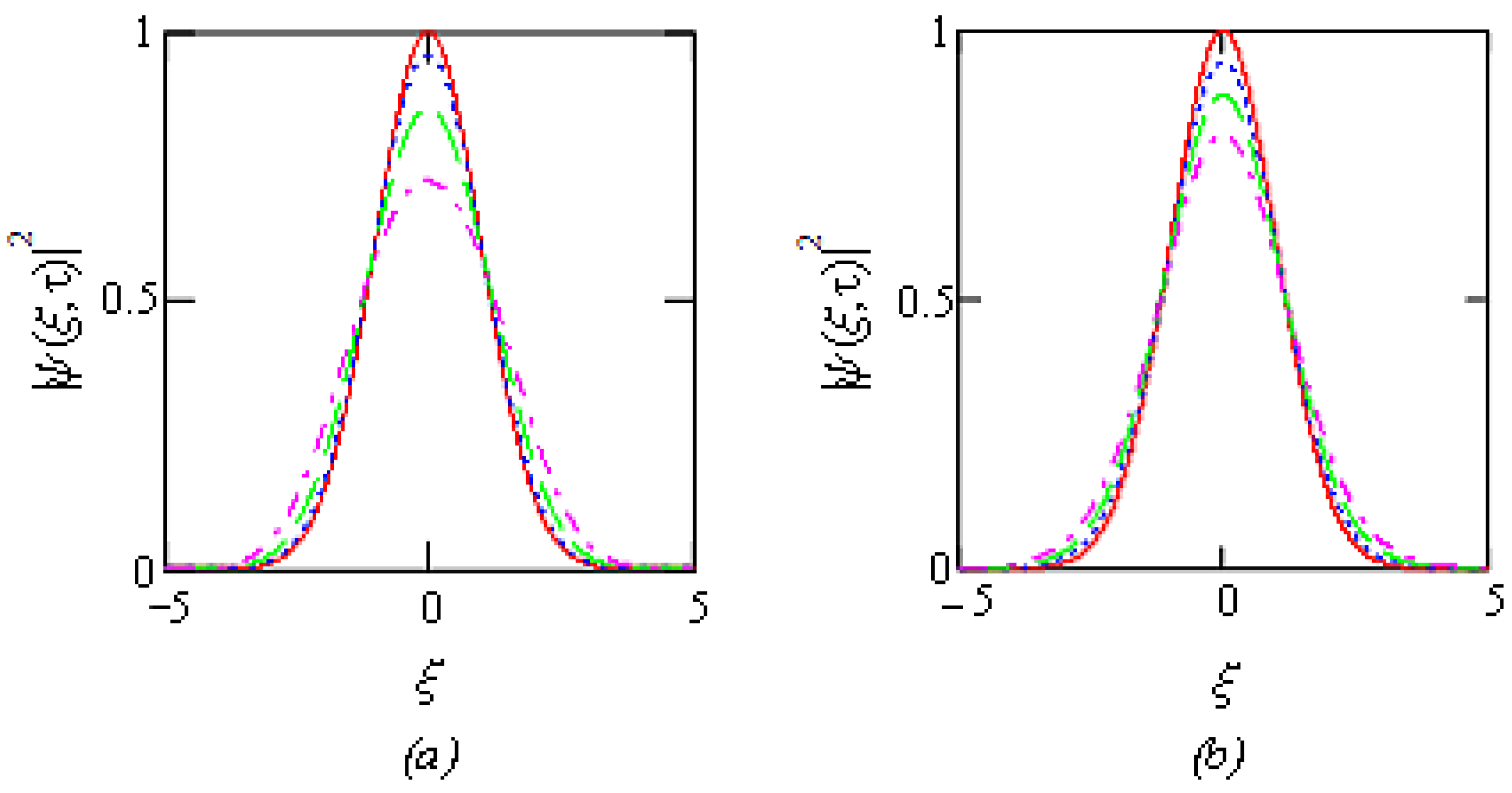
5.1.2. Suggesting Alternative Formulations in Fractional Calculus
5.2. Cube Root of Differential Operators
6. Relativistic-like Evolution Equation: A “Direct” Solving Method
6.1. Evolution Operator
6.2. Evolution Operator as McDonald Transform
6.3. Symmetry Transformations and “Polynomial” Solutions
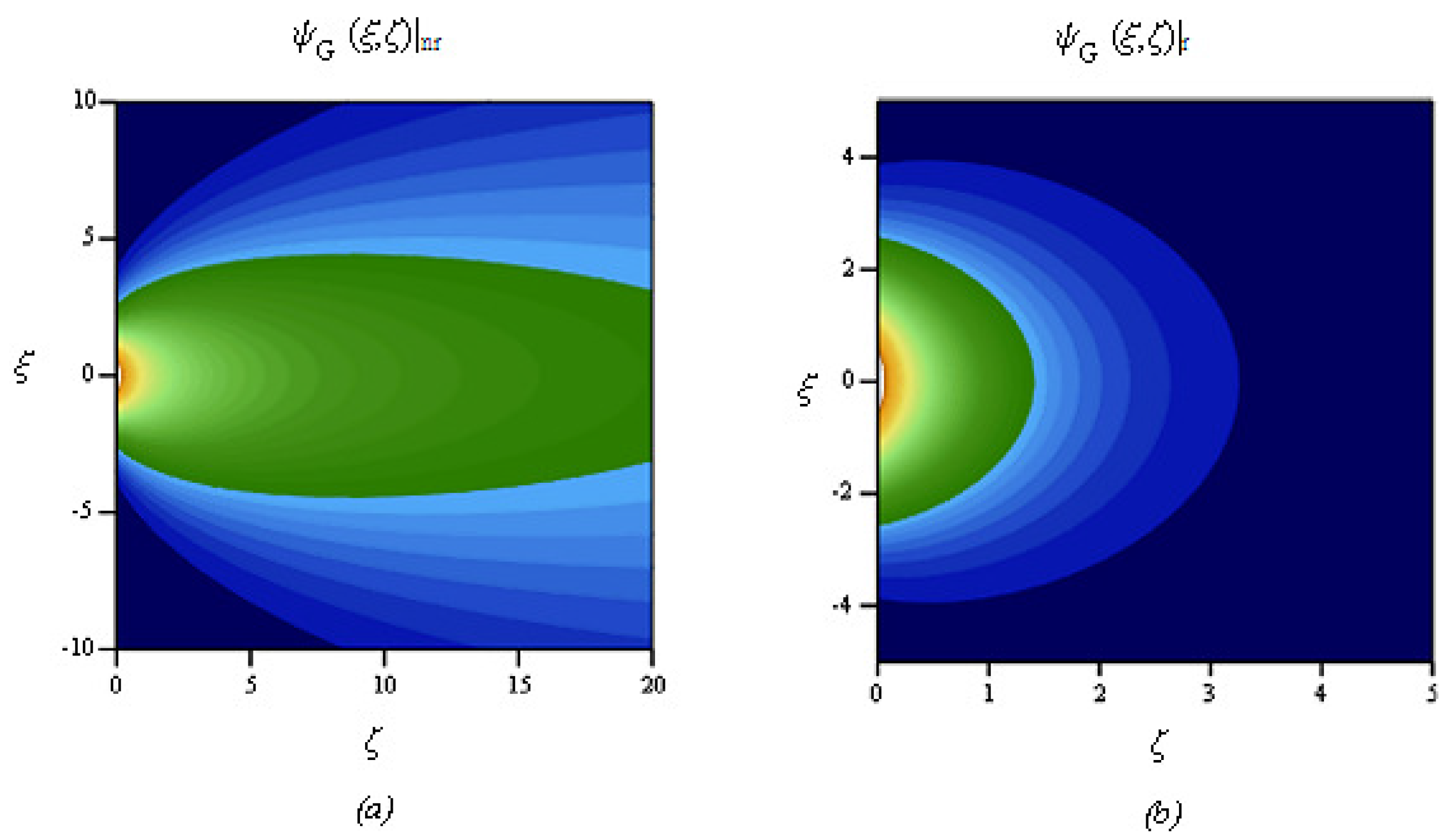
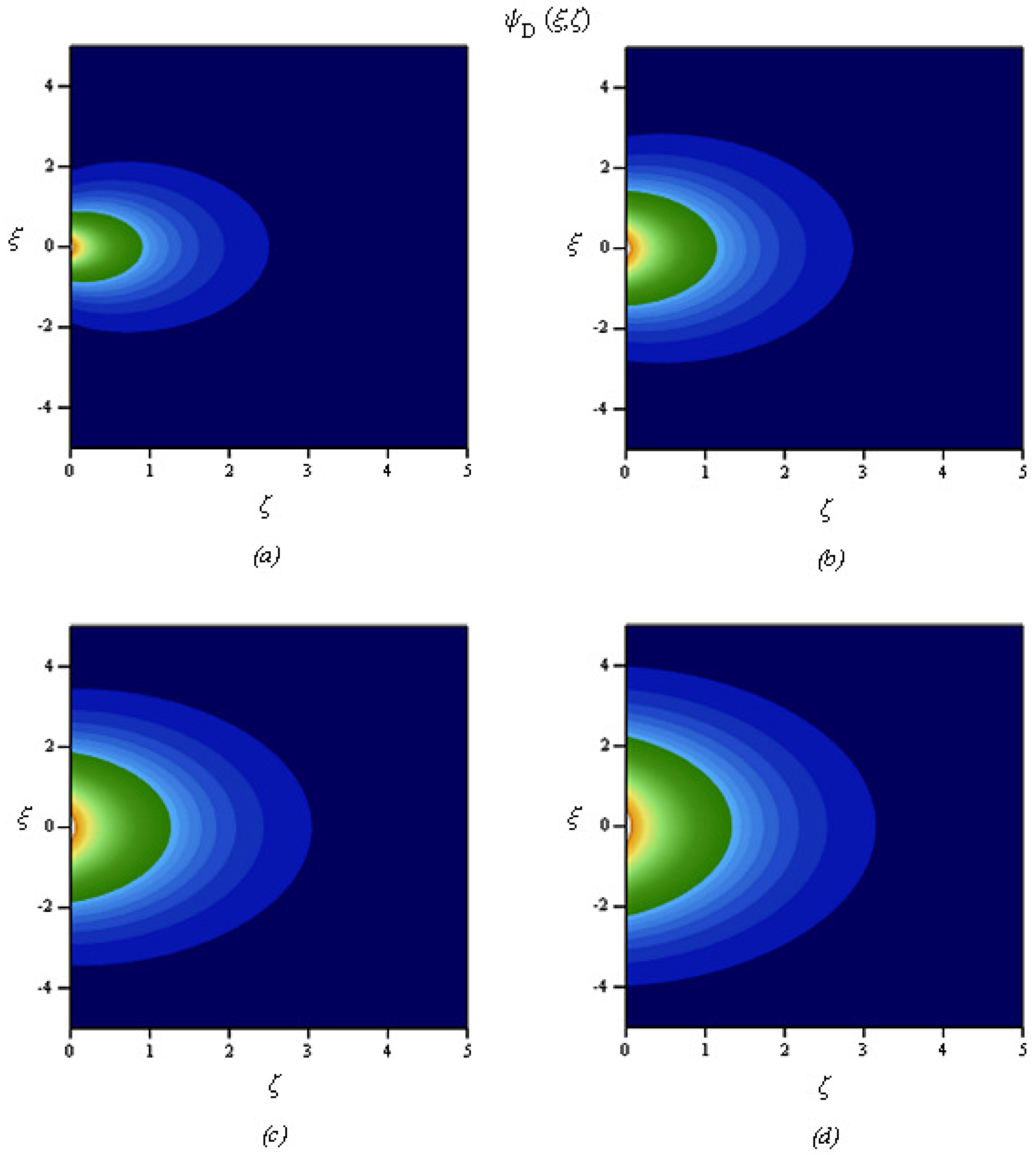
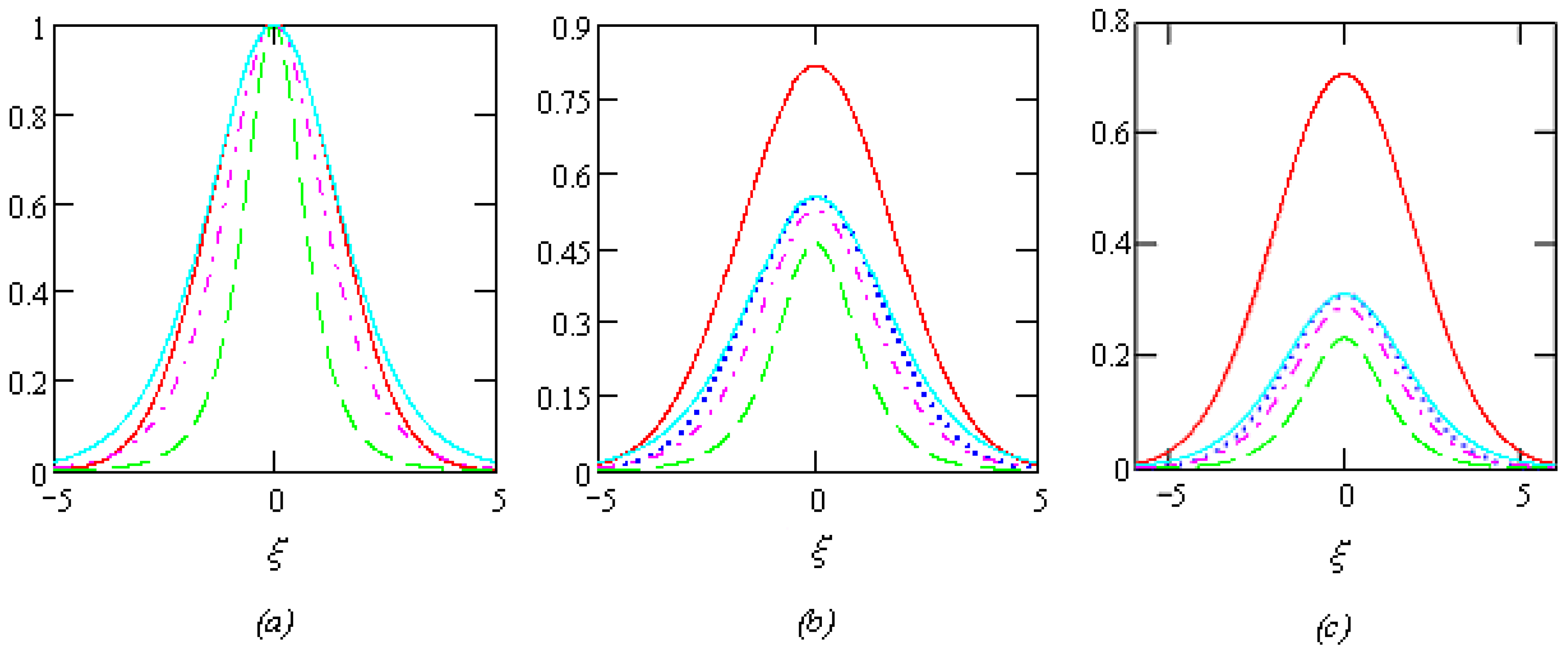
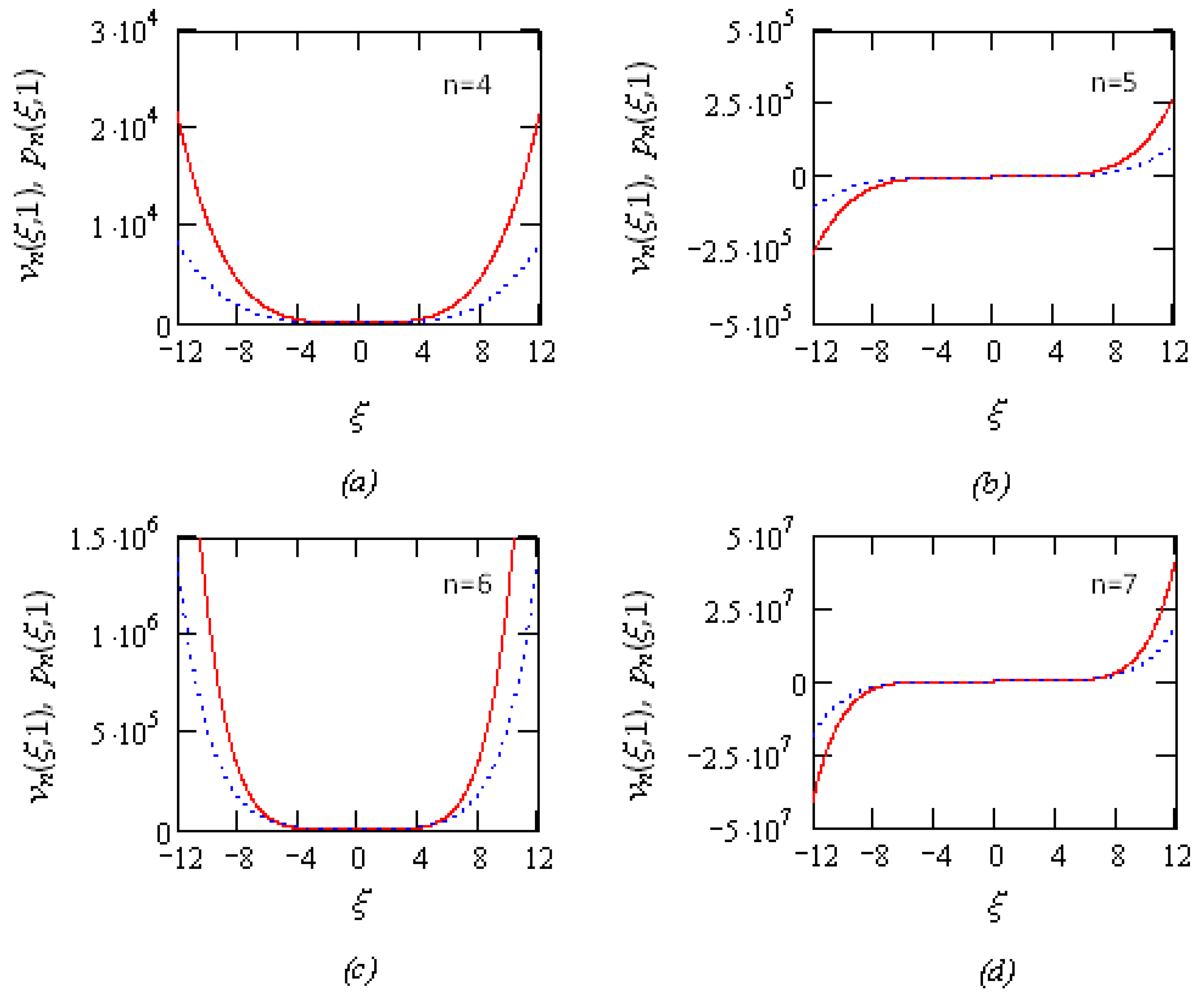
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Olver, P.J. Introduction to Partial Differential Equations; Springer: New York, NY, USA, 2014. [Google Scholar]
- Widder, D.V. The Heat Equation; Academic Press: London, UK, 1975. [Google Scholar]
- Ballentine, L.E. Quantum Mechanics; Prentice Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Marcuse, D. Light Transmission Optics; Van Nostrand Reinhold: New York, USA, 1972. [Google Scholar]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics; McGraw Hill: New York, NY, USA, 1953. [Google Scholar]
- Bjorken, J.D.; Drell, S.D. Relativistic Quantum Mechanics; McGraw Hill: New York, NY, USA, 1964. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Salpeter, E.E. Mass corrections to the fine structure of hydrogen-like atoms. Phys. Rev. 1952, 87, 328–343. [Google Scholar] [CrossRef]
- Lämmerzahl, C. The pseudodifferential operator square root of the Klein-Gordon equation. J. Math. Phys. 1993, 34, 3918–3932. [Google Scholar] [CrossRef]
- Kowalski, K.; Rembieliński, J. Salpeter equation and probability current in the relativistic Hamiltonian quantum mechanics. Phys. Rev. A 2011, 84, 012108. [Google Scholar] [CrossRef]
- Dattoli, G.; Sabia, E.; Górska, K.; Horzela, A.; Penson, K.A. Relativistic wave equations: An operational approach. J. Phys. A 2015, 48, 125203. [Google Scholar] [CrossRef]
- Babusci, D.; Dattoli, G.; Quattromini, M.; Ricci, P.E. A note on the extension of the Dirac method. App. Math. Comput. 2011, 218, 1495–1497. [Google Scholar] [CrossRef]
- Babusci, D.; Dattoli, G.; Quattromini, M.; Ricci, P.E.; Babusci, D. Extension of the dirac factorization and relevant applications. Bull. TICMI 2014, 18, 52–66. [Google Scholar]
- Torre, A.; Dattoli, G.; Quattromini, M.; Ricci, P.E. A note on the extension of the Dirac method. App. Math. Comput. 2011, 218, 1495–1497. [Google Scholar]
- Dirac, P.A.M. The quantum theory of the electron. Proc. R. Soc. Lond. A 1928, 117, 610–624. [Google Scholar] [CrossRef]
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. In Advances in Applied Mechanics; von Mises, R., von Kármán, T., Eds.; Academic Press Inc.: New York, NY, USA, 1948; pp. 171–199. [Google Scholar]
- Hopf, E. The partial differential equation ut + uux = μuxx. Comm. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Cole, J.D. On a quasi-linear parabolic equation occurring in aerodynamics. Appl. Math. 1951, 9, 225–236. [Google Scholar]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Polit. Econ 1973, 81, 637–659. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of rational option pricing. J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Torre, A. Paraxial wave equation: Lie-algebra based approach. In Mathematical Optics: Classical, Quantum, and Computational Methods; Lakshminarayanan, V., Calvo, M.L., Alieva, T., Eds.; CRC Press: New York, NY, USA, 2013; pp. 341–417. [Google Scholar]
- Kato, T. Perturbation Theory for Linear Operators; Springer-Verlag: Berlin, Germany, 1976. [Google Scholar]
- Appell, M.P. Sur l’équation et la théorie de la chaleur. J. Math. Pure Appl. 1892, 8, 187–216. [Google Scholar]
- Rosenbloom, P.C.; Widder, D.V. Expansions in terms of heat polynomials and associated functions. Trans. Am. Math. Soc. 1959, 92, 220–266. [Google Scholar] [CrossRef]
- Kemnitz, H. Polynomial expansions for solutions of . SIAM J. Math. Anal. 1982, 13, 640–650. [Google Scholar] [CrossRef]
- Magnus, W.; Oberhettinger, F.; Soni, R.P. Formulas and Theorems for the Special Functions of Mathematical Physics; Springer-Verlag: Berlin, Germany, 1966. [Google Scholar]
- Torre, A. The Appell transformation for the paraxial wave equation. J. Opt. 2011, 13, 015701.1–015701.14. [Google Scholar] [CrossRef]
- Torre, A. Appell transformation and canonical transforms. SIGMA 2011, 7. [Google Scholar] [CrossRef]
- Leutwiler, H. On the Appell transformation. In Potential Theory; Kràl, J., Ed.; Plenum Press: New York, NY, USA, 1988; pp. 215–222. [Google Scholar]
- Torre, A. Appell transformation and symmetry transformations for the paraxial wave equation. J. Opt. 2011, 13, 818–822. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: Oxford, UK, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujiilo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Di Paola, M.; Failla, G.; Pirrotta, A. Stationary and non-stationary stochastic response of linear fractional viscoelastic systems. Probab. Eng. Mech. 2012, 28, 85–90. [Google Scholar] [CrossRef]
- Di Lorenzo, S.; Di Paola, M.; Pinnola, F.P.; Pirrotta, A. Stochastic response of fractionally damped beams. Probab. Eng. Mech. 2014, 35, 37–43. [Google Scholar] [CrossRef]
- Di Matteo, A.; Lo Iacono, F.; Navarra, G.; Pirrotta, A. Innovative modeling of Tuned Liquid Column Damper motion. Commun. Nonlinear Sci. Numer. Simul. 2015, 23, 229–244. [Google Scholar] [CrossRef]
- Penson, K.A.; Górska, K. Exact and explicit probability densities for one-sided Levy stable distributions. Phys. Rev. Lett. 2010, 105, 210604. [Google Scholar] [CrossRef] [PubMed]
- Gorska, K.; Penson, K.A.; Babusci, D.; Dattoli, G.; Duchamp, G.H.E. Operator solutions for fractional Fokker-Planck equations. Phys. Rev. E 2012, 85, 031138. [Google Scholar] [CrossRef]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2011. [Google Scholar]
- Luke, Y.L. The Special Function and their Approximation; Academic Press: New York, NY, USA, 1969; Volume I. [Google Scholar]
- Ricci, P.E. Le funzioni pseudo-iperboliche e pseudo-trigonometriche. Pubbl. Istit. Mat. Appl. Fac. Ing. Univ. Stud. Roma 1978, 12, 37. [Google Scholar]
- Dattoli, G.; Migliorati, M.; Ricci, P.E. The Eisenstein Group and the Pseudo Hyperbolic Functions; ENEA Report: Rome, Italy, 2007. [Google Scholar]
- Shamir, J.; Cohen, N. Root and power transformations in optics. JOSA A 1995, 12, 2415–2423. [Google Scholar] [CrossRef]
- Gallier, J. Notes on Differential Geometry and Lie Groups. 2015. Available online: http://www.seas.upenn.edu/∼jean/diffgeom.pdf (accessed on 9 May 2015).
- Samko, G.S.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Mainardi, F. Fractional calculus: Some basic problems in continuum and statistical mechanics. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer Verlag: Wien, Austria, 1997; pp. 291–348. [Google Scholar]
- Wilcox, R.M. Exponential operators and parameter differentiation in quantum physics. J. Math. Phys. 1967, 8, 962–983. [Google Scholar] [CrossRef]
- Casas, F.; Murua, A.; Nadinic, M. Efficient computation of Zassenhaus formula. Comp. Phys. Comm. 2012, 183, 2386–2391. [Google Scholar] [CrossRef]
- Babusci, D.; Dattoli, G.; Quattromini, M. Relativistic equations with fractional and pseudo-differential operators. Phys. Rev. A 2011, 83, 062109. [Google Scholar] [CrossRef]
- Fikhtengolts, G.M. Kurs Differentsialnogo I Integralnogo Ischisleniya; Gostekhizdat: Moscow, Russia, 1947–1949; Volume I–III. [Google Scholar]
- Doetsch, G. Handbuch der Laplace Transformation; Birkhauser: Basel, Switzerland, 1972. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: London, UK, 1958. [Google Scholar]
- Appell, M.P. Sur une classe de polynômes. Ann. Sci. Ecole Norm. Super 1880, 9, 119–144. [Google Scholar]
- Dattoli, G.; Zukhovsky, K. Appèl polynomials series expansions. Int. Math. Forum 2010, 5, 649–662. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dattoli, G.; Torre, A. Root Operators and “Evolution” Equations. Mathematics 2015, 3, 690-726. https://doi.org/10.3390/math3030690
Dattoli G, Torre A. Root Operators and “Evolution” Equations. Mathematics. 2015; 3(3):690-726. https://doi.org/10.3390/math3030690
Chicago/Turabian StyleDattoli, Giuseppe, and Amalia Torre. 2015. "Root Operators and “Evolution” Equations" Mathematics 3, no. 3: 690-726. https://doi.org/10.3390/math3030690
APA StyleDattoli, G., & Torre, A. (2015). Root Operators and “Evolution” Equations. Mathematics, 3(3), 690-726. https://doi.org/10.3390/math3030690





