Direct Transformation of Laplace Equation’s Solution from Spherical to Cartesian Representation

Abstract

The description of the Earth’s gravitational field, governed by the fundamental potential equation (the Laplace equation), is conventionally expressed using spherical harmonics, yet the Cartesian formulation, using a Taylor series representation, offers significant algebraic advantages. This paper proposes a novel Direct Cartesian Method for generating spherical basis functions and coefficients directly within the Cartesian coordinate system, utilising the partial derivatives of the inverse distance ($1/R$) function. The present study investigates the structural correspondence between the Cartesian form of spherical basis functions and the high-order partial derivatives of $1/R$. The study reveals that spherical basis functions can be categorised into four distinct groups based on the parity of the degree n and order m. It is demonstrated that each spherical basis function is equivalent to a weighted summation of the partial derivatives of the inverse distance ($1/R$) with respect to Cartesian coordinates. Specifically, the basis functions are combined with those derivatives that share the same order of Z-differentiation and possess matching parities in their orders of differentiation with respect to X and Y. In order to facilitate the practical calculation of these high-degree derivatives, a recursive numerical algorithm has been developed. The method generates the polynomial coefficients for the numerator of the $1/R$ derivatives. A pivotal innovation is the implementation of a step-wise normalization scheme within the recursive relations. The integration of the recursive ratios of global normalization factors (including full Schmidt normalization) into each step of the algorithm effectively neutralises factorial growth, rendering the process immune to numerical overflow. The validity and numerical stability of the proposed method are demonstrated through a detailed step-by-step derivation of a sectorial basis function ($n=8,m=2$).

1. Introduction

1.1. The Gravitational Potential and the Laplace Equation

Newton’s law of universal gravitation (characterized by the inverse-square law) posits that the gravitational acceleration produced by a mass situated at the origin of a coordinate system, when observed from any given point in space, is inversely proportional to the square of the distance between the point and the origin. Additionally, the acceleration is a vector, and this vector’s direction is oriented towards the origin of the coordinate system where the mass is situated.

Laplace determined that this vector, at any given location in space, is the gradient of a scalar function called potential and can be constructed as the partial derivatives of the potential function.

Moreover, he observed an additional property: in source-free regions, the sum of the second derivatives of this scalar function (with respect to Cartesian coordinates) equals zero. This property is encapsulated in what is known as the Laplace differential equation [1].

$$\left({\displaystyle \frac{{\partial }^{2}U}{\partial X^2}}+{\displaystyle \frac{{\partial }^{2}U}{\partial Y^2}}+{\displaystyle \frac{{\partial }^{2}U}{\partial Z^2}}\right)=0.$$

This finding was later supplemented by Poisson, who stated that where masses are present, the right side of the equation contains a term with the density of the matter ($\rho$) [2]:

$$\left({\displaystyle \frac{{\partial }^{2}U}{\partial X^2}}+{\displaystyle \frac{{\partial }^{2}U}{\partial Y^2}}+{\displaystyle \frac{{\partial }^{2}U}{\partial Z^2}}\right)=-4\pi G\rho ,$$

where G is the gravitational constant and $\rho$ is the density of the material.

The potential generated at an external point $P(X,Y,Z)$ by a given mass element is inversely proportional to the distance r between the external point and the mass element. For the whole volume of the body, the volume integral should be calculated:

$$U=G{\int }_M{\displaystyle \frac{dm}{r}},$$

(1)

where G represents the gravitational constant, and the integration is performed over the domain M, which represents the entire spatial volume occupied by the attracting mass. In Equation (1), r denotes the Euclidean distance between the computation point P (defined by position vector $\mathbf{R}$) and the infinitesimal mass element $dm$ (defined by position vector $\mathit{\rho }$), i.e., $r=|\mathbf{R}-\mathit{\rho }|$. Mathematically, the term $1/r$ corresponds to the fundamental solution (or Green’s function) of the Laplace operator in three-dimensional unbounded space [3]. Since the gravitational potential satisfies the linear Poisson equation, the general solution for an arbitrary mass distribution is constructed by the superposition (convolution) of these elementary point-source solutions. The solution methods in spherical and Cartesian coordinate systems differ in how the ${\displaystyle \frac{1}{r}}$ function is expressed and how the integration in Equation (1) is performed.

• The spherical approach utilizes the generating function of Legendre polynomials (as detailed in Section 1.2).
• The Cartesian approach applies a 3D Taylor series expansion (as detailed in Section 1.3).

1.2. Laplace’s Equation in Spherical Coordinates

1.2.1. The General Solution in Spherical Coordinates

In the spherical coordinate representation of Laplace’s equation, the coordinates are the radius (R—the distance from the origin), the polar angle (or colatitude, $\vartheta$), and the longitude (or azimuth $\lambda$) angles. The Laplace equation takes the following form:

$${\displaystyle \frac{1}{R^2}}{\displaystyle \frac{\partial }{\partial R}}\left(R^2{\displaystyle \frac{\partial U}{\partial R}}\right)+{\displaystyle \frac{1}{R^{2}sin\vartheta }}\left(sin\vartheta {\displaystyle \frac{\partial U}{\partial \vartheta }}\right)+{\displaystyle \frac{1}{R^2{sin}^2\vartheta }}\left({\displaystyle \frac{{\partial }^{2}U}{\partial {\lambda }^2}}\right)=0.$$

This equation can be solved by the method of separation of variables (Fourier method), which is comprehensively described in [4]. A solution is sought which is the product of an R-dependent function $\mathcal{R}\left(R\right)$, a $\vartheta$-dependent function $P\left(\vartheta \right)$ and a $\lambda$-dependent function $\mathsf{\Lambda }\left(\lambda \right)$.

$$U(R,\theta ,\lambda )=\mathcal{R}\left(R\right)·P\left(\theta \right)·\mathsf{\Lambda }\left(\lambda \right).$$

Substituting and performing the necessary transformations, we obtain the following conditions for each function:

The form of the function $\mathcal{R}\left(R\right)$ must be either $R^n$ or $R^{-(n+1)}$, where n is an integer. In the following, for gravity calculations outside the mass volume of Earth, only the $R^{-(n+1)}$ term remains, as the potential for $R=\infty$ should be zero.

The function $\mathsf{\Lambda }\left(\lambda \right)$ must be a harmonic function, $cos\left(m\lambda \right)$ or $sin\left(m\lambda \right)$, and since it must be periodic in $2\pi$, m is also an integer. From these two conditions, it follows that the function $P\left(\vartheta \right)$ must be the solution of the following, the so-called Legendre differential equation [5]:

$${\displaystyle \frac{1}{sin\vartheta }}{\displaystyle \frac{\partial }{\partial \vartheta }}\left(sin\vartheta {\displaystyle \frac{\partial P\left(\vartheta \right)}{\partial \vartheta }}\right)+\left[n·(n+1)-{\displaystyle \frac{m^2}{{sin}^2\vartheta }}\right]P=0.$$

The solution to this problem requires two integer values, where n is called the degree, and m is called the order.

The solution of the Legendre differential equation is called Legendre polynomial for given n, if $m=0$, and associated Legendre function for $m\ne 0$, which can be obtained by the Rodrigues formula [6]:

$$P_{nm}\left(\vartheta \right)={\displaystyle \frac{{\left(1-{cos}^2\vartheta \right)}^{\frac{m}{2}}}{2^n·n!}}·{\displaystyle \frac{{\partial }^{n+m}{\left({cos}^2\vartheta -1\right)}^n}{\partial {(cos\vartheta )}^{n+m}}}.$$

The consequence of the derivation in these formulas shows that nonzero elements are obtained only for $m\le n$.

However, the physical meaning of the solution is best understood by expanding the reciprocal distance term $1/r$ in the potential integral (Equation (1)). Using the law of cosines, the distance r can be expressed as the difference between the vectors $\mathbf{R}$ (observation point) and $\mathit{\rho }$ (mass element):

$${\displaystyle \frac{1}{r}}={\displaystyle \frac{1}{|\mathbf{R}-\mathit{\rho }|}}={\displaystyle \frac{1}{\sqrt{R^2+{\rho }^2-2R\rho cos\psi }}}={\displaystyle \frac{1}{R\sqrt{1+{\left(\frac{\rho }{R}\right)}^2-2\frac{\rho }{R}cos\psi }}},$$

where $\psi$ is the angle between $\mathbf{R}$ and $\mathit{\rho }$. The validity of this expansion for the external gravitational field requires that the observation point is located outside the bounding sphere of the mass (${\displaystyle \frac{\rho }{R}}<1$). Under this condition, the term can be expanded into a convergent series using the generating function of Legendre polynomials $P_n(cos\psi )$:

$${\displaystyle \frac{1}{r}}=\sum _{n=0}^{\infty }{\displaystyle \frac{{\rho }^n}{R^{n+1}}}{P}_n\left(cos\psi \right).$$

Substituting this expansion back into Equation (1), and utilizing the addition theorem for spherical harmonics to separate the coordinates, leads to the standard spherical harmonic series form. Consequently, this approach yields the general solution for the gravitational potential $U(R,\vartheta ,\lambda )$ expressed in spherical coordinates:

$$U(R,\vartheta ,\lambda )=\sum _{n=0}^{\infty }\sum _{m=0}^n{\displaystyle \frac{1}{R^{n+1}}}{P}_{nm}\left(\vartheta \right)·\left[C_{nm}cos\left(m\lambda \right)+S_{nm}sin\left(m\lambda \right)\right].$$

For later use, we might factor out the spherical basis functions, which are the products of the power or radius, the Legendre function, and the cosine or sine of longitude. The basis function contains the coordinates of the observation point (R, $\vartheta$, $\lambda$). As the $R^n$ is in the denominator, the fraction was expanded by multiplying both the numerator and denominator by $R^n$—as we will see—to obtain Cartesian coordinates in the numerator.

The cosine and sine spherical basis functions are denoted with $C{B}_n^m$ and $S{B}_n^m$;

$$C{B}_n^m={\displaystyle \frac{R^n·P_{nm}\left(\vartheta \right)·cos\left(m\lambda \right)}{R^{2n+1}}},$$

(2)

$$S{B}_n^m={\displaystyle \frac{R^n·P_{nm}\left(\vartheta \right)·sin\left(m\lambda \right)}{R^{2n+1}}}.$$

(3)

The coefficients $C_{nm}$ and $S_{nm}$ characterize the mass distribution of the body. These coefficients are the integrals for the entire body, multiplied by the respective aforementioned functions of the spherical coordinates of body masses, and are specified as:

$$C_{nm}={\int }_M{\rho }^n·P_{nm}\left({\vartheta }^{\prime }\right)·cos\left(m{\lambda }^{\prime }\right)·dm,$$

(4)

$$S_{nm}={\int }_M{\rho }^n·P_{nm}\left({\vartheta }^{\prime }\right)·sin\left(m{\lambda }^{\prime }\right)·dm,$$

(5)

where $\rho$ is the radius (the distance from coordinate system origin), ${\vartheta }^{\prime }$ is the colatitude and $\lambda$ is the longitude of the respective mass, $dm$. The coefficients of Equations (4) and (5) are formally similar to the numerators of the spherical base functions in Equations (2) and (3).

As we do not know the actual distribution of the masses in Earth’s interior, the $C_{nm}$ and $S_{nm}$ coefficients are calculated using measurements of gravity-related quantities on Earth’s surface and in outer space.

Following this factoring out, the potential equation is represented as follows, as the linear combination of the basis functions ($C{B}_{nm}$ and $S{B}_{nm}$) where the multipliers are the respective coefficients ($C_{nm}$ and $S_{nm}$):

$$U(R,\vartheta ,\lambda )=\sum _{n=0}^{\infty }\sum _{m=0}^n\left[C{B}_n^m·C_{nm}+S{B}_n^m·S_{nm}\right].$$

1.2.2. Schmidt Normalization

Schmidt demonstrated that Legendre polynomials, in addition to being orthogonal, should also be normalized for the calculation of the actual values of the coefficients. Additionally, this normalization decreased the very high numeric values of the Legendre functions for higher n values.

This condition is satisfied if one multiplies the normalizing factor by the square of the Legendre function and then take its integral over the range $\vartheta =[0,\pi ]$ to obtain 1. This integral condition in spherical coordinates is given by:

$$k_n^m={\displaystyle \frac{4\pi }{{\int }_{\lambda =0}^{2\pi }{\int }_{\vartheta =0}^{\pi }{\left(P_{nm}\right)}^{2}sin\vartheta d\vartheta d\lambda }}.$$

That means the completed Schmidt normalization is defined as follows: for $m\ne 0$,

$$k_n^m=\sqrt{(2n+1)·2{\displaystyle \frac{(n-m)!}{(n+m)!}}},$$

(6)

and for $m=0$,

$$k_n^0=\sqrt{(2n+1)·{\displaystyle \frac{(n-m)!}{(n+m)!}}}.$$

(7)

Similarly, by combining Equations (6) and (7) we get:

$$k_n^m=\sqrt{2-{\delta }_{0,m}}·\sqrt{(2n+1)·2{\displaystyle \frac{(n-m)!}{(n+m)!}}}.$$

Using the fully normalized Schmidt coefficients, the normalized spherical base functions are

$$\begin{array}{c}\hfill \overline{C{B}_n^m}=k_n^m·C{B}_n^m,\\ \hfill \overline{S{B}_n^m}=k_n^m·S{B}_n^m,\end{array}$$

the fully normalized coefficients are

$$\begin{array}{c}\hfill \overline{C_{nm}}={\displaystyle \frac{1}{k_n^m}}·C_{nm},\\ \hfill \overline{S_{nm}}={\displaystyle \frac{1}{k_n^m}}·S_{nm},\end{array}$$

and with usage of the fully normalized coefficients and spherical base functions, the potential is:

$$U(R,\vartheta ,\lambda )=\sum _{n=0}^{\infty }\sum _{m=0}^n\left[\overline{C{B}_n^m}·{\overline{C}}_{nm}+\overline{S{B}_n^m}·{\overline{S}}_{nm}\right].$$

(8)

The significance of Equation (8) is that the Earth’s gravitational potential can be expressed in this form. For practical reasons, in the case of gravity models of Earth (e.g., EGM96), the Schmidt normalized coefficients are published [7].

1.3. The Potential in Cartesian Coordinate Representation

To interpret the gravity potential outside of a finite inhomogeneous body, we can again start from Equation (1). In this case, the $1/r$ function can be expressed as the inverse of the distance between body mass point ($x,y,z$) and the observation point ($X,Y,Z$). As the actual spatial distribution of the masses around the origin of the coordinate system is not known, a 3-dimensional Taylor series expansion can be applied to calculate the potential. The $1/r$ function in Equation (1) can be expressed:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{r}}={\displaystyle \frac{1}{R}}-\left(x{\displaystyle \frac{\partial }{\partial X}}{\displaystyle \frac{1}{R}}+y{\displaystyle \frac{\partial }{\partial Y}}{\displaystyle \frac{1}{R}}+z{\displaystyle \frac{\partial }{\partial Z}}{\displaystyle \frac{1}{R}}\right)\hfill \\ \hfill & +6{\displaystyle \frac{1}{2}}(x^2{\displaystyle \frac{{\partial }^2}{\partial X^2}}{\displaystyle \frac{1}{R}}+y^2{\displaystyle \frac{{\partial }^2}{\partial Y^2}}{\displaystyle \frac{1}{R}}+z^2{\displaystyle \frac{{\partial }^2}{\partial Z^2}}{\displaystyle \frac{1}{R}}\hfill \\ \hfill & +2xy{\displaystyle \frac{{\partial }^2}{\partial X\partial Y}}{\displaystyle \frac{1}{R}}+2xz{\displaystyle \frac{{\partial }^2}{\partial X\partial Z}}{\displaystyle \frac{1}{R}}+2yz{\displaystyle \frac{{\partial }^2}{\partial Y\partial Z}}{\displaystyle \frac{1}{R}})\pm \dots ,\hfill \end{array}$$

where x, y and z are the Cartesian coordinates of the masses, X, Y and Z are the Cartesian coordinates of the observation point. To calculate the potential, the partial derivatives of the $1/R$ function can be factored out, and the volume integral contains only the product of masses multiplied by the respective powers of their body coordinates, called multipole sources.

After this arrangement, the potential is the infinite sum of multipole sources of $n^{th}$ degree multiplied by the appropriate basis functions, which are the $n^{th}$ partial derivatives of the ${\displaystyle \frac{1}{R}}$ function.

If only one unit mass point is considered, whose coordinates are x, y and z, then the $n^{th}$ degree of the series is:

$$U^{\left(n\right)}=G{(-1)}^n\sum _{i+j+k=n}{x}^i{y}^j{z}^k{\displaystyle \frac{1}{n!}}·{\displaystyle \frac{{\partial }^n}{{\partial X}^i{\partial Y}^j{\partial Z}^k}}\left({\displaystyle \frac{1}{R}}\right).$$

The potential at the observation point $(X,Y,Z)$ can be expressed using the multipole coefficients $M^{(i,j,k)}$ as follows:

$$U(X,Y,Z)=G\sum _{n=0}^{\infty }{(-1)}^n\sum _{i+j+k=n}{M}^{(i,j,k)}·{\displaystyle \frac{1}{n!}}·{\displaystyle \frac{{\partial }^n}{\partial X^i\partial Y^j\partial Z^k}}\left({\displaystyle \frac{1}{R}}\right),$$

where the source coefficient (the $n^{th}$ degree multipole moment) is defined as:

$$M^{(i,j,k)}={\int }_M{x}^i{y}^j{z}^{k}dm,$$

where $i+j+k=n$, because multipole coefficients involve homogeneous polynomials of coordinates.

1.4. Objectives and Methodology

The primary objective of this study is to bridge the gap between the spherical and Cartesian representations of the potential field by developing a direct transformation method.

The methodology is founded upon two primary pillars: theoretical derivation and numerical algorithm development.

Firstly, the objective is to demonstrate analytically that normalised spherical basis functions can be constructed as a linear combination of Cartesian partial derivatives. This involves

• Systematically categorizing the basis functions into four parity-based groups.
• Establishing the exact summation formula that links the Cartesian derivatives to spherical harmonics.
• Verifying this relationship through the comparison of constituent monomials.

Secondly, to make this theoretical connection computationally viable, we develop a “Direct Numerical Method” for calculating the required partial derivatives of $1/R$. The specific objectives of this study are as follows:

• To define the set of valid exponent triplets $(i,j,k)$ representing the powers of the Cartesian coordinates ($X,Y,Z$) within the constituent monomials of the partial derivatives, strictly governed by homogeneity and parity constraints.
• To derive recursive relations for differentiation with respect to X and Y axes, and to establish a closed-form analytical formula for the coefficients of the pure Z-derivatives.
• To implement a step-wise normalization strategy. Rather than applying normalization factors at the conclusion of the calculation—a process which results in numerical overflow due to factorial growth—the method integrates the recursive ratios of these factors (including Schmidt normalization) directly into the recurrence relations.

Finally, to validate the proposed framework, the methodology includes a detailed numerical walkthrough for a specific case ($n=8$, $m=2$), aiming to confirm the precision of the algorithm.

2. Methods

Converting the Spherical Representation of the Laplace Equation into Cartesian Coordinates

To be able to compare the spherical representation with the Cartesian representation, the obvious way is to transform spherical coordinates into Cartesian coordinates [8]. The transformation between the representations is based on the transformation formulas:

$$x=\rho sin{\vartheta }^{\prime }cos{\lambda }^{\prime },y=\rho sin{\vartheta }^{\prime }sin{\lambda }^{\prime },z=\rho cos{\vartheta }^{\prime }.$$

(9)

In the inverse transformation, here we only need the formula for the radius:

$$\rho =\sqrt{x^2+y^2+z^2}.$$

Although Equation (9) describes the transformation for the internal mass coordinates ($\rho ,{\vartheta }^{\prime },{\lambda }^{\prime }$), an identical geometric transformation applies to the external observation point coordinates ($R,\vartheta ,\lambda$) to derive the Cartesian components ($X,Y,Z$) used in the basis functions in the numerators of Equations (2) and (3).

The following operations are required to convert the spherical coefficients ($C_{nm}$ and $S_{nm}$) and similarly the numerators of the basis functions ($C{B}_{nm}$ and $S{B}_{nm}$) to the Cartesian coordinate system:

• In the case where m is greater than 1, convert the trigonometric functions of multiple angles into single angles.
• Solve ${(1-{cos}^2{\vartheta }^{\prime })}^{k/2}={sin}^k{\vartheta }^{\prime }$, then convert every $\rho ·sin{\vartheta }^{\prime }·cos{\lambda }^{\prime }$ and $\rho ·cos{\vartheta }^{\prime }·cos{\lambda }^{\prime }$ expressions into x and y coordinates.
• After calculating all possible x and y coordinates, convert the remaining ${sin}^k{\vartheta }^{\prime }$ into ${(1-{cos}^2{\vartheta }^{\prime })}^{k/2}$.
• Convert every $\rho cos{\vartheta }^{\prime }$ into z coordinates.
• Finally, convert the remaining $\rho$s to $\sqrt{x^2+y^2+z^2}$.

As an example, the $n=2$ degree spherical coefficients and their actual form in spherical and Cartesian representation are shown in

Table 1. Spherical coefficients $(n=2)$ expressed in spherical and Cartesian coordinates.

Coeffs.	In Spherical Coordinates	In Cartesian Coordinates
$C_{20}$	${\displaystyle \frac{3{\rho }^2{cos}^2{\vartheta }^{\prime }}{2}}-{\displaystyle \frac{{\rho }^2}{2}}$	$-{\displaystyle \frac{x^2}{2}}-{\displaystyle \frac{y^2}{2}}+z^2$
$C_{21}$	$-3{\rho }^{2}cos{\vartheta }^{\prime }sin{\vartheta }^{\prime }cos{\lambda }^{\prime }$	$-3xz$
$S_{21}$	$-3{\rho }^{2}cos{\vartheta }^{\prime }sin{\vartheta }^{\prime }sin{\lambda }^{\prime }$	$-3yz$
$C_{22}$	$3{\rho }^2{sin}^2{\vartheta }^{\prime }{cos}^2{\lambda }^{\prime }-3{\rho }^2{sin}^2{\vartheta }^{\prime }{sin}^2{\lambda }^{\prime }$	$3(x^2-y^2)$
$S_{22}$	$6{\rho }^2{sin}^2{\vartheta }^{\prime }cos{\lambda }^{\prime }sin{\lambda }^{\prime }$	$6xy$

.

The significant benefit of the spherical coordinate representation is the reduction in the number of coefficients. Specifically, a solution of degree n takes the form of $2n+1$ terms in spherical coordinates, while the analogous solution in Cartesian coordinates involves $0.5n^2+1.5n+1$ terms. The disparity in the quantity of terms becomes more pronounced as an increment in n occurs (see

Table 2. Number of terms (coefficients or basis functions) for the respective degree, for Cartesian and spherical representation.

n	Number of Terms Using the Taylor Series-Based Cartesian Coordinates	Number of Terms Using the Spherical Coordinate System
1	3	3
2	6	5
3	10	7
4	15	9
5	21	11
6	28	13
n	$0.5n^2+1.5n+1$	$2n+1$

).

Using Equation (9), both coefficients and basis function of the spherical representation can be transformed into Cartesian coordinates. Upon analyzing the terms of the “transformed into Cartesian” spherical representation and the Taylor series (“true”) Cartesian representation, significant similarities can be observed among the coefficients and the basis functions in both representations.

Specifically, the basis functions of the Taylor series generated for $n=2$ degree are the second partial derivatives, and their relationships to the spherical basis functions $C{B}_2^0$, $C{B}_2^1$, $S{B}_2^1$, and $S{B}_2^2$ are shown in Figure 1. It can be seen that these spherical basis functions are proportional to the partial derivatives of the $1/R$ function. Additionally, comparing with Table 1, it can be noted that term $C_{22}$ can be calculated as the difference in the lower vertices of the triangle in Figure 1.

3. Results

3.1. New, Direct Transformation Method Between the Cartesian and the Spherical Coordinate Systems

Examining the higher-degree terms, notable similarities were identified when expressing the spherical and the Cartesian basis functions. Certain Cartesian basis functions exhibit a remarkable resemblance to the basis functions of the Cartesian-transformed spherical solution, as shown in Figure 1. For example, as noted in $n=2$:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2}{\partial Z^2}}{\displaystyle \frac{1}{R}}& =2C{B}_2^0,\hfill \\ \hfill {\displaystyle \frac{{\partial }^2}{\partial Y\partial Z}}{\displaystyle \frac{1}{R}}& =-S{B}_2^1,\hfill \\ \hfill {\displaystyle \frac{{\partial }^2}{\partial X\partial Z}}{\displaystyle \frac{1}{R}}& =-C{B}_2^1,\hfill \\ \hfill {\displaystyle \frac{{\partial }^2}{\partial X\partial Y}}{\displaystyle \frac{1}{R}}& ={\displaystyle \frac{S{B}_2^2}{2}}.\hfill \end{array}$$

These similarities led to the examination of the relationship between the Cartesian form of the spherical basis functions (Table 1) and the partial derivatives of $1/R$ into Cartesian coordinates.

During the development of a method to directly correlate these formulations, the basis functions of the spherical representation were systematically categorized into four distinct groups.

$$C{B}_n^{m\in \{0,2,\dots ,n\}},C{B}_n^{m\in \{1,3,\dots ,n\}},S{B}_n^{m\in \{1,3,\dots ,n\}},S{B}_n^{m\in \{2,4\dots ,n\}}.$$

Consequently, the original two groups of basis functions ($C{B}_n^m$ and $S{B}_n^m$) were categorized based on the parity of m. The four spherical basis function subcategories can be expressed as follows:

$$\begin{array}{c}\hfill C{B}_n^{even},C{B}_n^{odd},S{B}_n^{odd},S{B}_n^{even}.\end{array}$$

Within these subcategories, the powers of Cartesian coordinates X, Y, and Z appear in similar combinations. The basis functions expressed in Cartesian terms are derived from the partial derivatives of the function $1/R$. The derivatives of the highest order with respect to the Z coordinate are proportional to the initial elements of each of the four categories of spherical basis functions.

$$\begin{array}{cc}\hfill C{B}_n^0& \equiv {\displaystyle \frac{{\partial }^n}{\partial Z^n}}{\displaystyle \frac{1}{R}},\hfill \\ \hfill C{B}_n^1& \equiv {\displaystyle \frac{{\partial }^n}{\partial X\partial Z^{n-1}}}{\displaystyle \frac{1}{R}},\hfill \\ \hfill S{B}_n^1& \equiv {\displaystyle \frac{{\partial }^n}{\partial Y\partial Z^{n-1}}}{\displaystyle \frac{1}{R}},\hfill \\ \hfill S{B}_n^2& \equiv {\displaystyle \frac{{\partial }^n}{\partial X\partial Y\partial Z^{n-2}}}{\displaystyle \frac{1}{R}}.\hfill \end{array}$$

Analogously to the grouping of spherical basis functions, the basis functions of the Cartesian representation can also be organized into four groups. The initial members of these groups are the highest-order derivatives with respect to the Z coordinate, as shown above. The remaining members of each group are made up of partial derivatives of $1/R$, in which the differentiation order with respect to Z decreases by two in each subsequent term, while the total order of differentiation with respect to X and Y increases by two.

Thus, upon examining the basis functions of the Cartesian method, it is evident that for any degree n, the derivatives can be classified into the following four groups, each involving the same products of powers of the coordinates X, Y, and Z:

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^n}{\partial X^l\partial Y^{m-l}\partial Z^{n-m}}}{\displaystyle \frac{1}{R}},{\displaystyle \frac{{\partial }^n}{\partial X^{l+1}\partial Y^{m-l}\partial Z^{n-m-1}}}{\displaystyle \frac{1}{R}},\\ \hfill {\displaystyle \frac{{\partial }^n}{\partial X^l\partial Y^{m-l+1}\partial Z^{n-m-1}}}{\displaystyle \frac{1}{R}},{\displaystyle \frac{{\partial }^n}{\partial X^{l+1}\partial Y^{m-l+1}\partial Z^{n-m-2}}}{\displaystyle \frac{1}{R}},\end{array}$$

where m takes values from 0 to n in steps of 2 and l takes values from 0 to m in steps of 2.

Each group follows a distinct rule concerning the parity of the degree of partial derivatives with respect to coordinates. The parity of the partial derivative with respect to Z depends on n, while a rule independent of n applies to the parity of the partial derivatives with respect to X and Y for each group. Upon analysis of this observed rule, we can categorize the four groups as follows:

$$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^n}{\partial X^{\mathrm{even}}\partial Y^{\mathrm{even}}\partial Z^{n-m}}}{\displaystyle \frac{1}{R}},{\displaystyle \frac{{\partial }^n}{\partial X^{\mathrm{odd}}\partial Y^{\mathrm{even}}\partial Z^{n-m-1}}}{\displaystyle \frac{1}{R}},\\ \hfill {\displaystyle \frac{{\partial }^n}{\partial X^{\mathrm{even}}\partial Y^{\mathrm{odd}}\partial Z^{n-m-1}}}{\displaystyle \frac{1}{R}},{\displaystyle \frac{{\partial }^n}{\partial X^{\mathrm{odd}}\partial Y^{\mathrm{odd}}\partial Z^{n-m-2}}}{\displaystyle \frac{1}{R}},\end{array}$$

where $m\in \{0,2,\dots ,n\}$.

The groups are distinct and do not overlap, as they lack coordinate products with matching exponents. As a result, as illustrated in the final rows of

Table 3. Explicit algebraic forms of the fully normalized spherical basis functions for degree $n=3$. The functions $\overline{C{B}_n^m}$ and $\overline{S{B}_n^m}$ represent the Schmidt-normalized cosine and sine harmonic terms, respectively. The terms are systematically categorized into four subsets based on the parity of the order m and the harmonic character (cosine or sine). The final row, labeled “Constituent monomials,” identifies the specific combinations of Cartesian coordinate powers ($X^i{Y}^j{Z}^k/R^{2n+1}$) characterizing each group, serving as a structural reference for comparison with the Cartesian partial derivatives.

m	$\overline{{\mathit{CB}}_3^{\mathbf{even}}}$	$\overline{{\mathit{CB}}_3^{\mathbf{odd}}}$	$\overline{{\mathit{SB}}_3^{\mathbf{odd}}}$	$\overline{{\mathit{SB}}_3^{\mathbf{B}}}$
0	${\displaystyle \frac{Z^3-\frac{3Y^{2}Z}{2}-\frac{3X^{2}Z}{2}}{R^7}}·\sqrt{7}$
1		${\displaystyle \frac{\frac{X{Y}^2}{4}-X{Z}^2+\frac{X^3}{4}}{R^7}}·\sqrt{42}$	${\displaystyle \frac{-Y{Z}^2+\frac{X^{2}Y}{4}+\frac{Y^3}{4}}{R^7}}·\sqrt{42}$
2	${\displaystyle \frac{\frac{X^{2}Z}{2}-\frac{Y^{2}Z}{2}}{R^7}}·\sqrt{105}$			${\displaystyle \frac{\sqrt{105}XYZ}{R^7}}$
3		${\displaystyle \frac{-\frac{X^3}{4}+\frac{3X{Y}^2}{4}}{R^7}}·\sqrt{70}$	${\displaystyle \frac{-\frac{3X^{2}Y}{4}+\frac{Y^3}{4}}{R^7}}·\sqrt{70}$
Constituent monomials	${\displaystyle \frac{Z^3}{R^7}}$, ${\displaystyle \frac{Y^{2}Z}{R^7}}$, ${\displaystyle \frac{X^{2}Z}{R^7}}$	${\displaystyle \frac{X^3}{R^7}}$, ${\displaystyle \frac{X{Y}^2}{R^7}}$, ${\displaystyle \frac{X{Z}^2}{R^7}}$	${\displaystyle \frac{Y^3}{R^7}}$, ${\displaystyle \frac{X^{2}Y}{R^7}}$, ${\displaystyle \frac{Y{Z}^2}{R^7}}$	${\displaystyle \frac{XYZ}{R^7}}$

and

Table 4. The basis functions of the Cartesian representation for degree $n=3$, constructed from the partial derivatives of the inverse distance function ($1/R$). The expressions incorporate the binomial and factorial coefficients ($-\left({\displaystyle \genfrac{}{}{0pt}{}{n}{m}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{m}{l}}\right)/n!$) originating from the Taylor series expansion. The columns are organized according to the parity of the differentiation orders with respect to X and Y, mirroring the classification logic of Table 3. Note the identical structure of the “Constituent monomials” in the bottom row compared to the spherical formulation, demonstrating the direct correspondence between the highest-order Z-derivatives and the spherical basis functions.

m	$\frac{-\left(\genfrac{}{}{0pt}{}{\mathit{n}}{\mathit{m}}\right)\left(\genfrac{}{}{0pt}{}{\mathit{m}}{\mathit{l}}\right)}{\mathit{n}!}\frac{{\mathit{\partial }}^{\mathit{n}}}{\mathit{\partial }{\mathit{X}}^{\mathbf{even}}\mathit{\partial }{\mathit{Y}}^{\mathbf{even}}\mathit{\partial }{\mathit{Z}}^{\mathit{n}-\mathit{m}}}\frac{1}{\mathit{R}}$	$\frac{-\left(\genfrac{}{}{0pt}{}{\mathit{n}}{\mathit{m}}\right)\left(\genfrac{}{}{0pt}{}{\mathit{m}}{\mathit{l}}\right)}{\mathit{n}!}\frac{{\mathit{\partial }}^{\mathit{n}}}{\mathit{\partial }{\mathit{X}}^{\mathbf{odd}}\mathit{\partial }{\mathit{Y}}^{\mathbf{even}}\mathit{\partial }{\mathit{Z}}^{\mathit{n}-\mathit{m}}}\frac{1}{\mathit{R}}$	$\frac{-\left(\genfrac{}{}{0pt}{}{\mathit{n}}{\mathit{m}}\right)\left(\genfrac{}{}{0pt}{}{\mathit{m}}{\mathit{l}}\right)}{\mathit{n}!}\frac{{\mathit{\partial }}^{\mathit{n}}}{\mathit{\partial }{\mathit{X}}^{\mathbf{even}}\mathit{\partial }{\mathit{Y}}^{\mathbf{odd}}\mathit{\partial }{\mathit{Z}}^{\mathit{n}-\mathit{m}}}\frac{1}{\mathit{R}}$	$\frac{-\left(\genfrac{}{}{0pt}{}{\mathit{n}}{\mathit{m}}\right)\left(\genfrac{}{}{0pt}{}{\mathit{m}}{\mathit{l}}\right)}{\mathit{n}!}\frac{{\mathit{\partial }}^{\mathit{n}}}{\mathit{\partial }{\mathit{X}}^{\mathbf{odd}}\mathit{\partial }{\mathit{Y}}^{\mathbf{odd}}\mathit{\partial }{\mathit{Z}}^{\mathit{n}-\mathit{m}}}\frac{1}{\mathit{R}}$
0	${\displaystyle \frac{Z^3-\frac{3}{2}{Y}^{2}Z-\frac{3}{2}{X}^{2}Z}{R^7}}$
1		${\displaystyle \frac{6X{Z}^2-\frac{3}{2}X{Y}^2-\frac{3}{2}{X}^3}{R^7}}$	${\displaystyle \frac{6Y{Z}^2-\frac{3}{2}{X}^{2}Y-\frac{3}{2}{Y}^3}{R^7}}$
2	${\displaystyle \frac{6X^{2}Z-\frac{3}{2}{Y}^{2}Z-\frac{3}{2}{Z}^3}{R^7}}$			${\displaystyle \frac{15XYZ}{R^7}}$
	${\displaystyle \frac{6Y^{2}Z-\frac{3}{2}{X}^{2}Z-\frac{3}{2}{Z}^3}{R^7}}$
3		${\displaystyle \frac{X^3-\frac{3}{2}X{Z}^2-\frac{3}{2}X{Y}^2}{R^7}}$	${\displaystyle \frac{Y^3-\frac{3}{2}Y{Z}^2-\frac{3}{2}{X}^{2}Y}{R^7}}$
		${\displaystyle \frac{6X{Y}^2-\frac{3}{2}{X}^3-\frac{3}{2}X{Z}^2}{R^7}}$	${\displaystyle \frac{6X^{2}Y-\frac{3}{2}Y{Z}^2-\frac{3}{2}{Y}^3}{R^7}}$
Constituent monomials	${\displaystyle \frac{Z^3}{R^7}}$, ${\displaystyle \frac{Y^{2}Z}{R^7}}$, ${\displaystyle \frac{X^{2}Z}{R^7}}$	${\displaystyle \frac{X^3}{R^7}}$, ${\displaystyle \frac{X{Y}^2}{R^7}}$, ${\displaystyle \frac{X{Z}^2}{R^7}}$	${\displaystyle \frac{Y^3}{R^7}}$, ${\displaystyle \frac{X^{2}Y}{R^7}}$, ${\displaystyle \frac{Y{Z}^2}{R^7}}$	${\displaystyle \frac{XYZ}{R^7}}$

, the four groups of Cartesian basis functions align exactly with the equivalent groups of spherical basis functions, each representing the same combinations of the powers of coordinates.

3.1.1. Mathematical Justification of the Parity Grouping

The structural correspondence between the spherical and Cartesian basis functions presented above is mathematically rigorous. The exponents of the constituent monomials $X^i{Y}^j{Z}^k$ in both representations are constrained by identical parity rules, which we demonstrate below.

3.1.2. Proof for the Spherical Representation

The spherical basis functions are derived from the product of Legendre polynomials and azimuthal terms. The parity of the exponents i (for X) and j (for Y) is governed by the binomial expansion of the harmonic term ${(X+iY)}^m$. Two fundamental rules apply to every term:

• Azimuthal Parity Rule: The parity of the sum of horizontal exponents ($i+j$) is always identical to the parity of the order m.
• Homogeneity Rule: Since the basis functions are homogeneous polynomials of degree n, the sum of all exponents must satisfy $i+j+k=n$.

Based on the harmonic type (cosine or sine) and the parity of m, the specific constraints are derived as follows:

• Group $\overline{C{B}_n^{even}}$ (m is even): The cosine type corresponds to the Real part of the expansion, which contains only even powers of Y (thus j is even). Since m is even, i must also be even to satisfy the Azimuthal Parity Rule. Result: i is even, j is even.
• Group $\overline{C{B}_n^{odd}}$ (m is odd): As a cosine term, j remains even. However, since m is odd, i must be odd. Result: i is odd, j is even.
• Group $\overline{S{B}_n^{odd}}$ (m is odd): The sine type corresponds to the Imaginary part, which contains only odd powers of Y (thus j is odd). Since m is odd, i must be even. Result: i is even, j is odd.
• Group $\overline{S{B}_n^{even}}$ (m is even): As a sine term, j is odd. Since m is even, i must be odd. Result: i is odd, j is odd.

3.1.3. Proof for the Cartesian Representation

In the Taylor series expansion, the basis functions are partial derivatives of the reciprocal distance $1/R$. Since $1/R$ is an even function with respect to all coordinates $X,Y,Z$, the parity of the resulting derivative is strictly determined by the differentiation. Differentiating with respect to a specific coordinate produces a term where the exponent of that coordinate shares the same parity as the differentiation order.

Applying this rule to the four proposed Cartesian groups yields an exact match with the spherical results above:

• Differentiation $\partial X^{even}\partial Y^{even}$ yields terms with $X^{even}{Y}^{even}$.
• Differentiation $\partial X^{odd}\partial Y^{even}$ yields terms with $X^{odd}{Y}^{even}$.
• Differentiation $\partial X^{even}\partial Y^{odd}$ yields terms with $X^{even}{Y}^{odd}$.
• Differentiation $\partial X^{odd}\partial Y^{odd}$ yields terms with $X^{odd}{Y}^{odd}$.

The parity of the Z exponent (k) is automatically satisfied by the homogeneity condition $i+j+k=n$ in both systems. Thus, it is mathematically proven that the four groups of spherical harmonics and the four groups of Cartesian derivatives cover identical subsets of monomial terms.

Spherical basis functions are derived by summing terms within each group that includes the same number of partial derivatives with respect to Z. The equation that establishes a direct relationship between Cartesian derivatives and Schmidt normalized spherical basis functions is:

$$\begin{array}{cc}\hfill \overline{C{B}_n^m}& ={(-1)}^m·k_n^m·m!·\sum _{l\in \{0,2,\dots ,m\}}{(-1)}^n{\displaystyle \frac{1}{n!}}{\left(-1\right)}^{{\displaystyle \frac{l+2}{2}}+1}\left({\displaystyle \genfrac{}{}{0pt}{}{n}{m}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{m}{l}}\right){\displaystyle \frac{{\partial }^n}{\partial X^l\partial Y^{m-l}\partial Z^{n-m}}}{\displaystyle \frac{1}{R}},\hfill \\ \\ \hfill \overline{S{B}_n^m}& ={(-1)}^m·k_n^m·m!·\sum _{l\in \{1,3,\dots ,m\}}{(-1)}^n{\displaystyle \frac{1}{n!}}{\left(-1\right)}^{{\displaystyle \frac{l+1}{2}}+1}\left({\displaystyle \genfrac{}{}{0pt}{}{n}{m}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{m}{l}}\right){\displaystyle \frac{{\partial }^n}{\partial X^l\partial Y^{m-l}\partial Z^{n-m}}}{\displaystyle \frac{1}{R}},\hfill \end{array}$$

(10)

where $k_n^m$ refers to the Schmidt normalization factor, $\left({\displaystyle \genfrac{}{}{0pt}{}{n}{m}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{m}{l}}\right)$ represents the variations of a given derivative configuration, since differentiations can be performed in all possible orders. If all variations are taken into account, the number of basis functions in the Cartesian solution is $3^n$. If equivalent basis functions are summed, the total number reduces to ${0.5}^n+1.5n+1$. After conversion to the spherical method—as already indicated in the Table 2—this reduces further to $2·(n+1)$.

Figure 2 shows the third-order basis functions (partial derivatives) of the Cartesian representation.

• At the top vertex of the triangle lies the partial derivative: ${\displaystyle \frac{{\partial }^3}{\partial Z^3}}{\displaystyle \frac{1}{R}}$.
• At the bottom left corner: ${\displaystyle \frac{{\partial }^3}{\partial Y^3}}{\displaystyle \frac{1}{R}}$.
• At the bottom right corner: ${\displaystyle \frac{{\partial }^3}{\partial X^3}}{\displaystyle \frac{1}{R}}$.
• Moving away from the vertices of the triangle, the order of the partial derivatives with respect to the respective coordinates decreases.
• The upper rhombus within the triangle, highlighted by the bold black line in Figure 2, represents the starting elements of the four groups of spherical basis functions.
• The remaining components are derived by calculating the differences between terms that lie on the same horizontal axis, meaning they have an equal number of partial derivatives with respect to Z and are separated by two nodes of the triangular grid.

3.2. A Direct Numerical Method for Calculating the Partial Derivatives of $1/R$ Function

A method has been developed for the direct computation of the n-th degree partial derivatives of $1/R$, which are utilized in the Cartesian representation of the normalized spherical base functions, given by Equation (10).

The n-th degree partial derivative of the $1/R$ function consists of $A_{l,m-l,n-m}$ (a homogeneous polynomial of X, Y, and Z coordinates) divided by $R^{2n+1}$:

$${\displaystyle \frac{{\partial }^n}{\partial X^l\partial Y^{m-l}\partial Z^{n-m}}}{\displaystyle \frac{1}{R}}={\displaystyle \frac{A_{l,m-l,n-m}}{R^{2n+1}}},$$

(11)

where $A_{l,m-l,n-m}$ is an n-th degree numerator polynomial (see, for example, the ‘Results’ column of

Table 5. Explicit analytical derivation of the normalized spherical basis functions for degree $n=3$ via the Direct Cartesian Method. The table demonstrates the practical application of the general summation formula Equation (10) by mapping each target harmonic function ($\overline{C{B}_3^m},\overline{S{B}_3^m}$) to a specific weighted linear combination of the partial derivatives of the inverse distance function ($1/R$). The columns display the constituent derivatives with their associated correction factors, the intermediate algebraic substitution, and the final Cartesian polynomial forms, thereby validating the proposed transformation logic.

Normalized Spherical Basis Functions	Properly Summed and Then Corrected Cartesian Basis Functions	Substituted Intermediate Results	Results
$\overline{C{B}_3^0}$	${(-1)}^0·k_3^0·0!·{\displaystyle \frac{1}{3!}}$${\displaystyle \frac{{\partial }^3}{\partial Z^3}}{\displaystyle \frac{1}{R}}$	–	${\displaystyle \frac{Z^3-\frac{3Y^{2}Z}{2}-\frac{3X^{2}Z}{2}}{R^7}}·\sqrt{7}$
$\overline{C{B}_3^1}$	${(-1)}^1·k_3^1·1!·{\displaystyle \frac{3}{3!}}$${\displaystyle \frac{{\partial }^3}{\partial X\partial Z^2}}{\displaystyle \frac{1}{R}}$	${\displaystyle \frac{6X{Z}^2-\frac{3X{Y}^2}{2}-\frac{3X^3}{2}}{R^7}}·\left(-\sqrt{{\displaystyle \frac{7}{6}}}\right)$	${\displaystyle \frac{\frac{X{Y}^2}{4}-X{Z}^2+\frac{X^3}{4}}{R^7}}·\sqrt{42}$
$\overline{C{B}_3^2}$	${(-1)}^2·k_3^2·2!·{\displaystyle \frac{3}{3!}}$$\left[{\displaystyle \frac{{\partial }^3}{\partial Y^2\partial Z}}{\displaystyle \frac{1}{R}}-{\displaystyle \frac{{\partial }^3}{\partial X^2\partial Z}}{\displaystyle \frac{1}{R}}\right]$	$\left[{\displaystyle \frac{6Y^{2}Z-\frac{3X^{2}Z}{2}-\frac{3Z^3}{2}}{R^7}}-{\displaystyle \frac{6X^{2}Z-\frac{3Y^{2}Z}{2}-\frac{3Z^3}{2}}{R^7}}\right]·\sqrt{{\displaystyle \frac{7}{15}}}$	${\displaystyle \frac{\frac{X^{2}Z}{2}-\frac{Y^{2}Z}{2}}{R^7}}·\sqrt{105}$
$\overline{C{B}_3^3}$	${(-1)}^3·k_3^3·3!·{\displaystyle \frac{1}{3!}}$$\left[{\displaystyle \frac{{\partial }^3}{\partial X^3}}{\displaystyle \frac{1}{R}}-3·{\displaystyle \frac{{\partial }^3}{\partial X\partial Y^2}}{\displaystyle \frac{1}{R}}\right]$	$\left[{\displaystyle \frac{X^3-\frac{3X{Z}^2}{2}-\frac{3X{Y}^2}{2}}{R^7}}-{\displaystyle \frac{6X{Y}^2-\frac{3X^3}{2}-\frac{3X{Z}^2}{2}}{R^7}}\right]·\left(-\sqrt{{\displaystyle \frac{7}{10}}}\right)$	${\displaystyle \frac{-\frac{X^3}{4}+\frac{3X{Y}^2}{4}}{R^7}}·\sqrt{70}$
$\overline{S{B}_3^1}$	${(-1)}^1·k_3^1·1!·{\displaystyle \frac{3}{3!}}$${\displaystyle \frac{{\partial }^3}{\partial Y\partial Z^2}}{\displaystyle \frac{1}{R}}$	${\displaystyle \frac{6Y{Z}^2-\frac{3X^{2}Y}{2}-\frac{3Y^3}{2}}{R^7}}·\left(-\sqrt{{\displaystyle \frac{7}{6}}}\right)$	${\displaystyle \frac{-Y{Z}^2+\frac{X^{2}Y}{4}+\frac{Y^3}{4}}{R^7}}·\sqrt{42}$
$\overline{S{B}_3^2}$	${(-1)}^2·k_3^2·2!·{\displaystyle \frac{3·2}{3!}}$${\displaystyle \frac{{\partial }^3}{\partial XYZ}}{\displaystyle \frac{1}{R}}$	${\displaystyle \frac{15XYZ}{R^7}}·\sqrt{{\displaystyle \frac{7}{15}}}$	${\displaystyle \frac{XYZ}{R^7}}·\sqrt{105}$
$\overline{S{B}_3^3}$	${(-1)}^3·k_3^3·3!·{\displaystyle \frac{1}{3!}}$$\left[3·{\displaystyle \frac{{\partial }^3}{\partial X^2\partial Y}}{\displaystyle \frac{1}{R}}-{\displaystyle \frac{{\partial }^3}{\partial Y^3}}{\displaystyle \frac{1}{R}}\right]$	$\left[{\displaystyle \frac{6X^{2}Y-\frac{3Y{Z}^2}{2}-\frac{3Y^3}{2}}{R^7}}-{\displaystyle \frac{Y^3-\frac{3Y{Z}^2}{2}-\frac{3X^{2}Y}{2}}{R^7}}\right]·\left(-\sqrt{{\displaystyle \frac{7}{10}}}\right)$	${\displaystyle \frac{-\frac{3X^{2}Y}{4}+\frac{Y^3}{4}}{R^7}}·\sqrt{70}$

).

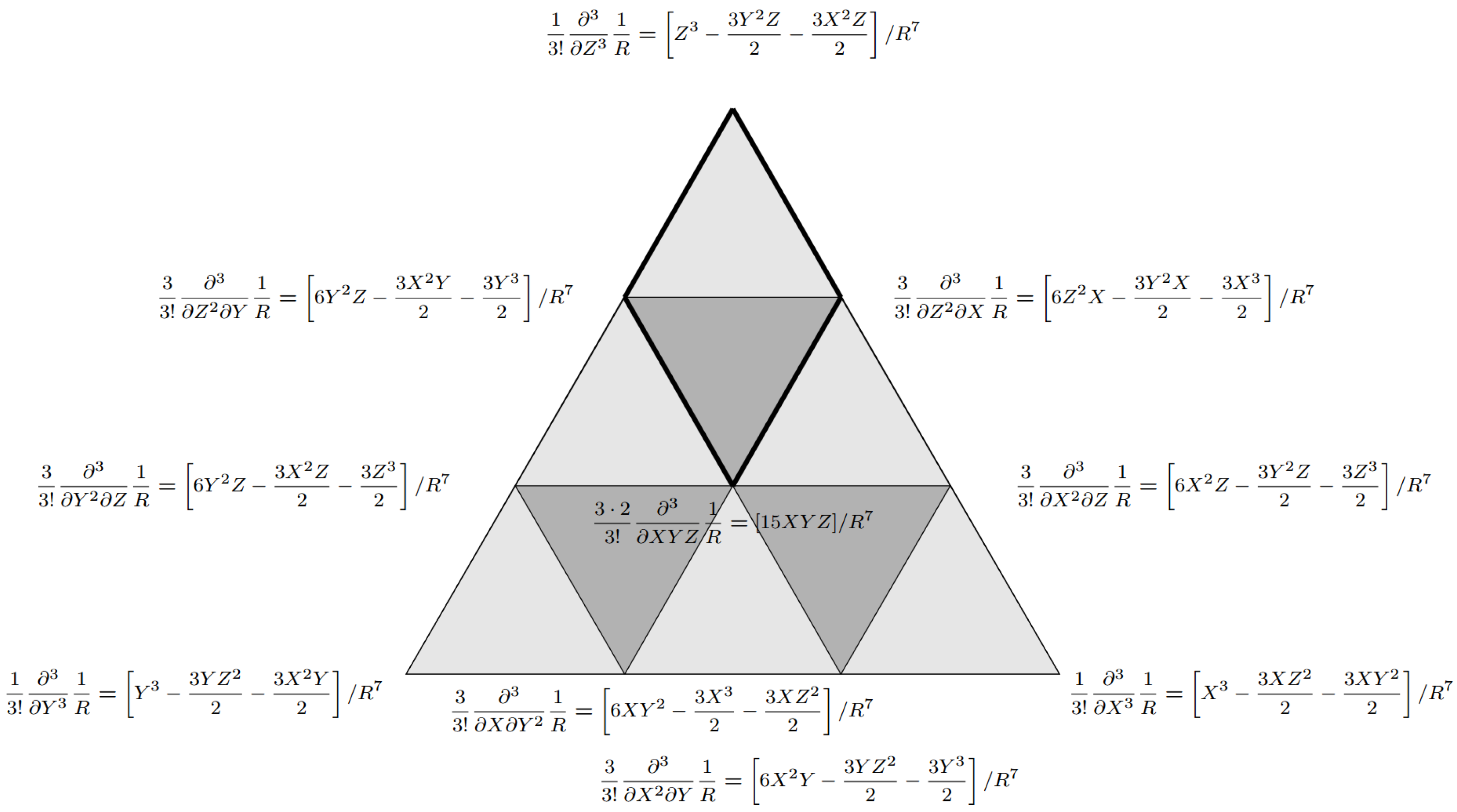
The numerator polynomial consists of polynomial terms of Cartesian coordinates multiplied by their respective coefficients:

$$A_{l,m-l,n-m}=\sum _{(i,j,k)\in \mathcal{T}(l,m-l,n-m)}{C}_{i,j,k}^{l,m-l,n-m}{X}^i{Y}^j{Z}^k,$$

(12)

where $\mathcal{T}(l,m-l,n-m)$ denotes the set of valid exponent triplets. The algorithm is designed to numerically determine, for each polynomial term, both the exponent triplet $(i,j,k)$ of the Cartesian monomials $X^i{Y}^j{Z}^k$ and their corresponding coefficients $C_{i,j,k}^{l,m-l,n-m}$.

In this notation, the superscripts ${\left(\right)}^{l,m-l,n-m}$ explicitly indicate the order of partial differentiation with respect to each coordinate axis: l corresponds to the number of differentiations with respect to X, $m-l$ to the number of differentiations with respect to Y, and $n-m$ to the number of differentiations with respect to Z.

3.2.1. Exponent Triplet Generation

The set $\mathcal{T}(l,m-l,n-m)$ (from Equation (12)) of all valid exponent triplets $(i,j,k)$ is strictly determined by two fundamental mathematical constraints: homogeneity and parity constraints.

1. Constraint: Homogeneity

The function, $f\left(R\right)={\displaystyle \frac{1}{R}}$, is a homogeneous function of degree $-1$. The partial differential operators ${\displaystyle \frac{\partial }{\partial X}}$, ${\displaystyle \frac{\partial }{\partial Y}}$, and ${\displaystyle \frac{\partial }{\partial Z}}$ are, themselves, homogeneous operators of degree $-1$.

It follows that the n-th order partial derivative is a homogeneous function of degree $-(1+n)$. Given that the denominator of the expression, $R^{2n+1}$, is a homogeneous function of degree $2n+1$, the numerator polynomial $A_{l,m-l,n-m}$ must necessarily be a homogeneous polynomial of degree n, such that the total degree of the fraction is $\left(n\right)-(2n+1)=-(n+1)$.

The condition of homogeneity implies that for every term in the polynomial $A_{l,m-l,n-m}$, the sum of the exponents must be exactly n. Therefore, for every element $(i,j,k)\in \mathcal{T}(l,m-l,n-m)$ of the set of exponents, the following must hold:

$$i+j+k=n,$$

where

$$n=(n-m)+(m-l)+l.$$

2. Constraint: Parity

The function ${\displaystyle \frac{1}{R}}={(X^2+Y^2+Z^2)}^{-1/2}$ is an even function with respect to all three coordinates ($X,Y,Z$), as $f\left(X\right)=f(-X)$, $f\left(Y\right)=f(-Y)$, and $f\left(Z\right)=f(-Z)$.

The operation of partial differentiation alters the parity of a function:

• The derivative of an even function is an odd function.
• The derivative of an odd function is an even function.

Consider the operator ${\displaystyle \frac{{\partial }^l}{\partial X^l}}$. When applied to the ${\displaystyle \frac{1}{R}}$ function:

• If l is even, the parity of the resulting function with respect to X remains even.
• If l is odd, the parity of the resulting function with respect to X becomes odd.

In general, the parity of the complete function ${\displaystyle \frac{{\partial }^n}{\partial X^l\partial Y^{m-l}\partial Z^{n-m}}}{\displaystyle \frac{1}{R}}$ with respect to X must be the same as the parity of l; its parity with respect to Y must be the same as $m-l$; and its parity with respect to Z must be the same as $n-m$.

As the denominator, $R^{2n+1}={(X^2+Y^2+Z^2)}^{(2n+1)/2}$ is also an even function with respect to all three variables; this parity constraint is inherited directly by the numerator polynomial, $A_{l,m-l,n-m}$.

The parity of a polynomial with respect to X is determined by the parity of its constituent $X^i$ exponents. For $A_{l,m-l,n-m}$ to satisfy the parity of l, every $X^i$ term must have an exponent i that has the same parity as l. The same holds true for Y and Z. This second set of constraints can be described by the following:

• l and i always have the same parity: if l is even, then i is also even; if l is odd, then i is also odd.
• $(m-l)$ and j always have the same parity: if $(m-l)$ is even, then j is also even; if $(m-l)$ is odd, then j is also odd.
• $(n-m)$ and k always have the same parity: if $(n-m)$ is even, then k is also even; if $(n-m)$ is odd, then k is also odd.

Number of terms

For a given degree n, order m, and index l, the number of terms satisfying the homogeneity and parity constraints is denoted by $\left|\mathcal{T}\right(l,m-l,n-m\left)\right|$. Based on the combinatorial constraints on the exponents i and j, three distinct cases arise:

$$\left|\mathcal{T}(l,m-l,n-m)\right|=\left\{\begin{array}{cc}{\displaystyle \frac{\left(\lfloor \frac{n}{2}\rfloor +1\right)\left(\lfloor \frac{n}{2}\rfloor +2\right)}{2}},\hfill & \mathrm{if}m\mathrm{is}\mathrm{even}\mathrm{and}l\mathrm{is}\mathrm{even},\hfill \\ {\displaystyle \frac{\lfloor \frac{n}{2}\rfloor \left(\lfloor \frac{n}{2}\rfloor +1\right)}{2}},\hfill & \mathrm{if}m\mathrm{is}\mathrm{even}\mathrm{and}l\mathrm{is}\mathrm{odd},\hfill \\ {\displaystyle \frac{\left(\lfloor \frac{n-1}{2}\rfloor +1\right)\left(\lfloor \frac{n-1}{2}\rfloor +2\right)}{2}},\hfill & \mathrm{if}m\mathrm{is}\mathrm{odd},\hfill \end{array}\right.$$

(13)

where $\lfloor \rfloor$ denotes the floor operation (rounding down).

3.2.2. Derivation of the Numerator Polynomial Coefficients

The coefficients of the $A_{l,m-l,n-m}$ numerator polynomial are generated using a recursive scheme. Each differentiation step ($n\to n+1$) represents a recursive relation that computes the new coefficients from the previous set.

Definition of the Recursive Realtions

Let $C_{i,j,k}^{l,m-l,n-m}$ denote the coefficient of the monomial $X^i{Y}^j{Z}^k$ within the n-th degree numerator polynomial, $A_n$. The coefficients ($C_{i,j,k}^{l+1,m-l,n-m}$ or $C_{i,j,k}^{l+1,m-l+1,n-m}$ or $C_{i,j,k}^{l+1,m-l,n-m+1}$) for the $(n+1)$-th order polynomial, $A_{n+1}$, are given by the following rules, depending on the variable of differentiation. The proof is presented in Appendix B.

Recursive computation of the coefficients under partial differentiation with respect to X:

$$C_{i,j,k}^{l+1,m-l,n-m}=(i+1)·C_{i+1,j-2,k}^{l,m-l,n-m}+(i+1)·C_{i+1,j,k-2}^{l,m-l,n-m}+\left(i-2(n+1)\right)·C_{i-1,j,k}^{l,m-l,n-m}.$$

(14)

Recursive computation of the coefficients under partial differentiation with respect to Y:

$$C_{i,j,k}^{l,m-l+1,n-m}=(j+1)·C_{i-2,j+1,k}^{l,m-l,n-m}+(j+1)·C_{i,j+1,k-2}^{l,m-l,n-m}+\left(j-2(n+1)\right)·C_{i,j-1,k}^{l,m-l,n-m}.$$

(15)

Recursive computation of the coefficients under partial differentiation with respect to Z:

$$C_{i,j,k}^{l,m-l,n-m+1}=(k+1)·C_{i-2,j,k+1}^{l,m-l,n-m}+(k+1)·C_{i,j-2,k+1}^{l,m-l,n-m}+\left(k-2(n+1)\right)·C_{i,j,k-1}^{l,m-l,n-m}.$$

(16)

The recursion is anchored by the 0-th-order derivative, $f=1/R$, for which the numerator polynomial is $A_0=1$. This provides the initial condition $C_{0,0,0}^{(0,0,0)}=1$, with all other coefficients being zero. Any term in the recurrence relations Equations (14)–(16) that references a coefficient with a negative exponent (e.g., $i-2<0$) is defined as zero.

3.2.3. Analytical Solution for the Z-Derivative

Coefficient of the “principal” $Z^n$ term of the Z-Derivative We examine the coefficient of the “principal” term, which is the term containing only the highest power of Z, $Z^{(n-m)+1}$, denoted $C_{0,0,(n-m)+1}^{0,0,(n-m)+1}$. Setting $i=0$, $j=0$, and $k=(n-m)+1$ in the Z-Derivative Equation (16):

$$\begin{array}{cc}\hfill C_{0,0,(n-m)+1}^{0,0,(n-m)+1}& =((n-m)+2)C_{-2,0,(n-m)+2}^{0,0,(n-m)}\hfill \\ & +((n-m)+2)C_{0,-2,(n-m)+2}^{0,0,(n-m)}\hfill \\ & +\left((n-m)+1)-2((n-m)+1)\right)C_{0,0,n-m}^{0,0,(n-m)}.\hfill \end{array}$$

The first two terms are zero, as they reference coefficients with negative (invalid) exponents. The third term, the only one to survive, simplifies as follows:

$$\left(\left(\right(n-m)+1)-2(n-m)-2\right)=(-(n-m)-1)=-((n-m)+1).$$

This yields a simple recurrence for the principal coefficient, $C_{0,0,(n-m)+1}^{0,0,(n-m)+1}$:

$$C_{0,0,(n-m)+1}^{0,0,(n-m)+1}=-((n-m)+1)·C_{0,0,(n-m)}^{0,0,(n-m)}.$$

The given recurrence relation can be transformed into a closed-form expression. Starting from the initial condition $C_{0,0,1}^{0,0,1}=-1$, the recurrence

$$C_{0,0,(n-m)}^{0,0,(n-m)}=-(n-m)·C_{0,0,(n-m)-1}^{0,0,(n-m)-1},$$

simplifies to

$$C_{0,0,(n-m)}^{0,0,(n-m)}={(-1)}^{(n-m)-1}·(n-m)!·(-1),$$

which leads to

$$C_{0,0,(n-m)}^{0,0,(n-m)}={(-1)}^{(n-m)}(n-m)!.$$

This demonstrates that the coefficient for the $Z^{(n-m)}$ term, represented as $C_{0,0,(n-m)}^{0,0,(n-m)}$, is

$$C_{0,0,(n-m)}^{0,0,(n-m)}={(-1)}^{(n-m)}(n-m)!.$$

Coefficient of the other terms of the Z-Derivative This analysis can be extended to the other terms of the Z-derivative, which have the form

$$X^{2r}{Y}^{2(q-r)}{Z}^{(n-m)-2q},$$

where $q\in \{0,\dots ,\lfloor (n-m)/2\rfloor \}$ and $r\in \{0,\dots ,r\}$

A similar, albeit more complex, recurrence relates the coefficient of these terms. Unwinding this q-based recurrence, applying the binomial theorem to the ${(X^2+Y^2)}^q$ term and substituting $C_{0,0,(n-m)}^{0,0,(n-m)}$ yields the general product formula

$$C_{2r,2(q-r),(n-m)-2q}^{0,0,(n-m)}=C_{0,0,(n-m)}^{0,0,(n-m)}·\prod _{s=1}^q\left[{\displaystyle \frac{-1}{{\left(2s\right)}^2}}((n-m)-2s+2)((n-m)-2s+1)\right]·\left({\displaystyle \genfrac{}{}{0pt}{}{q}{r}}\right),$$

$$\begin{array}{cc}\hfill C_{2r,2(q-r),(n-m)-2q}^{0,0,(n-m)}& ={(-1)}^{(n-m)}(n-m)!\hfill \\ & ·\prod _{s=1}^q\left[{\displaystyle \frac{-1}{{\left(2s\right)}^2}}((n-m)-2s+2)((n-m)-2s+1)\right]·\left({\displaystyle \genfrac{}{}{0pt}{}{q}{r}}\right).\hfill \end{array}$$

(17)

For Z-Derivatives: Analytical Simplification

The partial differentiation process is always initiated with respect to the Z coordinate. Consequently, in the base case where $m=0$ (implying purely zonal harmonics), the binomial weights $\left({\displaystyle \genfrac{}{}{0pt}{}{n}{m}}\right)$ and $\left({\displaystyle \genfrac{}{}{0pt}{}{m}{l}}\right)$ in Equation (10) all reduce to unity. The remaining normalization terms are the ${\displaystyle \frac{1}{n!}}$ and the Schmidt correction factor $k_n^m$, which is $\sqrt{(2·(n-m)+1)}$ in this case. Since for $m=0$, $n!$ is identical to $(n-m)!$, this term can be directly factored out from the raw coefficient in Equation (17), allowing for the exact analytical cancellation described above.The algorithm performs this analytical cancellation before any numerical computation. The resulting simplified formula, which is now free of the $(n-m)!$ growth, is then computed. The final and simplified coefficient for a specific monomial $X^{2r}{Y}^{2(q-r)}{Z}^{(n-m)-2q}$ is:

$$\begin{array}{cc}\hfill \overline{C_{0,0,(n-m)}^{2r,2(q-r),(n-m)-2q}}& =\sqrt{(2·(n-m)+1)}·{(-1)}^{(n-m)}\hfill \\ & ·\prod _{s=1}^q\left[{\displaystyle \frac{-1}{{\left(2s\right)}^2}}((n-m)-2s+2)((n-m)-2s+1)\right]·\left({\displaystyle \genfrac{}{}{0pt}{}{q}{r}}\right).\hfill \end{array}$$

(18)

For X/Y-Derivatives: Step-Wise Normalization

For the recursive branches, the normalization factors (${\displaystyle \frac{1}{n!}}$, $\left({\displaystyle \genfrac{}{}{0pt}{}{n}{m}}\right)$, $\left({\displaystyle \genfrac{}{}{0pt}{}{m}{l}}\right)$, and ${(-1)}^m{k}_n^{m}m!$) from Equation (10) are not applied at the end, but are applied at each step of the recursion. The factorial growth generated by the recurrence relations (Equations (14) and (15)) is immediately cancelled by applying a corresponding normalization factor ($F_{\mathrm{norm}}$). This ensures all computed coefficients remain bounded and immune to overflow. The normalization factors are decomposed into their recursive ratios ($F_n/F_{n-1}$) and are integrated directly into each step.

During the $n\to n+1$ step, the coefficient $\overline{C^{l+1,m-l,n-m}}$ or $\overline{C^{l,m-l+1,n-m}}$ is computed from the preceding coefficients multiplied by a recursive normalization factor ($F_{\mathrm{norm}}$).

A critical detail in Schmidt semi-normalization is the discontinuity between $m=0$ and $m>0$. The normalization factor includes a $\sqrt{2}$ multiplier for all orders $m>0$, which is absent for $m=0$. Consequently, the recursive ratio must account for this transition when $m=1$.

The corrected recursive normalization factor is composed of three components. To achieve full normalization, the correction term ($F_3$) is adjusted to account for the $\sqrt{2n+1}$ scaling factor inherent in the transition from degree $n-1$ to n:

$$F_{\mathrm{norm}}(n,m,l)=\underset{F_1:n!\mathrm{term}}{\underbrace{\left({\displaystyle \frac{1}{n}}\right)}}·\underset{F_2:\mathrm{Binomial}\mathrm{term}}{\underbrace{\left({\displaystyle \frac{n}{m-l\mathrm{or}l}}\right)}}·\underset{F_3:{\mathrm{k}}_n^m\mathrm{Schmidt}\mathrm{Norm}.}{\underbrace{\left({\displaystyle \frac{-m·{\sqrt{2}}^{{\delta }_{m,1}}}{\sqrt{(n+m)(n+m-1)}}}\sqrt{{\displaystyle \frac{2n+1}{2n-1}}}\right)}},$$

where n is the new total degree, m is the new total X/Y order, l is the X order, and ${\delta }_{m,1}$ is the Kronecker delta (which equals 1 if $m=1$, introducing the necessary $\sqrt{2}$ factor, and 0 otherwise).

The factor $F_{\mathrm{norm}}$ encapsulates the transition from iteration $n-1$ to n, derived directly from the coefficients in Equation (10). It is formulated as a product of three distinct components to maintain numerical precision:

• Factorial scaling ($F_1\approx 1/n$): Originates from the Taylor series expansion ($1/n!$) found in Equation (10), counteracting the factorial growth of higher-order derivatives.
• Combinatorial weight ($F_2$): Accounts for the binomial distribution of partial derivatives along the Cartesian axes.
• Normalization ($F_3$): The Schmidt normalization factor ($k_n^m$) standardizes the magnitude of the harmonics, ensuring consistent physical scaling, and gives the name $F_{\mathrm{norm}}$ to the combined coefficient.

Numerical Note: If the factorial and normalization terms were applied globally after computing the raw high-order derivatives of $1/R$, the calculation would fail due to arithmetic underflow (vanishing derivatives) and overflow (huge factorials). By applying these factors incrementally within each recursive step via $F_{\mathrm{norm}}$, the intrinsic decay of the derivatives is continuously balanced by the factorial term ($F_1$), while the Schmidt component ($F_3$) enforces the physical normalization, keeping the intermediate coefficients within a stable numerical range (∼1.0).

$F_{\mathrm{norm},X}$ (Differentiation with respect to X)

Substituting into the general form and merging the square roots for simplicity:

$$F_{\mathrm{norm},X}={\displaystyle \frac{-m·{\sqrt{2}}^{{\delta }_{m,1}}}{l}}\sqrt{{\displaystyle \frac{2n+1}{(2n-1)(n+m)(n+m-1)}}}.$$

$F_{\mathrm{norm},Y}$ (Differentiation with respect to Y)

Similarly for the Y-derivative (where the binomial term results in a factor of $1/(m-l)$):

$$F_{\mathrm{norm},Y}={\displaystyle \frac{-m·{\sqrt{2}}^{{\delta }_{m,1}}}{m-l}}\sqrt{{\displaystyle \frac{2n+1}{(2n-1)(n+m)(n+m-1)}}}.$$

By incorporating these recursive factors, the complete, numerically stable form of the recurrence relations is as follows:

The Normalized Recurrence Relations

• Normalized recursive computation of the coefficients under partial differentiation with respect to X

  $$\begin{array}{cc}\hfill \overline{C_{i,j,k}^{l+1,m-l,n-m}}& =F_{\mathrm{norm},X}·[(i+1)·C_{i+1,j-2,k}^{l,m-l,n-m}\hfill \\ \hfill & +(i+1)·C_{i+1,j,k-2}^{l,m-l,n-m}\hfill \\ \hfill & +\left(i-2(n+1)\right)·C_{i-1,j,k}^{l,m-l,n-m}].\hfill \end{array}$$

  (19)
• Normalized recursive computation of the coefficients under partial differentiation with respect to Y

  $$\begin{array}{cc}\hfill \overline{C_{i,j,k}^{l,m-l+1,n-m}}& =F_{\mathrm{norm},Y}·[(j+1)·C_{i-2,j+1,k}^{l,m-l,n-m}\hfill \\ \hfill & +(j+1)·C_{i,j+1,k-2}^{l,m-l,n-m}\hfill \\ \hfill & +\left(j-2(n+1)\right)·C_{i,j-1,k}^{l,m-l,n-m}].\hfill \end{array}$$

  (20)

This normalization method ensures numerical stability by avoiding the ill-conditioned multiplication of terms with an extreme dynamic range. It transforms the operation from a post-process multiplication (involving factorially large terms and infinitesimally small factors) into a sequential process where all intermediate values are kept near unity. This approach not only prevents numerical overflow but also inherently minimizes the propagation of compounding round-off errors.

3.3. Numerical Validation: A Step-by-Step Walkthrough ($n=8,m=2$)

To demonstrate the practical application and numerical stability of the Direct Cartesian Method, we present a step-by-step derivation for the degree $n=8$ and order $m=2$ case. The objective is to compute the normalized spherical basis functions $\overline{C{B}_8^2}$ and $\overline{S{B}_8^2}$ directly from Cartesian coordinates.

According to the summation formula derived in Equation (10), the target basis functions are constructed as a linear combination of the following Cartesian partial derivatives of order n:

For the computation of the cosine-term basis function ($\overline{C{B}_8^2}$), the summation requires derivatives where the order of X-differentiation (l) is even. Thus, we require

• The derivative of $1/R$ differentiated six times with respect to Z and two times with respect to X ($l=2$).
• The derivative of $1/R$ differentiated six times with respect to Z and two times with respect to Y ($l=0$).

$$\overline{C{B}_8^2}={\displaystyle \frac{\sqrt{17}\sqrt{70}}{210}}·{\displaystyle \frac{28}{8!}}\left({\displaystyle \frac{{\partial }^8}{\partial X^2\partial Z^6}}{\displaystyle \frac{1}{R}}-{\displaystyle \frac{{\partial }^8}{\partial Y^2\partial Z^6}}{\displaystyle \frac{1}{R}}\right).$$

For the computation of the sine-term basis function ($\overline{S{B}_8^2}$), the summation requires derivatives where l is odd. Thus, we require

• The derivative of $1/R$ differentiated six times with respect to Z, one time with respect to X, and one time with respect to Y ($l=1$).

$$\overline{S{B}_8^2}={\displaystyle \frac{\sqrt{17}\sqrt{70}}{210}}·{\displaystyle \frac{56}{8!}}\left({\displaystyle \frac{{\partial }^8}{\partial X\partial Y\partial Z^6}}{\displaystyle \frac{1}{R}}\right).$$

Every required derivative involves differentiating six times with respect to Z; therefore, the polynomial $A_{0,0,6}$ serves as the common base for all subsequent calculations.

3.3.1. Calculation of the Normalized Base Z-Derivative ($l=0,m-l=0,n-m=6$)

The Z-derivative numerator polynomial is expressed using Equation (12)

$$\overline{A_{0,0,6}}=\sum _{(i,j,k)\in \mathcal{T}(0,0,6)}{\overline{C_{i,j,k}}}^{0,0,6}{X}^i{Y}^j{Z}^k.$$

We determine the constituent terms (exponent triplets $i,j,k$) based on parity and homogeneity constraints. Since we differentiate six times with respect to Z, the sum of exponents is $i+j+k=6$, and all exponents must be even. The resulting index vectors are $[6,0,0],[4,2,0],[4,0,2],[2,2,2],[2,0,4],[2,4,0],[0,0,6],[0,6,0],[0,2,4],$ and $[0,4,2]$. This results in exactly 10 terms, which corresponds to Equation (13), i.e., the term-counting formula:

$$\left|\mathcal{T}(0,0,6)\right|={\displaystyle \frac{\left(\lfloor \frac{6}{2}\rfloor +1\right)\left(\lfloor \frac{6}{2}\rfloor +2\right)}{2}}=10.$$

The coefficients of the $X^{2r}{Y}^{2(q-r)}{Z}^{6-2q}$ monomial are calculated using the Normalized Formula for Z-Differentiation Equation (18).

$$\overline{C_{0,0,6}^{2r,2(q-r),6-2q}}={(-1)}^6\sqrt{13}·\prod _{s=1}^q\left[{\displaystyle \frac{-1}{{\left(2s\right)}^2}}(8-2s)(7-2s)\right]·\left({\displaystyle \genfrac{}{}{0pt}{}{q}{r}}\right),$$

where q ranges from 0 to 3, and r ranges from 0 to q.

Although the true sixth-order Z-derivative of $1/R$ would require multiplication by $n!$, our algorithm computes only the normalized values to maintain stability.

The resulting polynomial terms (using dimensionless coordinates for numerical stability) are derived from the values presented in

Table 6. Coefficients and monomials of the normalized Z-derivative for $(n-m)=6$, arranged by indices q and r, using Equation (18) ($\overline{A_{0,0,6}}=\overline{C_{0,0,6}^{2r,2(q-r),6-2q}}·X^{2r}{Y}^{2(q-r)}{Z}^{6-2q}$).

$\overline{{\mathit{A}}_{0,0,6}}$	r = 0	r = 1	r = 2	r = 3
q = 0	$\sqrt{13}{Z}^6$	–	–	–
q = 1	$-\sqrt{13}{\displaystyle \frac{15}{2}}{Y}^2{Z}^4$	$-\sqrt{13}{\displaystyle \frac{15}{2}}{X}^2{Z}^4$	–	–
q = 2	$\sqrt{13}{\displaystyle \frac{45}{8}}{Y}^4{Z}^2$	$\sqrt{13}{\displaystyle \frac{45}{4}}{X}^2{Y}^2{Z}^2$	$\sqrt{13}{\displaystyle \frac{45}{8}}{X}^4{Z}^2$	–
q = 3	$-\sqrt{13}{\displaystyle \frac{5}{16}}{Y}^6$	$-\sqrt{13}{\displaystyle \frac{15}{16}}{X}^2{Y}^4$	$-\sqrt{13}{\displaystyle \frac{15}{16}}{X}^4{Y}^2$	$-\sqrt{13}{\displaystyle \frac{5}{16}}{X}^6$

as follows:

$$\begin{array}{cc}\hfill \overline{A_{0,0,6}}=& \sqrt{13}·Z^6-\sqrt{13}{\displaystyle \frac{15}{2}}{Y}^2{Z}^4-\sqrt{13}{\displaystyle \frac{15}{2}}{X}^2{Z}^4\hfill \\ \hfill & +\sqrt{13}{\displaystyle \frac{45}{8}}{Y}^4{Z}^2+\sqrt{13}{\displaystyle \frac{45}{4}}{X}^2{Y}^2{Z}^2+\sqrt{13}{\displaystyle \frac{45}{8}}{X}^4{Z}^2\hfill \\ \hfill & -\sqrt{13}{\displaystyle \frac{5}{16}}{Y}^6-\sqrt{13}{\displaystyle \frac{15}{16}}{X}^2{Y}^4-\sqrt{13}{\displaystyle \frac{15}{16}}{X}^4{Y}^2-\sqrt{13}{\displaystyle \frac{5}{16}}{X}^6.\hfill \end{array}$$

3.3.2. Computation of the X-Derivative Branch

To obtain one of the term required for $\overline{C{B}_8^2}$, we differentiate the Z-derivative result two times with respect to X.

• Step 1: First X-derivative ($l=1,m-l=0,n-m=6$)

The numerator polynomial is expressed using Equation (12)

$$\overline{A_{1,0,6}}=\sum _{(i,j,k)\in \mathcal{T}(1,0,6)}\overline{C_{i,j,k}^{1,0,6}}{X}^i{Y}^j{Z}^k.$$

We determine the constituent terms (exponent triplets $i,j,k$) based on parity and homogeneity constraints. Since we differentiate six times with respect to Z and one time with respect to X, the sum of exponents is $i+j+k=7$, where j and k are even, and i is odd. The resulting index vectors are $[7,0,0]$, $[5,2,0]$, $[5,0,2]$,$[3,4,0]$, $[3,2,2]$, $[3,0,4]$, $[1,6,0]$, $[1,4,2]$, $[1,2,4]$, and $[1,0,6]$. This results in exactly 10 terms, which corresponds to Equation (13), i.e., the term-counting formula:

$$\left|\mathcal{T}(1,0,6)\right|={\displaystyle \frac{\left(\lfloor \frac{7-1}{2}\rfloor +1\right)\left(\lfloor \frac{7-1}{2}\rfloor +2\right)}{2}}=10.$$

To obtain the coefficients of the terms, we utilize the normalized recursive computation of the coefficients under partial differentiation with respect to X Equation (19):

$$\overline{C_{i,j,k}^{1,0,6}}={\displaystyle \frac{15}{2\sqrt{91}}}·\left[(i+1)·\overline{C_{i+1,j-2,k}^{0,0,6}}+(i+1)·\overline{C_{i+1,j,k-2}^{0,0,6}}+\left(i-14\right)·\overline{C_{i-1,j,k}^{0,0,6}}\right].$$

Since normalization is integrated into every step, the computed normalized values are:

$$\begin{array}{cc}\hfill \overline{A_{1,0,6}}=& {\displaystyle \frac{5\sqrt{105}}{32}}{X}^7+{\displaystyle \frac{15\sqrt{105}}{32}}{X}^5{Y}^2-{\displaystyle \frac{15\sqrt{105}}{4}}{X}^5{Z}^2\hfill \\ \hfill & +{\displaystyle \frac{15\sqrt{105}}{32}}{X}^3{Y}^4-{\displaystyle \frac{15\sqrt{105}}{2}}{X}^3{Y}^2{Z}^2+{\displaystyle \frac{15\sqrt{105}}{2}}{X}^3{Z}^4\hfill \\ \hfill & +{\displaystyle \frac{5\sqrt{105}}{32}}X{Y}^6-{\displaystyle \frac{15\sqrt{105}}{4}}X{Y}^4{Z}^2+{\displaystyle \frac{15\sqrt{105}}{2}}X{Y}^2{Z}^4-2\sqrt{105}X{Z}^6.\hfill \end{array}$$

• Step 2: Second X-derivative ($n=8$)

Using the Normalized Recurrence for X-Differentiation, we differentiate again with respect to X, using the same method we just described. The resulting polynomial terms (using dimensionless coordinates for numerical stability) are

$$\begin{array}{cc}\hfill \overline{A_{2,0,6}}=& -{\displaystyle \frac{\sqrt{17}\sqrt{70}}{24}}{X}^8-{\displaystyle \frac{23\sqrt{17}\sqrt{70}}{192}}{X}^6{Y}^2+{\displaystyle \frac{247\sqrt{17}\sqrt{70}}{192}}{X}^6{Z}^2\hfill \\ \hfill & -{\displaystyle \frac{7\sqrt{17}\sqrt{70}}{64}}{X}^4{Y}^4+{\displaystyle \frac{157\sqrt{17}\sqrt{70}}{64}}{X}^4{Y}^2{Z}^2-{\displaystyle \frac{29\sqrt{17}\sqrt{70}}{8}}{X}^4{Z}^4\hfill \\ \hfill & -{\displaystyle \frac{5\sqrt{17}\sqrt{70}}{192}}{X}^2{Y}^6+{\displaystyle \frac{67\sqrt{17}\sqrt{70}}{64}}{X}^2{Y}^4{Z}^2-{\displaystyle \frac{7\sqrt{17}\sqrt{70}}{2}}{X}^2{Y}^2{Z}^4\hfill \\ \hfill & +{\displaystyle \frac{101\sqrt{17}\sqrt{70}}{60}}{X}^2{Z}^6+{\displaystyle \frac{\sqrt{17}\sqrt{70}}{192}}{Y}^8-{\displaystyle \frac{23\sqrt{17}\sqrt{70}}{192}}{Y}^6{Z}^2\hfill \\ \hfill & +{\displaystyle \frac{\sqrt{17}\sqrt{70}}{8}}{Y}^4{Z}^4+{\displaystyle \frac{11\sqrt{17}\sqrt{70}}{60}}{Y}^2{Z}^6-{\displaystyle \frac{\sqrt{17}\sqrt{70}}{15}}{Z}^8.\hfill \end{array}$$

3.3.3. Computation of the Y-Derivative Branch

Next, we compute the derivatives required for the Y-component. We return to the Z-derivative ($n=6$) and differentiate recursively with respect to Y utilizing the normalized recursive computation of the coefficients under partial differentiation with respect to Y Equation (20).

• Step 1: First Y-derivative ($l=0,m-l=1,n-m=6$)

The numerator polynomial is expressed using Equation (12):

$$\overline{A_{0,1,6}}=\sum _{(i,j,k)\in \mathcal{T}(0,1,6)}\overline{C_{i,j,k}^{0,1,6}}{X}^i{Y}^j{Z}^k.$$

We determine the constituent terms (exponent triplets $i,j,k$) based on parity and homogeneity constraints. Since we differentiate six times with respect to Z and one time with respect to Y, the sum of exponents is $i+j+k=7$, where i and k are even, and j is odd. The resulting index triplets are

$$[0,7,0],[2,5,0],[0,5,2],[4,3,0],[2,3,2],[0,3,4],[6,1,0],[4,1,2],[2,1,4],[0,1,6].$$

This results in exactly 10 terms, which corresponds to Equation (13), i.e., the term-counting formula:

$$\left|\mathcal{T}(0,1,6)\right|={\displaystyle \frac{\left(\lfloor \frac{7-1}{2}\rfloor +1\right)\left(\lfloor \frac{7-1}{2}\rfloor +2\right)}{2}}=10.$$

To obtain the coefficients of the terms, we utilize the normalized recursive computation of the coefficients under partial differentiation with respect to Y Equation (20):

$$\overline{C_{i,j,k}^{0,1,6}}={\displaystyle \frac{15}{2\sqrt{91}}}·\left[(j+1)·\overline{C_{i-2,j+1,k}^{0,0,6}}+(j+1)·\overline{C_{i,j+1,k-2}^{0,0,6}}+\left(j-14\right)·\overline{C_{i,j-1,k}^{0,0,6}}\right].$$

Since normalization is integrated into every step, the computed normalized values are:

$$\begin{array}{cc}\hfill \overline{A_{0,1,6}}=& {\displaystyle \frac{5\sqrt{105}}{32}}{Y}^7+{\displaystyle \frac{15\sqrt{105}}{32}}{X}^2{Y}^5-{\displaystyle \frac{15\sqrt{105}}{4}}{Y}^5{Z}^2\hfill \\ \hfill & +{\displaystyle \frac{15\sqrt{105}}{32}}{X}^4{Y}^3-{\displaystyle \frac{15\sqrt{105}}{2}}{X}^2{Y}^3{Z}^2+{\displaystyle \frac{15\sqrt{105}}{2}}{Y}^3{Z}^4\hfill \\ \hfill & +{\displaystyle \frac{5\sqrt{105}}{32}}{X}^{6}Y-{\displaystyle \frac{15\sqrt{105}}{4}}{X}^{4}Y{Z}^2+{\displaystyle \frac{15\sqrt{105}}{2}}{X}^{2}Y{Z}^4-2\sqrt{105}Y{Z}^6.\hfill \end{array}$$

• Step 2: Second Y-derivative ($n=8$)

Using the Normalized Recurrence for Y-Differentiation, we differentiate again with respect to Y, using the same method we just described. The resulting polynomial terms (using dimensionless coordinates for numerical stability) are

$$\begin{array}{cc}\hfill \overline{A_{0,2,6}}=& -{\displaystyle \frac{\sqrt{17}\sqrt{70}}{24}}{Y}^8-{\displaystyle \frac{23\sqrt{17}\sqrt{70}}{192}}{X}^2{Y}^6+{\displaystyle \frac{247\sqrt{17}\sqrt{70}}{192}}{Y}^6{Z}^2\hfill \\ \hfill & -{\displaystyle \frac{7\sqrt{17}\sqrt{70}}{64}}{X}^4{Y}^4+{\displaystyle \frac{157\sqrt{17}\sqrt{70}}{64}}{X}^2{Y}^4{Z}^2-{\displaystyle \frac{29\sqrt{17}\sqrt{70}}{8}}{Y}^4{Z}^4\hfill \\ \hfill & -{\displaystyle \frac{5\sqrt{17}\sqrt{70}}{192}}{X}^6{Y}^2+{\displaystyle \frac{67\sqrt{17}\sqrt{70}}{64}}{X}^4{Y}^2{Z}^2-{\displaystyle \frac{7\sqrt{17}\sqrt{70}}{2}}{X}^2{Y}^2{Z}^4\hfill \\ \hfill & +{\displaystyle \frac{101\sqrt{17}\sqrt{70}}{60}}{Y}^2{Z}^6+{\displaystyle \frac{\sqrt{17}\sqrt{70}}{192}}{X}^8-{\displaystyle \frac{23\sqrt{17}\sqrt{70}}{192}}{X}^6{Z}^2\hfill \\ \hfill & +{\displaystyle \frac{\sqrt{17}\sqrt{70}}{8}}{X}^4{Z}^4+{\displaystyle \frac{11\sqrt{17}\sqrt{70}}{60}}{X}^2{Z}^6-{\displaystyle \frac{\sqrt{17}\sqrt{70}}{15}}{Z}^8.\hfill \end{array}$$

3.3.4. Synthesis of the Basis Function and Symmetry Analysis

Following the computation of the individual recursive branches, we construct the final normalized spherical basis function $\overline{C{B}_{8,2}}$ according to Equation (10). This requires the subtraction of the normalized polynomial terms obtained from the Y-derivative branch ($\overline{A_{0,2,6}}$) from those of the X-derivative branch ($\overline{A_{2,0,6}}$):

$$\overline{C{B}_{8,2}}={\displaystyle \frac{\overline{A_{2,0,6}}-\overline{A_{0,2,6}}}{R^{17}}}.$$

This result matches the value calculated from spherical coordinates as $P_{8,2}(cos\vartheta )cos\left(2\lambda \right)$. Dividing these final results by $R^{2n+1}$ yields the explicit Cartesian potential component for degree $n=8$ and order $m=2$.

$$\begin{array}{cc}\hfill {\displaystyle \frac{R^8{P}_8^2·cos\left(2\lambda \right)·k_n^m}{R^{17}}}& =\overline{C{B}_{8,2}}=(-{\displaystyle \frac{3\sqrt{17}\sqrt{70}}{64}}{X}^8-{\displaystyle \frac{3\sqrt{17}\sqrt{70}}{32}}{X}^6{Y}^2+{\displaystyle \frac{45\sqrt{17}\sqrt{70}}{32}}{X}^6{Z}^2\hfill \\ \hfill & +{\displaystyle \frac{45\sqrt{17}\sqrt{70}}{32}}{X}^4{Y}^2{Z}^2-{\displaystyle \frac{15\sqrt{17}\sqrt{70}}{4}}{X}^4{Z}^4\hfill \\ \hfill & +{\displaystyle \frac{3\sqrt{17}\sqrt{70}}{32}}{X}^2{Y}^6-{\displaystyle \frac{45\sqrt{17}\sqrt{70}}{32}}{X}^2{Y}^4{Z}^2+{\displaystyle \frac{3\sqrt{17}\sqrt{70}}{2}}{X}^2{Z}^6\hfill \\ \hfill & +{\displaystyle \frac{3\sqrt{17}\sqrt{70}}{64}}{Y}^8-{\displaystyle \frac{45\sqrt{17}\sqrt{70}}{32}}{Y}^6{Z}^2\hfill \\ \hfill & +{\displaystyle \frac{15\sqrt{17}\sqrt{70}}{4}}{Y}^4{Z}^4-{\displaystyle \frac{3\sqrt{17}\sqrt{70}}{2}}{Y}^2{Z}^6)/R^{17}.\hfill \end{array}$$

(21)

It is important to observe the inherent symmetry in the computation of $\overline{A_{2,0,6}}$ and $\overline{A_{0,2,6}}$. The recursive operations for the X branch and Y branch are mathematically identical under the permutation of X and Y coordinates. This symmetry is visually evident when comparing

Table 7. Recursive calculation of X-derivative terms ($n=7$).

${\mathit{X}}^{\mathit{i}}{\mathit{Y}}^{\mathit{j}}{\mathit{Z}}^{\mathit{k}}$	${\mathit{F}}_{\mathbf{norm},\mathit{X}}$	$\mathit{i}+1$	$\overline{{\mathit{C}}_{\mathit{i}+1,\mathit{j}-2,\mathit{k}}^{0,0,6}}$	$\overline{{\mathit{C}}_{\mathit{i}+1,\mathit{j},\mathit{k}-2}^{0,0,6}}$	$\mathit{i}-14$	$\overline{{\mathit{C}}_{\mathit{i}-1,\mathit{j},\mathit{k}}^{0,0,6}}$	$\overline{{\mathit{C}}_{\mathit{i},\mathit{j},\mathit{k}}^{1,0,6}}·{\mathit{X}}^{\mathit{i}}{\mathit{Y}}^{\mathit{j}}{\mathit{Z}}^{\mathit{k}}$
$X^7$	${\displaystyle \frac{15}{2\sqrt{91}}}$	8	0	0	$-7$	$-\sqrt{13}{\displaystyle \frac{5}{16}}$	${\displaystyle \frac{5\sqrt{105}}{32}}{X}^7$
$X^5{Y}^2$	${\displaystyle \frac{15}{2\sqrt{91}}}$	6	$-\sqrt{13}{\displaystyle \frac{5}{16}}$	0	$-9$	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	${\displaystyle \frac{15\sqrt{105}}{32}}{X}^5{Y}^2$
$X^5{Z}^2$	${\displaystyle \frac{15}{2\sqrt{91}}}$	6	0	$-\sqrt{13}{\displaystyle \frac{5}{16}}$	$-9$	$\sqrt{13}{\displaystyle \frac{45}{8}}$	$-{\displaystyle \frac{15\sqrt{105}}{4}}{X}^5{Z}^2$
$X^3{Y}^4$	${\displaystyle \frac{15}{2\sqrt{91}}}$	4	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	0	$-11$	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	${\displaystyle \frac{15\sqrt{105}}{32}}{X}^3{Y}^4$
$X^3{Y}^2{Z}^2$	${\displaystyle \frac{15}{2\sqrt{91}}}$	4	$\sqrt{13}{\displaystyle \frac{45}{8}}$	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	$-11$	$\sqrt{13}{\displaystyle \frac{45}{4}}$	$-{\displaystyle \frac{15\sqrt{105}}{2}}{X}^3{Y}^2{Z}^2$
$X^3{Z}^4$	${\displaystyle \frac{15}{2\sqrt{91}}}$	4	0	$\sqrt{13}{\displaystyle \frac{45}{8}}$	$-11$	$-\sqrt{13}{\displaystyle \frac{15}{2}}$	${\displaystyle \frac{15\sqrt{105}}{2}}{X}^3{Z}^4$
$X{Y}^6$	${\displaystyle \frac{15}{2\sqrt{91}}}$	2	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	0	$-13$	$-\sqrt{13}{\displaystyle \frac{5}{16}}$	${\displaystyle \frac{5\sqrt{105}}{32}}X{Y}^6$
$X{Y}^4{Z}^2$	${\displaystyle \frac{15}{2\sqrt{91}}}$	2	$\sqrt{13}{\displaystyle \frac{45}{4}}$	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	$-13$	$\sqrt{13}{\displaystyle \frac{45}{8}}$	$-{\displaystyle \frac{15\sqrt{105}}{4}}X{Y}^4{Z}^2$
$X{Y}^2{Z}^4$	${\displaystyle \frac{15}{2\sqrt{91}}}$	2	$-\sqrt{13}{\displaystyle \frac{15}{2}}$	$\sqrt{13}{\displaystyle \frac{45}{4}}$	$-13$	$-\sqrt{13}{\displaystyle \frac{15}{2}}$	${\displaystyle \frac{15\sqrt{105}}{2}}X{Y}^2{Z}^4$
$X{Z}^6$	${\displaystyle \frac{15}{2\sqrt{91}}}$	2	0	$-\sqrt{13}{\displaystyle \frac{15}{2}}$	$-13$	$\sqrt{13}$	$-2\sqrt{105}X{Z}^6$

(X-derivation) and

Table 8. Recursive calculation of Y-derivative terms ($n=7$) using Z-derivative ($n=6$) coefficients.

${\mathit{X}}^{\mathit{i}}{\mathit{Y}}^{\mathit{j}}{\mathit{Z}}^{\mathit{k}}$	${\mathit{F}}_{\mathbf{norm},\mathit{Y}}$	$\mathit{j}+1$	$\overline{{\mathit{C}}_{\mathit{i}-2,\mathit{j}+1,\mathit{k}}^{0,0,6}}$	$\overline{{\mathit{C}}_{\mathit{i},\mathit{j}+1,\mathit{k}-2}^{0,0,6}}$	$\mathit{j}-14$	$\overline{{\mathit{C}}_{\mathit{i},\mathit{j}-1,\mathit{k}}^{0,0,6}}$	$\overline{{\mathit{C}}_{\mathit{i},\mathit{j},\mathit{k}}^{0,1,6}}$
$Y^7$	${\displaystyle \frac{15}{2\sqrt{91}}}$	8	0	0	$-7$	$-\sqrt{13}{\displaystyle \frac{5}{16}}$	${\displaystyle \frac{5\sqrt{105}}{32}}{Y}^7$
$X^2{Y}^5$	${\displaystyle \frac{15}{2\sqrt{91}}}$	6	$-\sqrt{13}{\displaystyle \frac{5}{16}}$	0	$-9$	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	${\displaystyle \frac{15\sqrt{105}}{32}}{X}^2{Y}^5$
$Y^5{Z}^2$	${\displaystyle \frac{15}{2\sqrt{91}}}$	6	0	$-\sqrt{13}{\displaystyle \frac{5}{16}}$	$-9$	$\sqrt{13}{\displaystyle \frac{45}{8}}$	$-{\displaystyle \frac{15\sqrt{105}}{4}}{Y}^5{Z}^2$
$X^4{Y}^3$	${\displaystyle \frac{15}{2\sqrt{91}}}$	4	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	0	$-11$	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	${\displaystyle \frac{15\sqrt{105}}{32}}{X}^4{Y}^3$
$X^2{Y}^3{Z}^2$	${\displaystyle \frac{15}{2\sqrt{91}}}$	4	$\sqrt{13}{\displaystyle \frac{45}{8}}$	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	$-11$	$\sqrt{13}{\displaystyle \frac{45}{4}}$	$-{\displaystyle \frac{15\sqrt{105}}{2}}{X}^2{Y}^3{Z}^2$
$Y^3{Z}^4$	${\displaystyle \frac{15}{2\sqrt{91}}}$	4	0	$\sqrt{13}{\displaystyle \frac{45}{8}}$	$-11$	$-\sqrt{13}{\displaystyle \frac{15}{2}}$	${\displaystyle \frac{15\sqrt{105}}{2}}{Y}^3{Z}^4$
$X^{6}Y$	${\displaystyle \frac{15}{2\sqrt{91}}}$	2	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	0	$-13$	$-\sqrt{13}{\displaystyle \frac{5}{16}}$	${\displaystyle \frac{5\sqrt{105}}{32}}{X}^{6}Y$
$X^{4}Y{Z}^2$	${\displaystyle \frac{15}{2\sqrt{91}}}$	2	$\sqrt{13}{\displaystyle \frac{45}{4}}$	$-\sqrt{13}{\displaystyle \frac{15}{16}}$	$-13$	$\sqrt{13}{\displaystyle \frac{45}{8}}$	$-{\displaystyle \frac{15\sqrt{105}}{4}}{X}^{4}Y{Z}^2$
$X^{2}Y{Z}^4$	${\displaystyle \frac{15}{2\sqrt{91}}}$	2	$-\sqrt{13}{\displaystyle \frac{15}{2}}$	$\sqrt{13}{\displaystyle \frac{45}{4}}$	$-13$	$-\sqrt{13}{\displaystyle \frac{15}{2}}$	${\displaystyle \frac{15\sqrt{105}}{2}}{X}^{2}Y{Z}^4$
$Y{Z}^6$	${\displaystyle \frac{15}{2\sqrt{91}}}$	2	0	$-\sqrt{13}{\displaystyle \frac{15}{2}}$	$-13$	$\sqrt{13}$	$-2\sqrt{105}Y{Z}^6$

(Y-derivation). The structure of the calculation remains invariant; only the first column (the monomials $X^i{Y}^j{Z}^k$) and the last column (the results) differ, reflecting the interchange of exponents i and j.

Consequently, the resulting derivatives themselves exhibit symmetry. When calculating the difference $\overline{A_{2,0,6}}-\overline{A_{0,2,6}}$, this symmetry leads to the cancellation of specific terms. The final polynomial in Equation (21) consists of 12 terms, which is 3 fewer than the constituent polynomials (15 terms each).

The terms that vanish are those where the coefficients in both branches are identical due to X-Y symmetry. This occurs for monomials where the exponents of X and Y are equal ($i=j$). In the $n=8,m=2$ case, these nullified terms are

• $Z^8$ (where $i=j=0$);
• $X^2{Y}^2{Z}^4$ (where $i=j=2$);
• $X^4{Y}^4$ (where $i=j=4$).

This algebraic cancellation is exact and structurally guaranteed by the method, further simplifying the final expression of the sectorial basis functions.

Computation of $\overline{S{B}_{8,2}}$: The calculation of $\overline{S{B}_{8,2}}$ requires the derivative differentiated six times with respect to Z, one time with respect to X, and one time with respect to Y. We utilize the intermediate result $\overline{A_{0,1,6}}$ (calculated in the Y-branch step) and differentiate it recursively with respect to X using the normalized recursive computation of the coefficients under partial differentiation with respect to X Equation (19). This result matches the value calculated from spherical coordinates as $P_{8,2}(cos\vartheta )sin\left(2\lambda \right)$. Dividing these final results by $R^{2n+1}$ yields the explicit Cartesian potential component for degree $n=8$ and order $m=2$.

The result is

$$\begin{array}{cc}\hfill {\displaystyle \frac{R^8{P}_8^2·sin\left(2\lambda \right)·k_n^m}{R^{17}}}& =\overline{S{B}_{8,2}}=(-{\displaystyle \frac{3\sqrt{17}\sqrt{70}}{32}}{X}^{7}Y-{\displaystyle \frac{9\sqrt{17}\sqrt{70}}{32}}{X}^5{Y}^3+{\displaystyle \frac{45\sqrt{17}\sqrt{70}}{16}}{X}^{5}Y{Z}^2\hfill \\ \hfill & -{\displaystyle \frac{9\sqrt{17}\sqrt{70}}{32}}{X}^3{Y}^5+{\displaystyle \frac{45\sqrt{17}\sqrt{70}}{8}}{X}^3{Y}^3{Z}^2-{\displaystyle \frac{15\sqrt{17}\sqrt{70}}{2}}{X}^{3}Y{Z}^4\hfill \\ \hfill & -{\displaystyle \frac{3\sqrt{17}\sqrt{70}}{32}}X{Y}^7+{\displaystyle \frac{45\sqrt{17}\sqrt{70}}{16}}X{Y}^5{Z}^2\hfill \\ \hfill & -{\displaystyle \frac{15\sqrt{17}\sqrt{70}}{2}}X{Y}^3{Z}^4+3\sqrt{17}\sqrt{70}XY{Z}^6)/R^{17}.\hfill \end{array}$$

3.4. Numerical Stability and Operating Range

While the primary focus of this derivation is analytical, assessing the numerical behavior of the resulting formulas is essential for practical implementation. To evaluate the operational limits, the proposed method was tested against a standard double-precision reference implementation (MATLAB R2022b built-in functions based on standard recurrences [9]).

The numerical experiments confirm that the Direct Cartesian Method maintains high precision up to degree $n\approx 130$. It is acknowledged that specialized numerical “evaluators,” such as the approaches by Holmes and Featherstone [10] or Fukushima [11], can achieve significantly higher degrees (up to $2^{32}$ degrees) using techniques like exponent extension. However, these methods typically operate as purely numerical evaluators, obscuring the underlying algebraic structure. In contrast, our method retains the analytical structure of the derivatives.

Beyond the $n\approx 130$ threshold, precision naturally degrades in our direct double-precision implementation due to the finite representation of floating-point numbers: catastrophic cancellation affects the zonal terms ($m=0$, near $n\approx 170$) and compounding rounding errors appear in the recursive summation of sectoral terms ($n=m$, starting from $n\approx 115$). Consequently, the method is verified as numerically robust for degrees $n\le 100$, which is adequate for the intended analytical applications.

4. Conclusions

This study examined the similarity between the basis functions employed in the Cartesian coordinate system’s solution to the potential, which are derivable from the partial derivatives of $1/R$, and those used in the spherical coordinate system’s solution. The latter were computed using the Rodrigues formula and subsequently converted to Cartesian coordinates, outlined in Section 1.2 and the Section Converting the Spherical Representation of the Laplace Equation into Cartesian Coordinates.

My analysis, illustrated in Table 3 and Table 4, demonstrated that these basis functions can be categorized into four distinct groups. Within these groups, Cartesian basis functions differentiated an identical number of times with respect to the Z coordinate, and possessing matching parities in their orders of differentiation with respect to X and Y independently, are summed, after multiplication by appropriate coefficients as specified in Equation (10), to derive the normalized spherical basis function corresponding to specific values of n and m. Figure 2 offers an illustrative explanation of this method, and the validity of the approach is further corroborated by Table 5, which presents the results of substituting into Equation (10) for the $n=3$ case.

To facilitate the practical application of this theoretical connection, a Direct Numerical Method was developed for calculating the partial derivatives of the $1/R$ function. As defined in Equation (11), the derivative is decomposed into a denominator $R^{2n+1}$ and a homogeneous numerator polynomial $A_{l,m-l,n-m}$. This numerator is further resolved into constituent monomials $X^i{Y}^j{Z}^k$ multiplied by their respective coefficients $C_{i,j,k}^{l,m-l,n-m}$ Equation (12). We established that the valid exponent triplets $(i,j,k)$—representing the powers of the Cartesian coordinates within the derivative terms—are strictly determined by homogeneity ($i+j+k=n$) and parity constraints. The values of these coefficients are generated algorithmically: the initial Z-derivatives are determined using a closed-form analytical formula Equation (18), while the coefficients for the X and Y branches are computed via the derived recurrence relations Equations (19) and (20).

Crucially, to address numerical stability, we introduced a step-wise normalization scheme. By incorporating the recursive ratios of the normalization factors directly into the recurrence formulas, the algorithm is designed to mitigate factorial growth. This ensures that intermediate coefficients remain within a manageable numerical range. Comprehensive numerical testing at higher degrees is planned for future research.

The effectiveness of the proposed method is demonstrated for a representative case in Section 3.3. We presented a step-by-step derivation of the normalized spherical basis functions for degree $n=8$ and order $m=2$ ($\overline{C{B}_{8,2}}$ and $\overline{S{B}_{8,2}}$). This walkthrough confirmed that the method correctly reproduces the target functions through the weighted summation of the recursively generated, normalized Cartesian derivatives.

Furthermore, the derived Direct Cartesian formulation offers distinct advantages for specific applications, particularly in satellite geodesy and orbit determination where precise higher-order partial derivatives are required for force modeling. This necessitates the computation of the full gravitational gradient tensor, a problem also heavily researched in the context of recursive algorithms, such as those discussed by Casotto et al. [12] and Tsoulis [13].

Unlike spherical coordinates, which encounter singularities at the poles—a limitation explicitly addressed by non-singular Cartesian formulations like those of Pines [14], Cunningham [15], and Metris et al. [16]—the derivatives in our proposed method remain well-defined globally. Additionally, the transparent structure of the polynomial coefficients allows for direct analytical manipulation and a step-wise normalization that distinguishes it from purely numerical evaluation schemes.

Future Work: Key areas for future development include the extension to degrees $n>100$, GPU implementation, and integration into existing geodesy software (e.g., GMT).