1. Introduction
Industry 5.0 has revolutionized traditional manufacturing by incorporating advanced information and communication technologies, including cyber–physical systems (CPSs), big data analytics, machine learning, and the Internet of Things (IoT). This change has led intelligent manufacturing into a new era dominated by digitalization and services. The emergence of these technologies not only enables the manufacturing industry to better meet the increasingly personalized demands of the market but also enhances its overall competitiveness. In this dynamic context, research aimed at optimizing manufacturing processes, especially in areas such as production scheduling, becomes crucial.
Efficient production scheduling is extremely important to optimize the cost-effectiveness and productivity of manufacturing systems, especially in flexible job shops. Over the years, the flexible job shop scheduling problem (FJSP) has been extensively studied [
1]. However, historically, FJSP research has focused on optimizing machine resources but neglected labor resource management. In the modern manufacturing industry, labor resource management has gradually become a key factor in determining the performance of the whole system.
With the development of Industry 5.0, the importance of human–machine integration has become increasingly prominent [
2]. This trend has mainly been driven by two factors: escalating labor costs and the need for more adaptive and resilient production systems [
3]. Dual-Resource Constraint (DRC) systems [
4], which combine human and machine resources, have received extensive attention in the field of flexible job shop scheduling. These systems leverage multi-skilled workers and flexible work schedules to increase resource utilization, improve worker satisfaction, and increase the overall productivity. Multiple studies [
5,
6] have investigated the flexible job shop problem (FJSP) involving multi-skilled workers and their impact on the processing time. Nevertheless, workers acquire their multiple skills through training, which incurs substantial training costs [
7]. Consequently, shops tend to employ a higher proportion of single-skilled workers or a limited number of skilled workers.
Moreover, numerous studies have demonstrated that flexible working time arrangements play a pivotal role in promoting a work–life balance among employees and enhancing the overall company’s productivity [
8]. The production tasks change from batch to batch in the shop, which usually leads to changes in the number of people responsible for production. Nevertheless, a standard work system in workshops is to assign a fixed number of workers to each batch of tasks, and they work for a continuous and fixed period, such as from 9 a.m. to 5 p.m. [
9]. Although this method can effectively use the available human resources, redundancy can occur when the tasks are too few. For example, a job requires only four people to complete production. Still, with a fixed arrangement of five people, the work efficiency will be the same, and the personnel cost will significantly increase. Moreover, in the case of there being too many tasks, measures such as extra overtime are required due to insufficient staff. In such cases, flexible working time arrangements present a potential solution to optimize labor deployment, reduce personnel costs, and enhance operational efficiency.
Hence, a DRFJSP considering workers with flexible working time arrangements and machines with versatile functions is presented. This approach aligns with the Industry 5.0 paradigm by emphasizing adaptability, resilience, and the integration of human and machine resources. To address the computational complexity of dual-resource scheduling in smart manufacturing, this study adopted the forensic-based investigation (FBI) algorithm due to a strategic rationale: the interpopulation cooperation mechanism inherent in the FBI algorithm uniquely mirrors the dynamic coupling of machines and workers in DRC systems. Unlike traditional genetic algorithms that often struggle with premature convergence, an FBI’s two-stage investigation-tracking mechanism systematically balances exploration and exploitation at the multi-objective Pareto frontier. The remaining parts of this paper are organized as follows. A literature review is presented in
Section 2. In
Section 3 the scheduling problem and formal description are elaborated. In
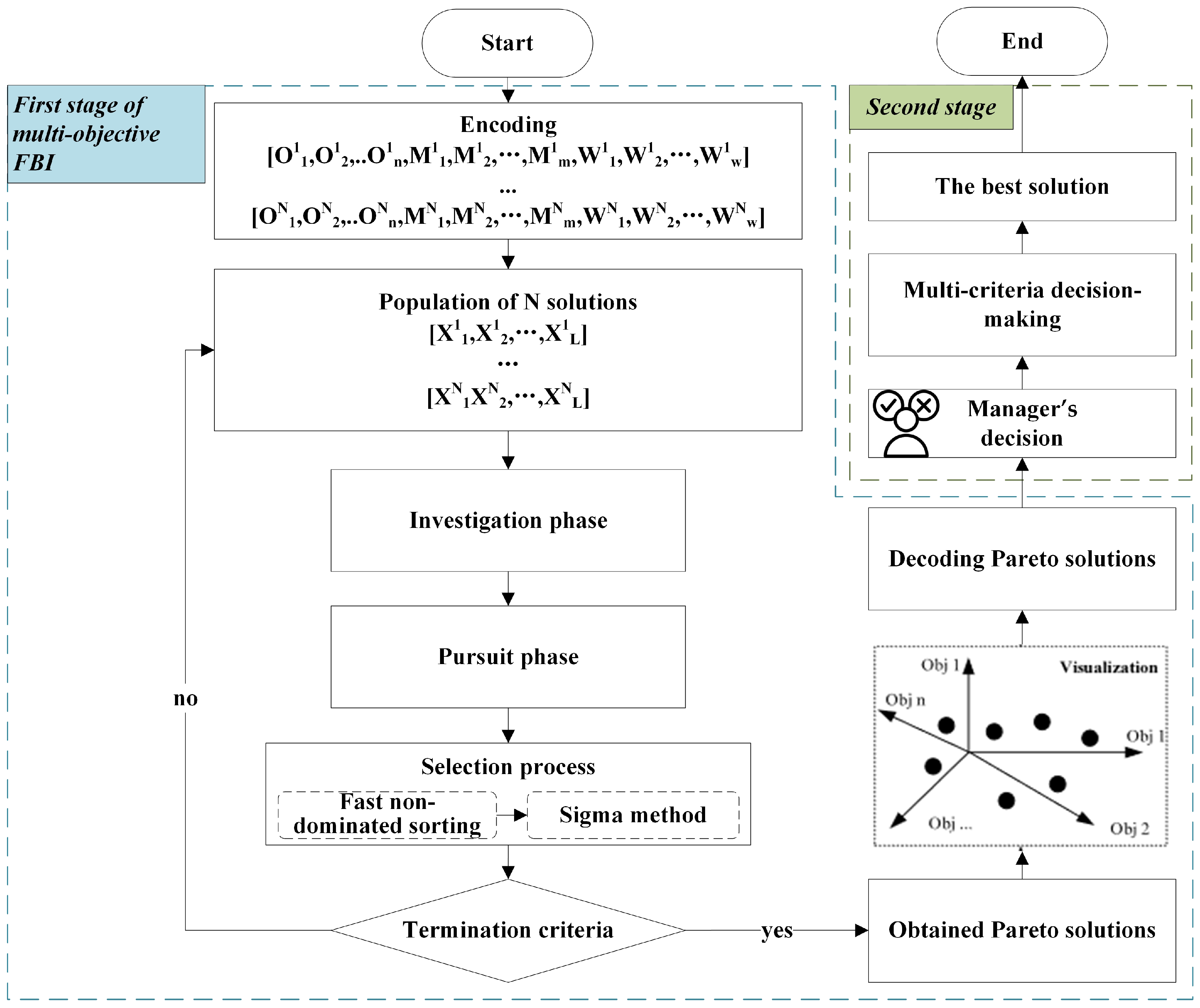
Section 4, the two-stage FBI-based algorithm is introduced. The case study and analyses are described in
Section 5. Finally, the conclusions and future perspectives are stated in
Section 6.
2. Literature Review
Industry 5.0 highlights a human-centric approach that prioritizes sustainable development and production flexibility [
10]. In manufacturing, production systems must both serve and rely on human resources [
11]. This paper investigates two areas: (1) the impact of working hours on workers and (2) the influence of human-inspired decision-making on algorithmic scheduling in production systems. In highly automated manufacturing environments, human intervention remains essential for tasks that cannot or should not be automated due to technical, socioeconomic, or ethical reasons. The goal of automation is not to replace workers, but to de-skill tasks so that workers can use their expertise, intelligent tools, and assistive systems to focus on decision-making and control. Therefore, human resources are the core of the production process, and their management and utilization require in-depth research [
12].
Production scheduling plays an essential role in the implementation of production. It can organically combine various elements (human resources, machines, materials, rules, and the environment) of the production process [
13]. Within this, dual-resource scheduling, especially a dual-resource scheduling problem that considers both worker resources and machine resources, has been widely studied by researchers. Further research has explored various facets of the DRFJSP, often extending the problem scope or constraints. For instance, Gong [
14] introduced a double flexible job shop problem (DFJSP), optimizing the processing time, green production, and human factors using a hybrid genetic algorithm. Yu [
15] studied distributed assembly hybrid flow shops with dual-resource constraints (DAHFSSP-DRC), minimizing the total tardiness using a knowledge-based iterated greedy algorithm. Mlekusch [
16] considered a dual-resource-constrained re-entrant flexible flow shop, common in screen printing, minimizing the makespan using constraint programming and a hybrid genetic algorithm. Renna [
17] applied game theory (Gale–Shapley model) for worker assignment in DRC job shops, showing its benefits, especially with varying worker efficiencies. Li [
18] specifically focused on worker shift arrangements in the FJSP, using a two-stage algorithm to minimize overdue days while managing shifts. Xiao [
19] tackled stochastic processing times in the DR-SJSSP using a robust scheduling approach and a two-stage assignment strategy solved using MO-HEDA. Li [
20] addressed sustainability (makespan, energy, ergonomics) in the SFJSPCDR using a survival duration-guided NSGA-III. Wei [
21] proposed an inverse scheduling approach for the RCFJISP to handle uncertainties by adjusting machine, worker, and process parameters using an improved memetic algorithm. Berti [
22] incorporated aging workforce effects and fatigue into DRC job shop scheduling, evaluating the impact of rest allowances. Seifi [
23] formulated MILP models for simultaneous machine and worker assignment in shift-based potash mining operations. Santos [
24] integrated machine scheduling (batch job shop) and personnel allocation in large-scale facilities using a rolling horizon framework. While these studies have significantly advanced the understanding of the DRFJSP, exploring areas like double flexibility [
14], assembly [
15], re-entrance [
16], worker assignment strategies [
17,
19,
20], shift scheduling [
18,
23], sustainability [
20], uncertainty/robustness [
21], and worker characteristics like fatigue/aging [
22], relatively few have specifically examined the impact of flexible working time arrangements, where workers operate within defined total hour limits rather than in fixed shifts or on simple multi-skilling assignments, on the scheduling performance and cost.
Flexible working time arrangements, which allow employees to manage their work hours outside the traditional “9 to 5” framework, have been shown to enhance employee motivation and productivity [
25]. Baridula [
26] highlighted their role in increasing employee retention in Nigerian manufacturing firms. Jarrahi [
9] suggested that personal digital infrastructure facilitates the implementation of flexible working time systems. Despite these benefits, the impact of flexible working time arrangements on production scheduling remains underexplored. Therefore, this study distinguished itself by explicitly modeling and optimizing a DRFJSP variant that incorporates workers with flexible working time arrangements alongside versatile machines. Unlike studies focusing on fixed shifts or multi-skilling costs, our work investigated the potential cost and efficiency benefits derived from allowing workers flexible start/end times within overall working hour constraints, addressing a gap in optimizing adaptable human resource deployment in modern manufacturing.
In recent years, Delgoshaei [
27] systematically reviewed the evolution of dual-resource scheduling approaches, identifying a paradigm shift toward the hybrid metaheuristics incorporating human factors that are a key foundation for our work. For the dual-resource-constrained flexible job shop scheduling problem (DRFJSP), a variety of metaheuristic methods have been widely used to cope with its NP-hard nature and obtain high-quality solutions in finite time. Metaheuristics have become a research hotspot because of their advantages regarding response time requirements in actual production systems [
28]. However, as the well-known No Free Lunch (NFL) theorem [
29] indicates, no metaheuristic is the most suitable for all optimization problems. This has motivated researchers to modify existing algorithms or develop new ones to solve various optimization problems [
30], such as the DRFJSP. Metaheuristics can be classified into evolution-based, population-based, human-based, physics-based, systems-based, and biology-based approaches [
31]. Traditional evolutionary algorithms such as genetic algorithms (GAs) and particle swarm optimization (PSO) have been widely used, but they often suffer from parameter sensitivity. For example, Mlekusch [
16] demonstrated the effectiveness of constraint programming combined with genetic algorithms for re-entrant flow shops, achieving a 12–18% better makespan than pure GA implementations. However, their hybrid approach requires complex parameter coordination between constraint propagation and evolutionary operators, increasing the implementation complexity. Similarly, Lu [
32] developed a memetic algorithm hybridizing a local search with genetic operators for assembly sequence variations, reducing the energy consumption by 17% compared to PSO-based approaches. The PSO implementation by Zhang [
33] also led to local convergence due to the improper setting of the speed factor. Liu’s [
34] improved biological migration algorithm demonstrated that parameter reduction can reduce the number of iterations by 35%. Therefore, a heuristic algorithm with low parameter tuning is especially useful for resource-constrained production systems that require fast response times.
Recent work has also extended the objectives beyond makespan minimization. Akbar [
35] applied a variant of NSGA to balance tardiness and labor productivity, revealing an inherent conflict between these objectives that informed our Pareto frontier analysis. Yu [
15] found that incorporating a knowledge-guided greedy search into the distributed assembly problem reduced the computation time by 28% compared to the Chinese implementation while maintaining a similar solution quality, supporting our hybrid decoding strategy. However, neither study addressed the critical integration problem concerning flexible working time constraints. The FBI algorithm is an optimization algorithm based on human behavior [
36], and its algorithm performance is relatively excellent, especially since it does not require any complex parameters that would seriously affect the algorithm’s performance. It has been applied to and shown excellent results in the solution of problems in various fields, such as solar cell model parameter optimization, pavement pothole identification [
37], and project scheduling [
38]. Despite this, the application of the FBI algorithm to solve flexible job shop scheduling problems such as the DRFJSP is still limited. On the one hand, the original FBI algorithm is mainly designed for continuous optimization problems, and on the other hand, its structure is only suitable for single-objective optimization tasks, which restricts its application in multi-constrained, discrete, and multi-objective environments.
To address combinatorial optimization problems, continuous optimization algorithms often require modifications to their operators. For instance, crossover operations can replace addition operations to better suit discrete problem spaces [
39,
40]. However, more efficient approaches involve developing new discrete algorithms specifically tailored for combinatorial optimization, which increases the scaling cost and time. Some researchers [
41] have identified the efficacy of the encoding and decoding methodology in transforming the design space into the problem space, and through the development of suitable coding and decoding techniques, it has become feasible to effectively enhance current algorithm versions, providing them with the capability to address combinatorial optimization problems. Hence, this paper presents a general hybrid coding and decoding method based on a technical characteristic of codecs so that the continuous optimization algorithm can quickly solve the combined optimization problem and reduce the cost and time consumption of developing a discrete version. Furthermore, since the dual-resource flexible job shop scheduling problem (DRFJSP) involves multiple objectives, the original forensic-based investigation (FBI) algorithm, designed for single-objective optimization, needed to be extended to handle multi-objective problems. Extensions of single-objective algorithms to multi-objective algorithms typically fall into four categories: dominance-based, decomposition-based, indicator-based, and hybrid selection mechanism-based approaches [
42]. Among these, the dominance-based approach [
42,
43], which relies on the concept of Pareto dominance, is widely used and effective for finding a diverse set of trade-off solutions. Therefore, we employed a Pareto-based dominance method, specifically the fast non-dominated sorting approach, to extend the FBI algorithm for multi-objective optimization.
However, solving the DRFJSP using a multi-objective FBI algorithm yields a set of Pareto-optimal solutions, presenting a challenge for decision-makers in selecting the most satisfactory solution. To address this, multi-criteria decision-making (MCDM) methods were employed. The analytical hierarchy process (AHP) is a well-established MCDM method that effectively combines qualitative and quantitative analysis, making it suitable for scenarios with a limited number of objectives [
44]. The AHP has been widely applied to multi-objective decision-making in combinatorial optimization problems [
45,
46], enabling managers to make informed decisions based on the production status and objectives. Due to its advantages of requiring less information and offering short decision times, this study applied AHP to the decision-making process for multi-objective scheduling problems in job shop environments.
5. Case Study
Three experiments were conducted to verify the correctness of the proposed DRFJSP model and the effectiveness of the TSFBI algorithm. The first experiment used the well-known solver Gurobi to solve the problem in order to verify the correctness of the model. The second experiment compared the performance of the TSFBI algorithm with that of the NSGA-II algorithm using three common metrics, and the third experiment verified the algorithm’s ability to obtain satisfactory solutions from the Pareto solutions through the AHP decision process.
All tests were run on a 3.1 GHz E5-2603V4 processor and a 64 GB server using the python3.7 programming language.
5.1. Instance Construction and Parameter Setting
Since there were no test cases for the DRFJSP, this study extended 51 test cases (el01–el51) for the la01–la40 benchmark [
50], BRData [
51] Mk01–Mk10 cases, and a simple case [
52]. Among them, the first 50 instances were utilized in Experiment 1 and 2, whereas the final sample was reserved for Experiment 3. The categorization of the test cases, as outlined by Liu et al. [
53], involved three classifications: small-, medium-, and large-scale. The instance construction was performed using the parameters outlined in
Table 2.
Different machines are operated by workers with different skill levels, the operating costs are equal for workers of each skill level, and the basic cost is equal. The unit time cost of the workers operating each machine obeys a uniform distribution [20, 70]. The standard time ST, the minimum working time LBT, and the maximum working time UBT of each worker are set according to each task period (TP). The task period is determined by the lower bound of the maximum completion time of the standard examples (LBCT-SE). That is, the TP is twice the lower bound of the maximum completion time of the standard example; the ST is 0.5 times the TP, the LBT is 0.2 times the TP, the UBT is 0.7 times the TP, the minimum number of workers per category is one, and the largest number of workers in each category is twice the total number of machines. The parameter settings of the TSFBI are shown in
Table 3.
The core variables of the job quantity and machine quantity, including the number of jobs (
n), the number of operations per job (
ni), the total number of machines (
m), and the set of candidate machines for each operation (
Mij), along with their standard processing times, were directly inherited from the original FJSP benchmark instances. The range of job quantities (
n) and machine quantities (
m) for instances el01–el40 is shown in
Table 4. These instances cover a spectrum of sizes, categorized as small- (e.g., 5 × 10), medium- (e.g., 10 × 10, 5 × 20), and large-scale (e.g., 10 × 20, 15 × 15, 10 × 30), as defined by Liu et al. [
53].
For the dual-resource aspect, we introduced a set of workers, W. The total number of workers (w) for each instance was set as equal to the number of machines (w = 2 m). To model basic worker qualifications and assignments, we assumed the following.
Option A (if all workers can operate all machines): All workers in the set W were considered capable of operating any machine, k ().
Option B (if workers were assigned to machines/had differing skill levels): Workers were conceptually divided into groups of different skill levels or pools. For simplicity, in this study, we assumed each worker was capable of operating a randomly assigned subset of machines, ensuring each machine had at least ‘a’ candidate workers, or workers were grouped, and each group was assigned to specific machines, reflecting basic specialization. While the model allowed for the consideration of worker–machine-specific processing times (), for these extended instances, we assumed that the processing time primarily depended on the job, operation, and machine (inherited from the base benchmark) and was uniform across all qualified workers for that machine.
Worker-related costs and time constraints were generated based on the parameters defined in
Table 2. Specifically, the unit time cost for worker l completing operation
on machine k (
) was randomly generated for each worker–machine assignment within the uniform distribution [20, 70], reflecting potential minor variations in the operating cost even if workers’ skills were assumed to be comparable. The basic salary for each worker (
) was drawn from the uniform distribution [800, 1200].
Flexible working time constraints (LBT, ST, UBT) for each worker were determined relative to the instance’s task period (TP), which was derived from the lower-bound makespan of the original benchmark instance, as detailed in
Table 2. The minimum (a) and maximum (b) number of workers allowed per class/task were set as defined in
Table 2.
This extension process aimed to create a diverse set of DRFJSP instances grounded in established FJSP structures, allowing for the evaluation of the performance of the proposed model and TSFBI algorithm in handling the added complexity of worker resource allocation and flexible working time constraints.
The parameter settings for the TSFBI, such as the population size (
N = 30) and maximum number of generations (
T = 300), were chosen based on common practices in the related literature and preliminary computational tests to ensure a balance between the solution quality and computational time. It is acknowledged that these parameters can influence algorithm performance. While the FBI algorithm itself does not rely on traditional crossover and mutation operators, the parameters governing its investigation and pursuit phases (embedded within Equations (17)–(23)) and the overall population size/generation count are important. The results of a preliminary sensitivity analysis are shown in
Figure 5 and
Table 4 to demonstrate the impact of key parameters.
To investigate the influence of key parameters on the performance of the TSFBI algorithm, a preliminary sensitivity analysis was conducted. We focused on the population size (N) and the maximum number of generations (T), as these often significantly impact metaheuristic performance. Several representative instances (e.g., el01, el16, and el26, representing small, medium, and large scales) were selected.
The results indicate that increasing the population size beyond 30 offered marginal improvements in the makespan at the cost of a significantly increased computation time. Similarly, running the algorithm for more than 300 generations yielded diminishing returns for these instances. While the chosen parameters (N = 30, T = 300) appeared to provide a reasonable trade-off for the benchmark instances used, the optimal parameter settings might vary depending on the problem size and complexity. Further comprehensive parameter tuning could be beneficial for specific industrial applications.
5.2. Performance Metrics
To evaluate the effectiveness of the proposed TSFBI algorithm, the following three common evaluation criteria were used [
38,
54]. These metrics reflect the quality of non-dominated solutions obtained based on the dominance, distribution, convergence, and diversity of Pareto solutions.
The C-metric (
C) represents the degree of dominance of two non-dominated sets. The metric maps an ordered pair (
A, B) to a range from zero to one, where
A and
B are two dominated solution sets, to determine the relative convergence, as shown in Equation (25). If
C (
A,
B) = 1, then all solutions of
A dominate the solutions of
B, and if
C (
A,
B) = 0, then all solutions of
B dominate the solutions of
A.
Spacing metric (
SM): this indicator shows the inhomogeneity of the distribution of solutions obtained along the Pareto front (
PF). It is expressed as
where
denotes the Euclidean distance between consecutive solutions and
represents the average of all values of
and a lower value of the
SM represents better algorithm performance.
Hyper-volume ratio (
HVR): the hyper-volume (
HV) indicates the volume of all the solutions in the
PF. The
HV of a
PF is expressed as
where
vi is the hypercube formed between a solution in the obtained
PF and the reference point. In the case of a minimization criterion, the reference point in the solution space is obtained by considering the maximum values of each normalized objective from the combined
PF, i.e., (1,1,1). The
HV is normalized to obtain the
HVR by dividing the
HV of an obtained
PF by the
HV of a
PF*. A higher value of the
HVR represents wider coverage and better convergence for the
PF.
5.3. Experiment I: Testing the Validity of the DRFJSP Model
To verify the validity of the mixed-integer programming model established in this paper, we used Gurobi 9.5.0 [
55] to solve the model. At the same time, in order to verify the effectiveness of the TSFBI designed in this paper, the resulting TSFBI solution and Gurobi solution were compared and analyzed for the same example. The maximum running time for Gurobi was set to 3600 s. The results are shown in the table, where ‘/’ means that Gurobi could not obtain a better solution within 3600 s. “
” denotes the discrepancy in the performance results between the TSFBI algorithm and Gurobi.
In
Table 5, where the best value is in bold, the first column presents data from 40 instances, while the second and third columns indicate the sizes of these instances. The fourth and fifth columns show the objective values obtained using the Gurobi and TSFBI algorithms for each instance, along with the differences between the two. From an analysis of the results in
Table 5, it can be observed that for smaller instances and certain medium-sized instances (such as el16–el20), Gurobi was able to achieve optimal solutions within the specified runtime. However, for larger instances, Gurobi failed to produce a solution within the allotted time. Additionally, the results obtained using the TSFBI were closely aligned with those of Gurobi, which suggests the effectiveness of the TSFBI algorithm to a certain extent. Moreover, for large-scale instances, the TSFBI was able to provide approximate solutions, indicating that the TSFBI algorithm studied may be more suitable for practical large-scale production scheduling optimization.
5.4. Experiment II: Testing the Performance of the TSFBI
The performance of the TSFBI was assessed in two ways. First, a comparison test was conducted to evaluate the proposed encoding methods. Second, a multi-objective Pareto performance test was carried out to assess the TSFBI using three criteria.
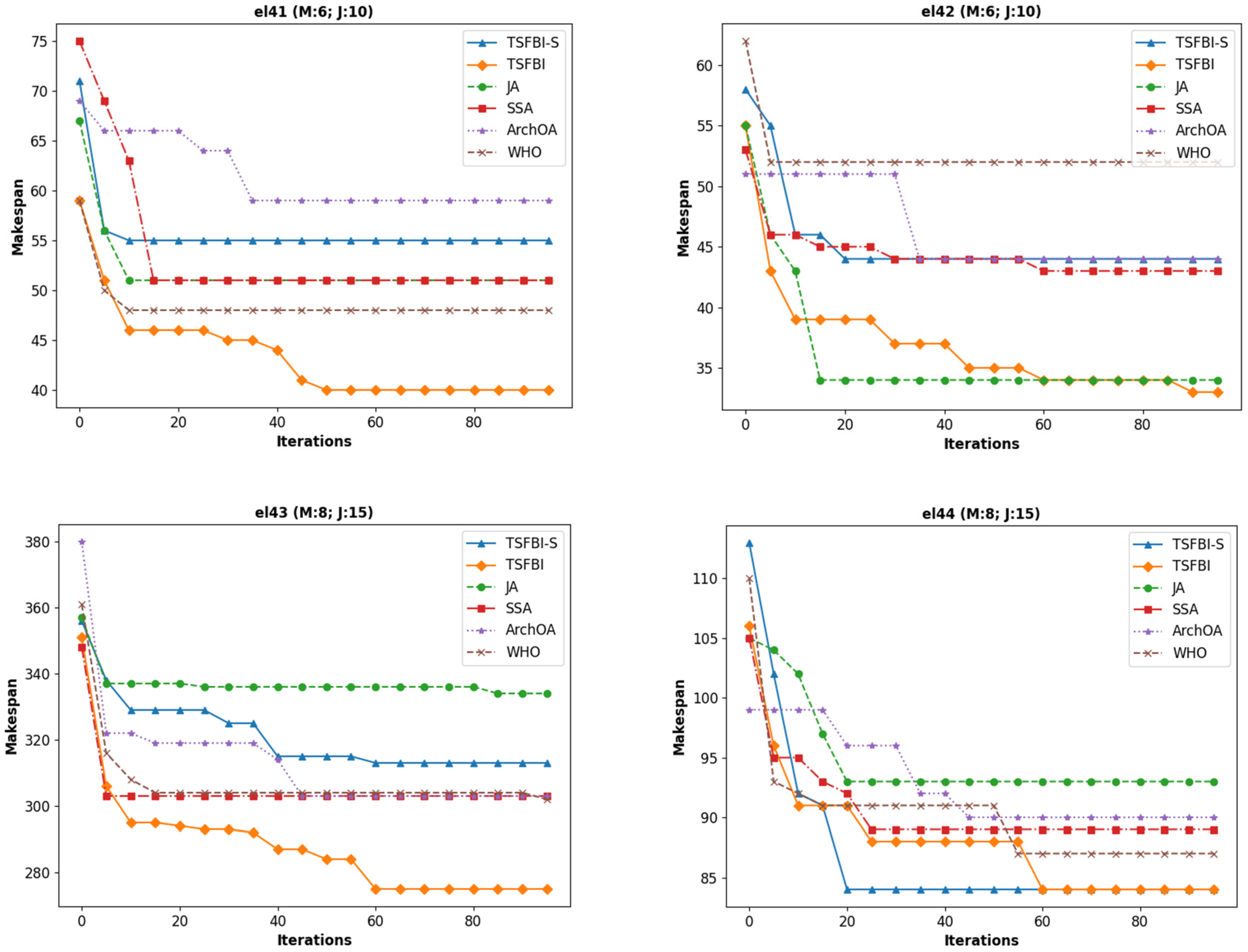
The initial test utilized el41–el50 for the verification of the compared encoding methods [
56], including the TSFBI-S, where the TSFBI-S represented our proposed TSFBI framework but utilized an alternative encoding method adopted from Shi et al. [
57] for comparison purposes. This comparison aimed to validate the effectiveness of the hybrid encoding technique proposed in this paper. To further illustrate the potential of the proposed codec technique in solving flexible job shop scheduling problems, newer metaheuristic algorithms were selected separately according to the classification of optimization algorithms presented in article [
57]. These included the JA [
58] and SSA [
59] algorithms based on animal social behavior, the ArchOA [
60] algorithm based on physical processes, and the WHO [
61] algorithm inspired by biology.
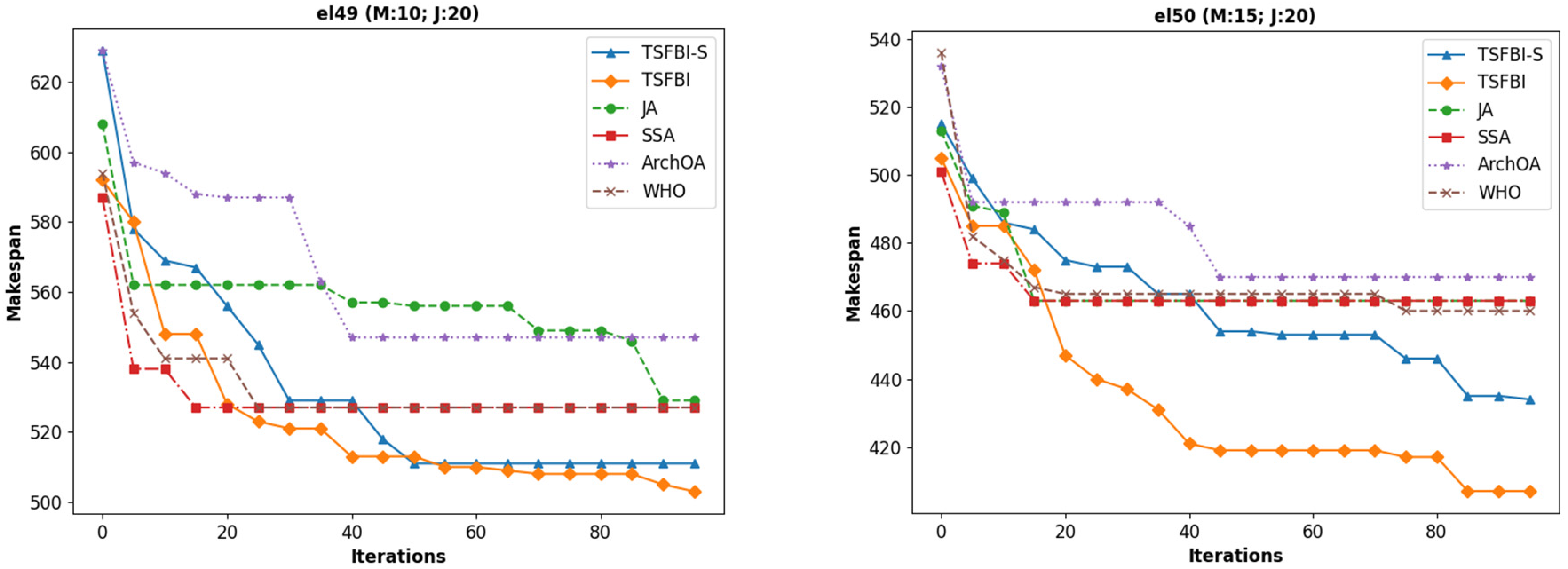
The experimental results are shown in
Figure 6,
Figure 7 and
Figure 8, where the x-axis of each figure represents the number of iterations completed by the algorithm, the y-axis represents the maximum completion time, and the captions refer to the different examples.
We know from the experimental results that the proposed codec method facilitates the rapid application of new continuous optimization algorithms in combinatorial optimization problems such as the DRFJSP, and the FBI algorithm always obtained better solutions when solving the FJSP than the other algorithms.
The results presented in
Figure 6,
Figure 7 and
Figure 8 demonstrate the effectiveness of the proposed hybrid encoding method, enabling the application of continuous optimization algorithms like the FBI to the discrete DRFJSP. Notably, the FBI algorithm consistently converged to better solutions (lower makespan) than those of JA, SSA, ArchOA, and WHO within the same number of iterations across most Mk benchmark instances, highlighting its potential for solving complex scheduling problems efficiently.
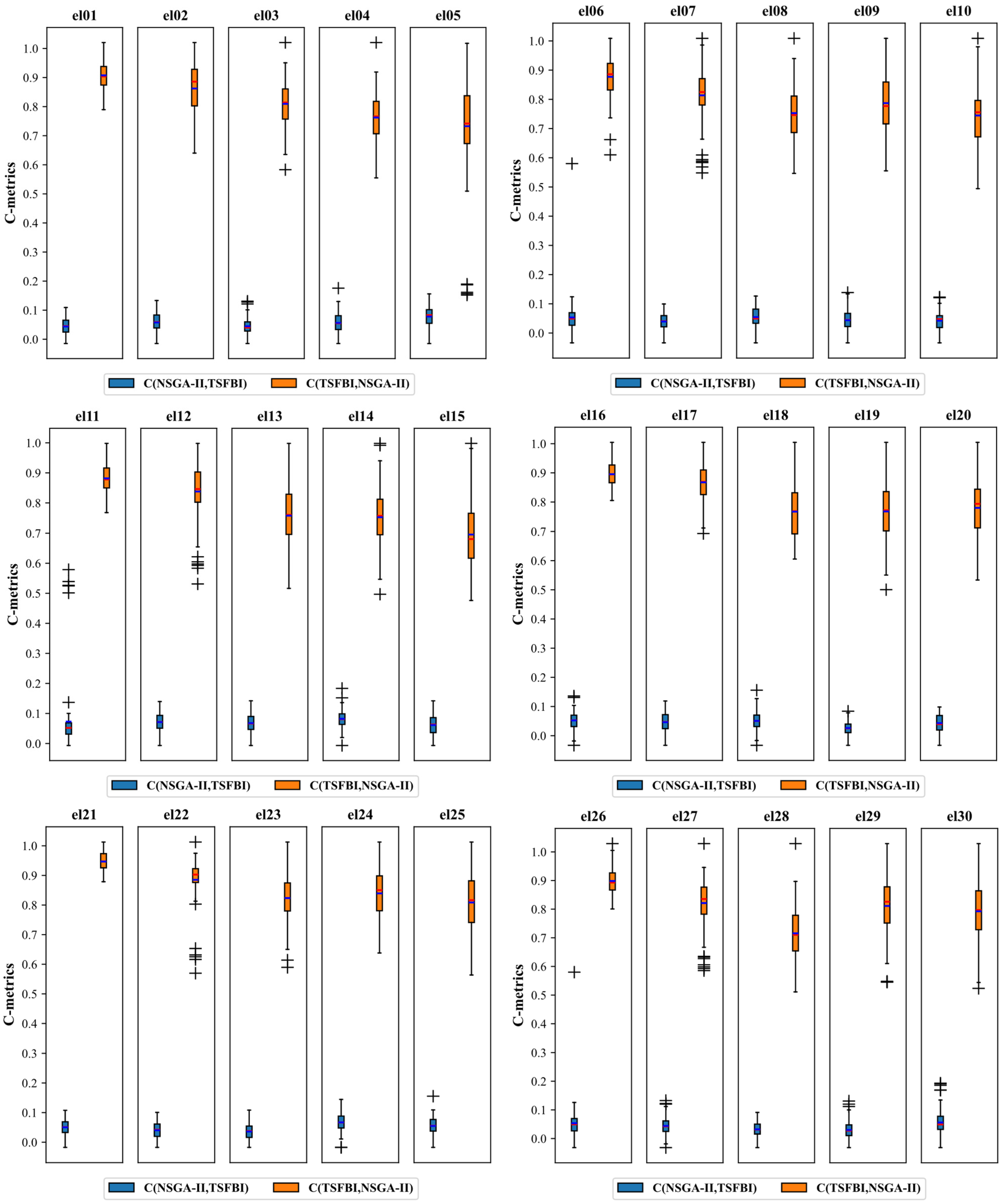
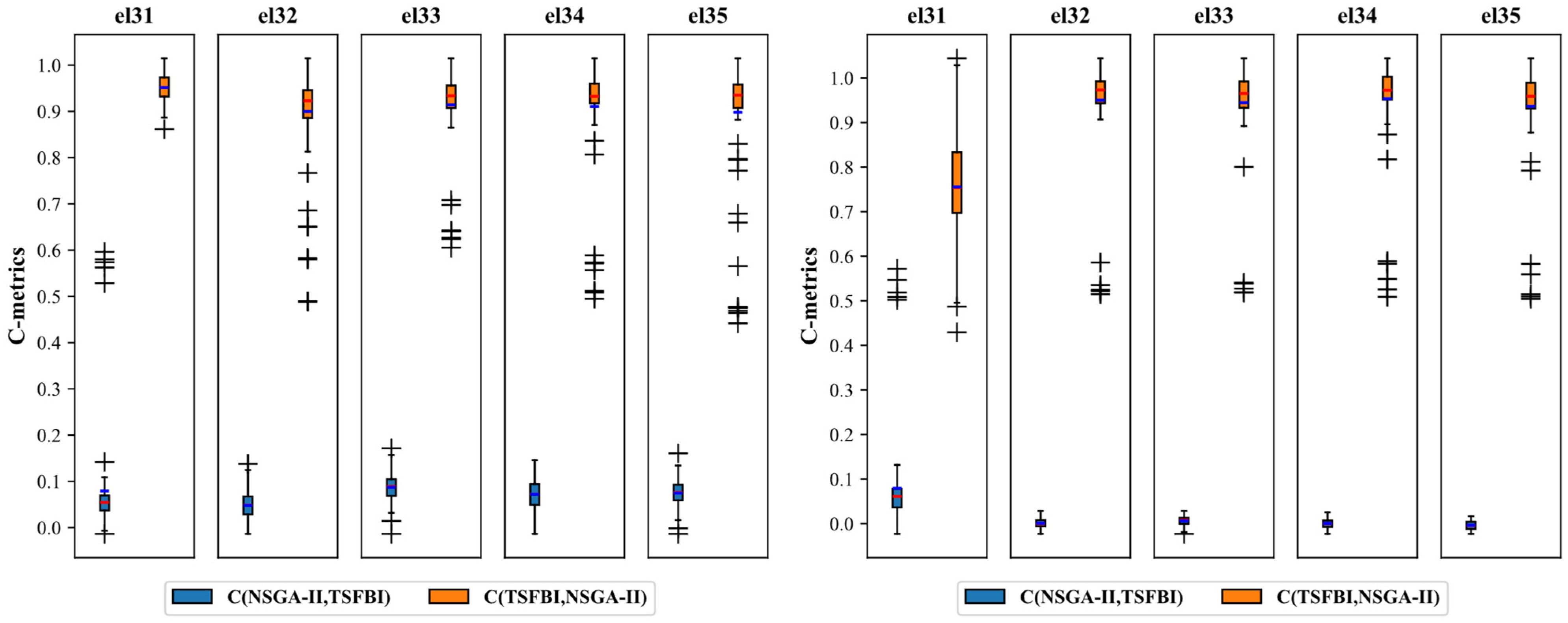
The extended instances (el01–el40) were optimized using the TSFBI and the NSGA-II, and three metrics, the C-metric, SM, and HVR, were statistically calculated. The statistics for the C-metrics are shown in
Figure 9. To visually demonstrate the variances in the distribution of the solutions produced by the TSFBI and NSGA-II, we utilized box plots. Each plot compares five instances, with a total of eight plots encompassing instances el01–el40. The
x-axis of each plot depicts the TSFBI and NSGA-II categories, while the y-axis represents the C-metrics.
Figure 9 illustrates the C-metric comparison between the TSFBI and NSGA-II. Recalling that
C(
A,
B) represents the fraction of solutions in B dominated by solutions in A, the generally high values observed for
C(
TSFBI,
NSGA-II) indicate that a large proportion of NSGA-II solutions were dominated by TSFBI solutions. Conversely, the generally low values for
C(
NSGA-II,
TSFBI) indicate that only a small proportion of TSFBI solutions were dominated by NSGA-II solutions. This demonstrates that the TSFBI algorithm achieved superior dominance performance in acquiring Pareto sets compared to the NSGA-II algorithm.
As shown in
Table 6, where the best value is in bold, the solutions obtained by the TSFBI were better than those obtained by NSGA-II in terms of their distribution, convergence, and diversity.
As shown in
Figure 9 and
Table 6, the TSFBI algorithm significantly outperformed the well-established NSGA-II algorithm across the tested instances (el01–el40). Specifically, the superior C-metric values indicate that the TSFBI generates Pareto sets with better dominance characteristics. Furthermore, the lower SM values suggest a more uniform distribution of solutions along the Pareto front, while the higher HVR values demonstrate better convergence and the wider coverage of the objective space. These combined results strongly suggest that the TSFBI is more effective than NSGA-II in finding a diverse and high-quality set of trade-off solutions for the DRFJSP, thus offering better support for decision-making regarding the scheduling efficiency and cost.
5.5. Experiment III on AHP Decision-Making Process
The Pareto solutions obtained using the TSFBI for the optimization calculation for the simple case are shown in
Figure 10. This study focused on two objectives, namely the completion time and worker cost, with a particular emphasis on the worker cost. The importance of these objectives was determined by assigning them ratings from 1 to 9 to construct the judgment matrix A. Therefore, the decision-maker’s preference for minimizing the worker cost was set at 8, while a rating of 1 is assigned to the minimization of the makespan. Using the weight calculation steps in
Section 4.2, the weight vector was calculated:
To clarify the calculation process, for each Pareto solution,
i (visualized in
Figure 10), the objective values (
for the makespan,
for the worker cost) were determined. These objective values were then normalized (using a specific normalization method, e.g., using the sum in Equation (24)). The normalized values for solution
i were plugged into Equation (24), along with the decision-maker’s weight vector
w = (1/9, 8/9) (Equation (30)) derived from the judgment matrix A (Equation (31)). This calculation yielded the
score for solution i, as is present in the vector in Equation (32), and based on Equation (32), the satisfaction vector was calculated, and the best value was achieved by solution 5. Solution 5 refers to the specific Pareto-optimal solution corresponding to the fifth score (0. 99234093) in the
vector. Based on the AHP analysis aiming to maximize this score, it was identified as the preferred solution in this context.
In this illustrative example, the preference for minimizing the worker cost (rating of 8) over the makespan (rating of 1) was assumed based on a hypothetical scenario where cost control was a primary concern for the decision-maker. In a real-world application, this judgment matrix would be established based on the actual preferences and strategic goals of the factory management. Different managers or changing priorities might lead to a different matrix A and consequently a different final solution selection. Future studies could explore the impact of varying weight assignments on the final scheduling decision through sensitivity analysis to assess the robustness of the chosen solution under different preference scenarios.
Figure 10 illustrates the Pareto front obtained for the simple case, clearly showing the trade-off between minimizing the makespan (f1) and minimizing worker costs (f2). For instance, solutions in the lower-left part of the front offered a shorter makespan but incurred higher worker costs, while solutions in the upper-right part achieved lower worker costs at the expense of a longer makespan. Solution 4, selected through the AHP with a strong preference towards minimizing worker costs (weight of 8/9 for f2), represented the most satisfactory compromise according to this specific preference structure, even though it did not have the absolute lowest makespan or the absolute lowest cost among all the Pareto solutions.
6. Conclusions
With increasing labor costs and the need for fine-grained production management, the consideration of human and machine resources in the scheduling process is receiving increasing attention. This article presents a human-centered approach to addressing the dual-resource flexible job shop scheduling problem and its solution. It explores the utilization of and dependence on human resources from two perspectives. First, the article discusses the incorporation of employees’ flexible working hours, constrained by minimum and maximum limits and often linked to work–life balance considerations, into the scheduling model. Second, it proposes a two-stage algorithm, drawing on the forensic-based investigation algorithm of human problem-solving behavior, to effectively solve the dual-resource flexible job shop scheduling problem (DRFJSP). By delegating scheduling decisions to managers, the method enables the creation of more flexible and dependable scheduling plans. By effectively optimizing both the makespan and worker costs, the proposed TSFBI algorithm provides manufacturers with valuable tools to improve the scheduling efficiency (reducing production lead times) and enhance cost-effectiveness (controlling labor expenditures) in complex dual-resource-constrained environments. The generation of a Pareto front allows for informed decision-making based on the desired balance between these critical objectives. The main findings of the paper are as follows:
In this paper, we discuss the impact of flexible working time arrangements on worker costs and production efficiency and formally describe the problem in a multi-objective mixed-integer linear programming model.
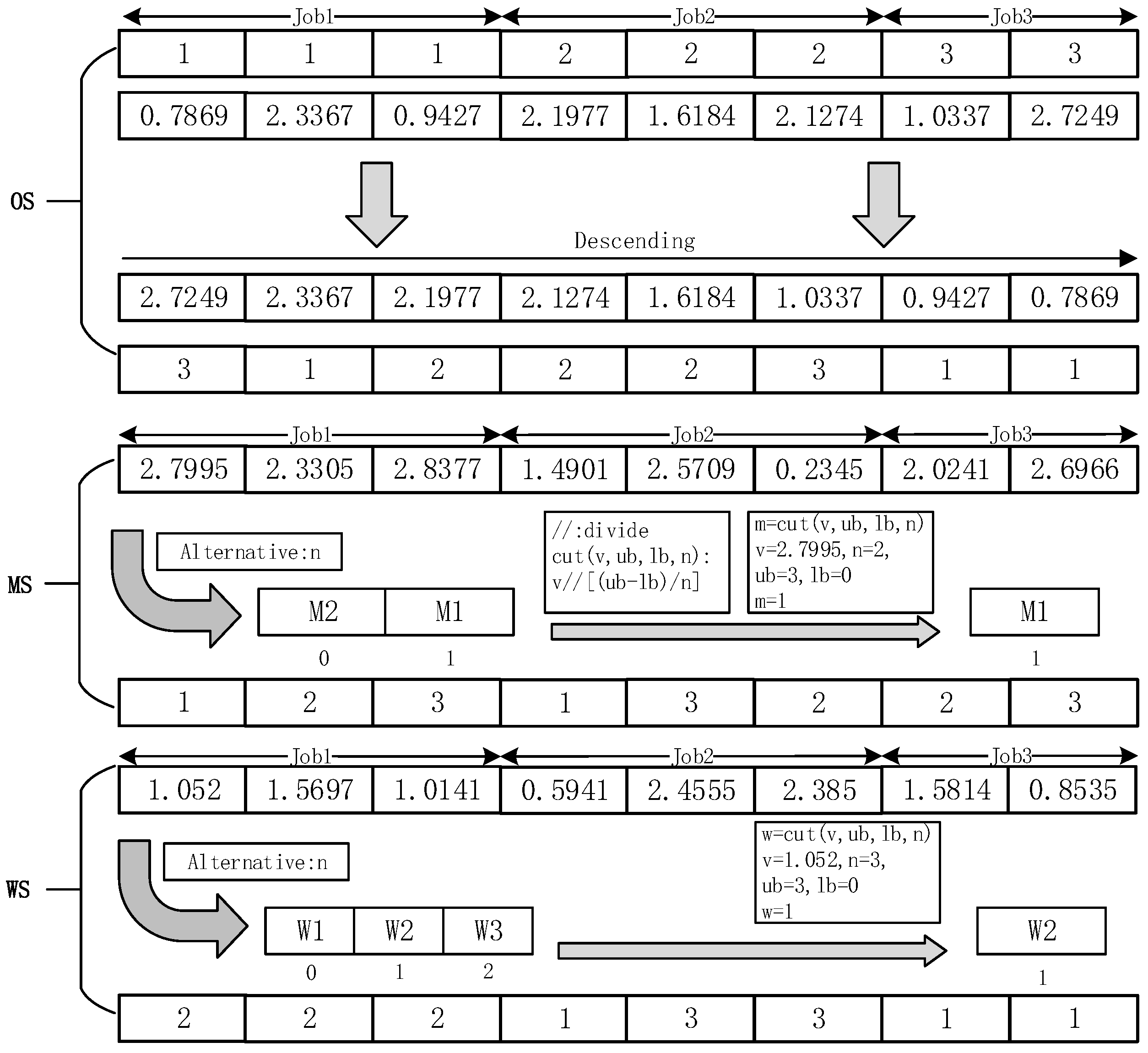
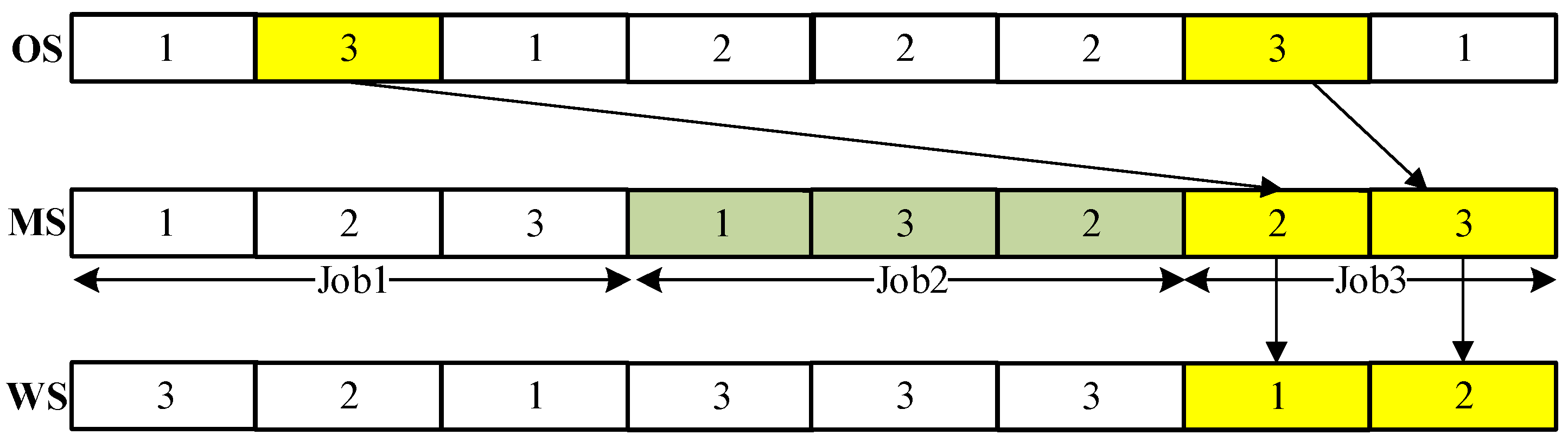
A two-stage approach based on the forensic-based investigation (TSFBI) is proposed to solve the model. First, the mapping relationship between the scheduling solution and the suspect vector of the DRFJSP is constructed using a hybrid codec approach, which ensures that the suspect vector is equivalent to a feasible scheduling solution. Second, the dominance relation of the solution is determined through fast non-dominated sorting, and a quantitative comparison operator is used to ensure the population’s diversity while not increasing the time complexity. Finally, the Pareto solutions are examined analytically through the AHP to obtain a satisfactory scheduling solution.
Three experiments were designed to verify the performance of the proposed TSFBI algorithm. The first experiment demonstrated the accuracy of the mixed-integer programming model established. The second experiment verified the effectiveness and efficiency of the proposed TSFBI algorithm. Comparing its results against those of the widely used NSGA-II algorithm demonstrated the TSFBI’s superiority in handling the DRFJSP, particularly in terms of the dominance, distribution, convergence, and diversity of the obtained Pareto solutions (as indicated by the C-metric, SM, and HVR, respectively). Furthermore, comparisons with several other recent metaheuristics (JA, SSA, ArchOA, WHO) using the proposed encoding method indicated the strong performance of the underlying FBI optimization engine for this type of problem. The third experiment examined the use of the AHP to obtain the optimal solution and proved the ability of the TSFBI to obtain the most suitable scheduling solution.
Despite the promising results, this study has several limitations that warrant acknowledgment. Firstly, the DRFJSP model operates under deterministic assumptions, neglecting stochastic events common in real manufacturing, such as machine breakdowns, processing time variability, or unexpected worker unavailability. Secondly, the validation primarily relied on benchmark instances; further testing with real-world industrial data is needed to confirm the practical applicability and robustness of the model and algorithm. Thirdly, certain operational details, such as worker skill levels, learning effects, or shift changeover times, were simplified or omitted. Furthermore, future research could broaden the comparative analysis by including the consideration of other established multi-objective algorithms, such as MOEA/D and SPEA2, to provide a more comprehensive benchmark of the TSFBI algorithm’s performance. Finally, while a preliminary sensitivity analysis was performed, a more comprehensive investigation into parameter tuning for the TSFBI algorithm could potentially further enhance its performance. To conclude, our work here has practical significance regarding the proposed model and research implications. Future research will focus on addressing these limitations by incorporating stochastic elements into the model (e.g., using simulation-based optimization or robust optimization techniques), validating the approach using industrial case studies, considering more detailed human factors (like skills and fatigue), and conducting extensive parameter optimization.