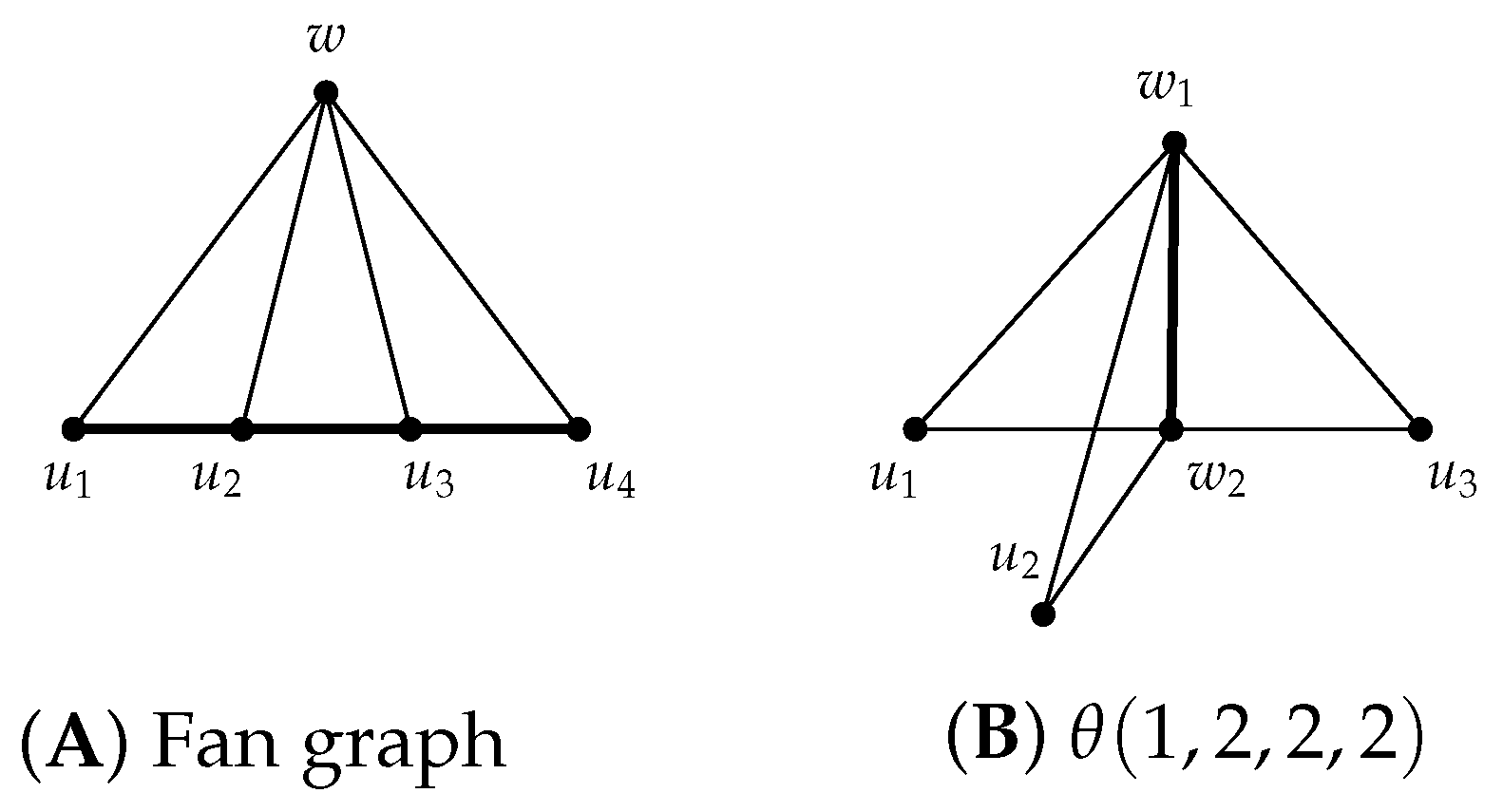1. Basic Notions
Throughout this paper, denotes an undirected, loopless graph with vertex set and edge set . The endpoint vertices u and v of an edge are said to be adjacent. A subgraph , where and , consisting of all edges of G with endpoints in X, is called an induced subgraph of G and is denoted by . A clique is a subgraph induced by a set of vertices in which every pair of vertices is adjacent. The clique number of G, denoted , is the maximum order of a clique in G, and the complete graph on r vertices is denoted .
The set of vertices adjacent to a vertex is called the open neighborhood of u and is denoted by . The subgraph induced by is called the closed neighborhood of u, denoted by . A vertex v is simplicial in G if every pair of its neighbors is adjacent in G, or equivalently, if is a clique.
A graph is said to be connected if there is a path between every pair of vertices. Otherwise, G is disconnected. The deletion of a set , denoted , is the subgraph induced by the complement of X. A separator of a connected graph G is a set such that is disconnected. A separator X is said to be minimal if no proper subset of X is also a separator, and it is maximal if X is not properly contained in any other separator. A cut-vertex is a separator consisting of a single vertex. A block of G is a maximal connected subgraph of G that has no cut-vertex. The graph G is said to be k-connected if no separator of G has fewer than k vertices.
Let be a separator of G whose deletion produces connected components induced by the nonempty, pairwise disjoint sets with . The induced subgraphs , for , are called the derived subgraphs of G relative to the separator . A derived subgraph is said to be minimal if no proper subset of H is also a derived subgraph, and it is maximal if H is not properly contained in any other derived subgraph.
2. Preliminaries
A list assignment to the graph is a function L that assigns a finite set of colors to each vertex . A proper L-coloring of G is a function such that for all , and whenever . The graph G is said to be k-choosable if it admits a proper L-coloring for every list assignment L where for all . The smallest integer k such that G is k-choosable is called the choice number of G, denoted .
The
chromatic number of
G, denoted
, is defined analogously, with the restriction that the list assignment
L assigns the same set of
k colors to all vertices. It is known that
. There are graphs for which
is arbitrarily larger than
, as shown in [
1], for instance. We note here that list assignments will often be adapted in a recursive process. Specifically, for a list assignment
L to a graph
G and a subset
A of colors, we let
denote the list assignment obtained from
L by removing each color
from
for all
. We refer the reader to [
2] for other basic definitions and notations.
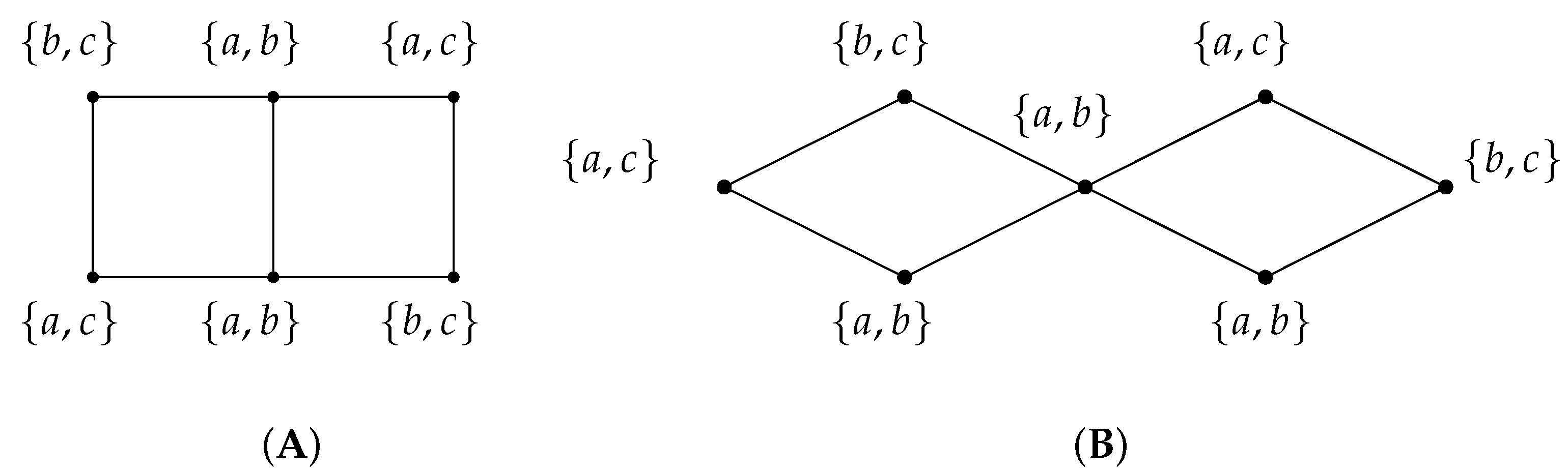
Figure 1A depicts the smallest graph
G for which
. In this example,
, but any choice of colors from the specified lists results in at least one pair of adjacent vertices receiving the same color. By Brooks’ theorem for the choice number [
3],
, and thus
.
The concept of list coloring was introduced in the late 1970s independently by Vizing [
4] and by Erdős, Rubin, and Taylor [
3]. Ever since, significant work has been carried out (see, e.g., Refs. [
5,
6,
7,
8,
9,
10,
11]) to identify classes of chromatic-choosable graphs. List colorings generalize classic proper vertex colorings and admit numerous applications in scheduling, resource management, and optimization where constraints are localized.
One of the most direct applications is in university scheduling and examination timetabling, where each course or event is restricted to certain time slots due to instructor availability or room constraints. These slot limitations translate into list assignments for vertices in a conflict graph, where edges represent overlaps in student enrollments. A successful list coloring guarantees a feasible schedule with no conflicts, and the choice number gives a lower bound on the minimum number of time slots needed under all feasible scenarios [
12].
In wireless communications, list coloring arises in frequency assignment problems, where each transmitter can only use specific frequency bands due to regulatory, physical, or environmental constraints. The interference graph models transmitters as vertices, and an edge between two vertices indicates they cannot share the same frequency. Because each transmitter may have its own subset of permitted frequencies, list coloring ensures an interference-free assignment while respecting local constraints. This has profound implications for the design and deployment of modern cellular and wireless networks [
13].
Compiler optimization, particularly register allocation, also benefits from list coloring techniques. In register allocation, variables in a program must be assigned to physical CPU registers. When certain variables are constrained to specific registers due to architectural limitations or prior usage, this problem becomes a list coloring instance. Solving it effectively improves runtime performance and reduces memory load, which is especially important in embedded and performance-critical systems [
14].
A graph
G is said to be
chromatic-choosable if
. Cycles, cliques, and trees are examples of chromatic-choosable graphs [
3]. For the reader, we list a few well-known results related to this topic for certain classes of graphs, in particular, the complete multipartite and multi-bridge graphs.
Theorem 1 (Erdös, Rubin, and Taylor [
3])
. The complete k-partite graph is chromatic-choosable. Theorem 2 (Galvin [
8])
. The line graph of any bipartite multigraph is chromatic-choosable. Theorem 3 (Gravier and Maffray [
9])
. If , then the complete k-partite graph is chromatic-choosable. We point out here that
is not chromatic-choosable since it contains the subgraph in
Figure 1 (
minus two edges), whose choice number is bigger than 2. Moreover, it was shown in [
7] that
is chromatic-choosable.
Theorem 4 (Kierstead [
15])
. Let G denote the complete k-partite graph . Then, . We note here that the previous statement implies that when and when .
Theorem 5 (Kierstead et al. [
16])
. Let G denote the complete k-partite graph . Then, . Theorem 6 (Hoffman and Johnson. [
1])
. Let denote a complete bipartite graph. Then, Theorem 7 (Enomoto et al. [
17])
. Let denote the complete k-partite graph . Then, Theorem 8 (Enomoto et al. [
17])
. Suppose , and let G denote the complete k-partite graph . Then, . Theorem 9 (Allagan and Johnson [
5])
. Let G denote the complete k-partite graph . Then, if . Theorem 10 (Allagan and Johnson [
5])
. Let G denote the complete k-partite graph , . Then, Theorem 11 (Erdős, Rubin, and Taylor [
3])
. A connected graph G is 2-choosable if and only if the core of G is , an even cycle, or of the form , where t is a positive integer. A reminder that the core of a graph G is the graph obtained from G by successively deleting its leaves (vertices of degree 1) until none remain. As such, most results only focus on the potential “core” of some graphs.
The next theorem is arguably the most well-known result by Noel, Reed, and Wu [
10] as an attempt to characterize chromatic-choosable graphs (with
); the statement was originally known as Ohba’s conjecture [
11].
Theorem 12 (Noel, Reed, and Wu [
10])
. If , then G is chromatic-choosable. It shows that when the chromatic number is large relative to the order of the graph, the chromatic number is also large enough to equal the choice number. However, there are still several classes of chromatic-choosable graphs whose chromatic numbers are low relative to their orders. For instance, any cycle (of any order) is chromatic-choosable, and Ohba’s theorem only shows that bipartite graphs of an order smaller than 6 are chromatic-choosable.
Theorem 13 (Allagan and Bobga [
7])
. Suppose is a multi-bridge graph with . G is chromatic-choosable if and only if G contains an odd cycle or G is of the form , where t is a positive integer. Theorem 14 (Erdős, Rubin, and Taylor [
3])
. If G is a connected graph that is neither a complete graph nor an odd cycle, then . Corollary 1. For any graph G, .
These results highlight the structural properties of chromatic-choosable graphs and motivate further exploration of graph classes with this property. Our work aims to identify other classes of chromatic-choosable graphs. We begin with chordal graphs, also known as triangulated graphs, in the next section.
3. Choice Number of Chordal Graphs
A graph
G is
chordal if every cycle of length
has a
chord. Traditionally, a chord is an edge of
G connecting two non-consecutive vertices of the cycle. We found this definition problematic in the context of this paper, which might explain why chordal graphs are often referred to as
triangulated graphs. As a subclass of perfect graphs, chordal graphs have at least one simplicial vertex. See [
18] for instance. For this reason, we (re)define a
chord as an edge of a cycle (of length greater than 3) that contributes to the formation of
, a triangle, and its removal yields a cycle of length at least 4.
Figure 2 shows two well-known chordal graphs. Moreover, the edges
,
are chords in the Fan graph while the edge
is the only chord in
.
Theorem 15. Chordal graphs are chromatic-choosable.
Proof. Let be a chordal graph with . To show that G is k-choosable, we must demonstrate that any list assignment L satisfying for all permits a proper L-coloring of G.
Since G is a chordal graph, there is a perfect elimination ordering (PEO), denoted as , of the vertices of G. By definition, in this ordering, for each vertex , the set of neighbors of appearing later in the ordering, , forms a clique.
We construct a proper L-coloring of G by coloring the vertices in the reverse order of the PEO, starting with and proceeding to . At each step i, we assign a color to from its available list such that the coloring remains proper.
To begin, consider the vertex . Since , assign any color from to . Now, consider . By the properties of the PEO, the only neighbors of that are already colored are in the clique formed by its higher-index neighbors. Because the size of this clique is at most (since ), there will always be at least one available color in that is distinct from the colors of its neighbors. Assign this color to .
This process continues inductively. At each step i, when coloring , its higher-index neighbors form a clique. Thus, the number of colors already used by its neighbors is at most . Since , there is always at least one available color in that does not conflict with the colors of its neighbors. Assign this color to .
By iterating this procedure through the reverse PEO, we construct a proper L-coloring of G. Therefore, . Since by definition, it follows that . □
We note here that because chordal graphs admit perfect elimination orderings, any greedy list-coloring strategy can color them successfully if each vertex has a list of size at least
. This structure ensures that list coloring does not require more colors than ordinary coloring, a result that is also confirmed in a recent paper by Vasudevan et al. for perfect graphs [
19].
A
k-tree is a graph constructed from a
k-clique by repeatedly adding new vertices, each connected to all vertices of an existing
k-clique. It is well-known that
k-trees are chordal graphs.
Figure 2A,B show two non-isomorphic 2-trees, which are well-known to be chordal graphs.
Corollary 2. Every k-tree is -choosable for all .
Other well-known members of the family of chordal graphs, shown in [
2,
18,
20,
21], for instance, include forests, fan graphs, split graphs, interval graphs,
k-sun, trivially perfect graphs, threshold graphs, windmill graphs, and strongly chordal graphs.
Remark 1. It is tempting to assume that graphs that admit clique separators are likely to be chromatic-choosable. Figure 1 shows two counterexamples: (A) when the clique separator is of size 2 and (B) when the clique separator is of size 1. This demonstrates that the presence of clique separators is not sufficient to guarantee chromatic choosability. In the next section, we look at
chordless graphs, which are graphs whose induced cycles of a length greater than 3 do not have any chord. See
Figure 1, for example. Moreover, chordless graphs, which are also known as triangle-free graphs, are not necessarily planar, and they include all bipartite graphs. Our results not only cover some triangle-free graphs (with a neighborhood condition) but also cover graphs that are neither triangulated nor triangle-free; they are known as
non-chordal. In general, a non-chordal graph can easily be derived from a chordless graph by adding a sequence of chords to any cycle of length greater than 3, while ensuring that the graph does not become chordal or fully triangulated.
4. Choice Number of Some Chordless and Non-Chordal Graphs
Theorem 16. Let be the derived subgraphs of a graph G, induced by a set X. Assume that for all . Furthermore, suppose that for every pair of vertices , the neighborhoods of u and v outside X in are disjoint, i.e., Then, the choice number of G satisfies: Proof. Let L be a list assignment to the vertices of G such that for all . We will show that G has a proper L-coloring under the given conditions.
Begin by properly coloring , which is k-choosable by assumption. Since , there is a proper L-coloring of . For each vertex , let be the color assigned to u by . Let denote the set of neighbors of in for . By the hypothesis for all , the sets are pairwise disjoint.
For each , remove the color from the list of each vertex . This operation results in a reduced list assignment . Since , it follows that .
Now consider the subgraph . For each , the hypothesis ensures that there is a proper -coloring of . Since the sets are pairwise disjoint, no two vertices in different share the same reduced list, ensuring that the proper coloring of each is independent of the others. By combining the proper -colorings of all , we obtain a proper L-coloring of G.
If for all , then G requires at most k colors in total, and . If for some , then the reduction process may require an additional color, and , hence the result. □
Theorem 17. (Decomposition Theorem)
. Let be the minimal derived subgraphs of a graph G, induced by the sets , such that for every , . If , then Proof. Let L be a list assignment to G where for all . We construct a proper L-coloring as follows. First, color . Since , there is a proper coloring of . Fix this coloring and record the colors assigned to vertices in separators shared between and other subgraphs. Then, adjust the lists for all . For each vertex , remove the color from if w is adjacent to . By the disjoint neighborhood condition, each w is adjacent to at most one , so .
Now, color each remaining subgraph . Since , the reduced list with admits a proper coloring . The union defines a proper L-coloring for G. Therefore, one of the following cases holds:
- 1.
If for all , then . The reduced lists (size k) suffice for , so .
- 2.
If for some , the initial list size ensures after adjustments, so .
Hence, the result. □
We illustrate the decomposition process of Theorem 17 in the next example.
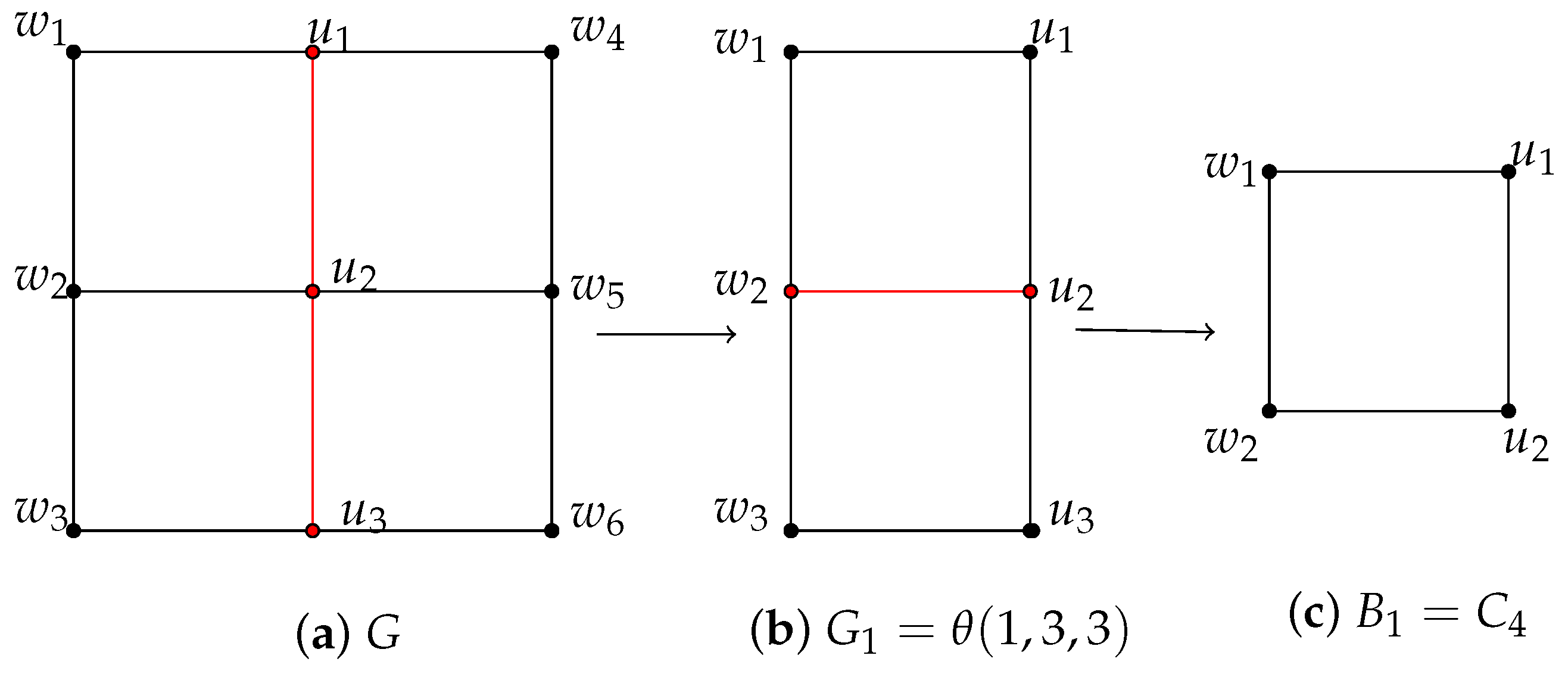
Example 1. Choice number of a grid: A decomposition.
Consider
, the Cartesian product of two paths
, which forms a
grid graph with
. To compute the choice number
, we illustrate in
Figure 3a decomposition of
G into derived subgraphs.
Consider the maximal separator,
. Note that, for each
, the neighborhood
, where
, satisfies the condition
for
. So,
produces the derived subgraphs
. For an illustration purpose, we only show the graph
in
Figure 3 and consider
and
, independently.
Further, we let and be the separators of and , respectively. The decomposition process ends with G being divided into four ’s, denoted by .
To compute , assign a list L with for each . Since , for , i.e., , it follows from Theorem 17 (second assertion) that . Moreover, because and , we have .
Remark 2. The previous two theorems give some insight into how to construct and even recognize some classes of chromatic-choosable graphs. So, given a graph G, it suffices to verify that the choice number of one of its components (given the separators’ condition) is bigger than that of any other component. This can be achieved by sufficiently increasing the size of the clique in one of the components either through the graph “join” operation or by connecting any pair of non-adjacent vertices in the case of graphs with even cycles. To see this, add an edge between two non-adjacent vertices for one or both of the two induced cycles in Figure 1B. The resulting graph is chromatic-choosable since its chromatic number is 3. In general, one can add enough chords to cycles (of length greater than 3) of a chordless graph without becoming fully chordal. Thus, one can form a non-chordal graph that is chromatic-choosable by adding a chord to any cycle of a 2-colorable chordless graph. Moreover, this process can be extended to derive a large class of chromatic-choosable non-chordal graphs, and the next two corollaries, which follow from Theorem 17, affirm their existence.
Corollary 3. Suppose are the derived subgraphs of G induced by the sets such that for every , . If , then .
Corollary 4. Suppose are the derived subgraphs of G induced by the sets such that for every , . If for each , and is chromatic-choosable, then G is chromatic-choosable.
5. Estimates of the Choice Number of Some Chordless
Now, we present some results on an upper bound on the choice numbers of the Cartesian product of two graphs, which are special families of chordless graphs. We note that these results apply to non-chordal graphs as well as they are easily formed from these chordless graphs, as mentioned in Remark 2.
For the reader, the Cartesian product of graphs G and H, denoted by , is the graph with vertex set , where is adjacent to whenever and , or and .
Theorem 18. Suppose that , , and are disjoint and non-empty; , ; and no vertex in has, in G, more than r neighbors in . Then, .
Proof. Let and suppose that L is a list assignment to G such that for all . Because , there is a proper L-coloring of . [More precisely, there is a proper L-restricted-to- coloring of .] Define on by . By the hypothesis of the Theorem, , for all , and, therefore, there is a proper -coloring of . Putting this coloring together with , we have a proper L-coloring of G. L was arbitrary, so . □
Corollary 5. For , .
Proof. Let the vertices of be ; let and . Then, and are disjoint and non-empty, , and every vertex in is adjacent in to exactly one vertex in . Further, induces in G, and induces in G. The conclusion follows from Theorem 18 by induction on n. □
Each of the graphs in the next two corollaries contains the subgraph , giving a lower bound of their choice number. The upper bound follows from Corollary 5, giving each result.
Corollary 6. For , , .
Corollary 7. For , , .
We note that both Corollary 6 and Corollary 7 follow from a result by Alon and Tarsi, who showed that every bipartite planar graph is 3-choosable [
22]. Also, it is worth noting that by Corollary 1,
for all
. Therefore,
when
m is odd. Together with Corollary 7, we can conclude the next result.
Corollary 8. For , , .
Corollary 9. Suppose that has degree in H; then, .
Proof. can be formed by connecting to a disjoint copy of G in such a way that every vertex of the added G has r neighbors in . □
Corollary 9 is just a special case of an obvious application of Theorem 18, in which is partitioned into and for some partition of into . In Corollary 9, .
We close this section with a more general upper bound on the choice number of the Cartesian product of any two graphs.
Theorem 19. with equality when .
Proof. If G and H are two graphs of order at most n, then and , with the last equality following from Theorem 2. □
Corollary 10. If , then is chromatic-choosable.
6. Conclusions
The results presented in this paper provide new insights into the relationship between the structure of a graph and its choice number, particularly for chordal, chordless, and some non-chordal graphs. Together, the corollaries and the example illustrate a connection between chromatic-choosability and graph decompositions, offering new tools to identify classes of chromatic-choosable graphs that are chordless or non-chordal. The question of whether there might be non-chordal graphs that are 2-choosable, thus chromatic-choosable, was answered affirmatively by Erdös et al. [
3] when they characterized all 2-choosable graphs, mainly that every component of such graphs must be 2-choosable. We hope that the results presented here will help further characterize 3-choosable graphs given some earlier work in this respect by Alon et al. [
22] when they showed that every bipartite planar graph is 3-choosable; our results make no distinctions between planar and non-planar graphs as every bipartite graph is chordless and non-chordal graphs include all multipartite graphs with 3 or more parts. Finally, we observe that the bound of Theorem 17 is tight for planar graphs, as Voigt and a few other researchers [
23,
24,
25] have found some examples of planar triangle-free graphs (having more than two odd holes) that are not 3-choosable.