Failure Mode of Tunnel Face Under Transient Unsaturated Seepage with Temperature Influence
Abstract
1. Introduction
2. Suction Stress and Apparent Cohesion Under Transient Unsaturated Seepage
2.1. Suction Stress and Apparent Cohesion in Unsaturated Soils
2.2. Impact of Temperature
2.3. Analytical Solution to Transient Unsaturated Seepage
3. Failure Mode of Tunnel Face Under Transient Unsaturated Seepage
3.1. Three-Dimensional Logarithmic Spiral Failure Mechanism
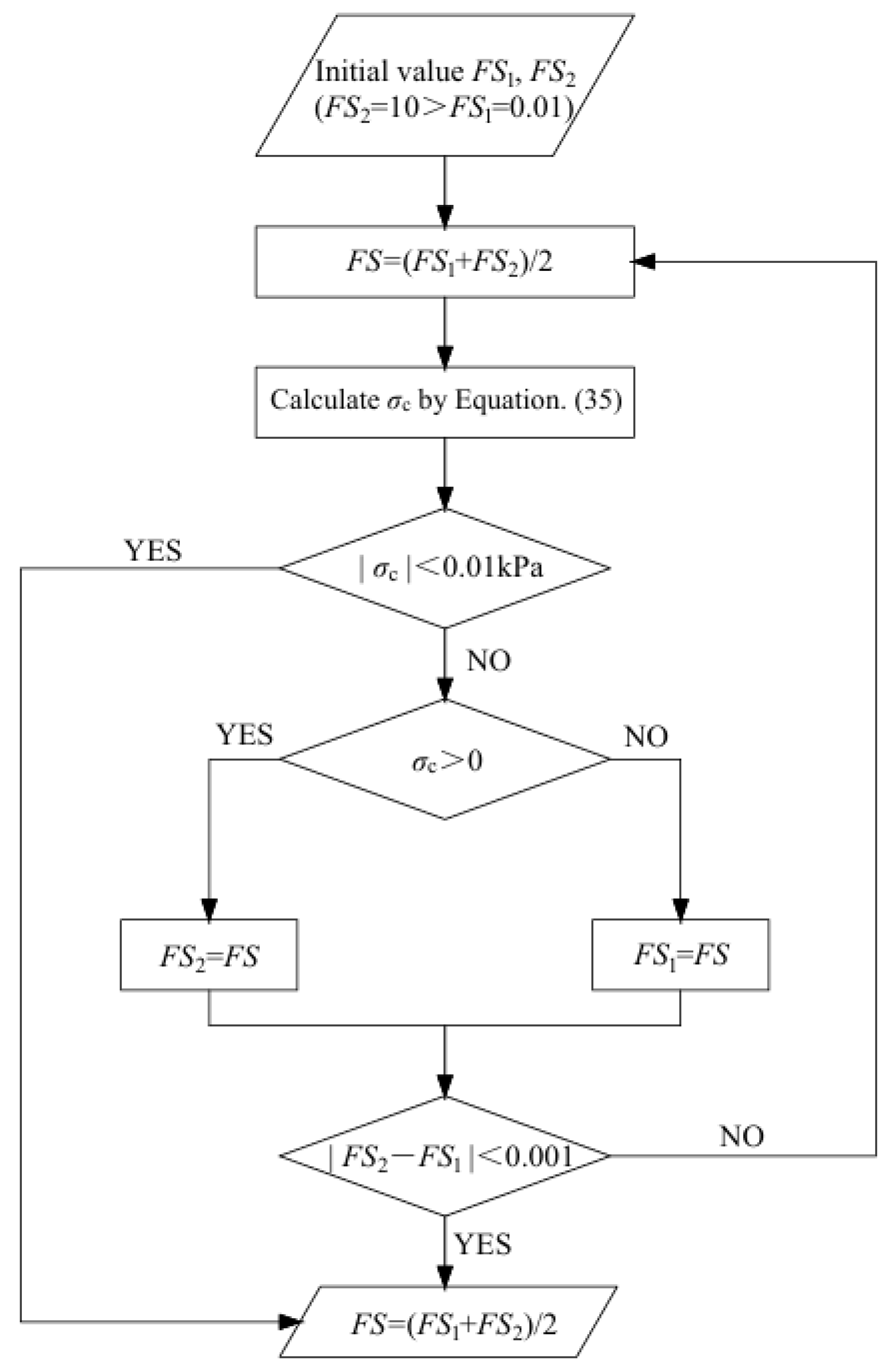
3.2. Strength Reduction Technique and Safety Factor
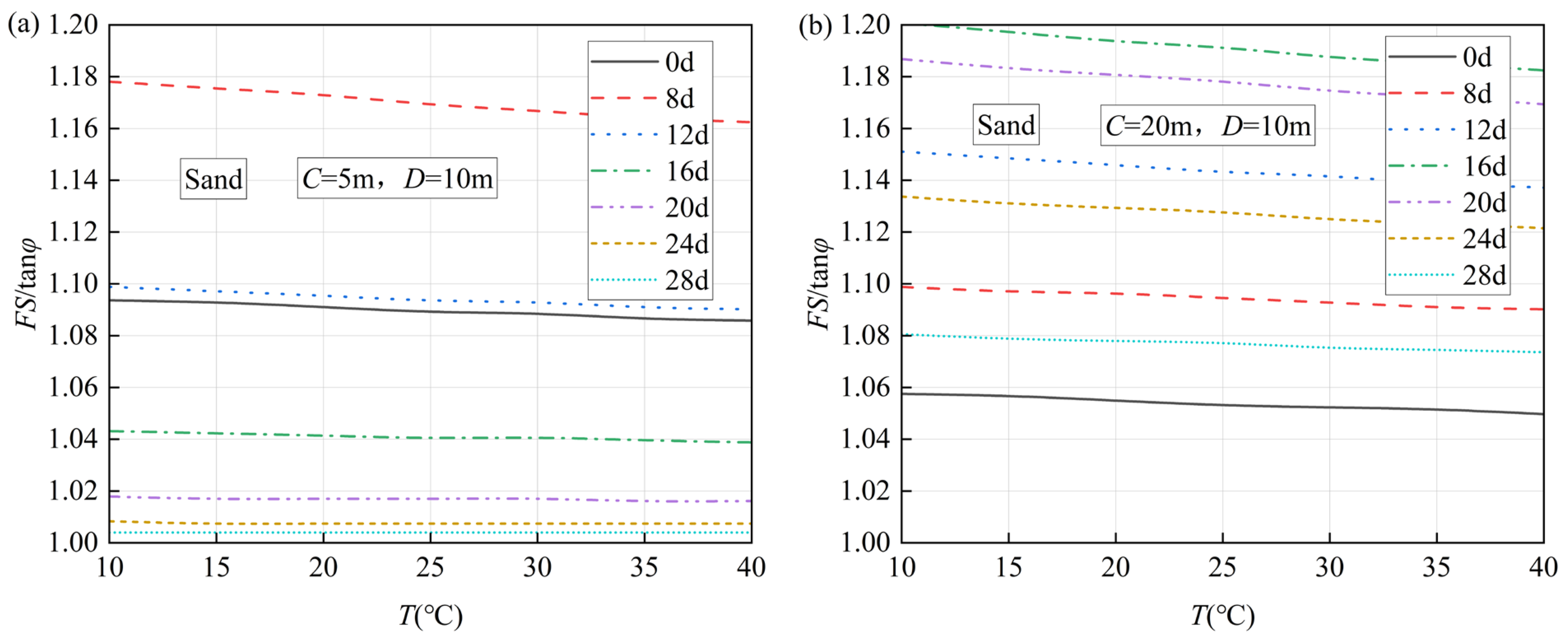
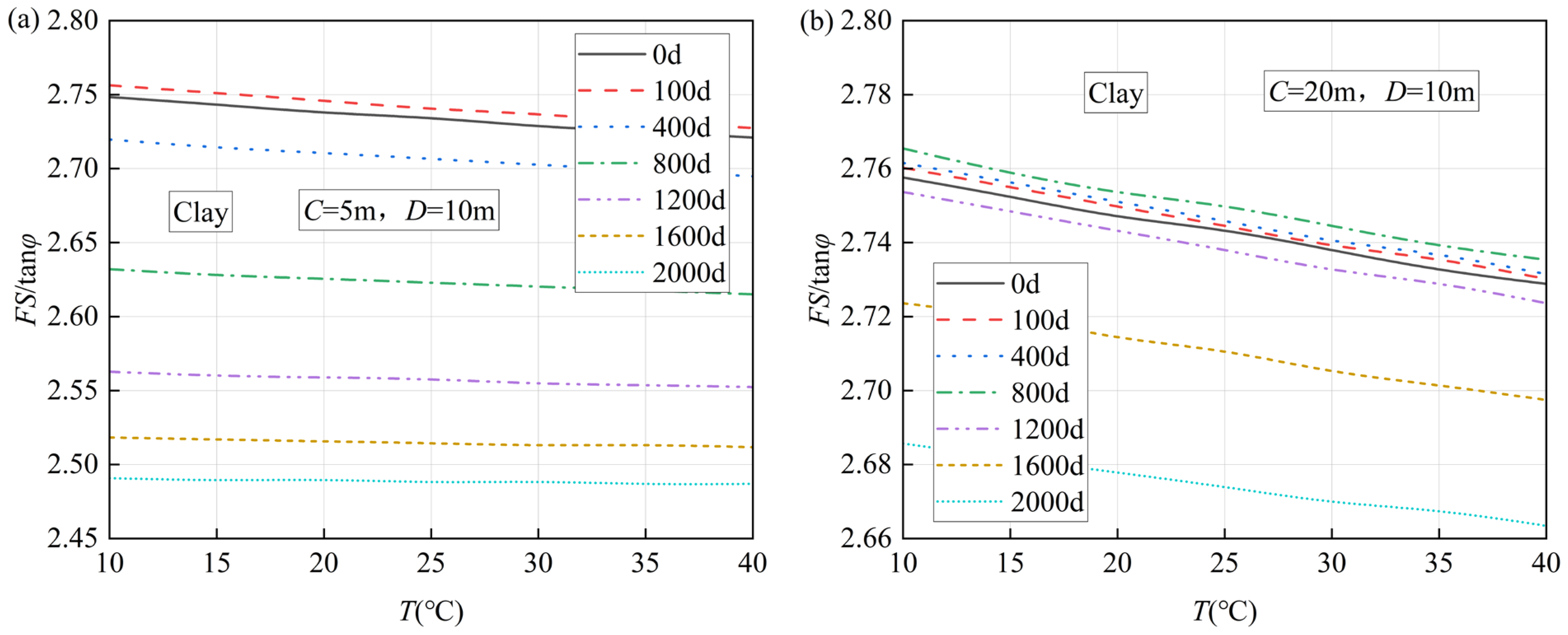
4. Parametric Analysis and Discussions
- (1)
- Layer thickness dependency: Thinner unsaturated soil layers experience earlier turning points and more pronounced safety factor variations. For example,
- (a)
- At D = 10 m and C/D = 0.5:
- (i)
- Sand: days.
- (ii)
- Silt: days.
- (iii)
- Clay: days.
- (b)
- At D = 10 m and C/D = 2:
- (i)
- Sand: days.
- (ii)
- Silt: days.
- (iii)
- Clay: days.
- (2)
- Convergence behavior: the safety factors gradually approach no-suction conditions, with thinner soil layers achieving this equilibrium state faster.
- (3)
- Early infiltration phase: during initial infiltration stages, saturation degrees and suction stresses near the groundwater level remain relatively unaffected, resulting in minimal safety factor variations.
- (4)
- Temperature changes affect the safety factor of the inflection point in unsaturated transient seepage. An increased temperature leads to a lower safety factor, and this impact is more significant in tunnels with greater depth-to-diameter ratios.
5. Conclusions
- (1)
- Rainfall-induced unsaturated transient seepage and ground temperature changes can lead to significant variations in unsaturated effects and temperature responses in unsaturated soils, particularly in silt and clay.
- (2)
- As the seepage progresses over time, the safety factor first rises, then falls, and gradually nears the value under no-suction conditions. Thinner soil layers reach equilibrium faster. This implies that considering transient unsaturated seepage is beneficial for tunnel face stability during excavation.
- (3)
- As temperatures change, so does the inflection point of the safety factor in unsaturated transient seepage. Higher temperatures lower the safety factor in tunnels with larger depth-to-diameter ratios. And the sensitivity to temperature changes is in the order: clay > silt sand.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, D.; Zeng, L.; Lv, Z.; Yu, X.C.; Liu, C.; Jiang, A.M.; Jiang, X.Y.; Li, Q.; Yang, Y.X. Failure Mode of Deep-Buried Rectangular Chamber and Upper Bound Solution of Surrounding Rock Pressure. Mathematics 2025, 13, 69. [Google Scholar] [CrossRef]
- Chambon, P.; Corte, J.F. Shallow tunnels in cohesionless soil: Stability of tunnel face. J. Geotech. Eng. 1994, 120, 1148–1165. [Google Scholar] [CrossRef]
- Kamata, H.; Mashimo, H. Centrifuge model test of tunnel face reinforcement by bolting. Tunn. Undergr. Space Technol. 2003, 18, 205–212. [Google Scholar] [CrossRef]
- Shan, J.T.; Wu, Y.M.; Yang, X.L. Three-dimensional stability of two-step slope with crack considering temperature effect on unsaturated soil. J. Cent. South Univ. 2025, 32, 1–19. [Google Scholar] [CrossRef]
- Kirsch, A. Experimental Investigation of the Face Stability of Shallow Tunnels in Sand. Acta Geotech. 2010, 5, 43–62. [Google Scholar] [CrossRef]
- Berthoz, N.; Branque, D.; Subrin, D.; Wong, H.; Humbert, E. Face failure in homogeneous and stratified soft ground: Theoretical and experimental approaches on 1g EPBS reduced scale model. Tunn. Undergr. Space Technol. 2012, 30, 25–37. [Google Scholar] [CrossRef]
- Vermeer, P.A.; Ruse, N.; Marcher, T. Tunnel heading stability in drained ground. Felsbau 2002, 20, 8–18. [Google Scholar]
- Mollon, G.; Dias, D.; Soubra, A.H. Probabilistic analysis and design of circular tunnels against face stability. Int. J. Geomech. 2009, 9, 237–249. [Google Scholar] [CrossRef]
- Yang, X.L.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek–Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Yang, X.L.; Wang, J.M. Ground movement prediction for tunnels using simplified procedure. Tunn. Undergr. Space Technol. 2011, 26, 462–471. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Yang, X.L. Pseudo-dynamic analysis of a 3D tunnel face in inclined weak strata. Undergr. Space 2023, 12, 156–166. [Google Scholar] [CrossRef]
- Anagnostou, G.; Kovári, K. The face stability of slurry-shield-driven tunnels. Tunn. Undergr. Space Technol. 1994, 9, 165–174. [Google Scholar] [CrossRef]
- Oreste, P.P.; Dias, D. Stabilisation of the Excavation Face in Shallow Tunnels Using Fibreglass Dowels. Rock Mech. Rock Eng. 2012, 45, 499–517. [Google Scholar] [CrossRef]
- Anagnostou, G.; Perazzelli, P. The stability of a tunnel face with a free span and a non-uniform support. Geotechnik 2013, 36, 40–50. [Google Scholar] [CrossRef]
- Yang, X.L.; Yin, J.H. Slope stability analysis with nonlinear failure criterion. J. Eng. Mech. 2004, 130, 267–273. [Google Scholar] [CrossRef]
- Yang, X.L.; Yin, J.H. Upper bound solution for ultimate bearing capacity with a modified Hoek–Brown failure criterion. Int. J. Rock Mech. Min. Sci. 2005, 42, 550–560. [Google Scholar] [CrossRef]
- Yang, X.L.; Li, L.; Yin, J.H. Seismic and static stability analysis for rock slopes by a kinematical approach. geotechnik 2004, 54, 543–549. [Google Scholar] [CrossRef]
- Mollon, G.; Phoon, K.K.; Dias, D.; Henry, W.; Emmanuel, H. Validation of a new 2D failure mechanism for the stability analysis of a pressurized tunnel face in a spatially varying sand. J. Eng. Mech. 2011, 137, 8–21. [Google Scholar] [CrossRef]
- Leca, E.; Dormieux, L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material. Géotechnique 1990, 40, 581–606. [Google Scholar] [CrossRef]
- Subrin, D.; Wong, H. Stabilité du front d’un tunnel en milieu frottant: Un nouveau mécanisme de rupture 3D. Comptes Rendus Mécanique 2002, 330, 513–519. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 1363–1388. [Google Scholar] [CrossRef]
- Liang, W.B.; Zhao, J.H.; Li, Y.; Chang, G.Z.; Su, W. Unified solution of Coulomb’s active earth pressure for unsaturated soils without crack. Appl. Mech. Mater. 2012, 170, 755–761. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, X.; Fan, W. Overturning stability of a rigid retaining wall for foundation pits in unsaturated soils. Int. J. Geomech. 2016, 16, 06015013. [Google Scholar] [CrossRef]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Lu, N.; Likos, W.J. Suction stress characteristic curve for unsaturated soil. J. Geotech. Geoenviron. Eng. 2006, 132, 131–142. [Google Scholar] [CrossRef]
- Li, T.Z.; Yang, X.L. New approach for face stability assessment of tunnels driven in nonuniform soils. Comput. Geotech. 2020, 121, 103412. [Google Scholar] [CrossRef]
- Li, T.Z.; Dias, D.; Li, Z.W. Failure potential of a circular tunnel face under steady-state unsaturated flow condition. Comput. Geotech. 2020, 117, 103231. [Google Scholar] [CrossRef]
- Xie, Y.; Liao, H.; Zhou, D. Temperature Effect on Stability of Tunnel Face Under Unsaturated Seepage Condition. Appl. Sci. 2024, 15, 298. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W. Hillslope Hydrology and Stability; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Srivastava, R.; Yeh, T.C.J. Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils. Water Resour. Res. 1991, 27, 753–762. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, D.; He, Y.; Zhang, H.; Chen, J.; Ren, S.; Zhou, Z. Study on cooling measures and ventilation cooling device of high ground temperature tunnel. J. Therm. Anal. Calorim. 2024, 149, 3347–3365. [Google Scholar] [CrossRef]
- Vahedifard, F.; Thota, S.K.; Cao, T.D.; Samarakoon, R.A.; McCartney, J.S. Temperature-dependent model for small-strain shear modulus of unsaturated soils. J. Geotech. Geoenviron. Eng. 2020, 146, 04020136. [Google Scholar] [CrossRef]
- Thota, S.K.; Vahedifard, F. Closed-form modeling of matric suction in unsaturated soils under undrained heating. Geomech. Energy Environ. 2022, 32, 100370. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, S.; Shi, J.; Liang, F.; Zaman, M. Temperature-Dependent SWCC Model for Unsaturated Soil. Int. J. Geomech. 2024, 24, 04024071. [Google Scholar] [CrossRef]
- Hou, C.T.; Yang, X.L. 3D stability analysis of tunnel face with influence of unsaturated transient flow. Tunn. Undergr. Space Technol. 2022, 123, 104414. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46, W05515. [Google Scholar] [CrossRef]
- Vahedifard, F.; Leshchinsky, B.A.; Mortezaei, K.; Lu, N. Active earth pressures for unsaturated retaining structures. J. Geotech. Geoenviron. Eng. 2015, 141, 04015048. [Google Scholar] [CrossRef]
- Grant, S.A.; Salehzadeh, A. Calculation of temperature effects on wetting coefficients of porous solids and their capillary pressure functions. Water Resour. Res. 1996, 32, 261–270. [Google Scholar] [CrossRef]
- Shahrokhabadi, S.; Vahedifard, F.; Ghazanfari, E.; Foroutan, M. Earth pressure profiles in unsaturated soils under transient flow. Eng. Geol. 2019, 260, 105218. [Google Scholar] [CrossRef]
- Thota, S.K.; Vahedifard, F. Stability analysis of unsaturated slopes under elevated temperatures. Eng. Geol. 2021, 293, 106317. [Google Scholar] [CrossRef]
- Godt, J.W.; Şener-Kaya, B.; Lu, N.; Baum, R.L. Stability of infinite slopes under transient partially saturated seepage conditions. Water Resour. Res. 2012, 48, W05505. [Google Scholar] [CrossRef]
- Gardner, W.R. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, D. An Analytical Framework for Assessing the Unsaturated Bearing Capacity of Strip Footings under Transient Infiltration. Mathematics 2023, 11, 3480. [Google Scholar] [CrossRef]
- Hou, C.T.; Yang, X.L. Three-dimensional face stability of tunnels in unsaturated soils with nonlinear soil strength. Int. J. Geomech. 2021, 21, 06021006. [Google Scholar] [CrossRef]
- Hou, C.T.; Yang, X.L. Seismic stability of 3D tunnel face considering tensile strength cut-off. KSCE J. Civ. Eng. 2020, 24, 2232–2243. [Google Scholar] [CrossRef]
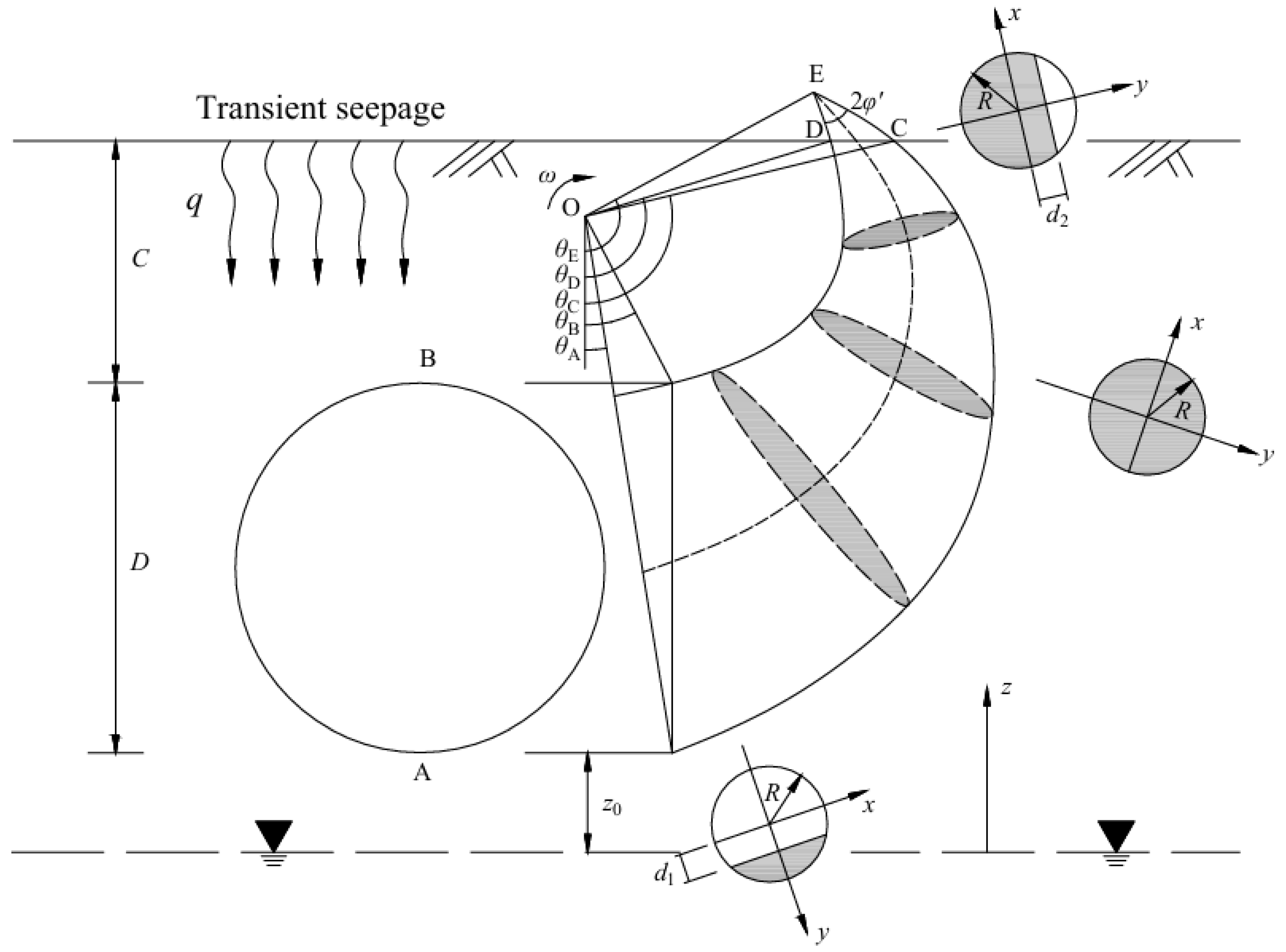

| Soil Type | c′/γD | ||||||
|---|---|---|---|---|---|---|---|
| Sand | 0.7 | 35 | 0.04 | 0.41 | 0.05 | ||
| Silt | 0.5 | 30 | 0.07 | 0.45 | 0.10 | ||
| Clay | 0.13 | 25 | 0.10 | 0.58 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Zhou, D.; Liao, H.; Zhu, J. Failure Mode of Tunnel Face Under Transient Unsaturated Seepage with Temperature Influence. Mathematics 2025, 13, 1311. https://doi.org/10.3390/math13081311
Xie Y, Zhou D, Liao H, Zhu J. Failure Mode of Tunnel Face Under Transient Unsaturated Seepage with Temperature Influence. Mathematics. 2025; 13(8):1311. https://doi.org/10.3390/math13081311
Chicago/Turabian StyleXie, Yi, De Zhou, Hong Liao, and Jianqun Zhu. 2025. "Failure Mode of Tunnel Face Under Transient Unsaturated Seepage with Temperature Influence" Mathematics 13, no. 8: 1311. https://doi.org/10.3390/math13081311
APA StyleXie, Y., Zhou, D., Liao, H., & Zhu, J. (2025). Failure Mode of Tunnel Face Under Transient Unsaturated Seepage with Temperature Influence. Mathematics, 13(8), 1311. https://doi.org/10.3390/math13081311





