Abstract
This study considers a simple automotive supply chain that includes an automobile manufacturer with demand information and financial advantages and a financially constrained automobile lessor. The manufacturer can decide whether to provide financing support to the lessor, as follows: when the manufacturer offers trade credit contracts, this is seller financing, and the lessor does not need to borrow from banks; if the manufacturer only provides wholesale price contracts, then the lessor must rely on bank financing. By constructing a signaling game, we delve into the interactive relationship between the manufacturer’s contract decisions and the lessor’s optimal financing strategies under both symmetric and asymmetric demand information scenarios. The findings show that, under symmetric information, the decisions of the manufacturer and the lessor are primarily driven by demand price sensitivity, with no significant financing conflicts between the two parties. However, under asymmetric information, their decisions are also closely related to the degree of demand fluctuation, leading to the emergence of financing conflicts. The innovation of this study lies in its incorporation of demand information asymmetry into the analytical framework governing manufacturers’ contract decisions and lessors’ financing strategies. This provides valuable theoretical insights and practical guidance for automotive supply chains operating under financial constraints.
Keywords:
supply chain management; decision analysis; bank financing; seller financing; signaling game MSC:
90B06
1. Introduction
In recent years, the Chinese car rental market has shown a steady growth trend. The market size of China’s car rental industry was about CNY 87 billion in 2020, and by 2023, this scale had reached CNY 132.5 billion [1]. The car rental industry not only meets the needs of various scenarios such as individual users, business travel, and charter tourism, but also promotes the upgrading and transformation of the entire automotive industry [2]. The problem of capital shortage poses a significant challenge to lessors. Over 98% of the operating entities in the car rental industry are private enterprises, mostly small- and medium-sized enterprises. Among them, more than 50% of lessors have financial problems and need timely internal or external financial intervention [3]. Usually, lessors facing capital constraints turn to the following two main sources of financing support: bank financing and seller financing. For example, CAR Inc. obtained a loan from China Merchants Bank for vehicle procurement and operational funding support. Meanwhile, many lessors have expanded their use of seller financing [4]. For example, car manufacturers (such as Volvo) provide seller financing to lessors (Ping An Leasing) to alleviate the pressure on them. Seller financing is widely used worldwide, especially in emerging economies and low- and middle-income countries [5]. Scholars have analyzed why firms specializing in production also offer seller financing when bank financing is available [6] and have studied whether the financially constrained party should choose bank financing or seller financing when both parties have the same understanding of demand information [7,8,9].
Lessors not only face the problem of capital shortage, but also the problem of a lack of market demand information. When new products are launched on the market, manufacturers usually have a better understanding of market demand [10]. This is because manufacturers conduct a lot of market research at the early stage of product design to ensure that the product design is highly consistent with market demand [11,12]. FAW Group, an automobile manufacturer in China, accurately grasps market demand (such as vehicle models and power types) through in-depth consumer research in the design phase, providing scientific guidance for the design of automotive products [13]. However, some lessors may fail to fully understand the diverse needs of consumers, resulting in a certain disconnect between services and market demand. For example, with the popularization of new energy vehicles, consumer demand for new energy vehicle rentals is gradually increasing, but some lessors may not have adjusted their vehicle configurations in time to meet this emerging demand [14]. This information asymmetry not only affects the collaborative efficiency of the supply chain, but may also lead to problems such as inventory accumulation and stockouts, thereby weakening the competitiveness of the entire supply chain [15]. Information in the supply chain is not only a resource, but also an important basis for corporate decision making [16]. Xiaomi, a mobile phone manufacturer, can dynamically adjust its production plan by sharing market demand data in real time, avoiding product overstock caused by market changes. Therefore, the issue of demand information asymmetry between manufacturers and lessors deserves attention.
Driven by the above discussion, we aim to investigate whether manufacturers are willing to provide financing and the financing choices of lessors when both bank financing and seller financing are available, in the context of demand information asymmetry. Ref. [17] showed that the wholesale price contracts offered by manufacturers in bank financing can signal market demand information. Refs. [18,19,20,21] found that the trade credit contracts offered by manufacturers in seller financing also have an information-signaling role. Focusing on the stage when new automotive products are first introduced to the market and manufacturers’ have an advantage in demand information, we discuss manufacturers’ use of wholesale price contracts or trade credit contracts to signal demand to lessors, and the optimal contract choice for manufacturers and the optimal financing strategy for lessors. Specifically, we investigate the following questions: (1) What are the manufacturer’s contract choice and the lessor’s optimal financing decision under symmetric demand information? (2) What are the manufacturer’s optimal contract choice and the lessor’s optimal financing decision under asymmetric demand information, given the lessor’s information inference? (3) How does information asymmetry affect the optimal choices of the manufacturer and the lessor?
To answer the above questions, we establish a signaling game model that involves an informed automobile manufacturer (she) and a financially constrained lessor (he) who purchases automotive products from the manufacturer. The manufacturer first decides whether to provide financing to the lessor and correspondingly sets wholesale price contracts or trade credit contracts. Then, the lessor makes a financing decision and determines the leasing price and order quantity, leasing the vehicles to the end market. The market’s rental demand is uncertain and price-sensitive.
The results of this study are novel and interesting. First, the existing literature mainly focuses on the contract selection and financing decisions of supply chain participants in a symmetric information environment [7,22], and generally concludes that the manufacturer has a significant advantage in choosing trade credit contracts. However, by introducing a price sensitivity function, this paper reveals that the contract choices of the manufacturer and the financing decisions of the lessor are also affected by the price sensitivity coefficient. Specifically, when the price sensitivity coefficient is low, the manufacturer tends to adopt wholesale price contracts, while the lessor prefers bank financing. Conversely, when the price sensitivity coefficient is high, the manufacturer is more willing to provide financing to the lessor (i.e., choose trade credit contracts) and the lessor is more inclined to select seller financing. Second, the existing literature rarely explores the impact of demand information asymmetry on supply chain decisions. This study finds that under the context of demand information asymmetry, the contract choices of the manufacturer are significantly affected by the degree of demand fluctuation. When demand fluctuation is below a certain threshold, the manufacturer is more inclined to use wholesale price contracts to signal demand. However, when demand fluctuation exceeds this threshold, the manufacturer is more willing to provide financing to the lessor and chooses trade credit contracts. Meanwhile, the lessor consistently prefers bank financing throughout this process. This finding extends the research boundary of [9]. Finally, this paper further examines the impact of the inference effect on supply chain decisions. The inference effect can harm the interests of the signal sender, and the impact of the inference effect on the signal receiver is significantly different. This difference affects the decision-making behavior of the manufacturer and the lessor in an environment of demand information asymmetry. This finding is consistent with the results of [23,24].
The structure of this paper is as follows: Section 2 briefly reviews the related literature. Section 3 outlines the model and basic assumptions. Section 4 introduces the contract decisions under symmetric information. Section 5 analyzes the contract design under asymmetric demand information. Section 6 explores the impact of asymmetric information on optimal contract selection. Section 7 provides a numerical example. Section 8 summarizes the study and discusses potential directions for future research.
2. Literature Review
In recent years, a considerable amount of academic research has been conducted on the intersection of supply chain operations and financing, for example, refs. [6,25,26,27,28,29,30,31,32,33,34]. This paper is related to several strands of research, including supply chain financing and signaling models under demand information asymmetry.
2.1. Supply Chain Financing
There is a substantial amount of research on supply chain financing. Most scholars have considered the financing choices of capital-constrained supply chains under symmetric demand information. Ref. [22] assumed that the retailer is capital-constrained, showing that properly priced seller financing is more favorable than bank financing, inducing the retailer to increase their order quantities and thereby enhancing the efficiency of the supply chain. Ref. [9] compared bank financing and seller financing under the newsvendor model, arguing that, within a certain production cost threshold, the manufacturer and the supply chain prefer bank financing; otherwise, they prefer seller financing. Ref. [35] explored the impact of bank financing on seller financing, using liquid equity as an analytical tool. The study showed that the stronger the liquidity of bank financing for the supplying firm, the more seller financing that the supplying firm can provide to downstream firms. Ref. [36] found that when firms need to borrow funds for capacity choice, seller financing can minimize the incentives for capital shifting and evasion. Ref. [37] conducted a theoretical analysis of seller financing under the real options framework, suggesting that seller financing can serve as a coordination mechanism. Ref. [38] found that financial interconnections between firms may lead retailers to provide trade credit financing for the entire market capacity. Ref. [39] considered a novel type of retailer-sponsored financing (RSF), where the retailer shares the loan repayment responsibilities of capital-constrained suppliers to help them obtain bank financing. On the other hand, some scholars have considered the signaling role of trade credit contracts in capital-constrained supply chains under information asymmetry. Ref. [40], considering the default risk of downstream firms, argued that trade credit contracts provide upstream suppliers with a relatively reliable means of identifying the default rates of downstream firms. Ref. [19] found that upstream suppliers can use the information transmission mechanism of trade credit contracts to reduce information asymmetry within the supply chain. Ref. [41] examined the incentive effects of trade credit contracts in a supply chain consisting of a single risk-neutral manufacturer and a single risk-averse retailer, where the retailer had private information about selling costs. Ref. [18] studied the impact of the potential signaling role of trade credit contracts on the strategic relationship between bank financing and seller financing. The existing literature mainly focuses on the financing choices of capital-constrained supply chains under symmetric demand information and the signaling incentive effects of trade credit contracts on sales costs and other information. However, research on the financing choices of capital-constrained supply chains under asymmetric demand information is relatively limited.
2.2. Signaling Model Under Demand Information Asymmetry
The second type of work examines signaling models under asymmetric demand information, which does not consider financial constraints and, thus, does not consider trade credit contracts. On the one hand, scholars have studied the downstream supply chain signaling demand to the upstream through its decision variables. For example, ref. [42] studied the use of option contracts to signal demand information. Ref. [43] studied a supply chain with one large supplier and one small supplier competing in supplying components to a manufacturer, quantifying the information value of the large supplier and the manufacturer and the competitive value of alternative procurement options under the condition that the small supplier had private information. Ref. [44] considered the signaling model of retailers with private information in both single-channel and dual-channel scenarios and found that, when channel competition was introduced, retailers preferred to signal low market demand to manufacturers to reduce competition but amplify the double marginalization effect. Ref. [45] constructed a signaling model in the context of retailers having private demand information, considering that manufacturers decide on product quality and can intrude into the supply chain. On the other hand, scholars have considered the upstream supply chain signaling demand to the downstream or consumers through its decision variables. Ref. [24] considered a second-order supply chain with one manufacturer and two retailers, studying the impact of signaling on manufacturer price distortion. Ref. [17] introduced a wholesale price contract under the condition that the manufacturer had private demand information, arguing that manufacturers can signal demand through wholesale prices, and discussed the separating and pooling equilibria of the signaling model. Ref. [46] studied the optimal decisions of members in a capital-constrained supply chain when manufacturers with private demand signals used guaranteed credit financing contracts for signaling. Similar to [46], this paper examines the signaling of demand information by the manufacturer using wholesale price contracts or trade credit contracts in an environment of asymmetric demand information and analyzes the optimal decisions of members in a capital-constrained supply chain.
Table 1 summarizes the main differences between this study and the existing literature. While prior studies have touched on supply chain financing and signaling models, the signaling mechanism of trade credit contracts under asymmetric demand information has seldom been explored. This paper investigates the signaling role of trade credit contracts and analyzes the manufacturer’s contract choices and the lessor’s optimal financing decisions under asymmetric demand information, highlighting the significant role of information advantage in capital-constrained supply chain management practice.

Table 1.
The difference between this paper and the related literature.
3. Model and Assumptions
3.1. Model
We consider an automotive supply chain where a financially constrained lessor (referred to as “he”) purchases automotive products from a well-capitalized manufacturer (referred to as “she”) and subsequently provides car leasing services to the end market. The lessor has no initial capital and needs to purchase the products before the leasing season begins [46]). The manufacturer offers the lessor both wholesale price contracts and trade credit contracts . If the lessor chooses bank financing, that is, to accept the wholesale price contracts from the manufacturer, or if the lessor opts for seller financing, that is, to accept the trade credit contracts from the manufacturer, similar to [9], the trade credit price covers both the wholesale price and the interest rate, so that the lessor does not need to pay any money for the goods when placing the order. Considering the limited liability of the lessor, the lessor determines the leasing price and order quantity based on the manufacturer’s contract and promises to repay the loan when the leasing period expires.
The unit production cost for the manufacturer is . Since automobiles are high-value products, the fixed cost of ordering is negligible compared to the value of the automobiles themselves. Therefore, we ignore the cost of the lessor. Consumers choose a long-term rental model and rent a batch of cars from the lessor at the beginning of the period, with the rental period being (where ), and the cars are returned at the end of the period. The per-unit vehicle leasing price per unit time is , which remains stable throughout the rental period .
The market random demand is a price-dependent inverse demand function, , where is the market saturation demand, satisfying , and is the price sensitivity, satisfying . is a random variable used to reflect randomness. Similar to the prior literature [46], we consider that the random demand distribution is one of two possible types, and the probability of high () is and that of low () is . The manufacturer knows the exact demand information, but the retailer only knows the prior probability distribution (). The demand is evenly distributed between 0 and , where . The distribution function is , which satisfies the first-order stochastic dominance condition. A high-value signal implies a random larger demand, for any result , and has a higher probability of receiving at least than , hence , where .
To facilitate calculations, the order quantity is transformed into , where is the inventory factor. We need to solve for , which requires solving for first. Market demand is uncertain, and if the lessor orders too many vehicles, it will lead to a vehicle inventory surplus and increased costs. Therefore, it is necessary to match market demand to ensure that all vehicles are rented out to maximize revenue. Here, we use the effective number of vehicles rented out per unit time to represent the number of vehicles that can bring in rental income. First, when the market random demand is greater than or equal to the order quantity , all vehicles are rented out. When the market random demand is less than the order quantity , only some of the vehicles are rented out. Therefore, the effective number of vehicles rented out per unit time can be expressed as follows: .
3.2. Assumptions
Assumption 1.
The bank, the manufacturer, and the lessor are all risk-neutral and fully rational [22].
Assumption 2.
The banking market is perfectly competitive [46].
Assumption 3.
According to [47], the lessor can only order vehicles at the beginning of the period and sell them at the end of the period, ensuring that the vehicle configuration remains unchanged within period .
Assumption 4.
Similar to [48], a single leasing period is roughly equal to the optimal period for vehicle retention, and the contract lasts only one leasing period. If there are multiple leasing periods, a new contract needs to be signed after the end of one leasing period.
We use the superscripts and to denote symmetric information and separating equilibrium, respectively. The subscripts and represent the market demand type obtained by the manufacturer and the supplier’s belief about the market type, respectively, where , . For example, represents the price of the trade credit contract in the separating equilibrium when the manufacturer obtains the high market demand type and the lessor has a high-demand belief. Table 2 summarizes the main parameters used in the paper.

Table 2.
Notation and their explanation.
The sequence of events
(1) Prior to the leasing season, the lessor obtains the initial distribution of beliefs about the market demand .
(2) After observing the market demand, the manufacturer simultaneously offers the following two types of contracts: a wholesale price contract and a trade credit contract.
(3) The lessor updates his belief about the manufacturer’s type, decides whether to finance from the bank or the car manufacturer, and announces the corresponding order quantity. If the lessor chooses to finance from the bank, that is, to accept the wholesale price contract, while the competitive bank simultaneously announces the interest rate, the lessor borrows from the bank and pays the full amount to the manufacturer. If the lessor decides to finance from the car manufacturer, he does not need to pay anything to the manufacturer after placing the order.
(4) When the market rental demand is realized, the lessor makes the repayment.
4. Benchmark: Contract Decisions Under Symmetric Information
In the context of symmetric demand information conditions, this section examines the manufacturer’s decision to provide either wholesale price contracts in bank financing or trade credit contracts in seller financing. By comparing and analyzing these two scenarios, we derive the manufacturer’s optimal contract choice under symmetric information and the corresponding financing strategies adopted by the lessor.
4.1. Wholesale Price Contract Decisions in Bank Financing
Under the condition of symmetric information, the manufacturer first determines the wholesale price contract . After observing , each bank announces the interest rate . The lessor chooses the order quantity based on the wholesale price contract. The lessor borrows from the bank and pays this amount to the manufacturer for the products. Once the market leasing demand is realized, the lessor repays the bank loan.
We will derive the equilibrium decisions of the bank market, the manufacturer, and the lessor in a backward manner. According to the previous assumptions, the bank market is competitive, and the expected profit of the bank lending to the lessor is zero, that is, the expected repayment amount of the lessor equals the cost of the bank’s loan. After the lease term expires, the lessor’s profit is , his expected repayment amount to the bank is , and the bank’s cost is . Therefore, the bank’s zero-profit function is as follows:
Under the condition of bank financing, considering the limited liability of the lessor, the profit maximization problem of the lessor is as follows:
In Equation (2), the function is equal to for and 0 otherwise. When the lessor chooses , according to the bank’s zero-profit condition, the lessor expects the corresponding interest rate . At the end of the period, the lessor receives the rental revenue , which will be used to repay the debt (including the principal and interest of the loan).
In bank financing, the manufacturer has already recovered the full payment for the products when the lessor places an order, so the manufacturer does not bear any default risk. Therefore, the profit maximization problem of the manufacturer is as follows:
We can obtain the optimal decisions of supply chain members in bank financing, as shown in Lemma 1.
Lemma 1.
In bank financing, when the manufacturer and the lessor have symmetric information, the manufacturer offers a wholesale price contract ; the lessor sets a leasing price ; and the order quantity is .
Proof of Lemma 1.
See Appendix A. □
From Lemma 1, we observe that since the market demand is visible to both parties, both rely on the true market demand to make decisions throughout the game. The profits of both are directly affected by the market demand and the expected profit increases with an increase in the market demand. The optimal wholesale price of the manufacturer and the leasing price of the lessor are independent of the parameters of the demand distribution (i.e., ). The optimal wholesale price is positively correlated with the manufacturer’s production cost . The higher the production cost, the higher the wholesale price, and vice versa. This is negatively correlated with the price sensitivity . The higher the sensitivity, the more inclined the manufacturer and lessor are to set lower prices. In addition, the longer the leasing period , the lower the leasing price.
4.2. Trade Credit Contract Decisions in Seller Financing
The manufacturer first determines the trade credit contract , and the lessor chooses the leasing price and order quantity without immediate payment. The manufacturer then delivers the goods. Once the market demand is realized, if the lessor’s revenue exceeds the manufacturer can collect the principal and interest from the lessor.
Therefore, the profit maximization problem for the lessor is as follows:
In seller financing, the profit maximization problem for the manufacturer is as follows:
The solutions are denoted as , , and . Lemma 2 below describes the optimal decision outcomes for each supply chain participant in seller financing when market demand information is symmetric.
Lemma 2.
In seller financing, when the manufacturer and the lessor have symmetric information about demand, the manufacturer offers a trade credit contract , the lessor sets a leasing price , and the order quantity is .
Proof of Lemma 2.
See Appendix A. □
Similar to Lemma 1, Lemma 2 indicates that under the symmetric information benchmark, the trade credit price set by the manufacturer is only related to the manufacturer’s production cost and price sensitivity . The leasing price set by the lessor is also negatively correlated with the rental period . Both are independent of the parameters of the demand distribution (i.e., ) and the market saturation demand . The lessor’s order quantity is positively correlated with the parameters of the demand distribution (i.e., ) and the market saturation demand .
4.3. The Optimal Contract Decisions Under Symmetric Information
Under symmetric information, both the manufacturer and the lessor are aware of the market demand and can make decisions based on the principle of maximizing their own profits. According to Lemma 1 and Lemma 2, we can easily derive Proposition 1.
Proposition 1.
Under symmetric information, when both financing forms are feasible, the optimal decisions of the manufacturer and the lessor are related to the price sensitivity , specifically as follows: (1) When , the manufacturer’s wholesale price is less than the trade credit price, i.e., ; when , the wholesale price is greater than the trade credit price, i.e., . (2) When , the lessor’s leasing price under the wholesale price contract is less than the leasing price under the trade credit contract, i.e., ; when , the leasing price under the wholesale price contract is greater than the leasing price under the trade credit contract, i.e., . (3) When , the lessor’s order quantity under the wholesale price contract is greater than the order quantity under the trade credit contract, i.e., ; when , the order quantity under the wholesale price contract is less than the order quantity under the trade credit contract, i.e., .
Proof of Proposition 1.
See Appendix A. □
Products with a low price sensitivity often have a certain degree of market stability and brand loyalty. Under symmetric information, consumers are less sensitive to leasing prices, and higher brand loyalty leads to relatively stable market demand. Since the manufacturer has to bear the risk of the lessor’s default, the trade credit price offered by the manufacturer is higher than the wholesale price. Although this increase in the trade credit price raises the lessor’s leasing price, its impact on market leasing demand and the manufacturer’s order quantity is relatively small. By offering a lower wholesale price, the manufacturer can increase the profit margin for the lessor. This encourages the lessor to either lower the leasing price to increase the leasing volume or actively promote the product without worrying about the lessor raising the leasing price to maximize profit. Therefore, in a market with a low price sensitivity, a lower wholesale price helps to expand market share.
When price sensitivity is high, consumers are very sensitive to changes in leasing prices, and the product faces intense market competition with lower brand loyalty. The manufacturer must reduce prices to maintain competitiveness. To avoid excessively low pricing that affects the manufacturer’s profit and to alleviate the lessor’s financial pressure, the manufacturer can offer flexible trade credit contracts. This encourages the lessor to order more while allowing them to maintain leasing services at a lower leasing price. In a market with a high price sensitivity, flexible trade credit pricing helps to stabilize market share.
Next, we analyze the optimal contract choice of the manufacturer and financing choice of the lessor under symmetric information about demand, leading to Proposition 2.
Proposition 2.
Under symmetric information, when both financing forms are feasible, the optimal contract choice of the manufacturer and the financing choice of the lessor are related to the price sensitivity , mainly manifested as follows: (1) When , the manufacturer prefers to offer a wholesale price contract; otherwise, the manufacturer prefers to offer a trade credit contract. (2) When , the lessor prefers bank financing; otherwise, the lessor prefers seller financing.
Proof of Proposition 2.
See Appendix A. □
Proposition 2 indicates that under symmetric information, there is no financing conflict between the manufacturer and the lessor. When the price sensitivity is high, meaning that the loyalty to the automotive product is low, seller financing is more advantageous than bank financing. Under symmetric information, when the price sensitivity is low, meaning that brand loyalty to the automotive product is high and consumers are less sensitive to leasing prices, the price of the trade credit contract offered by the manufacturer is higher than that of the wholesale price contract. This lower wholesale price encourages the lessor to order a larger quantity and set a lower leasing price, resulting in higher profits for the manufacturer. Therefore, the manufacturer prefers to offer a wholesale price contract.
When the price sensitivity is high, the leasing price will quickly affect leasing demand. The manufacturer prefers the lessor to set a lower leasing price and order a larger quantity. A trade credit contract can increase the lessor’s willingness to purchase. The lessor expands market leasing demand by lowering the leasing price, thereby earning more profit. Although the manufacturer’s unit profit margin decreases, the increased order quantity results in higher overall benefits. Therefore, the manufacturer prefers to offer a trade credit contract.
5. Contract Design Under Asymmetric Information
When the manufacturer possesses private demand information, she can signal demand information to the lessor through either wholesale price contracts or trade credit contracts. This section primarily addresses the design issues of the wholesale price contracts and trade credit contracts provided by the manufacturer in bank financing and seller financing scenarios. By comparing and analyzing these two scenarios, we derive the manufacturer’s optimal contract choices under information asymmetry and the corresponding financing strategies of the lessor. For simplicity, when the manufacturer has a higher demand, we refer to this manufacturer as an H-type manufacturer; otherwise, we call them an L-type manufacturer.
5.1. Wholesale Price Contract Design in Bank Financing
The previous section analyzed the decisions of the manufacturer and the lessor under symmetric information and found that, under symmetric information, the lessor would determine a higher order quantity for products with a high market demand. However, under asymmetric information, where market demand is the manufacturer’s private information, an L-type manufacturer might pretend to be an H-type manufacturer to obtain a higher order quantity. If the lessor perceives a higher demand forecast, his optimal order quantity will be higher. Therefore, an L-type manufacturer, aiming to maximize their expected profit, has the incentive to pretend to receive a higher market demand (i.e., mimic the H-type manufacturer) so that the lessor forms a belief about high market demand and sets a higher order quantity. Conversely, an H-type manufacturer has the incentive to separate themselves so that the lessor can infer the high-demand forecast. Thus, the H-type manufacturer must bear the signaling burden of distinguishing themselves from the L-type manufacturer.
In this case, the L-type manufacturer has the incentive to imitate the wholesale price set by the H-type manufacturer. If successful, this would lead the lessor to mistakenly believe that the market has a high demand and order the quantity corresponding to a high market demand. However, since the true market type is low demand, the demand realized under the high order quantity will be low. Due to the lack of a direct and credible channel for information exchange, and anticipating that the lessor will infer market demand from the wholesale price, the H-type manufacturer will proactively disclose the true market demand information in the wholesale price. That is, the lessor can infer the corresponding high or low market demand from the manufacturer’s separating wholesale price and make order quantity decisions to maximize his own profit. Therefore, under asymmetric demand information, the optimal problem for the H-type manufacturer is as follows:
The H-type manufacturer sets a signaling value (which may not be equal to the value under symmetric information). If the L-type manufacturer also chooses to pretend to be an H-type manufacturer, their maximum profit would be . However, if the L-type manufacturer does not disguise themselves and instead chooses the wholesale price corresponding to low demand, the lessor will respond with an order quantity corresponding to the low-demand scenario, resulting in a profit of for the manufacturer (i.e., the profit under symmetric information). When does not exceed , the L-type manufacturer has no incentive to disguise themselves and a separating equilibrium can be achieved under the signaling condition. To prove the existence of this separating equilibrium, it is also necessary to show that the H-type manufacturer has no incentive to deviate from any other non-equilibrium wholesale price contract.
Proposition 3 demonstrates the existence of a separating equilibrium in which the manufacturer uses a wholesale price contract to signal demand information and describes the wholesale price decisions of the manufacturer and the order quantity decisions of the lessor.
Proposition 3.
Under the condition of asymmetric demand information, a separating equilibrium exists in the costly signaling game where the manufacturer uses the wholesale price to signal market demand information. In this equilibrium, (1) the L-type manufacturer offers her symmetric information contract . (2) The H-type manufacturer offers a wholesale price contract , which is lower than the symmetric information counterpart , i.e., . (3) According to the wholesale price contract , the lessor’s leasing price is lower than the symmetric information counterpart , i.e., . (4) According to the wholesale price contract , the lessor’s order quantity is higher than the symmetric information counterpart , i.e., .
Proof of Proposition 3.
See Appendix A. □
Proposition 3 indicates that a separating equilibrium, in which the H-type manufacturer separates the L-type manufacturer using cost, can exist in the long term. According to Lemma 1, the wholesale prices of the L-type and H-type manufacturers are the same under symmetric information, and these prices are only related to the manufacturers’ production costs and price sensitivity . If the L-type manufacturer successfully mimics the H-type manufacturer, this will lead to an increase in order quantities and, consequently, higher profits. Therefore, the L-type manufacturer will continue to mimic the H-type manufacturer in the long term if it is profitable to do so. To prevent the L-type manufacturer from mimicking her, the H-type manufacturer will choose a wholesale price lower than that under symmetric information, thereby voluntarily reducing her unit profit margin to separate herself from the L-type manufacturer. The profit loss resulting from the downward distortion of the wholesale price is the additional cost that the H-type manufacturer pays to achieve signal information, namely, the “signaling cost”. The lessor infers a high market demand from the downwardly distorted wholesale price offered by the H-type manufacturer and, as a result, sets a lower leasing price and a higher order quantity to meet market needs.
5.2. Trade Credit Contract Design in Seller Financing
Considering that the manufacturer has private information about demand, the manufacturer signals information to the lessor by choosing an appropriate trade credit contract to maximize her total expected profit. Therefore, we analyze the signaling game under asymmetric information and examine the separating equilibrium.
In the previous analysis of the symmetric information scenario, we observed that, for any given trade credit contract, the manufacturer tends to induce the lessor to set a higher order quantity. If the lessor perceives a higher market demand, his optimal order quantity will be higher. Therefore, the L-type manufacturer has an incentive to mimic the H-type manufacturer to induce the lessor to set a higher order quantity. As a result, the H-type manufacturer must bear the burden of signaling to distinguish herself from the L-type manufacturer. To understand how a trade credit contract should signal higher demand information, we solve for the most efficient separating equilibrium, which is the profit-maximizing separating equilibrium for the H-type manufacturer. The most efficient separating equilibrium is the unique Perfect Bayesian Equilibrium (PBE) that satisfies the intuitive criterion of [49].
The separating equilibrium must satisfy the following properties. First, the L-type manufacturer should prefer to reveal her true type rather than mimicking the H-type manufacturer. This means that, in the separating equilibrium, the L-type manufacturer will adopt her preferred symmetric information strategy. Second, the H-type manufacturer should prefer to stick to her equilibrium strategy rather than deviating from it, which would save signaling costs and lead the lessor to believe that the market demand is low. To determine the most profitable separating equilibrium, the H-type manufacturer solves the following problem:
The two constraints in Equation (7) ensure that imitation is unprofitable for the L-type and H-type manufacturers, respectively. In the signaling game, only the first constraint (i.e., the non-imitation condition for demand types) is binding. To prove the existence of this separating equilibrium, we also need to show that the H-type manufacturer has no incentive to deviate to any other off-equilibrium wholesale price contract. We define , which reflects the degree of random demand fluctuation. Proposition 4 below demonstrates the existence of a separating equilibrium in seller financing, where the manufacturer has private demand information and uses a trade credit contract to signal demand, and characterizes the optimal decisions of the supply chain participants.
Proposition 4.
When and , the most efficient separating equilibrium in which the trade credit contract signals market demand information exists. In this equilibrium, (1) the L-type manufacturer offers her symmetric information contract . (2) The H-type manufacturer offers a trade credit contract , which is higher than the symmetric information counterpart , i.e., . (3) According to the wholesale price contract , the lessor’s leasing price is higher than the symmetric information counterpart , i.e., ; (4) According to the wholesale price contract , the lessor’s order quantity is lower than the symmetric information counterpart , i.e., .
Proof of Proposition 4.
See Appendix A. □
Proposition 4 indicates that the manufacturer’s trade credit contract decisions are related to the price sensitivity and the degree of random demand fluctuation . When or , substituting and into and , respectively, we have . This shows that the L-type manufacturer mimics the trade credit price of the H-type manufacturer to induce the lessor to increase their order quantity, which reduces her profit. Driven by profit motives, the L-type manufacturer will signal true and reliable information. Therefore, the H-type manufacturer does not need to pay additional costs to achieve the separating equilibrium, realizing “costless separation”.
Similarly, when and , indicating a low price sensitivity and minor fluctuations in market stochastic demand, if the L-type manufacturer mimics the H-type manufacturer in an attempt to increase the lessor’s order quantity, the L-type manufacturer will gain higher profits. As a rational decision maker, the L-type manufacturer will inevitably distort the information. This suggests that, if the optimal decision for the H-type manufacturer is to set , then the L-type manufacturer will definitely choose the same trade credit price to seek higher profits. To enable the lessor to accurately understand the true state of market demand, the H-type manufacturer will select a trade credit price higher than that of the H-type manufacturer under symmetric information, achieving a separating equilibrium. The profit loss resulting from the upward distortion of the trade credit price is the additional cost paid by the manufacturer to realize information sharing, namely, the “signaling cost”.
5.3. The Optimal Contract Decisions Under Asymmetric Information
When the manufacturer possesses private demand information, she signals demand information to the lessor through wholesale price contracts and trade credit contracts, which causes a certain loss in her profit and also distorts the lessor’s decision to some extent. Therefore, it is very necessary to analyze the optimal decisions of supply chain members under asymmetric information. By analyzing the decision variables of the manufacturer and the lessor under the two financing strategies, we obtain Proposition 5.
Proposition 5.
Under asymmetric demand information, when both financing forms are feasible, the optimal decisions of the manufacturer and the lessor are different, mainly manifested as follows: (1) When and , the manufacturer’s wholesale price is less than the trade credit price , i.e., ; otherwise, the wholesale price is greater than the trade credit price , i.e., . (2) The lessor’s leasing price decision in bank financing is lower than the leasing price decision in seller financing , i.e., . (3) The lessor’s ordering decision in bank financing is higher than the ordering decision in seller financing , i.e., .
Proof of Proposition 5.
See Appendix A. □
According to Proposition 3, it is known that the costly separating equilibrium, in which the manufacturer signals demand information through a wholesale price contract, has long existed. Proposition 4 indicates that a costly separating equilibrium exists when and . However, when or , a costless separation occurs. In Propositions 1 and 2, we have already analyzed the impact of price sensitivity on the decisions of the manufacturer and the lessor. This section mainly focuses on the impact of the degree of random demand fluctuation on their decisions. It was previously analyzed that, under symmetric information in a low price-sensitive market, the wholesale price is lower than the trade credit price. When the degree of random demand fluctuation is small, the H-type manufacturer distorts the wholesale price downward and the trade credit price upward to separate herself from the L-type manufacturer. This results in further widening of the gap between the trade credit price and the wholesale price compared to the symmetric information scenario. Consequently, the differences in leasing prices and order quantities are also enlarged compared to the symmetric information case.
When , the degree of demand fluctuation increases and the H-type manufacturer continues to distort the wholesale price downward to separate herself from the L-type manufacturer, incurring a higher signaling cost. However, under a trade credit contract, costless separation can be achieved. The H-type manufacturer adopts the trade credit price under symmetric information, which is lower than the separating wholesale price level.
Based on the different decision variables of the manufacturer and the lessor under asymmetric demand information, we derive the optimal contract choice for the manufacturer and the optimal financing decision for the lessor under asymmetric information. Thus, Proposition 6 can be obtained.
Proposition 6.
Under asymmetric information, the decisions of the supply chain members are as follows: (1) When and , if the manufacturer has private demand information, she prefers to offer a wholesale price contract to signal demand information because the manufacturer’s profit under the wholesale price contract is greater than the profit under the trade credit contract , i.e., ; otherwise, the manufacturer prefers to offer a trade credit contract. (2) The lessor is more inclined to choose bank financing under asymmetric information, because the lessor’s profit in bank financing is greater than the profit in seller financing , i.e., .
Proof of Proposition 6.
See Appendix A. □
Proposition 6 indicates that under asymmetric information, the optimal contract choice of the manufacturer and the optimal financing decision of the lessor are influenced not only by price sensitivity , but also by the degree of random demand fluctuation . When the degree of market demand fluctuation is low, the gap between the trade credit price and the wholesale price for the H-type manufacturer under asymmetric information is further widened compared to the symmetric information scenario. Consequently, the differences in leasing prices and order quantities are also enlarged compared to the symmetric information case. Therefore, when the degree of demand fluctuation is low, the wholesale price contract remains a better choice for the manufacturer. Generally speaking, the greater the degree of demand fluctuation, the higher the risk for the manufacturer when using trade credit. However, since the manufacturer does not need to pay signaling costs when using a trade credit contract to signal demand information under high fluctuation, it becomes more advantageous than a wholesale price contract. The trade credit price serves as an incentive mechanism to ensure the lessor’s order quantity and cash flow when the degree of demand fluctuation is high. When fluctuation is low, the necessity of this incentive mechanism diminishes, making the wholesale price contract more favorable than the trade credit contract.
For the lessor, when the degree of market demand fluctuation is low, the wholesale price is lower than the trade credit price, resulting in lower purchasing costs and inducing higher order quantities. In this case, financing from the bank is more profitable. When the degree of demand fluctuation is high, although the trade credit price is lower and the lessor’s per-unit purchasing cost is reduced, the induced order quantity is far less than that under the wholesale price contract. Therefore, financing from the bank remains the better choice.
6. The Impact of Information Asymmetry on Optimal Contract Decisions
According to Proposition 2, we know that when information is symmetric, if the price sensitivity is low, the manufacturer tends not to provide financing, only offering a wholesale price contract, and the lessor is also more willing to seek bank financing; when the price sensitivity is high, the manufacturer tends to provide seller financing, offering a trade credit contract, and the lessor is also more willing to choose seller financing. According to Proposition 4, we know that the lessor is more inclined to choose bank financing under asymmetric information, while the manufacturer tends not to provide financing when demand fluctuation is small, that is, offering a wholesale price contract; when demand fluctuation is large, the manufacturer is more willing to provide financing to the lessor, that is, offering a trade credit contract. We notice that under asymmetric demand information, the manufacturer’s contract choice and the lessor’s financing choice change, and this change is mainly due to the inference effect.
In signaling games, scholars have studied the inference effect under high-cost separation. The inference effect stems from the information asymmetry between the signal sender and the information receiver. Ref. [23] pointed out that the inference effect refers to the pricing distortion by the signal sender, and the signal receiver infers the signal based on the distorted pricing. We considered bank financing and seller financing in symmetric and asymmetric demand information scenarios to determine the impact of the inference effect on supply chain members, obtaining Proposition 7.
Proposition 7.
The impact of the inference effect on supply chain members in bank financing is as follows: (1) The inference effect makes the manufacture worse off in both bank financing and seller financing. (2) The inference effect leaves the lessor better off in bank financing and worse off in seller financing.
Proof of Proposition 7.
See Appendix A. □
Proposition 7 shows the impact of asymmetric information on the manufacturer and the lessor. The inference effect always harms the interests of the signal sender. According to Proposition 1, when the demand information is symmetric, the wholesale price set by the manufacturer is lower than the trade credit price. When the fluctuation of market demand is small, the high-demand manufacturer achieves separation by distorting the wholesale price downward and the trade credit price upward. This upward distortion of the trade credit price further increases the trade credit price under asymmetric information, leading to a sharp drop in the lessor’s order quantity. Therefore, the manufacturer pays a greater signaling cost under the trade credit contract. When the demand information is symmetric, the wholesale price set by the manufacturer is higher than the trade credit price. When the fluctuation of demand is large, if the manufacturer uses a wholesale price contract, they still need to pay a signaling cost to achieve separation. However, if they use a trade credit contract to signal demand, they can achieve cost-free separation. At this time, the manufacturer’s trade credit price is equal to the trade credit price under symmetric information. Correspondingly, the lessor’s leasing price and order quantity are also at the symmetric information level. Naturally, the trade credit contract is a better choice. In bank financing, the downward distortion of the manufacturer’s wholesale price makes the uninformed lessor infer a high-demand state of the market, thereby setting a lower leasing price and a higher order quantity, thus benefiting from it. In seller financing, the upward distortion of the trade credit price leads to a decrease in the lessor’s order quantity, so the inference effect is disadvantageous to the lessor. As a rational lessor, they are naturally more inclined to choose bank financing.
7. An Illustrating Example
Ref. [50] analyzed the development status of the global car rental market in 2024, where the scale of China’s car rental market was USD 24 billion, with a projected market saturation level of USD 80 billion and an average rental duration of 80 days. We appropriately modify the data to fit the conditions of our model, and we assume that the market demand , the rental period , and the market saturation level . Then, we adopt the data from [51] and set the unit car production cost to . To facilitate comparison with the decisions of manufacturers and lessors under asymmetric information, we set when studying the decisions of the manufacturer and lessor under symmetric information.
7.1. Equilibrium Decisions of Supply Chain Members
As shown in Figure 1a, in a market environment with symmetric demand information, the critical point in the manufacturer’s optimal decision regarding the relationship between the wholesale price and the trade credit price is at the price sensitivity () index of 4, as follows: when , the manufacturer offers a lower wholesale price; whereas when , trade credit contracts with a lower price level are provided. The lessor’s decision also exhibits clear price sensitivity under this symmetric information scenario, as shown in Figure 1b, as follows: when , the lessee’s order quantity under bank financing is higher than that under seller financing; conversely, when , the lessor will choose a higher order quantity under seller financing.
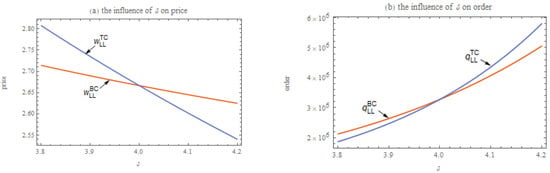
Figure 1.
The influence of on manufacturer’s price and lessor’s order under symmetric information (, , , and ).
However, in a market environment with asymmetric demand information, in order to effectively signal demand, the manufacturer needs to distort pricing strategies to transmit demand information to the market, which leads to a significant shift in their pricing decisions, as shown in Figure 2a. Specifically, when the degree of market demand fluctuation is below a certain threshold, the manufacturer distorts the trade credit price upward and the wholesale price downward to achieve separation. Conversely, when the degree of market demand fluctuation exceeds this critical value, the manufacturer adopts the trade credit price under symmetric demand information to achieve costless separation. Under this asymmetric information market environment, the lessor infers the market demand situation by observing the manufacturer’s price signals and then formulates their ordering decision strategy. As shown in Figure 2b, in bank financing, the lessor always maintains a higher order quantity decision in seller financing.
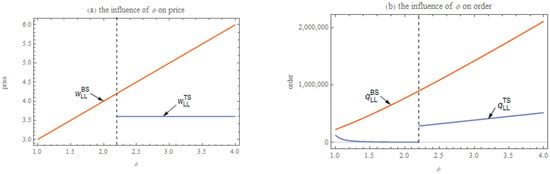
Figure 2.
The influence of on manufacturer’s price and lessor’s order under asymmetric information (, , , , and ).
7.2. Equilibrium Profits of Supply Chain Members
Figure 3a,b reveal that under symmetric demand information, the profits of both the manufacturer and the lessor are significantly and directly affected by price sensitivity. Specifically, when , the profit level is higher when the manufacturer offers wholesale price contracts and the lessor chooses bank financing. Conversely, when , the profit advantage is more pronounced when the manufacturer offers trade credit contracts and the lessor opts for seller financing. In a market environment with symmetric information, the financing choices of the manufacturer and the lessor tend to align, indicating that there is no financing conflict between the two. This conclusion is consistent with the analysis in Proposition 2.
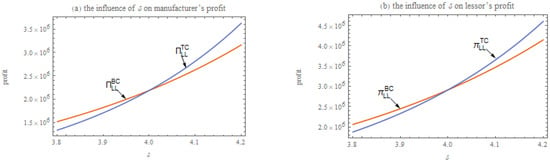
Figure 3.
The influence of on manufacturer’s and lessor’s profit under symmetric information (, , , and ).
Furthermore, we examined the profit performance of the manufacturer and the lessor under asymmetric demand information. In particular, Figure 4a shows that the manufacturer’s profit is not only affected by price sensitivity, but also significantly influenced by the degree of random demand fluctuation. By setting , we found the following patterns in the manufacturer’s profit decisions: when the degree of market demand fluctuation is low, the manufacturer achieves higher profits by offering wholesale price contracts to signal information. However, when the degree of market demand fluctuation is high, the manufacturer can realize a higher profit level by using trade credit contracts as a signaling tool. In addition, the analysis in Figure 4b indicates that, under asymmetric demand information, regardless of how market demand fluctuates, the lessor will always prefer bank financing. This leads to a financing conflict between the manufacturer and the lessor. This relationship is consistent with Proposition 6.
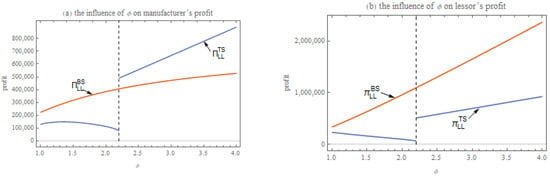
Figure 4.
The influence of on manufacturer’s and lessor’s profit under asymmetric information (, , , , and ).
8. Conclusions
Lessors face financial constraints and the challenge of information asymmetry. Therefore, we study a supply chain consisting of an automotive manufacturer and a financially constrained lessor, considering the manufacturer’s optimal decisions and the lessor’s financing issues under asymmetric demand information. The manufacturer, who possesses private information about demand, can signal demand through wholesale price contracts and trade credit contracts. To determine the possible financing choices of the lessor, we investigate bank financing and seller financing.
Our contributions are as follows. First, our research examines the financing decisions of capital-constrained supply chains under demand information asymmetry, thereby complementing the existing literature. Second, by designing wholesale price contracts and trade credit contracts to signal demand information, we call on manufacturers to pay attention to the signaling role of contracts and provide practical guidance for manufacturers to decide whether and when to finance the lessor based on market demand conditions. Third, we reveal the factors affecting the lessor’s financing strategy, providing an empirical basis for the choice of financing methods made by the lessor. Finally, we find that, under certain conditions, there is a conflict of choice preferences between the manufacturer and the lessor, which provides a direction for supply chain coordination. Specifically, the lessor is more willing to choose bank financing under asymmetric information, while the manufacturer prefers not to provide financing to the lessor when demand fluctuations are small, that is, to choose a wholesale price contract, in which case there is no financing conflict between them. However, when demand fluctuations are large, the manufacturer is more willing to provide financing to the lessor, that is, to choose a trade credit contract. In this case, there is a financing conflict between the manufacturer and the lessor. The manufacturer can take corresponding measures to guide this situation, such as offering the lessor certain interest subsidies to encourage him to choose seller financing.
The main findings of this study are summarized as follows:
(1) Previous scholars have found that, under symmetric demand information, manufacturers have a natural advantage in using trade credit contracts [22], and the financially constrained party prefers bank financing within a certain production cost threshold [9]. Based on the demand price sensitivity function we set up, we find that, under symmetric demand information, the manufacturer’s contract choice and the lessor’s financing strategy are also affected by price sensitivity . When the price sensitivity is below a certain threshold, the manufacturer is more willing to offer a wholesale price contract and the lessor is more inclined to choose bank financing. In contrast, when is above a certain threshold, the manufacturer is more likely to provide financing to the lessor, that is, to choose trade credit contracts, and the lessor is also more willing to opt for seller financing.
(2) Ref. [17] studied the manufacturer’s downward distortion of the wholesale price to signal demand. This paper reaches the same conclusion and extends the case of trade credit contracts signaling demand, comparing the two. We find that low-demand manufacturers achieve separation from high-demand manufacturers by upwardly distorting the trade credit price. The upward distortion of pricing deviates from the manufacturer’s optimal level, incurring signaling costs. Under asymmetric demand information, the manufacturer’s contract choice is influenced by the degree of demand fluctuation . When is below a certain threshold, the manufacturer is more inclined to use a wholesale price contract to signal demand information. However, when is above a certain threshold, the manufacturer prefers to provide financing to the lessor, choosing trade credit contracts. In contrast, the lessor always has a stronger preference for bank financing.
(3) Similar to [23,24], the inference effect under asymmetric information always harms the interests of the signal sender. When the degree of market demand fluctuation is small, the manufacturer achieves separation by distorting the contract price, and the manufacturer incurs a higher signaling cost under a trade credit contract. When the degree of demand fluctuation is large, the manufacturer can achieve costless separation by using a trade credit contract to signal demand. The lessee benefits from the inference under the wholesale price contract but is harmed by the inference under the trade credit contract.
Finally, we will discuss some possible extensions of the current model. First, in our model, we assume that a single manufacturer sells products to a single lessor. However, in reality, it is more common for multiple manufacturers to sell products competitively to a single lessor, or for a single manufacturer to sell products competitively to multiple lessors. This is a direction for future research. Another interesting direction is whether the lessor’s choice between the two financing strategies would differ if the lessor held private information. Finally, we assume that both the manufacturer and the lessor are risk-neutral. The implications of relaxing this risk neutrality of one or both members in the channel can be tested in future research.
Author Contributions
Conceptualization, S.X., and J.X.; methodology, S.X.; software, J.X.; validation, S.X., and J.X.; formal analysis, J.X.; investigation, S.X.; resources, J.X.; data curation, S.X.; writing—original draft preparation, S.X.; writing—review and editing, S.X., and J.X.; visualization, S.X.; supervision, J.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 72071074 and the Hunan Province Natural Science Foundation of China, grant number 2022JJ30110.
Data Availability Statement
The original contributions presented in this study are included in the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Proof of Lemma 1.
The first-order derivative of the lessor’s profit function with respect to the leasing price yields the following: .
The second-order derivative of the lessor’s profit function with respect to the leasing price yields the following:
It is easy to obtain that the first-order derivative is greater than 0 and the second-order derivative is less than 0. Setting the first-order derivative equal to 0, we find the following:
The first-order derivative of the lessor’s profit function with respect to yields the following:
The second-order derivative yields the following: .
It is easy to obtain that the first-order derivative is greater than 0 and the second-order derivative is less than 0, so we obtain the following: .
By solving the equations for and simultaneously, we obtain the following: ; .
Substituting this into the manufacturer’s profit function and taking the first-order derivative of the manufacturer’s profit function with respect to yields the following:
The second-order derivative yields the following:
It is easy to obtain that the first-order derivative is greater than 0 and the second-order derivative is less than 0, so we obtain the following: .
Then, can be calculated as follows: .
The lessor’s order quantity is as follows: .
The manufacturer’s profit is as follows: .
The lessor’s profit is as follows: . □
Proof of Lemma 2.
The first-order derivative of the lessor’s profit function with respect to the leasing price is as follows: .
The second-order derivative is as follows:
It is easy to see that the first-order derivative is greater than 0 and the second-order derivative is less than 0. Setting the first-order derivative as equal to 0, we obtain the following:
The first-order derivative of the lessor’s profit function with respect to the inventory factor is as follows: .
The second-order derivative is as follows: .
It is easy to see that the first-order derivative is greater than 0 and the second-order derivative is less than 0. Therefore, we obtain the following: .
By combining the equations for and , we obtain the following:
Substituting this into the manufacturer’s profit function and taking the first-order derivative of the manufacturer’s profit function with respect to the trade credit price, we obtain the following: .
The second-order derivative is as follows:
It is easy to see that the first-order derivative is greater than 0 within the range , while the second-order derivative is less than 0 within this range. Therefore, we obtain the following: .
Thus, we can calculate the following:
The manufacturer’s profit is as follows: .
The lessor’s profit is as follows: . □
Proof of Proposition 1.
Part (1). Under symmetric information, the price of the manufacturer with a high demand in wholesale price contract is and that in trade credit contract is . When , we have the following: .
Part (2). Under symmetric information, the leasing price of the lessor with a high demand in wholesale price contract is and that in trade credit contract is . When , we have the following: .
Part (3). Under symmetric information, the order quantity of the lessor with a high demand in wholesale price contract is and that in trade credit contract is . When , we have the following: . □
Proof of Proposition 2.
Part (1). Under symmetric information, the profit of the manufacturer with a high demand in wholesale price contract is and that in trade credit contract is . When , we have the following: .
Part (2). Under symmetric information, the profit of the lessor with a high demand in wholesale price contract is and that in trade credit contract is . When , we have the following: . □
Proof of Proposition 3.
Construct the Lagrangian function as follows:
The KKT conditions are as follows: ; ; ; , where and are the Lagrange multipliers.
When , then , we can obtain , and when substituting it into , we find it is always less than or equal to 0. When , then , we obtain and , and when substituting these solutions into the second constraint to check if they satisfy, only satisfies, so is the optimal solution.
From this, we can obtain the following: , , .
The manufacturer’s profit is as follows: .
The lessor’s profit is as follows: . □
Proof of Proposition 4.
Construct the Lagrangian function as follows:
The KKT conditions are as follows: , , , , where and .
When , then . We can obtain and substitute it into the constraint . Setting , we obtain the following range: or . When , and we obtain the solutions and . Substituting these two solutions into the second constraint, only satisfies it, so .
Thus, we have the following:
The manufacturer’s profit is as follows:
□
Proof of Proposition 5.
Part (1). Under asymmetric information, when and , the price of the manufacturer with a high demand in wholesale price contract is and that in trade credit contract is , so we have the following: .
Part (2). Under asymmetric information, the leasing price of the lessor with a high demand in wholesale price contract is and that in trade credit contract is , so we have the following: .
Part (3). Under symmetric information, the order quantity of the lessor with a high demand in wholesale price contract is and that in trade credit contract is , so we have the following: . □
Proof of Proposition 6.
Part (1). Under asymmetric information, when and , the profit of the manufacturer with a high demand in wholesale price contract is and that in trade credit contract is , so we have the following: .
Part (2). Under asymmetric information, the profit of the lessor with a high demand in wholesale price contract is and that in trade credit contract is , so we have the following: . □
Proof of Proposition 7.
Part (1). According to the wholesale price of the separate equilibrium, it is easy to obtain the profit of the high-demand manufacturer under the separate equilibrium. Compared to the profit under symmetric information, we have . According to the trade credit price of the separating equilibrium, it is easy to obtain the profit of the high-demand manufacturer under the separate equilibrium. Compared to the profit under symmetric information, we have .
Part (2). According to the order quantity under the separation equilibrium, we have the retailer’s profit under the separation equilibrium, and comparing it with the profit under the symmetric information, it is easy to obtain . According to the order quantity under the separation equilibrium, we have the retailer’s profit under the separation equilibrium, and comparing it with the profit under the symmetric information, it is easy to obtain . □
References
- Institute, CIRN. Annual Research and Consultation Report of Panorama Survey and Investment Strategy on China Industry 2023. 2024. Available online: https://www.chinairn.com/report/20240219/110838267.html?id=1902501&name=WuAoYan (accessed on 1 March 2025).
- Yoshizawa, D.; Nakamoto, Y.; Kagawa, S. Reduction of life-cycle CO2 emissions by expanding car-sharing services: A case study on Japan. J. Environ. Manag. 2023, 344, 118637. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Duan, Y.; Jia, S. An optimization Model Combining Operator-Based Relocation With User-Based Relocation for Electric Carsharing Systems. Transp. Res. Rec. 2022, 2676, 827–846. [Google Scholar] [CrossRef]
- Khotanlou, M.; Kazemiolum, M.; Ziyaei, F. The Impact of Corporate Reputation on Financial Leverage and Trade Credit. Financ. Manag. Strategy 2025, 13, 99–116. [Google Scholar]
- Wu, D.; Zhang, B.; Baron, O. A trade credit model with asymmetric competing retailers. Prod. Oper. Manag. 2019, 28, 206–231. [Google Scholar] [CrossRef]
- Chod, J. Inventory, risk shifting, and trade credit. Manag. Sci. 2017, 63, 3207–3225. [Google Scholar] [CrossRef]
- Deng, S.; Gu, C.; Cai, G.G.; Li, Y. Financing Multiple Heterogeneous Suppliers in Assembly Systems: Buyer Finance vs. Bank Finance. Manuf. Serv. Oper. Manag. 2018, 20, 53–69. [Google Scholar] [CrossRef]
- Fabbri, D.; Klapper, L.F. Bargaining power and trade credit. J. Corp. Financ. 2016, 41, 66–80. [Google Scholar] [CrossRef]
- Jing, B.; Chen, X.; Cai, G. Equilibrium financing in a distribution channel with capital constraint. Prod. Oper. Manag. 2012, 21, 1090–1101. [Google Scholar] [CrossRef]
- Bao, W.; Ni, J.; Singh, S. Informal lending in emerging markets. Mark. Sci. 2018, 37, 123–137. [Google Scholar] [CrossRef]
- Guan, X.; Chen, Y.J. The interplay between information acquisition and quality disclosure. Prod. Oper. Manag. 2017, 26, 389–408. [Google Scholar] [CrossRef]
- Guo, L.; Iyer, G. Information acquisition and sharing in a vertical relationship. Mark. Sci. 2010, 29, 483–506. [Google Scholar] [CrossRef]
- Caldieraro, F.; Zhang, J.Z.; Cunha Jr, M.; Shulman, J.D. Strategic information transmission in peer-to-peer lending markets. J. Mark. 2018, 82, 42–63. [Google Scholar] [CrossRef]
- Yao, Z.; Gendreau, M.; Li, M.; Ran, L.; Wang, Z. Service operations of electric vehicle carsharing systems from the perspectives of supply and demand: A literature review. Transp. Res. Part C Emerg. Technol. 2022, 140, 103702. [Google Scholar] [CrossRef]
- Ersahin, N.; Giannetti, M.; Huang, R. Trade credit and the stability of supply chains. J. Financ. Econ. 2024, 155, 103830. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, J.; Zhu, G. Incentive of retailer information sharing on manufacturer volume flexibility choice. Omega 2021, 100, 102210. [Google Scholar] [CrossRef]
- Jiang, B.; Tian, L.; Xu, Y.; Zhang, F. To share or not to share: Demand forecast sharing in a distribution channel. Mark. Sci. 2016, 35, 800–809. [Google Scholar] [CrossRef]
- Arca, P.; Atzeni, G.; Deidda, L. The signaling role of trade credit: Evidence from a counterfactual analysis. J. Corp. Financ. 2023, 80, 102414. [Google Scholar] [CrossRef]
- Biais, B.; Gollier, C. Trade credit and credit rationing. Rev. Financ. Stud. 1997, 10, 903–937. [Google Scholar] [CrossRef]
- Burkart, M.; Ellingsen, T. In-kind finance: A theory of trade credit. Am. Econ. Rev. 2004, 94, 569–590. [Google Scholar] [CrossRef]
- Lee, Y.W.; Stowe, J.D. Product risk, asymmetric information, and trade credit. J. Financ. Quant. Anal. 1993, 28, 285–300. [Google Scholar] [CrossRef]
- Kouvelis, P.; Zhao, W. Financing the newsvendor: Supplier vs. bank, and the structure of optimal trade credit contracts. Oper. Res. 2012, 60, 566–580. [Google Scholar] [CrossRef]
- Cao, E.; Chen, G. Information sharing motivated by production cost reduction in a supply chain with downstream competition. Nav. Res. Logist. 2021, 68, 898–907. [Google Scholar] [CrossRef]
- Gal-Or, E.; Geylani, T.; Dukes, A.J. Information sharing in a channel with partially informed retailers. Mark. Sci. 2008, 27, 642–658. [Google Scholar] [CrossRef]
- Bansal, A.; Panwar, A.; Unhelkar, B.; Mittal, M. Optimizing Inventory for Imperfect and Gradually Deteriorating Items Under Multi-Level Trade Credit in a Sustainable Supply Chain. Mathematics 2025, 13, 752. [Google Scholar] [CrossRef]
- Barrot, J.N. Trade credit and industry dynamics: Evidence from trucking firms. J. Financ. 2016, 71, 1975–2016. [Google Scholar] [CrossRef]
- Goyal, S.K. Economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 1985, 36, 335–338. [Google Scholar] [CrossRef]
- Ho, C.-H.; Ouyang, L.-Y.; Su, C.-H. Optimal pricing, shipment and payment policy for an integrated supplier–buyer inventory model with two-part trade credit. Eur. J. Oper. Res. 2008, 187, 496–510. [Google Scholar] [CrossRef]
- Jacobson, T.; Von Schedvin, E. Trade credit and the propagation of corporate failure: An empirical analysis. Econometrica 2015, 83, 1315–1371. [Google Scholar] [CrossRef]
- Kong, G.; Rajagopalan, S.; Zhang, H. Revenue sharing and information leakage in a supply chain. Manag. Sci. 2013, 59, 556–572. [Google Scholar] [CrossRef]
- Kouvelis, P.; Zhao, W. Supply chain contract design under financial constraints and bankruptcy costs. Manag. Sci. 2016, 62, 2341–2357. [Google Scholar] [CrossRef]
- Moorthy, S.; Srinivasan, K. Signaling quality with a money-back guarantee: The role of transaction costs. Mark. Sci. 1995, 14, 442–466. [Google Scholar] [CrossRef]
- Protopappa-Sieke, M.; Seifert, R.W. Interrelating operational and financial performance measurements in inventory control. Eur. J. Oper. Res. 2010, 204, 439–448. [Google Scholar] [CrossRef]
- Yang, S.A.; Birge, J.R. Trade credit, risk sharing, and inventory financing portfolios. Manag. Sci. 2018, 64, 3667–3689. [Google Scholar] [CrossRef]
- Shenoy, J.; Williams, R. Trade credit and the joint effects of supplier and customer financial characteristics. J. Financ. Intermediation 2017, 29, 68–80. [Google Scholar] [CrossRef]
- de Véricourt, F.; Gromb, D. Financing capacity with stealing and shirking. Manag. Sci. 2019, 65, 5128–5141. [Google Scholar] [CrossRef]
- Silaghi, F.; Moraux, F. Trade credit contracts: Design and regulation. Eur. J. Oper. Res. 2022, 296, 980–992. [Google Scholar] [CrossRef]
- Avinadav, T.; Shamir, N. Partial vertical ownership, capacity investment, and information exchange in a supply chain. Manag. Sci. 2023, 69, 6038–6056. [Google Scholar] [CrossRef]
- Zha, Y.; Chen, K.; Dong, L.; Yu, Y. Financing Supplier Through Retailer’s Credit. Prod. Oper. Manag. 2024, 33, 721–736. [Google Scholar] [CrossRef]
- Smith, J.K. Trade credit and informational asymmetry. J. Financ. 1987, 42, 863–872. [Google Scholar] [CrossRef]
- Wang, Z.-H.; Qi, L.; Zhang, Y.; Liu, Z. A trade-credit-based incentive mechanism for a risk-averse retailer with private information. Comput. Ind. Eng. 2021, 154, 107101. [Google Scholar] [CrossRef]
- Cachon, G.P.; Fisher, M. Supply chain inventory management and the value of shared information. Manag. Sci. 2000, 46, 1032–1048. [Google Scholar] [CrossRef]
- Özer, Ö.; Raz, G. Supply chain sourcing under asymmetric information. Prod. Oper. Manag. 2011, 20, 92–115. [Google Scholar] [CrossRef]
- Li, Z.; Gilbert, S.M.; Lai, G. Supplier encroachment under asymmetric information. Manag. Sci. 2014, 60, 449–462. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, J.; Zaccour, G. Market targeting and information sharing with social influences in a luxury supply chain. Transp. Res. Part E Logist. Transp. Rev. 2020, 133, 101822. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Q. The informational role of guarantee contracts. Eur. J. Oper. Res. 2022, 301, 191–202. [Google Scholar] [CrossRef]
- Liang, L.; Tian, L.; Xie, J.; Xu, J.; Zhang, W. Optimal pricing model of car-sharing: Market pricing or platform pricing. Ind. Manag. Data Syst. 2021, 121, 594–612. [Google Scholar] [CrossRef]
- Lagadic, M.; Verloes, A.; Louvet, N. Can carsharing services be profitable? A critical review of established and developing business models. Transp. Policy 2019, 77, 68–78. [Google Scholar] [CrossRef]
- Cho, I.-K.; Kreps, D.M. Signaling games and stable equilibria. Q. J. Econ. 1987, 102, 179–221. [Google Scholar] [CrossRef]
- Research, G.V. Car Rental Market Size, Share & Trends Analysis Report by Vehicle (Luxury Cars, Executive Cars), By Application (Local Usage, Airport Transport), By Booking Mode, By Region, and Segment Forecasts, 2025–2030. 2024. Available online: https://www.grandviewresearch.com/industry-analysis/car-rental-market (accessed on 1 March 2025).
- He, L.; Hu, Z.; Zhang, M. Robust repositioning for vehicle sharing. Manuf. Serv. Oper. Manag. 2020, 22, 241–256. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).