Truncated-Exponential-Based General-Appell Polynomials
Abstract
1. Introduction
2. Some Properties of Truncated-Exponential-Based General-Appell Polynomials
3. Special Cases of Truncated-Exponential-Based General-Appell Polynomials
3.1. Truncated Exponential Based Hermite Type Polynomials
3.2. Truncated-Exponential-Based Laguerre–Frobenius Euler Polynomials
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- Dattoli, G.; Cesarano, C.; Sacchetti, D. A note on truncated polynomials. Appl. Math. Comput. 2003, 134, 595–605. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Araci, S.; Khan, W.A.; Acikgoz, M. A note on the truncated-exponential based Apostol-type polynomials. Symmetry 2019, 11, 538. [Google Scholar] [CrossRef]
- Duran, U.; Açıkgöz, M. Truncated Fubini polynomials. Mathematics 2019, 7, 431. [Google Scholar] [CrossRef]
- Duran, U.; Açıkgöz, M. On degenerate truncated special polynomials. Mathematics 2020, 8, 144. [Google Scholar] [CrossRef]
- Kumam, W.; Srivastava, H.M.; Wani, S.A.; Araci, S.; Kumam, P. Truncated-exponential-based Frobenius–Euler polynomials. Adv. Differ. Equ. 2019, 2019, 530. [Google Scholar] [CrossRef]
- Raza, N.; Fadel, M.; Cesarano, C. A note on q-truncated exponential polynomials. Carpathian Math. Publ. 2024, 16, 128–147. [Google Scholar] [CrossRef]
- Costabile, F.A.; Khan, S.; Ali, H. A study of the q-truncated exponential–Appell polynomials. Mathematics 2024, 12, 3862. [Google Scholar] [CrossRef]
- Andrews, L.C. Special Functions for Engineers and Applied Mathematicians; Macmillan: New York, NY, USA, 1985. [Google Scholar]
- Dattoli, G.; Migliorati, M.; Srivastava, H.M. A class of Bessel summation formulas and associated operational methods. Fract. Calc. Appl. Anal. 2004, 7, 169–176. [Google Scholar]
- Roman, S. The Umbral Calculus; Academic Press Inc.: New York, NY, USA, 1984. [Google Scholar]
- Sheffer, I.M. Note on Appell polynomials. Bull. Am. Math. Soc. 1945, 51, 739–744. [Google Scholar] [CrossRef]
- Khan, S.; Raza, N. General-Appell polynomials within the context of monomiality principle. Int. J. Anal. 2013, 2013, 328032. [Google Scholar] [CrossRef]
- Khan, S.; Yasmin, G.; Khan, R.; Hassan, N.A.M. Hermite-based Appell polynomials: Properties and applications. J. Math. Anal. Appl. 2009, 351, 756–764. [Google Scholar] [CrossRef]
- Khan, S.; Al-Saad, M.W.; Khan, R. Laguerre-based Appell polynomials: Properties and applications. Math. Comput. Model. 2010, 52, 247–259. [Google Scholar] [CrossRef]
- Zayed, M.; Wani, S.A.; Subzar, M.; Riyasat, M. Certain families of differential equations associated with the generalized 1-parameter Hermite–Frobenius Euler polynomials. Math. Comput. Model. Dyn. Syst. 2024, 30, 683–700. [Google Scholar] [CrossRef]
- Costabile, F.A.; Longo, E. A determinantal approach to Appell polynomials. J. Comput. Appl. Math. 2010, 234, 1528–1542. [Google Scholar] [CrossRef]
- Yang, Y. Determinant representations of Appell polynomial sequences. Oper. Matrices 2008, 2, 517–524. [Google Scholar] [CrossRef]
- Costabile, F. Modern Umbral Calculus: An Elementary Introduction with Applications to Linear Interpolation and Operator Approximation Theory; Walter de Gruyter GmbH Co. KG: Berlin, Germany, 2019; Volume 72. [Google Scholar]
- Costabile, F.A.; Gualtieri, M.I.; Napoli, A. Polynomial Sequences: Basic Methods, Special Classes, and Computational Applications; Walter de Gruyter GmbH, Co. KG: Berlin, Germany, 2023. [Google Scholar]
- Costabile, F.A.; Gualtieri, M.I.; Napoli, A. Bivariate general Appell interpolation problem. Numer. Algorithms 2022, 91, 531–556. [Google Scholar] [CrossRef]
- Khan, S.; Yasmin, G.; Ahmad, N. A note on truncated exponential-based Appell polynomials. Bull. Malays. Math. Sci. Soc. 2017, 40, 373–388. [Google Scholar] [CrossRef]
- Dattoli, G.; Chiccoli, C.; Lorenzutta, S.; Maino, G.; Torre, A. Theory of generalized Hermite polynomials. Comput. Math. Appl. 1994, 28, 71–83. [Google Scholar] [CrossRef]
- Dattoli, G.; Torre, A.; Mancho, A.M. The generalized Laguerre polynomials, the associated Bessel functions and application to propagation problems. Radiat. Phys. Chem. 2000, 59, 229–237. [Google Scholar] [CrossRef]
- Carlitz, L. Eulerian numbers and polynomials. Math. Mag. 1959, 32, 247–260. [Google Scholar] [CrossRef]
- Araci, S.; Riyasat, M.; Wani, S.A.; Khan, S. Differential and integral equations for the 3-variable Hermite-Frobenius-Euler and Frobenius-Genocchi polynomials. Appl. Math. Inf. Sci. 2017, 11, 1335–1346. [Google Scholar] [CrossRef]
- Ma, W.X. Bilinear equations, Bell polynomials and linear superposition principle. J. Phys. Conf. Ser. 2013, 411, 012021. [Google Scholar] [CrossRef]
- Ma, W.X. Trilinear equations, Bell polynomials, and resonant solutions. Front. Math. China 2013, 8, 1139–1156. [Google Scholar] [CrossRef]
- Ma, W.X. Bilinear equations and resonant solutions characterized by Bell polynomials. Rep. Math. Phys. 2013, 72, 41–56. [Google Scholar] [CrossRef]
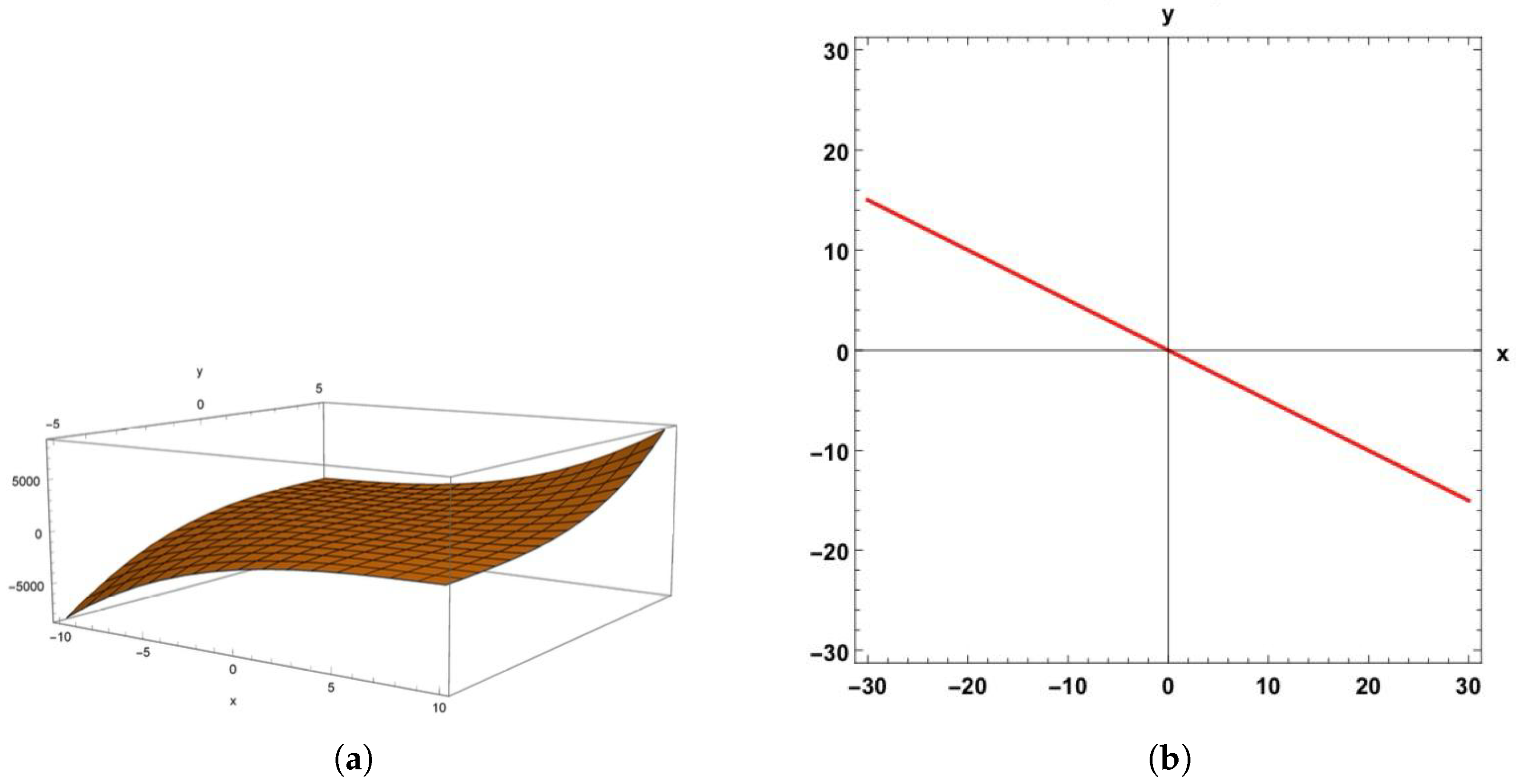
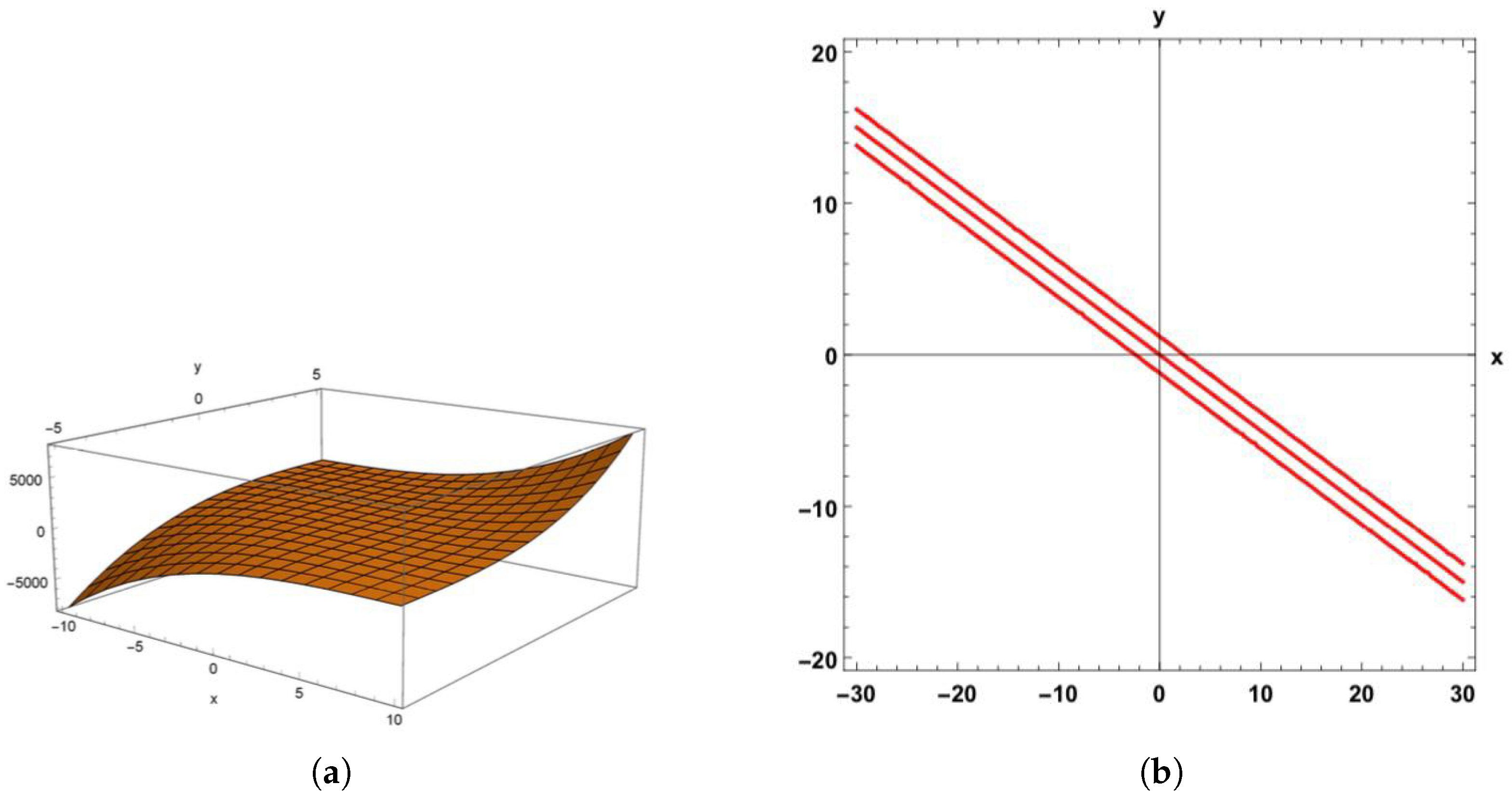
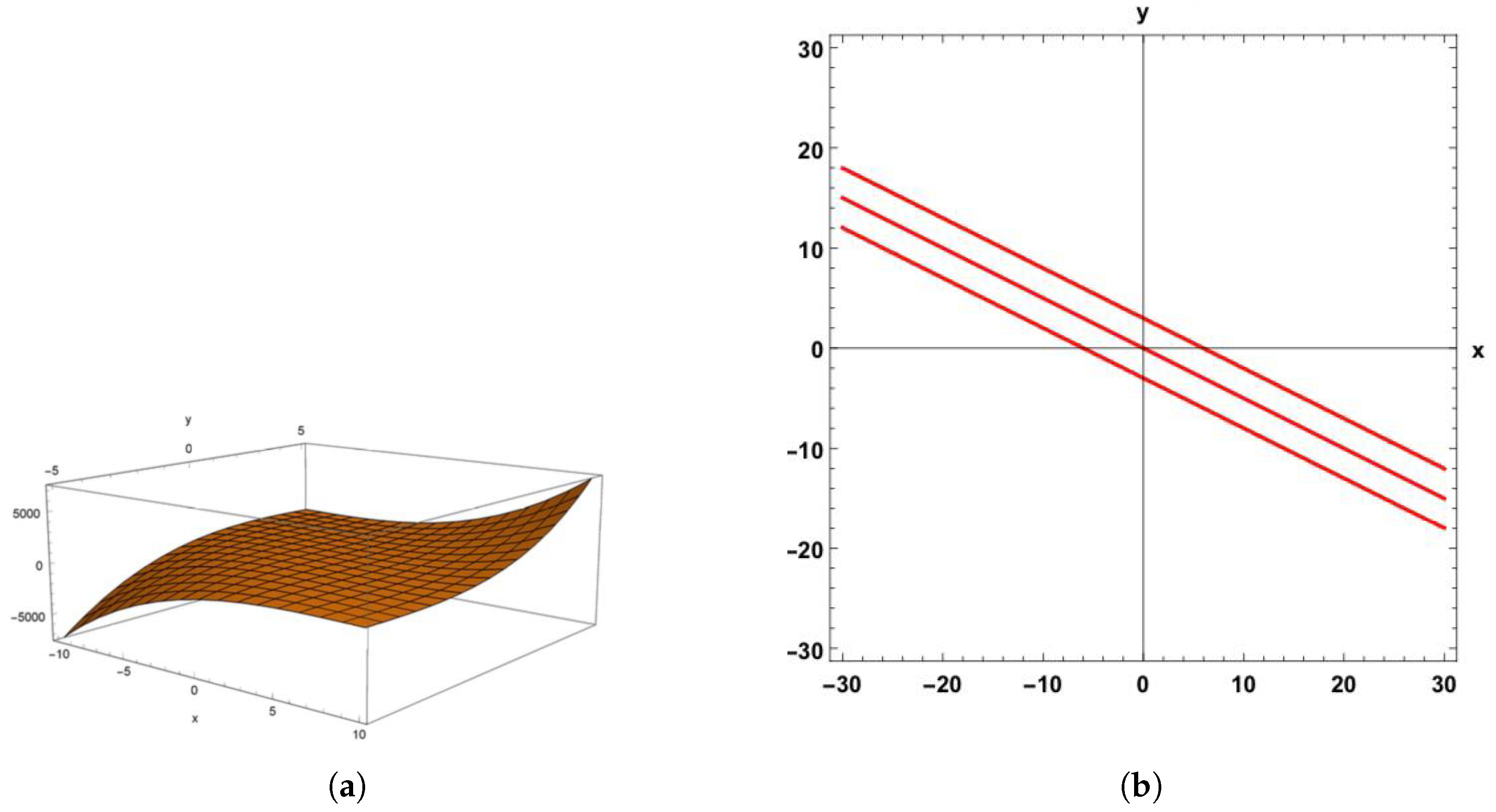
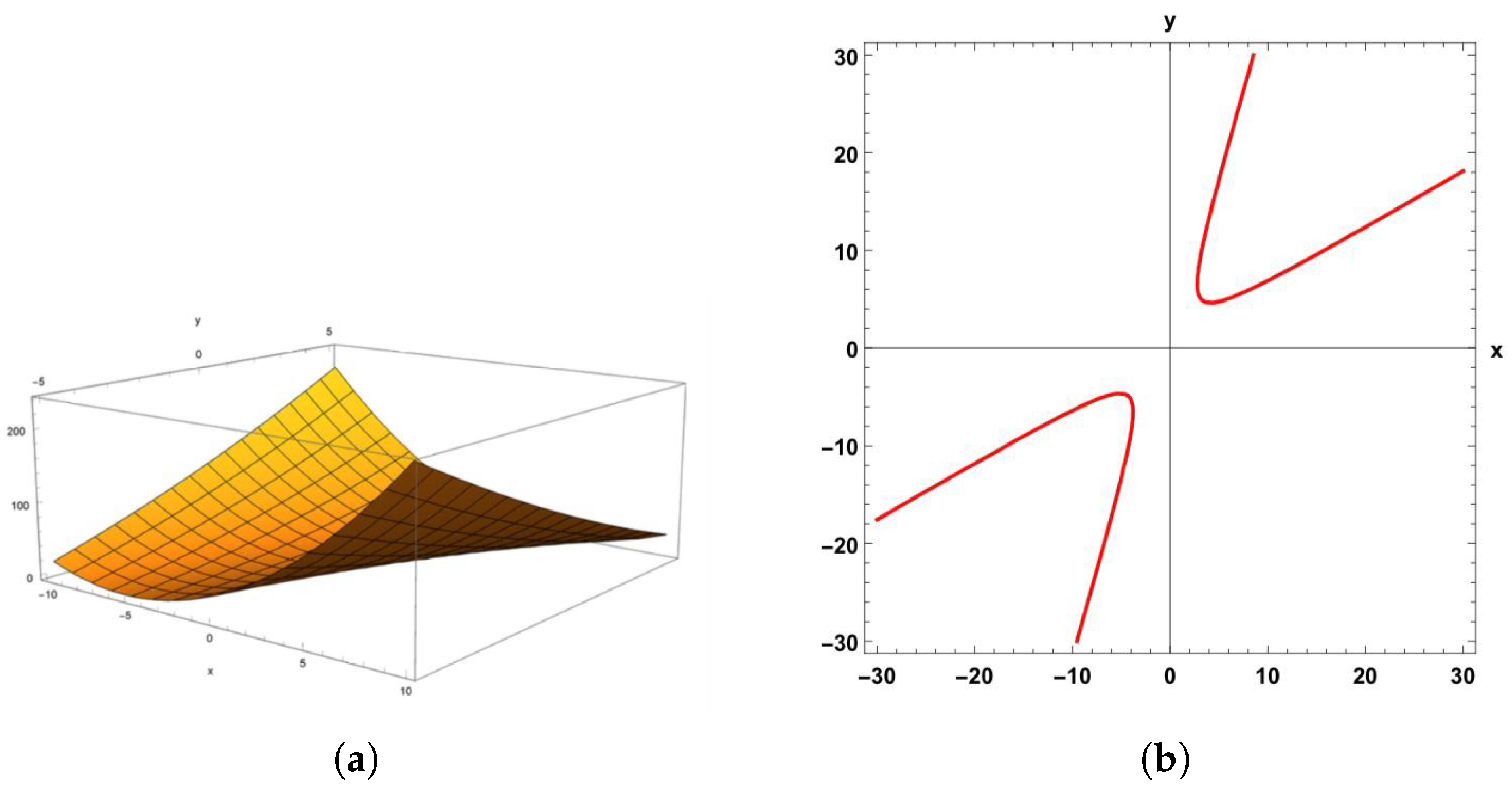


| j | |
| 0 | 1 |
| 1 | |
| 2 | |
| 3 |
| j | |
| 0 | 1 |
| 1 | |
| 2 | |
| 3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özat, Z.; Çekim, B.; Özarslan, M.A.; Costabile, F.A. Truncated-Exponential-Based General-Appell Polynomials. Mathematics 2025, 13, 1266. https://doi.org/10.3390/math13081266
Özat Z, Çekim B, Özarslan MA, Costabile FA. Truncated-Exponential-Based General-Appell Polynomials. Mathematics. 2025; 13(8):1266. https://doi.org/10.3390/math13081266
Chicago/Turabian StyleÖzat, Zeynep, Bayram Çekim, Mehmet Ali Özarslan, and Francesco Aldo Costabile. 2025. "Truncated-Exponential-Based General-Appell Polynomials" Mathematics 13, no. 8: 1266. https://doi.org/10.3390/math13081266
APA StyleÖzat, Z., Çekim, B., Özarslan, M. A., & Costabile, F. A. (2025). Truncated-Exponential-Based General-Appell Polynomials. Mathematics, 13(8), 1266. https://doi.org/10.3390/math13081266







