Predictive Maintenance for Cutter System of Roller Laminator
Abstract
1. Introduction
2. Applications of Machine Learning in PdM
- Signal type: Various studies have utilized sound, current, and vibration signals for condition monitoring. These signals have been processed and analyzed to distinguish different machine states effectively. Notably, vibration and current signals yield higher classification accuracy compared to sound signals. Vibration signals are also more commonly used in mechanical fault diagnostics. Given these advantages, this study selects voltage singles of vibrations extracted using an accelerometer as the primary signal type.
- Signal transformation: The raw signals captured by sensors are typically discontinuous time-domain signals. According to the reviewed literature, such signals are challenging to classify directly and require transformation into alternative feature representations for effective model training. Common transformation techniques include converting time-domain signals into frequency-domain features using FFT or employing DWT and STFT for time-frequency analysis. Since the cutting action of the roller laminating machine’s cutter system is completed within approximately one second, frequency-domain analysis provides a more efficient and effective approach for feature extraction.
- Model type: Machine learning is widely used for classification in PdM. Traditional machine learning models, such as SVM and RF, require manual feature extraction but are effective for smaller datasets. On the other hand, deep learning models, including DNN and CNN, can automatically learn complex patterns from data without extensive feature engineering. These models are particularly useful for capturing nonlinear relationships but require larger datasets and higher computational resources. While deep learning can enhance classification performance, it also introduces challenges such as increased training time and the risk of overfitting when dealing with limited data. Considering the constraints of this study, machine learning methods are chosen as the primary approach for anomaly classification, balancing model complexity with data availability and computational efficiency.
3. Research Methods
3.1. Hardware Architecture for Singal Collection
3.2. Singal Preprocessing
- Step 1: signal decomposition. The time-domain signal of length N is divided into even and odd sequences, as shown in Equations (2) and (3):
- Step 2: recursive DFT computation. The even and odd sequences are processed separately using recursive DFT, as expressed in Equations (4) and (5):
- Step 3: sequence combination. As shown in Equation (6), the odd-sequence DFT is rotated using the Twiddle Factor Wk,N = e−j2πk/N and then combined with the even-sequence DFT:
3.3. Frequency-Domain Feature Extraction
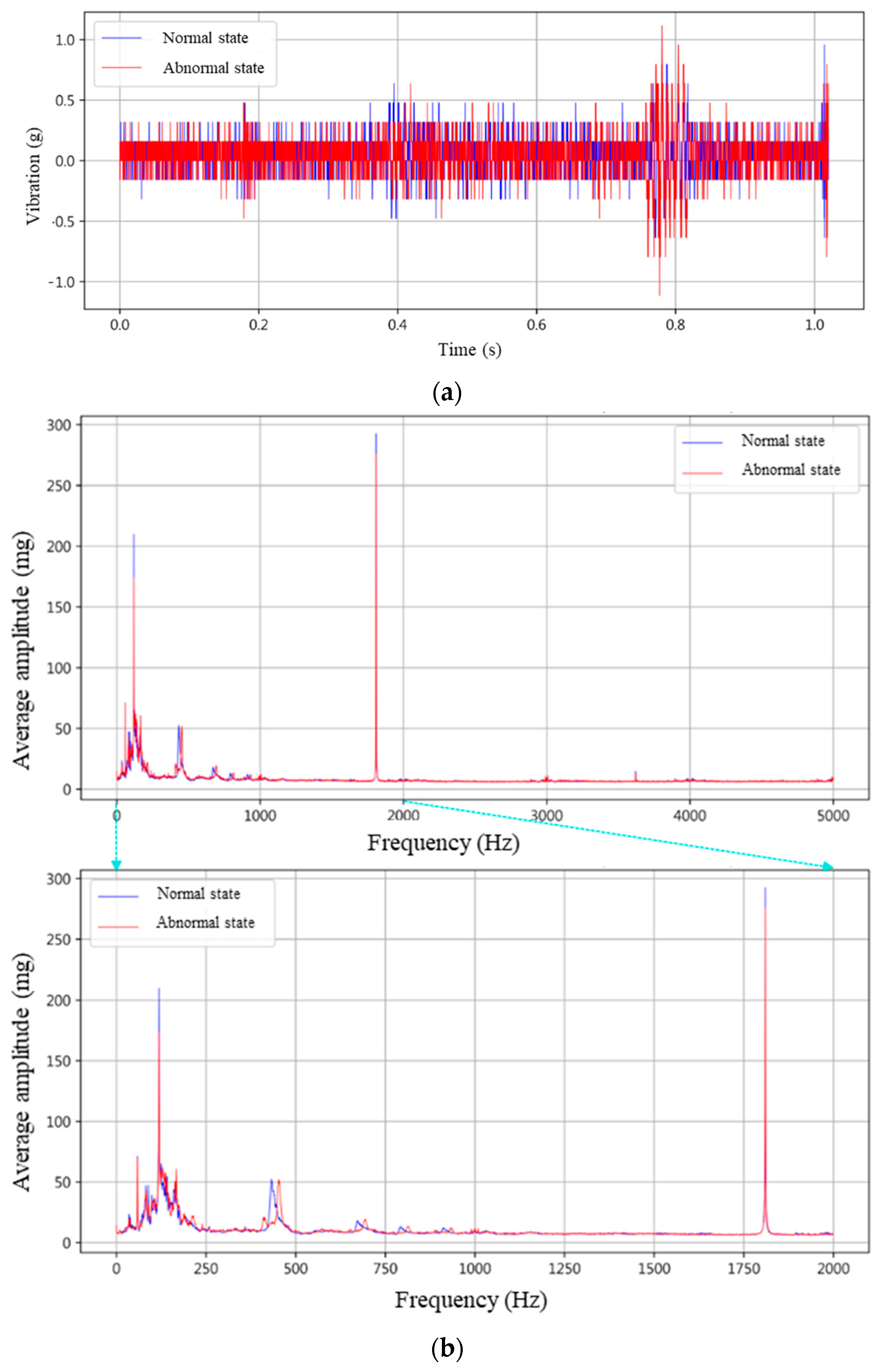
- Step 1: critical frequency component detection. Detecting critical frequency components involves analyzing the frequency domain to extract features that differentiate between normal and abnormal states. The amplitude spectrum is derived using:
- Step 2: critical frequency band identification. Identifying meaningful frequency bands is essential for effective signal analysis, and clustering techniques play a crucial role in this process. The k-means clustering is employed for its efficiency in partitioning data, with cluster quality evaluated using a widely used metric, silhouette score, which quantifies the cohesion and separation of clusters. The process begins by defining a range of potential cluster numbers, typically from 2 to 10. For each number of clusters, the k-means is applied, and the silhouette score is computed to assess clustering performance. Mathematically, the silhouette score for a clustering result is defined as
- Step 3: critical feature extraction. After frequency-domain analysis identifies critical frequency bands, irrelevant bands are removed to achieve dimensionality reduction. The study further extracts statistical features to extract physically meaningful features for each band, including maximum, mean, standard deviation, skewness, and kurtosis:
3.4. Supervised Machine Learning Algorithms
4. Experiment Results
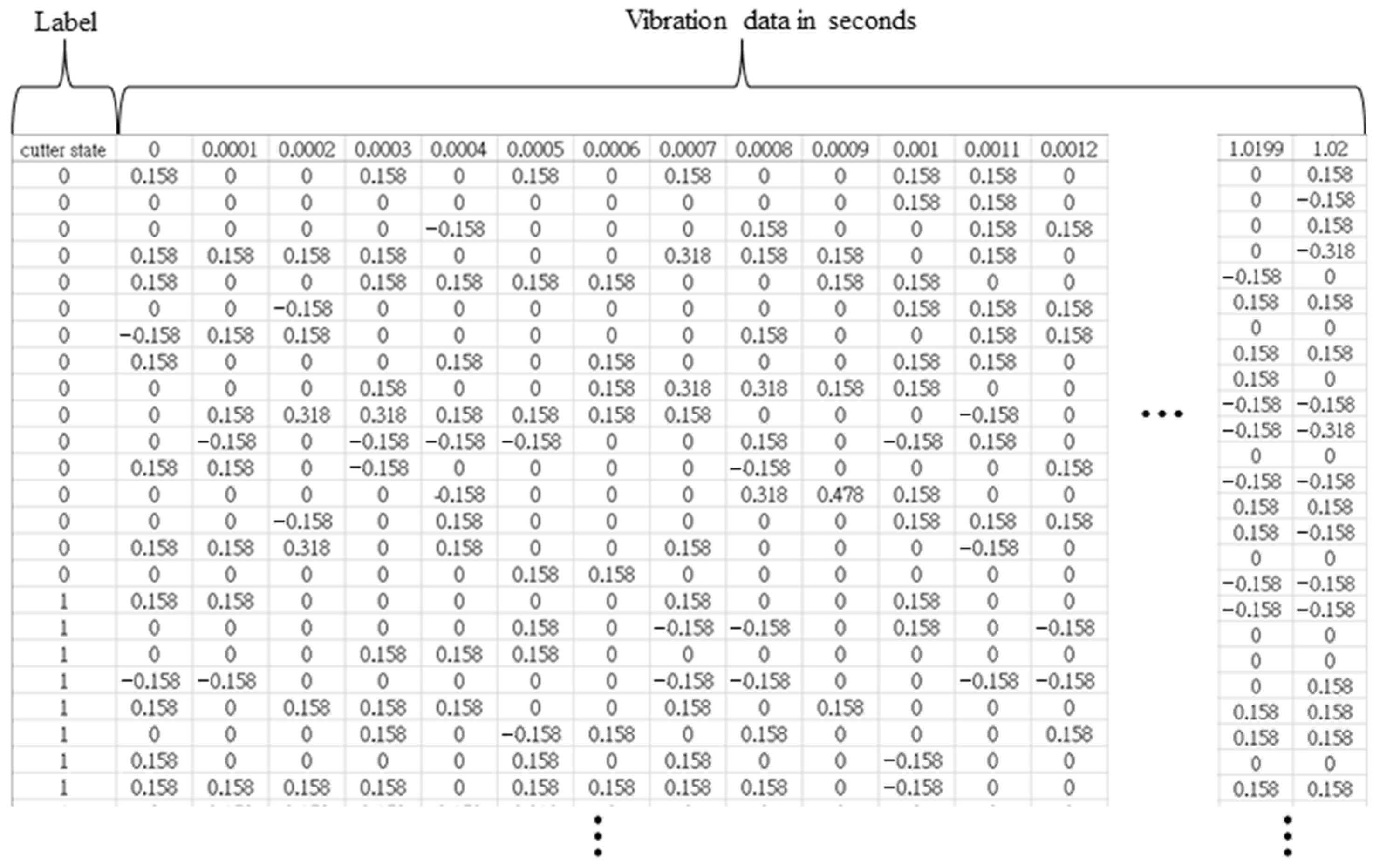
4.1. Data Collection and Labeling
4.2. Feature Engineering for Vibration Singals
4.3. Model Training and Comparison
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Achouch, M.; Dimitrova, M.; Ziane, K.; Sattarpanah Karganroudi, S.; Dhouib, R.; Ibrahim, H.; Adda, M. On predictive maintenance in industry 4.0: Overview, models, and challenges. Appl. Sci. 2022, 12, 8081. [Google Scholar] [CrossRef]
- Romanssini, M.; de Aguirre, P.C.C.; Compassi-Severo, L.; Girardi, A.G. A review on vibration monitoring techniques for predictive maintenance of rotating machinery. Eng 2023, 4, 1797–1817. [Google Scholar] [CrossRef]
- Carvalho, T.P.; Soares, F.A.; Vita, R.; Francisco , P.R.D.; Basto, J.P.; Alcalá, S.G. A systematic literature review of machine learning methods applied to predictive maintenance. Comput. Ind. Eng. 2019, 137, 106024. [Google Scholar] [CrossRef]
- Cerrada, M.; Zurita, G.; Cabrera, D.; Sánchez, R.V.; Artés, M.; Li, C. Fault diagnosis in spur gears based on genetic algorithm and random forest. Mech. Syst. Signal Process. 2016, 70, 87–103. [Google Scholar] [CrossRef]
- Madhusudana, C.K.; Kumar, H.; Narendranath, S. Face milling tool condition monitoring using sound signal. Int. J. Syst. Assur. Eng. Manag. 2017, 8, 1643–1653. [Google Scholar] [CrossRef]
- Kanawaday, A.; Sane, A. Machine learning for predictive maintenance of industrial machines using IoT sensor data. In Proceedings of the 2017 8th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 24–26 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 87–90. [Google Scholar]
- Madhusudana, C.K.; Gangadhar, N.; Kumar, H.; Narendranath, S. Use of discrete wavelet features and support vector machine for fault diagnosis of face milling tool. Struct. Durab. Health Monit. 2018, 12, 111. [Google Scholar]
- Bonci, A.; Longhi, S.; Nabissi, G.; Verdini, F. Predictive maintenance system using motor current signal analysis for industrial robot. In Proceedings of the 2019 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Zaragoza, Spain, 10–13 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1453–1456. [Google Scholar]
- Sikder, N.; Bhakta, K.; Al Nahid, A.; Islam, M.M. Fault diagnosis of motor bearing using ensemble learning algorithm with FFT-based preprocessing. In Proceedings of the 2019 International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 10–12 January 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 564–569. [Google Scholar]
- Esakimuthu Pandarakone, S.; Mizuno, Y.; Nakamura, H. A comparative study between machine learning algorithm and artificial intelligence neural network in detecting minor bearing fault of induction motors. Energies 2019, 12, 2105. [Google Scholar] [CrossRef]
- Ali, M.Z.; Shabbir, S.K.M.N.; Liang, X.; Zhang, Y.; Hu, T. Machine learning-based fault diagnosis for single-and multi-faults in induction motors using measured stator currents and vibration signals. IEEE Trans. Ind. Appl. 2019, 55, 2378–2391. [Google Scholar] [CrossRef]
- Magadán, L.; Suárez, F.J.; Granda, J.C.; García, D.F. Real-time monitoring of electric motors for detection of operating anomalies and predictive maintenance. In Proceedings of the Science and Technologies for Smart Cities: 5th EAI International Summit, SmartCity360, Braga, Portugal, 4–6 December 2019; Springer International Publishing: Cham, Switzerland, 2020; pp. 301–311. [Google Scholar]
- Saberi, A.N.; Sandirasegaram, S.; Belahcen, A.; Vaimann, T.; Sobra, J. Multi-sensor fault diagnosis of induction motors using random forests and support vector machine. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; IEEE: Piscataway, NJ, USA, 2020; Volume 1, pp. 1404–1410. [Google Scholar]
- Pollak, A.; Temich, S.; Ptasiński, W.; Kucharczyk, J.; Gąsiorek, D. Prediction of belt drive faults in case of predictive maintenance in industry 4.0 platform. Appl. Sci. 2021, 11, 10307. [Google Scholar] [CrossRef]
- Xiang, C.; Ren, Z.; Shi, P.; Zhao, H. Data-driven fault diagnosis for rolling bearing based on dit-fft and xgboost. Complexity 2021, 2021, 4941966. [Google Scholar] [CrossRef]
- Giri, A.; Mehendale, N.; Waghode, N. Optimized fault detection and classification for 3-phase electric drives–an AI/ML approach. In Proceedings of the 2022 International Conference on Innovations in Science and Technology for Sustainable Development (ICISTSD), Kollam, India, 25–26 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 80–87. [Google Scholar]
- Raouf, I.; Lee, H.; Kim, H.S. Mechanical fault detection based on machine learning for robotic RV reducer using electrical current signature analysis: A data-driven approach. J. Comput. Des. Eng. 2022, 9, 417–433. [Google Scholar] [CrossRef]
- Hosseinpour-Zarnaq, M.; Omid, M.; Biabani-Aghdam, E. Fault diagnosis of tractor auxiliary gearbox using vibration analysis and random forest classifier. Inf. Process. Agric. 2022, 9, 60–67. [Google Scholar] [CrossRef]
- Aburakhia, S.; Shami, A. SB-PdM: A tool for predictive maintenance of rolling bearings based on limited labeled data. Softw. Impacts 2023, 16, 100503. [Google Scholar] [CrossRef]
- Souza, J.C.S.D.; Honorato Júnior, O.; Tiago Filho, G.L.; Carpinteiro, O.A.S.; Biancardine Júnior, H.S.D.; Santos, I.F.S.D. Application of machine learning models in predictive maintenance of Francis hydraulic turbines. Rev. Bras. Recur. Hídricos 2024, 29, e48. [Google Scholar] [CrossRef]
- Hakami, A. Strategies for overcoming data scarcity, imbalance, and feature selection challenges in machine learning models for predictive maintenance. Sci. Rep. 2024, 14, 9645. [Google Scholar] [CrossRef] [PubMed]
- Khalil, A.F.; Rostam, S. Machine learning-based predictive maintenance for fault detection in rotating machinery: A case study. Eng. Technol. Appl. Sci. Res. 2024, 14, 13181–13189. [Google Scholar] [CrossRef]





| Reference | Application Field | Feature Extraction | Methodology |
|---|---|---|---|
| [4] | Gearbox | Time-domain statistics, FFT, WPT | Combined time, frequency, and time-frequency domain features, applied GA for feature reduction, and used RF for classification. |
| [5] | Face milling tool | DWT of sound signal | Compared multiple classifiers with DT-selected DWT features. |
| [6] | Film-slitting machine | DM of time, tension, pressure, width, diameter | Used ARIMA for prediction and four supervised models for classification. |
| [7] | Face milling tool | DWT of vibration signal | Applied DWT and DT feature selection with SVM for classification. |
| [8] | Belt transmission system | DWT of current signal | Analyzed belt looseness using wavelet energy decomposition. |
| [9] | Motor bearing | FFT of vibration signal | Used FFT with normalized features and RF model for fault classification. |
| [10] | Bearing | FFT of current signal | Compared SVM, KNN, and CNN with increasing training data volume. |
| [11] | Induction motor | WPT of current and vibration signals | Used WPT features with SVM and KNN classifiers for fault classification. |
| [12] | Pump | FFT of vibration signal | Compared FFT-based features of pumps with different maintenance cycles. |
| [13] | Eccentricity fault | FFT of current and vibration signals | Combined time- and frequency-domain features, used RF for feature selection, and SVM for classification. |
| [14] | Belt transmission system | FFT of vibration signal | Used autoencoder with FFT features from horizontal and vertical sensors. |
| [15] | Bearing | FFT of vibration signal | Used FFT features with XGBoost after standardization and parameter tuning. |
| [16] | Stator winding faults | FFT of current and axial flux signals | Used FFT and PSD features with six classifiers for fault classification. |
| [17] | 6-axis robotic arm | Waveform, statistical, kinetic features of current signal | Used correlation and chi-square tests for feature selection and applied four classifiers. |
| [18] | Tractor gearbox | DWT of vibration signal | Compared RF and MLP performance with and without CFS feature selection. |
| [19] | Bearing | FFT, STFT, WPT of vibration signal | Used SB-PdM V1.0 software and similarity metrics for comparison. |
| [20] | Hydraulic turbines | FFT of vibration signal | Compared MLP and RBFNN classifiers using FFT features under cavitation and normal states. |
| [21] | Non-woven materials machinery | Time-domain raw sensor data of vibration and temperature | GAN-generated data with LSTM features and five classifiers |
| [22] | Rotating machinery | FFT of vibration signal | FFT-based feature extraction with ensemble classifiers. |
| Features | Metrics Models | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) | TP | TN | FP | FN |
|---|---|---|---|---|---|---|---|---|---|
| 32 critical frequency from FFT | LR | 88.72 | 85.98 | 86.79 | 86.38 | 92 | 136 | 14 | 15 |
| RF | 94.16 | 93.33 | 92.45 | 92.89 | 98 | 144 | 8 | 7 | |
| SVM | 91.44 | 97.73 | 81.13 | 88.66 | 86 | 149 | 20 | 2 | |
| 15 statistical features from 3 critical bands of FFT | LR | 87.55 | 84.91 | 84.91 | 84.91 | 90 | 135 | 16 | 16 |
| RF | 93.77 | 92.45 | 92.45 | 92.45 | 98 | 143 | 8 | 8 | |
| SVM | 94.94 | 95.15 | 92.45 | 93.78 | 98 | 146 | 8 | 5 | |
| 12 statistical features from 2 components of DWT | LR | 73.93 | 70.10 | 64.15 | 67.00 | 68 | 119 | 38 | 29 |
| RF | 79.77 | 72.88 | 81.13 | 76.79 | 86 | 122 | 20 | 32 | |
| SVM | 78.60 | 71.43 | 80.19 | 75.56 | 85 | 117 | 21 | 34 | |
| 384 statistical features from 64 scales of CWT | LR | 84.05 | 80.37 | 81.13 | 80.75 | 86 | 139 | 20 | 21 |
| RF | 91.44 | 88.89 | 90.57 | 89.72 | 96 | 130 | 10 | 12 | |
| SVM | 89.49 | 88.35 | 85.85 | 87.08 | 91 | 139 | 15 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.-H.; Wang, C.-W.; Mayol, A.P.; Jan, C.-M.; Yang, T.-Y. Predictive Maintenance for Cutter System of Roller Laminator. Mathematics 2025, 13, 1264. https://doi.org/10.3390/math13081264
Chen S-H, Wang C-W, Mayol AP, Jan C-M, Yang T-Y. Predictive Maintenance for Cutter System of Roller Laminator. Mathematics. 2025; 13(8):1264. https://doi.org/10.3390/math13081264
Chicago/Turabian StyleChen, Ssu-Han, Chen-Wei Wang, Andres Philip Mayol, Chia-Ming Jan, and Tzu-Yi Yang. 2025. "Predictive Maintenance for Cutter System of Roller Laminator" Mathematics 13, no. 8: 1264. https://doi.org/10.3390/math13081264
APA StyleChen, S.-H., Wang, C.-W., Mayol, A. P., Jan, C.-M., & Yang, T.-Y. (2025). Predictive Maintenance for Cutter System of Roller Laminator. Mathematics, 13(8), 1264. https://doi.org/10.3390/math13081264







