Generalized Grönwall Inequality and Ulam–Hyers Stability in ℒp Space for Fractional Stochastic Delay Integro-Differential Equations
Abstract
1. Introduction
- As far as we know, this is the first comprehensive analysis of the well-posedness of the solutions of FSIDEs and UHS concerning Cap-KFrD in the space.
- We prove all results for the Cap-KFrD, which generalizes Cap-FrD and Cap-HFrD, such that our results are consistent with Cap-FrD when holds and match with Cap-HFrD when holds.
- Most results related to FDSDEs and FSIDEs have been established in the space; however, we establish these results in the space.
- This research work presents a generalized Grönwall inequality regarding Cap-KFrD.
2. Preliminaries
- , there is such as
- The , , and satisfies
3. Generalized Results
4. Stability Results
5. Example
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Cap-KFrD | Caputo–Katugampola fractional derivative |
| Cap-FrD | Caputo fractional derivative |
| Cap-HFrD | Caputo–Hadamard fractional derivative |
| Ex-Un | Existence and uniqueness |
| SFDEs | Stochastic fractional differential equations |
| FSIDEs | Fractional stochastic integro-differential equations |
| UHS | Ulam–Hyers stability |
References
- Subramanian, M.; Manigandan, M.; Zada, A.; Gopal, T.N. Existence and Hyers-Ulam stability of solutions for nonlinear three fractional sequential differential equations with nonlocal boundary conditions. Int. J. Nonlinear Sci. Numer. Simul. 2024, 24, 3071–3099. [Google Scholar] [CrossRef]
- Mohammed Djaouti, A.; Khan, Z.A.; Imran Liaqat, M.; Al-Quran, A. A novel technique for solving the nonlinear fractional-order smoking model. Fractal Fract. 2024, 8, 286. [Google Scholar] [CrossRef]
- Gunasekar, T.; Raghavendran, P.; Santra, S.S.; Majumder, D.; Baleanu, D.; Balasundaram, H. Application of Laplace transform to solve fractional integro-differential equations. J. Math. Comput. Sci. 2024, 33, 225–237. [Google Scholar] [CrossRef]
- Din, A.; Li, Y.; Khan, F.M.; Khan, Z.U.; Liu, P. On Analysis of fractional order mathematical model of Hepatitis B using Atangana–Baleanu Caputo (ABC) derivative. Fractals 2022, 30, 2240017. [Google Scholar] [CrossRef]
- Zeng, S.; Baleanu, D.; Bai, Y.; Wu, G. Fractional differential equations of Caputo-Katugampola type and numerical solutions. Appl. Math. Comput. 2017, 315, 549–554. [Google Scholar] [CrossRef]
- Ma, L.; Chen, Y. Analysis of Caputo–Katugampola fractional differential system. Eur. Phys. J. Plus 2024, 139, 171. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Nagy, A.M.; Al-Ajami, T.M. Numerical solutions of fractional optimal control with Caputo–Katugampola derivative. Adv. Differ. Equ. 2021, 2021, 425. [Google Scholar] [CrossRef]
- Boucenna, D.; Ben Makhlouf, A.; Naifar, O.; Guezane-Lakoud, A.; Hammami, M.A. Linearized stability analysis of Caputo-Katugampola fractional-order nonlinear systems. J. Nonlinear Funct. Anal. 2018, 2018, 27. [Google Scholar]
- Nazeer, N.; Asjad, M.I.; Azam, M.K.; Akgül, A. Study of results of katugampola fractional derivative and chebyshev inequailities. Int. J. Appl. Comput. Math. 2022, 8, 225. [Google Scholar] [CrossRef]
- Van Hoa, N.; Vu, H.; Duc, T.M. Fuzzy fractional differential equations under Caputo–Katugampola fractional derivative approach. Fuzzy Sets Syst. 2019, 375, 70–99. [Google Scholar]
- Omaba, M.E.; Sulaimani, H.A. On Caputo–Katugampola fractional stochastic differential equation. Mathematics 2022, 10, 2086. [Google Scholar] [CrossRef]
- Elbadri, M. An approximate solution of a time fractional Burgers’ equation involving the Caputo-Katugampola fractional derivative. Partial. Differ. Equations Appl. Math. 2023, 8, 100560. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S.; Alabdala, A.T.; Redhwan, S.S.; Bazighifan, O.; Ali, A.H.; Iambor, L.F. Symmetrical solutions for non-local fractional integro-differential equations via caputo–katugampola derivatives. Symmetry 2023, 15, 662. [Google Scholar] [CrossRef]
- Sadek, L.; Jarad, F. The general Caputo–Katugampola fractional derivative and numerical approach for solving the fractional differential equations. Alex. Eng. J. 2025, 121, 539–557. [Google Scholar] [CrossRef]
- Nagy, A.M.; Issa, K. An accurate numerical technique for solving fractional advection–diffusion equation with generalized Caputo derivative. Z. Angew. Math. Phys. 2024, 75, 164. [Google Scholar] [CrossRef]
- Dai, Q.; Zhang, Y. Stability of nonlinear implicit differential equations with Caputo–Katugampola fractional derivative. Mathematics 2023, 11, 3082. [Google Scholar] [CrossRef]
- Tran, M.D.; Ho, V.; Van, H.N. On the stability of fractional differential equations involving generalized Caputo fractional derivative. Math. Probl. Eng. 2020, 2020, 1680761. [Google Scholar] [CrossRef]
- Singh, J.; Agrawal, R.; Baleanu, D. Dynamical analysis of fractional order biological population model with carrying capacity under Caputo-Katugampola memory. Alex. Eng. J. 2024, 91, 394–402. [Google Scholar] [CrossRef]
- Oliveira, D.S.; Capelas de Oliveira, E. On a Caputo-type fractional derivative. Adv. Pure Appl. Math. 2019, 10, 81–91. [Google Scholar] [CrossRef]
- Batiha, I.M.; Abubaker, A.A.; Jebril, I.H.; Al-Shaikh, S.B.; Matarneh, K. A numerical approach of handling fractional stochastic differential equations. Axioms 2023, 12, 388. [Google Scholar] [CrossRef]
- Chen, J.; Ke, S.; Li, X.; Liu, W. Existence, uniqueness and stability of solutions to fractional backward stochastic differential equations. Appl. Math. Sci. Eng. 2022, 30, 811–829. [Google Scholar] [CrossRef]
- Moualkia, S.; Xu, Y. On the existence and uniqueness of solutions for multidimensional fractional stochastic differential equations with variable order. Mathematics 2021, 9, 2106. [Google Scholar] [CrossRef]
- Ali, A.; Hayat, K.; Zahir, A.; Shah, K.; Abdeljawad, T. Qualitative analysis of fractional stochastic differential equations with variable order fractional derivative. Qual. Theory Dyn. Syst. 2024, 23, 120. [Google Scholar] [CrossRef]
- Li, S.; Khan, S.U.; Riaz, M.B.; AlQahtani, S.A.; Alamri, A.M. Numerical simulation of a fractional stochastic delay differential equations using spectral scheme: A comprehensive stability analysis. Sci. Rep. 2024, 14, 6930. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Vijayakumar, V.; Shukla, A.; Chauhan, S. A note on asymptotic stability of semilinear thermoelastic system. Qual. Theory Dyn. Syst. 2022, 21, 75. [Google Scholar] [CrossRef]
- Abouagwa, M.; Bantan, R.A.; Almutiry, W.; Khalaf, A.D.; Elgarhy, M. Mixed Caputo fractional neutral stochastic differential equations with impulses and variable delay. Fractal Fract. 2021, 5, 239. [Google Scholar] [CrossRef]
- Doan, T.S.; Huong, P.T.; Kloeden, P.E.; Vu, A.M. Euler-Maruyama scheme for Caputo stochastic fractional differential equations. J. Comput. Appl. Math. 2020, 380, 112989. [Google Scholar] [CrossRef]
- Umamaheswari, P.; Balachandran, K.; Annapoorani, N. Existence and stability results for Caputo fractional stochastic differential equations with Lévy noise. Filomat 2020, 34, 1739–1751. [Google Scholar] [CrossRef]
- Li, M.; Niu, Y.; Zou, J. A result regarding finite-time stability for Hilfer fractional stochastic differential equations with delay. Fractal Fract. 2023, 7, 622. [Google Scholar] [CrossRef]
- Mirzaee, F.; Samadyar, N. On the numerical solution of fractional stochastic integro-differential equations via meshless discrete collocation method based on radial basis functions. Eng. Anal. Bound. Elem. 2019, 100, 246–255. [Google Scholar] [CrossRef]
- Cui, J.; Yan, L. Existence result for fractional neutral stochastic integro-differential equations with infinite delay. J. Phys. A Math. Theor. 2011, 44, 335201. [Google Scholar] [CrossRef]
- Badr, A.A.; El-Hoety, H.S. Monte-Carlo Galerkin Approximation of Fractional Stochastic Integro-Differential Equation. Math. Probl. Eng. 2012, 2012, 709106. [Google Scholar] [CrossRef]
- Ahmed, H.M.; El-Borai, M.M. Hilfer fractional stochastic integro-differential equations. Appl. Math. Comput. 2018, 331, 182–189. [Google Scholar] [CrossRef]
- Kamrani, M. Numerical solution of stochastic fractional differential equations. Numer. Algorithms 2015, 68, 81–93. [Google Scholar] [CrossRef]
- Ramkumar, K.; Ravikumar, K.; Varshini, S. Fractional neutral stochastic differential equations with Caputo fractional derivative: Fractional Brownian motion, Poisson jumps, and optimal control. Stoch. Anal. Appl. 2021, 39, 157–176. [Google Scholar] [CrossRef]
- Zou, J.; Luo, D. A new result on averaging principle for Caputo-type fractional delay stochastic differential equations with Brownian motion. Appl. Anal. 2024, 103, 1397–1417. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; Wang, J.; Jin, C.; Li, J.; Xu, W. A note on averaging principles for fractional stochastic differential equations. Fractal Fract. 2024, 8, 216. [Google Scholar] [CrossRef]
- Luo, D.; Wang, X.; Caraballo, T.; Zhu, Q. Ulam–Hyers stability of Caputo-type fractional fuzzy stochastic differential equations with delay. Commun. Nonlinear Sci. Numer. Simul. 2023, 121, 107229. [Google Scholar] [CrossRef]
- Zou, J.; Luo, D. On the averaging principle of Caputo type neutral fractional stochastic differential equations. Qual. Theory Dyn. Syst. 2024, 23, 82. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, P. Averaging principle for fractional stochastic differential equations with Lp convergence. Appl. Math. Lett. 2022, 130, 108024. [Google Scholar] [CrossRef]
- Djaouti, A.M.; Liaqat, M.I. Theoretical Results on the pth Moment of ϕ-Hilfer Stochastic Fractional Differential Equations with a Pantograph Term. Fractal Fract. 2025, 9, 134. [Google Scholar] [CrossRef]
- Otrocol, D.; Ilea, V. Ulam stability for a delay differential equation. Open Math. 2013, 11, 1296–1303. [Google Scholar] [CrossRef]
- Chen, C.; Dong, Q. Existence and Hyers–Ulam stability for a multi-term fractional differential equation with infinite delay. Mathematics 2022, 10, 1013. [Google Scholar] [CrossRef]
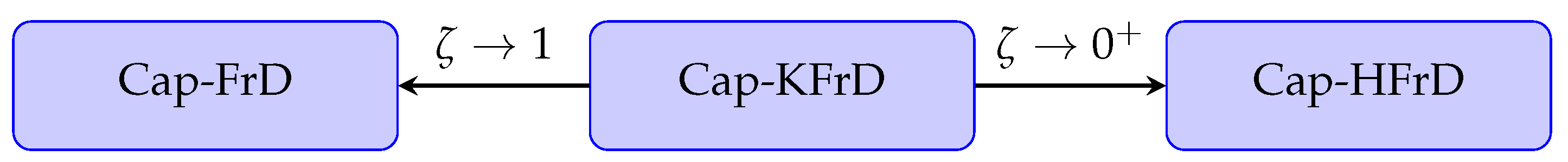
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djaouti, A.M.; Liaqat, M.I. Generalized Grönwall Inequality and Ulam–Hyers Stability in ℒp Space for Fractional Stochastic Delay Integro-Differential Equations. Mathematics 2025, 13, 1252. https://doi.org/10.3390/math13081252
Djaouti AM, Liaqat MI. Generalized Grönwall Inequality and Ulam–Hyers Stability in ℒp Space for Fractional Stochastic Delay Integro-Differential Equations. Mathematics. 2025; 13(8):1252. https://doi.org/10.3390/math13081252
Chicago/Turabian StyleDjaouti, Abdelhamid Mohammed, and Muhammad Imran Liaqat. 2025. "Generalized Grönwall Inequality and Ulam–Hyers Stability in ℒp Space for Fractional Stochastic Delay Integro-Differential Equations" Mathematics 13, no. 8: 1252. https://doi.org/10.3390/math13081252
APA StyleDjaouti, A. M., & Liaqat, M. I. (2025). Generalized Grönwall Inequality and Ulam–Hyers Stability in ℒp Space for Fractional Stochastic Delay Integro-Differential Equations. Mathematics, 13(8), 1252. https://doi.org/10.3390/math13081252






