Differential Quadrature Method for Bending Analysis of Asymmetric Circular Organic Solar Cells Resting on Kerr Foundation in Hygrothermal Environment
Abstract
1. Introduction
2. Formulation of the Problem
2.1. Displacement Field
- The transverse normal stress is negligible when compared to the in-plane stresses and .
- The strains involved are very small due to the minimal displacements.
- The lateral displacement consists of two components: the shear component and the bending component .
- The in-plane displacements have two components: (a) The bending components and are analogous to the displacements and in classical plate theory. Their expressions are given by(b) The shear components and of the displacements and , in terms of , induce parabolic variations in the shear stresses and across the plate’s cross-section. These shear stresses are zero at the top and bottom surfaces of the plate, i.e., at and .
2.2. Hygrothermal Field
2.3. Kerr Foundation
2.4. Strain and Stress Field Relations
3. Governing Equations
4. Solution Methods
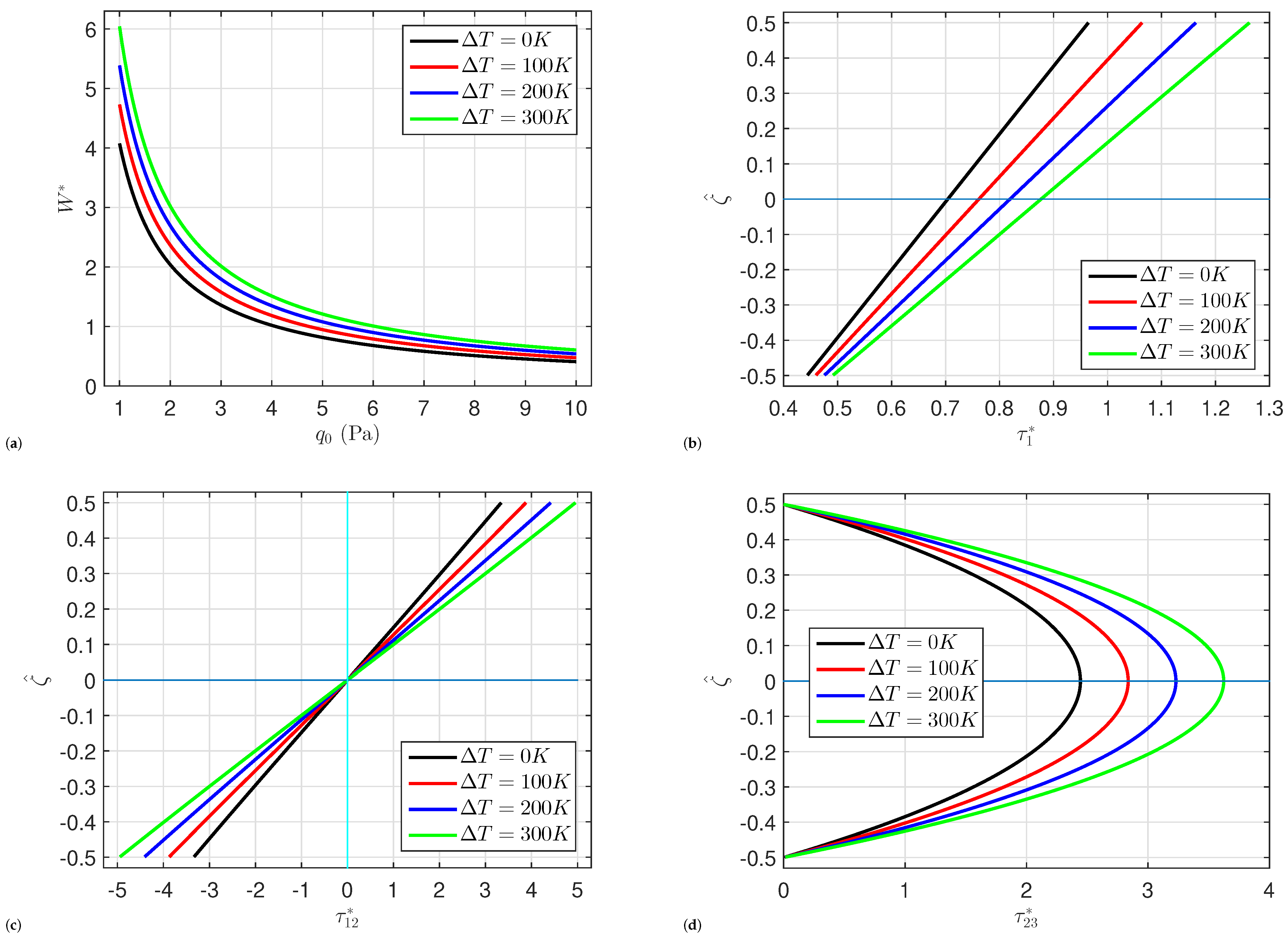
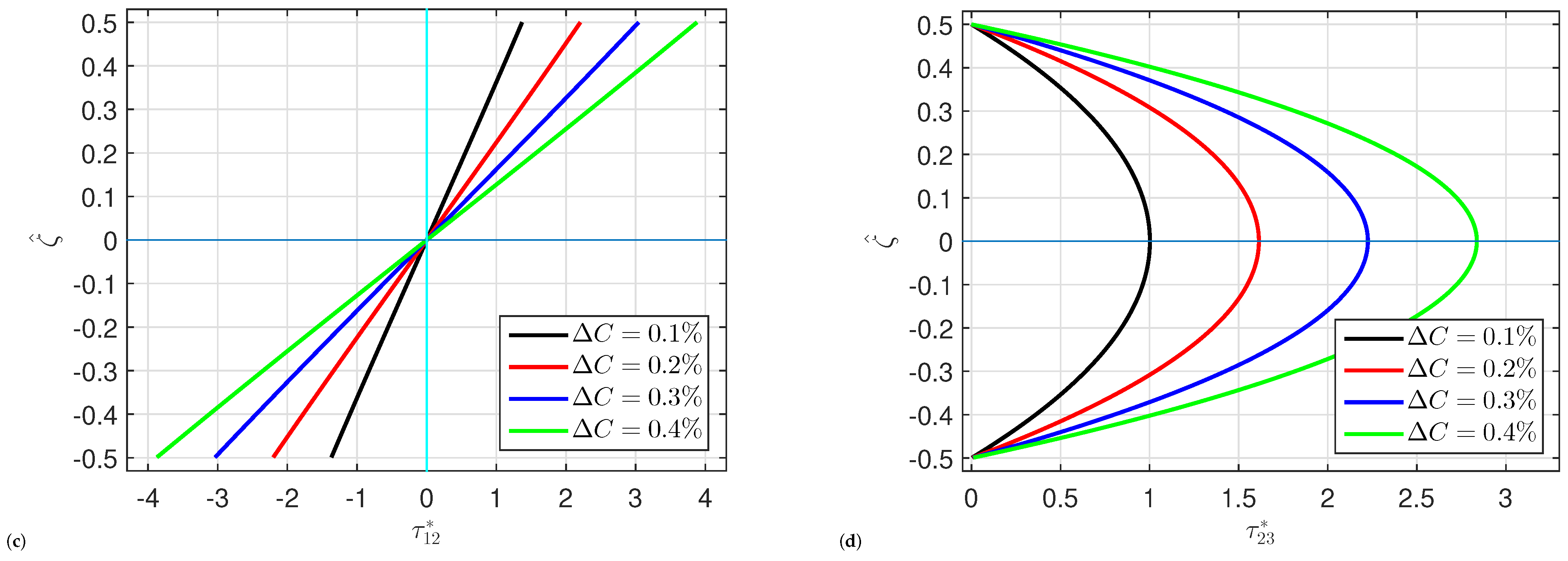
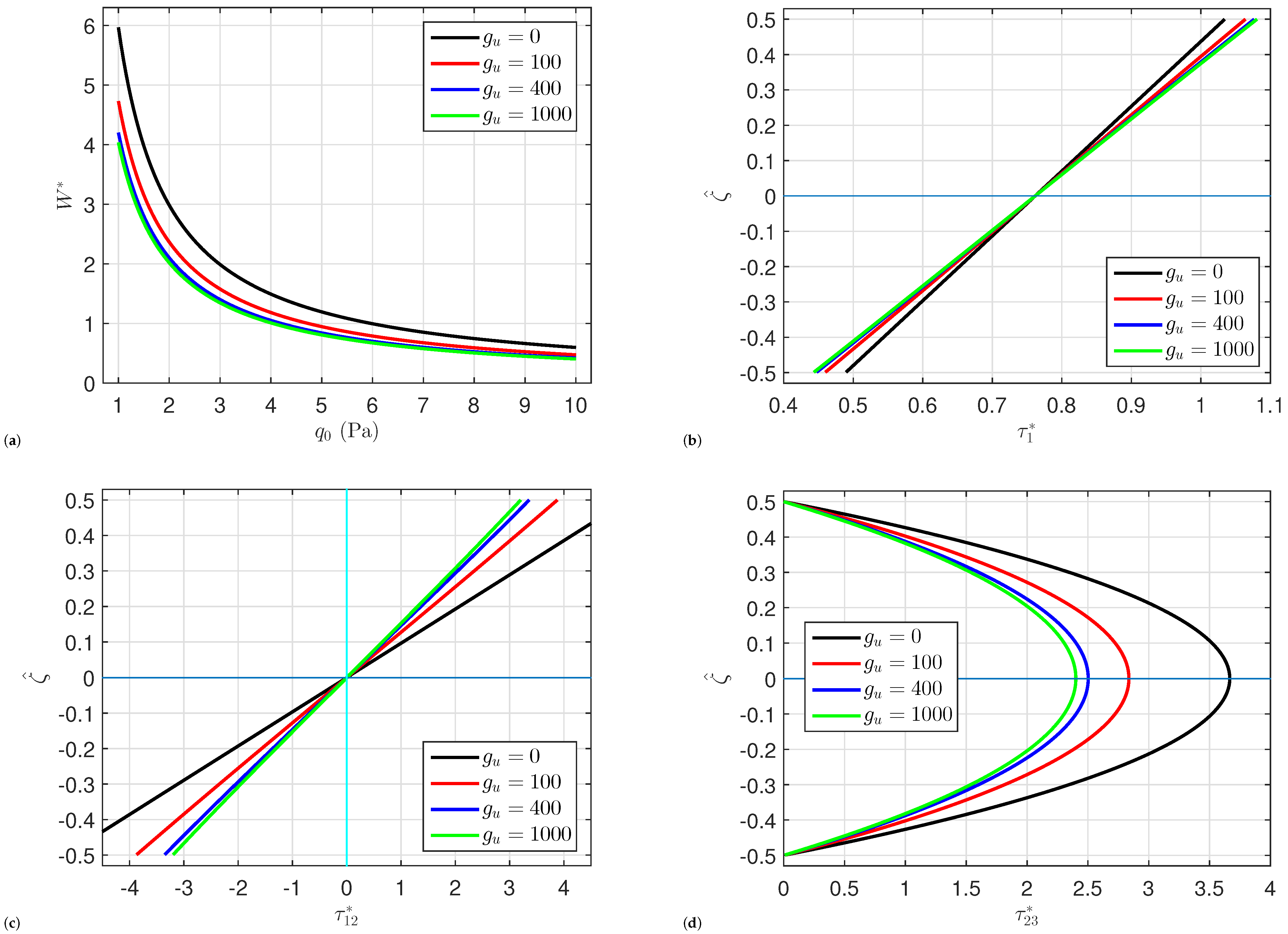
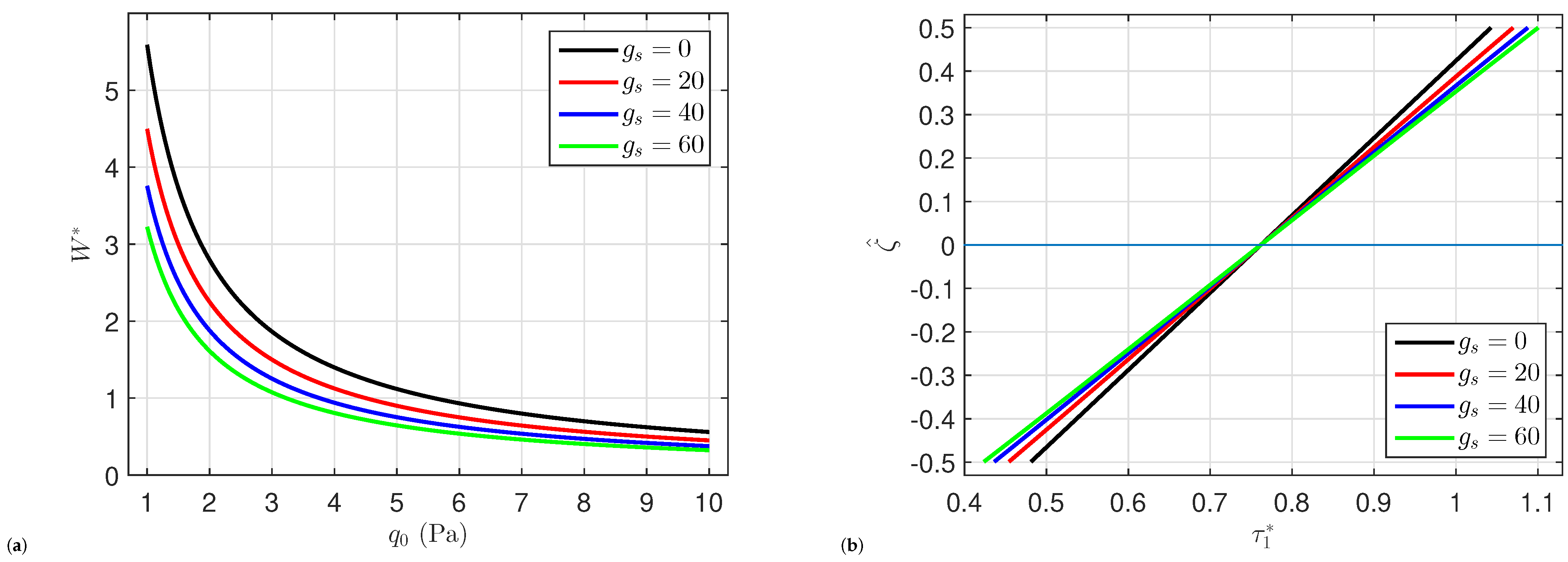
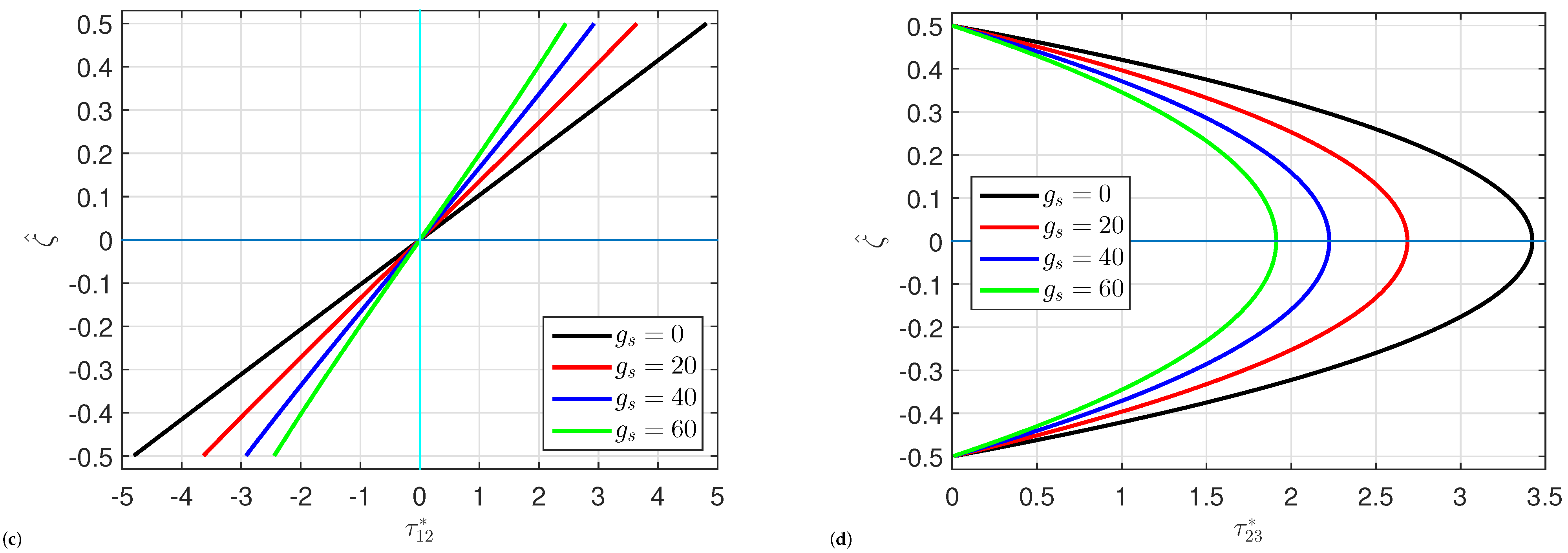
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Comello, S.; Reichelstein, S.; Sahoo, A. The road ahead for solar PV power. Renew. Sustain. Energy Rev. 2018, 92, 744–756. [Google Scholar]
- Guney, M.S. Solar power and application methods. Renew. Sustain. Energy Rev. 2016, 57, 776–785. [Google Scholar] [CrossRef]
- Bayoumi, A.S.A.; El-Sehiemy, R.A.; Badawy, M.; Elhosseini, M.; Aljohani, M.; Abaza, A. Optimizing multi-layer perovskite solar cell dynamic models with hysteresis consideration using artificial rabbits optimization. Mathematics 2023, 11, 4912. [Google Scholar] [CrossRef]
- Kalowekamo, J.; Baker, E. Estimating the manufacturing cost of purely organic solar cells. Sol. Energy 2009, 83, 1224–1231. [Google Scholar] [CrossRef]
- Kumavat, P.P.; Sonar, P.; Dalal, D.S. An overview on basics of organic and dye sensitized solar cells, their mechanism and recent improvements. Renew. Sustain. Energy Rev. 2017, 78, 1262–1287. [Google Scholar]
- Cardinaletti, I.; Vangerven, T.; Nagels, S.; Cornelissen, R.; Schreurs, D.; Hruby, J.; Vodnik, J.; Devisscher, D.; Kesters, J.; D’Haen, J.; et al. Organic and perovskite solar cells for space applications. Sol. Energy Mater. Sol. Cells 2018, 182, 121–127. [Google Scholar]
- Mbule, P.; Wang, D.; Grieseler, R.; Schaaf, P.; Muhsin, B.; Hoppe, H.; Mothudi, B.; Dhlamini, M. Aluminum-doped ZnO thin films deposited on flat and nanostructured glass substrates: Quality and performance for applications in organic solar cells. Sol. Energy 2018, 172, 219–224. [Google Scholar] [CrossRef]
- van Franeker, J.J.; Voorthuijzen, W.P.; Gorter, H.; Hendriks, K.H.; Janssen, R.A.; Hadipour, A.; Andriessen, R.; Galagan, Y. All-solution-processed organic solar cells with conventional architecture. Sol. Energy Mater. Sol. Cells 2013, 117, 267–272. [Google Scholar]
- Li, Q.; Wu, D.; Gao, W.; Tin-Loi, F.; Liu, Z.; Cheng, J. Static bending and free vibration of organic solar cell resting on Winkler-Pasternak elastic foundation through the modified strain gradient theory. Eur. J. Mech.-A/Solids 2019, 78, 103852. [Google Scholar]
- Li, Q.; Wu, D.; Gao, W.; Tin-Loi, F. Size-dependent instability of organic solar cell resting on Winkler–Pasternak elastic foundation based on the modified strain gradient theory. Int. J. Mech. Sci. 2020, 177, 105306. [Google Scholar]
- Duc, N.D.; Seung-Eock, K.; Quan, T.Q.; Long, D.D.; Anh, V.M. Nonlinear dynamic response and vibration of nanocomposite multilayer organic solar cell. Compos. Struct. 2018, 184, 1137–1144. [Google Scholar]
- Dat, N.D.; Anh, V.M.; Quan, T.Q.; Duc, P.T.; Duc, N.D. Nonlinear stability and optimization of thin nanocomposite multilayer organic solar cell using Bees Algorithm. Thin-Walled Struct. 2020, 149, 106520. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Q.; Wu, D.; Chen, X.; Yu, Y.; Gao, W. Geometrically nonlinear dynamic analysis of organic solar cell resting on Winkler-Pasternak elastic foundation under thermal environment. Compos. Part B Eng. 2019, 163, 121–129. [Google Scholar]
- Wang, Y.; Tham, L.; Cheung, Y. Beams and plates on elastic foundations: A review. Prog. Struct. Eng. Mater. 2005, 7, 174–182. [Google Scholar] [CrossRef]
- Avey, M.; Tornabene, F.; Aslanova, N.M.; Sofiyev, A.H. The Application of the Modified Lindstedt–Poincaré Method to Solve the Nonlinear Vibration Problem of Exponentially Graded Laminated Plates on Elastic Foundations. Mathematics 2024, 12, 749. [Google Scholar] [CrossRef]
- Gu, M.; Cai, X.; Fu, Q.; Li, H.; Wang, X.; Mao, B. Numerical analysis of passive piles under surcharge load in extensively deep soft soil. Buildings 2022, 12, 1988. [Google Scholar] [CrossRef]
- Kolahchi, R.; Safari, M.; Esmailpour, M. Dynamic stability analysis of temperature-dependent functionally graded CNT-reinforced visco-plates resting on orthotropic elastomeric medium. Compos. Struct. 2016, 150, 255–265. [Google Scholar]
- Pasternak, P. On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants; Gosudarstvennoe Izdatelstro Liberaturi po Stroitelstvui Arkhitekture: Moscow, Russia, 1954. [Google Scholar]
- Kerr, A.D. Elastic and viscoelastic foundation models. J. Appl. Mech. 1964, 31, 491–498. [Google Scholar]
- Shimpi, R.P. Refined plate theory and its variants. AIAA J. 2002, 40, 137–146. [Google Scholar]
- Reddy, J. A refined nonlinear theory of plates with transverse shear deformation. Int. J. Solids Struct. 1984, 20, 881–896. [Google Scholar]
- Touratier, M. An efficient standard plate theory. Int. J. Eng. Sci. 1991, 29, 901–916. [Google Scholar] [CrossRef]
- Soldatos, K. A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mech. 1992, 94, 195–220. [Google Scholar] [CrossRef]
- Karama, M.; Afaq, K.; Mistou, S. Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. Int. J. Solids Struct. 2003, 40, 1525–1546. [Google Scholar] [CrossRef]
- Tounsi, A.; Al-Dulaijan, S.; Al-Osta, M.A.; Chikh, A.; Al-Zahrani, M.; Sharif, A.; Tounsi, A. A four variable trigonometric integral plate theory for hygro-thermo-mechanical bending analysis of AFG ceramic-metal plates resting on a two-parameter elastic foundation. Steel Compos. Struct. Int. J. 2020, 34, 511–524. [Google Scholar]
- Matouk, H.; Bousahla, A.A.; Heireche, H.; Bourada, F.; Bedia, E.; Tounsi, A.; Mahmoud, S.; Tounsi, A.; Benrahou, K. Investigation on hygro-thermal vibration of P-FG and symmetric S-FG nanobeam using integral Timoshenko beam theory. Adv. Nano Res. 2020, 8, 293–305. [Google Scholar]
- Refrafi, S.; Bousahla, A.A.; Bouhadra, A.; Menasria, A.; Bourada, F.; Tounsi, A.; Bedia, E.A.; Mahmoud, S.; Benrahou, K.H.; Tounsi, A. Effects of hygro-thermo-mechanical conditions on the buckling of FG sandwich plates resting on elastic foundations. Comput. Concr. Int. J. 2020, 25, 311–325. [Google Scholar]
- Sobhy, M. Differential quadrature method for magneto-hygrothermal bending of functionally graded graphene/Al sandwich-curved beams with honeycomb core via a new higher-order theory. J. Sandw. Struct. Mater. 2021, 23, 1662–1700. [Google Scholar] [CrossRef]
- Kneifati, M.C. Analysis of plates on a Kerr foundation model. J. Eng. Mech. 1985, 111, 1325–1342. [Google Scholar] [CrossRef]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Safarpour, M.; Rahimi, A.; Alibeigloo, A.; Bisheh, H.; Forooghi, A. Parametric study of three-dimensional bending and frequency of FG-GPLRC porous circular and annular plates on different boundary conditions. Mech. Based Des. Struct. Mach. 2021, 49, 707–737. [Google Scholar] [CrossRef]
- Sobhy, M. 3-D elasticity numerical solution for magneto-hygrothermal bending of FG graphene/metal circular and annular plates on an elastic medium. Eur. J. Mech.-A/Solids 2021, 88, 104265. [Google Scholar] [CrossRef]
- Al Mukahal, F.H.H.; Alsebai, F.; Sobhy, M. Applying levy and DQ methods to hygrothermal deformation of piezoelectric/GPLs plates with porosities lying on elastic foundations using a quasi-3D plate theory. Mathematics 2025, 13, 764. [Google Scholar] [CrossRef]
- Mustafa, A.; Salama, R.S.; Mohamed, M. Semi-analytical analysis of drug diffusion through a thin membrane using the differential quadrature method. Mathematics 2023, 11, 2998. [Google Scholar] [CrossRef]
- Golmakani, M.; Vahabi, H. Nonlocal buckling analysis of functionally graded annular nanoplates in an elastic medium with various boundary conditions. Microsyst. Technol. 2017, 23, 3613–3628. [Google Scholar] [CrossRef]
- Demir, O.; Balkan, D.; Peker, R.C.; Metin, M.; Arikoglu, A. Vibration analysis of curved composite sandwich beams with viscoelastic core by using differential quadrature method. J. Sandw. Struct. Mater. 2020, 22, 743–770. [Google Scholar] [CrossRef]
- Sobhy, M. Piezoelectric bending of GPL-reinforced annular and circular sandwich nanoplates with FG porous core integrated with sensor and actuator using DQM. Arch. Civ. Mech. Eng. 2021, 21, 78. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Reddy, J.; Wang, C.; Kitipornchai, S. Axisymmetric bending of functionally graded circular and annular plates. Eur. J. Mech.-A/Solids 1999, 18, 185–199. [Google Scholar] [CrossRef]
- Yun, W.; Rongqiao, X.; Haojiang, D. Three-dimensional solution of axisymmetric bending of functionally graded circular plates. Compos. Struct. 2010, 92, 1683–1693. [Google Scholar] [CrossRef]
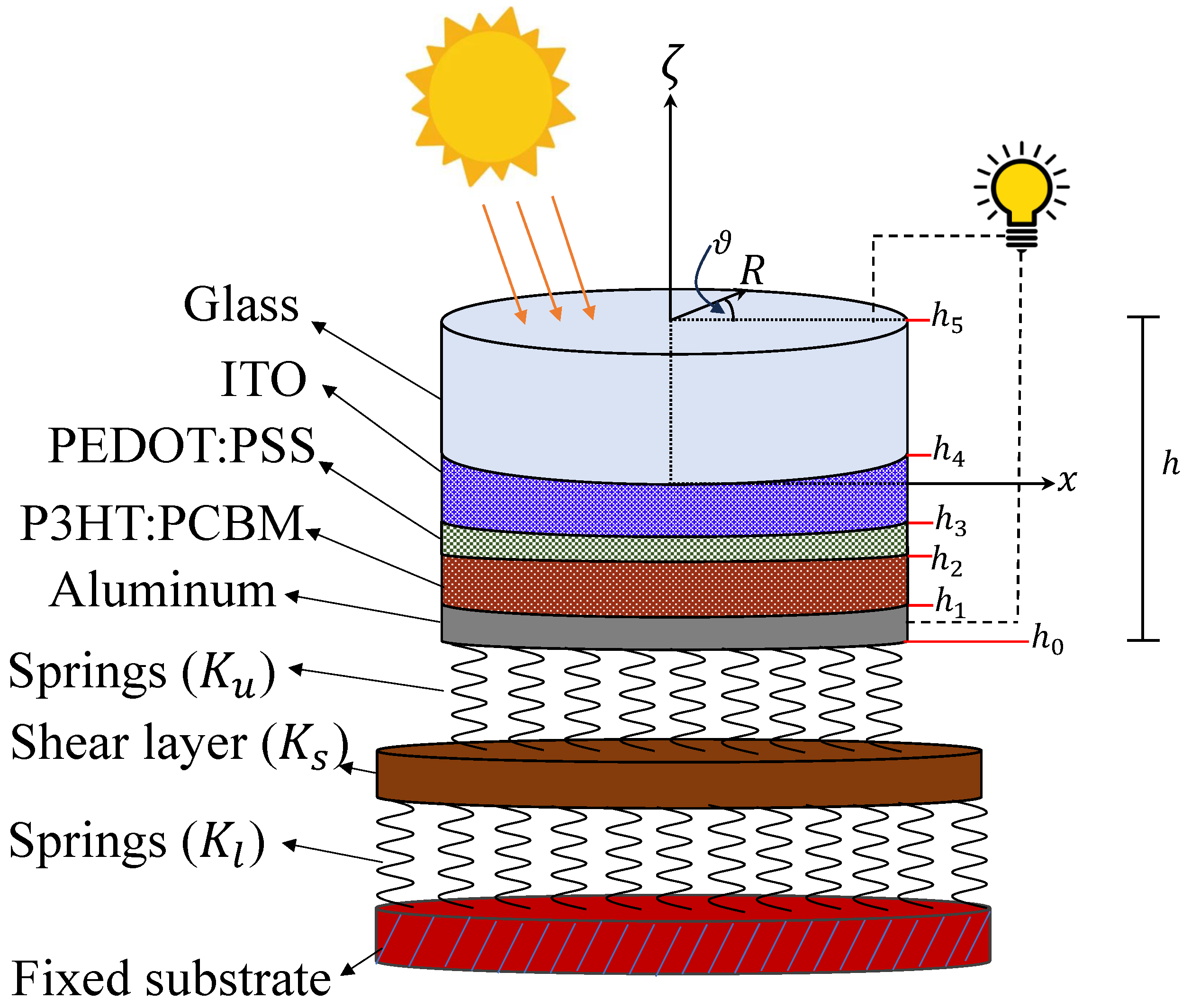



| Layer | Material | Thickness (h) | E (GPa) | (g/cm3) | (K−1) | (wt.%H2O)−1 | |
|---|---|---|---|---|---|---|---|
| 1 | Aluminum | 70 | |||||
| 2 | P3HT:PCBM | 6 | |||||
| 3 | PEDOT:PSS | 1 | |||||
| 4 | ITO | 116 | |||||
| 5 | Glass | 69 |
| n | |||||||
|---|---|---|---|---|---|---|---|
| 5 | 0.586 | 1.215 | 2.772 | 2.384 | 1.215 | 5.468 | |
| 7 | 0.585 | 1.218 | 3.114 | 2.382 | 1.218 | 6.269 | |
| 9 | 0.575 | 1.219 | 3.361 | 2.340 | 1.219 | 6.757 | |
| 11 | 0.575 | 1.219 | 3.353 | 2.342 | 1.219 | 6.740 | |
| 13 | 0.575 | 1.219 | 3.352 | 2.341 | 1.219 | 6.737 | |
| 15 | 0.575 | 1.219 | 3.352 | 2.341 | 1.219 | 6.737 | |
| Source | 2 | 4 | 6 | 8 | 10 | 15 | 20 | ||
|---|---|---|---|---|---|---|---|---|---|
| 0.05 | Present | 2.559 | 1.335 | 1.249 | 1.202 | 1.171 | 1.148 | 1.112 | 1.091 |
| Ref [37] | 2.561 | 1.405 | 1.284 | 1.222 | 1.184 | 1.157 | 1.117 | 1.094 | |
| Ref [40] | 2.551 | 1.400 | 1.280 | 1.218 | 1.179 | 1.152 | 1.112 | 1.089 | |
| Ref [39] | 2.554 | 1.402 | 1.282 | 1.220 | 1.181 | 1.155 | 1.114 | 1.092 | |
| 0.1 | Present | 2.661 | 1.384 | 1.293 | 1.244 | 1.212 | 1.189 | 1.153 | 1.132 |
| Ref [37] | 2.667 | 1.457 | 1.330 | 1.267 | 1.227 | 1.200 | 1.160 | 1.137 | |
| Ref [40] | 2.626 | 1.438 | 1.313 | 1.250 | 1.210 | 1.183 | 1.142 | 1.119 | |
| Ref [39] | 2.639 | 1.444 | 1.320 | 1.257 | 1.217 | 1.190 | 1.149 | 1.126 | |
| 0.15 | Present | 2.832 | 1.466 | 1.366 | 1.315 | 1.282 | 1.258 | 1.221 | 1.200 |
| Ref [37] | 2.844 | 1.542 | 1.407 | 1.340 | 1.300 | 1.272 | 1.231 | 1.208 | |
| Ref [40] | 2.751 | 1.500 | 1.368 | 1.302 | 1.262 | 1.234 | 1.193 | 1.169 | |
| Ref [39] | 2.781 | 1.515 | 1.384 | 1.318 | 1.278 | 1.250 | 1.208 | 1.184 | |
| 0.2 | Present | 3.070 | 1.580 | 1.469 | 1.414 | 1.379 | 1.355 | 1.317 | 1.296 |
| Ref [37] | 3.093 | 1.661 | 1.514 | 1.444 | 1.401 | 1.373 | 1.331 | 1.307 | |
| Ref [40] | 2.925 | 1.586 | 1.445 | 1.376 | 1.334 | 1.306 | 1.263 | 1.239 | |
| Ref [39] | 2.979 | 1.613 | 1.473 | 1.404 | 1.362 | 1.333 | 1.289 | 1.265 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abazid, M.A.; Alali, M.; Sobhy, M. Differential Quadrature Method for Bending Analysis of Asymmetric Circular Organic Solar Cells Resting on Kerr Foundation in Hygrothermal Environment. Mathematics 2025, 13, 1203. https://doi.org/10.3390/math13071203
Abazid MA, Alali M, Sobhy M. Differential Quadrature Method for Bending Analysis of Asymmetric Circular Organic Solar Cells Resting on Kerr Foundation in Hygrothermal Environment. Mathematics. 2025; 13(7):1203. https://doi.org/10.3390/math13071203
Chicago/Turabian StyleAbazid, Mohammad A., Muneer Alali, and Mohammed Sobhy. 2025. "Differential Quadrature Method for Bending Analysis of Asymmetric Circular Organic Solar Cells Resting on Kerr Foundation in Hygrothermal Environment" Mathematics 13, no. 7: 1203. https://doi.org/10.3390/math13071203
APA StyleAbazid, M. A., Alali, M., & Sobhy, M. (2025). Differential Quadrature Method for Bending Analysis of Asymmetric Circular Organic Solar Cells Resting on Kerr Foundation in Hygrothermal Environment. Mathematics, 13(7), 1203. https://doi.org/10.3390/math13071203






