Abstract
This paper introduces an integrated inventory model that employs customized neural networks to tackle the challenge of non-stationary demand for newsvendor-type products, such as vegetables and fashion items. In this newsvendor context, demand is intertemporal-dependent and influenced by external factors such as prices, promotions, and holidays. Contrary to traditional machine-learning-based inventory models that assume stationary and independent demand, our method accounts for the temporal dynamics and the impact of external factors on demand. Our customized neural network model integrates demand estimation with inventory optimization, circumventing the potential suboptimality of sequential estimation and optimization methods. We conduct a case study on optimizing the vegetable ordering decisions for a supermarket. The findings indicate the proposed model’s effectiveness in enhancing ordering decisions, thereby reducing inventory costs by up to 21.14%. By customizing an integrated neural network, this paper presents a precise and cost-effective inventory management solution to address real-world complexities of demand, like seasonality and external factor dependency. The proposed approach is particularly beneficial for retailers in industries dealing with perishable items and market volatility, enabling them to mitigate waste (e.g., unsold vegetables) and stockouts (e.g., seasonal fashion items). This directly confronts challenges related to sustainability and profitability. Furthermore, the integrated framework provides a methodological inspiration for adapting neural networks to other time-sensitive supply chain problems.
Keywords:
ordering optimization; non-stationary demand; external feature; integrated method; neural networks MSC:
90B05
1. Introduction
Inventory optimization is a critical challenge in operations management and supply chain management. The newsvendor model is widely used for the inventory control of items such as perishables, seasonal goods, and fast-fashion products. It helps to solve the problem of finding the optimal ordering quantity under demand uncertainty, assisting firms in striking a balance between overage and underage. In this model, the product demand is characterized by a stochastic variable, and ordering decisions are required to be made before sales start. A large order quantity may lead to overage costs, as the unsold products should be dealt with at the end of the sales period. Conversely, a small order quantity may result in underage costs, with the unmet demand lost. The decision-maker needs to determine the order quantity to minimize the total costs. Traditional newsvendor models are optimized based on the assumption that the random demand follows a known distribution; see textbook discussion in [1,2], etc. However, this assumption is often impractical, as the underlying demand distribution typically remains unknown [3], with only demand observations being available for analysis [4,5,6,7,8,9].
Recently, machine-learning-based inventory models have emerged, which base inventory decisions on observed demand data without relying on assumptions about the underlying demand distribution. An intuitive machine-learning-based approach is to first estimate the demand distribution using machine learning methods based on historical demand data and to then optimize the ordering decisions using this estimated distribution. Nevertheless, this sequential method introduces an estimation error into the subsequent optimization process, resulting in suboptimal ordering decisions [4]. To mitigate this issue, researchers have introduced end-to-end methodologies that integrate prediction and optimization to derive ordering decisions directly from data. These approaches usually employ not only historical demand data but also demand-related feature information, such as product characteristics, promotions, prices, and the day of the week. For example, studies [5,6,10] utilize neural networks to approximate the mapping from features to ordering decisions. They reformulate the newsvendor problem to align with the training objectives of neural networks, thereby enabling the direct learning of order quantity from historical demand data and associated feature information. Nonetheless, the majority of these data-driven inventory optimization approaches assume that demand is independent and identically distributed (i.i.d.), a premise that frequently does not hold in practical scenarios. For instance, in the realms of seasonal product sales, the fashion industry, and the rapidly evolving electronics market, demand is influenced by external factors, including product characteristics, promotion, and prices, while also exhibiting intertemporal dependence.
Despite the widespread occurrence of time-varying demand influenced by multiple external factors in inventory management across industries, the current literature addressing this multifaceted challenge for the data-driven newsvendor remains notably sparse. To the best of our knowledge, only Qi et al. [9] explores this problem within the newsvendor context, extending earlier methodologies from [4,11] through enhanced linear regression and kernel methods. However, an important opportunity remains unaddressed in existing studies: while prior methodologies (e.g., linear regression and kernel methods) have advanced the handling of demand complexity, the literature has not yet fully explored the integration of neural networks (NNs) for modeling the complex relationships between historical demand, external factors, and ordering decisions. Specifically, fully connected networks demonstrate strong performance in inventory management with i.i.d. data [5,6]. Long short-term memory (LSTM) performs well on sequential data [12,13,14,15]. Therefore, this paper aims to fill this gap by incorporating hybrid neural networks to enhance the effectiveness of addressing non-stationary demand in the newsvendor context.
In this paper, we propose a novel approach that integrates estimation and optimization through a customized, hybrid neural network. The integrated neural network framework is tailored to simultaneously process the intertemporal correlations of demand and incorporate the impact of non-temporal features on inventory decisions. The framework leverages neural networks’ proven effectiveness in inventory management [5,6,10] and LSTM’s capacity to model temporal dependencies [12,13,14,15,16]. The proposed method adopts the integrated estimation-and-optimization paradigm to avoid suboptimality caused by separated steps [4]. We test our method on a real-world dataset for vegetable ordering decisions. The results show that our method significantly reduces costs by up to 21.14%, outperforming benchmark methods, including the conventional LSTM-based method. This confirms that our model can effectively handle the complex relationship between historical demand, related features, and ordering decisions.
The main contributions of this paper are threefold. First, it extends the data-driven newsvendor research by considering both the non-linear effects of demand autocorrelation and external factors on ordering decisions. This provides a more realistic representation of the demand dynamics in the newsvendor context. Secondly, we introduce a novel integrated approach that leverages customized hybrid neural networks. This innovation in methodology broadens the application of neural networks in operations research and quantile regression. Lastly, the results of numerical experiments on real-world data demonstrate that our method outperforms conventional LSTM-based approaches. These findings provide valuable insights for enhancing decision-making processes in supply chain management.
The subsequent sections are structured as follows. Following this introductory section, Section 2 provides a comprehensive review of the relevant literature. Section 3 describes the problem, introduces the custom hybrid neural network, and details the integrated framework designed for ordering optimization. Section 4 presents numerical experiments performed to employ the customized neural network for the ordering optimization of vegetables for a supermarket. Section 5 presents the experimental results and discusses the theoretical and practical implications. Finally, Section 6 concludes this paper and proposes directions for further investigation.
2. Literature Review
In this study, we propose an integrated neural-network-based method for the data-driven newsvendor problem with intertemporal-dependent demand and external features. Our study is related to three streams of literature: the data-driven newsvendor with independent and identically distributed (i.i.d.) demand, data-driven inventory management with non-i.i.d. demand, and neural-network-based methods for the newsvendor.
The newsvendor problem is a classic model in inventory management. The literature offers a comprehensive review of the classic newsvendor problem and its extensions, as seen in references [17,18]. Our study is aligned with data-driven methodologies, which are increasingly popular in this field. When using data-driven methods for the newsvendor problem, a typical parametric method is to assume a specific form for the demand distribution while allowing its parameters (e.g., mean and variance in a norm distribution) to be unknown. These parameters are estimated from the collected data, and the resulting demand distribution is used for further inventory optimization. Our approach differs by not making any assumptions about the demand distribution, classifying it as a nonparametric method. Moreover, it aligns with integrated data-driven approaches, where ordering decisions are optimized directly using historical data. The sample average approximation (SAA) method is a well-known example of this, as detailed in references [7,19,20,21]. The SAA method relies solely on historical demand data and the i.i.d. demand assumption. Some studies explore the impact of external features information on demand and employ machine learning to address the newsvendor problem. For example, studies [4,22] incorporate linear regression into the newsvendor model, while studies [5,6,23] combine neural networks with the model to capture complex relationships. However, these studies generally assume i.i.d. demand or i.i.d. random disturbances, a simplification that may not hold in cases where demand changes over time [24].
Recent research in data-driven inventory optimization has increasingly focused on addressing the challenges by non-i.i.d demand [8,25,26,27,28,29,30]. Cao and Shen [29] introduces a double parallel feedforward network approach for handling time-dependent demand, utilizing quantile regression techniques to derive optimal inventory decisions for newsvendors directly from historical demand data. Dehaybe et al. [30] employs deep reinforcement learning to optimize the lot size for a single-item multi-period inventory system with non-stationary demand. These studies, however, primarily rely on demand data alone, i.e., only taking into account demand autocorrelation, without considering the impact of external factors. Qi et al. [9] extends the research of Ban and Rudin [4] by theoretically proving the out-of-sample performance bounds of learning algorithms in the presence of autocorrelated and non-stationary demand. We extend the literature by addressing the newsvendor problem, where demand is autocorrelated and influenced by external features, and by proposing a novel approach for learning inventory decisions through customizing novel integrated neural networks.
There has been a burgeoning body of research that incorporates neural networks within the fields of operations management and supply chain management. Recent studies have primarily focused on improving demand forecasting accuracy using neural networks, as evidenced by the literature [16,31,32,33,34,35,36,37]. As mentioned earlier, studies [5,6,23] develop end-to-end data-driven newsvendor methods integrating demand forecasting and inventory optimization based on neural networks. Qi et al. [10] proposes an end-to-end learning approach for the multi-period inventory problem with uncertain demand and random lead time by designing a novel neural network to learn inventory decisions directly from historical data. Inspired by Qi et al. [10], we develop a novel end-to-end neural network. It integrates the predictive capabilities of long short-term memory (LSTM) networks [12] on sequential data [13,14,15,16] with the complex relationship-capturing ability of fully connected networks. The hybrid approach can effectively address the complexity introduced by time-correlated demand and external demand-related feature information in the newsvendor problem.
To sum up, recent research has made strides in addressing non-i.i.d. demand for inventory management through advanced machine learning techniques. However, a critical gap persists in the integration of external feature information and the handling of time-correlated demand within a unified framework. Existing methods predominantly focus on demand autocorrelation or isolated external factors, with limitations in capturing the multifaceted drivers of demand variability. Our work bridges this gap by introducing a hybrid neural network model that synergizes LSTM networks for temporal pattern recognition with fully connected networks to incorporate external features. This end-to-end approach not only optimizes inventory decisions under autocorrelated demand but also leverages contextual data, offering a robust solution for real-world applications. By unifying these elements, our contribution advances the theoretical and practical scope of data-driven newsvendor models, enabling more adaptive and resilient inventory management systems.
3. Methodology
In this section, we present the customized neural-network-based methodology for tackling the challenges of the newsvendor problem with intertemporal-dependent demand and external features. Section 3.1 provides a detailed description of the problem, highlighting the challenges posed by the lack of a known demand distribution and the presence of non-stationary demand. In Section 3.2, we introduce the core of our approach, where we develop a custom neural network with a specialized loss function and hybrid architecture tailored to the non-stationary demand. Section 3.3 outlines the integrated framework of our approach, detailing the steps involved in data preprocessing, transforming, neural network design, hyperparameter tuning, and model training and evaluation. The proposed method ensures a systematic and efficient approach to inventory optimization, leveraging the learning power of neural networks and data-driven insights.
3.1. Problem Description
In the newsvendor problem, the decision-maker confronts the challenge of determining the optimal order quantity before the uncertain demand is realized. Let the random demand be denoted by , order decision by , and the demand realization by d. In the event of overordering, where , the excess quantities incur overage costs. We denote as the unit overage cost. Conversely, underordering, characterized by , leads to lost sales due to unmet demand. We denote as the unit underage cost. The decision-maker’s objective is to find an ordering strategy that minimizes the expected total cost. Thus, the optimization problem is formulated as
where . With the demand distribution function denoted by , the optimal ordering decision is obtained by , where . The parameter can be conceptualized as the “target service level” at which the decision-maker achieves the minimum expected inventory cost [5]. However, in practice, the demand distribution is often unknown. The decision-maker makes ordering decisions based on historical demand observations and external demand-related feature data, such as price, product characteristics, and holiday effects. Denote the historical observations of demand as , with n indicating the sample size. Denote the external feature data as , where represents the observed values of . Certain studies, including but not limited to studies [4,5,6], employ machine learning to characterize the relationship between external features and decisions. We denote the relationship as . These methods are grounded in the principle of empirical risk minimization (ERM), which aims to minimize the average newsvendor cost over the available data. Consequently, the optimization problem becomes
Unfortunately, these studies do not account for the autocorrelation of demand. In this paper, we simultaneously consider the impact of demand autocorrelation and external demand-related feature information in the inventory decision-making process. We denote the time steps for demand autocorrelation as T and the demand history vector as . By developing a customized neural network, we propose an integrated learning method that takes and as inputs and outputs the ordering quantity decision, denoted as .
3.2. Custom Hybrid Neural Network
A hybrid neural network is customized for the integrated inventory model. We customize the operational loss function of the ordering optimization problem for the neural network. The customized loss function allows for learning ordering decisions directly from data. The loss function is then smoothened by the Huber approximation, enabling its use in neural network training. Subsequently, the architecture of custom hybrid neural networks is specifically designed to handle the intertemporal dependencies in demand and incorporate the influence of external features. Furthermore, performance metrics for model evaluation are specified to align with our inventory optimization problem.
3.2.1. Custom Newsvendor Loss Function
Based on the principle of empirical risk minimization (ERM), the optimization problem for the newsvendor problem with intertemporal-dependent demand and external features is formulated by
With , Problem (3) is normalized as
It is obvious that Problem (4) is equivalent to the problem of quantile regression [38]. Thus, this study extends the methodological research on quantile regression. Moreover, as neural networks are typically trained based on stochastic gradient methods [39], the gradients of the objective function are needed. However, the gradient of does not exist when . Therefore, following studies [29,40,41], the Huber approximation is used to smooth Equation (4); that is,
where
and is a smoothing parameter with a small real value. The Huber approximation introduces a quadratic region near to ensure differentiability, while maintaining linearity in the tails to mitigate outlier sensitivity. Equation (5) is employed as the objective function (also known as loss function) in the integrated neural-network-based methods in the numerical experiments.
3.2.2. Hybrid Neural Network Structure
The immediate objective of the integrated learning method is to determine the optimal mapping function , which effectively captures the complex relationship between input data (historical demand sequence and external features) and the resulting ordering decisions. To tackle this challenge, a tailored hybrid neural network is developed, with its configuration depicted in Figure 1. This custom hybrid neural network is designed with two separate input layers, three hidden layers, and one output layer. Within this framework, the external feature data and the historical demand observations are processed independently by their respective dedicated hidden layers. Subsequently, their processed outputs are concatenated and further refined by the third hidden layer, prior to generating the final ordering decision outputs.
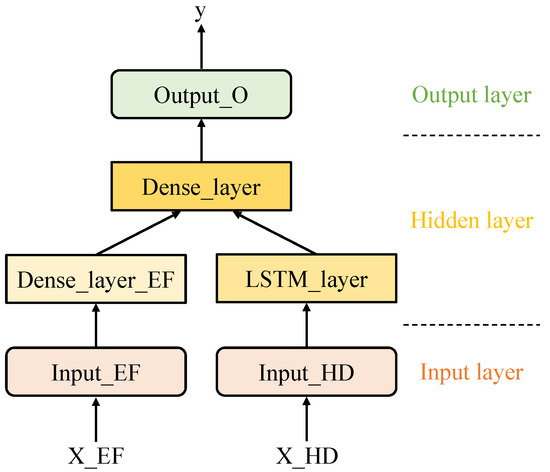
Figure 1.
The architecture of the custom hybrid neural network.
In the input layers of the hybrid neural network, the Input_EF layer processes the current period’s external feature data (i.e., ), represented as a 2D tensor with dimension . The Input_HD layer accepts the historical demand sequence (i.e., ), formatted as a 3D tensor with dimension . The external feature data serve to encapsulate the impact of external factors on decisions, whereas the historical demand data are employed to capture demands’ temporal dependencies influencing decisions. There are three components in the hidden layers. A fully connected layer, named Dense_layer_EF, is linked directly to the Input_EF layer, and an LSTM layer, named LSTM_layer, is connected to the Input_HD layer. The Dense_layer_EF is set for processing external feature information. The LSTM_layer leverages the good performance of LSTM’s ability to process sequential data, capturing the temporal correlation of demand. The LSTM’s gating mechanisms (forget, input, and output gates) dynamically control the flow of information to model long-term trends and seasonal fluctuations. Subsequently, the processed outputs from the Dense_layer_EF and LSTM_layer are then concatenated via a fully connected layer, Dense_layer, which is designed to integrate the effects of both external features and historical demand on decision making. Lastly, the Output_O layer produces the order quantity decisions.
The custom hybrid neural network architecture separates the impact of different input data on decisions and reduces node-to-node connections, thereby simplifying the network structure and lowering computational demands. The key hyperparameters of the custom hybrid neural network, such as the number of units in each hidden layer and the batch size in gradient-based training, are optimized via grid search and repeated random sub-sampling validation (RRSSV) as detailed in Section 3.3.
3.2.3. Performance Metrics
Given that our focus is on the optimization of ordering quantities rather than demand prediction, traditional model evaluation metrics such as mean squared error (MSE) and mean absolute error (MAE) are insufficient for accurately measuring the decision-making errors of our approaches. Instead, we employ metrics that are relevant to inventory management performance. The primary metric used is the out-of-sample average newsvendor cost on the test set, which is calculated as
where
To better illustrate the cost-saving advantage of our model, we calculate the percentage improvement in newsvendor cost compared to the most costly model (baseline cost), which is formulated as
Moreover, we analyze the service level of the models. Service level in the newsvendor problem is defined as the probability of not experiencing a stockout, which is a frequently used performance metric in inventory management [42]. The target service level (TSL) corresponds to the cost parameter . The target service level varies by industry and even by product due to differences in product price, ordering costs, salvage value, out-of-stock costs, etc. These differences result in the difference in the overage cost and in the underage cost in the newsvendor problem, and thus the difference in . We estimate the realized service level (RSL) by the proportion of instances in the test set that did not experience stockouts. We also calculate the service level gap (ΔSL) between the realized service level and the target service level. A smaller service level gap indicates better model performance. The formula for estimating the realized service level and calculating the service level gap is given, respectively, by
By utilizing these performance metrics, we are able to comprehensively evaluate the effectiveness of the neural-network-based models in inventory optimization.
3.3. Integrated Newsvendor Framework
For the considered data-driven newsvendor, we propose an integrated method with a tailored hybrid neural network. The experimental framework of our approach is presented in Figure 2. We summarize the framework into five steps, including data preprocessing, data transforming, integrated neural network design, hyperparameter tuning, and model training and evaluation. Each of these steps is explained in detail below.
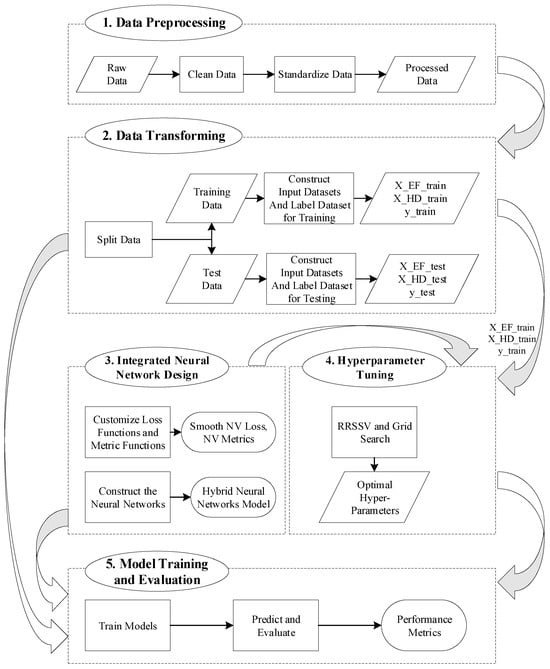
Figure 2.
The framework of the integrated newsvendor approach based on custom hybrid neural networks.
(1) Data Preprocessing. The initial phase of the experiment involves the collection of experimental data. The experimental data consist of historical demand data and external demand-related feature data, such as product prices and product characteristics. Subsequent to data collection, the raw data are subjected to a cleaning process. This processing includes the handling of outliers and the imputation of missing data. In addition, data standardization is crucial for ensuring comparability, with methods including min-max scaling, z-score standardization, and log transformation. Following these preprocessing steps, the resulting dataset is denoted as , where each element represents an observation in one period.
(2) Data Transforming. In this phase, the processed data are split into a training set and a test set. Subsequently, the input datasets and the labels dataset are constructed separately for both the training and test sets. Given the temporal nature of time series data, the dataset is split such that the initial 80% of the observations are used for training and the remaining 20% for testing. In the construction of the input datasets, it is crucial to acknowledge the requirement of the proposed hybrid neural network, which necessitates the separation of external feature data () and historical demand data (). Taking the training set as an example and assuming a time step of T and a training set sample size of , the input set is structured as a two-dimensional array with dimension while the input set is configured as a three-dimensional array with dimension . The corresponding label dataset, , is a one-dimensional array with dimension . Figure 3 shows the dimensions of the datasets, and the specific formulas are given in Equations (13)–(15).
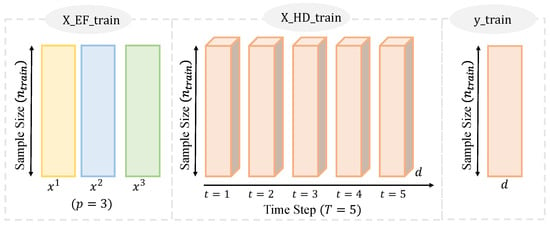
Figure 3.
Conceptual diagram of input datasets and label dataset.
(3) Integrated Neural Network Design. Define the loss function and construct the neural network structure based on Section 3.2.1 and Section 3.2.2, respectively.
(4) Hyperparameter Tuning. The process of hyperparameter tuning is conducted using a combination of repeated random sub-sampling validation (RRSSV) and grid search. Note that the hyperparameter tuning is exclusively performed on the training set, while the test set is reserved for subsequent model evaluation. The steps for hyperparameter tuning are detailed as follows.
- The entire training dataset, consisting of , is randomly partitioned into the training and validation set K times (e.g., five times). These partitions are denoted as for the training sets and for the validation sets, where .
- For each combination of the hyperparameters within the specified search space, the following occurs:
- (a)
- For each of the K random split datasets, the model is trained on the respective training set, , and the average newsvendor cost is computed as the evaluation metric on the validation set, .
- (b)
- The average performance metric across the K splits is then calculated.
- The hyperparameter combination that yields the lowest average evaluation metric across the K splits is selected as the optimal set of hyperparameters.
(5) Model Training and Evaluation. The model is developed using the optimal hyperparameters identified in the previous tuning phase. It is trained on the whole training dataset, . Subsequently, the trained model is applied to generate ordering decisions on the test set, . Finally, the model’s performance is assessed based on metrics in Section 3.2.3 and contrasted with those of other models to determine its relative efficacy.
4. Case Study: Order Quantity Optimization of Vegetables
We demonstrate the effectiveness of our proposed integrated method based on a hybrid neural network through a case study on the inventory optimization of vegetables for a supermarket. The process of implementing HNN-NV with the case study is shown in Figure 4. Details on data description, processing, and transformation are provided in Section 4.1. Section 4.2 discusses benchmark methods. Section 4.3 outlines the experimental setup and the process of hyperparameter tuning. The results are summarized in Section 5.
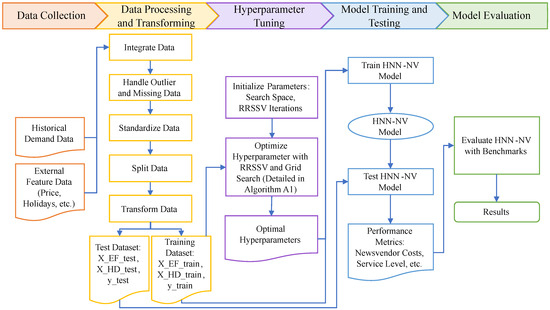
Figure 4.
Process of the case study with HNN-NV.
4.1. Data
The dataset employed in this section comprises comprehensive sales data for vegetable products in a supermarket, spanning a period from 1 July 2020 to 30 June 2023. In detail, the dataset contains sales quantities and pricing information for 244 stock-keeping units (SKUs) across six distinct vegetable categories. The demand for these vegetables varies over time and is influenced by various factors, including prices. The supermarket makes daily ordering decisions for each of these vegetable categories. Given the problem’s congruence with the newsvendor model, this study employs the dataset to evaluate the effectiveness of the proposed method. We conduct experiments separately for the six vegetable categories.
In the data preprocessing phase, we first aggregate the dataset based on the keys of date and vegetable category. For each group of date and category, we compute the cumulative sales quantities. Regarding pricing data within each group, we retain the highest and lowest prices, compute the weighted average price, and ascertain the occurrence of any discount promotions. Furthermore, by integrating the date information, we extract holiday-related characteristics to examine the impact of special dates on sales quantities. To address potential outliers in sales quantities, we employ the boxplot technique to detect outliers and subsequently apply smoothing techniques to adjust for these outliers. The temporal distribution of sales quantities for each vegetable category is visually represented in Figure 5. Figure 5 shows that the demand for the six vegetable categories displays cyclical fluctuation effects, with particularly significant fluctuations observed during holiday periods. Lastly, we use the min-max scaling method to standardize both the feature and sales data. In summary, the external features of the processed data are detailed in Table 1, and an excerpt of the first 10 data points of Category A is presented in Table 2. The processed data are then transformed into the training dataset and the test dataset. The first five data points of (with ), and are presented in Equations (16), (17), and (18), respectively.
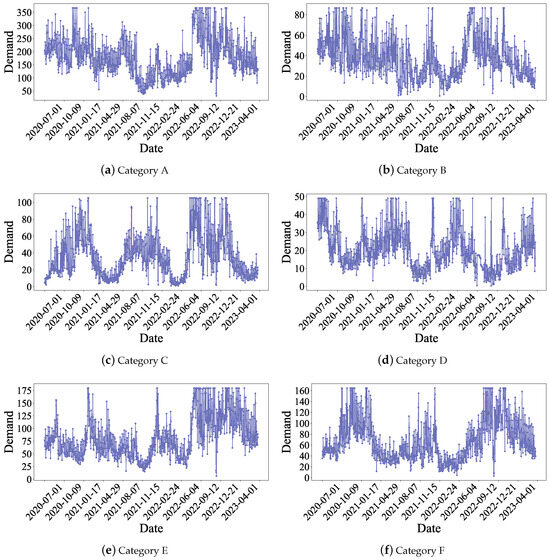
Figure 5.
Daily demand variations for six vegetable categories over July 2020–June 2023. Demand characteristics: cyclical fluctuation effects; significant fluctuations during holidays.

Table 1.
External feature in the processed data.

Table 2.
Samples of the processed data: the first ten data points of Category A.
4.2. Benchmark Methods
We conduct a suite of comparative experiments to verify the effectiveness of the customized neural network approach, which we denote as HNN-NV. We benchmark our proposed approach against a conventional long-short-term memory (LSTM) network for the newsvendor problem (denoted as LSTM-NV), aiming to demonstrate the performance benefits of our custom hybrid neural networks. LSTM-NV is inspired by studies [4,5,6,9,23], which suggest the use of integrated methods for the newsvendor problem. For LSTM-NV, we replace the conventional fully connected network employed in studies [5,6,23] with an LSTM network. This modification is aimed at capturing the intertemporal dependencies in demand, thereby making the comparison more reasonable. Additionally, the method proposed in these studies serves as a benchmark for comparison, denoted by NN-NV. The LSTM-NV model is configured with an LSTM layer as its hidden layer and is trained using the newsvendor loss function (refer to Equation (5)), utilizing X_mix_train as the input dataset and y_train (Equation (15)) as the corresponding label dataset. The X_mix_train with dimension is formulated as
Furthermore, to explore the utility of the integrated method, we compare different variations based on the custom architecture, including HNN-MSE and HNN-SEO. These models—HNN-MSE, HNN-SEO, and HNN-NV—share a similar neural network architecture and identical input and label data, differing only in their choice of loss functions. Both HNN-MSE and HNN-SEO employ the mean square error (MSE) as their loss function during model training. The HNN-MSE model employs an estimation-as-solution policy, directly using the model’s output as the order quantity decision, whereas the HNN-SEO model employs a sequential-estimation-and-optimization policy. Specifically, for the HNN-SEO model, the hybrid neural network model is first trained based on the MSE loss function, and predictions are generated for both the training and test sets. Subsequently, the prediction error for each observation is computed on the training set, denoted as . The SAA method is then applied to estimate the specific -quantile for the demand disturbance term, solving the following optimization problem:
Suppose that the optimal -quantile for Problem (20) is . For sample j, suppose that the predicted value of the hybrid neural network with MSE loss is ; then, the order quantity of the HNN-SEO method at a given level is .
4.3. Experimental Setup and Hyperparameter Optimization
All experiments are conducted within Python 3.8, and the neural-network-based models are developed with the widely used library, TensorFlow (version 2.6.0). The computational environment for these experiments comprises a computer system running Windows 11 (version 21H2), equipped with an Intel® Core™ i7-9700 CPU operating at 3.00 GHz and 24 GB of random-access memory (RAM).
The neural network models are optimized using the Adam algorithm. For the hidden layers, the sigmoid activation function is employed. To address the issue of overfitting, the training procedures are halted based on one of the two criteria: the completion of 500 epochs or the absence of loss reduction on the validation set for 30 consecutive epochs. The architecture of the neural networks, specifically the number of nodes in the hidden layers, and the batch size for stochastic gradient descent are determined via grid search and the RRSSV method, as described in detail in Appendix A.1, Algorithm A1. Through hyperparameter tuning, the selected batch size for HNN-NV is 8, LSTM_layer comprises 20 units, Dense_layer_EF contains 6 nodes, and Dense_layer consists of 2 nodes, taking vegetable category A as an example.
5. Results and Discussion
This section presents the empirical findings in the case study of HNN-NV and benchmark methods. Following this, we discuss the theoretical insights and practical implications that arise from the experimental results.
5.1. Results
We first detail the out-of-sample average newsvendor costs for each method. Specifically, we present the aggregate costs across the six vegetable categories. As shown in Table 3, HNN-NV achieves the lowest out-of-sample costs under all examined cost coefficients , with cost improvements ranging from 9.62% to 21.14% compared to the highest-cost methods. LSTM-NV’s costs are higher than those of both HNN-NV and HNN-SEO. HNN-MSE tends to have the highest out-of-sample costs at low or high levels. HNN-SEO, which enhances HNN-MSE with the SAA method for order quantity optimization, reduces costs but still falls short of HNN-NV. We exclude the results for NN-NV in this section due to its underperformance, which is detailed in Appendix A.2.

Table 3.
Percentage improvement in out-of-sample newsvendor costs.
Table 4 presents the outcomes of paired sample t-tests comparing HNN-NV against benchmark methods. The t-test results confirm the statistical significance of HNN-NV’s cost reductions across most scenarios. The exception occurs at , where the 95% confidence intervals for HNN-NV () and HNN-SEO () overlap, suggesting context-dependent tradeoffs worthy of further theoretical exploration.

Table 4.
Statistic analysis for out-of-sample newsvendor costs.
Figure 6 illustrates the average out-of-sample newsvendor cost, along with its components: underage costs and overage costs. When is small, HNN-NV experiences higher overage costs; that is, when the unit underage cost is lower than the unit overage cost, HNN-NV tends to reduce order quantities so as to minimize total costs. Conversely, when is large, HNN-NV reduces underage costs by increasing order quantities, which, in turn, reduces total costs. The observation is aligned with the optimization logic of the newsvendor model. Other methods do not exhibit similar cost-saving patterns, leading to higher total costs.
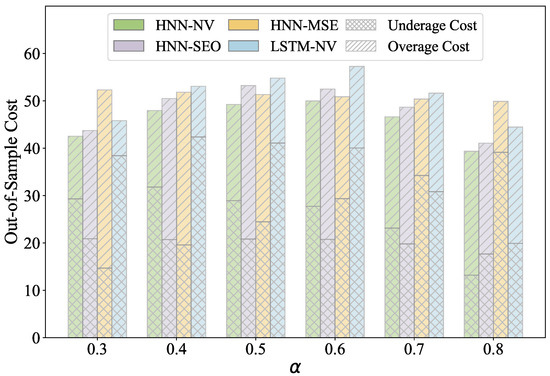
Figure 6.
Out-of-sample newsvendor costs.
Table 5 presents the realized average service level. The realized average service levels for HNN-NV are close to the target service level, as indicated by the small service level gap (ΔSL). The results are robust under different levels. These results show that the service level corresponding to the best-performance order quantities is close to the target service level.

Table 5.
Performance in service level.
Figure 7 illustrates the order quantities prescribed by HNN-NV in comparison to the actual demand for a representative vegetable category within the test dataset. As shown in Figure 7, the ordering decisions of HNN-NV align with the demand trend, thereby substantiating the earlier cost analysis findings. Additionally, as the cost coefficient increases, there is a noticeable upward trend in the order quantities predicted by HNN-NV. This adaptive ordering strategy is consistent with the theoretical results of the newsvendor model. Moreover, this trend correlates directly with the cost-saving patterns identified in Figure 6, affirming the model’s capability to optimize order quantities in response to different cost coefficients.
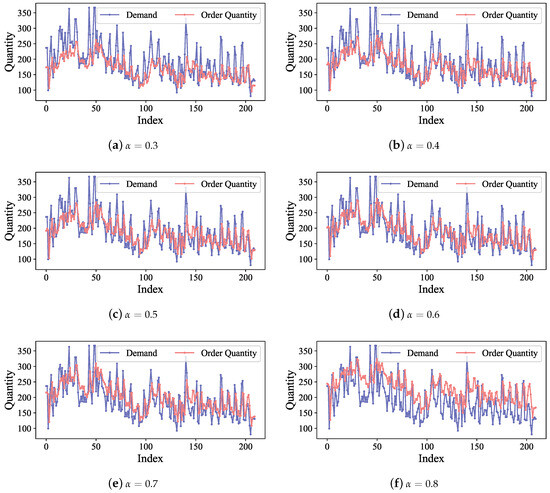
Figure 7.
The demands and order quantities prescribed by HNN-NV on the test set for the representative category. Analysis of the order quantity across varying values reveals a trend: at lower target service levels (small ), the order quantity typically falls short of demand. As the target service level () increases, the order quantity rises, frequently exceeding demand at higher target service levels.
5.2. Discussion
The experimental results validate the effectiveness of our proposed hybrid neural network framework (HNN-NV) for addressing non-stationary demand in the newsvendor problem. Theoretically, our HNN-NV method outperforms both the conventional LSTM-based method (LSTM-NV) and the standard fully connected neural-network-based method (NN-NV), highlighting the importance of hybrid architectures in simultaneously capturing both temporal dynamics and external factors. The inferior performance of generic neural networks without problem-specific architectural design underscores the need for domain-informed model development in management science and operations research. By integrating LSTM’s temporal modeling with fully connected layers for non-temporal features (e.g., weather, price fluctuations), HNN-NV effectively captures complex demand dynamics, advancing our understanding of inventory management under non-stationary conditions. Moreover, our integrated estimation-and-optimization approach (HNN-NV) is shown to be more cost-effective than the separate approach (HNN-SEO), in line with previous studies (e.g., Ban and Rudin [4]). The traditional MSE-based approach (HNN-MSE), which targets mean demand prediction, misaligns with the quantile-focused objective of newsvendor decisions. In contrast, HNN-NV is specifically designed to directly optimize the -quantile target of demand, thereby aligning prediction with the decision-making needs and resulting in enhanced cost efficiency, as supported by the literature (e.g., Oroojlooyjadid et al. [6]).
From a practical perspective, the HNN-NV approach offers valuable insights for inventory management, particularly in industries with perishable goods subject to non-stationary demand. Achieving cost reductions of up to 21.14% compared to benchmark methods, HNN-NV has the potential to generate substantial annual savings in high-volume supply chains, where even marginal efficiency gains translate into meaningful financial impacts. The adaptive ordering strategy, which adjusts quantities based on cost coefficients, provides a scalable solution for managing volatile demand patterns, as evidenced by its alignment with real-world vegetable demand trends. The close alignments of the service levels corresponding to the best-performance order quantities with the target service levels suggest that decision-makers can minimize inventory cost by effectively managing target service levels—a critical factor in industries with perishable goods. The suboptimal performance of the generic neural-network-based method (NN-NV) underscores the importance of domain-specific architectural design, advocating for customized machine learning solutions over one-size-fits-all approaches. These findings equip practitioners with a robust tool for optimizing inventory decisions, balancing cost efficiency and service reliability.
6. Conclusions
In practice, demand for newsvendor-type products often exhibits intertemporal dependence and is influenced by external factors such as price and promotions. This complexity has not been fully addressed in existing data-driven inventory optimization research. This paper presents a novel integrated learning method, HNN-NV, which leverages a customized hybrid neural network architecture. HNN-NV mitigates the risk of model mis-specification by relaxing specific assumptions about demand dynamics. It also overcomes the suboptimality issues associated with traditional separate estimation and optimization approaches by integrating demand estimation with order quantity optimization. Our case study on a supermarket’s vegetable ordering strategies demonstrates that HNN-NV has significant advantages in reducing decision costs. The results indicate that HNN-NV effectively captures demand autocorrelation and utilizes external feature information to optimize ordering decisions.
This paper’s findings offer valuable insights for customizing neural networks in inventory optimization under intertemporal-dependent demand and external feature information. However, our study has several limitations that warrant further investigation. The computational complexity of the customized hybrid neural network architecture, while delivering superior performance, requires more time for hyperparameter tuning with grid search than traditional LSTM-based benchmarks. In addition, the current case study focuses exclusively on vegetable ordering, leaving its effectiveness for other products (e.g., fast fashion and electronics) unverified. Furthermore, the offline training paradigm, while effective for historical pattern recognition, may exhibit suboptimal responsiveness to sudden demand shocks triggered by unforeseen events such as weather emergencies or supply chain disruptions. Additionally, the inherent black-box nature of neural networks introduces interpretability challenges that could affect decision-makers’ trust compared to transparent statistical models.
Future research should focus on enhancing both the technical aspects and practical applications of inventory management models. Technically, the development of simple models, potentially through the integration of knowledge distillation techniques, could reduce computational requirements. Investigating the application of reinforcement learning within inventory systems is a promising avenue for capturing the multi-dimensional complexity of demand, particularly in addressing the joint pricing and ordering problem in dynamic market environments. The incorporation of online learning algorithms can enhance the model’s ability to respond in real time to abrupt changes in demand. For more complex real-world scenarios, extending the model to handle multi-period and multi-product inventory management will necessitate an analysis of how products dynamically substitute for one another and share storage. Moreover, the development of interpretable models in data-driven inventory management is crucial. These models could help managers to understand the relationships between data inputs and decision outputs, thereby facilitating the broader adoption and practical implementation of these methods in industry settings.
Author Contributions
Conceptualization, M.C. and K.F.; methodology, M.C. and K.F.; software, M.C.; validation, M.C.; data curation, M.C.; writing—original draft, M.C.; writing—review and editing, M.C. and K.F.; visualization, M.C.; supervision, K.F.; funding acquisition, K.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Humanities and Social Sciences Foundation of Ministry of Education of China (Grant number 21YJA630016).
Data Availability Statement
The raw data and code supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Supplementary Material for Case Study
Appendix A.1. Hyperparameter Tuning for HNN-NV
The hyperparameter tuning process is based on grid search and repeated random sub-sampling validation (RRSSV), where RRSSV is described in Section 3.3. Algorithm A1 shows the details of the hyperparameter tuning procedure for HNN-NV in our case study.
| Algorithm A1 Hyperparameter optimization with RRSSV and grid search for HNN-NV | ||
| Input: X_EF_train: Input dataset for Input_EF layer | ||
| 1: | X_HD_train: Input dataset for Input_HD layer | |
| 2: | y_train: Label dataset | |
| 3: | α: Cost coefficient in Equation (5) | |
| 4: | K: RRSSV iterations | |
| 5: | ρ: Ratio of validation set | |
| 6: | : Search space for hyperparameters | |
| 7: | : Initial hyperparameter configuration | |
| Output: : Optimal hyperparameter configuration | ||
| 8: | : Minimal average validation cost | |
| 9: | // Define hyperparameter space | |
| 10: | // B: Batch size; : Number of units in LSTM_layer; | |
| 11: | // : Number of units in Dense_layer_EF; : Number of units in Dense_layer | |
| 12: | ||
| 13: | // Initialize optimal records | |
| 14: | , | |
| 15: | // Grid search loop | |
| 16: | for all do | |
| 17: | ▹ Current parameter configuration | |
| 18: | ▹ Cost record set | |
| 19: | // RRSSV iteration | |
| 20: | for k = 1 to K do | |
| 21: | , , , (, , ) | |
| ← GenerateSplit(, , , , k) | ||
| 22: | ← TrainValidate(, , , , | |
| , , , ) | ▹ Model training & validation | |
| 23: | ▹ Cost record | |
| 24: | ← Mean() | ▹ Compute mean cost |
| 25: | if then | |
| 26: | ||
| 27: | ||
| Key Function Specifications: | ||
| - GenerateSplit: Generates random training/validation split | ||
| - TrainValidate: Performs the following operations: | ||
| 1. Build the integrated Neural Network network: | ||
| • LSTM_layer: units | ||
| • Dense_layer_EF: units | ||
| • Dense_layer: units | ||
| • Loss function: Equation (5) | ||
| 2. Train in train set (, , ) with batch size b for a maximum of 500 iterations or early stopping with no loss improvement | ||
| 3. Compute newsvendor cost C in validation set (, , ) with Equation (7) | ||
Appendix A.2. Comparative Results with Traditional Neural Network-Based Method
In Section 5, we benchmark our proposed method, HNN-NV, against HNN-SEO, HNN-MSE, and LSTM-NV algorithms. We conduct a comparative analysis with a traditional neural-network-based method (denoted as NN-NV) proposed in the previous literature [5,6,23]. NN-NV, however, fails to account for the intertemporal dependence of demand. Table A1 shows that the out-of-sample newsvendor costs of NN-NV are significantly higher than those of the HNN-NV model, indicating that neglecting the intertemporal-dependent nature of vegetable demand can result in significant decision errors and lead to a substantial increase in inventory costs.

Table A1.
Out-of-sample newsvendor costs of HNN-NV and NN-NV.
Table A1.
Out-of-sample newsvendor costs of HNN-NV and NN-NV.
| α | HNN-NV | NN-NV | ||
|---|---|---|---|---|
| Mean (SEM) | Mean (SEM) | ΔNVC | t-Test p-Value | |
| 0.3 | 42.54 (1.76) | 67.97 (2.56) | 25.43 | 0.000 **** |
| 0.4 | 47.96 (2.06) | 79.72 (3.18) | 31.77 | 0.000 **** |
| 0.5 | 49.24 (2.22) | 88.84 (3.89) | 39.6 | 0.000 **** |
| 0.6 | 49.97 (2.34) | 91.29 (4.17) | 41.32 | 0.000 **** |
| 0.7 | 46.63 (2.29) | 89.09 (4.38) | 42.46 | 0.000 **** |
| 0.8 | 39.35 (1.73) | 76.46 (4.21) | 37.11 | 0.000 **** |
Notes: * p < 0.1, ** p < 0.05, *** p < 0.01, **** p < 0.001; Mean (SEM): the mean of out-of-sample newsvendor cost (the standard error of the mean); ΔNVC: the gap of the mean of out-of-sample newsvendor cost between the model and HNN-NV; t-test p-value: the p-value result of paired sample t-test between HNN-NV and the model.
References
- Zipkin, P.H. Foundations of Inventory Management; Irwin/McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Porteus, E.L. Foundations of Stochastic Inventory Theory; Stanford University Press: Redwood City, CA, USA, 2002. [Google Scholar]
- Scarf, H.E. A min-max solution of an inventory problem. In Studies in the Mathematical Theory of Inventory and Production; Arrow, K.J., Karlin, S., Scarf, H.E., Eds.; Stanford University Press: Redwood City, CA, USA, 1958; pp. 201–209. [Google Scholar]
- Ban, G.Y.; Rudin, C. The big data newsvendor: Practical insights from machine learning. Oper. Res. 2019, 67, 90–108. [Google Scholar] [CrossRef]
- Huber, J.; Müller, S.; Fleischmann, M.; Stuckenschmidt, H. A data-driven newsvendor problem: From data to decision. Eur. J. Oper. Res. 2019, 278, 904–915. [Google Scholar] [CrossRef]
- Oroojlooyjadid, A.; Snyder, L.V.; Takáč, M. Applying deep learning to the newsvendor problem. IISE Trans. 2020, 52, 444–463. [Google Scholar]
- Besbes, O.; Mouchtaki, O. How big should your data really be? Data-driven newsvendor: Learning one sample at a time. Manag. Sci. 2023, 69, 5848–5865. [Google Scholar] [CrossRef]
- Ren, K.; Bidkhori, H.; Shen, Z.J.M. Data-driven inventory policy: Learning from sequentially observed non-stationary data. Omega 2024, 123, 102942. [Google Scholar] [CrossRef]
- Qi, M.; Shen, Z.J.M.; Zheng, Z. Learning newsvendor problems with intertemporal dependence and moderate non-stationarities. Prod. Oper. Manag. 2024, 33, 1196–1213. [Google Scholar]
- Qi, M.; Shi, Y.; Qi, Y.; Ma, C.; Yuan, R.; Wu, D.; Shen, Z.J.M. A practical end-to-end inventory management model with deep learning. Manag. Sci. 2023, 69, 759–773. [Google Scholar] [CrossRef]
- Bertsimas, D.; Kallus, N. From Predictive to Prescriptive Analytics. Manag. Sci. 2020, 66, 1025–1044. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, Y.; Mao, S.; Chen, X.; Zou, H. LASSO and LSTM integrated temporal model for short-term solar intensity forecasting. IEEE Internet Things J. 2018, 6, 2933–2944. [Google Scholar] [CrossRef]
- Kim, M.; Lee, J.; Lee, C.; Jeong, J. Framework of 2D KDE and LSTM-based forecasting for cost effective inventory management in smart manufacturing. Appl. Sci. 2022, 12, 2380. [Google Scholar] [CrossRef]
- Ping, H.; Li, Z.; Shen, X.; Sun, H. Optimization of vegetable restocking and pricing strategies for innovating supermarket operations utilizing a combination of ARIMA, LSTM, and FP-growth algorithms. Mathematics 2024, 12, 1054. [Google Scholar] [CrossRef]
- Punia, S.; Nikolopoulos, K.; Singh, S.P.; Madaan, J.K.; Litsiou, K. Deep learning with long-short-term memory networks and random forests for demand forecasting in multi-channel retail. Int. J. Prod. Res. 2020, 58, 4964–4979. [Google Scholar]
- Qin, Y.; Wang, R.; Vakharia, A.J.; Chen, Y.; Seref, M.M.H. The newsvendor problem: Review and directions for future research. Eur. J. Oper. Res. 2011, 213, 361–374. [Google Scholar]
- DeYong, G.D. The price-setting newsvendor: Review and extensions. Int. J. Prod. Res. 2020, 58, 1776–1804. [Google Scholar]
- Levi, R.; Roundy, R.O.; Shmoys, D.B. Provably near-optimal sampling-based policies for stochastic inventory control models. Math. Oper. Res. 2007, 32, 821–839. [Google Scholar]
- Levi, R.; Perakis, G.; Uichanco, J. The data-driven newsvendor problem: New bounds and insights. Oper. Res. 2015, 63, 1294–1306. [Google Scholar] [CrossRef]
- Lin, M.; Huh, W.T.; Krishnan, H.; Uichanco, J. Technical note—Data-driven newsvendor problem: Performance of the sample average approximation. Oper. Res. 2022, 70, 1996–2012. [Google Scholar]
- Beutel, A.L.; Minner, S. Safety stock planning under causal demand forecasting. Int. J. Prod. Econ. 2012, 140, 637–645. [Google Scholar]
- Zhang, Y.; Gao, J. Assessing the performance of deep learning algorithms for newsvendor problem. In Proceedings of the Neural Information Processing: 24th International Conference (ICONIP), Guangzhou, China, 14–18 November 2017; Part I 24. pp. 912–921. [Google Scholar]
- Trapero, J.R.; Cardós, M.; Kourentzes, N. Empirical safety stock estimation based on kernel and GARCH models. Omega 2019, 84, 199–211. [Google Scholar]
- Alwan, L.C.; Xu, M.; Yao, D.Q.; Yue, X. The dynamic newsvendor model with correlated demand. Decis. Sci. 2016, 47, 11–30. [Google Scholar] [CrossRef]
- Carrizosa, E.; Olivares-Nadal, A.V.; Ramírez-Cobo, P. Robust newsvendor problem with autoregressive demand. Comput. Oper. Res. 2016, 68, 123–133. [Google Scholar]
- Lugosi, G.; Markakis, M.G.; Neu, G. On the hardness of learning from censored and nonstationary demand. INFORMS J. Optim. 2024, 6, 63–83. [Google Scholar] [CrossRef]
- Kilic, O.A.; Tarim, S.A. A simple heuristic for computing non-stationary inventory policies based on function approximation. Eur. J. Oper. Res. 2024, 316, 899–905. [Google Scholar]
- Cao, Y.; Shen, Z.J.M. Quantile forecasting and data-driven inventory management under nonstationary demand. Oper. Res. Lett. 2019, 47, 465–472. [Google Scholar] [CrossRef]
- Dehaybe, H.; Catanzaro, D.; Chevalier, P. Deep Reinforcement Learning for inventory optimization with non-stationary uncertain demand. Eur. J. Oper. Res. 2024, 314, 433–445. [Google Scholar]
- Choi, T.M.; Wen, X.; Sun, X.; Chung, S.H. The mean-variance approach for global supply chain risk analysis with air logistics in the blockchain technology era. Transp. Res. Part E: Logist. Transp. Rev. 2019, 127, 178–191. [Google Scholar]
- Loureiro, A.L.D.; Miguéis, V.L.; da Silva, L.F.M. Exploring the use of deep neural networks for sales forecasting in fashion retail. Decis. Support Syst. 2018, 114, 81–93. [Google Scholar]
- Cao, W.; Liu, H.; Zhang, X.; Zeng, Y. Residential load forecasting based on long short-term memory, considering temporal local attention. Sustainability 2024, 16, 11252. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Shabani, M.; Yousefi, M. An optimized model using LSTM network for demand forecasting. Comput. Ind. Eng. 2020, 43, 106435. [Google Scholar] [CrossRef]
- Niu, T.; Zhang, H.; Yan, X.; Miao, Q. Intricate supply chain demand forecasting based on graph convolution network. Sustainability 2024, 16, 9608. [Google Scholar] [CrossRef]
- Nasseri, M.; Falatouri, T.; Brandtner, P.; Darbanian, F. Applying machine learning in retail demand prediction—A comparison of tree-based ensembles and long short-term memory-based deep learning. Appl. Sci. 2023, 13, 11112. [Google Scholar] [CrossRef]
- Hurtado-Mora, H.A.; García-Ruiz, A.H.; Pichardo-Ramírez, R.; González-del-Ángel, L.J.; HerreraBarajas, L.A. Sales forecasting with LSTM, custom loss function, and hyperparameter optimization: A case study. Appl. Sci. 2024, 14, 9957. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar]
- Cannon, A.J. Quantile regression neural networks: Implementation in R and application to precipitation downscaling. Comput. Geosci. 2011, 37, 1277–1284. [Google Scholar]
- Chen, C. A finite smoothing algorithm for quantile regression. J. Comput. Graph. Stat. 2007, 16, 136–164. [Google Scholar]
- Goltsos, T.E.; Syntetos, A.A.; Glock, C.H.; Ioannou, G. Inventory-forecasting: Mind the gap. Eur. J. Oper. Res. 2022, 299, 397–419. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).