Enhancing Border Learning for Better Image Denoising
Abstract
1. Introduction
- The patch-wise autoencoder model is extended into a novel residual block to learn image mappings. This block is designed with a specific CNN configuration for efficient computation, demonstrating superior performance in peak GPU memory usage and average inference time.
- Compared to the basic residual block, the proposed residual block enhances the learning of border features, effectively eliminating high-frequency artifacts in feature maps propagated within the CNN. This improves the accuracy of high-frequency texture restoration in denoised results.
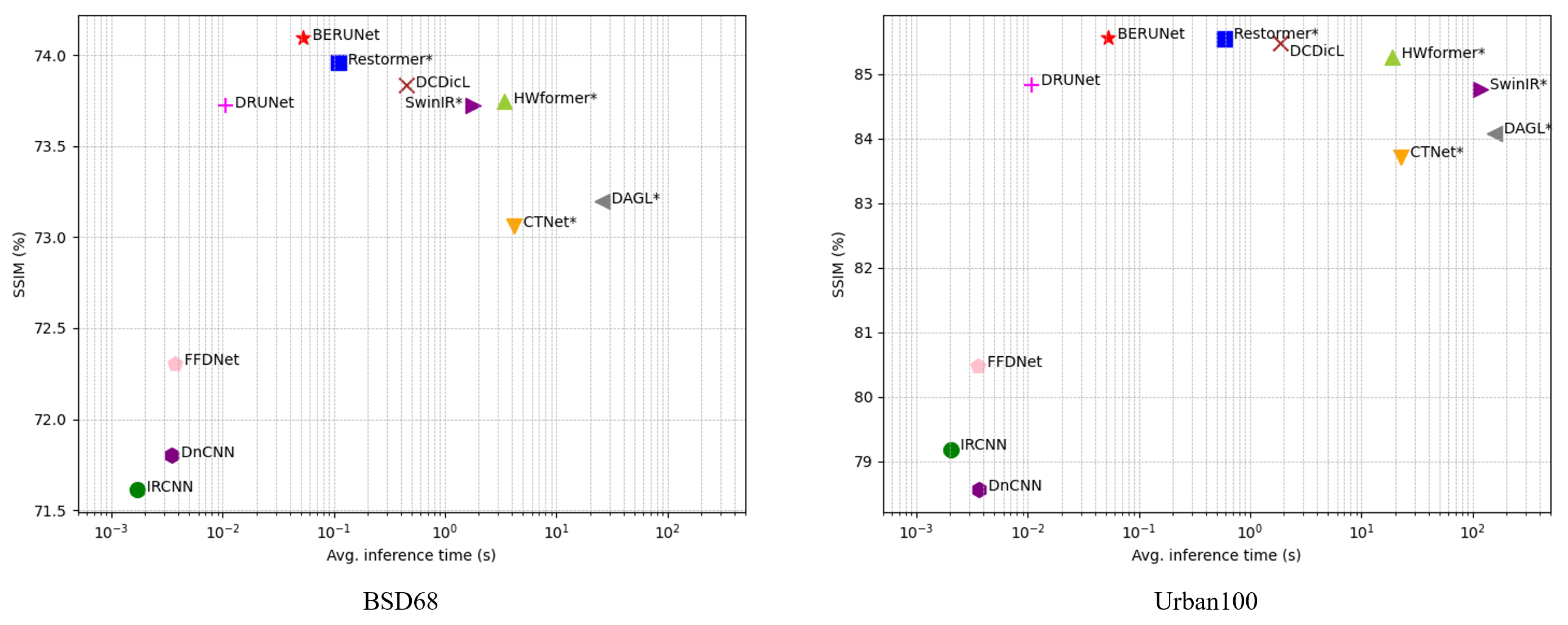
- Extensive comparisons with 19 state-of-the-art DNN-based methods on benchmark datasets Set12, BSD68, Kodak24, McMaster, Urban100, and SIDD across different noise removal tasks demonstrate that the proposed residual block enables U-Net-based denoisers to achieve outstanding performance in terms of PSNR, SSIM, visual quality, and average inference time.
2. Related Work
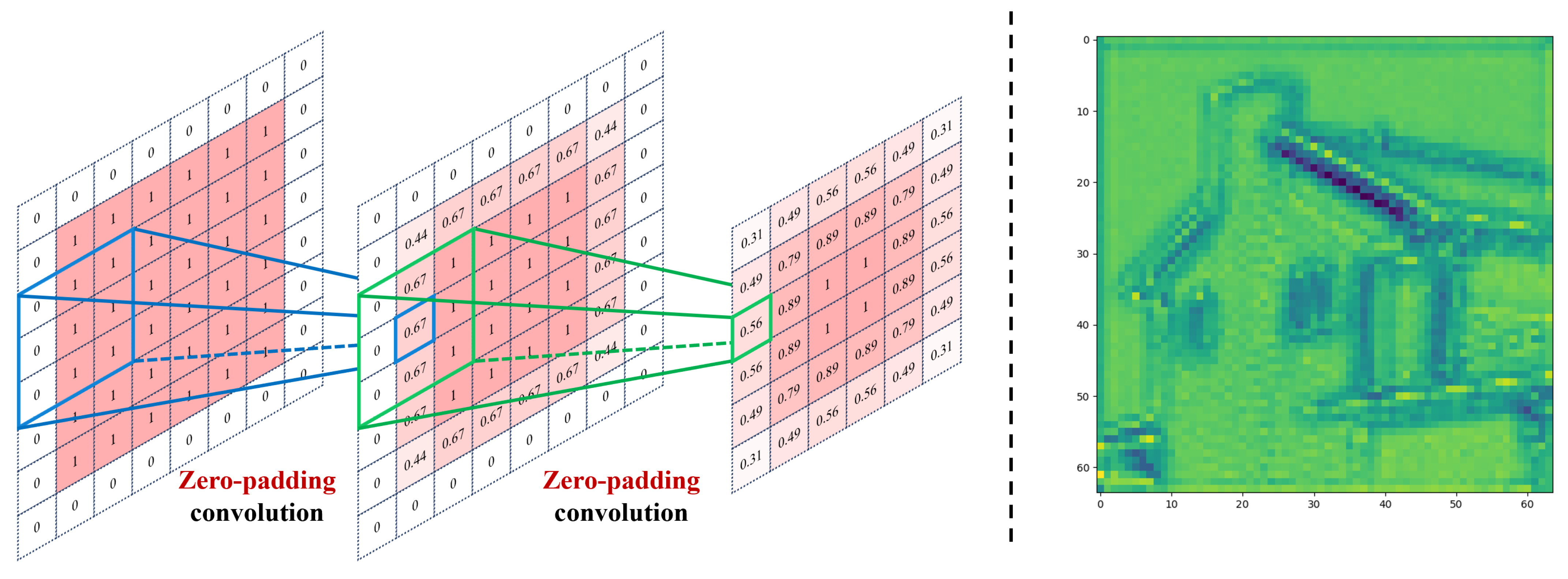
2.1. Solution to the Border Effect in CNNs
2.2. Patch-Wise Denoiser Learned from Whole Images
2.3. Autoencoders for Image Patch Denoising
3. Methodology
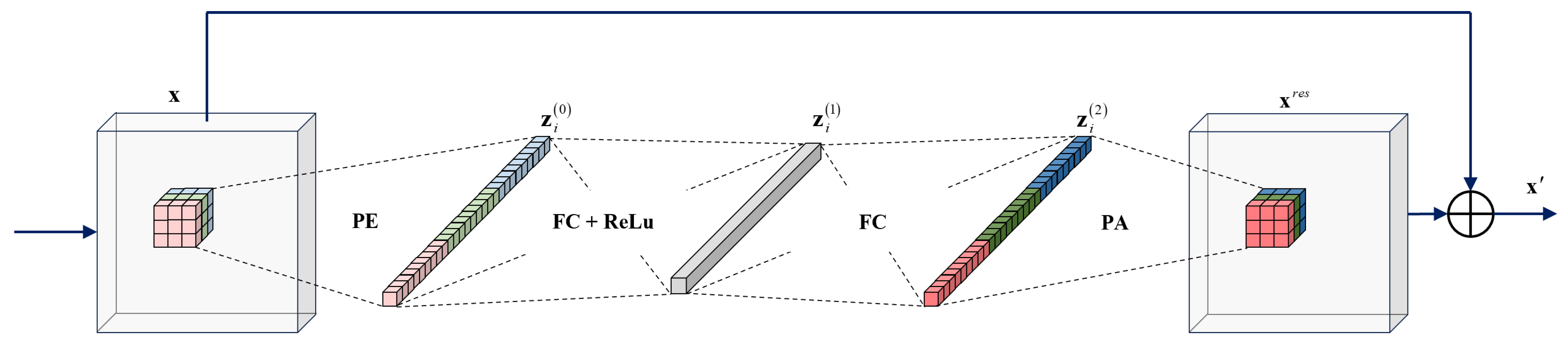
3.1. Learn Patch-Wise Mapping by Residual Autoencoder
3.2. From Patch-Wise Autoencoder to Image-Wise Mapping
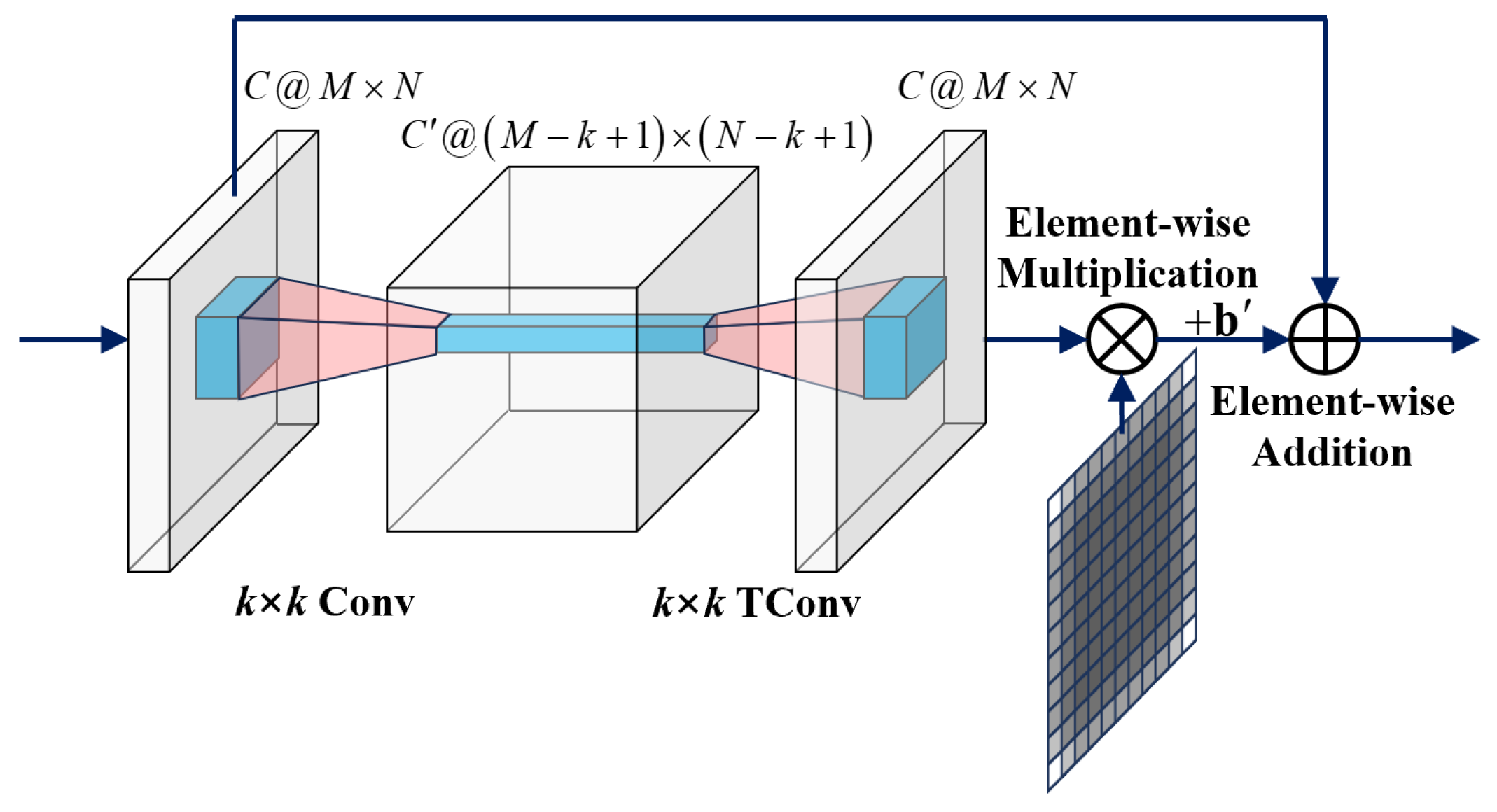
3.3. Accelerate Patch-Wise Autoencoder by Conv and TConv Layers
3.4. The Relationship and Difference with the Basic Residual Block
- The mask layer in BERBlock enhances the learning of border features in the image;
- The basic RBlock uses data padding/cropping to preserve the size of the hidden layers.
3.5. Network Architectures for Image Denoising
4. Experiments and Discussion
4.1. Implementation Details
4.1.1. Preparation of Data and Metrics for Experiments
4.1.2. Setting of Parameters for Training BERUNet
4.1.3. Necessity of Data Padding and Cropping for BERUNet
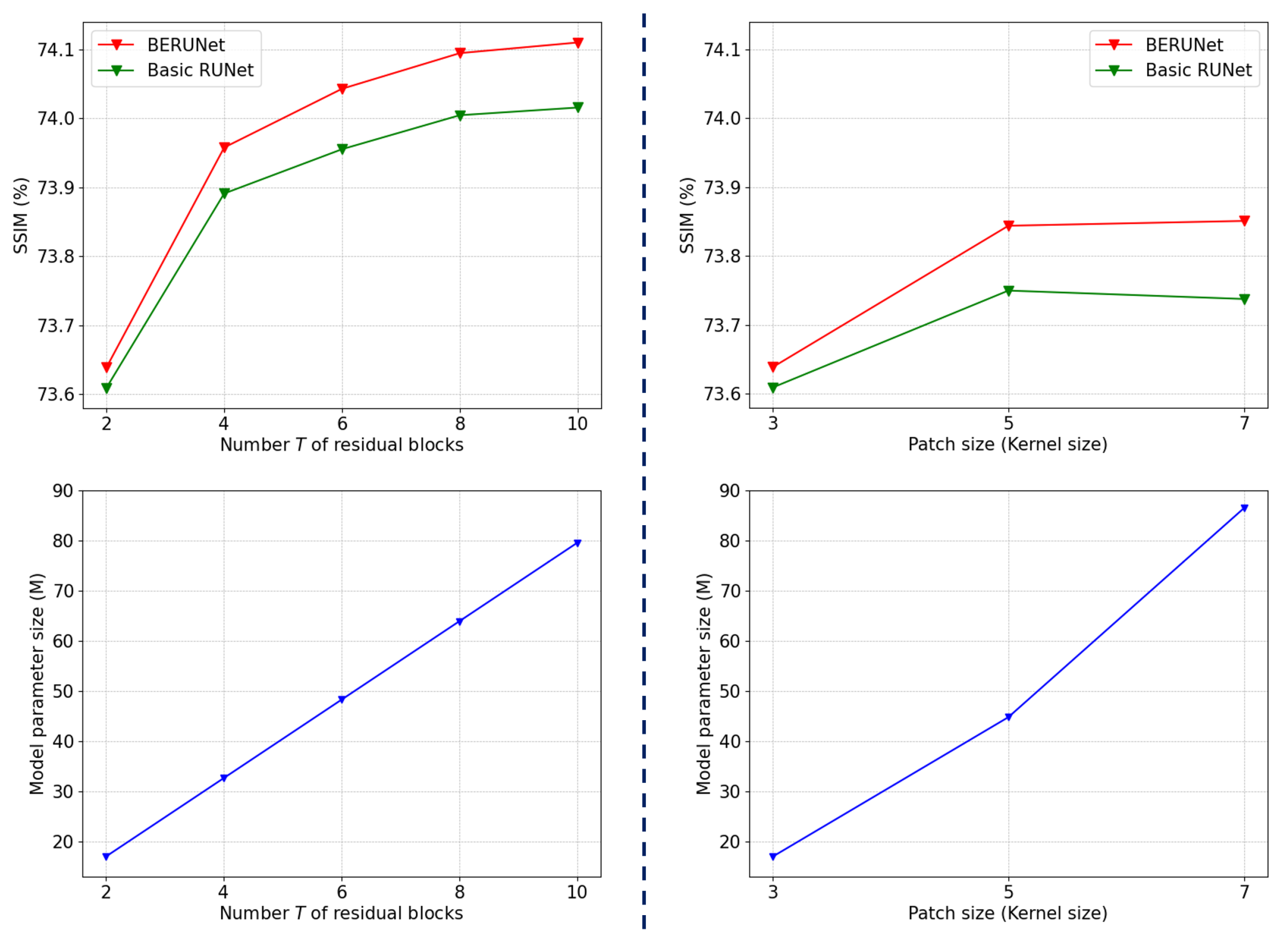
4.1.4. Selection of Architecture Hyperparameters for Image Denoising
4.2. Impact of Enhancing Border Learning on Image Denoising
4.2.1. Quantitative Analysis of the Denoising Metrics
4.2.2. Visualization Analysis of Feature Propagation Within DNN
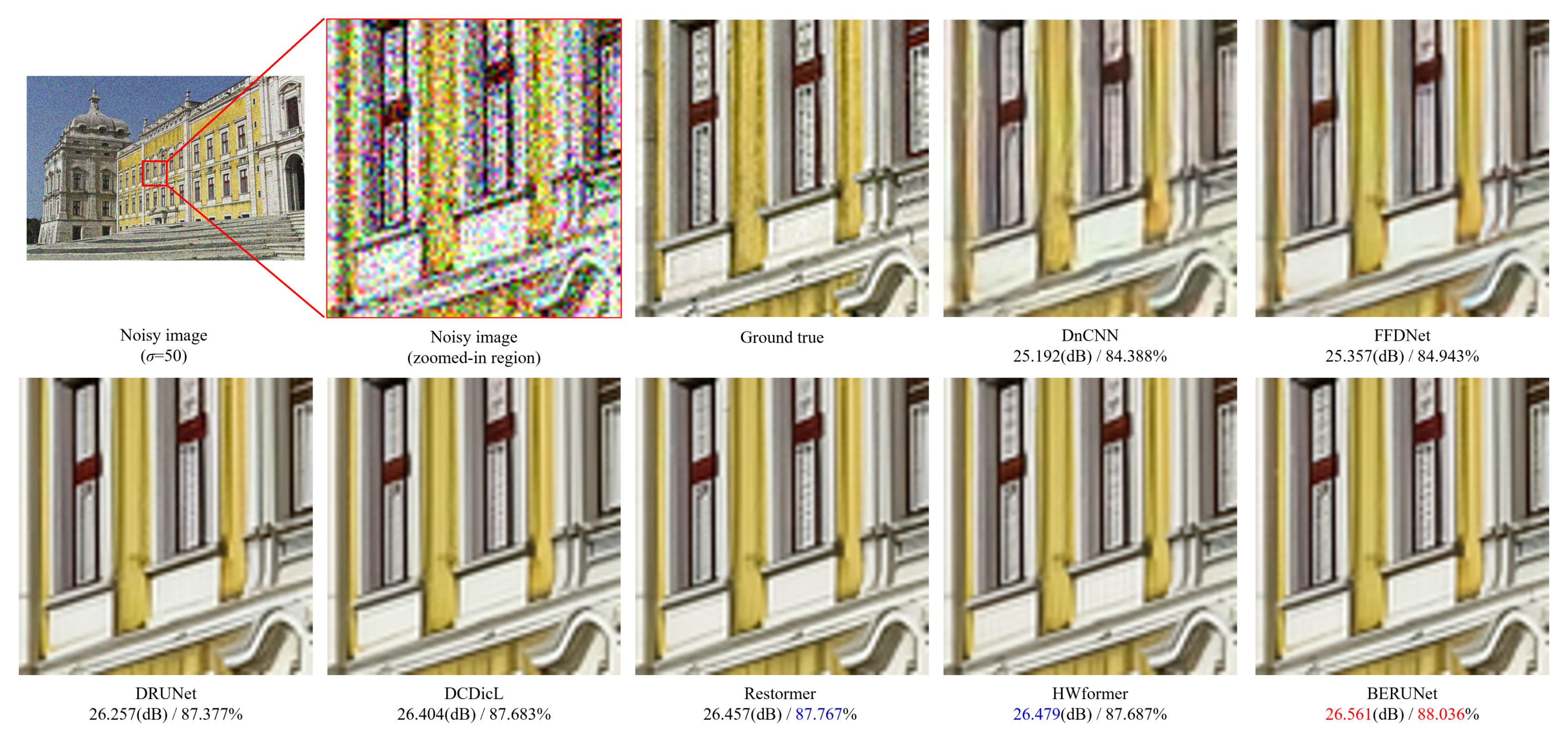
4.2.3. Visualization Analysis of Denoising Texture Accuracy
4.3. Comparison with Advanced DNN-Based Denoising Methods
4.3.1. Removal of Grayscale Synthetic Noise
4.3.2. Removal of Color Synthetic Noise
4.3.3. Removal of Real-World Noise
4.3.4. Advantages of BERUNet in Fast Denoising
4.3.5. Limitations of BERUNet in Image Denoising Task
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. Memnet: A persistent memory network for image restoration. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–27 October 2017; pp. 4539–4547. [Google Scholar]
- Wu, W.; Liu, S.; Xia, Y.; Zhang, Y. Dual residual attention network for image denoising. Pattern Recognit. 2024, 149, 110291. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Zuo, W.; Zhang, L.; Van Gool, L.; Timofte, R. Plug-and-play image restoration with deep denoiser prior. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 6360–6376. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Li, J.; Xu, C.; Huang, D.; Hoi, S.C. RUN: Rethinking the UNet Architecture for Efficient Image Restoration. IEEE Trans. Multimed. 2024, 26, 10381–10394. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, D.; Tan, S. Transfer CLIP for Generalizable Image Denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 25974–25984. [Google Scholar]
- Liu, D.; Wen, B.; Fan, Y.; Loy, C.C.; Huang, T.S. Non-local recurrent network for image restoration. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS), Montréal, QC, Canada, 3–8 December 2018; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Yan, Q.; Zhang, L.; Liu, Y.; Zhu, Y.; Sun, J.; Shi, Q.; Zhang, Y. Deep HDR imaging via a non-local network. IEEE Trans. Image Process. 2020, 29, 4308–4322. [Google Scholar] [CrossRef]
- Sehgal, R.; Kaushik, V.D. Deep Residual Network and Wavelet Transform-Based Non-Local Means Filter for Denoising Low-Dose Computed Tomography. Int. J. Image Graph. 2024, 2550072. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Cheng, Z.; Liu, T.; Zhai, J.; Hu, H. Polarimetric image denoising via non-local based cube matching convolutional neural network. Opt. Lasers Eng. 2025, 184, 108684. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Yan, Q.; Liu, S.; Xu, S.; Dong, C.; Li, Z.; Shi, J.Q.; Zhang, Y.; Dai, D. 3D Medical image segmentation using parallel transformers. Pattern Recognit. 2023, 138, 109432. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Wang, Z.X.; Yang, H.B.; Chen, Y.L.; Li, Y.; Pan, Q.; Wang, H.K.; Zhao, C.X. Hformer: Highly efficient vision transformer for low-dose CT denoising. Nucl. Sci. Tech. 2023, 34, 61. [Google Scholar] [CrossRef]
- Zheng, H.; Yong, H.; Zhang, L. Deep convolutional dictionary learning for image denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 630–641. [Google Scholar]
- Mou, C.; Wang, Q.; Zhang, J. Deep generalized unfolding networks for image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 17399–17410. [Google Scholar]
- Xu, W.; Zhu, Q.; Qi, N.; Chen, D. Deep sparse representation based image restoration with denoising prior. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 6530–6542. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9446–9454. [Google Scholar]
- Tran, L.D.; Nguyen, S.M.; Arai, M. GAN-based noise model for denoising real images. In Proceedings of the Asian Conference on Computer Vision, Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Niu, C.; Li, K.; Wang, D.; Zhu, W.; Xu, H.; Dong, J. Gr-gan: A unified adversarial framework for single image glare removal and denoising. Pattern Recognit. 2024, 156, 110815. [Google Scholar]
- Kawar, B.; Elad, M.; Ermon, S.; Song, J. Denoising diffusion restoration models. In Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS 2022), New Orleans, LO, USA, 28 November–9 December 2022; Volume 35, pp. 23593–23606. [Google Scholar]
- Zeng, H.; Cao, J.; Zhang, K.; Chen, Y.; Luong, H.; Philips, W. Unmixing Diffusion for Self-Supervised Hyperspectral Image Denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 17–21 June 2024; pp. 27820–27830. [Google Scholar]
- Liu, J.; Wang, Q.; Fan, H.; Wang, Y.; Tang, Y.; Qu, L. Residual denoising diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 17–21 June 2024; pp. 2773–2783. [Google Scholar]
- Hu, Y.; Niu, A.; Sun, J.; Zhu, Y.; Yan, Q.; Dong, W.; Woźniak, M.; Zhang, Y. Dynamic center point learning for multiple object tracking under Severe occlusions. Knowl.-Based Syst. 2024, 300, 112130. [Google Scholar]
- Lin, B.; Zheng, J.; Xue, C.; Fu, L.; Li, Y.; Shen, Q. Motion-aware correlation filter-based object tracking in satellite videos. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–13. [Google Scholar]
- Shi, W.; Caballero, J.; Theis, L.; Huszar, F.; Aitken, A.; Ledig, C.; Wang, Z. Is the deconvolution layer the same as a convolutional layer? arXiv 2016, arXiv:1609.07009. [Google Scholar]
- Islam, M.A.; Kowal, M.; Jia, S.; Derpanis, K.G.; Bruce, N.D.B. Position, Padding and Predictions: A Deeper Look at Position Information in CNNs. Int. J. Comput. Vis. 2024, 132, 3889–3910. [Google Scholar] [CrossRef]
- Garcia-Gasulla, D.; Gimenez-Abalos, V.; Martin-Torres, P. Padding aware neurons. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–2 October 2023; pp. 99–108. [Google Scholar]
- Gavrikov, P.; Keuper, J. On the interplay of convolutional padding and adversarial robustness. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 3981–3990. [Google Scholar]
- Liu, R.; Jia, J. Reducing boundary artifacts in image deconvolution. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 505–508. [Google Scholar]
- Zoran, D.; Weiss, Y. From learning models of natural image patches to whole image restoration. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 479–486. [Google Scholar]
- Xu, Z.; Sun, J. Image inpainting by patch propagation using patch sparsity. IEEE Trans. Image Process. 2010, 19, 1153–1165. [Google Scholar]
- Scetbon, M.; Elad, M.; Milanfar, P. Deep k-svd denoising. IEEE Trans. Image Process. 2021, 30, 5944–5955. [Google Scholar]
- Vaksman, G.; Elad, M.; Milanfar, P. LIDIA: Lightweight Learned Image Denoising with Instance Adaptation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Alsallakh, B.; Kokhlikyan, N.; Miglani, V.; Yuan, J.; Reblitz-Richardson, O. Mind the Pad–CNNs Can Develop Blind Spots. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 4 May 2021. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the 25th Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; Volume 25. [Google Scholar]
- Simonyan, K. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Nguyen, A.D.; Choi, S.; Kim, W.; Ahn, S.; Kim, J.; Lee, S. Distribution padding in convolutional neural networks. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4275–4279. [Google Scholar]
- Ning, C.; Gan, H.; Shen, M.; Zhang, T. Learning-based padding: From connectivity on data borders to data padding. Eng. Appl. Artif. Intell. 2023, 121, 106048. [Google Scholar]
- Innamorati, C.; Ritschel, T.; Weyrich, T.; Mitra, N. Learning on the Edge: Explicit Boundary Handling in CNNs. In Proceedings of the British Machine Vision Conference (BMVC), Newcastle, UK, 3–6 September 2018. [Google Scholar]
- Leng, K.; Thiyagalingam, J. Padding-Free Convolution Based on Preservation of Differential Characteristics of Kernels. In Proceedings of the 2023 International Conference on Machine Learning and Applications (ICMLA), Jacksonville, FL, USA, 15–17 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 233–240. [Google Scholar]
- Liu, G.; Dundar, A.; Shih, K.J.; Wang, T.C.; Reda, F.A.; Sapra, K.; Yu, Z.; Yang, X.; Tao, A.; Catanzaro, B. Partial convolution for padding, inpainting, and image synthesis. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 6096–6110. [Google Scholar]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [PubMed]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar]
- Dong, W.; Zhang, L.; Shi, G.; Li, X. Nonlocally centralized sparse representation for image restoration. IEEE Trans. Image Process. 2012, 22, 1620–1630. [Google Scholar]
- Simon, D.; Elad, M. Rethinking the CSC model for natural images. In Proceedings of the 33rd Annual Conference on Neural Information Processing Systems, Vancouver, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Herbreteau, S.; Kervrann, C. DCT2net: An interpretable shallow CNN for image denoising. IEEE Trans. Image Process. 2022, 31, 4292–4305. [Google Scholar]
- Bhatti, U.A.; Tang, H.; Wu, G.; Marjan, S.; Hussain, A. Deep learning with graph convolutional networks: An overview and latest applications in computational intelligence. Int. J. Intell. Syst. 2023, 2023, 8342104. [Google Scholar]
- Wang, D.; Fan, F.; Wu, Z.; Liu, R.; Wang, F.; Yu, H. CTformer: Convolution-free Token2Token dilated vision transformer for low-dose CT denoising. Phys. Med. Biol. 2023, 68, 065012. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation, parallel distributed processing, explorations in the microstructure of cognition, ed. de rumelhart and j. mcclelland. vol. 1. 1986. Biometrika 1986, 71, 6. [Google Scholar]
- Zhang, Y.; Zhang, E.; Chen, W. Deep neural network for halftone image classification based on sparse auto-encoder. Eng. Appl. Artif. Intell. 2016, 50, 245–255. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Burger, H.C.; Schuler, C.J.; Harmeling, S. Image denoising: Can plain neural networks compete with BM3D? In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 2392–2399. [Google Scholar]
- Xie, J.; Xu, L.; Chen, E. Image denoising and inpainting with deep neural networks. In Proceedings of the 26th Annual Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 25. [Google Scholar]
- Majumdar, A. Blind denoising autoencoder. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 312–317. [Google Scholar]
- Bhute, S.; Mandal, S.; Guha, D. Speckle Noise Reduction in Ultrasound Images using Denoising Auto-encoder with Skip connection. In Proceedings of the 2024 IEEE South Asian Ultrasonics Symposium (SAUS), Gujarat, India, 27–29 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–4. [Google Scholar]
- Agostinelli, F.; Anderson, M.R.; Lee, H. Adaptive multi-column deep neural networks with application to robust image denoising. In Proceedings of the 27th Annual Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; Volume 26. [Google Scholar]
- Lore, K.G.; Akintayo, A.; Sarkar, S. LLNet: A deep autoencoder approach to natural low-light image enhancement. Pattern Recognit. 2017, 61, 650–662. [Google Scholar] [CrossRef]
- Majumdar, A. Graph structured autoencoder. Neural Netw. 2018, 106, 271–280. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Tao, D. Non-local auto-encoder with collaborative stabilization for image restoration. IEEE Trans. Image Process. 2016, 25, 2117–2129. [Google Scholar] [CrossRef]
- Tran, L.; Liu, X.; Zhou, J.; Jin, R. Missing modalities imputation via cascaded residual autoencoder. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1405–1414. [Google Scholar]
- Daubechies, I.; Defrise, M.; De Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. J. Issued Courant Inst. Math. Sci. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Vasudevan, A.; Anderson, A.; Gregg, D. Parallel multi channel convolution using general matrix multiplication. In Proceedings of the 2017 IEEE 28th International Conference on Application-Specific Systems, Architectures and Processors (ASAP), Seattle, WA, USA, 10–17 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 19–24. [Google Scholar]
- Dumoulin, V.; Visin, F. A guide to convolution arithmetic for deep learning. arXiv 2016, arXiv:1603.07285. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1520–1528. [Google Scholar]
- Al-Saggaf, U.M.; Botalb, A.; Moinuddin, M.; Alfakeh, S.A.; Ali, S.S.A.; Boon, T.T. Either crop or pad the input volume: What is beneficial for Convolutional Neural Network? In Proceedings of the 2020 8th International Conference on Intelligent and Advanced Systems (ICIAS), Kuching, Indonesia, 13–15 July 2020; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Venkatesh, G.; Naresh, Y.; Little, S.; O’Connor, N.E. A deep residual architecture for skin lesion segmentation. In Proceedings of the OR 2.0 Context-Aware Operating Theaters, Computer Assisted Robotic Endoscopy, Clinical Image-Based Procedures, and Skin Image Analysis: First International Workshop (OR 2.0 2018), 5th International Workshop (CARE 2018), 7th International Workshop (CLIP 2018), Third International Workshop (ISIC 2018), Held in Conjunction with MICCAI 2018, Granada, Spain, 16–20 September 2018; Proceedings 5. Springer: Berlin, Heidelberg, 2018; pp. 277–284. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient transformer for high-resolution image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5728–5739. [Google Scholar]
- Fan, C.M.; Liu, T.J.; Liu, K.H. SUNet: Swin transformer UNet for image denoising. In Proceedings of the 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 1–28 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 2333–2337. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 2, pp. 416–423. [Google Scholar]
- Ma, K.; Duanmu, Z.; Wu, Q.; Wang, Z.; Yong, H.; Li, H.; Zhang, L. Waterloo exploration database: New challenges for image quality assessment models. IEEE Trans. Image Process. 2016, 26, 1004–1016. [Google Scholar] [CrossRef] [PubMed]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Abdelhamed, A.; Lin, S.; Brown, M.S. A high-quality denoising dataset for smartphone cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1692–1700. [Google Scholar]
- Roth, S.; Black, M.J. Fields of experts: A framework for learning image priors. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 2, pp. 860–867. [Google Scholar]
- Franzen, R. Kodak Lossless True Color Image Suite. 2024. Available online: https://r0k.us/graphics/kodak/index.html (accessed on 1 September 2024).
- Zhang, L.; Wu, X.; Buades, A.; Li, X. Color demosaicking by local directional interpolation and nonlocal adaptive thresholding. J. Electron. Imaging 2011, 20, 023016. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sapienza, D.; Franchini, G.; Govi, E.; Bertogna, M.; Prato, M. Deep Image Prior for medical image denoising, a study about parameter initialization. Front. Appl. Math. Stat. 2022, 8, 995225. [Google Scholar] [CrossRef]
- Saxe, A.M.; McClelland, J.L.; Ganguli, S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv 2013, arXiv:1312.6120. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; JMLR Workshop and Conference Proceedings. pp. 249–256. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Mou, C.; Zhang, J.; Wu, Z. Dynamic attentive graph learning for image restoration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 4328–4337. [Google Scholar]
- Tian, C.; Zheng, M.; Zuo, W.; Zhang, S.; Zhang, Y.; Lin, C.W. A cross Transformer for image denoising. Inf. Fusion 2024, 102, 102043. [Google Scholar] [CrossRef]
- Tian, C.; Zheng, M.; Lin, C.W.; Li, Z.; Zhang, D. Heterogeneous window transformer for image denoising. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 6621–6632. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Gu, S.; Zhang, L. Learning deep CNN denoiser prior for image restoration. In Proceedings of the IEEE Conference on Ccomputer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3929–3938. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar]
- Tian, C.; Xu, Y.; Zuo, W. Image denoising using deep CNN with batch renormalization. Neural Netw. 2020, 121, 461–473. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Cycleisp: Real image restoration via improved data synthesis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2696–2705. [Google Scholar]
- Chen, L.; Lu, X.; Zhang, J.; Chu, X.; Chen, C. Hinet: Half instance normalization network for image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 182–192. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Multi-stage progressive image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14821–14831. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Learning enriched features for fast image restoration and enhancement. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 1934–1948. [Google Scholar]
- Liu, K.; Du, X.; Liu, S.; Zheng, Y.; Wu, X.; Jin, C. DDT: Dual-branch deformable transformer for image denoising. In Proceedings of the 2023 IEEE International Conference on Multimedia and Expo (ICME), Brisbane, Australia, 10–14 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 2765–2770. [Google Scholar]
- Zhang, J.; Zhang, Y.; Gu, J.; Dong, J.; Kong, L.; Yang, X. Xformer: Hybrid X-Shaped Transformer for Image Denoising. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Chen, J.; Chen, J.; Chao, H.; Yang, M. Image blind denoising with generative adversarial network based noise modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3155–3164. [Google Scholar]
- Kim, C.; Kim, T.H.; Baik, S. Lan: Learning to adapt noise for image denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 25193–25202. [Google Scholar]
- Krull, A.; Buchholz, T.O.; Jug, F. Noise2void-learning denoising from single noisy images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2129–2137. [Google Scholar]
- Chihaoui, H.; Favaro, P. Masked and shuffled blind spot denoising for real-world images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2024; pp. 3025–3034. [Google Scholar]
- Chen, S.; Guo, W. Auto-encoders in deep learning—A review with new perspectives. Mathematics 2023, 11, 1777. [Google Scholar] [CrossRef]
- Chen, X.; Ding, M.; Wang, X.; Xin, Y.; Mo, S.; Wang, Y.; Han, S.; Luo, P.; Zeng, G.; Wang, J. Context autoencoder for self-supervised representation learning. Int. J. Comput. Vis. 2024, 132, 208–223. [Google Scholar]


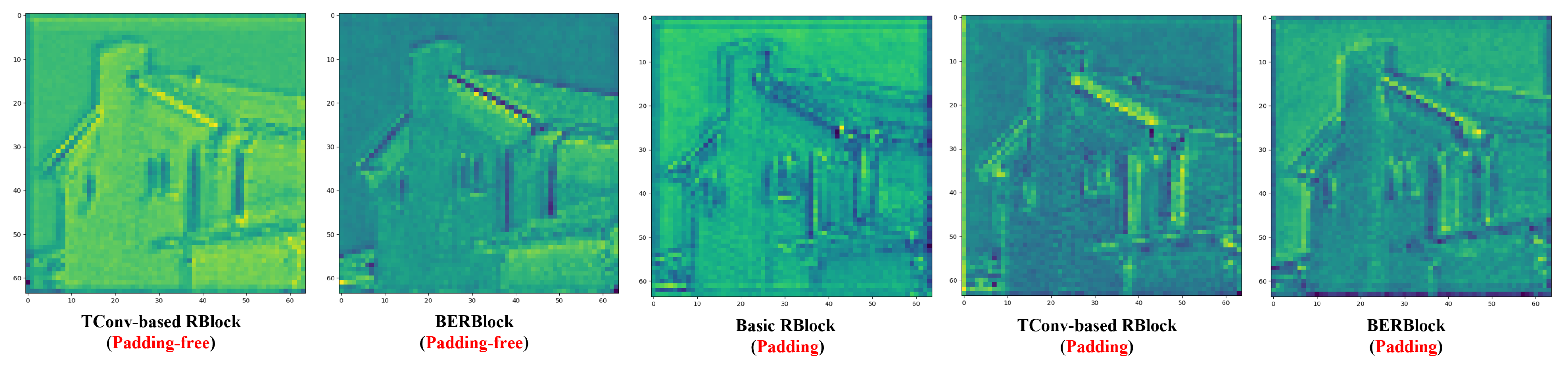






| Block Structure | Explicit BERBlock | Implicit BERBlock | Basic RBlock | TConv-Based RBlock | ||||
|---|---|---|---|---|---|---|---|---|
| Padding/Cropping | ✓ | × | ✓ | × | ✓ | × | ✓ | × |
| Parameter size (K) | 73.856 | 73.856 | 73.856 | 73.856 | ||||
| GFLOPs | 4.832 | 4.757 | 4.832 | 4.757 | 4.832 | - | 4.832 | 4.757 |
| Peak GPU memory (MB) | 501.286 | 494.715 | 84.782 | 84.713 | 64.282 | - | 64.282 | 64.281 |
| Average inference time (ms) | 3.495 | 3.364 | 0.840 | 0.850 | 0.664 | - | 0.667 | 0.666 |
| Parameter | Loss | Metrics | Set12 | BSD68 | Urban100 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initialization | Function | ||||||||||
| Orthogonal | L2 | PSNR (dB) SSIM (%) | 33.293 91.078 | 30.994 87.448 | 27.965 81.087 | 31.919 89.550 | 29.495 83.816 | 26.616 73.996 | 33.499 93.832 | 31.179 90.919 | 28.049 84.932 |
| Kaiming | L2 | PSNR (dB) SSIM (%) | 33.297 91.068 | 30.994 87.438 | 27.969 81.104 | 31.919 89.511 | 29.496 83.760 | 26.617 73.932 | 33.495 93.819 | 31.174 90.907 | 28.046 84.948 |
| Xavier | L2 | PSNR (dB) SSIM (%) | 33.297 91.090 | 30.995 87.452 | 27.972 81.116 | 31.919 89.539 | 29.495 83.793 | 26.619 73.958 | 33.498 93.830 | 31.179 90.920 | 28.054 84.962 |
| Xavier | L1 | PSNR (dB) SSIM (%) | 33.266 90.990 | 30.953 87.338 | 27.910 80.982 | 31.901 89.477 | 29.466 83.681 | 26.577 73.814 | 33.466 93.786 | 31.121 90.837 | 27.959 84.818 |
| Methods | Padding/ | Metrics | Set12 | BSD68 | Urban100 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cropping | |||||||||||
| Basic RUNet | ✓ | PSNR (dB) SSIM (%) | 33.299 91.082 | 30.995 87.437 | 27.963 81.088 | 31.919 89.511 | 29.495 83.738 | 26.618 73.881 | 33.495 93.816 | 31.175 90.893 | 28.045 84.913 |
| TConv-based RUNet | ✓ | PSNR (dB) SSIM (%) | 33.298 91.077 | 30.994 87.423 | 27.967 81.070 | 31.918 89.516 | 29.495 83.754 | 26.616 73.904 | 33.497 93.820 | 31.177 90.901 | 28.042 84.909 |
| × | PSNR (dB) SSIM (%) | 33.283 91.068 | 30.982 87.420 | 27.958 81.085 | 31.915 89.511 | 29.491 83.742 | 26.610 73.860 | 33.478 93.800 | 31.156 90.865 | 28.016 84.832 | |
| BERUNet | ✓ | PSNR (dB) SSIM (%) | 33.297 91.090 | 30.995 87.452 | 27.972 81.116 | 31.919 89.539 | 29.495 83.793 | 26.619 73.958 | 33.498 93.830 | 31.179 90.920 | 28.054 84.962 |
| × | PSNR (dB) SSIM (%) | 33.293 91.071 | 30.986 87.403 | 27.963 81.044 | 31.917 89.522 | 29.493 83.746 | 26.614 73.875 | 33.489 93.823 | 31.166 90.889 | 28.027 84.863 | |
| Methods | Padding/ | Metrics | Set12 | BSD68 | Urban100 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cropping | |||||||||||
| BERUNet vs. TConv-based RUNet | ✓ | p-value of PSNR p-value of SSIM | 0.268 0.018 | 0.520 0.026 | 0.159 0.007 | 0.269 <0.001 | 0.862 <0.001 | 0.043 <0.001 | 0.360 <0.001 | 0.279 <0.001 | 0.002 <0.001 |
| × | p-value of PSNR p-value of SSIM | 0.337 0.012 | 0.429 0.032 | 0.294 0.033 | 0.024 0.001 | 0.086 0.004 | 0.031 0.013 | <0.001 <0.001 | 0.026 0.008 | 0.058 0.019 | |
| BERUNet vs. basic RUNet | ✓ | p-value of PSNR p-value of SSIM | 0.471 0.036 | 0.505 0.045 | 0.302 0.033 | 0.589 <0.001 | 0.883 <0.001 | 0.399 <0.001 | 0.115 <0.001 | 0.025 <0.001 | 0.005 <0.001 |
| Methods | Primary | Metrics | Set12 | BSD68 | Urban100 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Architecture | |||||||||||
| DnCNN (2017) | FCN | PSNR (dB) SSIM (%) | 32.851 90.251 | 30.432 86.166 | 27.169 78.277 | 31.722 88.996 | 29.222 82.712 | 26.233 71.802 | 32.643 92.406 | 29.945 87.806 | 26.263 78.565 |
| IRCNN (2017) | FCN | PSNR (dB) SSIM (%) | 32.759 90.059 | 30.371 85.979 | 27.124 78.043 | 31.621 88.752 | 29.138 82.403 | 26.181 71.613 | 32.463 92.360 | 29.803 88.311 | 26.223 79.184 |
| FFDNet (2018) | FCN | PSNR (dB) SSIM (%) | 32.739 90.242 | 30.419 86.313 | 27.300 78.994 | 31.623 88.952 | 29.183 82.803 | 26.289 72.306 | 32.405 92.648 | 29.903 88.785 | 26.503 80.475 |
| DCDicL (2021) | Unfolding network + U-Net | PSNR (dB) SSIM (%) | 33.341 91.152 | 31.026 87.478 | 27.999 81.216 | 31.922 89.486 | 29.492 83.690 | 26.613 73.836 | 33.595 93.881 | 31.304 91.079 | 28.236 85.483 |
| DAGL (2021) | FCN + NLNN | PSNR (dB) SSIM (%) | 33.272 91.002 | 30.926 87.198 | 27.793 80.421 | 31.912 89.449 | 29.457 83.547 | 26.524 73.198 | 33.748 93.860 | 31.363 90.835 | 27.954 84.081 |
| SwinIR (2021) | FCN + Transformer | PSNR (dB) SSIM (%) | 33.377 91.108 | 31.037 87.431 | 27.956 81.017 | 31.948 89.534 | 29.494 83.698 | 26.582 73.721 | 33.726 93.911 | 31.339 90.953 | 28.060 84.764 |
| DRUNet (2022) | U-Net | PSNR (dB) SSIM (%) | 33.245 90.980 | 30.936 87.327 | 27.896 80.962 | 31.886 89.449 | 29.455 83.633 | 26.569 73.721 | 33.442 93.761 | 31.109 90.820 | 27.963 84.830 |
| Restormer (2022) | U-Net + Transformer | PSNR (dB) SSIM (%) | 33.346 91.150 | 31.042 87.535 | 28.006 81.209 | 31.947 89.561 | 29.521 83.831 | 26.639 74.103 | 33.671 93.889 | 31.393 91.095 | 28.332 85.551 |
| CTNet (2024) | Parallel Network + Transformer | PSNR (dB) SSIM (%) | 33.322 91.001 | 30.959 87.240 | 27.802 80.386 | 31.922 89.456 | 29.456 83.516 | 26.492 73.063 | 33.693 93.824 | 31.256 90.720 | 27.790 83.713 |
| HWformer (2024) | FCN + Transformer | PSNR (dB) SSIM (%) | 33.424 91.233 | 31.075 87.532 | 27.979 81.045 | 31.978 89.589 | 29.534 83.791 | 26.611 73.745 | 33.909 94.060 | 31.591 91.266 | 28.332 85.261 |
| BERUNet (Ours) | U-Net | PSNR (dB) SSIM (%) | 33.347 91.169 | 31.051 87.555 | 28.033 81.294 | 31.944 89.570 | 29.522 83.846 | 26.651 74.095 | 33.609 93.894 | 31.387 91.216 | 28.267 85.501 |
| Primary | Metrics | CBSD68 | Kodak24 | McMaster | Urban100 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Methods | Architecture | |||||||||||||
| DnCNN (2017) | FCN | PSNR (dB) SSIM (%) | 33.898 92.903 | 31.244 88.300 | 27.946 78.963 | 34.596 92.089 | 32.136 87.753 | 28.948 79.173 | 33.450 90.353 | 31.521 86.942 | 28.620 79.856 | 32.984 93.143 | 30.811 90.148 | 27.589 83.308 |
| IRCNN (2017) | FCN | PSNR (dB) SSIM (%) | 33.872 92.845 | 31.179 88.238 | 27.879 78.978 | 34.689 92.093 | 32.150 87.793 | 28.936 79.426 | 34.577 91.949 | 32.182 88.176 | 28.928 80.692 | 33.777 94.017 | 31.204 90.878 | 27.701 83.959 |
| FFDNet (2018) | FCN | PSNR (dB) SSIM (%) | 33.879 92.896 | 31.220 88.211 | 27.974 78.871 | 34.749 92.243 | 32.250 87.912 | 29.109 79.524 | 34.656 92.158 | 32.359 88.614 | 29.194 81.494 | 33.834 94.182 | 31.404 91.201 | 28.054 84.764 |
| BRDNet (2020) | Parallel Network + FCN | PSNR (dB) SSIM (%) | 34.103 92.909 | 31.431 88.470 | 28.157 79.423 | 34.878 92.492 | 32.407 88.560 | 29.215 80.401 | 35.077 92.691 | 32.745 89.433 | 29.520 82.649 | 34.421 94.616 | 31.993 91.941 | 28.556 85.769 |
| DCDicL (2021) | Unfolding network + U-Net | PSNR (dB) SSIM (%) | 34.335 93.468 | 31.728 89.289 | 28.551 81.040 | 35.385 92.999 | 32.972 89.275 | 29.960 82.190 | 35.483 93.328 | 33.238 90.454 | 30.200 84.906 | 34.903 95.111 | 32.771 92.998 | 29.875 88.838 |
| SwinIR (2021) | FCN + Transformer | PSNR (dB) SSIM (%) | 34.410 93.557 | 31.773 89.403 | 28.561 81.199 | 35.464 93.045 | 33.008 89.316 | 29.947 82.208 | 35.609 93.454 | 33.311 90.558 | 30.198 84.896 | 35.162 95.234 | 32.934 93.051 | 29.876 88.607 |
| DRUNet (2022) | U-Net | PSNR (dB) SSIM (%) | 34.287 93.435 | 31.676 89.247 | 28.494 81.029 | 35.312 92.918 | 32.894 89.171 | 29.869 82.075 | 35.392 93.245 | 33.131 90.306 | 30.069 84.604 | 34.826 95.054 | 32.609 92.826 | 29.611 88.348 |
| Restormer (2022) | U-Net + Transformer | PSNR (dB) SSIM (%) | 34.386 93.539 | 31.780 89.419 | 28.608 81.340 | 35.440 93.044 | 33.023 89.361 | 30.002 82.346 | 35.541 93.385 | 33.299 90.563 | 30.276 85.160 | 35.056 95.188 | 32.906 93.077 | 30.016 88.937 |
| CTNet (2024) | Parallel Network + Transformer | PSNR (dB) SSIM (%) | 34.374 93.490 | 31.716 89.249 | 28.455 80.745 | 35.395 92.963 | 32.915 89.147 | 29.782 81.702 | 35.544 93.308 | 33.221 90.281 | 30.038 84.130 | 35.119 95.172 | 32.859 92.915 | 29.733 88.214 |
| HWformer (2024) | FCN + Transformer | PSNR (dB) SSIM (%) | 34.412 93.546 | 31.784 89.386 | 28.580 81.191 | 35.483 93.076 | 33.037 89.376 | 29.959 82.243 | 35.641 93.461 | 33.362 90.570 | 30.240 84.818 | 35.261 95.293 | 33.100 93.191 | 30.139 88.981 |
| BERUNet (Ours) | U-Net | PSNR (dB) SSIM (%) | 34.394 93.563 | 31.782 89.460 | 28.596 81.365 | 35.447 93.080 | 33.036 89.438 | 29.981 82.390 | 35.592 93.449 | 33.290 90.569 | 30.262 85.004 | 35.114 95.221 | 32.903 93.102 | 29.996 88.956 |
| Methods | CycleISP (2020) | HINet (2021) | MPRNet (2021) | Restormer (2022) | DGUNet+ (2022) | MIRNetv2 (2022) | DDT (2023) | CTNet (2024) | DRANet (2024) | Xformer (2024) | BERUNet (Ours) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Primary architecture | FCN + NLNN | Multi-stage FCN | Multi-stage U-Net | U-Net + Transformer | Unfolding network + U-Net | FCN + UNet + Transformer | U-Net + Transformer | Parallel Network + Transformer | Parallel Network + FCN | U-Net + Transformer | U-Net |
| PSNR (dB) SSIM (%) | 39.439 91.744 | 39.776 92.017 | 39.630 91.957 | 39.929 92.146 | 39.800 92.064 | 39.757 92.005 | 39.749 92.010 | 38.377 90.475 | 39.427 91.796 | 39.891 92.154 | 39.847 92.119 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, X.; Zhu, Y.; Qi, L.; Hu, Y.; Sun, J.; Zhang, Y. Enhancing Border Learning for Better Image Denoising. Mathematics 2025, 13, 1119. https://doi.org/10.3390/math13071119
Ge X, Zhu Y, Qi L, Hu Y, Sun J, Zhang Y. Enhancing Border Learning for Better Image Denoising. Mathematics. 2025; 13(7):1119. https://doi.org/10.3390/math13071119
Chicago/Turabian StyleGe, Xin, Yu Zhu, Liping Qi, Yaoqi Hu, Jinqiu Sun, and Yanning Zhang. 2025. "Enhancing Border Learning for Better Image Denoising" Mathematics 13, no. 7: 1119. https://doi.org/10.3390/math13071119
APA StyleGe, X., Zhu, Y., Qi, L., Hu, Y., Sun, J., & Zhang, Y. (2025). Enhancing Border Learning for Better Image Denoising. Mathematics, 13(7), 1119. https://doi.org/10.3390/math13071119







