Analyzing Coupled Delayed Fractional Systems: Theoretical Insights and Numerical Approaches

Abstract

In this work, we investigate the theoretical properties of a generalized coupled system of finite-delay fractional differential equations involving Caputo derivatives. We establish rigorous criteria to ensure the existence and uniqueness of solutions under appropriate assumptions on the problem parameters and constituent functions, employing contraction mapping principles and Schauder’s fixed-point theorem. Then, we examine the Ulam–Hyers stability of the proposed system. To illustrate the main findings, three examples are provided. Moreover, we provide numerical solutions using the Adams–Bashforth–Moulton method. The practical significance of our results is demonstrated through illustrative examples, highlighting applications in predator–prey dynamics and control systems.

1. Introduction

Fractional calculus has received a lot of interest lately for modeling complex systems that exhibit memory and nonlocal interactions because of its capacity to generalize conventional derivatives and integrals to noninteger orders [1,2,3,4]. Specifically, Caputo fractional derivatives (CapFDs) provide a strong framework for characterizing dynamical systems in which the evolution of variables depends on both past and present states [5,6].

Theoretical studies concerning the uniqueness and existence of solutions for linked Caputo fractional differential equations (CapFDEs) have applications in many different fields of science. Essential tools for determining the unique conditions under which the solutions to these equations exist are provided by contraction mapping principles that are specifically designed for fractional calculus and fixed-point theorems [7,8,9,10,11]. Furthermore, resistance against minor perturbations is ensured by studying the Ulam–Hyers stability of solutions, which is essential for forecasting the long-term behavior of complex systems [12,13]. Many studies (e.g., [14,15,16]) have examined the existence, uniqueness, and Ulam–Hyers stability results for a nonlinear coupled system including Caputo fractional derivatives.

Illustrative examples, such as applications to predator–prey models which capture dynamics where populations show memory of previous interactions, indicate the usefulness of CapFDEs in ecological dynamics [1,17]. Beyond ecology, CapFDEs find use in a wide range of fields, including epidemiology (to model the spread of disease using historical infection rates), finance (to replicate price fluctuations driven by past market trends), and control systems with delayed feedback mechanisms [6,18]. Younis et al. [19] used the fixed-point method to connect with Chua’s dynamic, incorporating the Atangana–Baleanu–Caputo (ABC) fractional derivative using a two-step Lagrange polynomial. Qaraad et al. [20] focused on the oscillation and asymptotic behavior of certain third-order nonlinear delay differential equations with distributed deviating arguments. In [21], the authors used fixed-point theorems to investigate the existence and uniqueness results for a CapFDE with finite delay. Ref. [22] investigated the existence, uniqueness, and stability results for a specific type of coupled system incorporating FDEs. The authors of [23] showed the existence and uniqueness of solutions for a coupled system of sequential FDEs of Caputo type with nonlocal integral boundary conditions. Reference [24] discussed recent results about Ulam stabilities of nonlinear integral equations. Wang and Zhang examined the Ulam–Hyers–Mittag–Leffler stability of the subsequent CapFDE in [25]:

$${}^{C}D_{\varrho }^{\alpha }\mu \left(\varrho \right)=f(\varrho ,\mu \left(\varrho \right),\nu \left(g\left(\varrho \right)\right),\mu \left({\tau }_i\left(\varrho \right)\right),\varrho \in I=[0,b]\subset \mathbb{R},\alpha \in (0,1).$$

Tunç [26] discussed new findings related to the Ulam–Hyers–Mittag–Leffler stability of CapFDEs with finite delay:

$$\left\{\begin{array}{cc}{}^{C}D_{\varrho }^{\alpha }\nu \left(\varrho \right)=\sum _{i=1}^N{F}_i(\varrho ,\nu \left(\varrho \right),\nu \left({\tau }_i\left(\varrho \right)\right),\varrho \in [0,b],\hfill & \\ \nu \left(\varrho \right)=\phi \left(\varrho \right),\varrho \in [-h,0],\hfill \end{array}\right.$$

where $\varrho \in [0,b]$, $0<b\in \mathbb{R}$, $v\left(\varrho \right)\in \mathbb{R}$, ${}^{C}D_{\varrho }^{\alpha }v\left(\varrho \right)$ is the CapFD of $v\left(\varrho \right)$ with a lower limit zero of order $\alpha$, $\alpha \in (0,1)$, $F_i\in C([0,b]\times {\mathbb{R}}^2,\mathbb{R})$, ${\tau }_i\in C([0,b],[-h,b])$, $h>0$, ${\tau }_i\left(\varrho \right)\le \varrho$ with $0\le {\tau }_i\left(\varrho \right)\le h_i$, $0<h_i\in \mathbb{R}$, $h=max\left(h_i\right)$, $i=1,2,\dots ,N$.

To extend the presented problems to a coupled system for the analysis of uniqueness, existence, and Ulam–Hyers stability, we consider the following coupled system of CapFDEs:

$$\left\{\begin{array}{c}{}^{C}D_{\varrho }^{\alpha }\mu \left(\varrho \right)=\sum _{i=1}^N{F}_i(\varrho ,\mu \left(\varrho \right),\nu \left(\varrho \right),\mu \left({\tau }_i\left(\varrho \right)\right),\nu \left({\sigma }_i\left(\varrho \right)\right)),\varrho \in [0,b],\hfill \\ {}^{C}D_{\varrho }^{\alpha }\nu \left(\varrho \right)=\sum _{j=1}^M{G}_j(\varrho ,\mu \left(\varrho \right),\nu \left(\varrho \right),\mu \left({\eta }_j\left(\varrho \right)\right),\nu \left({\xi }_j\left(\varrho \right)\right)),\varrho \in [0,b],\hfill \end{array}\right.$$

(1)

with the initial conditions

$$\left\{\begin{array}{cc}\mu \left(\varrho \right)=\phi \left(\varrho \right),\hfill & \varrho \in [-h,0],\hfill \\ \nu \left(\varrho \right)=\psi \left(\varrho \right),\hfill & \varrho \in [-h,0],\hfill \end{array}\right.$$

(2)

Therein, the following are defined:

• $\mu \left(\varrho \right)$ and $\nu \left(\varrho \right)$ are the unknown functions and $\varphi ,\psi \in C\left(\right[-h,0],\mathbb{R})$.
• ${}^{C}D_{\varrho }^{\alpha }$ denotes the CapFD of order $\alpha$ with $\alpha \in (0,1)$.
• $F_i\in C(I\times {\mathbb{R}}^4,\mathbb{R})$ and $G_j\in C(I\times {\mathbb{R}}^4,\mathbb{R})$ are given continuous functions.
• ${\tau }_i\left(\varrho \right)$, ${\sigma }_i\left(\varrho \right)$, ${\eta }_j\left(\varrho \right)$, and ${\xi }_j\left(\varrho \right)$ are given continuous delay functions satisfying
  ${\tau }_i\left(\varrho \right),{\sigma }_i\left(\varrho \right),{\eta }_j\left(\varrho \right),{\xi }_j\left(\varrho \right){\in }_j\left(\varrho \right)\in C(I,[-h,b])$, $b,h>0$
  and $0\le {\tau }_i\left(\varrho \right),{\sigma }_i\left(\varrho \right),{\eta }_j\left(\varrho \right),{\xi }_j\left(\varrho \right)\le \varrho \le b$.

In this paper, we conduct a comprehensive theoretical analysis of the coupled system of CapFDEs with finite delays, as formulated in Equations (1) and (2). Our study focuses on establishing the existence and uniqueness results under appropriate conditions, leveraging contraction mapping principles and Schauder’s fixed-point theorem. Additionally, we explore the Ulam–Hyers stability of the proposed system, ensuring its robustness in practical applications. To support our theoretical findings, we implement numerical simulations using the Adams–Bashforth–Moulton method [27], which not only validates our analytical results but also provides deeper insights into the behavior of the system in real-world scenarios. The fractional-order modeling framework presented in this work is particularly relevant for capturing nonlocal interactions and memory effects, making it applicable across diverse fields such as control systems and predator–prey dynamics.

The main contributions of this study are as follows:

• Theoretical Analysis: We establish the existence, uniqueness, and Ulam–Hyers stability criteria for the coupled system of CapFDEs with delays.
• Numerical Validation: We implement the Adams–Bashforth–Moulton method to numerically approximate solutions, reinforcing our theoretical results.
• Application: We demonstrate the practical applicability of our findings through a variety of illustrative examples, applications, and numerical simulations.

Bridging theoretical advancements with numerical and applied perspectives, this research provides a solid foundation for the further exploration and application of fractional-order differential models in complex systems.

The structure of this paper is as follows: Section 2 provides an overview and fundamental ideas. In Section 3, we give the existence, uniqueness, and Ulam–Hyers stability of the system’s solutions. Section 4 and Section 5 give some examples and applications. The conclusion and suggestions for further research are in the final section.

2. Preliminaries

Some well-known fundamental definitions of fractional calculus as well as a few lemmas required for this study are given in this section.

Define the Banach space $\left(C\right([0,b],\mathbb{R}),\parallel ·\parallel )$, where $\parallel \mu \parallel ={sup}_{\varrho \in [0,b]}\left|\mu \left(\varrho \right)\right|$ for any $\mu \in C\left(\right[0,b],\mathbb{R})$.

Definition 1

([2]). A Riemann–Liouville fractional integral of order α for a function f is defined by

$$I_0^{\alpha }f\left(\varrho \right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{\displaystyle \frac{f\left(s\right)}{{(\varrho -s)}^{1-\alpha }}}ds,\varrho >0,\alpha >0,$$

provided the right side is pointwise-defined on ${\mathbb{R}}^{+},{\mathbb{R}}^{+}=[0,\infty )$, where $\mathrm{\Gamma }(·)$ is the gamma function.

Definition 2

([2]). The CapFD of order α for a function $f:{\mathbb{R}}^{+}\to \mathbb{R}$ can be written as

$${}^{C}D_{\varrho }^{\alpha }\mu \left(\varrho \right)={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}{\int }_0^{\varrho }{\displaystyle \frac{{\mu }^{\prime }\left(\tau \right)}{{(\varrho -\tau )}^{\alpha }}}d\tau ,\varrho >0,0<\alpha <1.$$

Remark 1.

Composition with Power Functions: The CapFD of a power function ${\varrho }^{\beta }$ for $\beta >0$ is given by

$${}^{C}D_{\varrho }^{\alpha }{\varrho }^{\beta }=\left\{\begin{array}{cc}{\displaystyle \frac{\mathrm{\Gamma }(\beta +1)}{\mathrm{\Gamma }(\beta -\alpha +1)}}{\varrho }^{\beta -\alpha },\hfill & \mathrm{if}\beta >\alpha -1,\hfill \\ 0,\hfill & \mathrm{if}\beta =\alpha -1.\hfill \end{array}\right.$$

Lemma 1

([1]). If $\alpha >0$, $\beta >0$, $\varrho \in [0,b]$, and $\nu \left(\varrho \right)\in L[0,b]$, then

$${}^{C}D_{\varrho }^{\alpha }{I}_{\varrho }^{\alpha }\nu \left(\varrho \right)=\nu \left(\varrho \right),I_{\varrho }^{\alpha }{I}_{\varrho }^{\beta }\nu \left(\varrho \right)=I_{\varrho }^{\alpha +\beta }\mu \left(\varrho \right).$$

Lemma 2

([2]). Assume that $\nu \in C\left(\right(0,+\infty ),\mathbb{R})$ with a CapFD of order $\alpha >0$ that belongs to $\mu \in C^n((0,+\infty ),\mathbb{R})$; then,

$$I_{\varrho }^{\alpha }{}^{C}D_{\varrho }^{\alpha }\nu \left(\varrho \right)=\nu \left(\varrho \right)-\sum _{k=0}^{n-1}{\displaystyle \frac{{\nu }^{\left(k\right)}\left(0\right)}{k!}}{\varrho }^k,$$

where n is the smallest integer greater than or equal to α.

Lemma 3

([28]). Suppose that $n\in \mathbb{N}$, and $n-1<\alpha <n$. Then, we have

$$I_{\varrho }^{\alpha }{[}^C{D}_{\varrho }^{\alpha }\nu \left(\tau \right)]=\nu \left(\tau \right)+c_0+c_1\tau +c_2{\tau }^2+\cdots +c_{n-1}{\tau }^{n-1},$$

where $c_i\in \mathbb{R}$, $i=0,1,2,\dots ,n-1$. Hence, the following CapFDE

$${}^{C}D_{\varrho }^{\alpha }\nu \left(\tau \right)=0,$$

has a general solution which is expressed by

$$\nu \left(\tau \right)=c_0+c_1\tau +c_2{\tau }^2+\cdots +c_{n-1}{\tau }^{n-1}.$$

Lemma 4

([28]). Let $0<\alpha <1$, and let $f:[0,b]\to \mathbb{R}$ be continuous. Then, ν is a solution of the fractional integral equation

$$\nu \left(\varrho \right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}f\left(s\right)ds,\varrho >0,$$

if and only if ν is a solution to the initial value problem for the CapFDE

$${}^{C}D_{\varrho }^{\alpha }\nu \left(\varrho \right)=f\left(\varrho \right),\varrho \in [0,b],$$

$$\nu \left(0\right)=0.$$

Lemma 5

(Banach fixed-point theorem [29]). Let $(X,d)$ be a nonempty complete metric space, and let $T:X\to X$ be a contraction mapping, i.e., there exists a constant $0\le k<1$ such that

$$d\left(T\right(\mu ),T(\nu \left)\right)\le kd(\mu ,\nu )\mathrm{for}\mathrm{all}\mu ,\nu \in X.$$

Then, T has a unique fixed point ${\mu }^{*}\in X$.

Lemma 6

(Schauder fixed-point theorem [29]). Let X be a nonempty, convex, and closed subset of a Banach space, and let $T:X\to X$ be a continuous and compact (i.e., $T\left(X\right)$ is relatively compact) mapping. Then, T has at least one fixed point in X.

3. Main Results

The existence, uniqueness, and Ulam–Hyers stability of the operator, which determines whether or not it has fixed points, will be proved by the following results. Then, we give some examples and applications.

Definition 3.

Consider the coupled system of CapFDEs with delays:

$$\left\{\begin{array}{cc}{}^{C}D_{\varrho }^{\alpha }\mu \left(\varrho \right)=\sum _{i=1}^N{F}_i\left(\varrho ,\mu \left(\varrho \right),\nu \left(\varrho \right),\mu \left({\tau }_i\left(\varrho \right)\right),\nu \left({\sigma }_i\left(\varrho \right)\right)\right),\hfill & \varrho \in [0,b],\hfill \\ {}^{C}D_{\varrho }^{\alpha }\nu \left(\varrho \right)=\sum _{j=1}^M{G}_j\left(\varrho ,\mu \left(\varrho \right),\nu \left(\varrho \right),\mu \left({\eta }_j\left(\varrho \right)\right),\nu \left({\xi }_j\left(\varrho \right)\right)\right),\hfill & \varrho \in [0,b],\hfill \end{array}\right.$$

(3)

with initial conditions

$$\mu \left(\varrho \right)=\varphi \left(\varrho \right),\nu \left(\varrho \right)=\psi \left(\varrho \right),\varrho \in [-h,0],$$

where $\alpha \in (0,1)$, $F_i,G_j$ are continuous and bounded, and ${\tau }_i,{\sigma }_i,{\eta }_j,{\xi }_j\in C([0,b],[-h,b])(b,h>0)$ are continuous delay functions satisfying $0\le {\tau }_i\left(\varrho \right),{\sigma }_i\left(\varrho \right),{\eta }_j\left(\varrho \right),{\xi }_j\left(\varrho \right)\le \varrho \le b$.

Using the properties of CapFD and Lemma 3, the coupled systems (1)–(2) can be transformed into the following coupled system of Volterra integral equations:

$$\left\{\begin{array}{c}\mu \left(\varrho \right)=\phi \left(0\right)+{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}\sum _{i=1}^N{F}_i(s,\mu \left(s\right),\nu \left(s\right),\mu \left({\tau }_i\left(s\right)\right),\nu \left({\sigma }_i\left(s\right)\right))ds,\hfill \\ \nu \left(\varrho \right)=\psi \left(0\right)+{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}\sum _{j=1}^M{G}_j(s,\mu \left(s\right),\nu \left(s\right),\mu \left({\eta }_j\left(s\right)\right),\nu \left({\xi }_j\left(s\right)\right))ds,\hfill \end{array}\right.$$

(4)

for $\varrho \in [0,b]$, and

$$\mu \left(\varrho \right)=\varphi \left(\varrho \right),\nu \left(\varrho \right)=\psi \left(\varrho \right),\mathrm{for}\varrho \in [-h,0].$$

To establish the existence and uniqueness of solutions for the coupled systems (1)–(2) using the Banach and Schauder fixed-point theorems, we make the following assumptions on the system functions $F_i$ and $G_j$, the fractional-order $\alpha$, and the parameters ${\tau }_i$, ${\sigma }_i$, ${\eta }_j$, and ${\xi }_j$:

(H1)

For all $i=1,\dots ,N$ and $j=1,\dots ,M$, we have the following:

• $F_i:[0,b]\times {\mathbb{R}}^4\to \mathbb{R}$ and $G_j:[0,b]\times {\mathbb{R}}^4\to \mathbb{R}$ are continuous.
• $F_i$ and $G_j$ are bounded: There exist constants $M_F,M_G>0$ such that

  $$\underset{(\varrho ,x_1,x_2,x_3,x_4)\in [0,b]\times {\mathbb{R}}^4}{sup}\left|F_i(\varrho ,x_1,x_2,x_3,x_4)\right| \le M_F,$$

  $$\underset{(\varrho ,x_1,x_2,x_3,x_4)\in [0,b]\times {\mathbb{R}}^4}{sup}\left|G_j(\varrho ,x_1,x_2,x_3,x_4)\right| \le M_G.$$

(H2)

The delay functions satisfy the following:

• ${\tau }_i,{\sigma }_i,{\eta }_j,{\xi }_j\in C([0,b],[-h,b])$ for all $i,j$.
• ${\tau }_i\left(\varrho \right),{\sigma }_i\left(\varrho \right),{\eta }_j\left(\varrho \right),{\xi }_j\left(\varrho \right)\le \varrho$ for all $\varrho \in [0,b]$.

(H3)

$\varphi ,\psi \in C\left(\right[-h,0],\mathbb{R})$ are given continuous initial functions.

(H4)

For all $i=1,\dots ,N$ and $j=1,\dots ,M$, $F_i$ and $G_j$ satisfy Lipschitz conditions, with constants $L_F,L_G>0$ such that for all $(\varrho ,x_1,x_2,x_3,x_4),(\varrho ,y_1,y_2,y_3,y_4)\in [0,b]\times {\mathbb{R}}^4$,

$$|F_i(\varrho ,x_1,x_2,x_3,x_4)-F_i(\varrho ,y_1,y_2,y_3,y_4)| \le L_F\sum _{k=1}^4|x_k-y_k|,$$

$$|G_j(\varrho ,x_1,x_2,x_3,x_4)-G_j(\varrho ,y_1,y_2,y_3,y_4)| \le L_G\sum _{k=1}^4|x_k-y_k|.$$

Theorem 1

(existence theorem). Under the assumptions (H1)–(H3), the system (3) has at least one solution $(\mu ,\nu )\in C\left(\right[-h,b],\mathbb{R})\times C\left(\right[-h,b],\mathbb{R})$.

Proof. 

We will provide the proof in the following steps.

Step 1: Equivalent Integral System.

The Caputo derivative ${}^{C}D_{\varrho }^{\alpha }$ is inverted using the fractional integral ${\mathcal{I}}_{\varrho }^{\alpha }$ with the aid of Lemma 3. Consequently, for $\varrho \in [0,b]$, the system can be rewritten as

$$\begin{array}{cc}\hfill \mu \left(\varrho \right)& =\varphi \left(0\right)+{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}\sum _{i=1}^N{F}_i\left(s,\mu \left(s\right),\nu \left(s\right),\mu \left({\tau }_i\left(s\right)\right),\nu \left({\sigma }_i\left(s\right)\right)\right)ds,\hfill \\ \hfill \nu \left(\varrho \right)& =\psi \left(0\right)+{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}\sum _{j=1}^M{G}_j\left(s,\mu \left(s\right),\nu \left(s\right),\mu \left({\eta }_j\left(s\right)\right),\nu \left({\xi }_j\left(s\right)\right)\right)ds,\hfill \end{array}$$

and for $\varrho \in [-h,0]$,

$$\mu \left(\varrho \right)=\varphi \left(\varrho \right),\nu \left(\varrho \right)=\psi \left(\varrho \right).$$

Therein, ${\tau }_i\left(s\right)\le 0$, $\mu \left({\tau }_i\left(s\right)\right)=\varphi \left({\tau }_i\left(s\right)\right)$, and this is similar for other delayed terms.

Step 2: Operator Formulation.

Define the Banach space as

$$E=C([-h,b],\mathbb{R})\times {C([-h,b],\mathbb{R}),\parallel (\mu ,\nu )\parallel }_E=max\left\{{\parallel \mu \parallel }_C,{\parallel \nu \parallel }_C\right\}.$$

Define the operator $T:E\to E$ as

$$T(\mu ,\nu )\left(\varrho \right)=(T_{\mu },T_{\nu })(\mu ,\nu )\left(\varrho \right)=\left\{\begin{array}{cc}\left(\varphi \left(\varrho \right),\psi \left(\varrho \right)\right),\hfill & \varrho \in [-h,0],\hfill \\ \left(\varphi \left(0\right)+{\mathcal{I}}^{\alpha }\sum _{i=1}^N{F}_i(·),\psi \left(0\right)+{\mathcal{I}}^{\alpha }\sum _{j=1}^M{G}_j(·)\right),\hfill & \varrho \in [0,b].\hfill \end{array}\right.$$

that is,

$$\begin{array}{cc}\hfill T_{\mu }(\mu ,\nu )\left(\varrho \right)& =\varphi \left(0\right)+{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}\sum _{i=1}^N{F}_i\left(s,\mu \left(s\right),\nu \left(s\right),\mu \left({\tau }_i\left(s\right)\right),\nu \left({\sigma }_i\left(s\right)\right)\right)ds,\hfill \\ \hfill T_{\nu }(\mu ,\nu )\left(\varrho \right)& =\psi \left(0\right)+{\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}\sum _{j=1}^M{G}_j\left(s,\mu \left(s\right),\nu \left(s\right),\mu \left({\eta }_j\left(s\right)\right),\nu \left({\xi }_j\left(s\right)\right)\right)ds.\hfill \end{array}$$

Step 3: Continuity of$\mathit{T}$.

Let $({\mathit{\mu }}_{\mathit{n}},{\mathit{\nu }}_{\mathit{n}})\to (\mathit{\mu },\mathit{\nu })$ in $\mathit{E}$. For $\mathit{\varrho }\in [\mathbf{0},\mathit{b}]$,

$$\begin{array}{cc}\hfill & \left|{\mathit{T}}_{\mathit{\mu }}({\mathit{\mu }}_{\mathit{n}},{\mathit{\nu }}_{\mathit{n}})\left(\mathit{\varrho }\right)-{\mathit{T}}_{\mathit{\mu }}(\mathit{\mu },\mathit{\nu })\left(\mathit{\varrho }\right)\right|\le {\displaystyle \frac{\mathbf{1}}{\mathbf{\Gamma }\left(\mathit{\alpha }\right)}}{\int }_{\mathbf{0}}^{\mathit{\varrho }}{(\mathit{\varrho }-\mathit{s})}^{\mathit{\alpha }-\mathbf{1}}\hfill \\ \hfill & \times \sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}\left|{\mathit{F}}_{\mathit{i}}(\mathit{s},{\mathit{\mu }}_{\mathit{n}}\left(\mathit{s}\right),{\mathit{\nu }}_{\mathit{n}}\left(\mathit{s}\right),{\mathit{\mu }}_{\mathit{n}}\left({\mathit{\tau }}_{\mathit{i}}\left(\mathit{s}\right)\right),{\mathit{\nu }}_{\mathit{n}}\left({\mathit{\sigma }}_{\mathit{i}}\left(\mathit{s}\right)\right))-{\mathit{F}}_{\mathit{i}}(\mathit{s},\mathit{\mu }\left(\mathit{s}\right),\mathit{\nu }\left(\mathit{s}\right),\mathit{\mu }\left({\mathit{\tau }}_{\mathit{i}}\left(\mathit{s}\right)\right),\mathit{\nu }\left({\mathit{\sigma }}_{\mathit{i}}\left(\mathit{s}\right)\right))\right|\mathit{ds}\hfill \\ \hfill & \le {\displaystyle \frac{\mathbf{1}}{\mathbf{\Gamma }\left(\mathit{\alpha }\right)}}{\int }_{\mathbf{0}}^{\mathit{b}}{(\mathit{\varrho }-\mathit{s})}^{\mathit{\alpha }-\mathbf{1}}\sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\parallel {\left({\mathit{F}}_{\mathit{i}}\right)}_{\mathit{n}}-\left({\mathit{F}}_{\mathit{i}}\right)\parallel }_{\mathit{C}}\mathit{ds}.\hfill \end{array}$$

Since ${\mathit{F}}_{\mathit{i}}$ is a continuous function and, by the dominated convergence theorem, we have

$$\begin{array}{cc}\hfill & \left|{\mathit{T}}_{\mathit{\mu }}({\mathit{\mu }}_{\mathit{n}},{\mathit{\nu }}_{\mathit{n}})\left(\mathit{\varrho }\right)-{\mathit{T}}_{\mathit{\mu }}(\mathit{\mu },\mathit{\nu })\left(\mathit{\varrho }\right)\right|\le {\displaystyle \frac{{\mathit{b}}^{\mathit{\alpha }}}{\mathbf{\Gamma }(\mathit{\alpha }+\mathbf{1})}}{\parallel ({\mathit{\mu }}_{\mathit{n}},{\mathit{\nu }}_{\mathit{n}})-(\mathit{\mu },\mathit{\nu })\parallel }_{\mathit{E}}\to \mathbf{0}\mathrm{as}\mathit{n}\to \infty .\hfill \end{array}$$

Also, with the same process, one has

$$\begin{array}{cc}\hfill & \left|{\mathit{T}}_{\mathit{\nu }}({\mathit{\mu }}_{\mathit{n}},{\mathit{\nu }}_{\mathit{n}})\left(\mathit{\varrho }\right)-{\mathit{T}}_{\mathit{\nu }}(\mathit{\mu },\mathit{\nu })\left(\mathit{\varrho }\right)\right|\le {\displaystyle \frac{\mathbf{1}}{\mathbf{\Gamma }\left(\mathit{\alpha }\right)}}{\int }_{\mathbf{0}}^{\mathit{b}}{(\mathit{\varrho }-\mathit{s})}^{\mathit{\alpha }-\mathbf{1}}\sum _{\mathit{j}=\mathbf{1}}^{\mathit{M}}{\parallel {\left({\mathit{G}}_{\mathit{j}}\right)}_{\mathit{n}}-\left({\mathit{G}}_{\mathit{j}}\right)\parallel }_{\mathit{C}}\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{b}}^{\mathit{\alpha }}}{\mathbf{\Gamma }(\mathit{\alpha }+\mathbf{1})}}{\parallel ({\mathit{\mu }}_{\mathit{n}},{\mathit{\nu }}_{\mathit{n}})-(\mathit{\mu },\mathit{\nu })\parallel }_{\mathit{E}}\to \mathbf{0}\mathrm{as}\mathit{n}\to \infty .\hfill \end{array}$$

Thus, $\mathit{T}$ is continuous.

Step 4: Compactness of $\mathit{T}$.

• Let ${\mathit{B}}_{\mathit{r}}={\mathbf{\{}(\mathit{\mu },\mathit{\nu })\in \mathit{E}:\parallel (\mathit{\mu },\mathit{\nu })\parallel }_{\mathit{E}}\le \mathit{r}\mathbf{\}}$. We show that $\mathit{T}\left({\mathit{B}}_{\mathit{r}}\right)$ is relatively compact via the Arzelá–Ascoli theorem.

Uniform Boundedness: For $(\mathit{\mu },\mathit{\nu })\in {\mathit{B}}_{\mathit{r}}$ and $\mathit{\varrho }\in [\mathbf{0},\mathit{b}]$,

$$\begin{array}{cc}\hfill & \left|\mathit{T}(\mathit{\mu },\mathit{\nu })\left(\mathit{\varrho }\right)\right| \le \mathit{max}\left\{|{\mathit{T}}_{\mathit{\mu }}(\mathit{\mu },\mathit{\nu })\left(\mathit{\varrho }\right)| + |{\mathit{T}}_{\mathit{\nu }}(\mathit{\mu },\mathit{\nu })\left(\mathit{\varrho }\right)|\right\}\hfill \\ \hfill & \le \left|\mathit{\varphi }\left(\mathbf{0}\right)\right| +{\displaystyle \frac{\mathit{N}·{\mathit{M}}_{\mathit{F}}}{\mathbf{\Gamma }(\mathit{\alpha }+\mathbf{1})}}{\mathit{b}}^{\mathit{\alpha }}+\left|\mathit{\psi }\left(\mathbf{0}\right)\right| +{\displaystyle \frac{\mathit{M}·{\mathit{M}}_{\mathit{G}}}{\mathrm{\Gamma }(\mathit{\alpha }+\mathbf{1})}}{\mathit{b}}^{\mathit{\alpha }},\hfill \end{array}$$

where $|{\mathit{F}}_{\mathit{i}}| \le {\mathit{M}}_{\mathit{F}}$ and $|{\mathit{G}}_{\mathit{j}}| \le {\mathit{M}}_{\mathit{G}}$. Choose $\mathit{r}={\mathbf{max}\mathbf{\{}\parallel \mathit{\varphi }\parallel }_{\mathit{C}}{,\parallel \mathit{\psi }\parallel }_{\mathit{C}}\mathbf{\}}+{\displaystyle \frac{(\mathit{N}{\mathit{M}}_{\mathit{F}}+\mathit{M}{\mathit{M}}_{\mathit{G}}){\mathit{b}}^{\mathit{\alpha }}}{\mathrm{\Gamma }(\mathit{\alpha }+\mathbf{1})}}$. Then, $\mathit{T}\left({\mathit{B}}_{\mathit{r}}\right)\subset {\mathit{B}}_{\mathit{r}}$.

Equicontinuity: For ${\mathit{\varrho }}_{\mathbf{1}},{\mathit{\varrho }}_{\mathbf{2}}\in [\mathbf{0},\mathit{b}]$, ${\mathit{\varrho }}_{\mathbf{1}}<{\mathit{\varrho }}_{\mathbf{2}}$,

$$\begin{array}{cc}\hfill & \left|{\mathit{T}}_{\mathit{\mu }}(\mathit{\mu },\mathit{\nu })\left({\mathit{\varrho }}_{\mathbf{2}}\right)-{\mathit{T}}_{\mathit{\mu }}(\mathit{\mu },\mathit{\nu })\left({\mathit{\varrho }}_{\mathbf{1}}\right)\right|\hfill \\ \hfill & \le {\displaystyle \frac{\mathbf{1}}{\mathrm{\Gamma }\left(\mathit{\alpha }\right)}}\left|{\int }_{\mathbf{0}}^{{\mathit{\varrho }}_{\mathbf{2}}}{({\mathit{\varrho }}_{\mathbf{2}}-\mathit{s})}^{\mathit{\alpha }-\mathbf{1}}\sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\mathit{F}}_{\mathit{i}}\mathit{ds}-{\int }_{\mathbf{0}}^{{\mathit{\varrho }}_{\mathbf{1}}}{({\mathit{\varrho }}_{\mathbf{1}}-\mathit{s})}^{\mathit{\alpha }-\mathbf{1}}\sum _{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\mathit{F}}_{\mathit{i}}\mathit{ds}\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{NM}}_{\mathit{F}}}{\mathrm{\Gamma }(\mathit{\alpha }+\mathbf{1})}}\left({\mathit{\varrho }}_{\mathbf{2}}^{\mathit{\alpha }}-{\mathit{\varrho }}_{\mathbf{1}}^{\mathit{\alpha }}\right)\le {\displaystyle \frac{{\mathit{NM}}_{\mathit{F}}}{\mathrm{\Gamma }(\mathit{\alpha }+\mathbf{1})}}\mathit{\alpha }({\mathit{\varrho }}_{\mathbf{2}}-{\mathit{\varrho }}_{\mathbf{1}})\left(\mathrm{by}\mathrm{mean}\mathrm{value}\mathrm{theorem}\right).\hfill \end{array}$$

Similarly, we have

$$\begin{array}{cc}\hfill & \left|{\mathit{T}}_{\mathit{\nu }}(\mathit{\mu },\mathit{\nu })\left({\mathit{\varrho }}_{\mathbf{2}}\right)-{\mathit{T}}_{\mathit{\nu }}(\mathit{\mu },\mathit{\nu })\left({\mathit{\varrho }}_{\mathbf{1}}\right)\right|\le \left|{\int }_{\mathbf{0}}^{{\mathit{\varrho }}_{\mathbf{2}}}{({\mathit{\varrho }}_{\mathbf{2}}-\mathit{s})}^{\mathit{\alpha }-\mathbf{1}}\sum _{\mathit{i}=\mathbf{1}}^{\mathit{M}}{\mathit{G}}_{\mathit{j}}\mathit{ds}-{\int }_{\mathbf{0}}^{{\mathit{\varrho }}_{\mathbf{1}}}{({\mathit{\varrho }}_{\mathbf{1}}-\mathit{s})}^{\mathit{\alpha }-\mathbf{1}}\sum _{\mathit{i}=\mathbf{1}}^{\mathit{M}}{\mathit{G}}_{\mathit{j}}\mathit{ds}\right|\hfill \\ \hfill & \le {\displaystyle \frac{{\mathit{NM}}_{\mathit{F}}}{\mathbf{\Gamma }(\mathit{\alpha }+\mathbf{1})}}\mathit{\alpha }({\mathit{\varrho }}_{\mathbf{2}}-{\mathit{\varrho }}_{\mathbf{1}}).\hfill \end{array}$$

Thus, $\left|\mathit{T}(\mathit{\mu },\mathit{\nu })\left({\mathit{\varrho }}_{\mathbf{2}}\right)-\mathit{T}(\mathit{\mu },\mathit{\nu })\left({\mathit{\varrho }}_{\mathbf{1}}\right)\right|\to \mathbf{0}\mathrm{as}\mathit{n}\to \infty$. Hence $\mathit{T}\left({\mathit{B}}_{\mathit{r}}\right)$ is equicontinuous.

• For $[-\mathit{h},\mathbf{0}]$, $\mathit{T}$ is constant and hence equicontinuous. By Arzelá–Ascoli theorem, $\mathit{T}$ is compact.

Since $\mathit{T}:{\mathit{B}}_{\mathit{r}}\to {\mathit{B}}_{\mathit{r}}$ is continuous and compact, Schauder’s theorem (Lemma 6) guarantees a fixed point $(\mathit{\mu },\mathit{\nu })=\mathit{T}(\mathit{\mu },\mathit{\nu })$, which solves the system (3). □

Theorem 2

(uniqueness theorem). Assume that assumptions (H2)–(H4) hold. For $\lambda >0$, if $2{\lambda }^{-\alpha }(N{L}_F+M{L}_G)<1$, then the system (3) has a unique solution $(\mu ,\nu )\in C\left(\right[-h,b],\mathbb{R})\times C\left(\right[-h,b],\mathbb{R})$.

Proof. 

Consider the operator $T:E\to E$ on the Banach space $E=C\left(\right[-h,b],\mathbb{R})\times C\left(\right[-h,b],\mathbb{R})$ with the Bielecki norm:

$${\parallel (\mu ,\nu )\parallel }_{E,\lambda }=\underset{\varrho \in [-h,b]}{sup}{e}^{-\lambda \varrho }\left|\mu \left(\varrho \right)\right| +\underset{\varrho \in [-h,b]}{sup}{e}^{-\lambda \varrho }\left|\nu \left(\varrho \right)\right|,\mathrm{for}\lambda >0.$$

The operator T is defined componentwise, as established in the existence proof. To complete the proof, we demonstrate that T is a contraction operator. For this purpose, we begin by estimating the Lipschitz constant. Specifically, for $\varrho \in [0,b]$, the difference in the $\mu$-component satisfies

$$\begin{array}{cc}\hfill e^{-\lambda \varrho }|T_{\mu }({\mu }_1,{\nu }_1)\left(\varrho \right)-T_{\mu }({\mu }_2,{\nu }_2)\left(\varrho \right)|& \le {\displaystyle \frac{2N{L}_F}{\mathrm{\Gamma }\left(\alpha \right)}}{e}^{-\lambda \varrho }{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}{e}^{\lambda s}ds·{\parallel ({\mu }_1-{\mu }_2,{\nu }_1-{\nu }_2)\parallel }_{E,\lambda }\hfill \\ \hfill & ={\displaystyle \frac{2N{L}_F}{\mathrm{\Gamma }\left(\alpha \right)}}{\lambda }^{-\alpha }\mathrm{\Gamma }\left(\alpha \right){\parallel ({\mu }_1-{\mu }_2,{\nu }_1-{\nu }_2)\parallel }_{E,\lambda }\hfill \\ \hfill & =2N{L}_F{\lambda }^{-\alpha }{\parallel ({\mu }_1-{\mu }_2,{\nu }_1-{\nu }_2)\parallel }_{E,\lambda }.\hfill \end{array}$$

(5)

Similarly, for the $\nu$-component,

$$\begin{array}{c}\hfill e^{-\lambda \varrho }|T_{\nu }({\mu }_1,{\nu }_1)\left(\varrho \right)-T_{\nu }({\mu }_2,{\nu }_2)\left(\varrho \right)| \le 2M{L}_G{\lambda }^{-\alpha }{\parallel ({\mu }_1-{\mu }_2,{\nu }_1-{\nu }_2)\parallel }_{E,\lambda }.\end{array}$$

(6)

Next, we show that T is a contraction. For $({\mu }_1,{\nu }_1),({\mu }_2,{\nu }_2)\in E$, and summing both components in (5) and (6), we obtain

$$\begin{array}{cc}\hfill & \parallel T({\mu }_1,{\nu }_1)-T({\mu }_2,{\nu }_2){\parallel }_{E,\lambda }\hfill \\ \hfill & \le \parallel T_{\mu }({\mu }_1,{\nu }_1)\left(\varrho \right)-T_{\mu }({\mu }_2,{\nu }_2)\left(\varrho \right){\parallel }_{E,\lambda }+{\parallel T_{\nu }({\mu }_1,{\nu }_1)\left(\varrho \right)-T_{\nu }({\mu }_2,{\nu }_2)\left(\varrho \right)\parallel }_{E,\lambda }\hfill \\ \hfill & \le 2{\lambda }^{-\alpha }(N{L}_F+M{L}_G){\parallel ({\mu }_1-{\mu }_2,{\nu }_1-{\nu }_2)\parallel }_{E,\lambda }.\hfill \end{array}$$

Since $2{\lambda }^{-\alpha }(N{L}_F+M{L}_G)<1$, this implies that $\lambda >{\left[2(N{L}_F+M{L}_G)\right]}^{1/\alpha }$. Thus, T is a contraction on $(E,\parallel ·{\parallel }_{E,\lambda })$. By the Banach fixed-point theorem (Lemma 5), T has a unique fixed point $(\mu ,\nu )\in E$, which is the unique solution to (3). □

We shall now present our third result to prove the stability of the Ulam–Hyers sense. Before that, we present the following definition:

Definition 4

($\epsilon$-approximate solution [13]). A pair $(\tilde{\mu },\tilde{\nu })\in C([-h,b],\mathbb{R})\times C([-h,b],\mathbb{R})$ is an ε-approximate solution of (3) if there exist functions ${\theta }_1,{\theta }_2\in C([0,b],\mathbb{R})$ with $|{\theta }_1\left(\varrho \right)| \le \epsilon$ and $|{\theta }_2\left(\varrho \right)| \le \epsilon$ for all $\varrho \in [0,b]$ such that

$$\left\{\begin{array}{c}{\displaystyle {}^{C}D_{\varrho }^{\alpha }\tilde{\mu }\left(\varrho \right)=\sum _{i=1}^N{F}_i(\varrho ,\tilde{\mu }\left(\varrho \right),\tilde{\nu }\left(\varrho \right),\tilde{\mu }\left({\tau }_i\left(\varrho \right)\right),\tilde{\nu }\left({\sigma }_i\left(\varrho \right)\right))+{\theta }_1\left(\varrho \right),}\hfill \\ {\displaystyle {}^{C}D_{\varrho }^{\alpha }\tilde{\nu }\left(\varrho \right)=\sum _{j=1}^M{G}_j(\varrho ,\tilde{\mu }\left(\varrho \right),\tilde{\nu }\left(\varrho \right),\tilde{\mu }\left({\eta }_j\left(\varrho \right)\right),\tilde{\nu }\left({\xi }_j\left(\varrho \right)\right))+{\theta }_2\left(\varrho \right),}\hfill \end{array}\right.$$

for $\varrho \in [0,b]$, and $\tilde{\mu }\left(\varrho \right)=\varphi \left(\varrho \right)$, $\tilde{\nu }\left(\varrho \right)=\psi \left(\varrho \right)$ for $\varrho \in [-h,0]$.

Theorem 3

(Ulam–Hyers stability). Assume that assumptions (H2)–(H4) hold. If ${\displaystyle \frac{2(N{L}_F+M{L}_G)b^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}<1$, then the system (3) is Ulam–Hyers stable: For every $\epsilon >0$ and ε-approximate solution $(\tilde{\mu },\tilde{\nu })$, there exists a unique exact solution $(\mu ,\nu )$ of (3) such that

$$\parallel \tilde{\mu }{-\mu \parallel }_C+{\parallel \tilde{\nu }-\nu \parallel }_C\le K\epsilon ,$$

where $K={\displaystyle \frac{2b^{\alpha }/\mathrm{\Gamma }(\alpha +1)}{1-2(N{L}_F+M{L}_G)b^{\alpha }/\mathrm{\Gamma }(\alpha +1)}}$.

Proof. 

Let $(\tilde{\mu },\tilde{\nu })$ be an $\epsilon$-approximate solution and $(\mu ,\nu )$ the exact solution. Define the errors:

$$e_1\left(\varrho \right)=\tilde{\mu }\left(\varrho \right)-\mu \left(\varrho \right),e_2\left(\varrho \right)=\tilde{\nu }\left(\varrho \right)-\nu \left(\varrho \right),\varrho \in [-h,b].$$

For $\varrho \in [0,b]$, the errors satisfy

$$e_1\left(\varrho \right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}\left[\sum _{i=1}^N\Delta F_i\left(s\right)+{\theta }_1\left(s\right)\right]ds,$$

$$e_2\left(\varrho \right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}\left[\sum _{j=1}^M\Delta G_j\left(s\right)+{\theta }_2\left(s\right)\right]ds,$$

where $\Delta F_i\left(s\right)=F_i(s,\tilde{\mu }\left(s\right),\tilde{\nu }\left(s\right),\tilde{\mu }\left({\tau }_i\left(s\right)\right),\tilde{\nu }\left({\sigma }_i\left(s\right)\right))-F_i(s,\mu \left(s\right),\nu \left(s\right),\mu \left({\tau }_i\left(s\right)\right),\nu \left({\sigma }_i\left(s\right)\right))$.

Using the Lipschitz continuity of $F_i$ and $G_j$,

$$|\Delta F_i\left(s\right)| \le L_F\left(|e_1\left(s\right)|+|e_2\left(s\right)|+|e_1\left({\tau }_i\left(s\right)\right)|+|e_2\left({\sigma }_i\left(s\right)\right)|\right),$$

$$|\Delta G_j\left(s\right)| \le L_G\left(|e_1\left(s\right)|+|e_2\left(s\right)|+|e_1\left({\eta }_j\left(s\right)\right)|+|e_2\left({\xi }_j\left(s\right)\right)|\right).$$

For $s\in [0,b]$, if ${\tau }_i\left(s\right)\le 0$, then $e_1\left({\tau }_i\left(s\right)\right)=0$; otherwise, $|e_1\left({\tau }_i\left(s\right)\right)| \le {sup}_{[0,b]}|e_1|=\parallel e_1{\parallel }_C$. This is similar for other delayed terms.

Now, we estimate the supremum as Let $E_1={\parallel e_1\parallel }_C$, $E_2={\parallel e_2\parallel }_C$, and $S=E_1+E_2$. Then,

$$|e_1\left(\varrho \right)| \le {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}\left[2N{L}_{F}S+\epsilon \right]ds,$$

$$|e_2\left(\varrho \right)| \le {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^{\varrho }{(\varrho -s)}^{\alpha -1}\left[2M{L}_{G}S+\epsilon \right]ds.$$

Evaluating the integrals gives the following:

$$|e_1\left(\varrho \right)| \le {\displaystyle \frac{2N{L}_{F}S+\epsilon }{\mathrm{\Gamma }(\alpha +1)}}{\varrho }^{\alpha },|e_2\left(\varrho \right)|\le {\displaystyle \frac{2M{L}_{G}S+\epsilon }{\mathrm{\Gamma }(\alpha +1)}}{\varrho }^{\alpha }.$$

For $\varrho \in [0,b]$, we obtain

$$E_1\le {\displaystyle \frac{2N{L}_{F}S+\epsilon }{\mathrm{\Gamma }(\alpha +1)}}{b}^{\alpha },E_2\le {\displaystyle \frac{2M{L}_{G}S+\epsilon }{\mathrm{\Gamma }(\alpha +1)}}{b}^{\alpha }.$$

Adding the inequalities for $E_1$ and $E_2$, we have

$$S=E_1+E_2\le {\displaystyle \frac{2(N{L}_F+M{L}_G)S+2\epsilon }{\mathrm{\Gamma }(\alpha +1)}}{b}^{\alpha }.$$

Rearranging gives the following:

$$S\left(1-{\displaystyle \frac{2(N{L}_F+M{L}_G)b^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\right)\le {\displaystyle \frac{2b^{\alpha }\epsilon }{\mathrm{\Gamma }(\alpha +1)}}.$$

Under the condition ${\displaystyle \frac{2(N{L}_F+M{L}_G)b^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}<1$, we obtain

$$S\le {\displaystyle \frac{2b^{\alpha }\epsilon /\mathrm{\Gamma }(\alpha +1)}{1-2(N{L}_F+M{L}_G)b^{\alpha }/\mathrm{\Gamma }(\alpha +1)}}=K\epsilon .$$

Thus, $\parallel \tilde{\mu }{-\mu \parallel }_C+{\parallel \tilde{\nu }-\nu \parallel }_C\le K\epsilon$, proving Ulam–Hyers stability. □

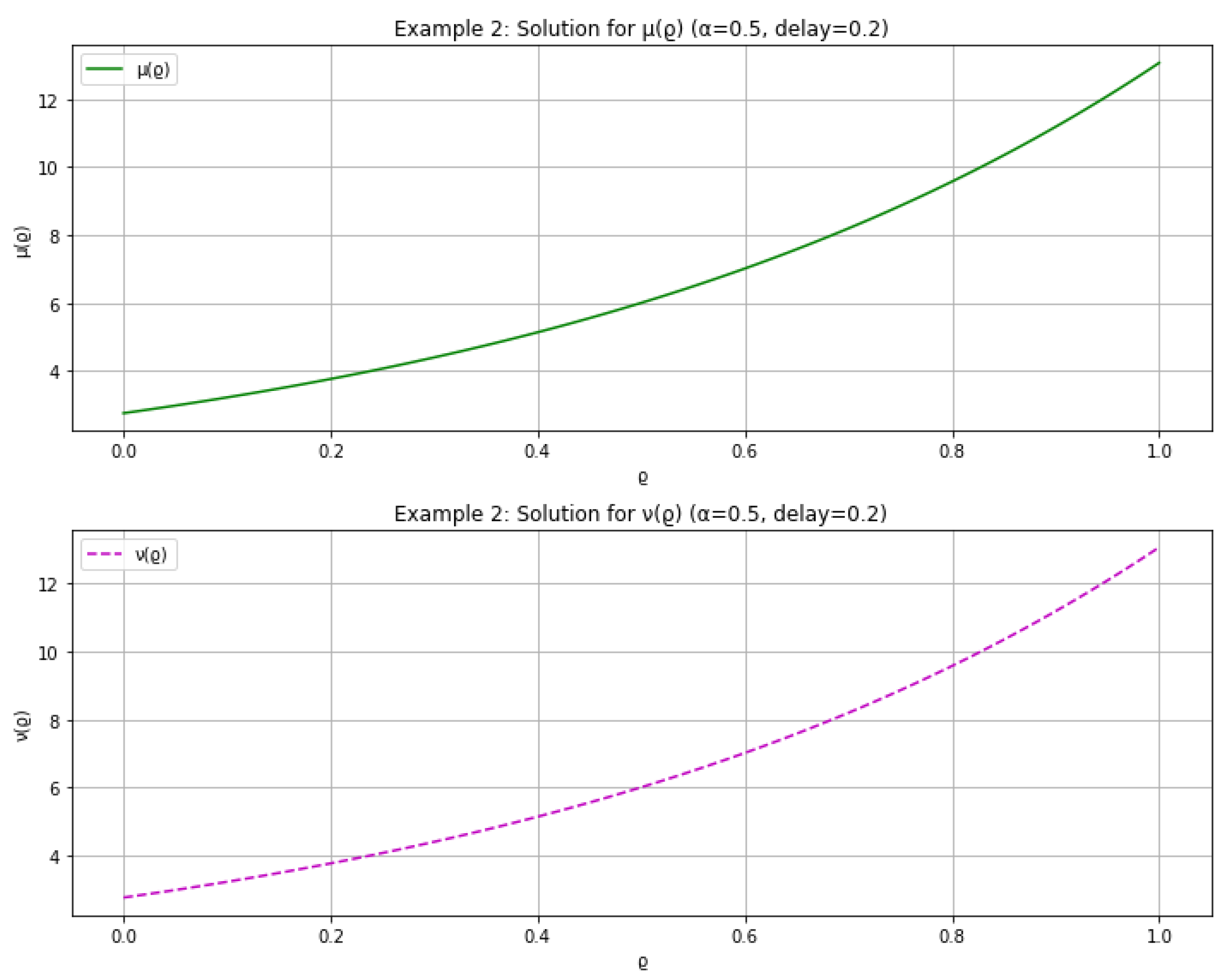
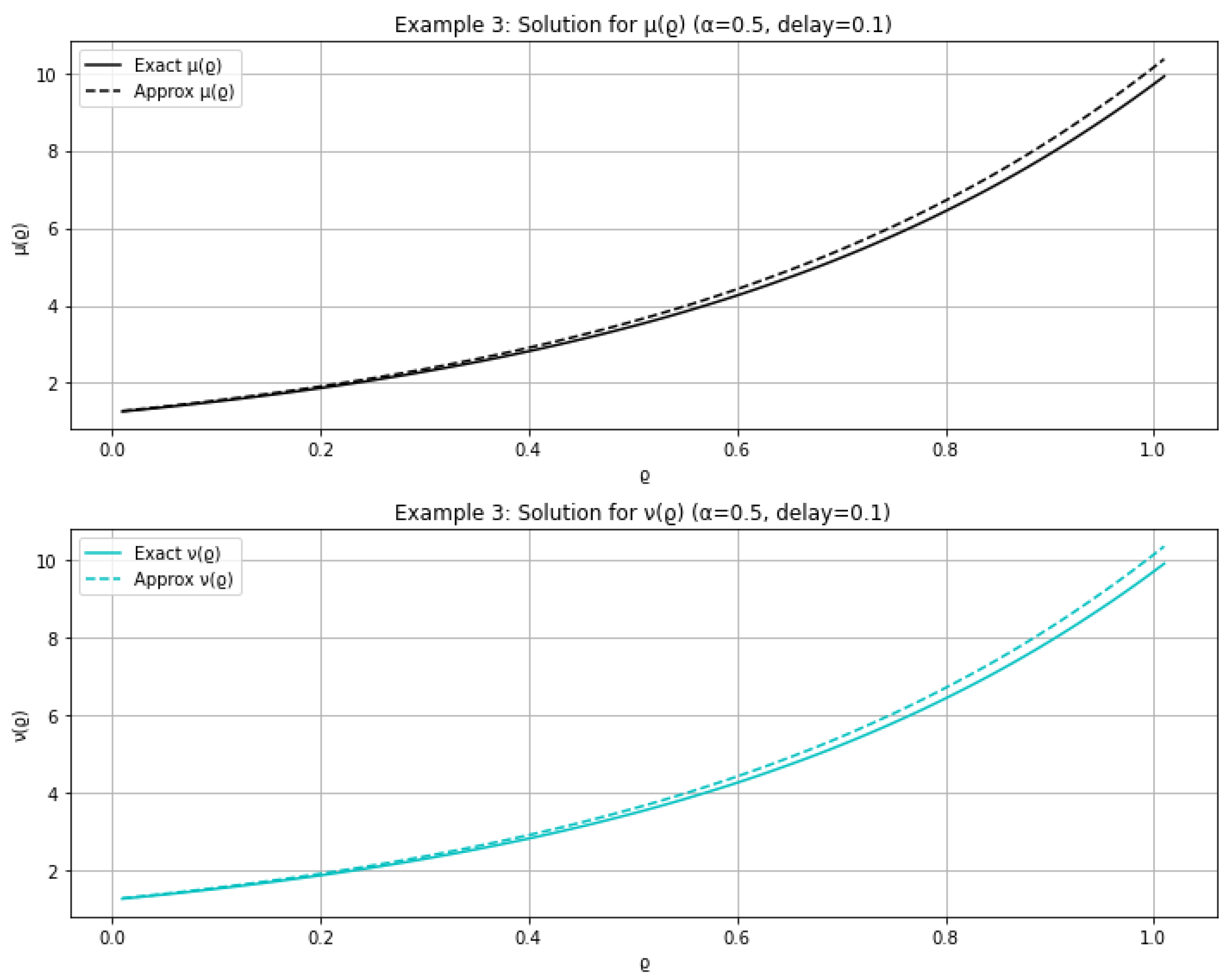
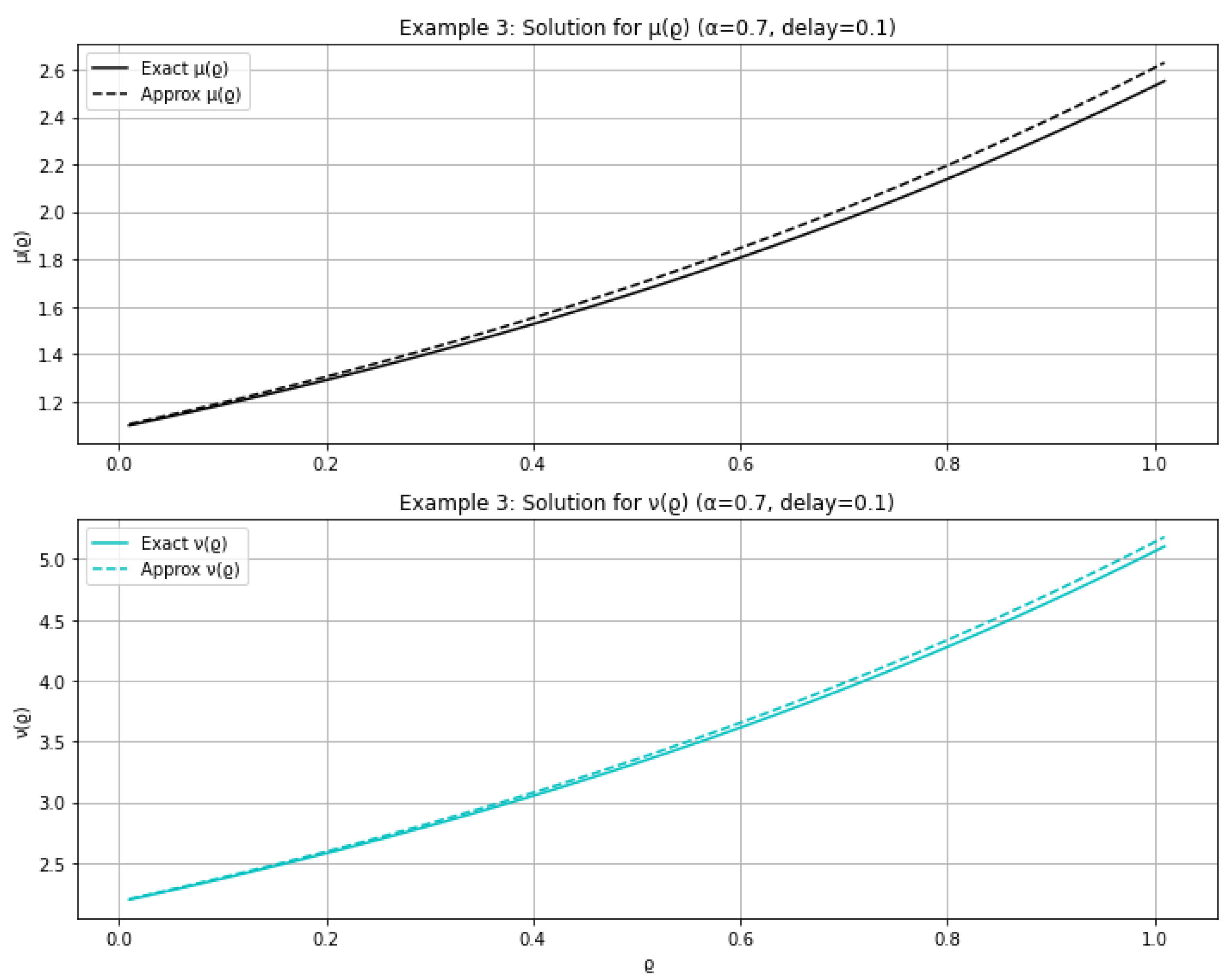
4. Examples

This section provides three examples to demonstrate the efficacy of the outcomes produced.

Example 1.

Consider the following coupled CapFDE system with delays:

$$\left\{\begin{array}{cc}{}^{C}D_{\varrho }^{0.5}\mu \left(\varrho \right)=0.2sin\left(\mu \left(\varrho \right)\right)+0.1\nu (\varrho -0.1),\hfill & \varrho \in [0,1],\hfill \\ {}^{C}D_{\varrho }^{0.5}\nu \left(\varrho \right)=0.1\mu (\varrho -0.1)+0.2cos\left(\nu \left(\varrho \right)\right),\hfill & \varrho \in [0,1],\hfill \end{array}\right.$$

(7)

with initial conditions

$$\mu \left(\varrho \right)=1,\nu \left(\varrho \right)=1,\varrho \in [-0.1,0].$$

Now, we will check the following hypotheses:

• For $F_1(\varrho ,\mu ,\nu ,\mu \left({\tau }_1\right),\nu \left({\sigma }_1\right))=0.2sin\left(\mu \right)+0.1\nu \left({\sigma }_1\right)$,

  $$|F_1| \le 0.2| sin\left(\mu \right)| +0.1|\nu \left({\sigma }_1\right)| \le 0.2\left(1\right)+0.1\left(1\right)=0.3.$$
• For $G_1(\varrho ,\mu ,\nu ,\mu \left({\eta }_1\right),\nu \left({\xi }_1\right))=0.1\mu \left({\eta }_1\right)+0.2cos\left(\nu \right)$,

  $$|G_1| \le 0.1|\mu \left({\eta }_1\right)| +0.2| cos\left(\nu \right)| \le 0.1\left(1\right)+0.2\left(1\right)=0.3.$$

Thus, $M_F=M_G=0.3$. For delay functions, we have ${\tau }_1\left(\varrho \right)=\varrho ,{\sigma }_1\left(\varrho \right)=\varrho -0.1,{\eta }_1\left(\varrho \right)=\varrho -0.1,and{\xi }_1\left(\varrho \right)=\varrho .$ All delays satisfy ${\tau }_1\left(\varrho \right),{\sigma }_1\left(\varrho \right),{\eta }_1\left(\varrho \right),{\xi }_1\left(\varrho \right)\le \varrho$. In addition, the initial conditions are $\varphi \left(\varrho \right)=1,\mathit{and}\psi \left(\varrho \right)=1\mathit{are}\mathit{continuous}\mathit{on}[-0.1,0]$, where $h=0.1$.

By Theorem 1, system (7) has at least one solution $(\mu ,\nu )\in C{([-0.1,1],\mathbb{R})}^2$. Figure 1 shows the simulation for Example 1.

Example 2.

Consider the following linear system:

$$\left\{\begin{array}{cc}{}^{C}D_{\varrho }^{0.5}\mu \left(\varrho \right)=0.1\mu \left(\varrho \right)+0.05\nu (\varrho -0.2),\hfill & \varrho \in [0,1],\hfill \\ {}^{C}D_{\varrho }^{0.5}\nu \left(\varrho \right)=0.05\mu (\varrho -0.2)+0.1\nu \left(\varrho \right),\hfill & \varrho \in [0,1],\hfill \end{array}\right.$$

(8)

with initial conditions

$$\mu \left(\varrho \right)=2,\nu \left(\varrho \right)=2,\varrho \in [-0.2,0].$$

Verification of Hypotheses

• For $F_1(\varrho ,\mu ,\nu ,\mu \left({\tau }_1\right),\nu \left({\sigma }_1\right))=0.1\mu +0.05\nu \left({\sigma }_1\right)$,

  $$|F_1(·)-F_1\left({·}^{\prime }\right)| \le 0.1|\mu -{\mu }^{\prime }| +0.05|\nu \left({\sigma }_1\right)-{\nu }^{\prime }\left({\sigma }_1\right)| \le 0.15\parallel (\mu -{\mu }^{\prime },\nu -{\nu }^{\prime }){\parallel }_C.$$
• For $G_1(\varrho ,\mu ,\nu ,\mu \left({\eta }_1\right),\nu \left({\xi }_1\right))=0.05\mu \left({\eta }_1\right)+0.1\nu$,

  $$|G_1(·)-G_1\left({·}^{\prime }\right)| \le 0.05|\mu \left({\eta }_1\right)-{\mu }^{\prime }\left({\eta }_1\right)| +0.1|\nu -{\nu }^{\prime }| \le 0.15\parallel (\mu -{\mu }^{\prime },\nu -{\nu }^{\prime }){\parallel }_C.$$

Thus, $L_F=L_G=0.15$. To verify the contraction condition, we have

$${\displaystyle \frac{2(N{L}_F+M{L}_G)b^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}={\displaystyle \frac{2(1·0.15+1·0.15)·1^{0.5}}{\mathrm{\Gamma }\left(1.5\right)}}={\displaystyle \frac{0.6}{0.886}}\approx 0.68<1.$$

By Theorem 2, system (8) has a unique solution. Figure 2 shows the simulation for Example 2.

Example 3.

Consider the following symmetric linear system:

$$\left\{\begin{array}{cc}{}^{C}D_{\varrho }^{0.5}\mu \left(\varrho \right)=0.1\mu \left(\varrho \right)+0.1\nu (\varrho -0.1),\hfill & \varrho \in [0,1],\hfill \\ {}^{C}D_{\varrho }^{0.5}\nu \left(\varrho \right)=0.1\mu (\varrho -0.1)+0.1\nu \left(\varrho \right),\hfill & \varrho \in [0,1],\hfill \end{array}\right.$$

(9)

with initial conditions

$$\mu \left(\varrho \right)=1,\nu \left(\varrho \right)=2,\varrho \in [-0.1,0].$$

Stability Verification

• Lipschitz constants: $L_F=L_G=0.1+0.1=0.2$.
• Stability constant K:

  $$K={\displaystyle \frac{2b^{\alpha }/\mathrm{\Gamma }(\alpha +1)}{1-2(N{L}_F+M{L}_G)b^{\alpha }/\mathrm{\Gamma }(\alpha +1)}}={\displaystyle \frac{2·1^{0.5}/0.886}{1-2(0.2+0.2)·1^{0.5}/0.886}}\approx 23.5.$$
• Error bound for an $\epsilon$-approximate solution with $\epsilon =0.01$:

  $$\parallel \tilde{\mu }{-\mu \parallel }_C+{\parallel \tilde{\nu }-\nu \parallel }_C\le 23.5·0.01=0.235.$$

The system (9) is Ulam–Hyers stable with stability constant $K\approx 23.5$.

The fractional-order $\alpha$ plays a crucial role in determining system stability. A lower $\alpha$ (e.g., $\alpha =0.5$, Figure 3) introduces stronger memory effects, which smooth oscillations and improve robustness to perturbations by reducing the Ulam–Hyers stability constant K. In contrast, a higher $\alpha$ (e.g., $\alpha =0.7$, Figure 4) weakens memory dependence, leading to faster dynamics but greater sensitivity to disturbances, resulting in a larger K. Although visual differences may be subtle in linear systems or short-term simulations, theoretical stability limits deteriorate as $\alpha$ increases, highlighting a tradeoff between responsiveness and robustness. These effects become more pronounced in nonlinear systems or over extended time horizons.

5. Applications

This section applies a coupled system of Caputo FDEs with delays to model control systems and predator–prey dynamics. The inclusion of fractional derivatives and communication delays provides a more realistic representation of control mechanisms and ecological interactions, offering insights into system stability and long-term behavior.

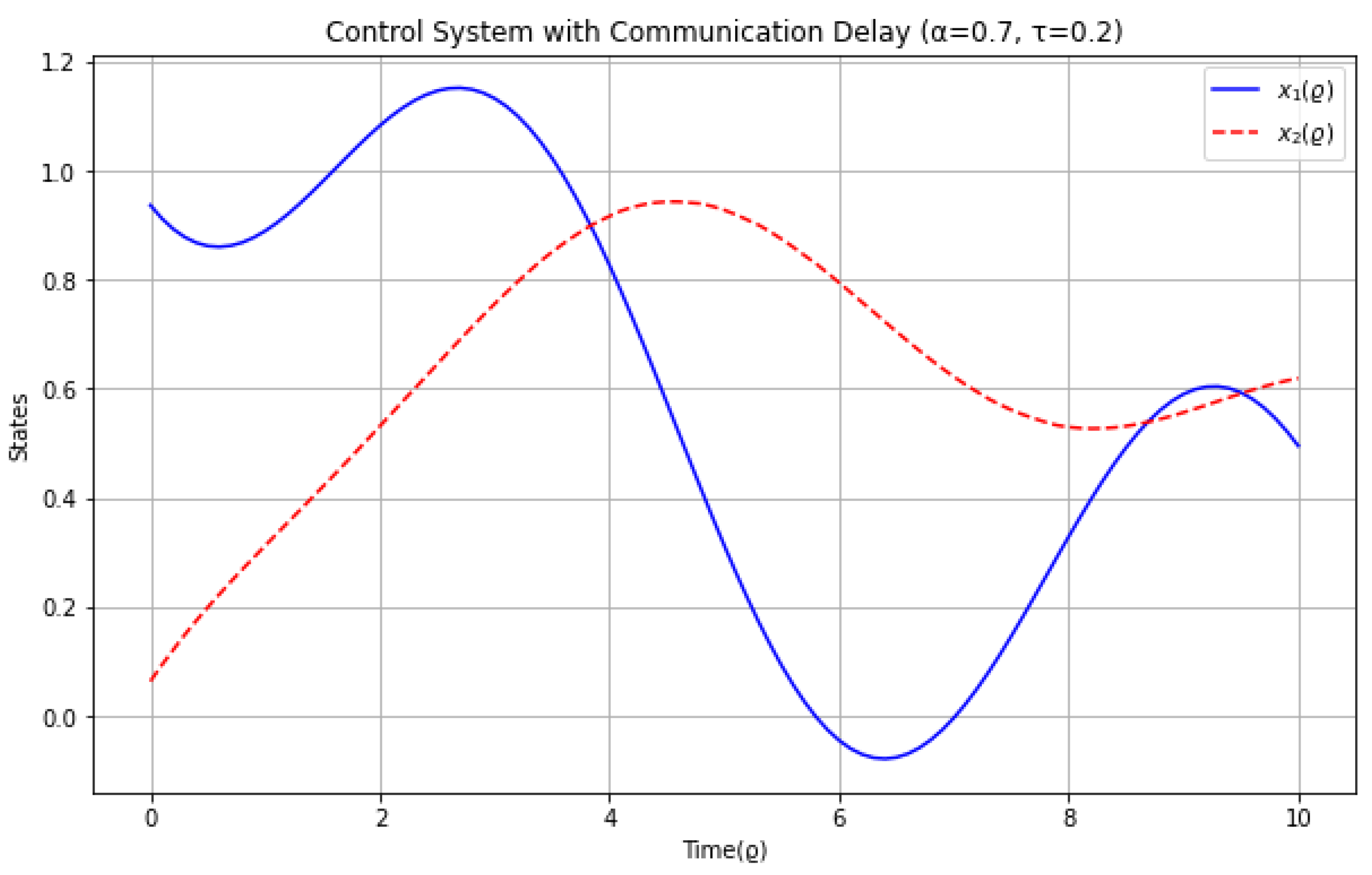
5.1. Control Systems with Communication Delays

The control system is modeled using a coupled system of Caputo FDEs with communication delays:

$$\left\{\begin{array}{c}{}^{C}D_{\varrho }^{\alpha }{x}_1\left(\varrho \right)=A{x}_1\left(\varrho \right)+Bu(\varrho -\tau ),\hfill \\ {}^{C}D_{\varrho }^{\alpha }{x}_2\left(\varrho \right)=C{x}_2\left(\varrho \right)+D{x}_1(\varrho -\tau ),\hfill \end{array}\right.$$

where $x_1\left(\varrho \right)$ and $x_2\left(\varrho \right)$ are the system states, $u\left(\varrho \right)$ is the control input, $\tau$ is the communication delay, $A,B,C,D$ are system parameters, and $\alpha$ is the fractional-order ($0<\alpha <1$).

The system is solved using the fractional Adams–Bashforth–Moulton predictor–corrector method [6], which is a numerical scheme for solving FDEs. The method involves the following steps:

• The time domain $\varrho \in [0,T]$ is discretized into N steps of size $h=T/N$.
• Predictor step: An initial estimate of the solution is calculated using the Adams–Bashforth fractional formula:

  $$\left\{\begin{array}{c}{x}_1^P\left({\varrho }_{n+1}\right)=x_1\left({\varrho }_n\right)+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\sum _{j=0}^n{b}_{j,n+1}{f}_1({\varrho }_j,x_1\left({\varrho }_j\right)),\hfill \\ x_2^P\left({\varrho }_{n+1}\right)=x_2\left({\varrho }_n\right)+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\sum _{j=0}^n{b}_{j,n+1}{f}_2({\varrho }_j,x_2\left({\varrho }_j\right)),\hfill \end{array}\right.$$

  where $b_{j,n+1}={(n+1-j)}^{\alpha }-{(n-j)}^{\alpha }$, $f_1(\varrho ,x_1\left(\varrho \right))=A{x}_1\left(\varrho \right)+Bu(\varrho -\tau )$, and $f_2(\varrho ,x_2\left(\varrho \right))=C{x}_2\left(\varrho \right)+D{x}_1(\varrho -\tau )$.
• Corrector step: The estimate is refined using the Adams–Moulton fractional formula:

  $$\left\{\begin{array}{c}{x}_1\left({\varrho }_{n+1}\right)=x_1\left({\varrho }_n\right)+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\left(f({\varrho }_{n+1},x_1^P\left({\varrho }_{n+1}\right))+\sum _{j=0}^n{a}_{j,n+1}{f}_1({\varrho }_j,x_1\left({\varrho }_j\right))\right),\hfill \\ x_2\left({\varrho }_{n+1}\right)=x_2\left({\varrho }_n\right)+{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}}\left(f({\varrho }_{n+1},x_2^P\left({\varrho }_{n+1}\right))+\sum _{j=0}^n{a}_{j,n+1}{f}_2({\varrho }_j,x_2\left({\varrho }_j\right))\right),\hfill \end{array}\right.$$

  where

  $$a_{j,n+1}=\left\{\begin{array}{cc}{n}^{r+1}-(n-r){(n+1)}^r,\hfill & j=0,\hfill \\ {(n-j+2)}^{r+1}+{(n-j)}^{r+1}-2{(n-j+1)}^{r+1},\hfill & 0<j\le n,\hfill \\ 1,\hfill & j=n+1,\hfill \end{array}\right.$$
• Delay handling: Delayed terms (e.g., $x_1(\varrho -\tau )$) are handled by interpolating historical data at $\varrho -\tau$.

The following parameters were used in the simulation: $\alpha =0.5$, $\tau =0.2$, $A=-0.1$, $B=0.2$, $C=-0.1$, $D=0.15$, $u(\varrho -\tau )=sin(\varrho -\tau )$, $x_1\left(0\right)=1.0$, $x_2\left(0\right)=0.0$, $\varrho \in [-0.2,10]$, and $h=0.1$. The simulation results are shown in Figure 5. The states $x_1\left(\varrho \right)$ and $x_2\left(\varrho \right)$ exhibit oscillatory behavior due to the delayed control input and state feedback. The fractional-order $\alpha =0.5$ introduces memory effects, resulting in smoother oscillations compared to integer-order models. Figure 5 illustrates the dynamic behavior of the control system.

5.2. Predator–Prey Dynamics

The predator–prey dynamics are modeled using a coupled system of Caputo FDEs with delays:

$$\left\{\begin{array}{c}{}^{C}D_{\varrho }^{\alpha }x\left(\varrho \right)=x\left(\varrho \right)\left(a-by\left(\varrho \right)-cx(\varrho -\tau )\right),\hfill \\ {}^{C}D_{\varrho }^{\alpha }y\left(\varrho \right)=y\left(\varrho \right)\left(-d+ex(\varrho -\tau )\right),\hfill \end{array}\right.$$

where $x\left(\varrho \right)$ is the prey population, $y\left(\varrho \right)$ is the predator population, $a,b,c,d,e$ are system parameters, $\tau$ is the time delay (e.g., gestation period), and $\alpha$ is the fractional order ($0<\alpha <1$). The system is solved using the fractional Adams–Bashforth–Moulton predictor–corrector method [6], which is a numerical scheme for solving FDEs. The method involves the predictor step to estimate the solution and the corrector step to refine the estimate with the same previous process. The time delay $\tau$ is handled by interpolating historical data at $\varrho -\tau$. The following parameters were used in the simulation: $\alpha =0.7$, $\tau =0.2$, $a=1.0$, $b=0.1$, $c=0.05$, $d=0.5$, $e=0.1$, $x\left(0\right)=10.0$, $y\left(0\right)=5.0$, $\varrho \in [-0.2,20]$, and $h=0.1$.

The simulation results are shown in Figure 6. The prey population ($x\left(\varrho \right)$) and predator population ($y\left(\varrho \right)$) exhibit oscillatory behavior due to the interaction between the species and the memory effects introduced by the fractional derivative. Figure 6 illustrates the dynamic behavior of the Predator–Prey.

6. Conclusions

In this paper, we have investigated the theoretical properties of a generalized coupled system of CapFDEs with finite delay. The existence, uniqueness, and Ulam–Hyers stability of solutions for our system have been our main concerns. By leveraging Banach’s and Schauder’s fixed-point theorems adapted to the fractional setting, we have derived sufficient conditions under which these properties hold, which are contingent upon appropriate assumptions on problem parameters and constituent functions. To illustrate the main findings, three examples were provided. Our theoretical insights can be applied to complicated systems such as ecological dynamics, as we have shown through practical applications, which include applications to the control and predator–prey models. We have used numerical simulations using the Adams–Bashforth–Moulton approach to solve these models. The numerical findings demonstrate the applicability of our theoretical framework in real-world scenarios. Finally, this study enhances our understanding and application of CapFDEs in analyzing and modeling complex systems with fractional-order dynamics. Future research directions may include extending these results to more intricate systems or exploring advanced numerical methods for solving FDEs using alternative fractional derivatives, such as the ABC derivative [30] or the Caputo–Fabrizio derivative [31].