Abstract
This study presents a novel mathematical model of a generalized magnetothermoelastic half-space based on the Green–Naghdi theorem, namely type-I and type-III. The half-space surface undergoes ramp-type heating and is positioned on a sturdy base to prevent movement. This research is novel as it employs Caputo’s definition of fractional derivatives within the context of Maxwell’s time-fractional equations. Laplace transform methods are used to obtain the solutions. Tzou’s iterative method has been used to calculate inversions of the Laplace transform. The findings include quantitative answers for temperature increase, strain, displacement, stress, induced magnetic field, and induced electric field distributions. The time-fraction parameter defined by Maxwell’s equation considerably influences all essential mechanical functions, but the thermal functions remain unchanged. In Maxwell’s equations, the time-fractional parameter functions augment the induced electric field inside the material, acting as a resistor to particle motion and the induced magnetic field, while concurrently facilitating the induced electric field. Moreover, the thermal, mechanical, and magnetoelectric waves of Green–Naghdi type-III propagate at a reduced velocity compared to type-I. The fundamental magnetic field substantially influences all examined functions.
Keywords:
thermoelasticity; electromagnetic; Maxwell’s equations; Green–Naghdi theorem; time-fractional; fractional derivatives; Caputo definition MSC:
74-10; 35Q61; 34K37
1. Introduction
The correlation between strain and magnetic fields in thermoelastic materials is increasingly intriguing due to its many applications in plasma physics, geophysics, and other disciplines. Internal magnetic fields, elevated temperatures, and temperature gradients in nuclear reactors significantly influence the comprehension of their operational mechanics. Magnetothermoelasticity is pertinent to this domain. This hybrid theory integrates electromagnetism and thermoelasticity [1,2]. Electromagnetic theory is regulated by hyperbolic partial differential equations, which, therefore, impose limitations on wave propagation velocities. The parabolic partial differential equation of heat conduction and hyperbolic partial differential equation of motion underpin Biot’s theory of thermoelasticity [3]. Despite the contradicting findings, the attributes of the second equation suggest that heat waves may propagate at an unrestricted velocity. Lord and Shulman developed the idea of generalized thermoelasticity with a singular relaxation time to address this problem. Furthermore, they introduced a novel and distinct principle of heat transfer to replace the traditional Fourier’s law of heat conduction (L-S) [4]. This control considers both the heat flow vector and its time derivative. Furthermore, it has an innovative element that serves as a respite throughout the procedure. The classification of the heat equation in this theory as wave-like imposes restrictions on the propagation velocities of thermal and elastic waves. The governing differential equations of this theory include the equations of motion and the constitutive relations for stress and strain, similar to both coupled and uncoupled theories. This theory was formulated by Dhaliwal and Sherief to include a broader anisotropic environment than previously considered [5]. In the examination of thermoelasticity, Green and Naghdi (G-N) suggested three possibilities for consideration. The models are based on specific entropy differences rather than inequality as their basis. The position of the heat flow vector is variable [6,7]. The Green–Naghdi theory encompasses three distinct classifications: type-I, type-II, and type-III. Each of these categories embodies a distinct assumption being proposed. The linear variation of type-I is determined by the conventional thermoelasticity mechanism. Energy wasting is absolutely prohibited under type-II regulations. The designation “type-II” pertains to a subgroup within the type-III classification. Type-III facilitates the use of energy in an inefficient way [7,8,9,10,11,12]. In discussions about magnetothermoelastic challenges, the generalized heat equation is often overlooked. This is true irrespective of whether the discussion pertains to coupled or uncoupled formulations. It is standard procedure to validate this method due to the little quantitative variance seen in the outcomes of these equations. Neglecting the whole generalized system of differential equations results in significant accuracy loss when accounting for short-term variations. This concept serves as an invaluable instrument for addressing a diverse array of problems, including heat gradients, and for assessing the consequences that manifest in a brief timeframe [1,13]. Leibniz was the first individual to provide the derivative of order one-half, marking the beginning of the whole history of fractional calculus [14,15]. Leibniz, Liouville, Grunwald, Letnikov, and Riemann are widely recognized as the pioneers of fractional order integrals and derivatives theory. The domain of fractional calculus and fractional differential equations offers a wealth of compelling literature and resources [14,16]. In recent years, physicists have used fractional-order derivatives and integrals, as well as fractional integro-differential equations, for various research endeavors [17,18]. The study of fractional-order electrodynamics is a novel area within academic discourse that merits exploration. Classical derivatives are local, meaning they represent changes in the vicinity of a point, while fractional derivatives may characterize changes throughout an interval. A fractional derivative has a nonlocal characteristic. This feature makes these derivatives appropriate for simulating many physical processes, including seismic vibrations and polymers. Among the several accessible methodologies, one that is particularly notable is the incorporation of fractional-order derivatives into Maxwell’s equations throughout both spatial and temporal domains [19,20,21,22,23]. To elucidate the dynamics of electromagnetic systems, including memory and energy dissipation, one may use expansions of Maxwell’s equations that include fractional-order derivatives [23]. In electrodynamics, the use of fractional-order derivatives offers an extra benefit in the form of the ability to represent the electric potential in terms of fractional-order poles [23,24]. Youssef is accountable for the development of the notion of fractional-order generalized thermoelasticity. The hypothesis is based on the fractional-order non-Fourier heat conduction equation [25] with the theory of generalized thermoelasticity with fractional-order strain, which is based on fractional-order equations of motion and arises from fractional-order stress–strain relationships [26]. Kumar et al. introduced a two-dimensional thermoelastic model for a homogeneous isotropic half-space with double porosity underlying an inviscid liquid half-space featuring temperature variations [27]. This study is unique since it seeks to address a problem concerning a generalized magnetothermoelastic half-space within the context of the Green–Naghdi theorem, type-I and type-III. This issue occurs when the surface of the half-space is subjected to the time-fractional Maxwell electromagnetic phenomenon. The Caputo fractional derivative formulation has been used for the time-fractional Maxwell’s equations.
2. The Problem Formulation
By assuming the space is occupied by an isotropic, generalized thermoelastic, electromagnetic, half-space, the magnetic vector field has been considered and acts tangent to the surface of the half-space when , and all the studied functions of the material are dependent only on one-dimension distance and the time variable .
gives the induced magnetic vector field due to the effect of the primary magnetic vector field , then, an induced electric intensity vector field will be generated as in Figure 1 [13,28,29,30]:
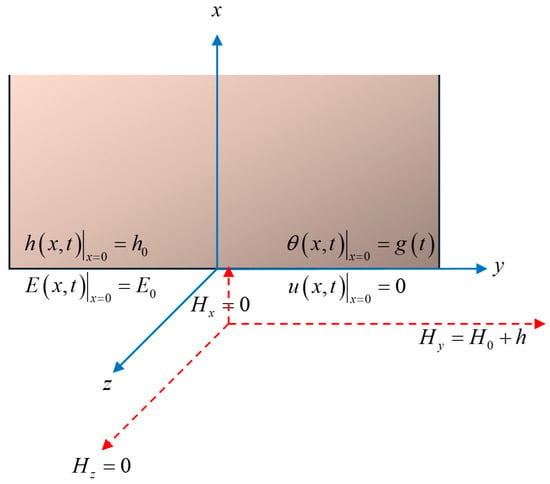
Figure 1.
The magnetothermoelastic material based on time-fractional Maxwell’s equations and subjected to ramp-type heat.
We assume the vectors and have a small magnitude in the context of the linear generalized thermoelasticity theory of Green–Naghdi. Hence, the vector of displacement takes the following form:
The magnetic intensity vector takes the following components [13,28,29,30]:
Due to the role of the left-hand, the electric intensity vector field must be perpendicular to the displacement vectors and the magnetic intensity vector.
Hence, the electric field vector has the following components:
Moreover, the current density vector must be in the same direction as the electric intensity vector . Thus, we have the following:
In general vector forms based on a fractional derivative definition, the time-fractional Maxwell’s equations can be written as follows [23]:
and
The fractional-order time-derivative operator will be applied in which the integer derivative gives the free-space situation, and the Caputo fractional derivative when , respectively, as in the following unified form [14,15,16,17,18,19,20,21,22,23,24,25,26]:
where and give the magnetic and electric permeabilities, respectively [2,6,13,23,31,32].
Equations (5)–(9) are supported by Ohm’s law, namely [2,6,13,23,31,32] as follows:
Ohm’s law gives the following equation [2,6,13,23,31,32]:
where gives the electric conductivity.
Lorentz’s force vector is given by the following law [2,6,13,23,31,32]:
Hence, from Equations (9), (12), and (13), we obtain the following:
After linearization, we obtain the following:
The strain components take the following forms [13]:
and
The stress components are given by the following relation [13]:
which has the following components [13]:
and
where defines the absolute temperature of the medium; is a reference temperature assumed to be such that ; and are Lamé’s moduli; ; and is the linear thermal expansion coefficient.
Equations of motion in general unified form are as follows [1,3,4]:
where gives the density of the material.
By inserting Equation (12) into Equation (9), we obtain the equation of motion in one-dimensional form as follows [2,6,13,29,31,32]:
By exciting the partial derivative concerning the variable and using Equation (17), Equation (23) takes the following new form:
The one-dimensional heat conduction equation of Green–Naghdi of type-I and type-III takes the following unified form [33,34,35]:
The unified form of Equation (25) can be applied to both type-I and type-III of the Green–Naghdi theorem as follows:
- (a)
- provides Green–Naghdi type-I.
- (b)
- provides Green–Naghdi type-III.
We may take as the main character of the Green–Naghdi theory, while gives the thermal conductivity, and denotes the specific heat at constant deformation.
Equation (5) for the current model takes the following form:
Substituting from Equation (12), we obtain [23] the following:
Also, Equation (6) takes the following form [23]:
By adding a one-order partial derivative with respect to the variable for Equation (27) and using Equation (28), we obtain the following equation [23]:
In addition, Equation (24) will take the following form [23]:
The following dimensionless variables will be applied for simplifications as follows [13,28,29,36]:
After omitting the primes for ease, the preceding equations have been simplified to the following system of differential equations:
and
where
The constitutive relations will be reduced to the following forms:
and
where .
The Laplace transform of Formula (10) and its derivatives are given by the following [14,15,16,17,18,19,20,21,22,23,24,25,26]:
The initial conditions of the current model are given as follows:
After applying initial conditions, form (37) will be in the following simple form [14,15,16,17,18,19,20,21,22,23,24,25,26]:
Then, we have the following:
and
where
The constitutive equations are given by the following:
and
By eliminating the three functions from Equations (40)–(42), we have the following characteristic equations:
where , and .
The solutions of Equation (46) bounded for have the following forms:
and
where are the roots of the characteristic equation:
By inserting Equations (47)–(49) into Equations (40)–(42), we obtain the following relations:
and
Then, we have the following:
and
Then, from the Equations (16) and (53), we have the following:
From Equations (43) and (54), we obtain the following:
To obtain the parameters , the following boundary conditions at the bounding surface of the half-space will be applied as follows:
- 1.
- The half-space connected to a rigid foundation enough to prevent the displacement of the material is the mechanical boundary condition, i.e.,
- 2.
- The surface of the half-space loaded thermally by ramp-type heat gives the thermal boundary condition, which is defined as follows:where is called the ramp-time heat parameter and is constant.
Applying the Laplace transform, the above condition takes the following form:
- 3.
- The magnetic and electric functions and must satisfy the continuity conditions around the surface and give the magnetic and electrical boundary conditions as follows [13]:andwhere give the magnetic and electric intensities in the free space, respectively.
In the free space, in the non-dimensional Maxwell’s equations in the Laplace transform domain, we can put , which give the following equations:
and
Eliminating between the above two equations, we obtain the following:
where .
The bounded solution of Equation (64) in a general form is given by the following:
From Equations (63) and (65), we obtain the following:
From Equations (62) and (66), we obtain the condition when as [13] follows:
Applying the boundary conditions (57), (59), and (67), we obtain the following system of linear equations in the unknown parameters :
and
Solving the system of linear Equations (68)–(70) gives complete solutions in the domain of the Laplace transform.
3. The Numerical Results and Discussion
The Laplace transform inversions may be determined using the iteration form indicated in the following equation [37]:
gives the unit of an imaginary number, while “” provides the real part of any complex function, and is an integer parameter that could be chosen such that the following applies:
To get a faster convergence for the above iteration, the parameter ““ may satisfy the following condition: [37,38].
Copper material has been used for the numerical calculations. The properties of the material and the parameters have been taken as follows [2,6,13,29,30,32]:
The dimensionless dimension variable has been taken as follows: .
Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 show the distributions of the temperature increment, the volumetric dilatation, displacement, stress, induced magnetic field, and induced electric field based on Green–Naghdi type-I and type-III, respectively, under the definition of the fractional-order derivative of Caputo for three different values of the fractional-order parameter where gives the traditional material of normal derivative, while gives the time-fractional Maxwell’s equations cases. The results have been obtained based on two different cases of the ramp-time heat parameter to stand on this parameter’s effects on all the studied functions.
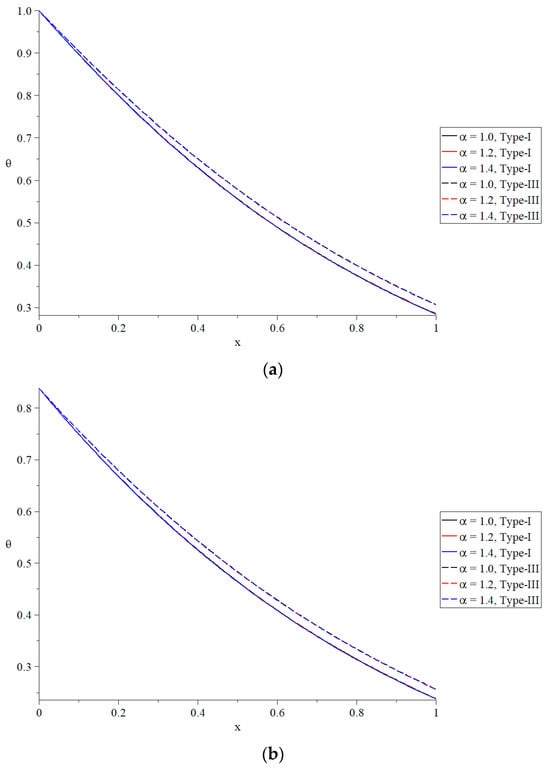
Figure 2.
The temperature increment distribution under different values of the time-fractional parameter of Maxwell’s equations. (a) The distribution of the temperature increment based on Green–Naghdi type-I and type-III when . (b) The distribution of the temperature increment based on Green–Naghdi type-I and type-III when .
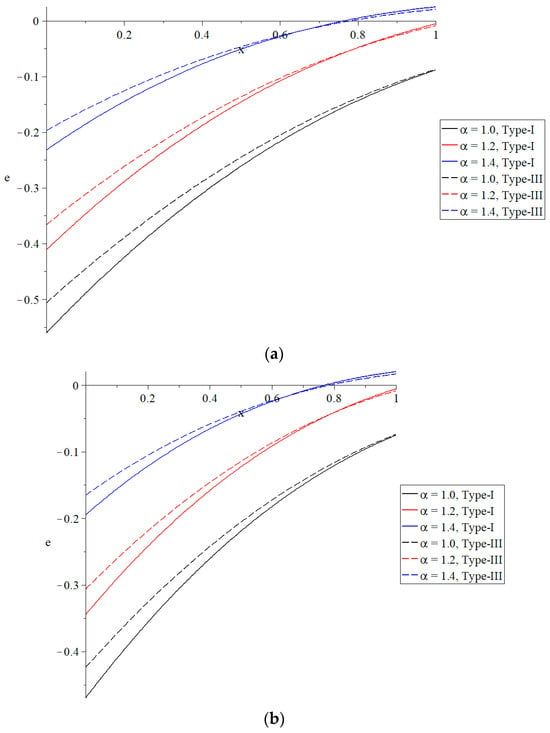
Figure 3.
The distribution of volumetric dilatation under different values of the time-fractional parameter of Maxwell’s equations. (a) The distribution of volumetric dilatation based on Green–Naghdi type-I and type-III when . (b) The distribution of volumetric dilatation based on Green–Naghdi type-I and type-III when .
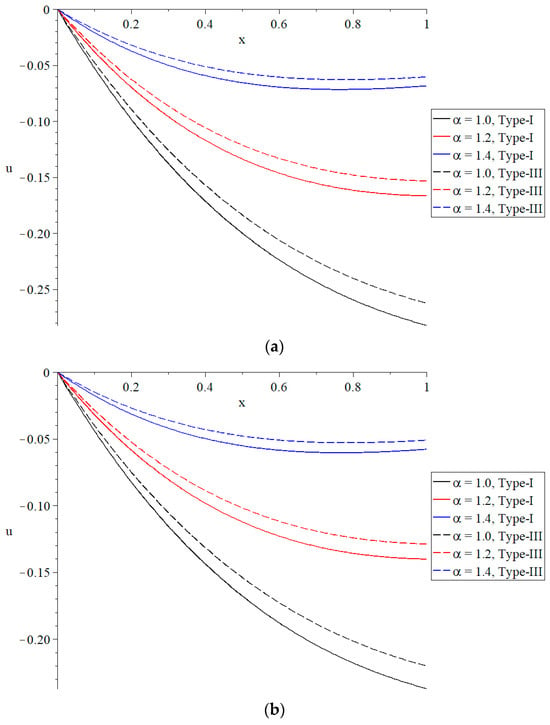
Figure 4.
The distribution of displacement under different values of the time-fractional parameter of Maxwell’s equations. (a) The distribution of displacement based on Green–Naghdi type-I and type-III when . (b) The distribution of displacement based on Green–Naghdi type-I and type-III when .
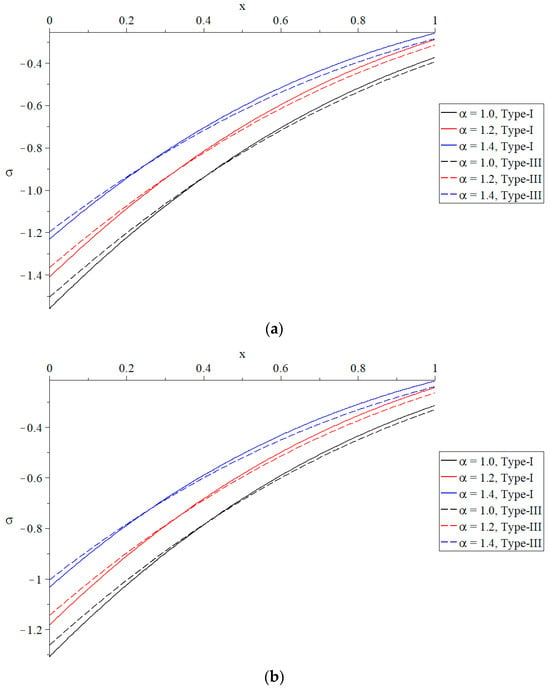
Figure 5.
The distribution of stress under different values of the time-fractional parameter of Max-well’s equations. (a) The distribution of stress based on Green–Naghdi type-I and type-III when . (b) The distribution of stress based on Green–Naghdi type-I and type-III when .
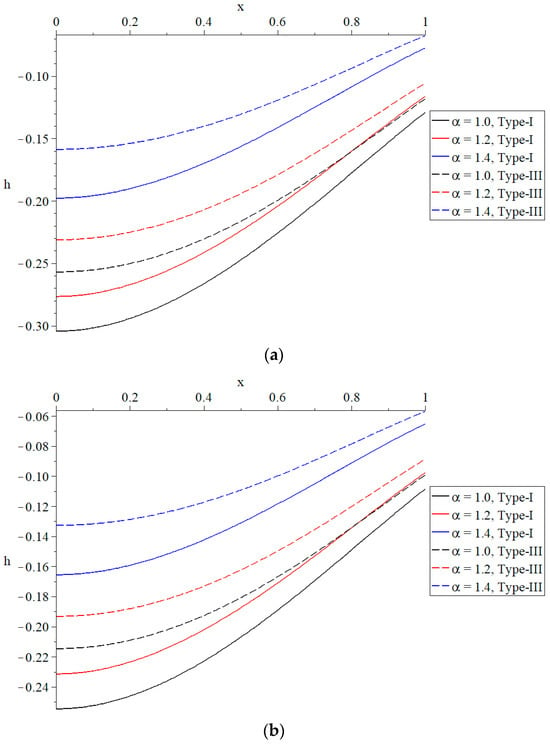
Figure 6.
The distribution of induced magnetic field under different values of the time-fractional parameter of Maxwell’s equations. (a) The distribution of the induced magnetic field based on Green–Naghdi type-I and type-III . (b) The distribution of the induced magnetic field based on Green–Naghdi type-I and type-III when .
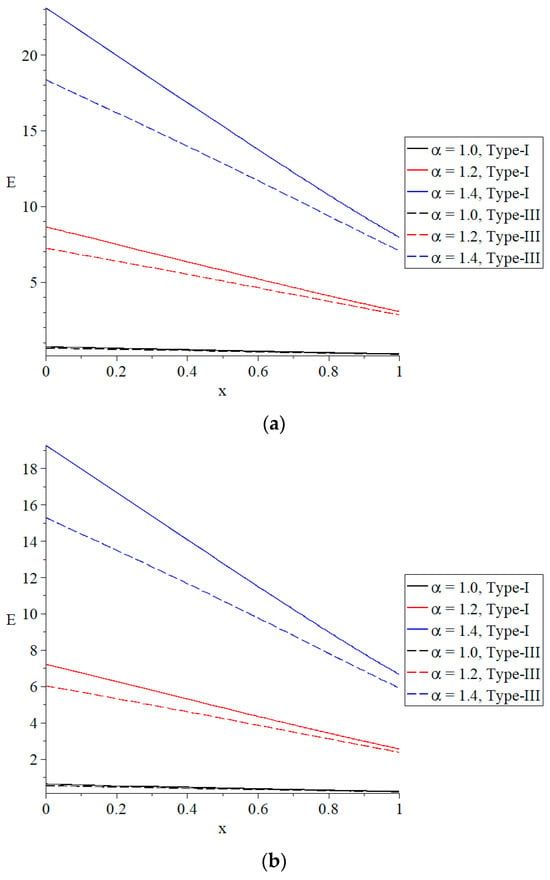
Figure 7.
The distribution of the induced electric field under different values of the time-fractional parameter of Maxwell’s equations. (a) The distribution of the induced electric field based on Green–Naghdi type-I and type-III when . (b) The distribution of the induced electric field based on Green–Naghdi type-I and type-III when .
Figure 2 depicts the impact of the time-fractional parameter in Maxwell’s equations on the temperature increment distribution, revealing a minimal effect. Figure 2a,b illustrate that the ramp-time heat parameter significantly influences the temperature increment, whereas an increase in the ramp-time heat parameter correlates with a reduction in the temperature increment. Moreover, the values of the temperature increment under Green–Naghdi type-I and type-III take the following order:
which means that the thermal wave based on Green–Naghdi type-I propagates with a more limited speed than type-III.
The effects of the time-fractional parameter on the volumetric dilatation distribution are shown in Figure 3, which indicates that the volumetric dilatation distribution is significantly affected. Within both categories shown in Figure 3a,b, it can be seen that an increase in the time-fractional parameter of Maxwell’s equations results in a reduction in the absolute value of volumetric dilatation. When compared to the results obtained from Green–Naghdi type-III, the volumetric dilatation values obtained from Green–Naghdi type-I are superior. Within the framework of Maxwell’s equations, the time-fractional parameter functions as a resistor to the deformation of the material. There is a considerable relationship between the ramp-time heat parameter and the distribution of volumetric dilatation; an increase in this parameter leads to a decrease in the absolute value of volumetric dilatation.
The absolute values of the volumetric dilatation take the following order:
The influence that the time-fractional parameter has on the distribution of displacement is seen in Figure 4, which may be found here. The magnitude of this influence is significant; as can be seen in Figure 4a,b, an increase in the time-fractional parameter results in a reduction in displacement for both species that were investigated. There is a significant improvement in the displacement values obtained from Green–Naghdi type-I in comparison to those obtained from Green–Naghdi type-III. A further purpose of the time-fractional parameter in Maxwell’s equations is to serve as a resistor to the movement of particles inside the medium. A decrease in the absolute displacement value is the consequence of an increase in the value of the ramp-time heat parameter, which has a substantial impact on the distribution of displacement. The absolute values of the displacement take the following order:
The influence of the time-fractional parameter in Maxwell’s equations on the distribution of stress is seen in Figure 5, which reveals that the effect is both significant and continuously growing. There is a correlation between a rise in the time-fractional parameter and an increase in the absolute stress value at the boundary surface as can be observed in both types of stress that are shown in Figure 5a,b. In comparison to Green–Naghdi type-III, the absolute levels of stress that were acquired from Green–Naghdi type-I were determined to be higher. In addition, the ramp-time heat parameter has a significant impact on the distribution of stress, and an increase in its value leads to a decrease in the relative magnitude of the absolute stress. The absolute values of the stress on the bounding plane of the half-space take the following order:
The influence that the time-fractional parameter in Maxwell’s equations has on the distribution of the magnetic field that is created is seen in Figure 6. An increase in the time-fractional parameter results in a reduction in the induced magnetic field as can be seen in Figure 6a,b for both kinds that were investigated. This is a considerable influence. When compared to the values generated by Green–Naghdi type-III, the induced magnetic field values that are acquired from Green–Naghdi type-I may be considered better. Maxwell’s equations include a time-fractional parameter that functions as a barrier to the magnetic field that is created inside the material under consideration. In addition, the ramp-time heat parameter has a major impact on the distribution of the magnetic field that is created. Furthermore, an increase in the value of this parameter leads to a decrease in the absolute magnitude of the magnetic field that is induced. The absolute values of the induced magnetic field take the following order:
The influence that the time-fractional parameter in Maxwell’s equations has on the distribution of the electric field that is created is seen in Figure 7. As can be observed in Figure 7a,b, the influence is significant; an increase in the time-fractional parameter coincides with an elevation in the generated electric field. This is the case for both kinds that were investigated. When compared to the values obtained from Green–Naghdi type-III, the induced electric field values obtained from Green–Naghdi type-I are exceptional. The creation of the induced electric field inside the material is made easier by the time-fractional parameter that is included in Maxwell’s equations. To add insult to injury, the ramp-time heat parameter has a substantial impact on the distribution of the produced electric field. As a consequence, a rise in its value leads to a decrease in the intensity of the induced electric field. The values of the induced electric field take the following order:
Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show the distributions of the temperature increment, the volumetric dilatation, displacement, stress, induced magnetic field, and induced electric field based on Green–Naghdi type-I and type-III, respectively, under the definition of the fractional-order derivative of Caputo when with different values of the primary magnetic field .
Figure 8.
The distribution of the temperature increment based on Green–Naghdi type-I and type-III with a different primary magnetic field when .
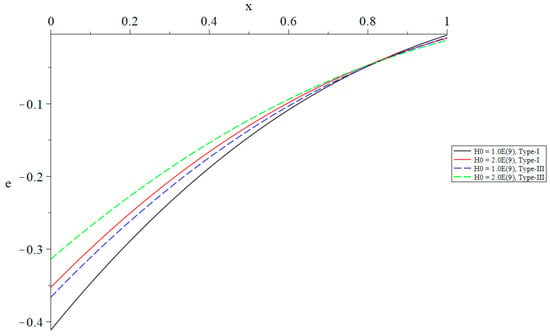
Figure 9.
The distribution of volumetric dilatation based on Green–Naghdi type-I and type-III with a different primary magnetic field when .
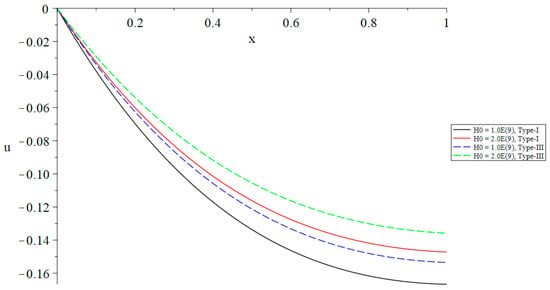
Figure 10.
The distribution of displacement based on Green–Naghdi type-I and type-III with a different primary magnetic field when .
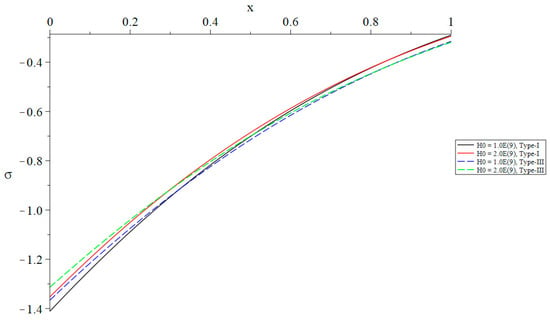
Figure 11.
The distribution of stress based on Green–Naghdi type-I and type-III with a different primary magnetic field when .
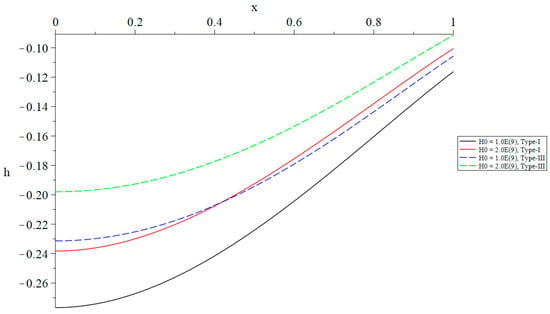
Figure 12.
The distribution of the induced magnetic field based on Green–Naghdi type-I and type-III with a different primary magnetic field when .
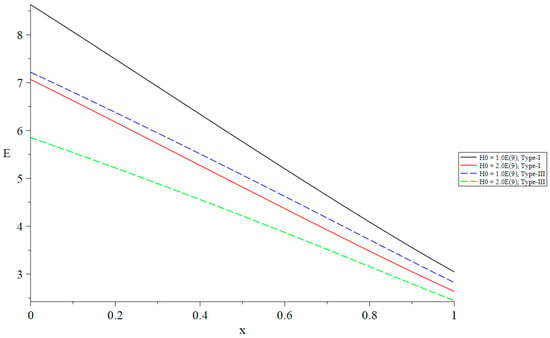
Figure 13.
The distribution of the induced electric field based on Green–Naghdi type-I and type-III with a different primary magnetic field when .
In Figure 8, it is shown that the primary magnetic field has a negligible impact on the temperature rise. Figure 9 demonstrates that the primary magnetic field has a significant impact on volumetric dilatation. Specifically, an increase in the primary magnetic field is correlated with a decrease in the absolute value of volumetric dilatation. An increase in the primary magnetic field is correlated with a decrease in the absolute value of the displacement as shown in Figure 10. This indicates that the primary magnetic field has a significant impact on displacement. An increase in the primary magnetic field is correlated with a decrease in the absolute magnitude of stress as shown in Figure 11. This demonstrates that the primary magnetic field has a significant impact on stress. Figure 12 demonstrates that the primary magnetic field has a significant impact on the induced magnetic field. This influence is such that an increase in the magnitude of the primary magnetic field leads to a decrease in the absolute value of the induced magnetic field. It is shown in Figure 13 that the primary magnetic field has a significant impact on the electromagnetic field. Specifically, a rise in the primary magnetic field is correlated with a decrease in the induced electric field.
4. Validation
We can see that the current results agree with the results of the paper [39].
5. Conclusions
Within the scope of this study, a novel and distinct mathematical model of a generalized magnetothermoelastic half-space with a single thermal relaxation period was presented. Taking into consideration time-fractional Maxwell’s equations, the model was constructed using Green–Naghdi theory type-I and type-III as its theoretical foundation. This model makes use of the definition of the Caputo fractional derivative, which is the fractional derivative that has been applied. It was determined that direct use of Laplace transform methods was the most effective method for this. For calculating the inverse Laplace transform, the iteration method that Tzou had created was used. It has been determined and described how the distributions of temperature increment, strain, displacement, stress, induced magnetic field, and induced electric field are distributed. These distributions have been determined and explained.
The distributions of temperature increment, strain, displacement, stress, induced magnetic field, and induced electric field based on Green–Naghdi type-I and type-III are significantly influenced by the time-fraction parameter in Maxwell’s equations. This is the case because the time-fraction parameter has a significant effect.
More than any other parameter, the time-fraction parameter has the greatest impact on these distributions.
The time-fractional parameter of Maxwell’s equations functions as a resistor to the movement of the particle, volumetric dilatation, and the induced magnetic field. On the other hand, it functions as a catalyst for the induced electric field that is present inside the material.
Thermal, mechanical, and magnetoelectric waves are all significantly impacted by the ramp-time heat parameter due to their considerable implications.
When it comes to mechanical and magnetoelectric waves, the ramp-time heat parameter has a substantial impact, although it has no impact whatsoever on the thermal temperature wave.
The pace at which thermal, mechanical, and magnetoelectric waves propagate under Green–Naghdi type-III is slower than the speed at which type-I waves propagate.
There are considerable effects that the main magnetic field has on all of the functions that were investigated.
Funding
This research work was funded by Umm Al-Qura University, Saudi Arabia under grant number 25UQU4250163GSSR02.
Data Availability Statement
No data are associated with the manuscript.
Acknowledgments
The authors extend their appreciation to Umm Al-Qura University, Saudi Arabia for funding this research work through grant number 25UQU4250163GSSR02.
Conflicts of Interest
The authors report there are no competing interests to declare.
Nomenclature
| Notation | Meaning |
| The induced magnetic vector field | |
| The induced electric intensity vector field | |
| The primary magnetic vector field | |
| Displacement functions | |
| The current density vector | |
| The magnetic permeabilities | |
| The electrical permeabilities | |
| The electric conductivity | |
| The strain components | |
| The Kronecker delta function | |
| The components of the stress tensor | |
| Lamé’s constants | |
| Temperature | |
| Reference temperature | |
| Time | |
| The ramp-time parameter | |
| The coefficient of linear thermal expansion | |
| The density | |
| Thermal conductivity | |
| The main character of the Green–Naghdi theory | |
| The specific heat at constant strain | |
| Longitudinal wave speed | |
| Thermal viscosity coefficient |
References
- Hetnarski, R.B.; Eslami, M.R.; Hetnarski, R.B.; Eslami, M.R. Basic laws of thermoelasticity. Therm. Stress.Adv. Theory Appl. 2019, 158, 1–43. [Google Scholar]
- Ezzat, M.A.; Youssef, H.M. Generalized magneto-thermoelasticity for an infinite perfect conducting body with a cylindrical cavity. Mater. Phys. Mech. 2013, 18, 156–170. [Google Scholar]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar]
- Sherief, H.H.; Darwish, A.A. A short time solution for a problem in thermoelasticity of an infinite medium with a spherical cavity. J. Therm. Stress. 1998, 21, 811–828. [Google Scholar] [CrossRef]
- Sadeghi, M.; Kiani, Y. Generalized magneto-thermoelasticity of a layer based on the Lord–Shulman and Green–Lindsay theories. J. Therm. Stress. 2022, 45, 319–340. [Google Scholar]
- Hendy, M.M.; Ezzat, M.A. A modified Green-Naghdi fractional order model for analyzing thermoelectric MHD. Int. J. Numer. Methods Heat Fluid Flow 2024, 34, 2376–2398. [Google Scholar] [CrossRef]
- Sarkar, N.; Lahiri, A. A three-dimensional thermoelastic problem for a half-space without energy dissipation. Int. J. Eng. Sci. 2012, 51, 310–325. [Google Scholar]
- Rezazadeh, M.; Tahani, M.; Hosseini, S.M. Thermoelastic damping in a nonlocal nano-beam resonator as NEMS based on the type III of Green–Naghdi theory (with energy dissipation). Int. J. Mech. Sci. 2015, 92, 304–311. [Google Scholar]
- Atwa, S.Y. Generalized magneto-thermoelasticity with two temperature and initial stress under Green–Naghdi theory. Appl. Math. Model. 2014, 38, 5217–5230. [Google Scholar]
- Othman, M.I.; Atwa, S.Y.; Farouk, R. The effect of diffusion on two-dimensional problem of generalized thermoelasticity with Green–Naghdi theory. Int. Commun. Heat Mass Transf. 2009, 36, 857–864. [Google Scholar]
- Sharma, S.; Sharma, K.; Bhargava, R.R. Effect of viscosity on wave propagation in anisotropic thermoelastic with Green-Naghdi theory type-II and type-III. Mater. Phys. Mech. 2013, 16, 144–158. [Google Scholar]
- Sherief, H.H.; Yosef, H.M. Short time solution for a problem in magnetothermoelasticity with thermal relaxation. J. Therm. Stress. 2004, 27, 537–559. [Google Scholar]
- Daftardar-Gejji, V. Fractional Calculus; Alpha Science International Limited: Oxford, UK, 2013. [Google Scholar]
- Li, C.; Cai, M. Theory and Numerical Approximations of Fractional Integrals and Derivatives; SIAM: Philadelphia, PA, USA, 2019. [Google Scholar]
- Almeida, R.; Tavares, D.; Torres, D.F. The Variable-Order Fractional Calculus of Variations; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Petrás, I. Fractional Derivatives, Fractional Integrals, and Fractional Differential Equations in MATLAB; IntechOpen: London, UK, 2011. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World scientific: Singapore, 2000. [Google Scholar]
- Baleanu, D.; Golmankhaneh, A.K.; Golmankhaneh, A.K.; Baleanu, M.C. Fractional electromagnetic equations using fractional forms. Int. J. Theor. Phys. 2009, 48, 3114–3123. [Google Scholar]
- Lazo, M.J. Gauge invariant fractional electromagnetic fields. Phys. Lett. A 2011, 375, 3541–3546. [Google Scholar]
- Jaradat, E.; Hijjawi, R.; Khalifeh, J. Maxwell’s equations and electromagnetic Lagrangian density in fractional form. J. Math. Phys. 2012, 53, 033505. [Google Scholar]
- Ortigueira, M.D.; Rivero, M.; Trujillo, J.J. From a generalised Helmholtz decomposition theorem to fractional Maxwell equations. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 1036–1049. [Google Scholar]
- Stefański, T.P.; Gulgowski, J. Formulation of time-fractional electrodynamics based on Riemann-Silberstein vector. Entropy 2021, 23, 987. [Google Scholar] [CrossRef]
- Machado, J.T.; Jesus, I.S.; Galhano, A.; Cunha, J.B. Fractional order electromagnetics. Signal Process. 2006, 86, 2637–2644. [Google Scholar]
- Youssef, H.M. Theory of fractional order generalized thermoelasticity. J. Heat Mass Transf. 2010, 132, 61301. [Google Scholar]
- Youssef, H.M. Theory of generalized thermoelasticity with fractional order strain. J. Vib. Control 2016, 22, 3840–3857. [Google Scholar]
- Kumar, R.; Pathania, V.; Gupta, V.; Barak, M.; Ahmad, H. Thermoelastic modeling with dual porosity interacting with an inviscid liquid. J. Appl. Comput. Mech. 2024, 10, 111–124. [Google Scholar]
- Ezzat, M.A.; Youssef, H.M. Generalized magneto-thermoelasticity in a perfectly conducting medium. Int. J. Solids Struct. 2005, 42, 6319–6334. [Google Scholar]
- Othman, M.I. Generalized Electromagneto-Thermoelastic Plane Waves by Thermal Shock Problem in a Finite Conductivity Half-Space with One Relaxation Time. Multidiscip. Model. Mater. Struct. 2005, 1, 231–250. [Google Scholar]
- Abbas, I.A. Generalized magneto-thermoelasticity in a nonhomogeneous isotropic hollow cylinder using the finite element method. Arch. Appl. Mech. 2009, 79, 41–50. [Google Scholar]
- Sarkar, N. Generalized magneto-thermoelasticity with modified Ohm’s Law under three theories. Comput. Math. Model. 2014, 25, 544–564. [Google Scholar]
- Tiwari, R. Magneto-thermoelastic interactions in generalized thermoelastic half-space for varying thermal and electrical conductivity. Waves Random Complex Media 2024, 34, 1795–1811. [Google Scholar]
- Hobiny, A.; Abbas, I.A. A GL photo-thermal theory upon new hyperbolic two-temperatures in a semiconductor material. Waves Random Complex Media 2021, 34, 4799–4812. [Google Scholar]
- Youssef, H.M.; El-Bary, A. Characterization of the photothermal interaction of a semiconducting solid sphere due to the mechanical damage, ramp-Type heating, and rotation under LS theory. Waves Random Complex Media 2024, 34, 547–572. [Google Scholar]
- Hobiny, A.D.; Abbas, I.A. The influences of thermal relaxation time and varying thermal conductivity in thermoelastic media. Case Stud. Therm. Eng. 2024, 56, 104263. [Google Scholar]
- Othman, M.I. Relaxation effects on thermal shock problems in an elastic half-space of generalized magneto-thermoelastic waves. Mech. Mech. Eng. 2004, 7, 165–178. [Google Scholar]
- Tzou, D.; Guo, Z.-Y. Nonlocal behavior in thermal lagging. Int. J. Therm. Sci. 2010, 49, 1133–1137. [Google Scholar]
- O¨zisik, M.N.; Tzou, D. On the wave theory in heat conduction. J. Heat Transfer. 1994, 116, 526–535. [Google Scholar]
- Al-Lehaibi, E.A.; Youssef, H.M. State-Space Approach to the Time-Fractional Maxwell’s Equations under Caputo Fractional Derivative of an Electromagnetic Half-Space under Four Different Thermoelastic Theorems. Fractal Fract. 2024, 8, 566. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).