Abstract
This paper presents an optimized nonlinear controller, the Integral Super-Twisting Sliding Mode Control (ISTSMC), for acute leukemia therapy. To enhance its performance, we introduce the RedFox Optimization Algorithm, a nature-inspired technique based on the hunting behavior of red foxes. This algorithm is utilized to fine-tune the controller parameters, ensuring optimal achievement of control objectives. We discuss the fundamentals of ISTSMC, Sliding Mode Control, and Synergetic Control, detailing their optimization methodology using the RedFox Algorithm. The effectiveness of ISTSMC is evaluated through numerical simulations and compared with traditional Sliding Mode Control (SMC) and Synergetic Control (SC). The results demonstrate that ISTSMC achieves superior performance with a steady state error of 53.85, a settling time of 59.60, and a transient time of 4.7942, significantly outperforming SMC and SC. Additionally, ISTSMC reduces leukemic cell levels to a safe threshold more efficiently while maintaining healthy cell populations within acceptable limits. These improvements highlight the potential of ISTSMC in optimizing chemotherapy administration, ensuring better patient outcomes while minimizing side effects.
Keywords:
acute leukemia; chemotherapy; Integral Super-Twisting Sliding Mode Control; nonlinear control MSC:
34H05; 93C95; 92F05
1. Introduction
Leukemias are cancers that develop in the bone marrow’s blood-forming tissues. Unlike many cancers, leukemia does not create solid tumors. Instead, it leads to an overproduction of abnormal white blood cells (leukemia cells and leukemic blast cells) that accumulate in the bloodstream and bone marrow. This accumulation interferes with the body’s ability to produce normal blood cells, making it harder to carry oxygen, control bleeding, or fight infections [1].
Leukemia is a general term used to describe blood cell cancers. The type depends on which blood cell is affected and how fast the disease develops [2]. Although leukemia occurs most often in adults over 55, it is also the most common childhood cancer, especially in children under 15. Leukemia is diagnosed through comprehensive testing of blood and bone marrow samples. This includes a detailed count of white blood cells, red blood cells, platelets, and leukemia cells. Along with a bone marrow examination, these tests help to confirm the presence of leukemia. Leukemia is categorized into four primary types based on how fast the disease progresses (acute or chronic) and the type of blood cell involved (lymphoblastic or myeloid). Acute leukemias advance rapidly, while chronic types progress more slowly [3].
Researchers funded by the National Cancer Institute (NCI) are advancing the field with breakthroughs in targeted therapies and immunotherapies, aiming to make leukemia treatments more effective and less harmful [4]. The standard treatments for adults have long been chemotherapy, radiation, and stem cell transplants. In recent years, targeted therapies have become part of the standard care for specific types of leukemia, focusing on proteins that regulate cancer cell growth and spread.
Different leukemia types require different therapeutic combinations. For example, adult acute lymphoblastic leukemia (ALL), which causes an overproduction of lymphocytes, progresses rapidly and needs aggressive treatment. Chemotherapy is a standard treatment but can be intolerable for older patients. Targeted therapies, which are currently being tested in clinical trials, may offer a less toxic alternative for older patients with a form of ALL known as B-cell ALL.
Acute myeloid leukemia (AML) is the most common acute leukemia in adults and causes an excess of abnormal blood cells. AML is often aggressive and challenging to treat, but certain gene mutations in AML cells can be targeted by new medications. Researchers are exploring genomic sequencing to help tailor the most effective treatments, including chemotherapy, targeted drugs, and stem cell transplants, for each patient [5].
Acute leukemia therapy involves complex, nonlinear systems characterized by dynamic variations, such as changes in blood cell counts, immune responses, and other physiological factors. A review of mathematical models of leukemia and its treatment is given by [6]. To manage such complexities effectively, advanced control techniques are required. A molecular targeted therapy, such as Imatinib, aims to reduce the size of the tumor cell mass while using the minimal effective drug dosage. This approach helps minimize both adverse effects and costs; the optimal control is determined through a discretization scheme [7]. The optimization problem includes two objective functions, which are solved using Pontryagin’s Maximum Principle, as presented in [8]. In [9], optimal control theory is used to present both continuous and bang-bang controls for various objectives and parameter choices, demonstrating a practical application of Pontryagin’s Maximum Principle through example calculations. In [10], a mathematical model of drug therapy for chronic myelogenous leukemia over a fixed time horizon describes disease dynamics through a system of ordinary differential equations, modeling the interaction between naive T cells, effector T cells, and leukemic cancer cells in a hypothetical patient, while incorporating both targeted and broad cytotoxic therapies.
This paper focuses on three advanced control strategies: Super-Twisting Sliding Mode Control (STSMC), Sliding Mode Control (SMC), and Synergetic Control, to design nonlinear controllers for acute leukemia therapy [11,12]. These controllers aim to maintain therapeutic levels of various parameters, such as drug concentrations and cell counts, within optimal bounds. SMC is commonly used to obtain the dynamics of a system along a sliding surface and has the capability to control under the effect of disturbances and model uncertainties [13]. SMC is a variable structure control as it has strong robustness to discontinuities. The various advantages of SMC include robust control in the presence of disturbance, parametric invariance, simple structure, and model order reduction. SMC has been used for the fault ride-through performance enhancement of DFIG-based wind turbines [14], chemotherapy control of brain tumors [15], and for a class of nonlinear systems with disturbances [16]. Chattering is the most common problem of SMC and can be significantly reduced by using higher-order SMCs, as they eliminate the reaching phase, thus ensuring fast convergence and robustness right from the initial time [17,18,19,20].
Traditional leukemia treatment strategies, such as chemotherapy and targeted therapy, often struggle with maintaining optimal drug dosages due to patient variability and dynamic physiological responses. While classical control techniques like Sliding Mode Control (SMC) and Synergetic Control (SC) offer robustness against uncertainties, they are prone to issues such as chattering and slow convergence, which can negatively impact treatment effectiveness [11]. The necessity of ISTSMC arises from its ability to provide finite-time convergence, enhanced disturbance rejection, and reduced chattering, making it a more reliable approach for drug administration in leukemia therapy [12]. Furthermore, by integrating the RedFox optimization algorithm, ISTSMC ensures adaptive and optimized control performance, addressing the limitations of conventional control strategies. These improvements make ISTSMC a crucial advancement in leukemia treatment, ensuring better patient outcomes while minimizing side effects.
Foxes are widespread across many parts of the world, with their presence spanning Europe, Asia, North America, and even certain Arctic regions. Their hunting behavior and survival tactics are quite unique. These predators remain active throughout the year, constantly searching for both domesticated and wild prey. They employ a range of clever techniques to deceive their targets while stealthily approaching, making them highly effective hunters. Their ability to adapt to different environments is largely due to their territorial instincts and strong social structures between juveniles and adults. To optimize these controllers and ensure the best performance under real-world conditions, we apply the RedFox Algorithm [21], a nature-inspired optimization algorithm. The RedFox Algorithm is based on the behavior of red foxes in their natural environment, specifically their hunting techniques, and is well-suited for handling dynamic optimization problems. The improved FOX optimization method, which incorporates adaptive spiral flight and multi-strategy fusion, is extensively compared against multiple swarm intelligence algorithms. This comparison is conducted using engineering optimization problems and the CEC2017 benchmark test functions, as discussed in [22] and the references therein.
Leukemia therapy, particularly in the context of acute forms, involves complex interactions between healthy and cancerous cells, as well as the effects of chemotherapeutic agents. The progression of these cell populations can often be modeled using the Gompertz growth law, which provides a mathematical framework for understanding their dynamics. In such models, the population of normal cells and leukemic cells evolve according to differential equations that account for growth rates, competition, and therapeutic interventions.
The concentration of the drug, represented as , plays a critical role in these dynamics. Chemotherapy is inherently dual-edged, as it impacts both diseased and healthy cells. The effectiveness of treatment is typically governed by therapy functions and , which quantify the impact of the drug on healthy and cancerous cells, respectively. While healthy cells are often more vulnerable, diseased cells may develop resistance, leading to complex non-monotonic responses.
To achieve an effective therapy, it is essential to optimize drug administration while adhering to practical constraints. These include limits on dosage levels, total drug quantity, and ensuring that the healthy cell population does not fall below a critical threshold required for patient survival. This forms a challenging optimal control problem, where the aim is to minimize the leukemic cell population at the end of therapy while respecting these constraints.
In comparison to previous studies, this work makes the following notable contributions:
- 1.
- A novel Integral Super-Twisting Sliding Mode Controller (ISTSMC) is proposed, providing convergence and enhanced robustness.
- 2.
- The RedFox algorithm is introduced to improve the tracking performance and efficiency of the ISTSMC.
- 3.
- A comprehensive comparative evaluation of nonlinear controllers, including Integral Super-Twisting Sliding Mode Control (ISTSMC), Sliding Mode Control (SMC), and Synergetic Control (SC) is presented.
This article is organized as follows: In Section 2, a mathematical model for leukemia therapy is presented in detail. The nonlinear controllers, Integral Super-Twisting Sliding Mode Control (ISTSMC), Sliding Mode Control (SMC), and Synergetic Control (SC) are described under the effects of monotonic and non-monotonic therapy in Section 3. The RedFox Algorithm with methodology is illustrated in Section 4. Numerical results are provided in Section 5, followed by the conclusion in the final section.
2. The Problem Statement
We examine a mathematical model for leukemia therapy, based on the assumption that a population of cells will grow according to Gompertz’s law. The Gompertz model was selected for this study due to its well-established ability to describe tumor growth dynamics, particularly in leukemia. Unlike the exponential model, which assumes unrestricted tumor growth, the Gompertz model accounts for the deceleration of cell proliferation as the tumor mass increases, making it more biologically realistic [2].
Let be the number of healthy or normal cells and be the number of diseased or leukemic cells. Let be the drug concentration in the body at moment in time t (i.e., the total number of therapeutic agents) c.f. [23,24]. To describe the dynamics of the number of cells and the drug concentration, we write the following system of equations:
where and c are positive real constants.
Notice the following:
- : the maximum possible number of healthy cells;
- : the maximum possible number of leukemic (diseased) cells;
- : the replication rates of normal cells;
- : the replication rates of leukemic cells;
- : the death rates of healthy and diseased cells, respectively;
- , : the therapy functions describe the effect of the drug on normal and leukemia cells, respectively;
- : the drug dissipation;
- c: the constant describes the interaction (competition) between normal and diseased cells;
- : the control function that can be looked upon as the quantity of the drug administered to a patient at moment t.
Moreover, we impose the following restrictions: one on the maximum amount of chemotherapy that can be administered at any given time t and another on the total cumulative dose of the chemotherapy throughout the entire treatment process:
with the parameters . For simplicity, we denote as , as , and as in what follows.
3. Controller Framework
In this section, we propose Integral Super-Twisting Sliding Mode Control (ISTSMC) to manage both monotonic and non-monotonic therapies. The goal is to eliminate all leukemic cells while maintaining a healthy level of normal cells by the conclusion of chemotherapy, ensuring the therapeutic agent is used safely throughout the process.
Notice that a relationship described under Michaelis–Mentis law is chosen to describe monotonic therapy function [23,24,25]; that is,
With the value of , the mathematical model (1) is under the effect of monotonic therapy.
In the context of non-monotonic therapy, represents the therapy function modeling the effect of the chemotherapeutic agent on normal cells. Unlike monotonic therapy, non-monotonic therapy introduces a threshold effect. The function gains a maximal value at a specific level , beyond which its effect diminishes. This is crucial for balancing the therapy’s impact on normal and leukemic cells.
A non-monotonic therapy function has been described as follows:
where , for all , ; for , , and for . Such a function represents an interaction with a threshold effect: the therapeutic effect increases up to a maximum value, , and then decreases for . Consequently, the maximum effect is achieved at . It is important to note that can be regarded as the maximum permissible dosage of the drug. The non-monotonic therapy function applied here is given by
where , and ensures the function exhibits the desired threshold behavior. This formulation helps manage the dosage of the chemotherapeutic agent to achieve optimal therapeutic effects while minimizing harm to normal cells.
3.1. Integral Super-Twisting Sliding Mode Control
This section introduces a novel approach called Integral Super-Twisting Sliding Mode Control (ISTSMC). The super-twisting algorithm is a specific variation of Sliding Mode Control (SMC) that mitigates chattering—undesirable high-frequency oscillations—while improving control performance. By incorporating an integral term, ISTSMC further enhances robustness, ensuring better error convergence, improved disturbance rejection, and higher steady state accuracy. As an advanced form of SMC, the super-twisting sliding mode controller employs a second-order technique to refine control precision and system stability. ISTSMC builds upon this foundation by integrating the benefits of both super-twisting and integral action, offering superior performance in applications requiring high robustness and minimal chattering.
To develop a control law for ISTSMC, we consider the tracking errors of all three states ; that is,
where represents, respectively, the error between the normal cells and their tracking references, the leukemic cells and their tracking references, the total amount of therapeutic agent and their tracking references. The aim of this work is to design the controller for the system with control .
The time derivatives of errors are given by
To design the Integral Super-Twisting Sliding Mode Controller (ISTSMC), we define the integral errors as follows:
where represents the tracking error, and is its integral. This integral term helps improve steady state accuracy and enhances robustness against disturbances. By incorporating integral errors, the ISTSMC ensures better convergence properties and minimizes steady state deviations.
Notice that
Next, we define a macro-variable S, which represents a linear combination of tracking errors, for the model (1) with the control input u:
where are the positive gains. The time derivative of S is given by
and substituting Equation (5), we have
For asymptotic convergence of ISTSMC, the time-derivative of sliding surface S is given by
where and have been explained in [24].
Next, we define the control input corresponding to the ISTSMC. For this, we write the control law
where the switching control for ISTSMC is given by
and
Substituting the time derivative values of and ; that is, and , to derive the control law for the monotonic therapy case, we obtain
Similarly, for the non-monotonic therapy case, the control law is given by
For the stability analysis, the following Lyapunov candidate is chosen for ISTSMC.
The time derivative of V is given by
Substituting Equation (9), we have
3.2. Sliding Mode Control
Sliding Mode Control (SMC) is a robust nonlinear control technique that forces a system’s state to reach and maintain a predefined surface, despite uncertainties and disturbances. In acute leukemia therapy, SMC can be applied to regulate drug dosage in chemotherapy, ensuring optimal treatment while minimizing side effects. By designing a sliding surface based on desired leukemic cell dynamics and healthy cell preservation, the SMC can adaptively adjust drug infusion rates, compensating for patient-specific variations and external disturbances. This approach enhances treatment efficacy, reduces toxicity, and helps maintain a stable immune response, improving patient outcomes.
The time derivative of S is given by
The control law for the monotonic therapy case is characterized as follows:
Similarly, for the non-monotonic therapy case, the control law is given by
For the stability of Sliding Mode Control (SMC), we consider the following Lyapunov function:
After taking the time derivative, we have
Substituting the value of (Equation (22)), we obtain
This guarantees the system’s stability and convergence of tracking error to zero.
3.3. Synergetic Control
Synergetic Control Technique for Acute Leukemia refers to an advanced control-theoretic approach that integrates multiple treatment strategies (chemotherapy, targeted therapy, immunotherapy) in a way that optimally suppresses leukemia while minimizing toxicity and drug resistance. This technique is inspired by synergetic control theory, which is commonly used in engineering and biological systems to achieve stable, adaptive, and coordinated control.
The time derivative of S is given by
The dynamic evaluation equation for S is given by
where is the convergence rate of states to .
Solving for u, we have the control law for SC to track the desired trajectory: The control law for the monotonic therapy case is given by
Similarly, for the non-monotonic therapy case, the control law for SC is given by
For the stability of synergetic control to track the desired trajectory, we consider the following Lyapunov candidate function:
After taking the time derivative, we have
Substituting the value of using the Equation (30), we obtain
and
where denotes the value of Lyapunov function at . In this way, the global exponential stability of the system is established.
4. RedFox Optimization Algorithm
The RedFox Algorithm (RFA) is a nature-inspired optimization method that mimics the hunting and foraging behavior of red foxes [21]. It is designed to balance exploration and exploitation while searching for optimal solutions in a complex search space. The algorithm utilizes multiple strategies, inspired by the ability of the red fox to adapt to environmental changes and its allocation of resources during hunting. The main features of the algorithm are as follows:
- Exploration and Exploitation Balance: RedFox emphasizes the dynamic adjustment between broad exploration of the search space (searching for new and better solutions) and exploitation (refining the solutions found so far).
- Position Update Mechanism: The algorithm’s search process is based on the metaphor of a red fox searching for food while avoiding predators. This adaptive mechanism allows it to efficiently find global solutions without becoming stuck in local optima.
- Adaptive Parameters: The RedFox algorithm adapts its search strategy during the optimization process, allowing it to effectively navigate both smooth and rugged landscapes, making it well-suited for optimizing nonlinear control parameters.
- Convergence Rate: The algorithm can converge quickly, especially when fine-tuned, making it useful for real-time applications like leukemia therapy, where time is of the essence.
4.1. Methodology: RedFox Algorithm for Optimizing Nonlinear Control
The RedFox Algorithm is applied to optimize the key parameters of the Super-Twisting Sliding Mode Control (STSMC) and Synergetic Control strategies. The following steps outline the proposed methodology:
4.1.1. Initialization
The parameters of both the STSMC and the synergetic control laws are initialized, with a range of possible values for each control parameter (e.g., sliding surface coefficients, gain parameters for STSMC, and interaction coefficients for Synergetic Control). These initial values serve as the starting point for the optimization process.
4.1.2. Objective Function Definition
An objective function is defined to measure the performance of the controllers. This function includes criteria such as the minimization of control effort, the tracking error of desired therapeutic trajectories, and the robustness to disturbances and uncertainties in the system. Mathematically, the objective function can be defined as
where:
- is the output of the system (e.g., drug concentration, cell count);
- is the reference trajectory;
- is the control input (e.g., drug dose);
- is the tracking error;
- are weighting coefficients; and
- T is the time horizon for performance evaluation.
The goal is to minimize this objective function to achieve accurate tracking and minimal control effort while ensuring robustness against disturbances.
4.1.3. RedFox Algorithm Execution
- Exploration Phase: The algorithm starts by exploring a wide solution space, trying to locate regions where optimal solutions may lie. During this phase, RedFox samples solutions from various areas to identify promising regions of the search space.
- Exploitation Phase: Once promising solutions are found, the RedFox algorithm refines them by focusing on local areas of the search space. This phase narrows down the search to optimize the most promising candidate solutions.
- Balance Adjustment: The algorithm dynamically adjusts its exploration–exploitation balance based on the feedback from the objective function. If the algorithm encounters a region where further refinement is beneficial, it increases the exploitation phase. Otherwise, it continues exploring new areas of the search space.
4.1.4. Parameter Optimization
The RedFox Algorithm fine-tunes the control parameters for both ISTSMC and Synergetic Control. Specifically, the algorithm optimizes the parameters that define the sliding surface in ISTSMC and the interaction coefficients in Synergetic Control. These parameters are crucial for achieving the desired performance in the leukemia therapy model.
The Redfox algorithm begins by initializing a diverse set of candidate solutions. Each solution is then assessed using a predefined fitness function, which quantifies its effectiveness in addressing the given problem. The algorithm proceeds iteratively, continuously refining the solution set through the following key steps:
- Selection: A subset of solutions is chosen based on their fitness values. These selected solutions serve as the foundation for generating the next generation of candidates.
- Crossover: New solutions are produced by combining elements from two parent solutions. This recombination process enables the algorithm to explore new regions of the solution space by merging advantageous characteristics from different individuals.
- Mutation: Random modifications are introduced to certain solutions, ensuring diversity in the population and reducing the risk of the algorithm converging prematurely to a suboptimal solution.
The iterative cycle continues until a predefined stopping criterion is satisfied. This criterion may be based on a fixed number of iterations, a desired level of fitness, or a combination of both. The Redfox algorithm has demonstrated its effectiveness in solving numerous optimization challenges. Its straightforward implementation and natural suitability for parallel processing make it a practical choice for a variety of applications. The fundamental workflow of the Redfox algorithm is illustrated in [26,27]. Moreover, the behaviour of Redfox is shown in Figure 1.
Figure 1.
RedFox hunting behavior.
4.1.5. Simulation and Validation
The optimized controllers are tested using simulated models of acute leukemia therapy. The simulations incorporate realistic variations in patient conditions, such as changes in immune response and drug absorption rates. The optimized controllers are evaluated for performance metrics including tracking error, robustness to disturbances, and control effort. The results are compared against baseline controllers to validate the improvements achieved by the RedFox optimization.
5. Simulations
In this section, we present the simulation results of the Integral Super-Twisting Sliding Mode Controller (ISTSMC), Sliding Mode Controller (SMC), and Synergetic Controller (SC), and compare their performance in both monotonic and non-monotonic therapy cases for leukemia. The simulations were conducted in MATLAB R2024b (Simulink) using the specified constants and model parameters from [18,24].
The model parameter values are listed in Table 1; D represents the maximum allowable total quantity of the chemotherapeutic drug used in this process. The parameter denotes the minimum safe number of normal cells, as a value below this threshold may lead to fatal consequences. The maximum permissible value of the control function , denoted as , is set to 1 for all the proposed controllers. The total amount of the therapeutic agent consumed can be determined by computing the area under the curve of .

Table 1.
Parameters’ values.
The controller gain values were determined using the RedFox Optimization algorithm and/or a trial-and-error approach. Table 2 provides the gain values for monotonic therapy, while Table 3 presents those for non-monotonic therapy. Furthermore, the performance of the proposed nonlinear controllers was analyzed, and their comparative evaluation is presented. The comparison is based on the convergence of the states with their desired references, steady state error, and their overall effectiveness.

Table 2.
Controller design parameters with monotonic therapy.

Table 3.
Controller design parameters with non-monotonic therapy.
5.1. Monotonic Therapy
In this section, we present the results of numerical experiments for ISTSMC, SMC, and Synergetic Control using monotonic therapy. The design constant values for the controllers under monotonic therapy are provided in Table 2. In the case of monotonic therapy using ISTSMC, the number of normal cells is illustrated in Figure 2, while the number of leukemic cells is depicted in Figure 3. Additionally, the quantity of chemotherapeutic agents is shown in Figure 4, and the control effort is represented in Figure 5.
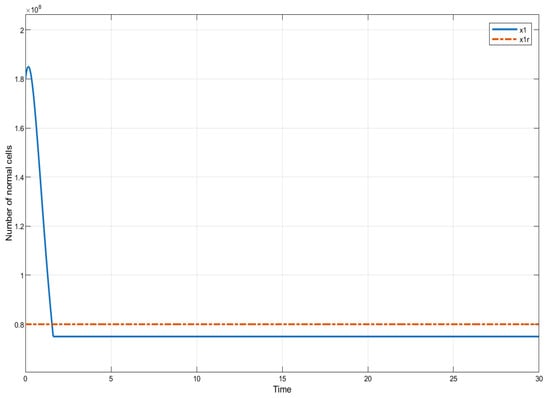
Figure 2.
ISTSMC: number of normal cells (monotonic therapy).
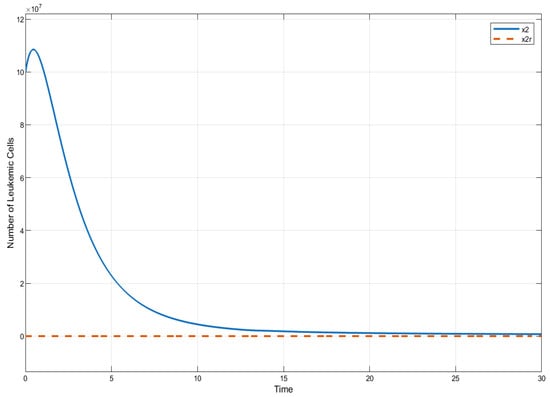
Figure 3.
ISTSMC: number of leukemiac cells (monotonic therapy).
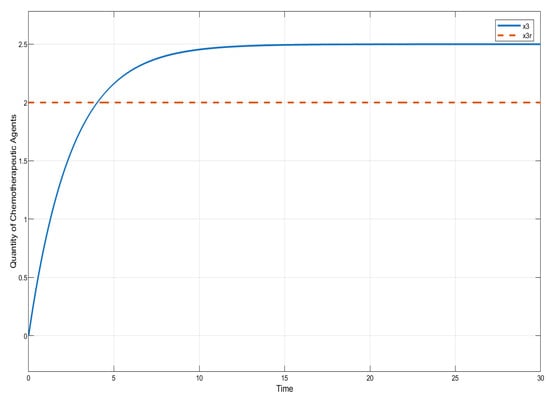
Figure 4.
ISTSMC: quantity of chemotherapeutic agents (monotonic therapy).
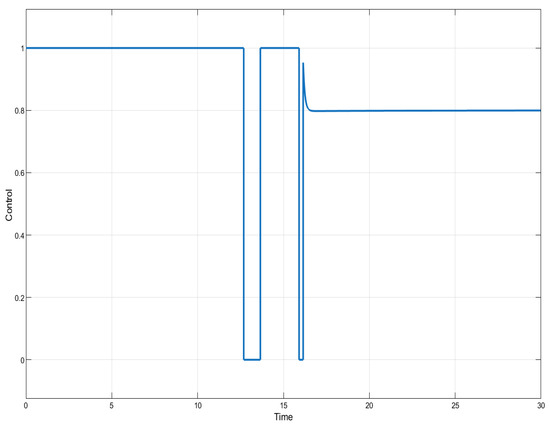
Figure 5.
ISTSMC: controller (monotonic therapy).
Figure 6 presents a comparative analysis of the proposed controllers (ISTSMC, SMC, and SC) with respect to the state , representing the number of leukemic cells. The results indicate that ISTSMC reduces leukemic cell levels to significantly faster than SMC and SC. Furthermore, at the end of therapy, the normal cell count remains above the minimum safe threshold .
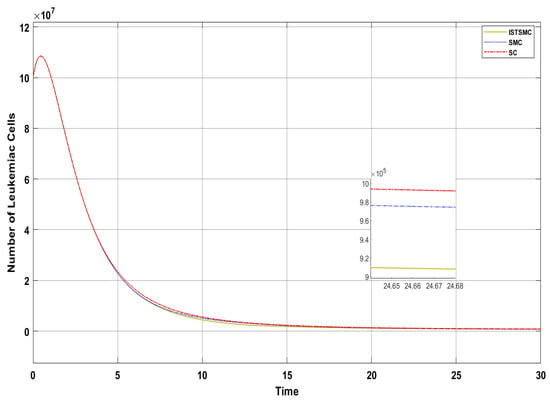
Figure 6.
Comparison of ISTSMC, SMC, and SC for the state (monotonic therapy).
Figure 4 compares the total amount of chemotherapeutic agents administered. While all controllers adhere to the designated reference, steady state errors are observed in ISTSMC, SMC, and SC. In addition, a comparison of the transient response characteristics of the state is shown in Table 4.

Table 4.
Comparison of transient response characteristics of state (monotonic therapy).
5.2. Non-Monotonic Therapy
In this section, we show the results of numerical experiments of ISTSMC, SMC, and Synergetic Control using non-monotonic therapy. The design constant values of the designed controllers under non-monotonic therapy are given by Table 2. The abscissa axis of all graphs in this section represents the non-dimensional time where 1 unit time equals [28].
In the case of ISTSMC with non-monotonic therapy, the number of normal cells is illustrated in Figure 7, while the number of leukemic cells is depicted in Figure 8. Moreover, the quantity of chemotherapeutic agents is shown in Figure 9, and the control is represented in Figure 10.
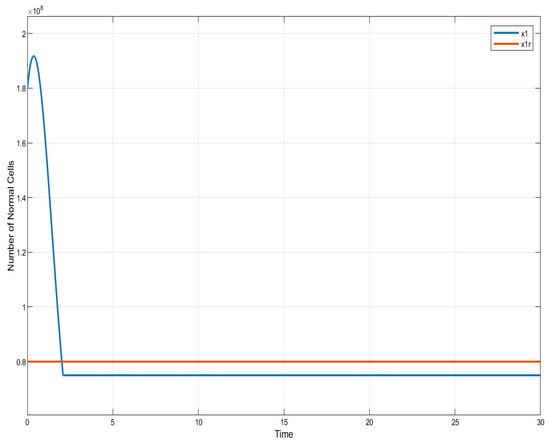
Figure 7.
ISTSMC: number of normal cells (non-monotonic therapy).
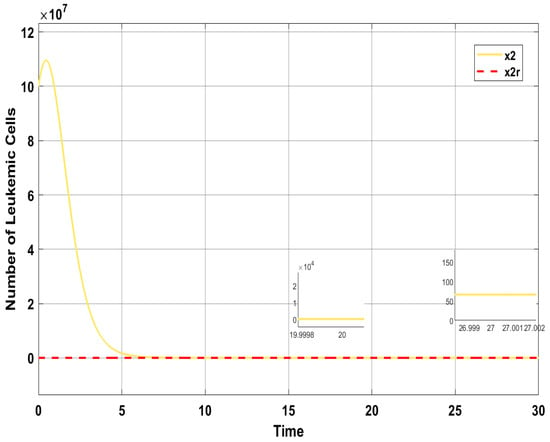
Figure 8.
ISTSMC: number of leukemic cells (non-monotonic therapy).
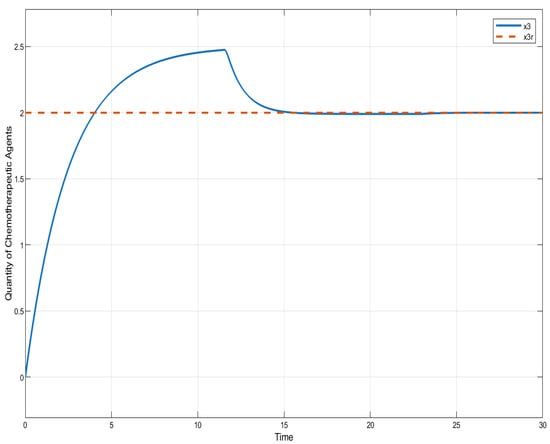
Figure 9.
ISTSC: quantity of chemotherapeutic agents (non-monotonic therapy).
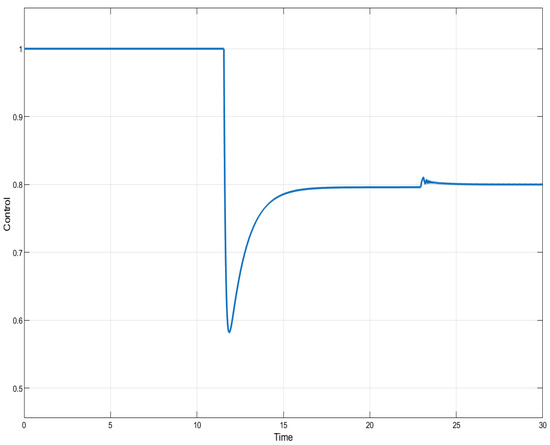
Figure 10.
ISTSMC: controller (non-monotonic therapy).
Figure 11 presents a comparative analysis of the proposed controllers (ISTSMC, SMC, and SC) with respect to state , representing the number of leukemic cells. The results indicate that ISTSMC reduces leukemic cell levels to significantly faster than both SMC and SC. Furthermore, at the end of therapy, the normal cell count remains above the minimum safe threshold .
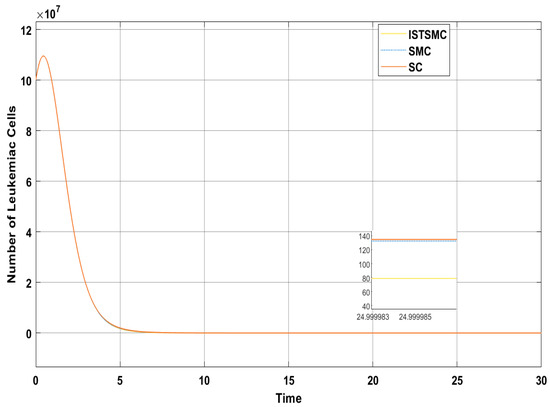
Figure 11.
Comparison of ISTSMC, SMC, and SC for the state (non-monotonic therapy).
Figure 9 compares the total amount of chemotherapeutic agents administered. While all controllers adhere to the designated reference, steady state errors are observed in both SMC and SC, whereas ISTSMC demonstrates superior tracking performance with zero steady state error.
The total amount of chemotherapeutic agent administered is 67 for ISTSMC, 60 for SMC, and 57 for the synergetic controller. Overall, the total drug consumption across all designed controllers under monotonic therapy remains below the maximum safe limit . A comparison of transient response characteristics of the state is shown in Table 5.

Table 5.
Comparison of transient response characteristics of state (non-monotonic therapy).
6. Conclusions
Acute leukemia is a fast-progressing cancer of the blood and bone marrow, characterized by the rapid growth of abnormal white blood cells. In this context, the control technique could be applied to mathematical or computational models of leukemia progression to regulate tumor growth or abnormal cell populations, optimize drug delivery schedules and dosages in chemotherapy, and simulate and predict the dynamics of leukemia under various treatment conditions, taking into account uncertainties like patient variability or external factors.
Based on the simulation results, the Integral Super-Twisting Sliding Mode Controller outperforms the sliding mode controller and synergetic controller in terms of convergence rate, steady state accuracy, chattering reduction, and improved transient response for both therapies. The non-monotonic therapy proves to be more effective than the monotonic therapy, as it achieves the objectives in a shorter time with faster convergence. One of the main reasons for selecting the RedFox algorithm is its ability to efficiently optimize the gains of the sliding mode controller and its variations. The concept might involve designing and testing an ISTSMC-based framework to stabilize and drive leukemia-related biomarkers (e.g., abnormal white blood cell counts) toward desired healthy levels, despite biological uncertainties and external disturbances. This could lead to optimized, personalized, and more effective treatment plans.
In future works, we can integrate the RedFox Optimization Algorithm with other metaheuristic techniques such as genetic algorithms, particle swarm optimization, or gray wolf optimizer to enhance parameter tuning for nonlinear controllers.
Author Contributions
Conceptualization, M.M.B.; Methodology, M.M.B.; Software, MATLAB R2024b (Simulink), M.M.B. and A.I.K.B.; Formal analysis, A.I.K.B.; Investigation, A.I.K.B.; Resources, A.I.K.B.; Writing—original draft, M.M.B.; Writing—review & editing, A.I.K.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Project No. KFU251228].
Data Availability Statement
All data supporting the findings of this study are available within the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| ISTSMC | Integral Super-Twisting Sliding Mode Control |
| SMC | Sliding Mode Control |
| SC | Synergetic Control |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| RFA | RedFox Algorithm |
| AML | Acute Myeloid Leukemia |
| ALL | Acute Lymphoblastic Leukemia |
| NCI | National Cancer Institute |
| CML | Chronic Myeloid Leukemia |
| Na | Maximum possible number of healthy cells |
| La | Maximum possible number of leukemic cells |
| Replication rate of normal cells | |
| Replication rate of leukemic cells | |
| Death rate of healthy cells | |
| Death rate of leukemic cells | |
| Drug dissipation rate | |
| Therapy function describing drug effect on normal cells | |
| Therapy function describing drug effect on leukemic cells | |
| Maximum amount of chemotherapy administered at a given time | |
| Total cumulative chemotherapy dosage | |
| State variables representing normal cells, leukemic cells, and drug concentration | |
| Control function representing drug dosage | |
| V | Lyapunov function |
| T | Convergence rate of states |
| S | Sliding surface |
References
- Afenya, E. Mathematical models of cancer and their relevant insights. In Handbook of Cancer Models with Applications; Series in Mathematical Biology and Medicine; World Scientific: Hackensack, NJ, USA, 2008; Volume 9, pp. 173–223. [Google Scholar]
- Araujo, R. A history of the study of solid tumor growth: The contribution of mathematical modelling. Bull. Math. Biol. 2004, 66, 1039–1091. [Google Scholar] [PubMed]
- Chakrabarty, A.; Pearce, S.M.; Nelson, R.P.; Rundell, A.E. Treating acute myeloid leukemia via HSC transplantation: A preliminary study of multi-objective personalization strategies. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 3790–3795. [Google Scholar]
- Mayo Clinic Staff. Cancer. Mayo Clinic. Available online: https://www.mayoclinic.org/diseasesconditions/cancer/symptoms-causes/syc-20370588 (accessed on 5 February 2025).
- How Is Leukemia Diagnosed? Available online: https://www.health.com (accessed on 5 February 2025).
- Chulián, S.; Rubio, Á.M.; Rosa, M.; Pérez-García, V.M. Mathematical models of Leukaemia and its treatment: A review. SeMA J. 2022, 79, 441–486. [Google Scholar]
- Rădulescu, I.R.; Cândea, D.; Halanay, A. Optimal control analysis of a leukemia model under imatinib treatment. Math. Comput. Simul. 2016, 121, 1–11. [Google Scholar]
- Todorov, Y.; Fimmel, E.; Bratus, A.S.; Semenov, Y.S.; Nuernberg, F. An optimal strategy for leukemia therapy: A multi-objective approach. Russ. J. Numer. Anal. Math. Model. 2012, 26, 589–604. [Google Scholar]
- Sharp, J.A.; Browning, A.P.; Mapder, T.; Burrage, K.; Simpson, M.J. Optimal control of acute myeloid leukaemia. J. Theoret. Biol. 2019, 470, 30–42. [Google Scholar]
- Nanda, S.; Moore, H.; Lenhart, S. Optimal control of treatment in a mathematical model of chronic myelogenous leukemia. Math. Biosci. 2007, 210, 143–156. [Google Scholar] [PubMed]
- Ahmad, S.; NasimUllah; Ahmed, N.; Ilyas, M.; Khan, W. Super twisting sliding mode control algorithm for developing artificial pancreas in type 1 diabetes patients. Biomed. Signal Process. Control 2017, 38, 200–211. [Google Scholar]
- Dey, B.S.; Bera, M.K.; Roy, B.K. Super twisting sliding mode control of cancer chemotherapy. In Proceedings of the 2018 15th International Workshop on Variable Structure Systems (VSS), Graz, Austria, 9–11 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 343–348. [Google Scholar]
- Hernández, A.G.G.; Fridman, L.; Levant, A.; Shtessel, Y.; Leder, R.; Monsalve, C.R.; Andrade, S.I. High-order sliding-mode control for blood glucose: Practical relative degree approach. Control Eng. Pract. 2013, 21, 747–758. [Google Scholar] [CrossRef]
- Firouzi, M.; Nasiri, M.; Mobayen, S.; Gharehpetian, G.B. Sliding Mode Controller-Based BFCL for Fault Ride-Through Performance Enhancement of DFIG-Based Wind Turbines. Complexity 2020, 2020, 1259539. [Google Scholar] [CrossRef]
- Zubair, M.; Rana, I.A.; Islam, Y.; Khan, S.A. Variable Structure Based Control for the Chemotherapy of Brain Tumor. IEEE Access 2021, 9, 107333–107346. [Google Scholar] [CrossRef]
- Jafari, M.; Mobayen, S. Second-order sliding set design for a class of uncertain nonlinear systems with disturbances: An LMI approach. Math. Comput. Simul. 2019, 156, 110–125. [Google Scholar]
- Ghazali, R.; Sam, Y.M.; Rahmat, M.F.; Hashim, A.W.I.M.; Zulfatman. Performance comparison between sliding mode control with PID sliding surface and PID controller for an electro-hydraulic positioning system. Int. J. Adv. Sci. Eng. Inform. Technol. 2011, 1, 447–452. [Google Scholar]
- Islam, Y.; Ahmad, I.; Zubair, M.; Shahzad, K. Double Integral sliding mode control of Leukemia Therapy. Biomed. Signal Process. Control 2020, 61, 102046. [Google Scholar] [CrossRef]
- Venkataraman, S.T.; Gulati, S. Control of Nonlinear Systems Using Terminal Sliding Modes. In Proceedings of the 1992 American Control Conference, Chicago, IL, USA, 24–26 June 1992; IEEE: Piscataway, NJ, USA, 1992; pp. 891–893. [Google Scholar]
- Utkin, V.I.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Polap, D.; Woźniak, M. Red fox optimization algorithm. Expert Syst. Appl. 2021, 166, 114107. [Google Scholar]
- Zhang, Z.; Wang, X.; Cao, L. FOX Optimization Algorithm Based on Adaptive Spiral Flight and Multi-Strategy Fusion. Biomimetics 2024, 9, 524. [Google Scholar] [CrossRef] [PubMed]
- Bratus, A.; Yegorov, I.; Yurchenko, D. Dynamic mathematical models of therapy processes against glioma and leukemia under stochastic uncertainties. Mecc. Mater. Strutt. 2016, 6, 131–138. [Google Scholar]
- Islam, Y.; Ahmad, I.; Zubair, M.; Islam, A. Adaptive terminal and supertwisting sliding mode controllers for acute Leukemia therapy. Biomed. Signal Process. Control 2022, 71, 103121. [Google Scholar]
- Bratus, A.; Fimmel, E.; Todorov, Y.; Semenov, Y.; Nürnberg, F. On strategies on a mathematical model for leukemia therapy. Nonlinear Anal. Real World Appl. 2012, 13, 1044–1059. [Google Scholar]
- Mughees, A.; Ahmad, I.; Jadoon, A.N. Enhanced Nonlinear Control for Trajectory Tracking Control of a Quad-Copter System Using Redfox Algorithm. IEEE Access 2024, 12, 86618–86630. [Google Scholar]
- Mohammed, H.; Rashid, T. FOX: A FOX-inspired optimization algorithm. Appl. Intell. 2023, 53, 1030–1050. [Google Scholar] [CrossRef]
- Tan, W.Y.; Hanin, L.G. (Eds.) Handbook of Cancer Models with Applications; Series in Mathematical Biology and Medicine; World Scientific: Singapore; Hackensack, NJ, USA, 2008; Volume 9. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).