A Model of Effector–Tumor Cell Interactions Under Chemotherapy: Bifurcation Analysis
Abstract
1. Introduction
2. The Mathematical Model
3. Analysis of Model Equilibria
4. Static Analysis
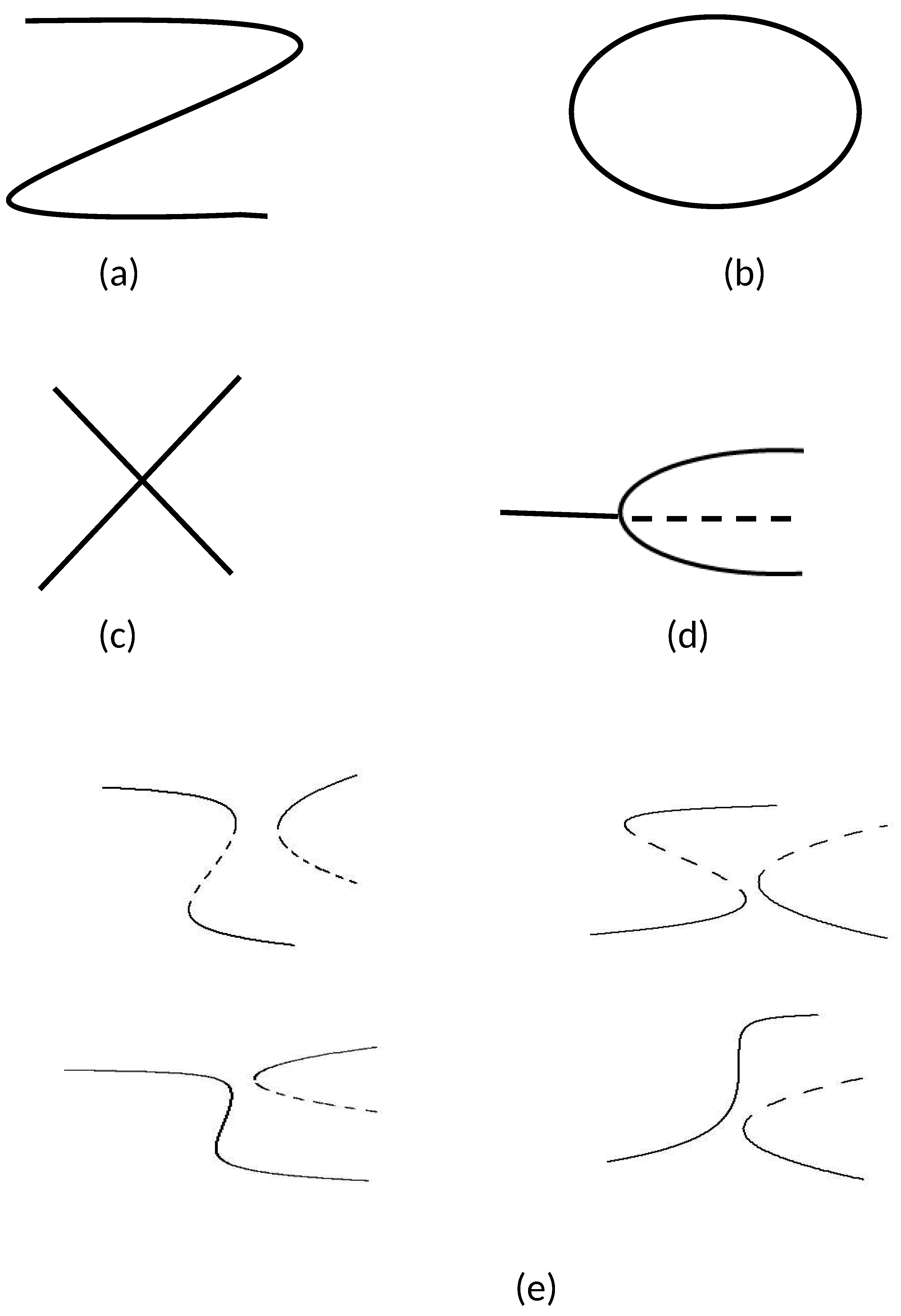
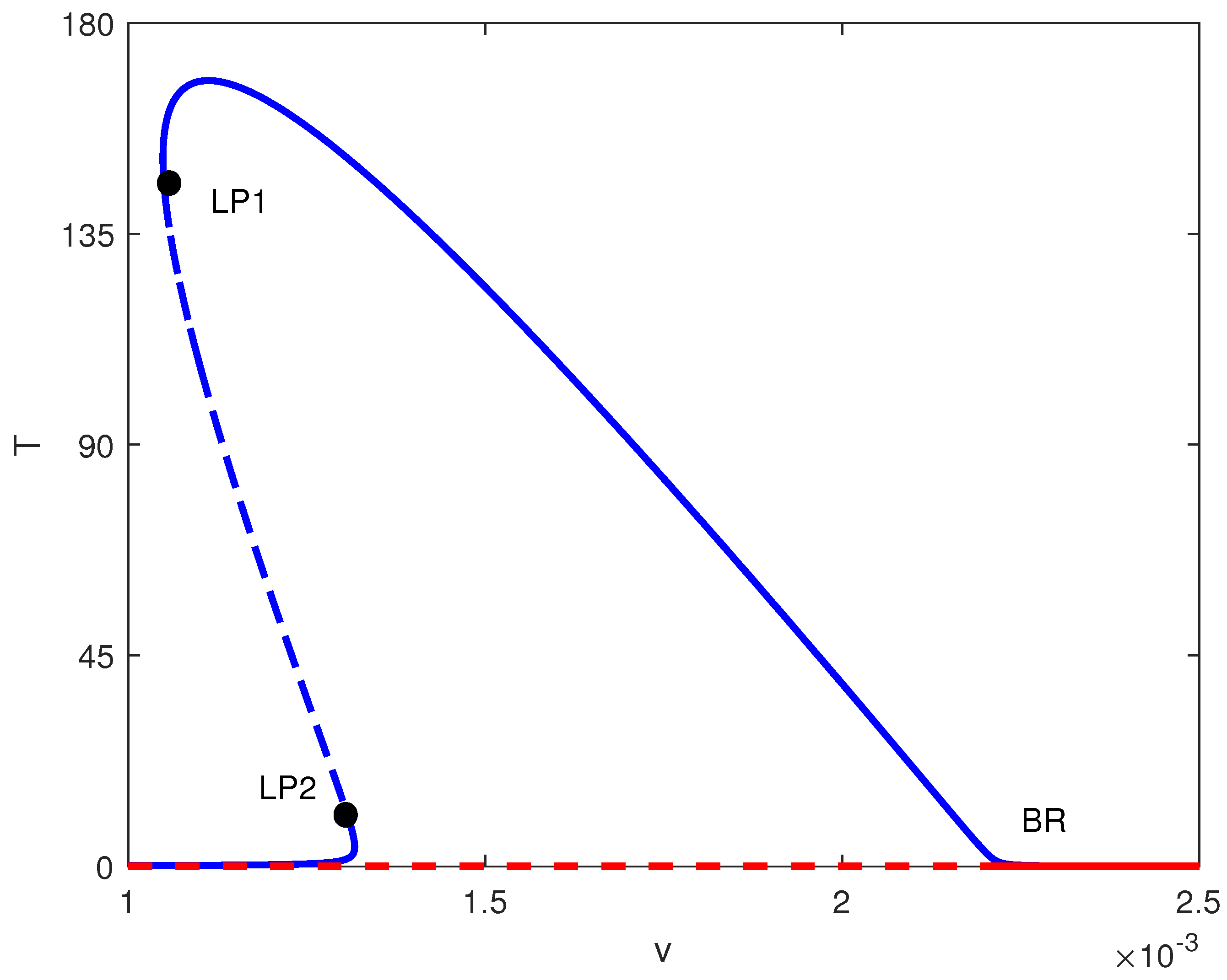
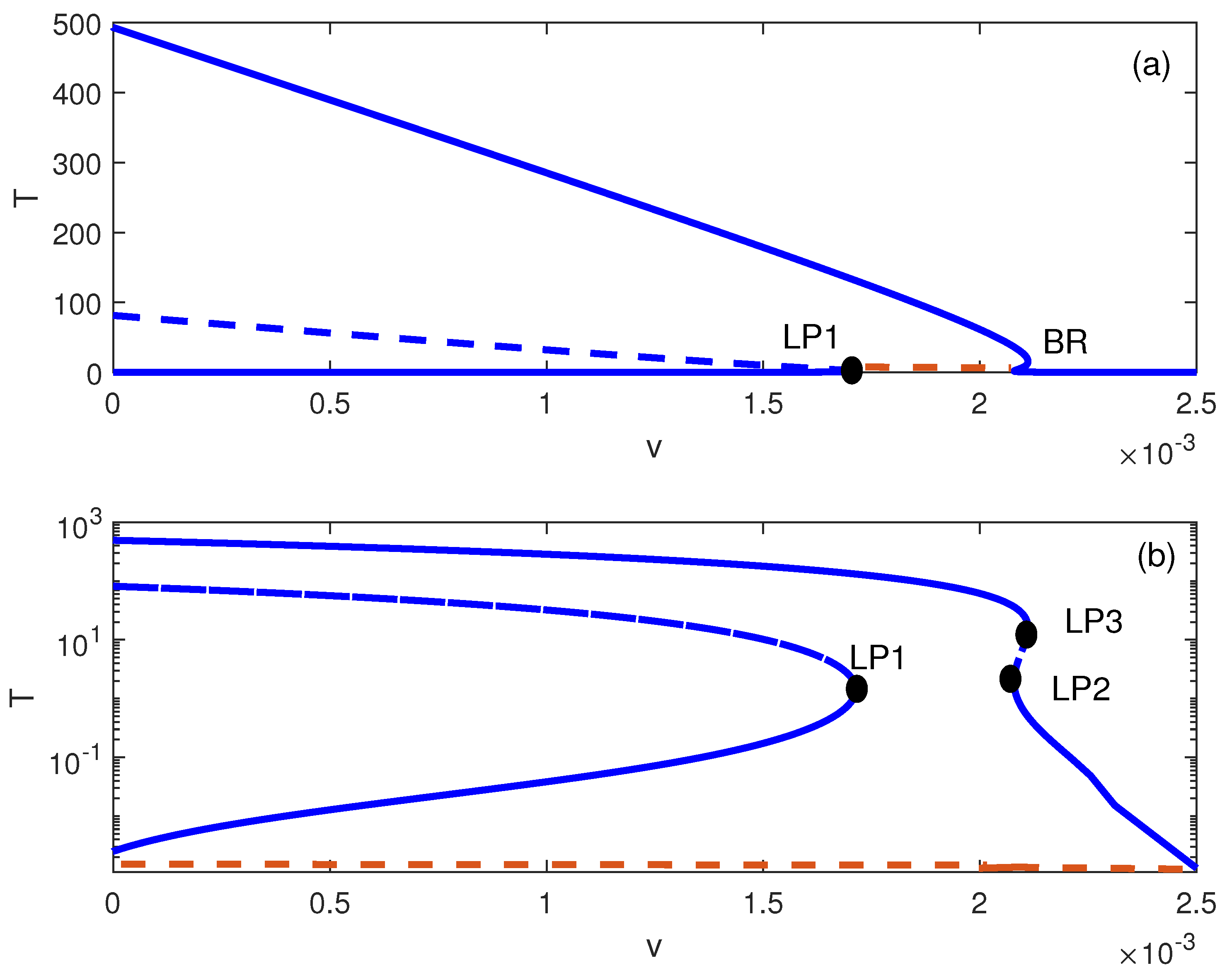
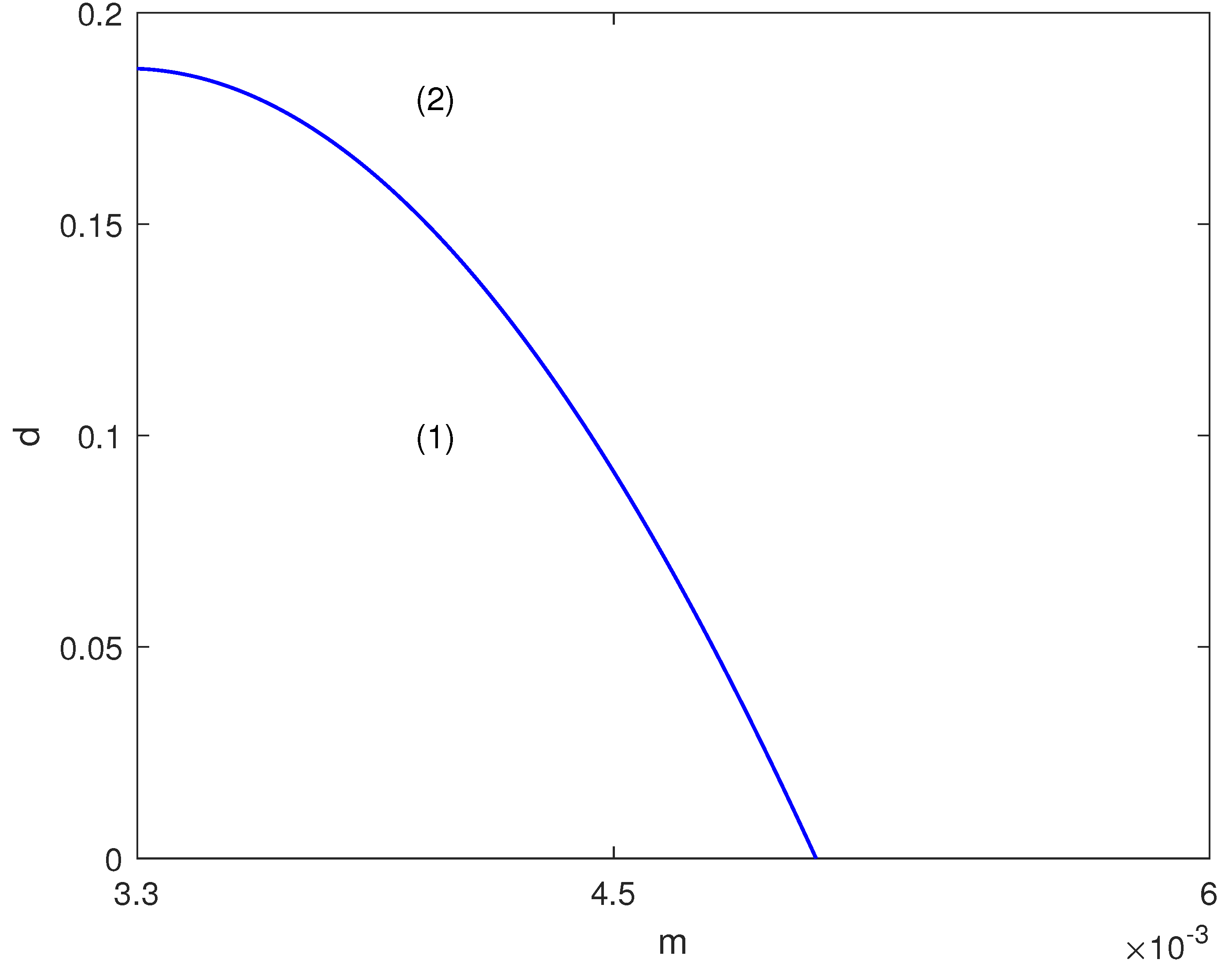
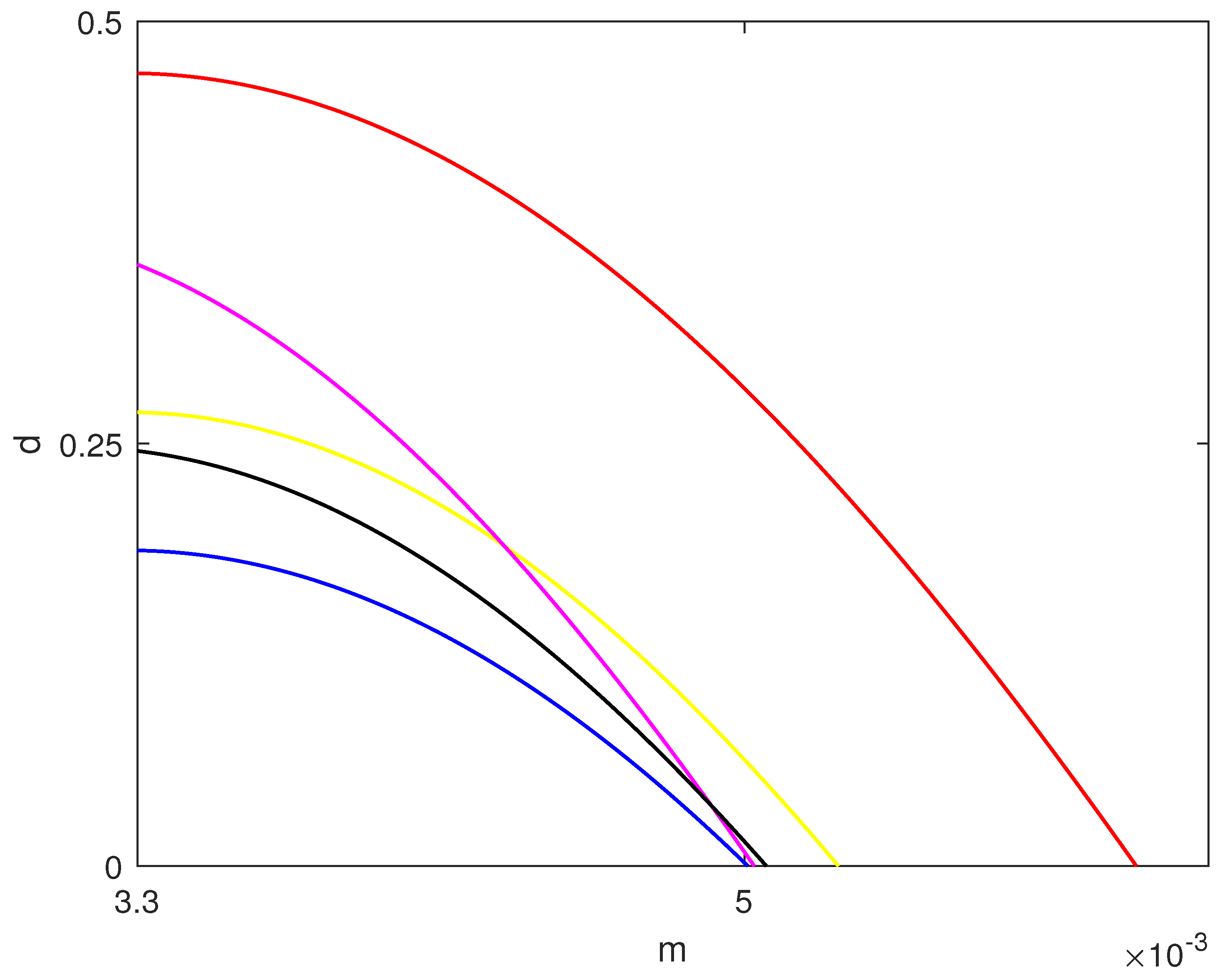
4.1. Hysteresis Singularity
4.2. Isola/Mushroom Singularity
4.3. Pitchfork Singularity
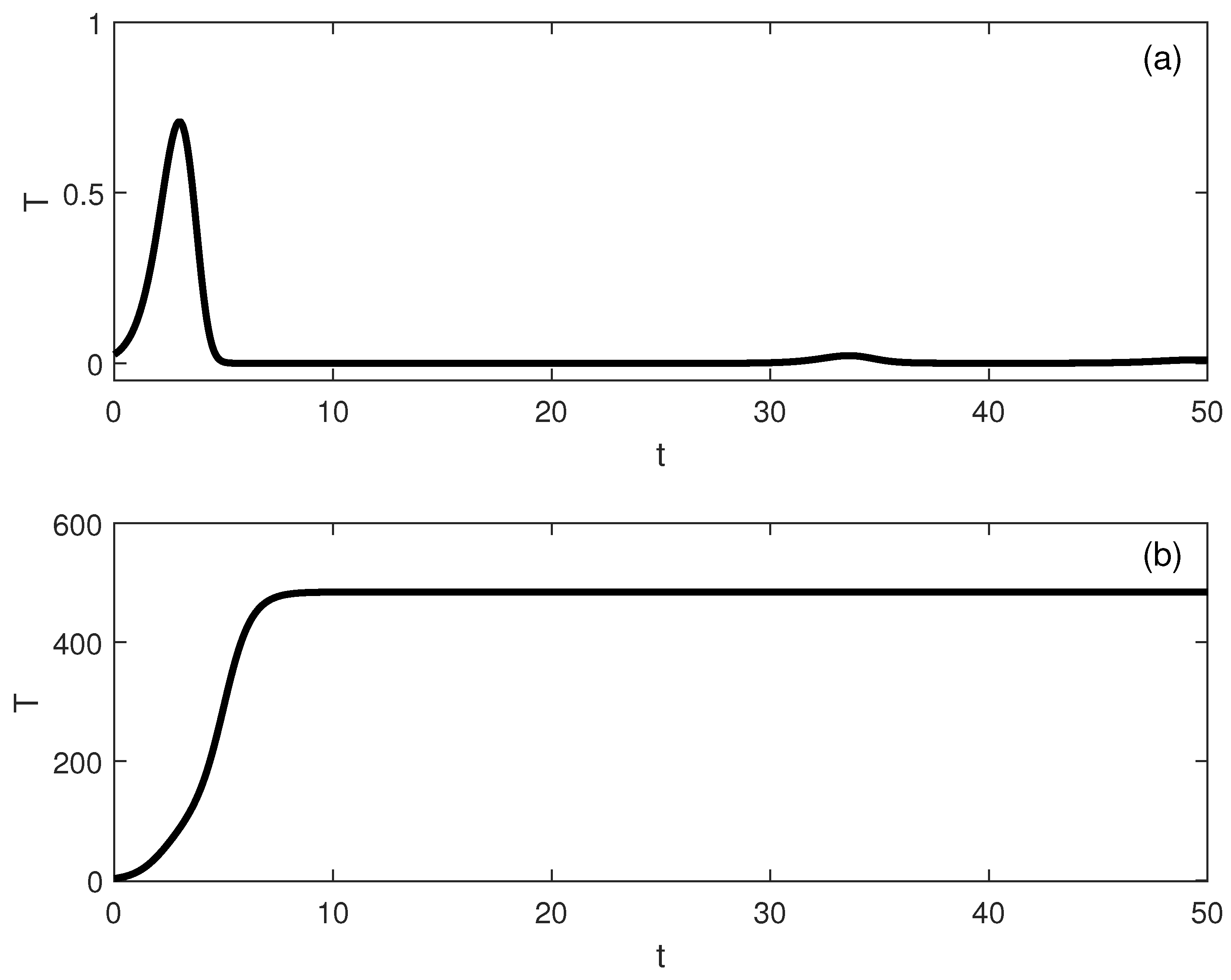
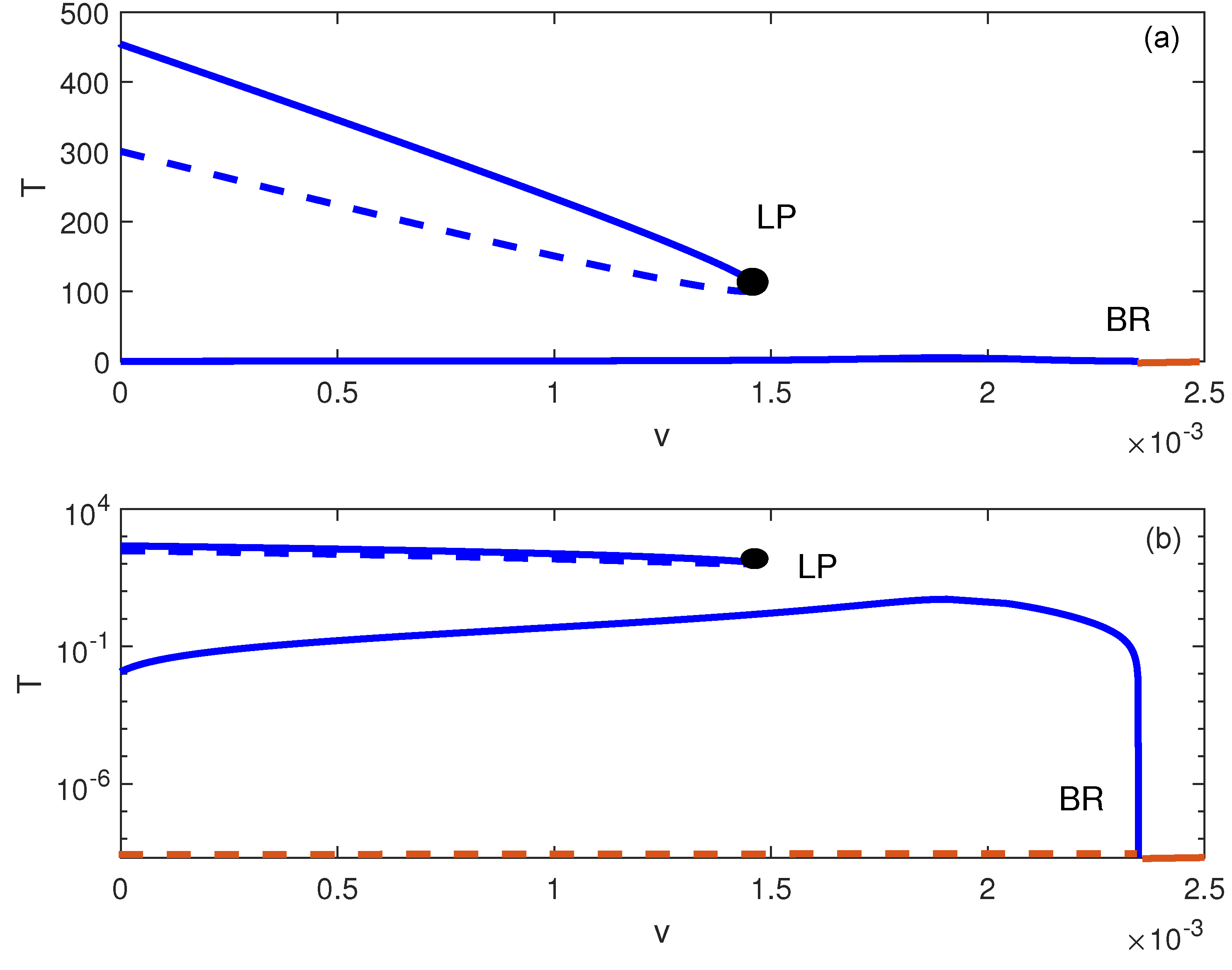
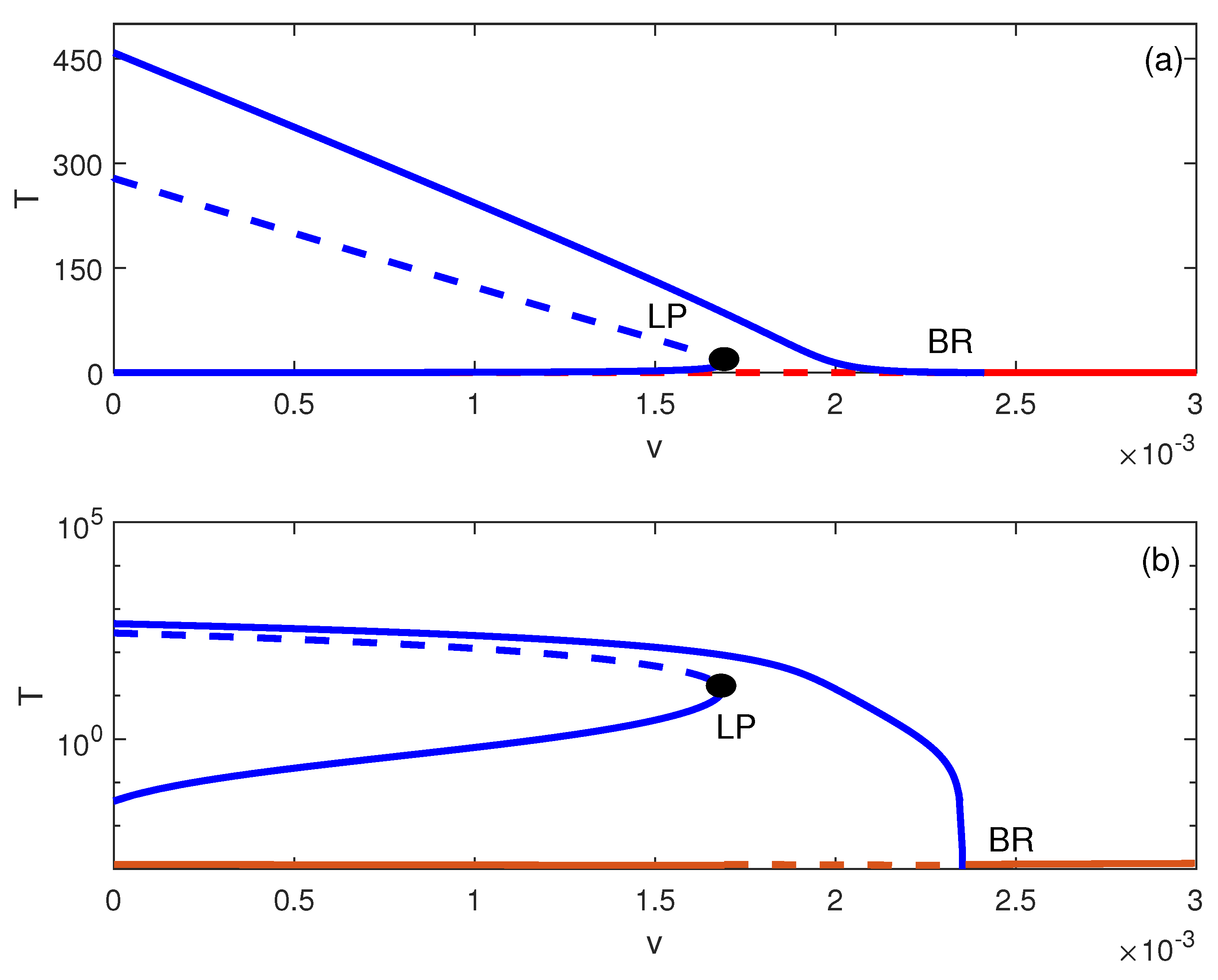
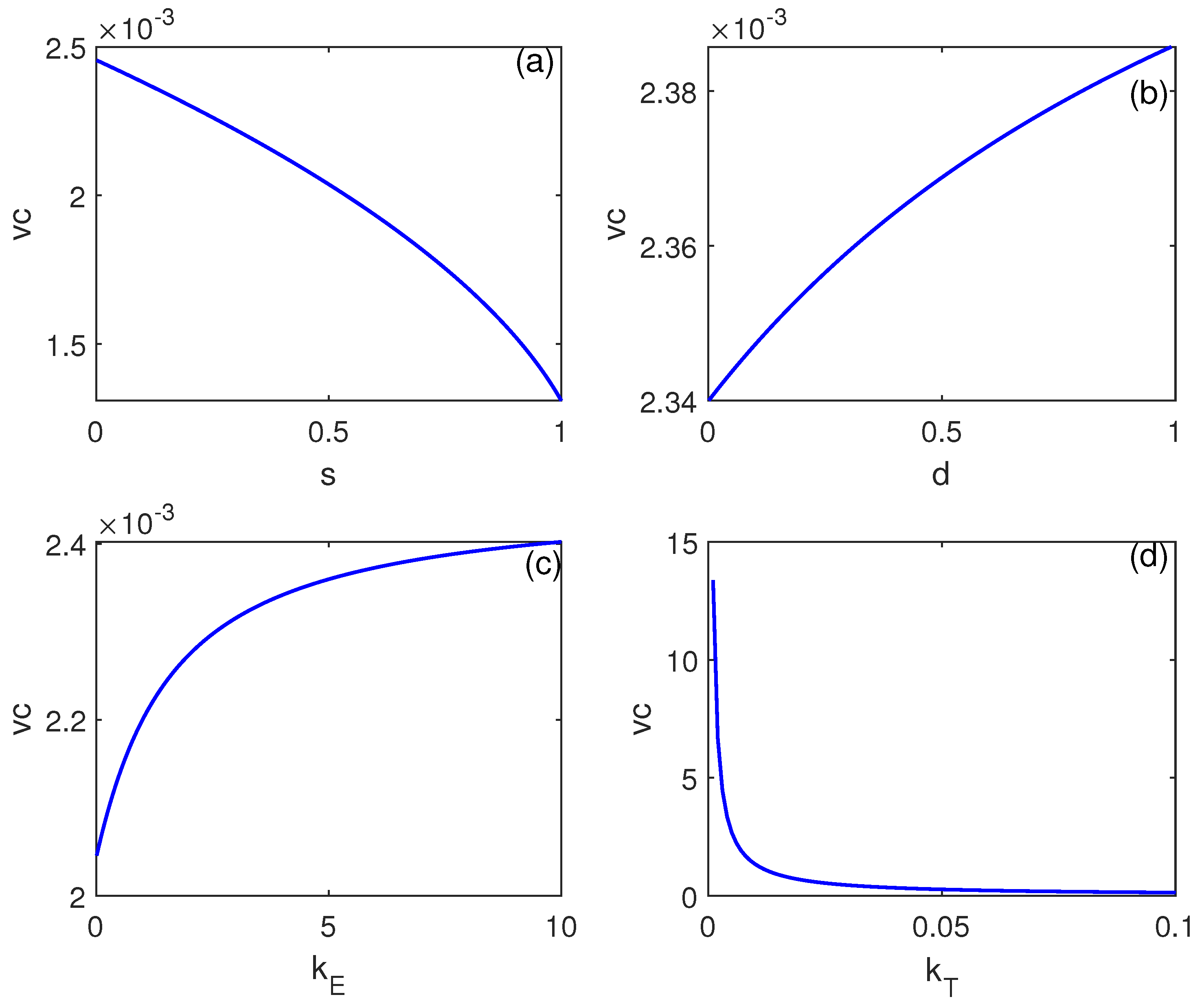
5. Dynamic Bifurcation
Numerical Simulations
6. Discussion
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Bray, F.; Laversanne, M.; Sung, H.; Ferlay, J.; Siegel, R.L.; Soerjomataram, I.; Jemal, A. Global cancer statistics 2022: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2024, 74, 229–263. [Google Scholar] [CrossRef] [PubMed]
- Rockne, R.C.; Scott, J.G. Introduction to Mathematical Oncology. JCO Clin. Cancer Inform. 2019, 3, 1–4. [Google Scholar]
- Araujo, R.P.; McElwain, D.L.S. A history of the study of solid tumour growth: The contribution of mathematical modelling. Bull. Math. Biol. 2004, 66, 1039–1091. [Google Scholar] [CrossRef] [PubMed]
- Enderling, H.; Wolkenhauer, O. Are all models wrong? Comput. Syst. Oncol. 2020, 1, e1008. [Google Scholar]
- Batmani, Y.; Khaloozadeh, H. Optimal drug regimens in cancer chemotherapy: A multi-objective approach. Comput. Biol. Med. 2013, 43, 2089–2095. [Google Scholar]
- Agur, Z.; Vuk-Pavlovic, S. Mathematical modeling in immunotherapy of cancer: Personalizing clinical trials. Mol. Ther. 2012, 20, 1–2. [Google Scholar][Green Version]
- Wang, Z.; Deisboeck, T.S. Mathematical modeling in cancer drug discovery. Drug Discov. Today 2014, 19, 145–150. [Google Scholar][Green Version]
- Yin, A.; Moes, D.J.; van Hasselt, J.G.; Swen, J.J.; Guchelaar, H.J. A review of mathematical models for tumor dynamics and treatment resistance evolution of solid tumors. CPT Pharmacometrics Syst. Pharmacol. 2019, 8, 720–737. [Google Scholar][Green Version]
- Kuznetsov, V.A.; Makalkin, I.A.; Taylor, M.A.; Perelson, A.S. Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar][Green Version]
- Robertson-Tessi, M.; El-Kareh, A.; Goriely, A. A mathematical model of tumor-immune interactions. J. Theor. Biol. 2012, 294, 56–73. [Google Scholar] [CrossRef]
- Kaur, G.; Ahmad, N. On study of immune response to tumor cells in prey-predator system. Int. Sch. Res. Not. 2014, 2014, 346597. [Google Scholar] [CrossRef]
- Benzekry, S.; Lamont, C.; Beheshti, A.; Tracz, A.; Ebos, J.M.; Hlatky, L.; Hahnfeldt, P. Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput. Biol. 2014, 10, e1003800. [Google Scholar] [CrossRef] [PubMed]
- Michor, F.; Beal, K. Improving cancer treatment via mathematical modeling: Surmounting the challenges is worth the effort. Cell 2015, 163, 1059–1063. [Google Scholar] [CrossRef] [PubMed]
- Murphy, H.; Jaafari, H.; Dobrovolny, H.M. Differences in predictions of ODE models of tumor growth: A cautionary example. BMC Cancer 2016, 16, 163. [Google Scholar] [CrossRef]
- Heesterman, B.L.; Bokhorst, J.M.; de Pont, L.M.; Verbist, B.M.; Bayley, J.P.; van der Mey, A.G.; Corssmit, E.P.; Hes, F.J.; van Benthem, P.P.; Jansen, J.C. Mathematical models for tumor growth and the reduction of overtreatment. J. Neurol. Surg. B Skull Base 2019, 80, 72–78. [Google Scholar] [CrossRef]
- Lestari, D.; Sari, E.R.; Arifah, H. Dynamics of a mathematical model of cancer cells with Chemotherapy. J. Phys. Conf. Ser. 2019, 1320, 012026. [Google Scholar] [CrossRef]
- Akhmetzhanov, A.R.; Kim, J.W.; Sullivan, R.; Beckman, R.A.; Tamayo, P.; Yeang, C.H. Modelling bistable tumour population dynamics to design effective treatment strategies. J. Theor. Biol. 2019, 474, 88–102. [Google Scholar] [CrossRef]
- Beckman, R.A.; Kareva, I.; Adler, F.R. How should cancer models be constructed? Cancer Control 2020, 27, 1073274820962008. [Google Scholar] [CrossRef]
- Kareva, I.; Luddy, K.A.; O’Farrelly, C.; Gatenby, R.A.; Brown, J.S. Predator-prey in tumor-immune interactions: A wrong model or just an incomplete one? Front. Immunol. 2021, 12, 668221. [Google Scholar] [CrossRef]
- Bashkirtseva, I.; Chukhareva, A.; Ryashko, L. Modeling and analysis of nonlineartumor-immune interaction under chemotherapy and radiotherapy. Math. Methods Appl. Sci. 2022, 45, 7983–7991. [Google Scholar] [CrossRef]
- Hamilton, P.T.; Anholt, B.R.; Nelson, B.H. Tumour immunotherapy: Lessons from predator-prey theory. Nat. Rev. Immunol. 2022, 22, 765–775. [Google Scholar] [CrossRef] [PubMed]
- Kareva, I.; Berezovskaya, F. Cancer immunoediting: A process driven by metabolic competition as a predator-prey-shared resource type model. J. Theor. Biol. 2015, 380, 463–472. [Google Scholar] [PubMed]
- Bazykin, A.D. Nonlinear Dynamics of Interacting Populations; World Scientific: Singapore, 1998. [Google Scholar]
- Golubovskaya, V.; Wu, L. Different Subsets of T Cells, Memory, Effector Functions, and CAR-T Immunotherapy. Cancers 2016, 8, 36. [Google Scholar] [CrossRef] [PubMed]
- De Pillis, L.G.; Radunskaya, A.E. Modeling tumor-immune dynamics, In Mathematical Models of Tumor-Immune System Dynamics; Eladdadi, A., Kim, P., Mallet, D., Eds.; Springer Proceedings in Mathematics & Statistics 107; Springer Science+Business Media: New York, NY, USA, 2014; pp. 59–108. [Google Scholar]
- López, A.G.; Seoane, J.M.; Sanjuán, M.A. A validated mathematical model of tumor growth including tumor-host interaction, cell-mediated immune response and chemotherapy. Bull. Math. Biol. 2014, 76, 2884–2906. [Google Scholar]
- Makhlouf, A.M.; El-Shennawy, L.; Elkaranshawy, H.A. Mathematical modelling for the role of CD4+T cells in tumor-immune interactions. Comput. Math. Methods Med. 2020, 2020, 7187602. [Google Scholar] [CrossRef]
- Song, G.; Tian, T.; Zhang, X. A mathematical model of cell-mediated immune response to tumor. Math. Biosci. Eng. 2020, 18, 373. [Google Scholar]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Springer: New York, NY, USA, 1990. [Google Scholar]
- Golubitsky, M.; Stewart, I.; Schaeffer, D.G. Singularities and Groups in Bifurcation Theory: Volume II; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Alhumaizi, K.; Aris, R. Surveying a Dynamical System: A Study of the Gray-Scott Reaction in a Two-Phase Reactor; Research Notes in Mathematics Series; Chapman & Hall/CRC: London, UK, 1995. [Google Scholar]
- Ajbar, A.; Alhumaizi, K. Dynamics of the Chemostat: A Bifurcation Theory Approach; Chapman and Hall/CRC: London, UK, 2011. [Google Scholar]
- Smith, L.M.; Motta, F.C.; Chopra, G.; Moch, J.K.; Nerem, R.R.; Cummins, B.; Roche, K.E.; Kelliher, C.M.; Leman, A.R.; Harer, J.; et al. An intrinsic oscillator drives the blood stage cycle of the malaria parasite Plasmodium falciparum. Science 2020, 368, 754. [Google Scholar]
- Greer, M.; Saha, R.; Gogliettino, A.; Yu, C.; Zollo-Venecek, K. Emergence of oscillations in a simple epidemic model with demographic data. R. Soc. Open Sci. 2020, 7, 191187. [Google Scholar]
- Dorraki, M.; Fouladzadeh, A.; Salamon, S.J.; Allison, A.; Coventry, B.J.; Abbott, D. On detection of periodicity in C-reactive protein (CRP) levels. Sci. Rep. 2018, 8, 11979. [Google Scholar] [CrossRef]
- Mazard, T.; Ychou, M.; Thezenas, S.; Poujol, S.; Pinguet, F.; Thirion, A.; Bleuse, J.P.; Portales, F.; Samalin, E.; Assenat, E. Feasibility of biweekly combination chemotherapy with capecitabine, irinotecan, and oxaliplatin in patients with metastatic solid tumors: Results of a two-step phase I trial: XELIRI and XELIRINOX. Cancer Chemother. Pharmacol. 2012, 69, 807–814. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqahtani, R.T. A Model of Effector–Tumor Cell Interactions Under Chemotherapy: Bifurcation Analysis. Mathematics 2025, 13, 1032. https://doi.org/10.3390/math13071032
Alqahtani RT. A Model of Effector–Tumor Cell Interactions Under Chemotherapy: Bifurcation Analysis. Mathematics. 2025; 13(7):1032. https://doi.org/10.3390/math13071032
Chicago/Turabian StyleAlqahtani, Rubayyi T. 2025. "A Model of Effector–Tumor Cell Interactions Under Chemotherapy: Bifurcation Analysis" Mathematics 13, no. 7: 1032. https://doi.org/10.3390/math13071032
APA StyleAlqahtani, R. T. (2025). A Model of Effector–Tumor Cell Interactions Under Chemotherapy: Bifurcation Analysis. Mathematics, 13(7), 1032. https://doi.org/10.3390/math13071032







