Research on Internal Response in Three-Dimensional Elastodynamic Time Domain Boundary Element Method
Abstract
1. Introduction
2. Internal Point Boundary Integral Equation
3. Numerical Processing
3.1. Numerical Discretization
3.2. Solutions for Influence Coefficient
3.3. Assemble
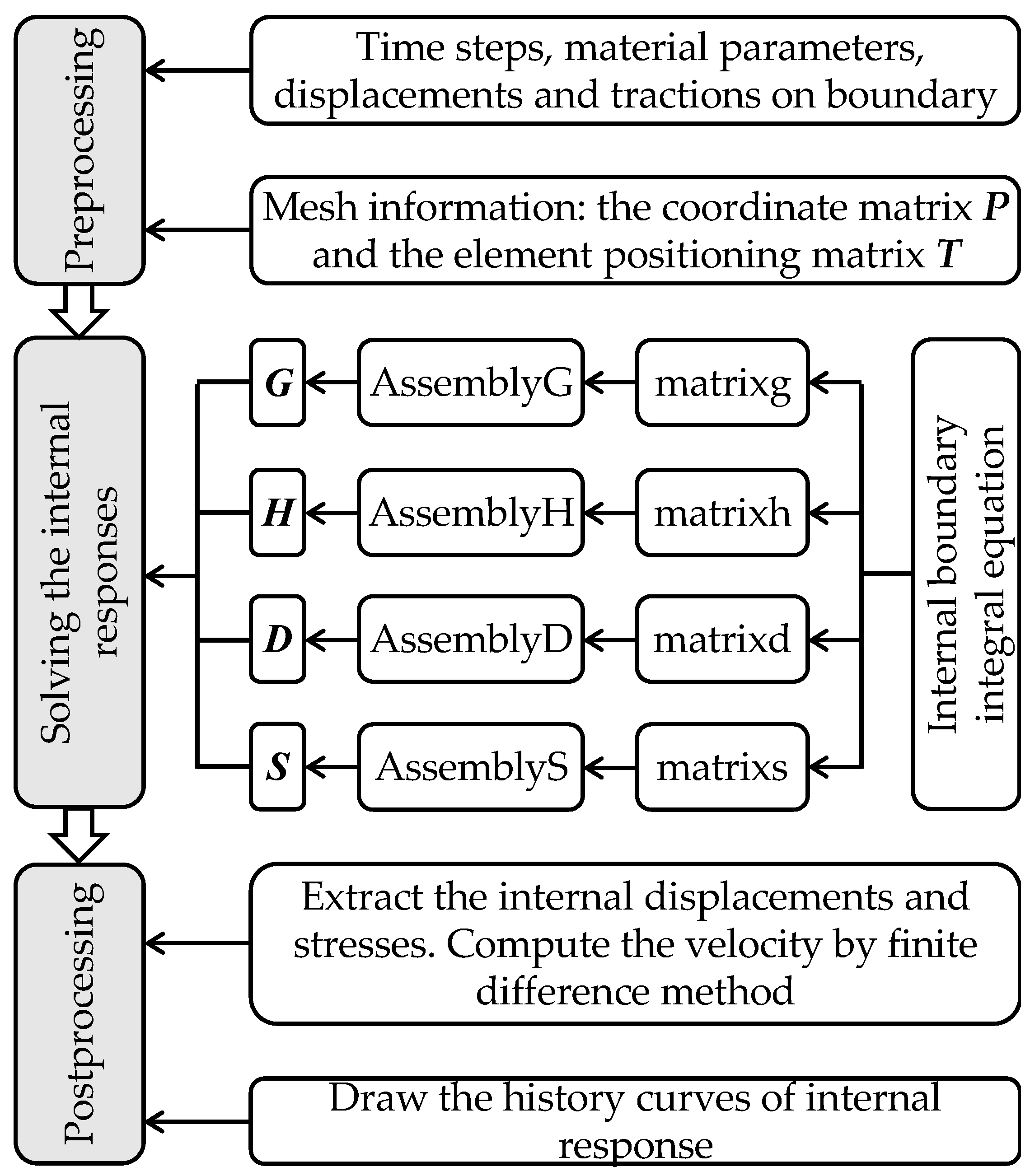
3.4. Programmatic Implementation
4. Calculation of Internal Velocities Using Finite Difference Methods
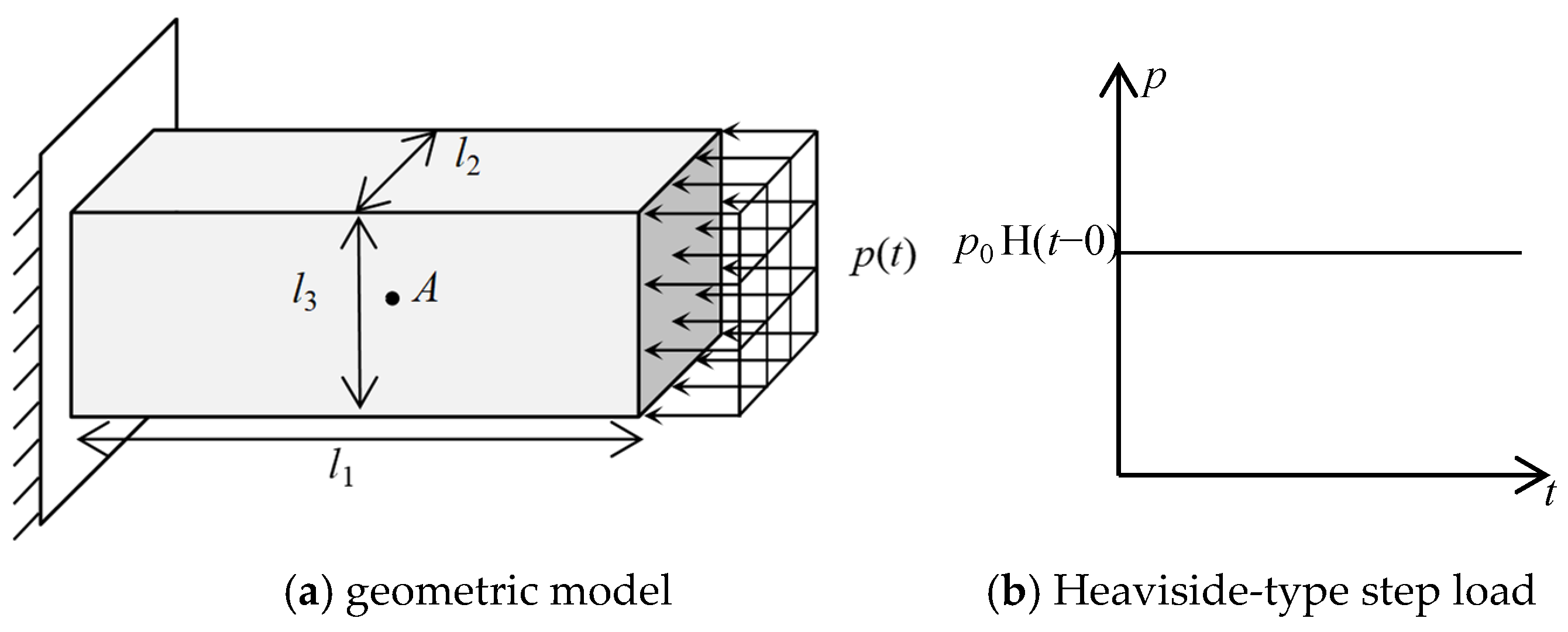
5. Example Verification Analysis
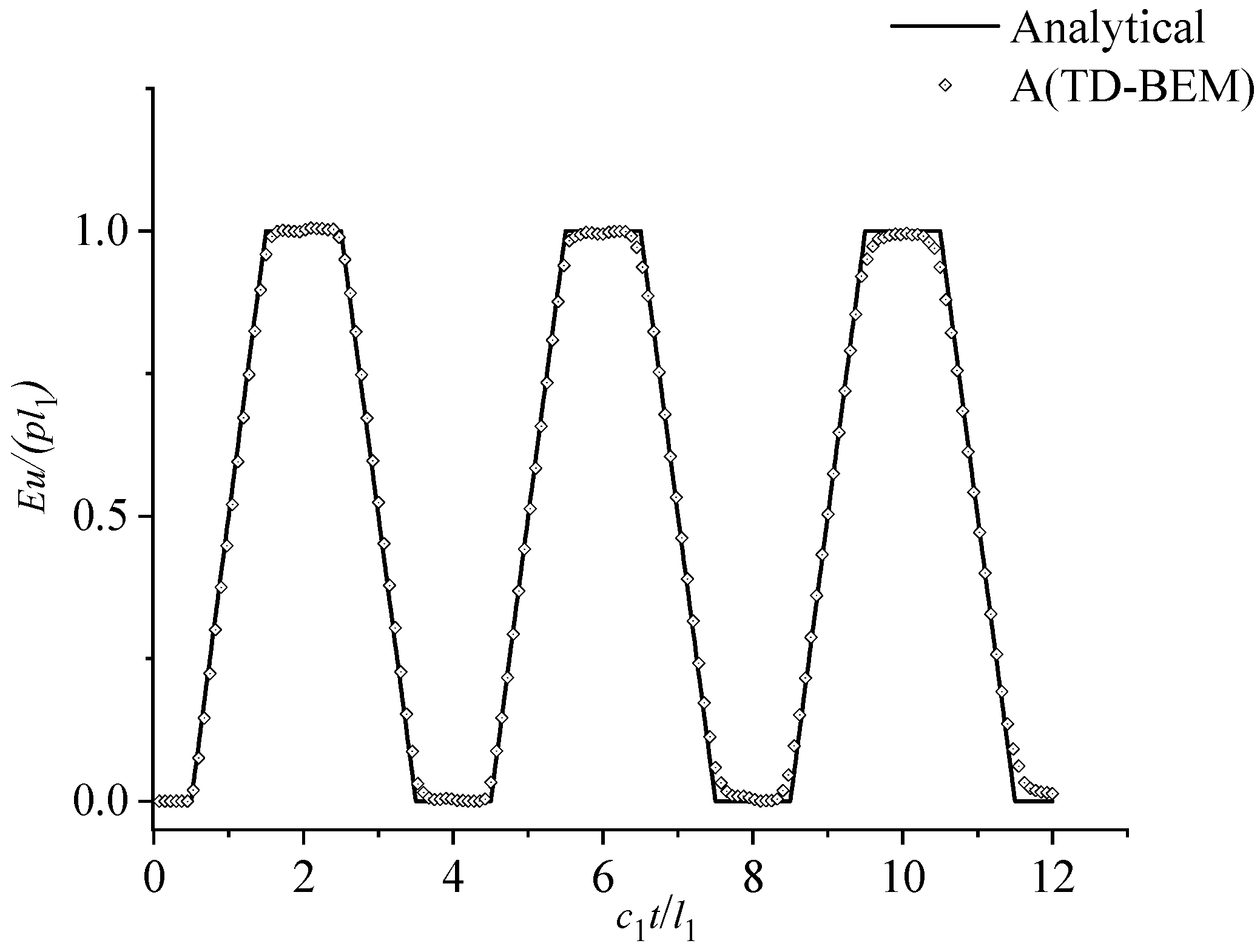
5.1. One-Dimensional Rod Example Validation Analysis
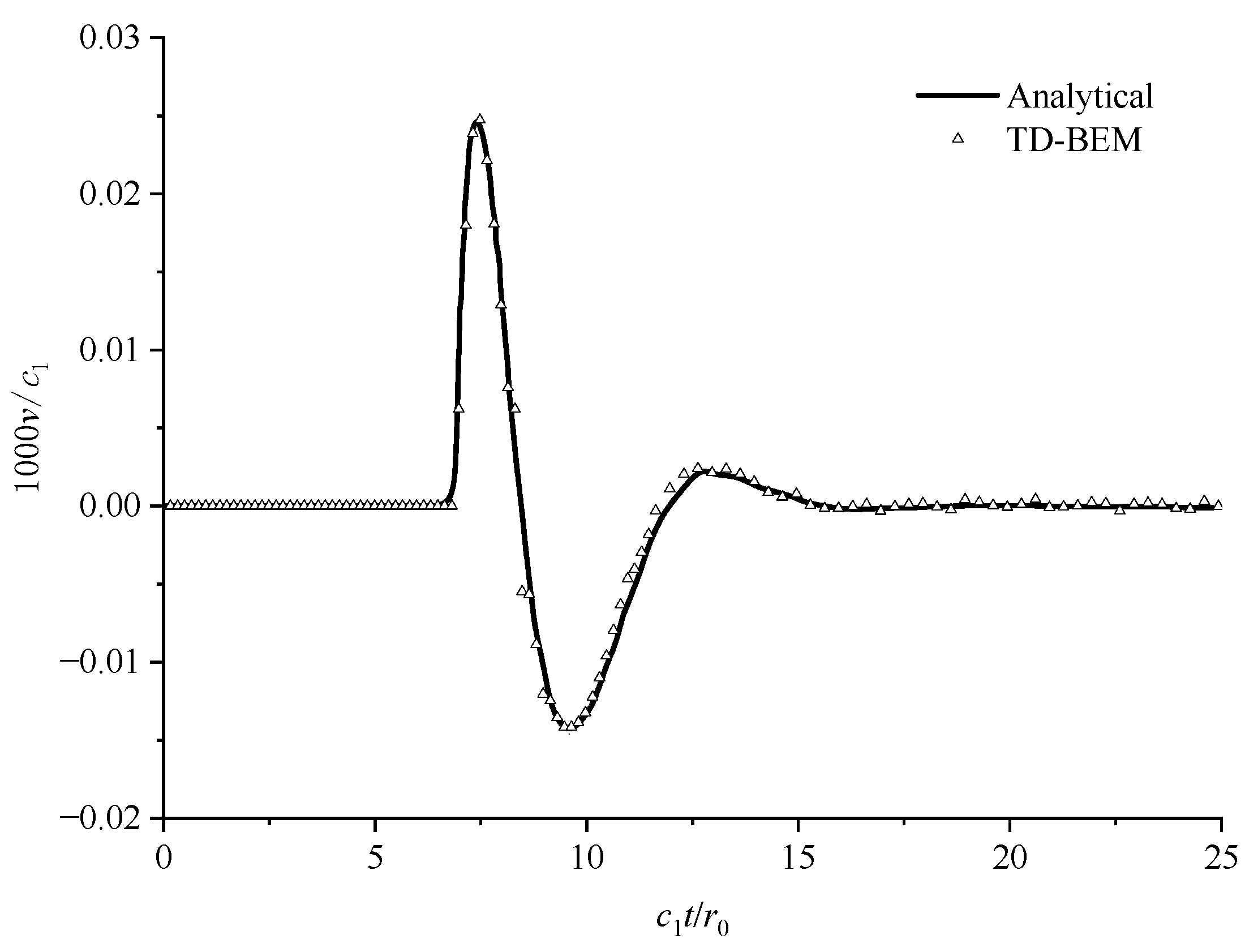
5.2. Infinite Domain with a Cavity Example Validation Analysis
6. Conclusions
- The displacement influence coefficient kernel function and the surface traction influence coefficient kernel function are derived, leading to the formulation of the internal stress boundary integral equation.
- The singular integrals that arise, particularly those associated with the time domain wavefront singularity, are solved analytically. The values of the functions that cause the wavefront singularity are determined, focusing on solving the time integral of the second derivative of the newly introduced Dirac function.
- The computational results show good agreement with the theoretical solution. From deriving the fundamental solution and establishing the equations to the subsequent analytical integration, all formulas and integral equations are mathematically rigorous and without any introduced errors, demonstrating that the TD-BEM is valid for solving internal stress problems.
- This paper provides further theoretical refinement of the TD-BEM for three-dimensional elastodynamics but has not yet delved into studying three-dimensional elastoplastic dynamics. Within the existing framework of the elastodynamics TD-BEM, the incorporation of an integral plastic term involving plastic strain, along with constitutive relations, enables the solution of elastoplastic problems. The further development of elastoplastic dynamic theory will be a key focus of our team’s future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Karabalis, D.L.; Beskos, D.E. Dynamic response of 3-D rigid surface foundations by time domain boundary element method. Earthq. Eng. Struct. Dyn. 1984, 12, 73–93. [Google Scholar]
- Beskos, D.E. Boundary element methods in dynamic analysis. Appl. Mech. Rev. 1997, 50, 149–197. [Google Scholar]
- Ahmad, S.; Banerjee, P.K. Time-domain transient elastodynamic analysis of 3-D problems by BEM. Int. J. Numer. Methods Eng. 1988, 26, 1709–1728. [Google Scholar] [CrossRef]
- Green, G.; Wheelhouse, T.; Lindsay, R. An essay on the application of mathematical analysis to the theories of electricity and magnetism. Phys. Today 1959, 12, 48. [Google Scholar]
- Kupradze, V.D.; Aleksidze, M.A. The method of functional equations for the approximate solution of certain boundary value problems. USSR Comput. Math. Math. Phys. 1964, 4, 82–126. [Google Scholar] [CrossRef]
- Jaswon, M.A. Integral equation methods in potential theory. Proc. R. Soc. Lond. A 1963, 275, 23–32. [Google Scholar]
- Brebbia, C.A. The Boundary Element Method for Engineers; Pentech Press: London, UK, 1978. [Google Scholar]
- Mansur, W.J.; Brebbia, C.A. Formulation of the boundary element method for transient problems governed by the scalar wave equation. Appl. Math. Model. 1982, 6, 307–311. [Google Scholar]
- Banerjee, P.K.; Ahmad, S.; Manolis, G.D. Transient elastodynamic analysis of three-dimensional problems by boundary element method. Earthq. Eng. Struct. Dyn. 1986, 14, 933–949. [Google Scholar]
- Marrero, M.; Dominguez, J. Numerical behaviour of time domain BEM for three-dimensional transient elastodynamic problems. Eng. Anal. Bound. Elem. 2003, 27, 39–48. [Google Scholar]
- Manolis, G.D.; Beskos, D.E. Boundary Element Methods in Elastodynamics; Unwin Hyman: London, UK, 1988. [Google Scholar]
- Coda, H.B.; Venturini, W.S. Three-dimensional transient BEM analysis. Comput. Struct. 1995, 56, 751–768. [Google Scholar]
- Hildenbrand, J.; Kuhn, G. Numerical computation of hypersingular integrals and application to the boundary integral equation for the stress tensor. Eng. Anal. Bound. Elem. 1992, 10, 209–217. [Google Scholar]
- Pan, E.; Yuan, F.G. Boundary element analysis of three-dimensional cracks in anisotropic solids. Int. J. Numer. Methods Eng. 2000, 48, 211–237. [Google Scholar]
- Panagiotopoulos, C.G.; Manolis, G.D. Three-dimensional BEM for transient elastodynamics based on the velocity reciprocal theorem. Eng. Anal. Bound. Elem. 2010, 35, 507–516. [Google Scholar]
- Qin, X.; Fan, Y.; Li, H.; Lei, W. A Direct Method for Solving Singular Integrals in Three-Dimensional Time-Domain Boundary Element Method for Elastodynamics. Mathematics 2022, 10, 286. [Google Scholar] [CrossRef]
- Lei, W.; Qin, X.; Li, H.; Fan, Y. Causality condition relevant functions-orientated analytical treatment on singularities in 3D TD-BEM. Appl. Math. Comput. 2022, 427, 127113. [Google Scholar]
- Pak, R.Y.S.; Guzina, B.B. Seismic soil-structure interaction analysis by direct boundary element methods—ScienceDirect. Int. J. Solids Struct. 1999, 36, 4743–4766. [Google Scholar]
- Pak, R.Y.S.; Bai, X.Y. A regularized boundary element formulation with weighted-collocation and higher-order projection for 3D time-domain elastodynamics. Eng. Anal. Bound. Elem. 2018, 93, 135–142. [Google Scholar]
- Pak, R.Y.S.; Bai, X.Y. On the stability of direct time-domain boundary element methods for elastodynamics. Eng. Anal. Bound. Elem. 2018, 96, 138–149. [Google Scholar]
- Israil, A.; Banerjee, P.K. Interior stress calculations in 2-d time-domain transient bem analysis. Int. J. Solids Struct. 1991, 27, 915–927. [Google Scholar]
- Carrer, J.A.M.; Mansur, W.J. Stress and Velocity in 2D Transient Elastodynamic Analysis by the Boundary Element Method. Eng. Anal. Bound. Elem. 1999, 23, 233–245. [Google Scholar]
- Schanz, M.; Antes, H. A new visco- and elastodynamic time domain boundary element formulation. Comput. Mech. 1997, 20, 452–459. [Google Scholar] [CrossRef]
- Antes, H.; Steinfeld, B.; Tröndle, G. Recent developments in dynamic stress analyses by time domain BEM. Eng. Anal. Bound. Elem. 1991, 8, 176–184. [Google Scholar] [CrossRef]
- Coda, H.B.; Venturini, W.S. Dynamic non-linear stress analysis by the mass matrix BEM. Eng. Anal. Bound. Elem. 2000, 24, 623–632. [Google Scholar] [CrossRef]
- Stokes, G.G. On the dynamical theory of diffraction. Trans. Camb. Philos. Soc. 1849, 9, 1–62. [Google Scholar]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity, 4th ed.; Dover: New York, NY, USA, 1944. [Google Scholar]
- De Hoop, A.T. Representation Theorems for the Displacement in an Elastic Solid and Their Application to Elastodynamic Diffraction Theory. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1958. [Google Scholar]
- Payton, R.G. An application of the dynamic Betti-Rayleigh reciprocal theorem to moving point loads in elastic media. Q. Appl. Math. 1964, 21, 299–313. [Google Scholar] [CrossRef]
- Aliabadi, M.H. The Boundary Element Method; Wiley: New York, NY, USA, 2002; Volume 2: Applications in Solids and Structures. [Google Scholar]

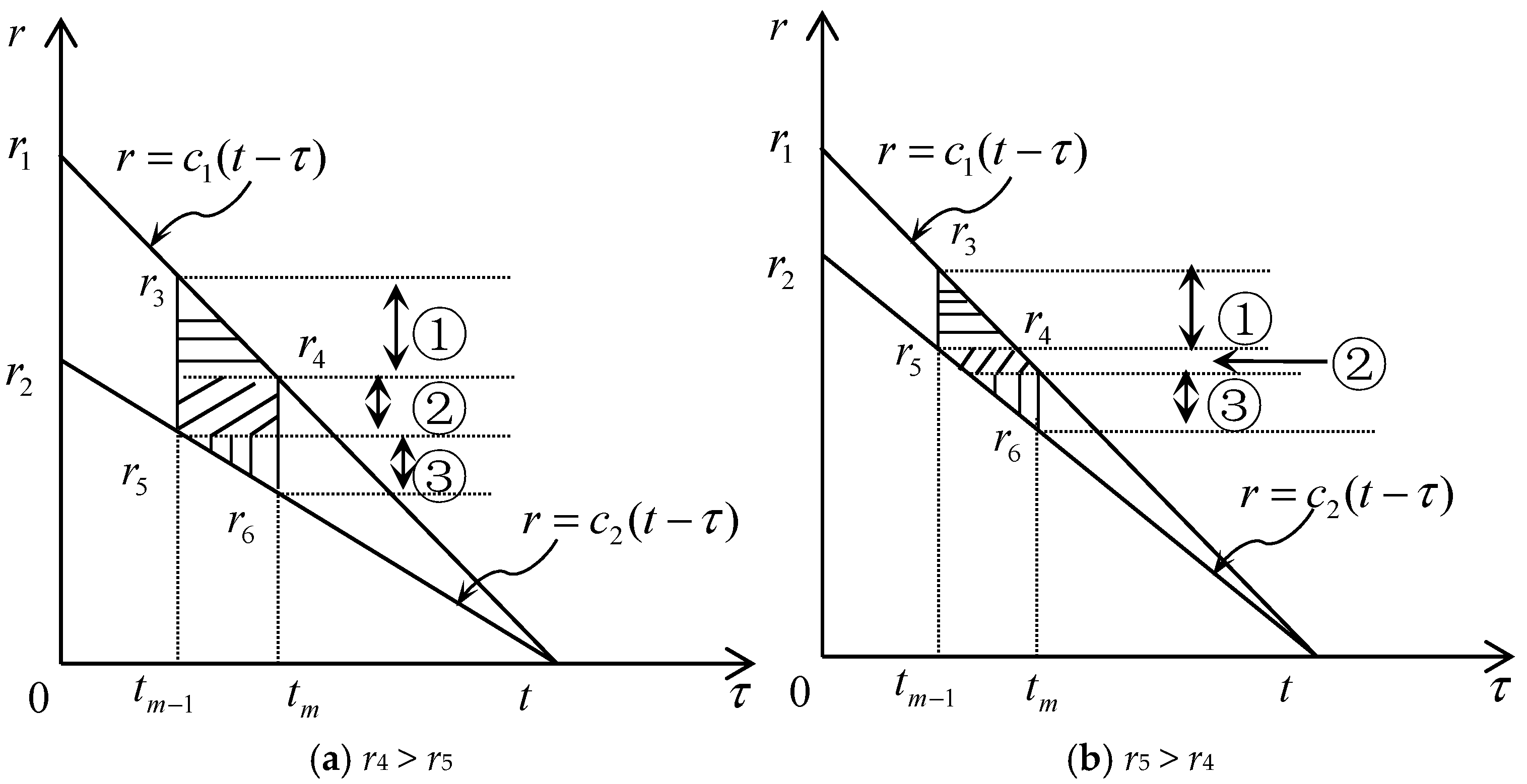



| 0 | 0 | |||
| 0 | 0 | |||
| 0 | 0 | |||
| 0 | 0 | |||
| 0 | 0 | |||
| 0 | 0 |
TD-BEM | Analytical | Error Percentage | TD-BEM | Analytical | Error Percentage | |
|---|---|---|---|---|---|---|
| (1) 1.0125 | 1.0682 | 1 | 6.82% | 0.5204 | 0.51 | 2.03% |
| (2) 2.0250 | 1.9527 | 2 | 2.36% | 1.0025 | 1 | 0.25% |
| (3) 2.9812 | 1.0235 | 1 | 2.35% | 0.5238 | 0.51 | 2.71% |
| (4) 5.0625 | 1.0487 | 1 | 4.87% | 0.6577 | 0.65 | 1.18% |
| (5) 6.0187 | 1.9350 | 2 | 3.25% | 0.9979 | 1 | 0.21% |
| (6) 6.975 | 1.0164 | 1 | 1.64% | 0.5329 | 0.52 | 2.48% |
| (7) 9.0562 | 1.0553 | 1 | 5.53% | 0.5745 | 0.56 | 2.58% |
| (8) 10.0125 | 1.9387 | 2 | 3.06% | 0.9959 | 1 | 0.41% |
| (9) 10.9687 | 1.0201 | 1 | 2.01% | 0.5419 | 0.53 | 2.24% |
| TD-BEM | Analytical | Error Percentage | TD-BEM | Error Percentage | |||
|---|---|---|---|---|---|---|---|
| (1) 7.6439 | 0.0121 | 0.0129 | 6.2% | (1) 7.1454 | 0.0179 | 0.0189 | 5.29% |
| (2) 8.4748 | 0.0232 | 0.0220 | 5.45% | (2) 7.4777 | 0.0247 | 0.0239 | 3.34% |
| (3) 9.6380 | 0.0112 | 0.0118 | 5.08% | (3) 7.9762 | 0.0128 | 0.0129 | 0.77% |
| (4) 5.0625 | −0.0057 | −0.0055 | 3.63% | (4) 9.638 | −0.0141 | −0.0145 | 1.02% |
| (5) 13.2938 | −0.0032 | −0.0030 | 6.89% | (5) 10.4688 | −0.0095 | −0.0102 | 6.86% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Li, H.; Qin, X.; Lei, W.; Liu, Y. Research on Internal Response in Three-Dimensional Elastodynamic Time Domain Boundary Element Method. Mathematics 2025, 13, 1025. https://doi.org/10.3390/math13071025
Li L, Li H, Qin X, Lei W, Liu Y. Research on Internal Response in Three-Dimensional Elastodynamic Time Domain Boundary Element Method. Mathematics. 2025; 13(7):1025. https://doi.org/10.3390/math13071025
Chicago/Turabian StyleLi, Lihui, Honjun Li, Xiaofei Qin, Weidong Lei, and Yan Liu. 2025. "Research on Internal Response in Three-Dimensional Elastodynamic Time Domain Boundary Element Method" Mathematics 13, no. 7: 1025. https://doi.org/10.3390/math13071025
APA StyleLi, L., Li, H., Qin, X., Lei, W., & Liu, Y. (2025). Research on Internal Response in Three-Dimensional Elastodynamic Time Domain Boundary Element Method. Mathematics, 13(7), 1025. https://doi.org/10.3390/math13071025






