Distributionally Robust Energy Optimization with Renewable Resource Uncertainty
Abstract
1. Introduction
- (1)
- A structural model for a microgrid that incorporates wind energy, energy storage, and demand response load is proposed, accounting for the uncertainty in the power generated by wind turbines. Energy storage is employed to enhance the grid’s capability to accommodate wind power.
- (2)
- We utilize the Wasserstein metric to construct the uncertainty set for wind power. Increasing the volume of historical data leads to a gradual convergence of the empirical distribution towards the true distribution. This convergence mitigates the conservatism of optimal decisions, thereby achieving more optimal operational costs while adhering to equipment constraints.
- (3)
- To address the optimization and scheduling challenges of the aforementioned microgrid, a two-stage RO approach is employed. This method offers increased flexibility compared to traditional single-stage RO.
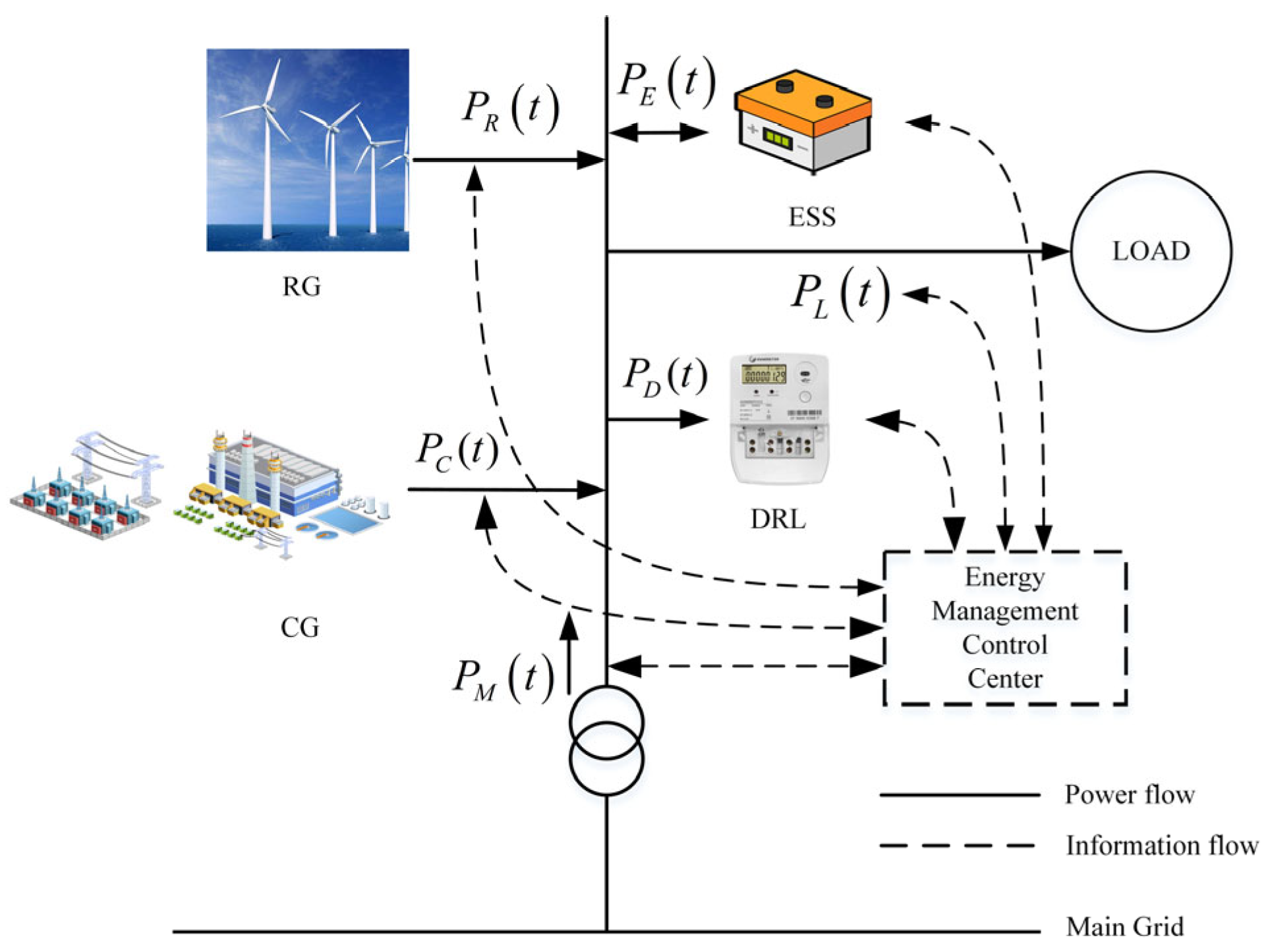
2. Microgrid Modeling
2.1. Electricity Transaction Cost
2.2. Demand Response Load
2.3. Conventional Generator
2.4. Energy Storage System
3. Uncertainty of RG
3.1. Wasserstein Metric
3.2. Uncertainty Sets
4. Energy Management Optimization
5. Experiment Validation and Discussion
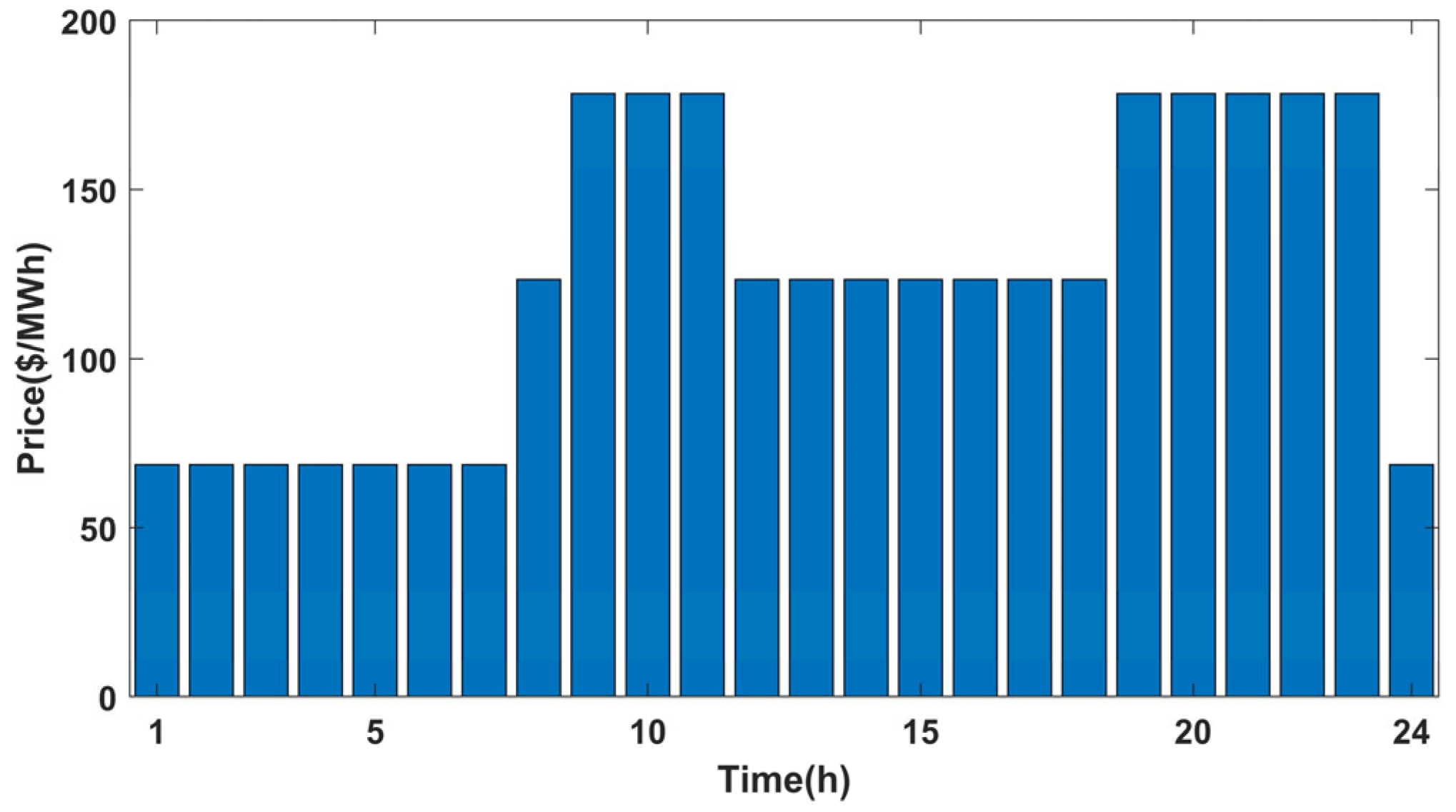
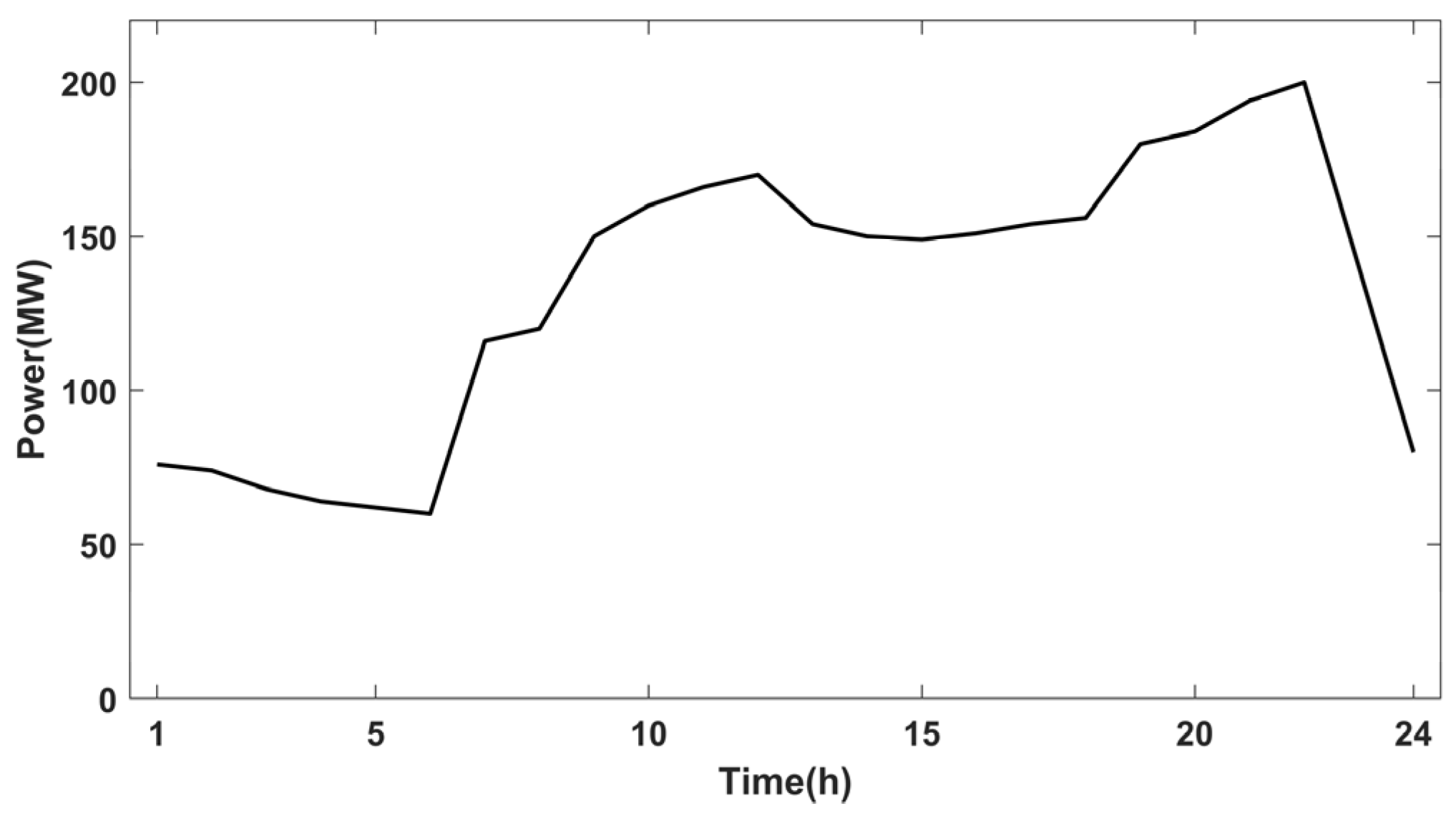
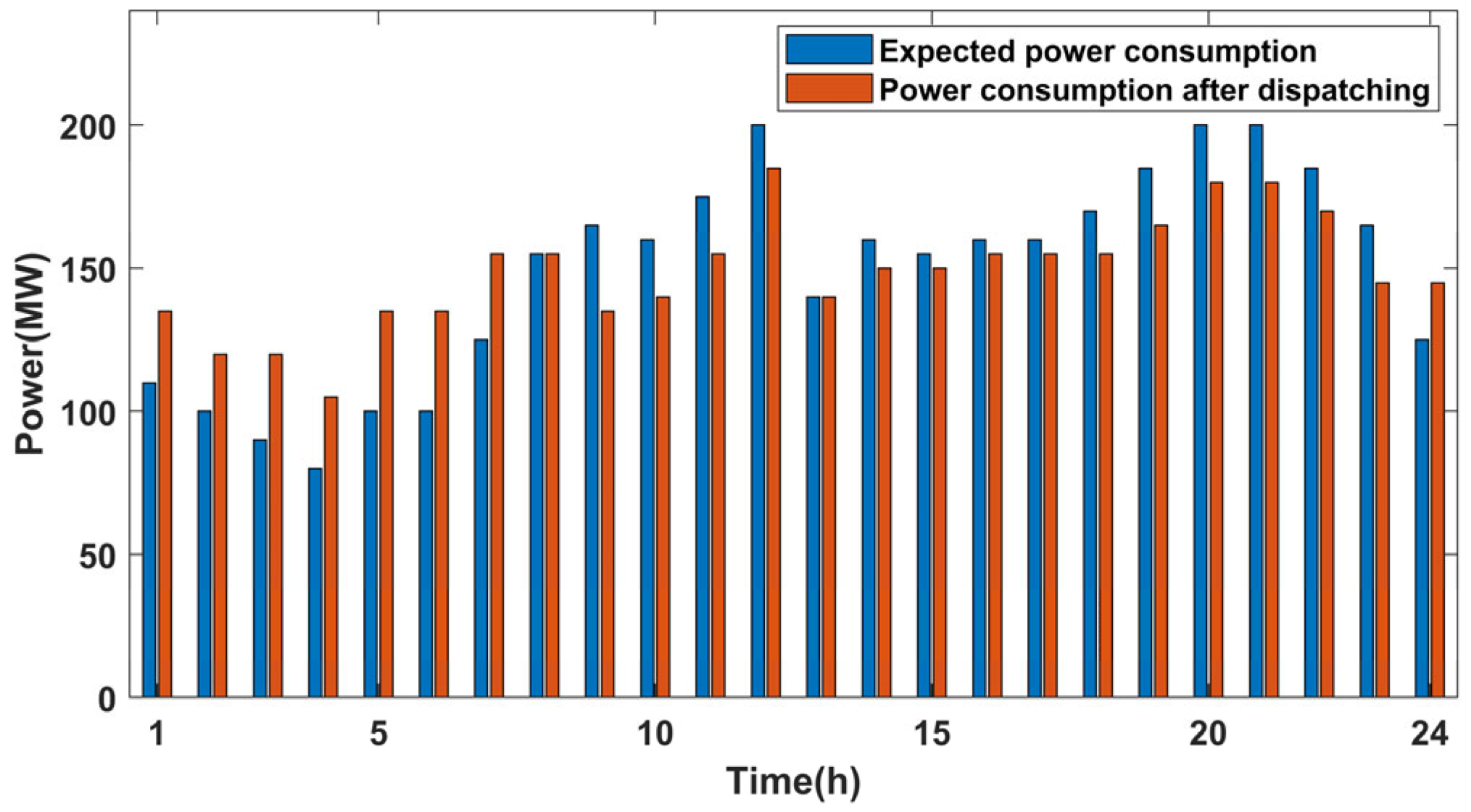
5.1. Economic Dispatch Scheme of Microgrid
5.2. Robustness Verification
5.3. Comparative Analysis with RO and SP
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zahedi, A. A Review of Drivers, Benefits, and Challenges in Integrating Renewable Energy Sources into Electricity Grid. Renew. Sustain. Energy Rev. 2011, 15, 4775–4779. [Google Scholar] [CrossRef]
- Lei, B.; Ren, Y.; Luan, H.; Dong, R.; Wang, X.; Liao, J.; Fang, S.; Gao, K. A Review of Optimization for System Reliability of Microgrid. Mathematics 2023, 11, 822. [Google Scholar] [CrossRef]
- Bertsimas, D.; Litvinov, E.; Sun, X.A.; Zhao, J.; Zheng, T. Adaptive Robust Optimization for the Security Constrained Unit Commitment Problem. IEEE Trans. Power Syst. 2013, 28, 52–63. [Google Scholar] [CrossRef]
- Ali, Z.M.; Diaaeldin, I.M.; H. E. Abdel Aleem, S.; El-Rafei, A.; Abdelaziz, A.Y.; Jurado, F. Scenario-Based Network Reconfiguration and Renewable Energy Resources Integration in Large-Scale Distribution Systems Considering Parameters Uncertainty. Mathematics 2021, 9, 26. [Google Scholar] [CrossRef]
- Fazlalipour, P.; Ehsan, M.; Mohammadi-Ivatloo, B. Risk-Aware Stochastic Bidding Strategy of Renewable Micro-Grids in Day-Ahead and Real-Time Markets. Energy 2019, 171, 689–700. [Google Scholar] [CrossRef]
- Gómez Sánchez, M.; Macia, Y.M.; Fernández Gil, A.; Castro, C.; Nuñez González, S.M.; Pedrera Yanes, J. A Mathematical Model for the Optimization of Renewable Energy Systems. Mathematics 2021, 9, 39. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Y.; Wang, J. A Chance-Constrained Two-Stage Stochastic Program for Unit Commitment With Uncertain Wind Power Output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar] [CrossRef]
- Ozturk, U.A.; Mazumdar, M.; Norman, B.A. A Solution to the Stochastic Unit Commitment Problem Using Chance Constrained Programming. IEEE Trans. Power Syst. 2004, 19, 1589–1598. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Q.; Wang, J.; Guan, Y. Expected Value and Chance Constrained Stochastic Unit Commitment Ensuring Wind Power Utilization. IEEE Trans. Power Syst. 2014, 29, 2696–2705. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khambadkone, A.M.; Khosravi, A. A Computational Framework for Uncertainty Integration in Stochastic Unit Commitment with Intermittent Renewable Energy Sources. Appl. Energy 2015, 152, 71–82. [Google Scholar] [CrossRef]
- Karami, M.; Shayanfar, H.A.; Aghaei, J.; Ahmadi, A. Scenario-Based Security-Constrained Hydrothermal Coordination with Volatile Wind Power Generation. Renew. Sustain. Energy Rev. 2013, 28, 726–737. [Google Scholar] [CrossRef]
- Zheng, Q.P.; Wang, J.; Liu, A.L. Stochastic Optimization for Unit Commitment—A Review. IEEE Trans. Power Syst. 2015, 30, 1913–1924. [Google Scholar] [CrossRef]
- Lorca, Á.; Sun, X.A. Adaptive Robust Optimization With Dynamic Uncertainty Sets for Multi-Period Economic Dispatch Under Significant Wind. IEEE Trans. Power Syst. 2015, 30, 1702–1713. [Google Scholar] [CrossRef]
- Dashtdar, M.; Flah, A.; Hosseinimoghadam, S.M.S.; Zangoui Fard, M.; Dashtdar, M. Optimization of Microgrid Operation Based on Two-Level Probabilistic Scheduling with Benders Decomposition. Electr. Eng. 2022, 104, 3225–3239. [Google Scholar] [CrossRef]
- Jabr, R.A.; Karaki, S.; Korbane, J.A. Robust Multi-Period OPF With Storage and Renewables. IEEE Trans. Power Syst. 2015, 30, 2790–2799. [Google Scholar] [CrossRef]
- Ju, C.; Ding, T.; Jia, W.; Mu, C.; Zhang, H.; Sun, Y. Two-Stage Robust Unit Commitment with the Cascade Hydropower Stations Retrofitted with Pump Stations. Appl. Energy 2023, 334, 120675. [Google Scholar] [CrossRef]
- Choi, J.; Shin, Y.; Choi, M.; Park, W.-K.; Lee, I.-W. Robust Control of a Microgrid Energy Storage System Using Various Approaches. IEEE Trans. Smart Grid 2019, 10, 2702–2712. [Google Scholar] [CrossRef]
- Shao, C.; Wang, X.; Shahidehpour, M.; Wang, X.; Wang, B. Security-Constrained Unit Commitment With Flexible Uncertainty Set for Variable Wind Power. IEEE Trans. Sustain. Energy 2017, 8, 1237–1246. [Google Scholar] [CrossRef]
- Wei, W.; Wang, J.; Mei, S. Dispatchability Maximization for Co-Optimized Energy and Reserve Dispatch With Explicit Reliability Guarantee. IEEE Trans. Power Syst. 2016, 31, 3276–3288. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, S.; Mathieu, J.L. Distributionally Robust Chance-Constrained Optimal Power Flow With Uncertain Renewables and Uncertain Reserves Provided by Loads. IEEE Trans. Power Syst. 2017, 32, 1378–1388. [Google Scholar] [CrossRef]
- Duan, C.; Jiang, L.; Fang, W.; Liu, J. Data-Driven Affinely Adjustable Distributionally Robust Unit Commitment. IEEE Trans. Power Syst. 2018, 33, 1385–1398. [Google Scholar] [CrossRef]
- Duan, C.; Jiang, L.; Fang, W.; Liu, J.; Liu, S. Data-Driven Distributionally Robust Energy-Reserve-Storage Dispatch. IEEE Trans. Ind. Inform. 2018, 14, 2826–2836. [Google Scholar] [CrossRef]
- Yixin, L.; Guo, L.; Wang, C. Economic Dispatch of Microgrid Based on Two Stage Robust Optimization. Proc. CSEE 2018, 38, 4013–4022. [Google Scholar]
- Duan, C. Distributionally Robust and Structure Exploiting Algorithms for Power System Optimization Problems. Ph.D. Thesis, The University of Liverpool, Liverpool, UK, 2018. [Google Scholar]
- Xiang, Y.; Liu, J.; Liu, Y. Robust Energy Management of Microgrid With Uncertain Renewable Generation and Load. IEEE Trans. Smart Grid 2016, 7, 1034–1043. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, Z.; Wang, Q.; Qi, W.; Ge, Y. Optimal Power Flow Method with Consideration of Uncertainty Sources of Renewable Energy and Demand Response. Front. Energy Res. 2024, 12, 1421277. [Google Scholar] [CrossRef]
- Hodge, B.-M.; Lew, D.; Milligan, M.; Gómez-Lázaro, E.; Larsén, X.G.; Giebel, G.; Holttinen, H.; Sillanpää, S.; Scharff, R.; Söder, L.; et al. Wind Power Forecasting Error Distributions: An International Comparison. In Proceedings of the 11th International Workshop on Large-Scale Integration of Wind Power into Power Systems 2012, Lisbon, Portugal, 13–15 November 2012. [Google Scholar]
- Peng, C.; Xie, P.; Pan, L.; Yu, R. Flexible Robust Optimization Dispatch for Hybrid Wind/Photovoltaic/Hydro/Thermal Power System. IEEE Trans. Smart Grid 2016, 7, 751–762. [Google Scholar] [CrossRef]

| Units | Parameters | Value |
|---|---|---|
| Grid interaction | 200 | |
| 200 | ||
| DR load | 40 | |
| 3565 | ||
| CG | 50 | |
| 5 | ||
| 0 | ||
| 90 | ||
| 500 | ||
| 40 | ||
| −40 | ||
| ESS | 600 | |
| 50 | ||
| 100 | ||
| 100 | ||
| 70 | ||
| , | 0.95 | |
| 50 |
| Sample Size | Wasserstein Ball Radius and Bounds | ||
|---|---|---|---|
| Upper Bound | Lower Bound | Radius | |
| 1000 | 72.67 | −60.13 | 1.15 |
| 2000 | 71.09 | −59.20 | 0.84 |
| 3000 | 58.86 | −46.03 | 0.60 |
| 4000 | 56.37 | −42.67 | 0.54 |
| 5000 | 50.50 | −37.36 | 0.51 |
| 6000 | 50.79 | −37.78 | 0.47 |
| 7000 | 51.96 | −28.88 | 0.46 |
| 8000 | 49.79 | −36.79 | 0.45 |
| 9000 | 49.77 | −36.69 | 0.45 |
| 10,000 | 49.36 | −36.23 | 0.44 |
| The Proposed DRO Model | ||||
|---|---|---|---|---|
| Sample Size | Average Costs | Standard Deviation | 95% Confidence Interval | Feasibility Probability |
| 1000 | 186,376 | 1914.82 | (184,932.13, 187,819.87) | 100 |
| 3000 | 174,895 | 2074.52 | (173,330.70, 176,459.30) | 99.62 |
| 5000 | 167,783 | 2202.05 | (166,234.54, 169,555.46) | 99.32 |
| 7000 | 166,354 | 2872.28 | (164,229.15, 168,560.85) | 99.14 |
| 10,000 | 163,527 | 3223.43 | (161,096.36, 165,957.64) | 99.01 |
| RO Model | |||
|---|---|---|---|
| Average Costs | Standard Deviation | 95% Confidence Interval | Feasibility Probability |
| 191,708 | 1851.14 | (190,312.14, 193,103.86) | 100 |
| SP Model | |||
|---|---|---|---|
| Average Costs | Standard Deviation | 95% Confidence Interval | Feasibility Probability |
| 160,337 | 4021.19 | (157,304.81, 163,369.19) | 97.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Cao, R.; Tang, D.; Wang, C.; Liu, X.; Hu, W. Distributionally Robust Energy Optimization with Renewable Resource Uncertainty. Mathematics 2025, 13, 992. https://doi.org/10.3390/math13060992
Wang Z, Cao R, Tang D, Wang C, Liu X, Hu W. Distributionally Robust Energy Optimization with Renewable Resource Uncertainty. Mathematics. 2025; 13(6):992. https://doi.org/10.3390/math13060992
Chicago/Turabian StyleWang, Zhangyi, Rui Cao, Dan Tang, Chunsheng Wang, Xiaoyu Liu, and Weiguang Hu. 2025. "Distributionally Robust Energy Optimization with Renewable Resource Uncertainty" Mathematics 13, no. 6: 992. https://doi.org/10.3390/math13060992
APA StyleWang, Z., Cao, R., Tang, D., Wang, C., Liu, X., & Hu, W. (2025). Distributionally Robust Energy Optimization with Renewable Resource Uncertainty. Mathematics, 13(6), 992. https://doi.org/10.3390/math13060992





