Generalized Cardinal Polishing Splines Signal Reconstruction
Abstract
1. Introduction
- Main Results
- 1.
- The elementary theory of GCP-splines signal processing is proposed. Z-transformation of expanded discrete GCP-splines and Fourier transformations of the continuous GCP-splines are proposed.
- 2.
- The GCP-splines signal reconstruction and filter based on the discrete convolution operation are proposed. The GCP-splines filters can output a reconstructed signal from the given discrete signal in spatial domain. The experimental results demonstrate lower approximation errors and enhanced performance compared to existing spline-based reconstruction techniques.
- 3.
- Differential signal reconstruction based on GCP-splines is proposed. The reconstructed differential signals based on the GCP-splines are proposed, and are complemented by convolution with appropriate finite-difference operators.
2. Preliminaries
2.1. B-splines
2.2. Polishing Spline
2.3. GCP-splines
3. GCP-splines Signal Processing
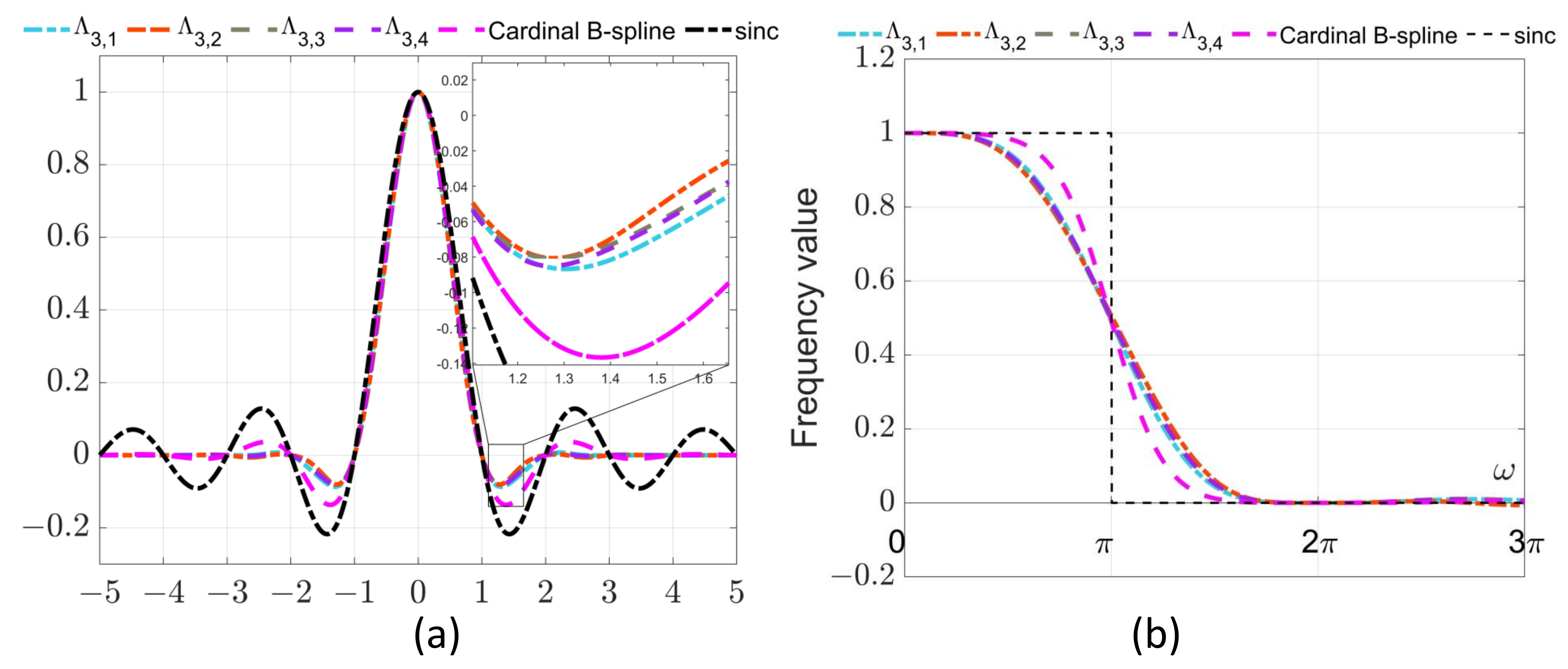
3.1. Fourier Transformation of Continuous GCP-splines
3.2. Z-Transformation of Expanded Discrete GCP-splines
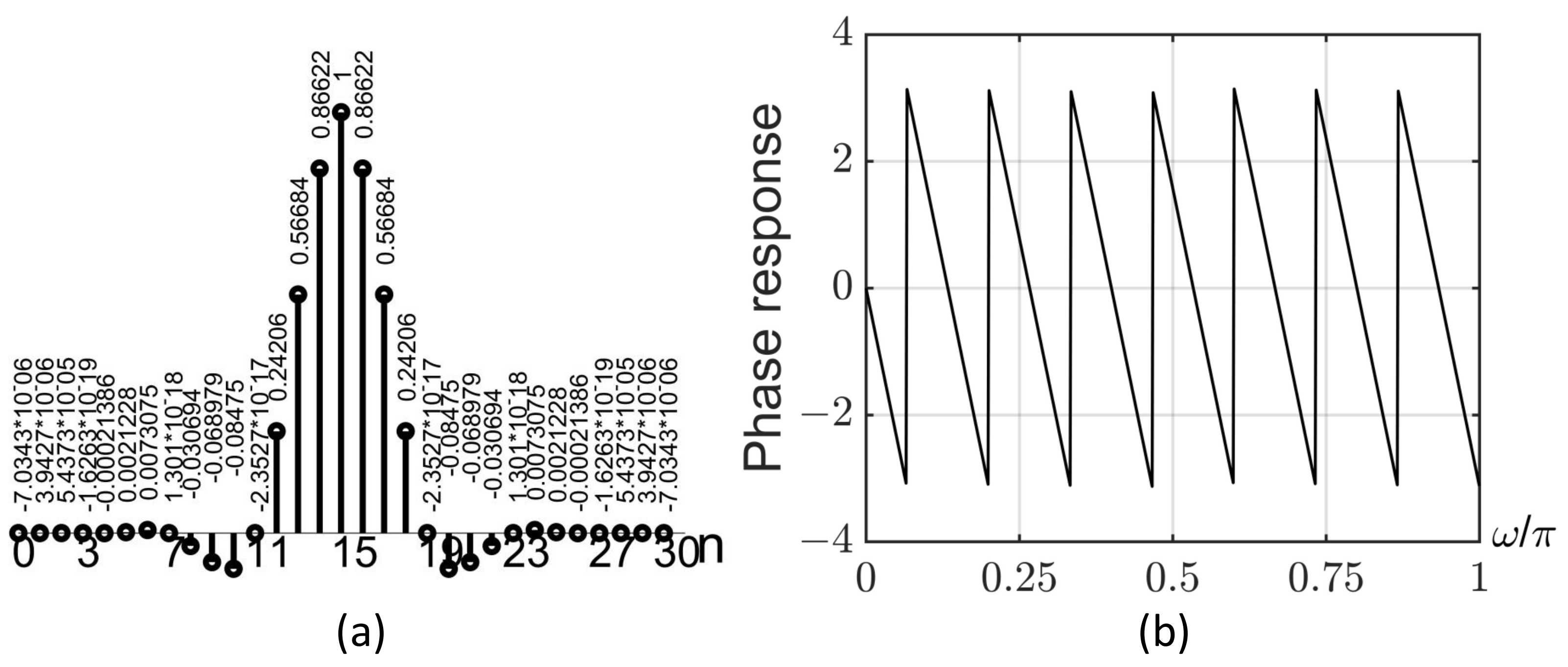
3.3. GCP-splines Signal Reconstruction and Filter
| Algorithm 1 GCP-splines differential signal reconstruction |
Input: Let N be the size of the original signal , the sampling factor m, with its coefficients of the average shift operator , and the parameter is only used to distinguish GCP-splines of the same order n, which is the r-th order derivative of the signal ; 1: ; 2: based on Equation (25); Output: Reconstructed differential signal data ; 3: function myDGCPfunc : 4: let ; 5: for to do 6: based on Equation (26). 7: end for |
3.4. Differential Signal Reconstruction
4. Simulated Experiments
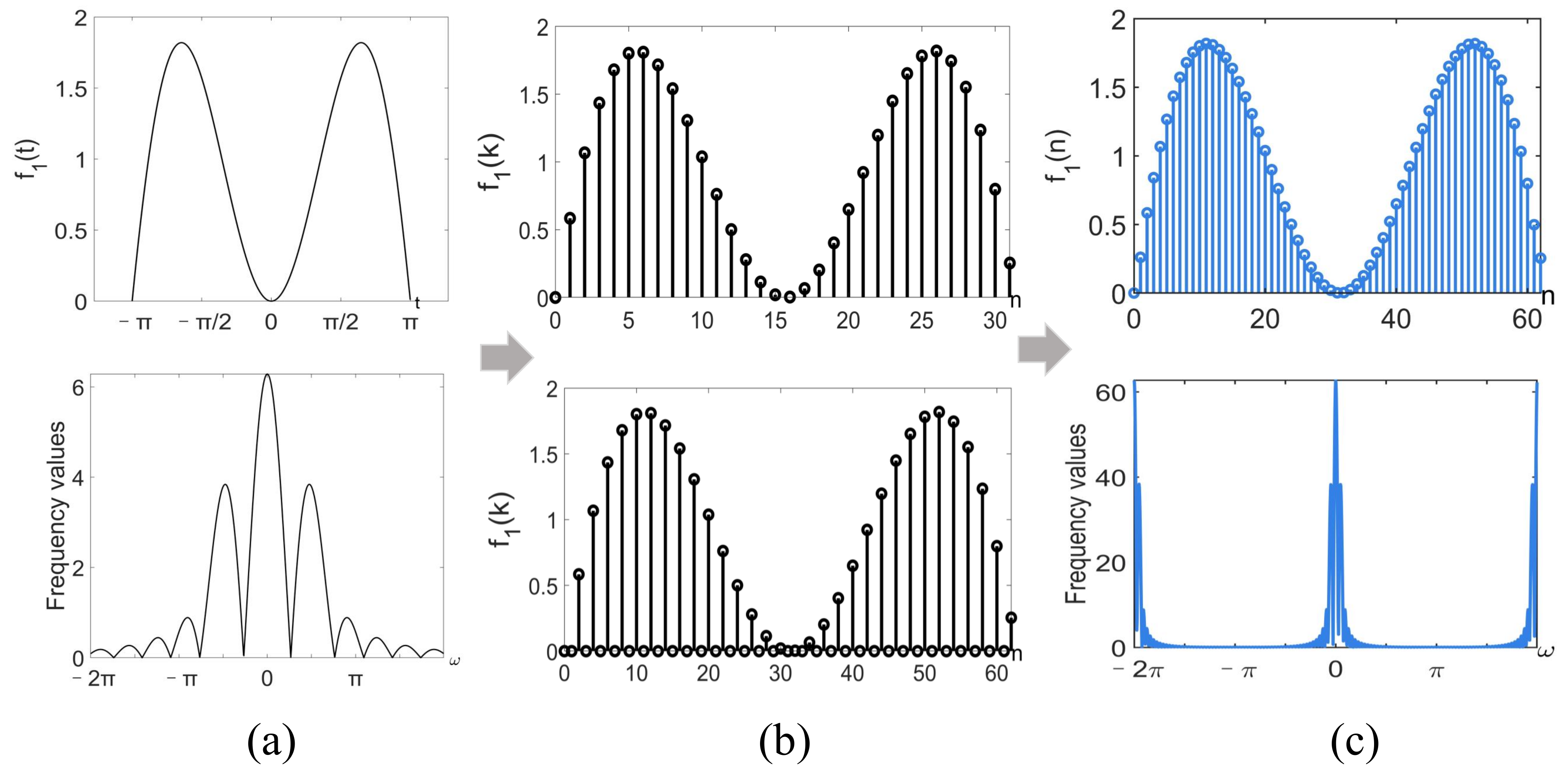
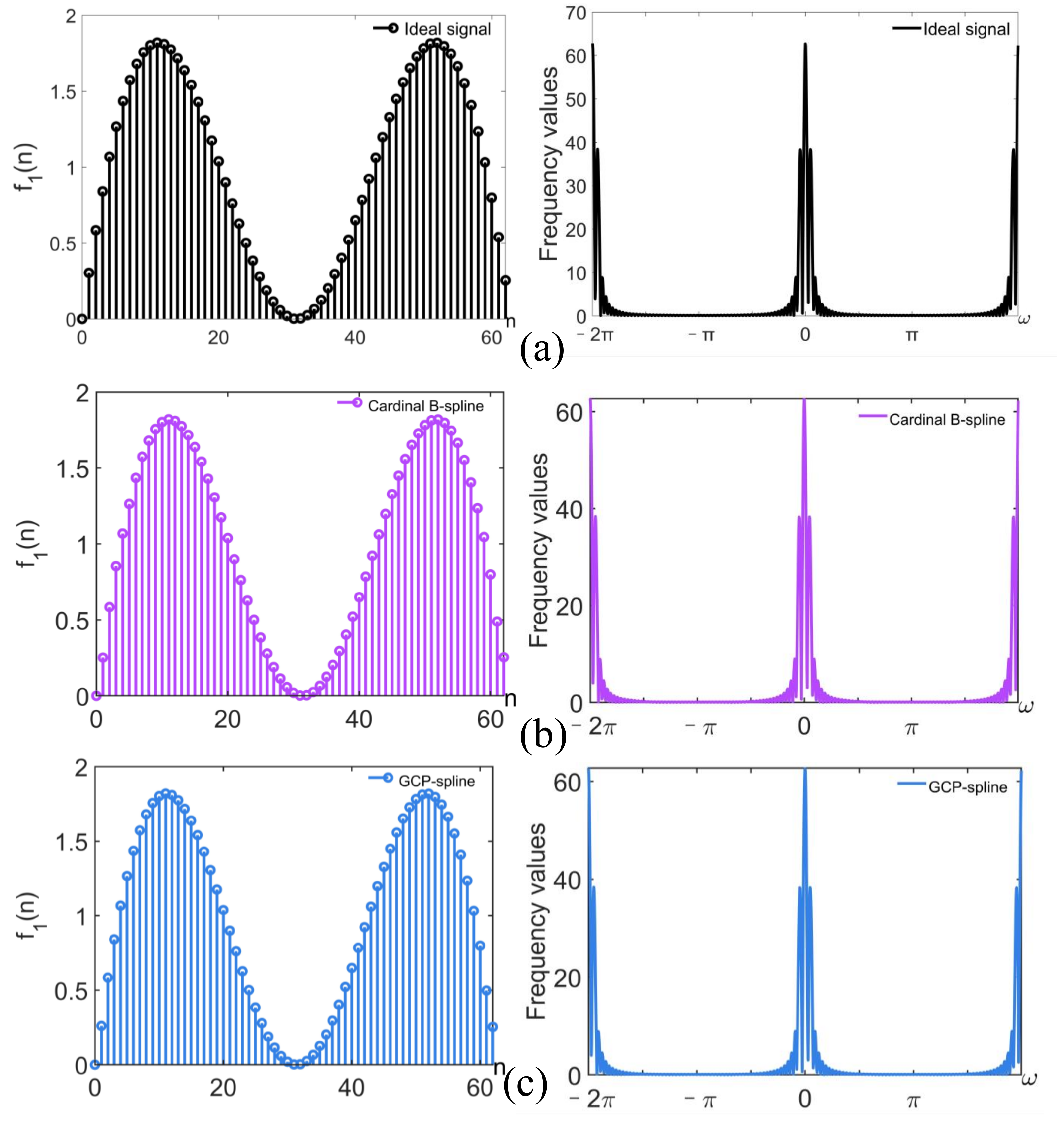
4.1. Analog Signal
4.2. Differential Signal
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, D.; Yuan, Z.; Cai, Z.; Zhu, D.; Shen, X. A New Local Optimal Spline Wavelet for Image Edge Detection. Mathematics 2025, 13, 42. [Google Scholar] [CrossRef]
- Qarariyah, A.; Yang, T.; Deng, F. A Solution-Structure B-Spline-Based Framework for Hybrid Boundary Problems on Implicit Domains. Mathematics 2024, 12, 3973. [Google Scholar] [CrossRef]
- Lodhi, R.K.; Darweesh, M.S.; Aydi, A.; Kolsi, L.; Sharma, A.; Ramesh, K. A Sixth-Order Cubic B-splines Approach for Solving Linear Boundary Value Problems: An In-Depth Analysis and Comparative Study. Mathematics 2024, 12, 3274. [Google Scholar] [CrossRef]
- Ma, X.; Shen, W. Generalized de Boor–Cox Formulas and Pyramids for Multi-Degree Spline Basis Functions. Mathematics 2023, 11, 367. [Google Scholar] [CrossRef]
- Zhang, B.; Zheng, H. A Variant Cubic Exponential B-splines Scheme with Shape Control. Mathematics 2021, 9, 3116. [Google Scholar] [CrossRef]
- Laome, L.; Budiantara, I.N.; Ratnasari, V. Estimation Curve of Mixed Spline Truncated and Fourier Series Estimator for Geographically Weighted Nonparametric Regression. Mathematics 2023, 11, 152. [Google Scholar] [CrossRef]
- Hsieh, S.; Andrews, H. Cubic splines for image interpolation and digital filtering. IEEE Trans. Acoust. Speech Signal Process. 1978, 26, 508–517. [Google Scholar] [CrossRef]
- Bohra, P.; Unser, M. Continuous-Domain Signal Reconstruction Using Lp-Norm Regularization. IEEE Trans. Signal Process. 2020, 68, 4543–4554. [Google Scholar] [CrossRef]
- Chen, J.; Cai, Z. A new class of explicit interpolatory splines and related measurement estimation. IEEE Trans. Signal Process. 2020, 68, 2799–2813. [Google Scholar] [CrossRef]
- Haro, B.B.; Vetterli, M. Sampling continuous-time sparse signals: A frequency-domain perspective. IEEE Trans. Signal Process. 2018, 66, 1410–1424. [Google Scholar] [CrossRef]
- Vlašić, T.; Seršić, D. Sampling and Reconstruction of Sparse Signals in Shift-Invariant Spaces: Generalized Shannon’s Theorem Meets Compressive Sensing. IEEE Trans. Signal Process. 2022, 70, 438–451. [Google Scholar] [CrossRef]
- Unser, M.; Aldroubi, A.; Eden, M.; Fellow, L. B-splines signal processing: Part I—Theory. IEEE Trans. Signal Process. 1993, 41, 821–833. [Google Scholar] [CrossRef]
- Zou, Q.; Zhu, L.; Wu, J.; Yang, Z. SplineGen: Approximating unorganized points through generative AI. Comput.-Aided Des. 2025, 178, 103809. [Google Scholar] [CrossRef]
- Huang, S. Implicit Uniform Rational Spline Reconstruction Method With Regularization Term. IEEE Access 2024, 12, 99012–99021. [Google Scholar] [CrossRef]
- Pang, D.; Ferrari, L.; Sankar, P. B-splines FIR filters. Circuits Syst. Signal Process. 1994, 13, 31–64. [Google Scholar] [CrossRef]
- Hosseini, M.; Plataniotis, K. Derivative kernels: Numerics and applications. IEEE Trans. Image Process. 2017, 26, 4596–4611. [Google Scholar] [CrossRef]
- Schoenberg, I.J. Spline functions and the problem of graduation. Proc. Nat. Acad. Sci. USA 1964, 52, 947–950. [Google Scholar] [CrossRef]
- Unser, M. Cardinal exponential splines: Part II—Think analog, act digital. IEEE Trans. Signal Process. 2005, 53, 1439–1449. [Google Scholar] [CrossRef]
- Unser, M.; Blu, T. Cardinal exponential splines: Part I—Theory and filtering algorithms. IEEE Trans. Signal Process. 2005, 53, 1425–1438. [Google Scholar] [CrossRef]
- Unser, M. B-splines signal processing: Part II—Efficient design and applications. IEEE Trans. Signal Process. 1993, 41, 834–848. [Google Scholar] [CrossRef]
- Bai, Y. On the Comparison of Trilinear, Cubic Spline, and Fuzzy Interpolation Methods in the High-Accuracy Measurements. IEEE Trans. Fuzzy Syst. 2010, 18, 1016–1022. [Google Scholar] [CrossRef]
- Lee, S.; Wolberg, G.; Shin, S.Y. Scattered data interpolation with multilevel B-splines. IEEE Trans. Vis. Comput. Graph. 1997, 3, 228–244. [Google Scholar] [CrossRef]
- Lü, Y.; Wang, G.; Yang, X. Uniform hyperbolic polynomial B-splines curves. Comput. Aided Geom. Des. 2002, 19, 379–393. [Google Scholar] [CrossRef]
- Qi, D.; Liang, Z. On the polish method by many-knot spline function (I). Numer. Math. J. Chin. Univ. 1979, 2, 196–209. [Google Scholar]
- Unser, M. Splines: A perfect fit for signal and image processing. IEEE Signal Process. Mag. 2002, 16, 22–38. [Google Scholar] [CrossRef]
- Ding, Q.; Wong, P.J.Y. Quintic non-polynomial spline for time-fractional nonlinear Schrdinger equation. Adv. Differ. Equ. 2020, 2020, 577. [Google Scholar] [CrossRef]
- Marinakis, V.; Fokas, A.S.; Kastis, G.A.; Protonotarios, N.E. Chebyshev Interpolation Using Almost Equally Spaced Points and Applications in Emission Tomography. Mathematics 2023, 11, 4757. [Google Scholar] [CrossRef]
- Blu, T.; Unser, M. Wavelets, fractals, and radial basis functions. IEEE Trans. Signal Process. 2002, 50, 543–553. [Google Scholar] [CrossRef]
- Chen, W.; Chen, T.; Wang, W. Hyperbolic polynomial B-splines with shape parameter. In Proceedings of the 2010 International Conference on Computer Application and System Modeling (ICCASM 2010), Taiyuan, China, 22–24 October 2010; pp. V10-441–V10-444. [Google Scholar] [CrossRef]
- Bruni, V.; Campagna, R.; Vitulano, D. Multicomponent signals interference detection exploiting HP-splines frequency parameter. Appl. Numer. Math. 2025, 209, 20–37. [Google Scholar] [CrossRef]
- Zhu, Y.; Han, X. C2 interpolation T-splines. Comput. Methods Appl. Mech. Eng. 2020, 362, 112835.1–112835.22. [Google Scholar] [CrossRef]
- Xie, J.; Xu, L.; Sun, M.; Xie, C.; Zhang, J. Quadratic Non-uniform Hyperbolic B-spline Curves. In Proceedings of the 2012 International Conference on Computer Science and Electronics Engineering, Hangzhou, China, 23–25 March 2012; pp. 508–511. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Yousif, M.A.; Mohammed, P.O.; Lupas, A.A.; Ibrahim, I.S.; Chorfi, N. Hyperbolic Non-Polynomial Spline Approach for Time-Fractional Coupled KdV Equations: A Computational Investigation. Symmetry 2024, 16, 1610. [Google Scholar] [CrossRef]
- Munoz, A.; Blu, T.; Unser, M. Least-squares image resizing using finite differences. IEEE Trans. Image Process. Soc. 2001, 10, 1365–1378. [Google Scholar] [CrossRef] [PubMed]
- Fahmy, O.M.; Fahmy, M.F.; Fahmy, G.F. E-spline based image interpolators. In Proceedings of the 2014 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Noida, India, 15–17 December 2014; pp. 61–66. [Google Scholar] [CrossRef]
- Schmitter, D.; Delgado-Gonzalo, R.; Unser, M. A family of smooth and interpolatory basis functions for parametric curve and surface representation. Appl. Math. Comput. 2016, 272 Pt 1, 53–63. [Google Scholar] [CrossRef][Green Version]
- Alexandru, R.; Dragotti, P.L. Reconstructing classes of non-bandlimited signals from time encoded information. IEEE Trans. Signal Process. 2020, 68, 747–763. [Google Scholar] [CrossRef]
- Debarre, T.; Aziznejad, S.; Unser, M. Hybrid-spline dictionaries for continuous-domain inverse problems. IEEE Trans. Signal Process. 2019, 67, 5824–5836. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Bostan, E.; Unser, M. Learning convex regularizers for optimal bayesian denoising. IEEE Trans. Signal Process. 2017, 66, 1093–1105. [Google Scholar] [CrossRef]
- Debarre, T.; Fageot, J.; Gupta, H.; Unser, M. B-Spline-Based Exact Discretization of Continuous-Domain Inverse Problems with Generalized TV Regularization. IEEE Trans. Inf. Theory 2019, 65, 4457–4470. [Google Scholar] [CrossRef]
- Dadi, L.; Aziznejad, S.; Unser, M. Generating Sparse Stochastic Processes Using Matched Splines. IEEE Trans. Signal Process. 2020, 68, 4397–4406. [Google Scholar] [CrossRef]
- Qi, D. On the many-knot cardinal δ-spline interpolation. Acta Sci. Nat. Univ. Jilinensis 1975, 3, 70–81. [Google Scholar]
- Qi, D.; Tian, Z.; Zhang, Y.; Feng, J. Numerical polishing method for curve fitting. Acta Math. Sin. 1975, 18, 173–184. [Google Scholar]
- Chen, J.; Cai, Z. Cardinal MK-spline signal processing: Spatial interpolation and frequency domain filtering. Inf. Sci. 2019, 495, 116–135. [Google Scholar] [CrossRef]
- Lan, T.; Cai, Z.; Ye, B. A Novel Spline Algorithm Applied to COVID-19 Computed Tomography Image Reconstruction. IEEE Trans. Ind. Inform. 2022, 18, 7804–7813. [Google Scholar] [CrossRef]
- Cai, Z.; Lan, T.; Zheng, C. Hierarchical MK splines: Algorithm and applications to data fitting. IEEE Trans. Multimed. 2017, 19, 921–934. [Google Scholar] [CrossRef]
- Sun, F.; Cai, Z. Cubic Polishing Spline-Based Algorithms for Industrial Image Processing. IEEE Trans. Ind. Inform. 2024, 20, 314–326. [Google Scholar] [CrossRef]
- Sun, F.; Cai, Z. A Family of Generalized Cardinal Polishing Splines. IEEE Trans. Image Process. 2023, 33, 1952–1964. [Google Scholar] [CrossRef]
- Hong, S.H.; Wang, L.; Truong, T.K.; Lin, T.C.; Wang, L.J. Novel approaches to the parametric cubic-spline interpolation. IEEE Trans. Image Process. 2012, 22, 1233–1241. [Google Scholar] [CrossRef]
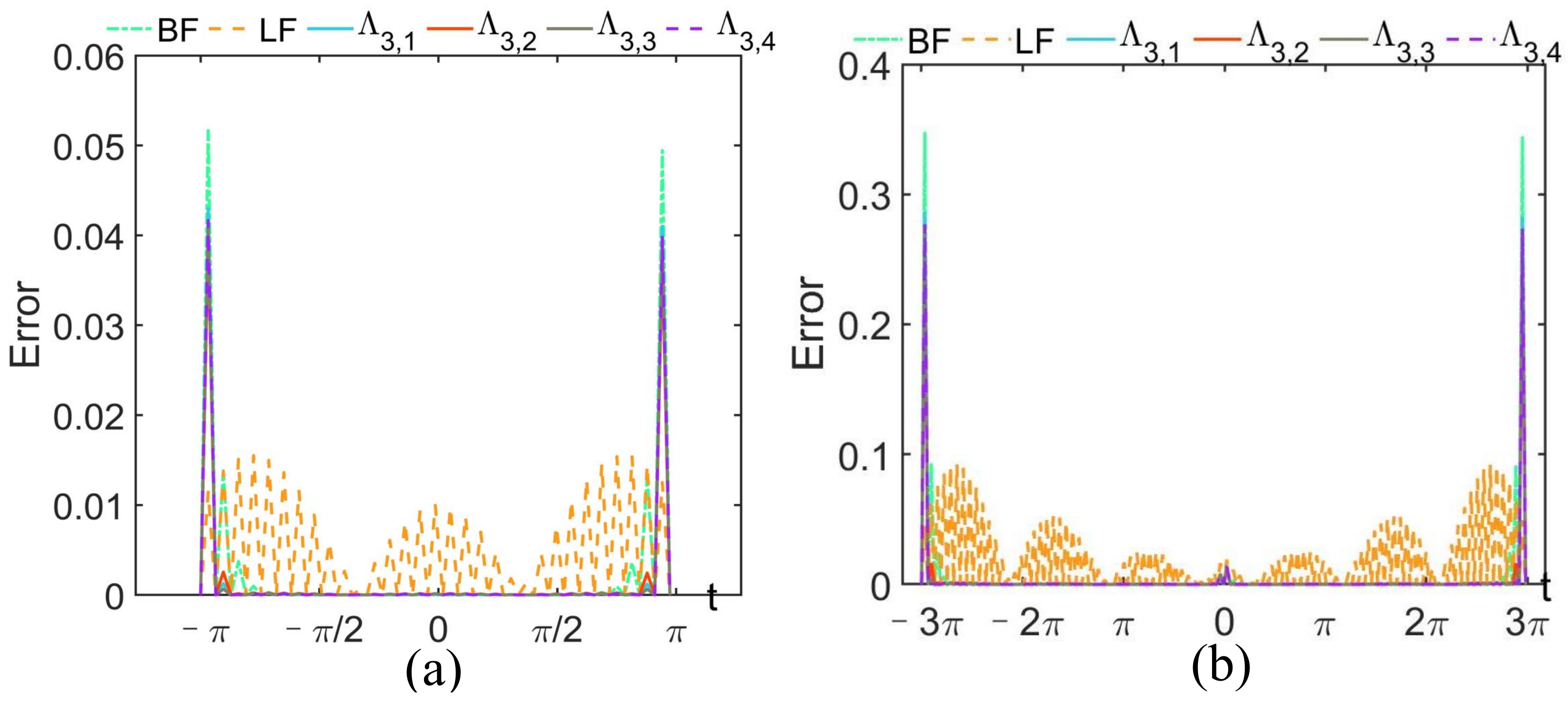
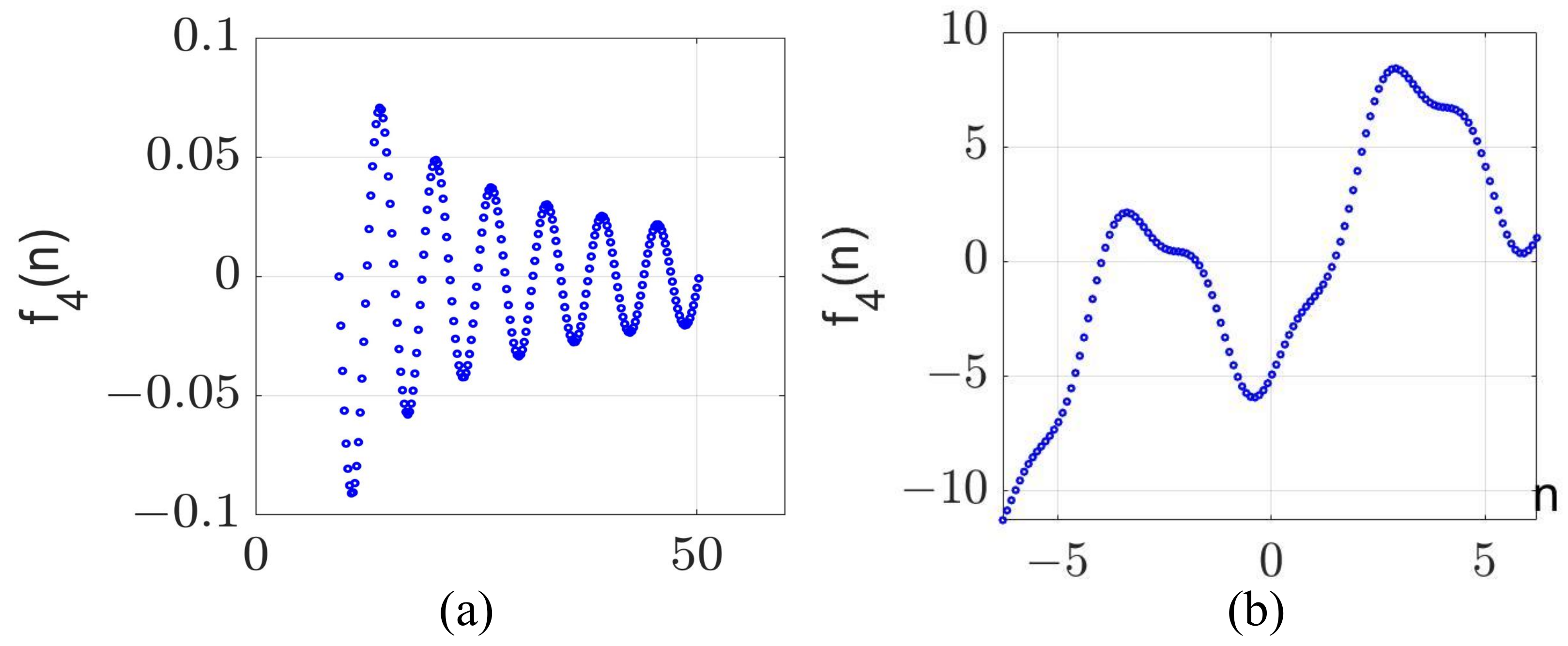


| Sample Step ℓ and Expanded Factor | ||||
| Functions | Filters | |||
| BF | ||||
| LF | ||||
| BF | ||||
| LF | ||||
| Sample Step ℓ and Expanded Factor | ||||
| Functions | Filters | |||
| BF | ||||
| LF | ||||
| BF | ||||
| LF | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, F.; Cai, Z. Generalized Cardinal Polishing Splines Signal Reconstruction. Mathematics 2025, 13, 983. https://doi.org/10.3390/math13060983
Sun F, Cai Z. Generalized Cardinal Polishing Splines Signal Reconstruction. Mathematics. 2025; 13(6):983. https://doi.org/10.3390/math13060983
Chicago/Turabian StyleSun, Fangli, and Zhanchuan Cai. 2025. "Generalized Cardinal Polishing Splines Signal Reconstruction" Mathematics 13, no. 6: 983. https://doi.org/10.3390/math13060983
APA StyleSun, F., & Cai, Z. (2025). Generalized Cardinal Polishing Splines Signal Reconstruction. Mathematics, 13(6), 983. https://doi.org/10.3390/math13060983








