Locality-Preserving Multiprojection Discriminant Analysis
Abstract
1. Introduction
- A novel convex discriminant analysis framework is established from the perspective of metric learning, which can learn a flexible number of discriminative projections to extract more discriminative features.
- An auto-optimized graph mechanism is cleverly integrated into the discriminant analysis framework, which automatically exploits the neighborships of each instance and further enhances the discriminative ability of the extracted features.
- An efficient iterative strategy is designed to solve the resultant optimization problem. Extensive experiments were conducted on the benchmark datasets to demonstrate the superiority of the proposed method.
2. Related Works
2.1. Linear Discriminant Analysis
2.2. Geometric Mean Metric Learning
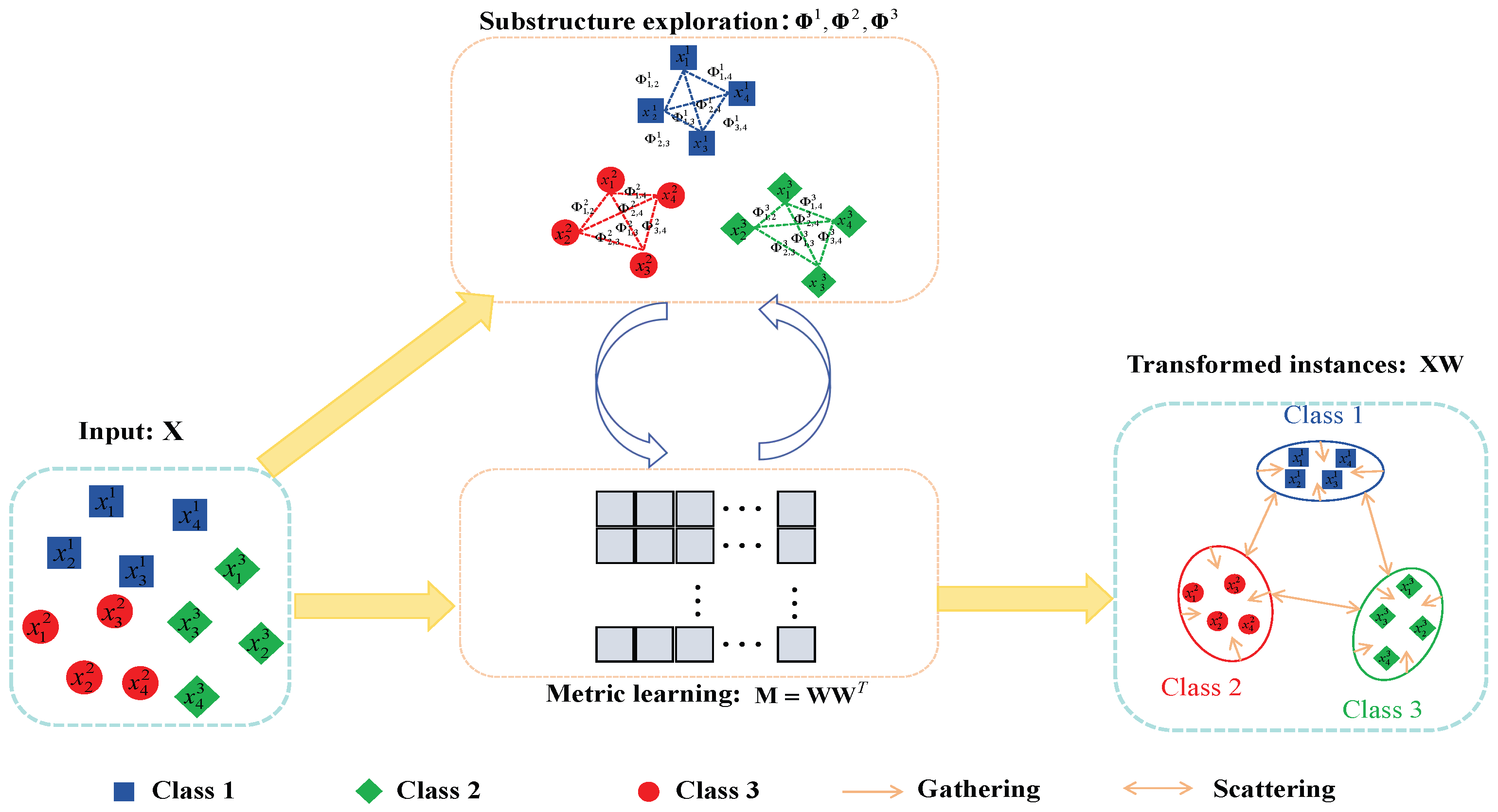
3. Proposed Method
3.1. Multiprojection Discriminant Analysis
3.2. Local Structure Exploitation
3.3. Objective Function
3.4. Optimization for LPMDA
| Algorithm 1 Algorithm for solving LPMDA |
| Input: Training instance matrix , label matrix , regularization parameter , weighting parameter , neighbors number k, reduced dimension r. Initialization: While not converged do 1. Update by solving problem (12) 2. Calculate according to Equation (15). end while , where denotes the Cholesky decomposition operation. Output: . |
3.5. Complexity and Convergence Analysis
3.6. Connections to Previous Discriminators
4. Experiments
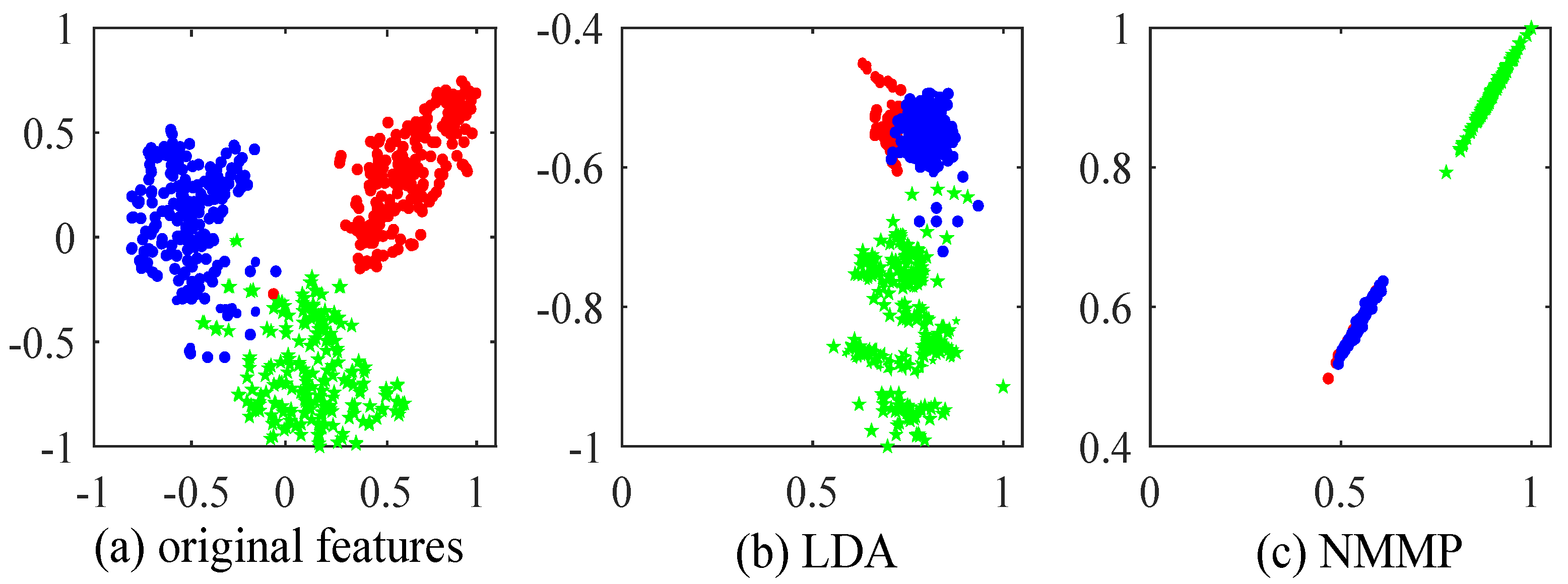
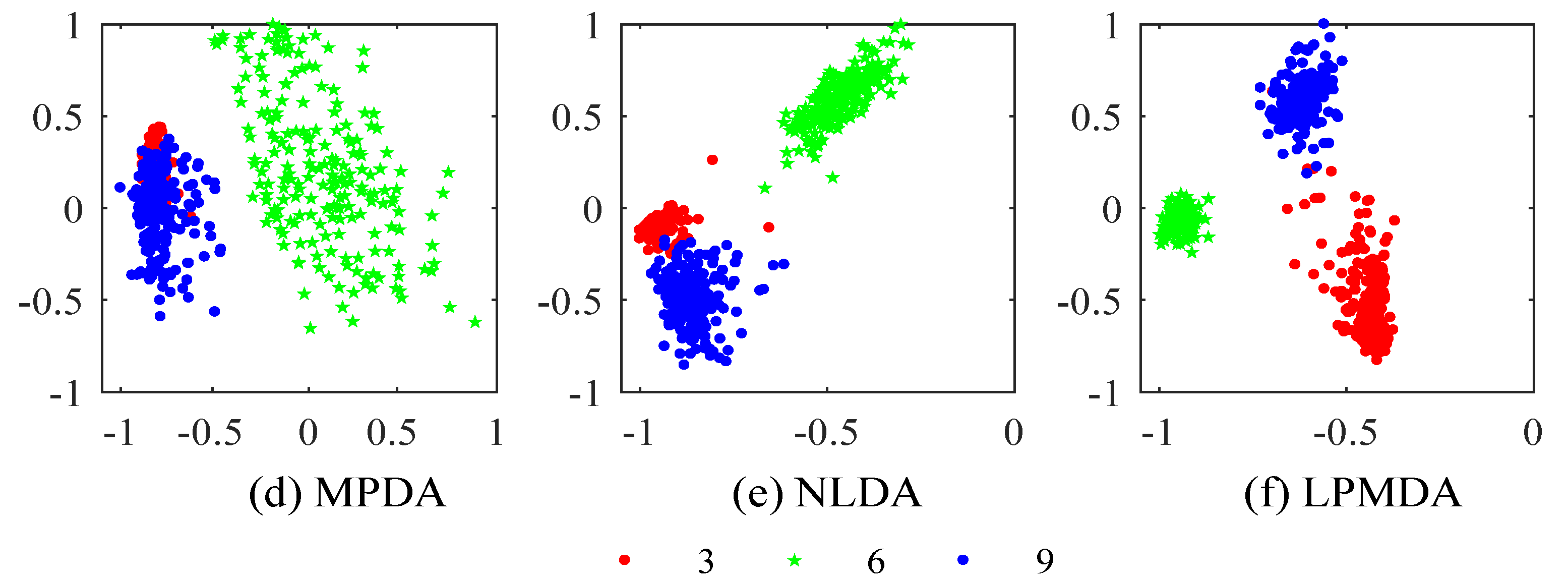
4.1. Experiments on Handwritten Digit Recognition
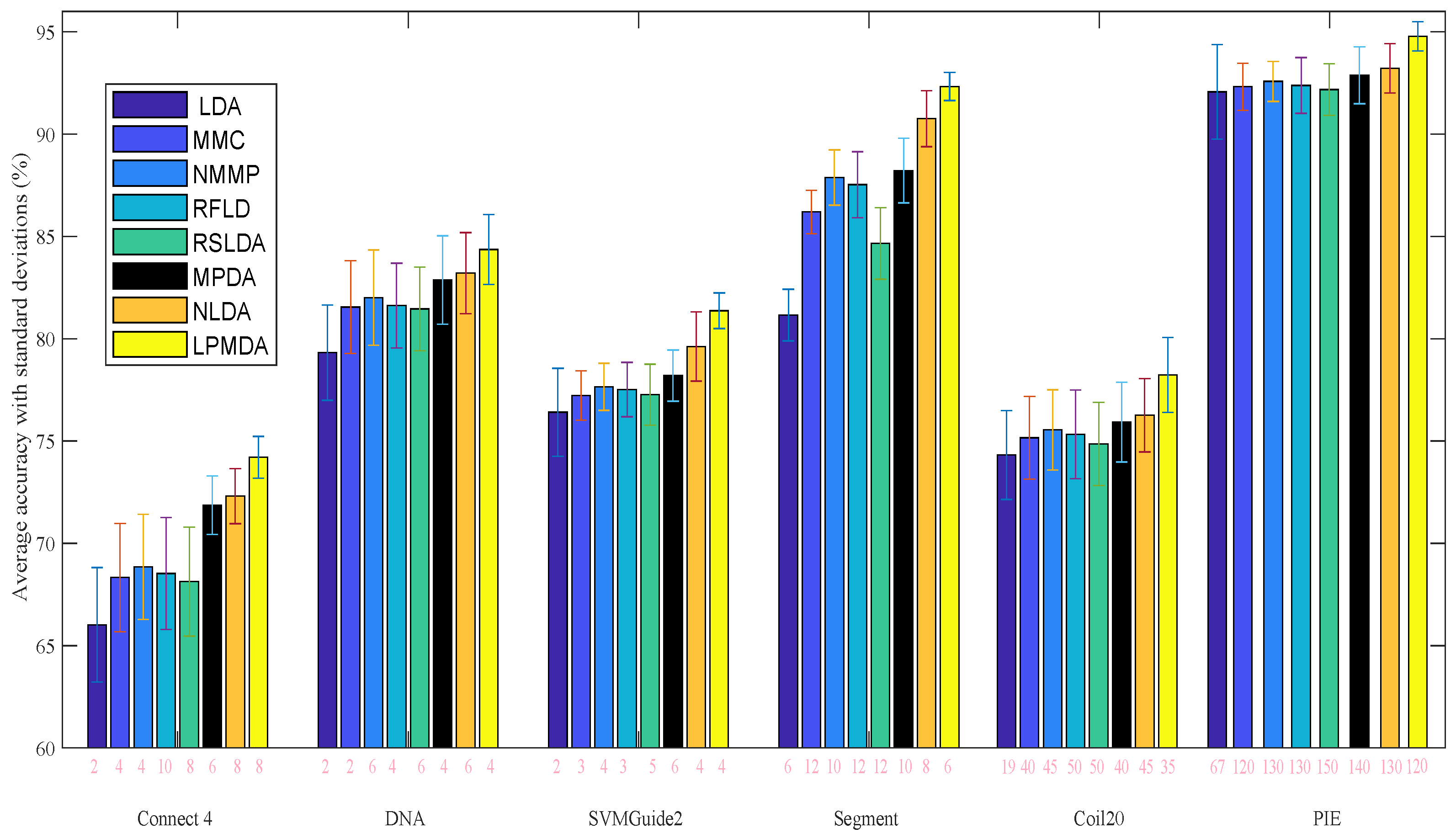
4.2. Experiments on Benchmark Datasets
4.3. Statistical Significance
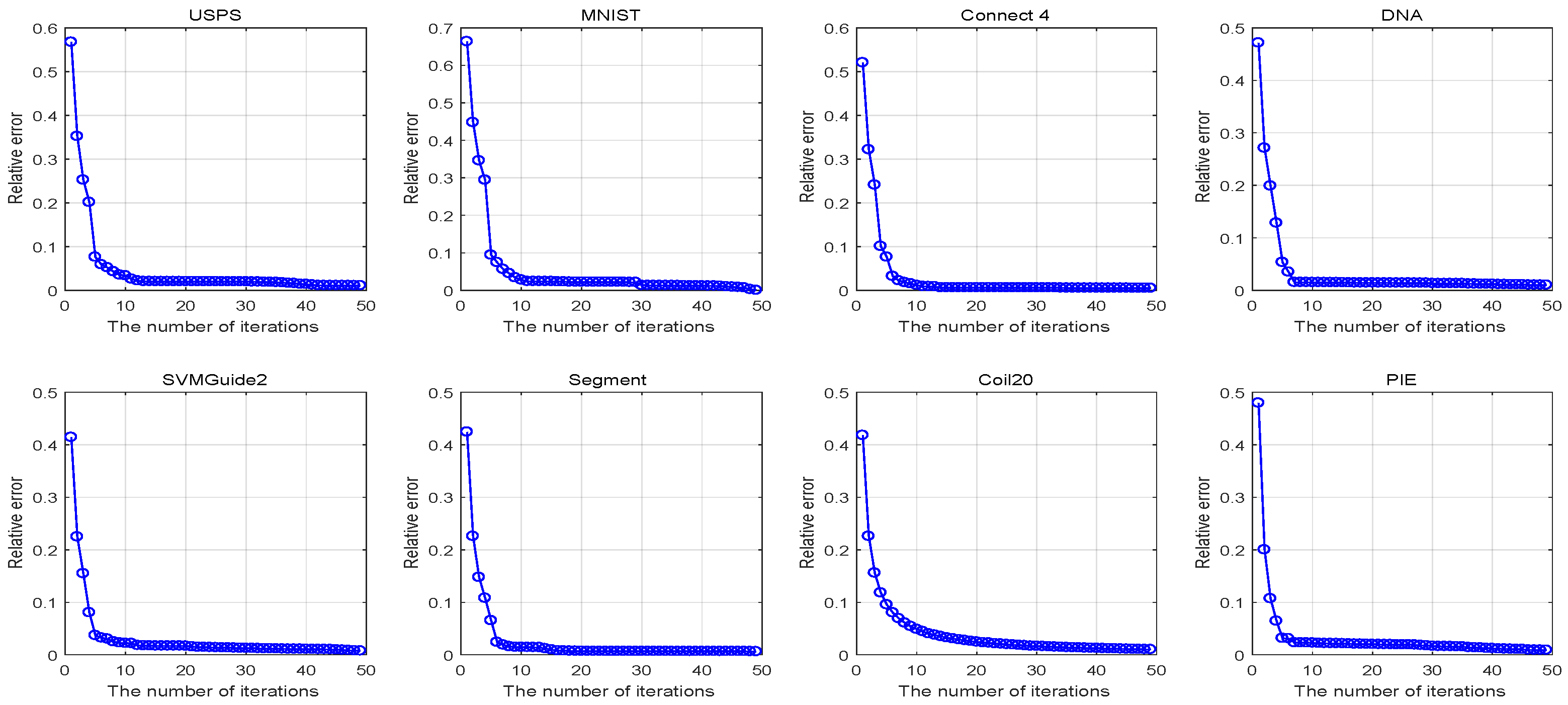
4.4. Convergence and Computational Performance
4.5. Ablation Study
- LPMDA1: LPMDA1 only replaces the trace ratio operation in LDA with the GMML similarity measure to obtain optimization problem (8), which can yield more features than the number of classes.
- LPMDA2: LPMDA2 incorporates auto-optimized graph embedding in LDA, resulting in the following optimization problem:
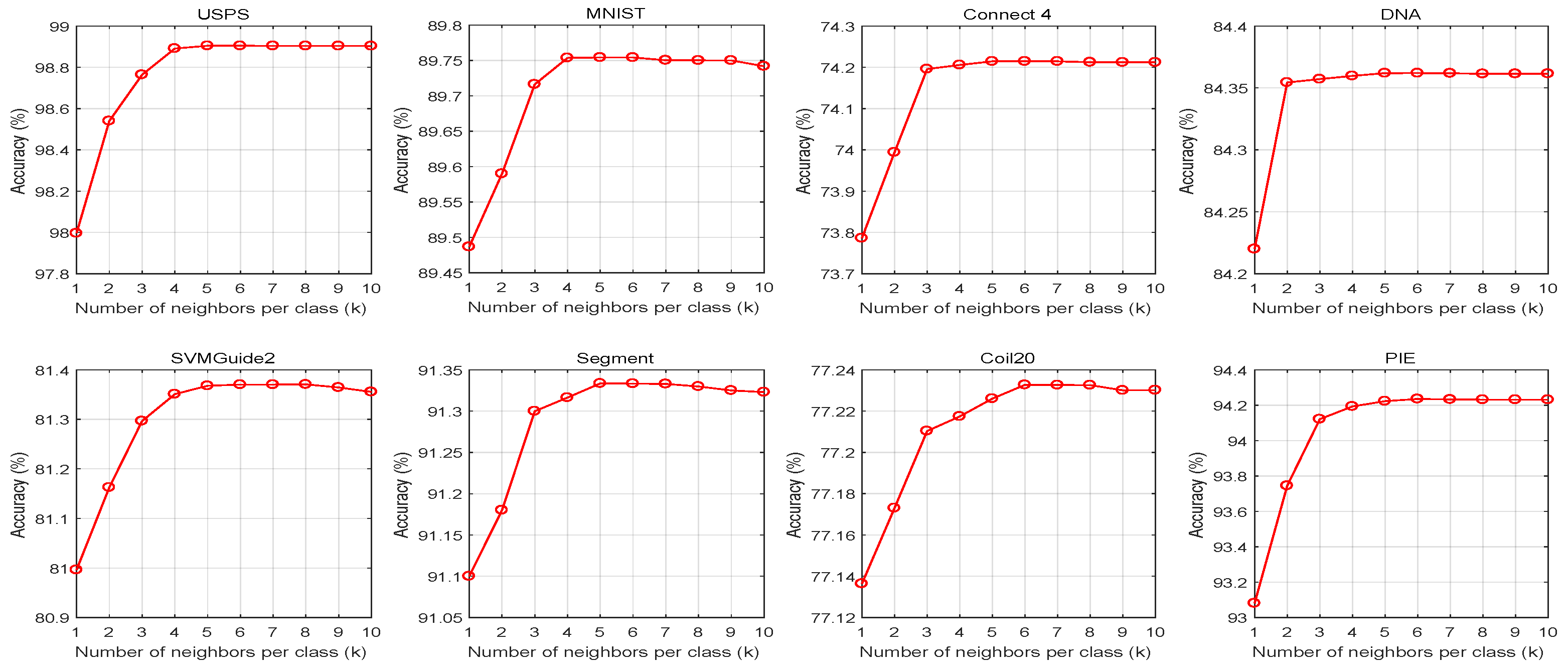
4.6. Parameter Sensitiveness
5. Conclusions and Future Work
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Wang, J.; Wang, L.; Nie, F.; Li, X. Fast Unsupervised Projection for Large-Scale Data. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 3634–3644. [Google Scholar] [CrossRef] [PubMed]
- Dorrity, M.W.; Saunders, L.M.; Queitsch, C.; Fields, S.; Trapnell, C. Dimensionality reduction by UMAP to visualize physical and genetic interactions. Nat. Commun. 2020, 11, 1537. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.; Yu, W.; Zi, Y.; Chow, T. An Enhanced Trace Ratio Linear Discriminant Analysis for Fault Diagnosis: An Illustrated Example Using HDD Data. IEEE Trans. Instrum. Meas. 2019, 68, 4629–4639. [Google Scholar] [CrossRef]
- Ma, J.; Xu, F.; Rong, X. Discriminative multi-label feature selection with adaptive graph diffusion. Pattern Recognit. 2024, 148, 110154. [Google Scholar] [CrossRef]
- Yin, W.; Ma, Z.; Liu, Q. Discriminative subspace learning via optimization on Riemannian manifold. Pattern Recognit. 2023, 139, 109450. [Google Scholar] [CrossRef]
- Xiang, C.; Fan, X.A.; Lee, T.H. Face Recognition Using Recursive Fisher Linear Discriminant. IEEE Trans. Image Process. 2006, 15, 2097–2105. [Google Scholar] [CrossRef]
- Hemmatpour, S.; Hashemi, H. Using PCA and RDA feature reduction techniques for ranking seismic attributes. J. Earth Space Phys. 2011, 37, 217–227. [Google Scholar]
- Fakhari, M.G.; Hashemi, H. Fisher Discriminant Analysis (FDA), a supervised feature reduction method in seismic object detection. Geopersia 2019, 9, 141–149. [Google Scholar]
- Yan, S.; Xu, D.; Zhang, B.; Zhang, H.; Yang, Q.; Lin, S. Graph Embedding and Extensions: A General Framework for Dimensionality Reduction. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 40–51. [Google Scholar] [CrossRef]
- Witten, D.M.; Tibshirani, R. Penalized Classification Using Fisher’s Linear Discriminant. J. R. Stat. Soc. Ser.-Stat. Methodol. 2011, 73, 753–772. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, T.; Long, H.; Shi, H.; Wang, J.; Yang, L. Fisher discrimination multiple kernel dictionary learning for robust identification of nonlinear features in machinery health monitoring. Inf. Sci. 2024, 677, 120862. [Google Scholar] [CrossRef]
- Ju, F.; Sun, Y.; Gao, J.; Hu, Y.; Yin, B. Kronecker-decomposable robust probabilistic tensor discriminant analysis. Inf. Sci. 2021, 561, 196–210. [Google Scholar] [CrossRef]
- Nie, F.; Wang, J.; Wang, H.; Li, X. Ratio Sum Versus Sum Ratio for Linear Discriminant Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1936, 44, 10171–10185. [Google Scholar]
- Li, H.; Jiang, T.; Zhang, K. Efficient and robust feature extraction by maximum margin criterion. IEEE Trans. Neural Netw. Learn. Syst. 2006, 17, 157–165. [Google Scholar] [CrossRef]
- Hayes, T.L.; Kanan, C. Lifelong Machine Learning with Deep Streaming Linear Discriminant Analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 13–19 June 2020; pp. 887–896. [Google Scholar]
- Bartan, B.; Pilanci, M. Neural Fisher Discriminant Analysis: Optimal Neural Network Embeddings in Polynomial Time. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 1647–1663. [Google Scholar]
- Uzun, B.; Cevikalp, H.; Saribas, H. Deep Discriminative Feature Models (ddfms) for Set Based Face Recognition and Distance Metric Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 5594–5608. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Shao, Y.; Yin, W.; Liu, M. Robust and Sparse Linear Discriminant Analysis via an Alternating Direction Method of Multipliers. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 915–926. [Google Scholar] [CrossRef]
- Loog, M.; Ginneken, B.V.; Duin, R. Dimensionality reduction of image features using the canonical contextual correlation projection. Pattern Recognit. 2005, 38, 2409–2418. [Google Scholar] [CrossRef]
- Zhu, M.; Martinez, A.M. Subclass Discriminant Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1274–1286. [Google Scholar]
- Webb, A.R. Introduction to Statistical Pattern Recognition. In Statistical Pattern Recognition; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Sugiyama, M. Dimensionality reduction of multimodal labeled data by local fisher discriminant analysis. J. Mach. Learn. Res. 2007, 8, 1027–1061. [Google Scholar]
- Li, Z.; Nie, F.; Chang, X.; Yi, Y. Beyond trace ratio: Weighted harmonic mean of trace ratios for multiclass discriminant analysis. IEEE Trans. Knowl. Data Eng. 2017, 29, 2100–2110. [Google Scholar] [CrossRef]
- Wa, H.; Wang, H.; Guo, G.; Wei, X. Separability-Oriented Subclass Discriminant Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 409–422. [Google Scholar]
- Luo, T.; Hou, C.; Nie, F.; Yi, D. Dimension reduction for non-gaussian data by adaptive discriminative analysis. IEEE Trans. Cybern. 2019, 49, 933–946. [Google Scholar] [CrossRef]
- Okada, T.; Tomita, S. An optimal orthonormal system for discriminant analysis. Pattern Recognit. 1985, 18, 139–144. [Google Scholar] [CrossRef]
- Ohta, R.; Ozawa, S. An Incremental Learning Algorithm of Recursive Fisher Linear Discriminant. In Proceedings of the International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009; pp. 2310–2315. [Google Scholar]
- Loog, M.; Duin, R. Linear Dimensionality Reduction via a Heteroscedastic Extension of LDA: The Chernoff Criterion. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 732–739. [Google Scholar]
- Zadeh, P.; Hosseini, R.; Sra, S. Geometric mean metric learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 2464–2471. [Google Scholar]
- Fan, Z.; Xu, Y.; Zhang, D. Local Linear Discriminant Analysis Framework Using Sample Neighbors. IEEE Trans. Neural Netw. Learn. Syst. 2011, 22, 1119–1132. [Google Scholar] [CrossRef]
- Nie, F.; Xiang, S.; Zhang, C. Neighborhood MinMax Projections. In Proceedings of the International Joint Conference on Artificial Intelligence, Hyderabad, India, 6–12 January 2007; pp. 993–998. [Google Scholar]
- Zhao, Z.; Chow, T. Robust linearly optimized discriminant analysis. Neurocomputing 2012, 79, 140–157. [Google Scholar]
- Zhu, F.; Gao, J.; Yang, J.; Ye, N. Neighborhood linear discriminant analysis. Pattern Recognit. 2022, 123, 108422. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, S. Manifold Partition Discriminant Analysis. IEEE Trans. Cybern. 2017, 47, 830–840. [Google Scholar] [CrossRef]
- Bhatia, R. Positive Definite Matrices. In Princeton; Princeton University Press: Princeton, NJ, USA, 2009; Volume 24. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Sim, T.; Baker, S.; Bsat, M. The cmu pose, illumination, and expression database. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1615–1618. [Google Scholar]
- Demiar, J.; Schuurmans, D. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Ma, J.; Zhou, S. Discriminative least squares regression for multiclass classification based on within-class scatter minimization. Appl. Intell. 2022, 52, 622–635. [Google Scholar] [CrossRef]


| Method | Computational Complexity |
|---|---|
| LDA [21] | |
| MMC [14] | |
| NMMP [31] | |
| RFLD [6] | |
| RSLDA [18] | |
| MPDA [34] | |
| NLDA [33] | |
| LPMDA |
| Methods | Definition of and | ♯ Features | Structure Preservation | |
|---|---|---|---|---|
| LDA [21] | | global | ||
| MMC [14] | | global | ||
| RFLD [6] | | global | ||
| RSLDA [18] | | global | ||
| NMMP [31] | | local | ||
| NLDA [33] | | local | ||
| LPMDA | | local |
| Class | USPS | MNIST | ||
|---|---|---|---|---|
| ♯Training | ♯Test | ♯Training | ♯Test | |
| 0 | 644 | 177 | 5923 | 980 |
| 1 | 1194 | 359 | 6742 | 1135 |
| 2 | 1005 | 264 | 5958 | 1032 |
| 3 | 731 | 198 | 6131 | 1010 |
| 4 | 658 | 166 | 5842 | 982 |
| 5 | 652 | 200 | 5421 | 892 |
| 6 | 556 | 160 | 5918 | 958 |
| 7 | 664 | 170 | 6265 | 1028 |
| 8 | 645 | 147 | 5851 | 974 |
| 9 | 542 | 166 | 5949 | 1009 |
| Data | LDA | MMC | NMMP | RFLD | RSLDA | MPDA | NLDA | LPMDA |
|---|---|---|---|---|---|---|---|---|
| USPS | 94.02 ± 1.21 | 95.33 ± 1.33 | 96.73 ± 1.51 | 96.55 ± 1.31 | 97.21 ± 1.51 | 98.01 ± 1.62 | 97.21 ± 1.55 | 98.89 ± 0.81 |
| (1) | (140) | (160) | (160) | (130) | (110) | (160) | (150) | |
| MNIST | 83.18 ± 1.66 | 84.52 ± 1.73 | 85.67 ± 1.55 | 85.72 ± 1.45 | 87.32 ± 1.62 | 88.53 ± 1.71 | 87.51 ± 1.60 | 89.75 ± 0.85 |
| (1) | (120) | (130) | (140) | (110) | (100) | (130) | (140) |
| Dataset | # Classes | # Instances | # Features |
|---|---|---|---|
| Connect 4 | 3 | 44,473 | 126 |
| DNA | 3 | 3186 | 180 |
| SVMGuide2 | 3 | 391 | 20 |
| Segment | 7 | 2310 | 19 |
| Coil20 | 20 | 1440 | 256 |
| PIE | 68 | 11,554 | 1024 |
| Dataset | LDA | MMC | NMMP | RFLD | RSLDA | MPDA | NLDA | LPMDA |
|---|---|---|---|---|---|---|---|---|
| USPS | 0.213 | 0.387 | 1.675 | 0.721 | 1.369 | 2.912 | 2.163 | 0.392 |
| MNIST | 0.376 | 0.433 | 1.832 | 1.026 | 1.576 | 3.685 | 2.825 | 0.453 |
| Connect4 | 1.368 | 1.830 | 6.122 | 4.651 | 5.216 | 12.377 | 6.933 | 1.836 |
| DNA | 1.231 | 1.682 | 5.331 | 3.685 | 4.921 | 11.937 | 6.387 | 1.721 |
| SVMGuide2 | 0.086 | 0.122 | 0.468 | 0.329 | 0.453 | 0.975 | 0.637 | 0.151 |
| Segment | 0.131 | 0.173 | 0.621 | 0.467 | 0.526 | 1.265 | 0.861 | 0.210 |
| Coil20 | 0.168 | 0.261 | 0.821 | 0.587 | 0.733 | 1.733 | 1.233 | 0.311 |
| PIE | 11.612 | 16.33 | 89.375 | 60.31 | 72.891 | 179.321 | 92.331 | 17.833 |
| Dataset | USPS | MNIST | Connect 4 | DNA | SVMGuide2 | Segment | Coil20 | PIE |
|---|---|---|---|---|---|---|---|---|
| LPMDA1 | 96.30 ± 0.92 | 87.03 ± 0.87 | 71.21 ± 1.12 | 82.11 ± 1.67 | 79.61 ± 1.22 | 88.63 ± 0.76 | 75.81 ± 1.26 | 92.36 ± 1.02 |
| (150) | (140) | (8) | (7) | (6) | (6) | (40) | (135) | |
| LPMDA2 | 95.51 ± 2.33 | 85.61 ± 1.01 | 69.01 ± 1.21 | 80.38 ± 2.07 | 78.51 ± 0.91 | 89.26 ± 0.78 | 76.85 ± 0.98 | 91.48 ± 0.85 |
| (1) | (1) | (2) | (2) | (2) | (6) | (19) | (67) | |
| LPMDA | 98.89 ± 0.81 | 89.75 ± 0.85 | 74.21 ± 1.02 | 84.36 ± 1.71 | 81.37 ± 0.87 | 91.33 ± 0.69 | 77.23 ± 1.83 | 94.23 ± 0.72 |
| (150) | (140) | (6) | (4) | (4) | (6) | (35) | (120) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J. Locality-Preserving Multiprojection Discriminant Analysis. Mathematics 2025, 13, 962. https://doi.org/10.3390/math13060962
Ma J. Locality-Preserving Multiprojection Discriminant Analysis. Mathematics. 2025; 13(6):962. https://doi.org/10.3390/math13060962
Chicago/Turabian StyleMa, Jiajun. 2025. "Locality-Preserving Multiprojection Discriminant Analysis" Mathematics 13, no. 6: 962. https://doi.org/10.3390/math13060962
APA StyleMa, J. (2025). Locality-Preserving Multiprojection Discriminant Analysis. Mathematics, 13(6), 962. https://doi.org/10.3390/math13060962






