ZNN-Based Gait Optimization for Humanoid Robots with ALIP and Inequality Constraints
Abstract
1. Introduction
- Proposing an adaptive gait optimization algorithm based on angular momentum: A cost function is constructed to balance tracking errors and system smoothness. Adaptive parameters and physical limits are used as constraints, and adaptive parameters adjust the error between the expected angular momentum and the current estimated angular momentum online, dynamically adjusting the next foot placement to avoid oscillations or tipping problems caused by deadbeat control.
- Proposing a novel neural network ISPTAF-ZNN: A strong predefined-time convergence activation function is designed, with an integral term in the activation function to enhance the ZNN’s disturbance resistance. The ISPTAF-ZNN neural dynamics formula is derived, and Lyapunov stability theory is used to prove its strong predefined-time convergence and robustness.
2. Preliminaries and Problem Formulation
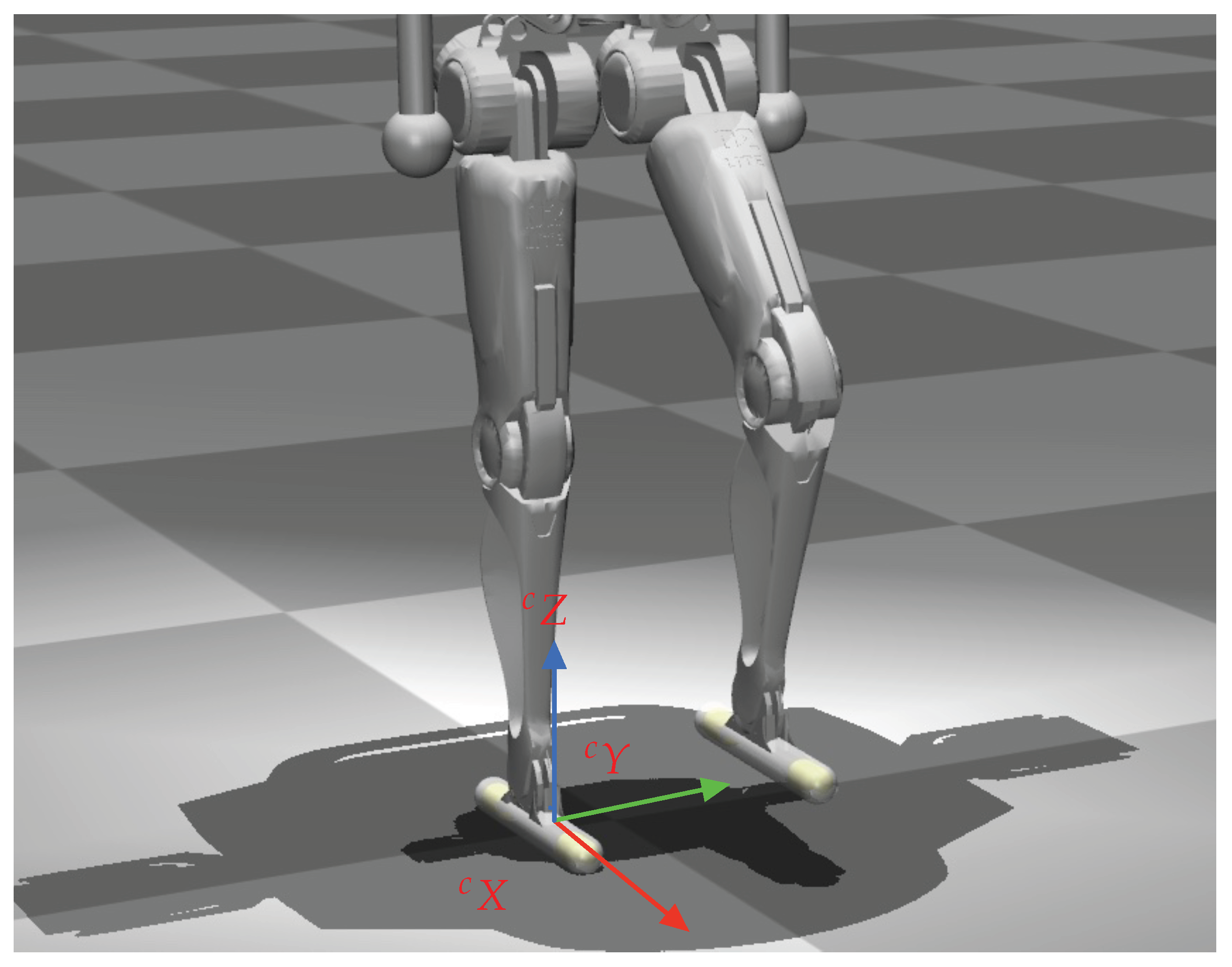
2.1. Preliminaries
2.2. AFP-QP Scheme
3. ISPTAF-ZNN Solver
4. Analysis of Convergence and Robustness
- (i)
- (ii)
- For , the ZNN (12) can be represented as the dynamic nonlinear equation , where the autonomous and independent subsystems are given bywhere . and are the scalar components of the vector and . Choose a Lyapunov function as . The corresponding time derivative isSolving this ordinary differential equation yieldsSubstituting the initial condition into the above equation gives . Substituting into the equation, we getDefine the residence time as . According to the solution (21), it is clear that when , we have . Moreover, since the given is radially unbounded, we have . According to Definition (1), we haveThis means that the ISPTAF-ZNN (12) is strongly predefined-time stable within the time .
- For , the subsystem can be simplified asThe derivative of isThe Equation (24) shows that for , will not monotonically increase. Therefore, for all subsystems, the residual error vector remains zero within .
- For , the perturbed ISPTAF-ZNN (16) consists of subsystems in the time interval . Let , each subsystem can be represented asChoose , and assume the parameters satisfy . Taking the derivative of and substituting Equation (25), we getAccording to Theorem 1, the closed-loop system (26) weakly or strongly converges within the predefined-time . When , the entire system simplifies toAccording to Theorem 1, the residual error of each subsystem (27) decays to zero in a strongly predefined-time manner. The convergence time is . Therefore, for the ISPTAF-ZNN (16), the external disturbance can be suppressed within the predefined-time , and the residual error converges to zero within the strong predefined-time .
- For , the subsystem can be represented asThe derivative of isWhen the parameters satisfy , Equation (24) shows that will not monotonically increase within and will be able to suppress the external disturbance.
5. Simulation Results and Analysis
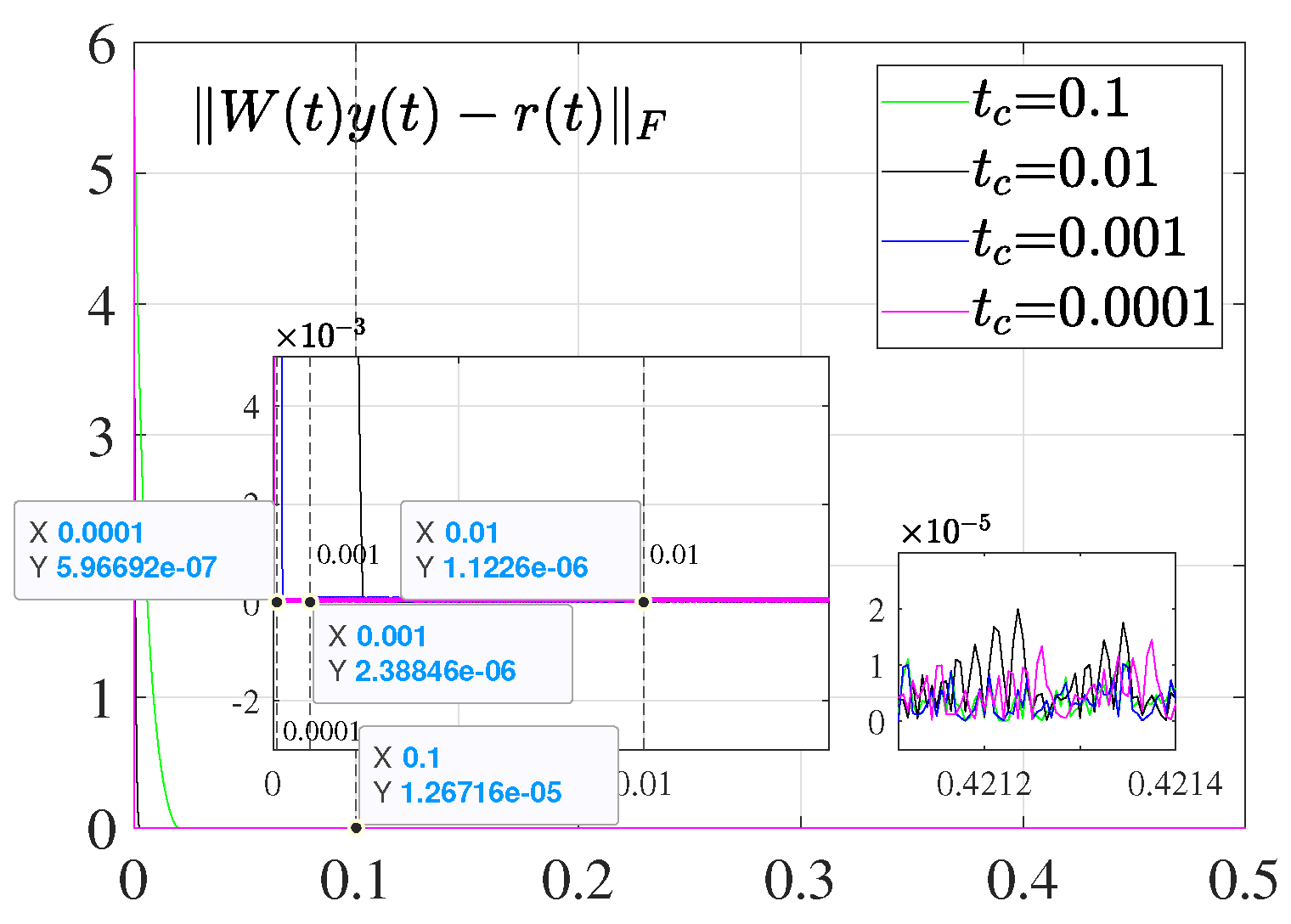
5.1. ZNN Solver Performance Verification
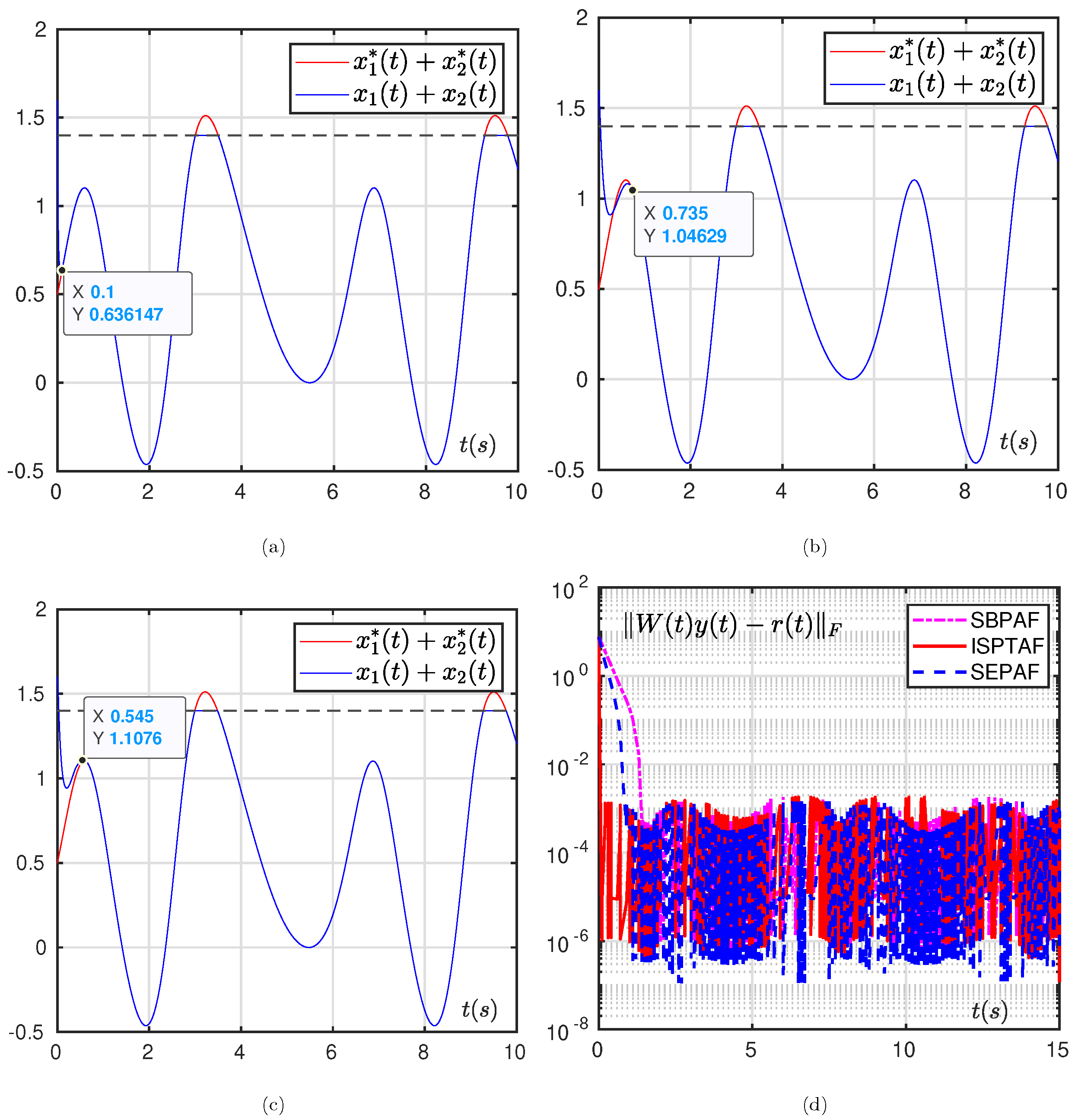
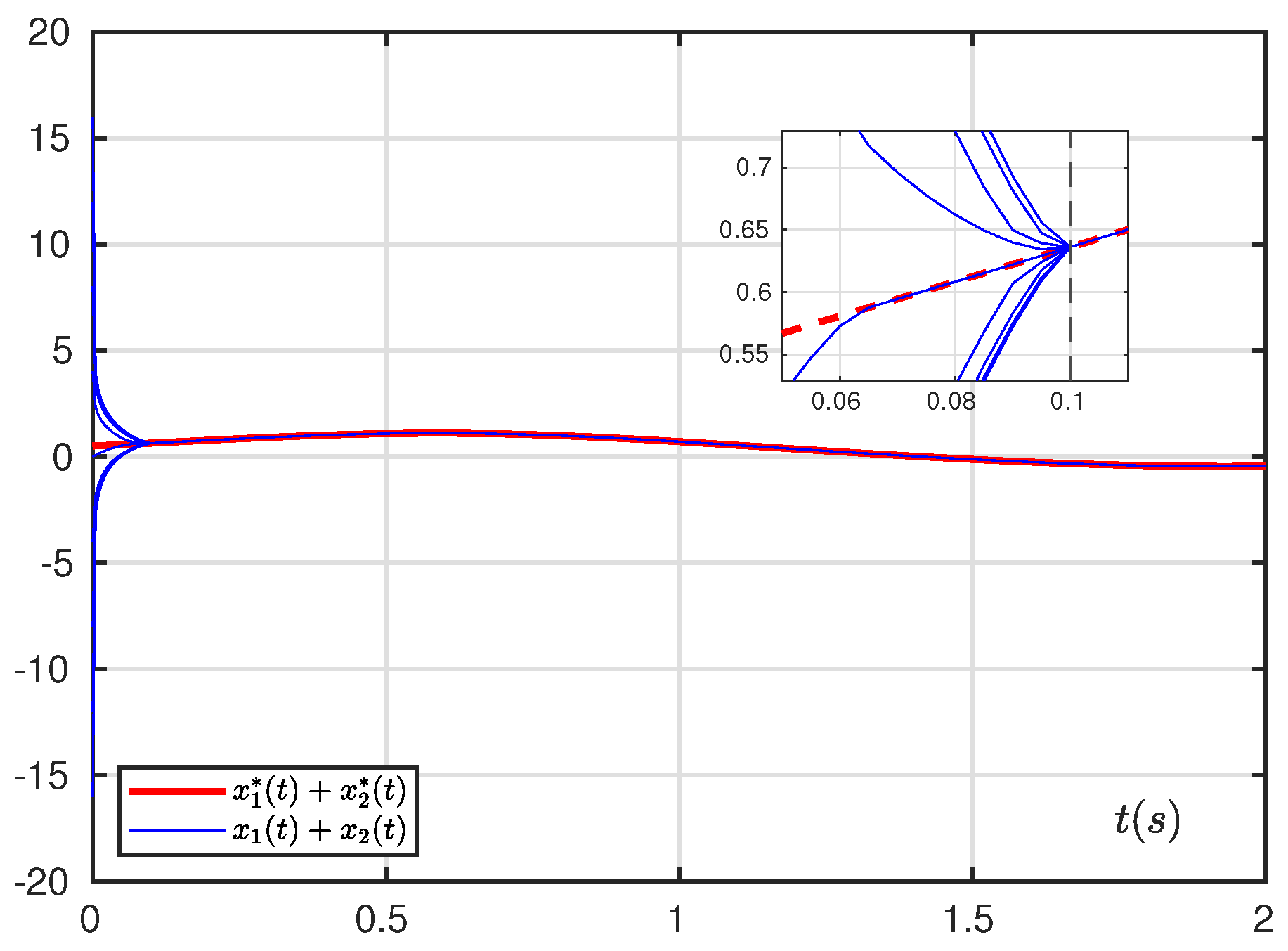
5.1.1. Without Noise Case
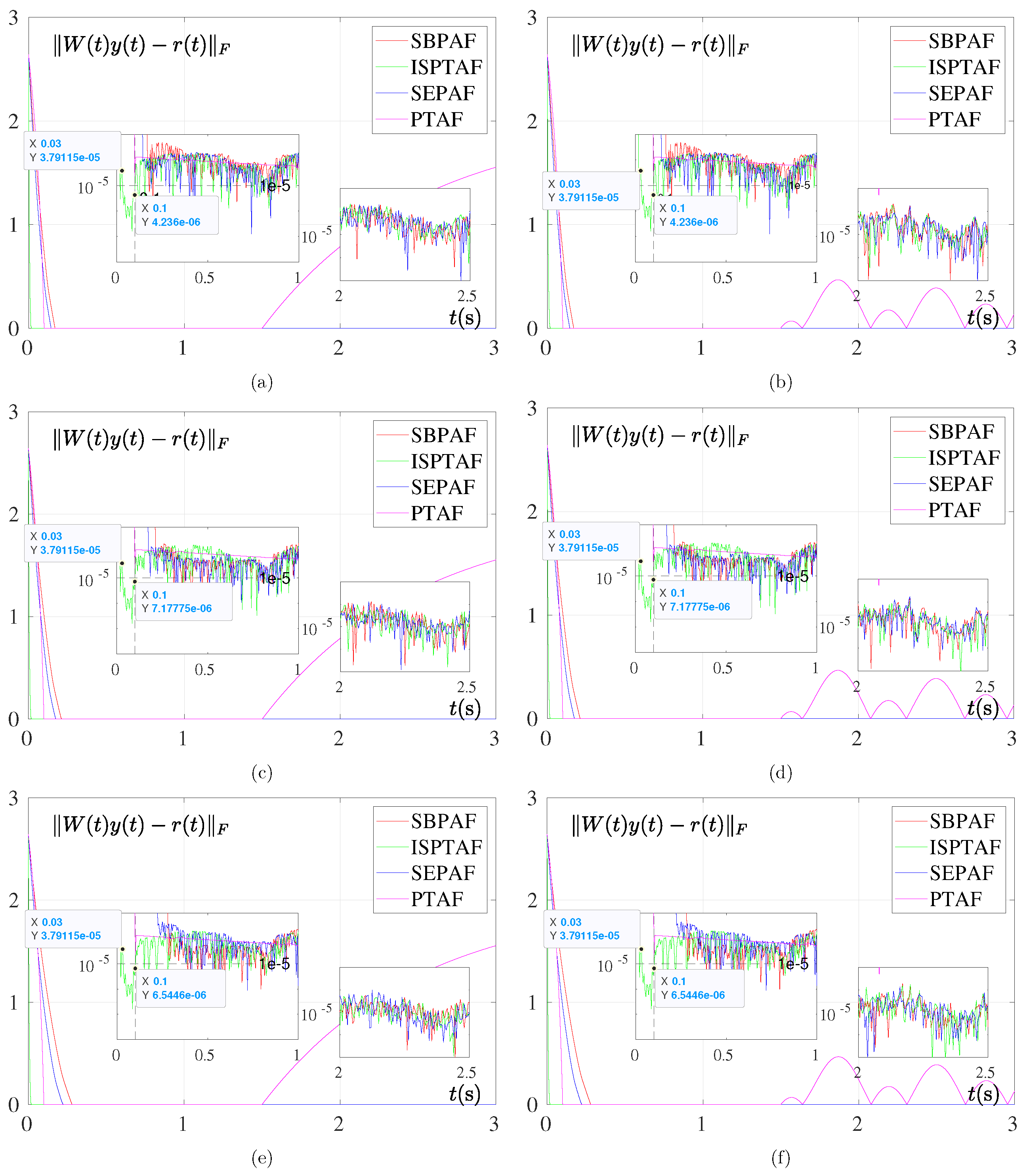
5.1.2. Under Noise Case
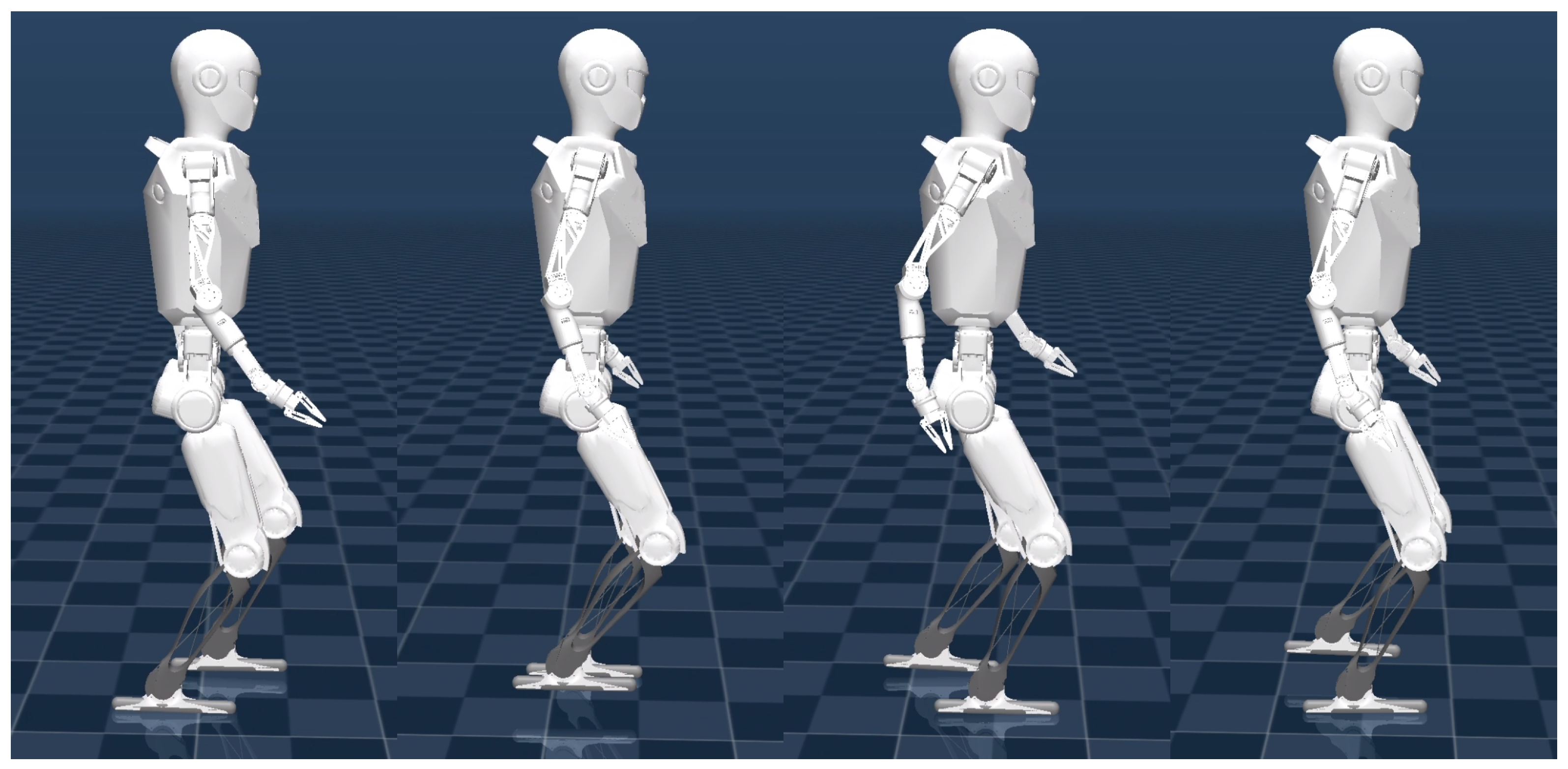
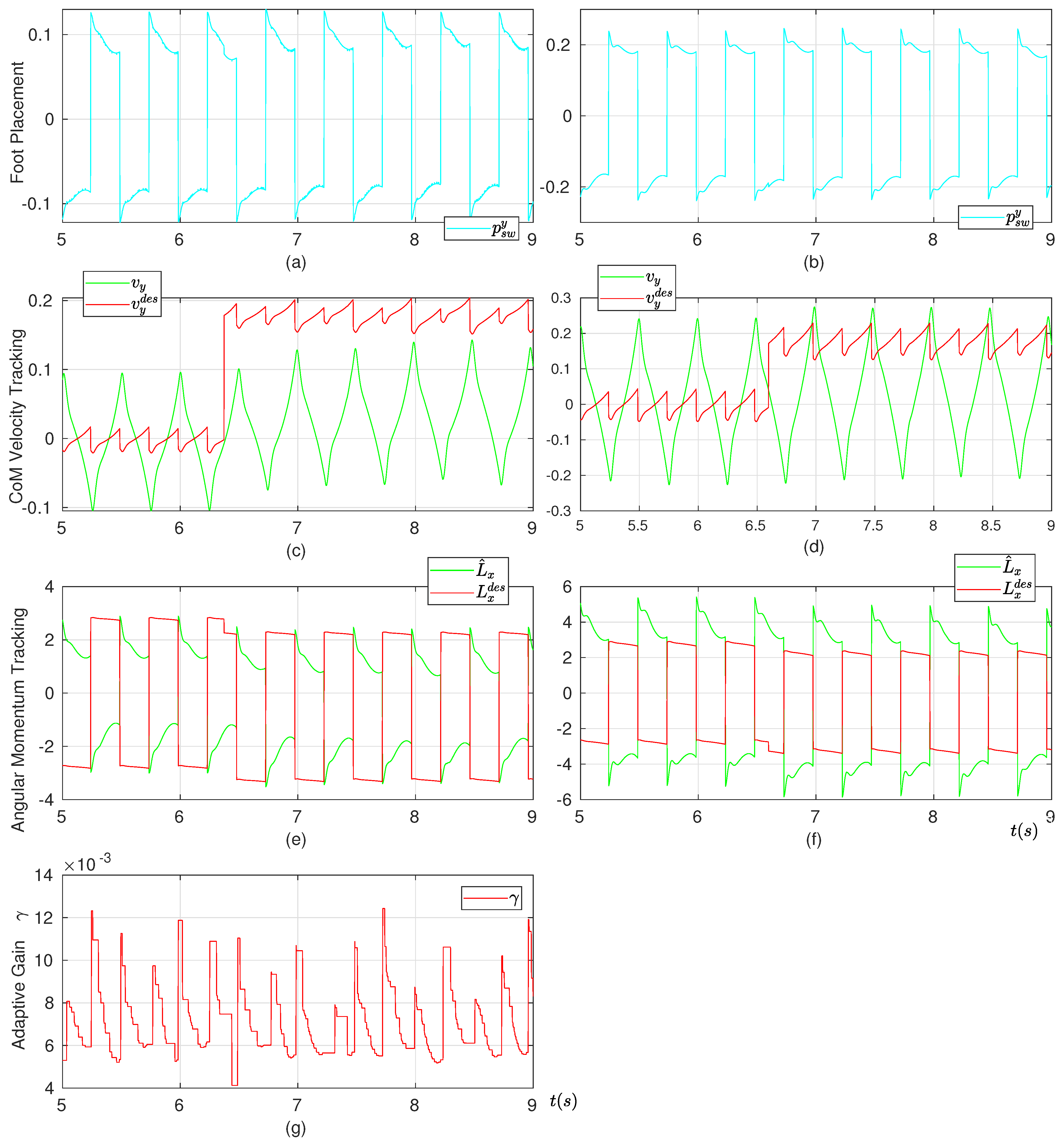
5.1.3. Foot Placement Optimization VERIFICATION
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ALIP | Angular Momentum Linear Inverted Pendulum |
| AF | Activation Function |
| AFP-QP | Adaptive Foot Placement Quadratic Programming |
| CoM | Center of Mass |
| GNN | Gradient-based Neural Networks |
| NCP | Nonlinear Complementarity Problem |
| ISPTAF | Integral Strong Predefined-time Activation Function |
| RNN | Recurrent Neural Networks |
| LIP | Linear Inverted Pendulum |
| TVQP | Time-Varying Quadratic Programming |
| SAPAF | Sign-bi-power Activation Function |
| SEPAF | Sign-exponential-power Activation Function |
| ZNN | Zeroing Neural Networks |
References
- Hu, K.; Chen, Z.; Kang, H.; Tang, Y. 3D vision technologies for a self-developed structural external crack damage recognition robot. Autom. Constr. 2024, 159, 105262. [Google Scholar] [CrossRef]
- Wang, T.; Chevallereau, C. Stability analysis and time-varying walking control for an under-actuated planar biped robot. Robot. Auton. Syst. 2011, 59, 444–456. [Google Scholar] [CrossRef]
- Westervelt, E.R.; Grizzle, J.W.; Koditschek, D.E. Hybrid zero dynamics of planar biped walkers. IEEE Trans. Autom. Control 2003, 48, 42–56. [Google Scholar] [CrossRef]
- Powell, M.J.; Ames, A.D. Mechanics-based control of underactuated 3D robotic walking: Dynamic gait generation under torque constraints. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 555–560. [Google Scholar]
- Gong, Y.; Grizzle, J. One-step ahead prediction of angular momentum about the contact point for control of bipedal locomotion: Validation in a lip-inspired controller. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2832–2838. [Google Scholar]
- Wang, W.; Liu, C.; Zhao, H.; Song, Z. Improved Deadbeat-Direct Torque and Flux Control for PMSM With Less Computation and Enhanced Robustness. IEEE Trans. Ind. Electron. 2023, 70, 2254–2263. [Google Scholar] [CrossRef]
- Wang, Z.; Chai, J.; Sun, X.; Lu, H. Predictive deviation filter for deadbeat control. IET Electr. Power Appl. 2020, 14, 1041–1049. [Google Scholar] [CrossRef]
- Zheng, L.; Yu, W.; Xu, Z.; Zhang, Z.; Deng, F. Design, Analysis, and Application of a Discrete Error Redefinition Neural Network for Time-Varying Quadratic Programming. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 13646–13657. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, T.; Zheng, L.; Luo, Y. A quadratic programming based neural dynamic controller and its application to UAVs for time-varying tasks. IEEE Trans. Veh. Technol. 2021, 70, 6415–6426. [Google Scholar] [CrossRef]
- Wang, B.; Sun, S.; Ren, W. Distributed continuous-time algorithms for optimal resource allocation with time-varying quadratic cost functions. IEEE Trans. Control Netw. Syst. 2020, 7, 1974–1984. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, Y.; Zheng, L.; Li, S.; Yu, Z.; Li, Y. A new varying-parameter convergent-differential neural-network for solving time-varying convex QP problem constrained by linear-equality. IEEE Trans. Autom. Control 2018, 63, 4110–4125. [Google Scholar] [CrossRef]
- Yi, Z. Convergence Analysis of Recurrent Neural Networks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 13. [Google Scholar]
- Wen, U.P.; Lan, K.M.; Shih, H.S. A review of Hopfield neural networks for solving mathematical programming problems. Eur. J. Oper. Res. 2009, 198, 675–687. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, D.; Wang, J. A recurrent neural network for solving Sylvester equation with time-varying coefficients. IEEE Trans. Neural Networks 2002, 13, 1053–1063. [Google Scholar] [CrossRef]
- Jin, L.; Li, S. Nonconvex function activated zeroing neural network models for dynamic quadratic programming subject to equality and inequality constraints. Neurocomputing 2017, 267, 107–113. [Google Scholar] [CrossRef]
- Li, W.; Wu, H.; Jin, L. A Lower Dimension Zeroing Neural Network for Time-Variant Quadratic Programming Applied to Robot Pose Control. IEEE Trans. Ind. Inform. 2024, 20, 11835–11843. [Google Scholar] [CrossRef]
- Zuo, Q.; Li, K.; Xiao, L.; Li, K. Robust finite-time zeroing neural networks with fixed and varying parameters for solving dynamic generalized Lyapunov equation. IEEE Trans. Neural Networks Learn. Syst. 2021, 33, 7695–7705. [Google Scholar] [CrossRef]
- Li, W.; Ma, X. Comparisons of Slack Variable, NCP Function, and Penalty Function Based ZNNs for Solving Equality-and Inequality-Constrained QP Problems With Robotic Applications. In Proceedings of the 2022 International Conference on Advanced Robotics and Mechatronics (ICARM), Guilin, China, 3–5 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 226–231. [Google Scholar]
- Li, S.; Chen, S.; Liu, B. Accelerating a recurrent neural network to finite-time convergence for solving time-varying Sylvester equation by using a sign-bi-power activation function. Neural Process. Lett. 2013, 37, 189–205. [Google Scholar] [CrossRef]
- Xiao, L.; Zhang, Y.; Jia, L.; He, Y. A ZNN-based sliding mode control strategy for solving synchronization problems of chaotic systems with application in memristor oscillator. J. Frankl. Inst. 2023, 360, 12101–12124. [Google Scholar] [CrossRef]
- Jin, J.; Chen, W.; Qiu, L.; Zhu, J.; Liu, H. A noise tolerant parameter-variable zeroing neural network and its applications. Math. Comput. Simul. 2023, 207, 482–498. [Google Scholar] [CrossRef]
- Li, W.; Liao, B.; Xiao, L.; Lu, R. A recurrent neural network with predefined-time convergence and improved noise tolerance for dynamic matrix square root finding. Neurocomputing 2019, 337, 262–273. [Google Scholar] [CrossRef]
- Jin, J.; Chen, W.; Ouyang, A.; Yu, F.; Liu, H. A time-varying fuzzy parameter zeroing neural network for the synchronization of chaotic systems. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 8, 364–376. [Google Scholar] [CrossRef]
- Jin, J.; Zhu, J.; Gong, J.; Chen, W. Novel activation functions-based ZNN models for fixed-time solving dynamirc Sylvester equation. Neural Comput. Appl. 2022, 34, 14297–14315. [Google Scholar] [CrossRef]
- Gong, Y.; Grizzle, J.W. Zero dynamics, pendulum models, and angular momentum in feedback control of bipedal locomotion. J. Dyn. Syst. Meas. Control 2022, 144, 121006. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Lagrange multipliers and optimality. SIAM Rev. 1993, 35, 183–238. [Google Scholar] [CrossRef]
- Chen, B.; Chen, X.; Kanzow, C. A penalized Fischer-Burmeister NCP-function. Math. Program. 2000, 88, 211–216. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y. Recurrent neural networks for real-time computation of inverse kinematics of redundant manipulators. In Machine Intelligence: Quo Vadis? World Scientific: Singapore, 2004; pp. 299–319. [Google Scholar]
- Cui, Z.; Huang, Y.; Li, W.; Chiu, P.W.Y.; Li, Z. Noise-Resistant Adaptive Gain Recurrent Neural Network for Visual Tracking of Redundant Flexible Endoscope Robot with Time-Varying State Variable Constraints. IEEE Trans. Ind. Electron. 2023, 71, 2694–2704. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, L.; Zhang, Z. An anti-disturbance integral recursive neural network for solving time-varying matrix inversion. In Proceedings of the 2021 36th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Nanchang, China, 28–30 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 271–275. [Google Scholar]
- Utkin, V.; Shi, J. Integral sliding mode in systems operating under uncertainty conditions. In Proceedings of the Proceedings of 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; IEEE: Piscataway, NJ, USA, 1996; Volume 4, pp. 4591–4596. [Google Scholar]
- Sánchez-Torres, J.D.; Gómez-Gutiérrez, D.; López, E.; Loukianov, A.G. A class of predefined-time stable dynamical systems. IMA J. Math. Control Inf. 2018, 35, i1–i29. [Google Scholar] [CrossRef]
- Li, W.; Ma, X.; Luo, J.; Jin, L. A strictly predefined-time convergent neural solution to equality-and inequality-constrained time-variant quadratic programming. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 4028–4039. [Google Scholar] [CrossRef]

| AF | Expression | Predefined-Time Convergence | Robustness |
|---|---|---|---|
| SBPAF [22] | No | Yes | |
| SEPAF [22] | Weakly | Yes | |
| PTAF [33] | Strong | No | |
| ISPTAF (18) | Strong | Yes |
| Convergence Accuracy | Convergence Time | ||
|---|---|---|---|
| AF | |||
| ISPTAF | 8 | 0.1 | |
| 6 | 0.1 | ||
| 4 | 0.1 | ||
| PTAF | 8 | 0.1 | |
| 6 | 0.1 | ||
| 4 | 0.1 | ||
| SEPAF | 8 | 0.19 | |
| 6 | 0.32 | ||
| 4 | 0.408 | ||
| SBPAF | 8 | 0.18 | |
| 6 | 0.315 | ||
| 4 | 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jiang, H.; Mou, H.; Li, Q.; Zhang, J. ZNN-Based Gait Optimization for Humanoid Robots with ALIP and Inequality Constraints. Mathematics 2025, 13, 954. https://doi.org/10.3390/math13060954
Liu Y, Jiang H, Mou H, Li Q, Zhang J. ZNN-Based Gait Optimization for Humanoid Robots with ALIP and Inequality Constraints. Mathematics. 2025; 13(6):954. https://doi.org/10.3390/math13060954
Chicago/Turabian StyleLiu, Yuanji, Hao Jiang, Haiming Mou, Qingdu Li, and Jianwei Zhang. 2025. "ZNN-Based Gait Optimization for Humanoid Robots with ALIP and Inequality Constraints" Mathematics 13, no. 6: 954. https://doi.org/10.3390/math13060954
APA StyleLiu, Y., Jiang, H., Mou, H., Li, Q., & Zhang, J. (2025). ZNN-Based Gait Optimization for Humanoid Robots with ALIP and Inequality Constraints. Mathematics, 13(6), 954. https://doi.org/10.3390/math13060954






