Device Independent Quantum Private Queries Based on Quantum Key Distribution

Abstract

Symmetric private information retrieval (SPIR) protocol is proposed for users to retrieve items from a database holder without revealing the retrieval address, and meanwhile the users cannot learn any additional entries of the database. Quantum key distribution (QKD)-based quantum private queries (QPQs) are the most practical protocols for the SPIR problem. However, most existing protocols assume ideal devices. To overcome this drawback, we propose a device independent QPQ protocol based on QKD with imperfect sources and detectors. By constructing the semi-definite programming optimization problem, we give the CHSH test threshold and prove the correctness of our protocol. We use the shift and permutation post-processing technique to further improve the security. We compare the performance of our protocol with a recent full device-independent QPQ. and discuss their relative advantages. The simulation results show that our protocol improves database security, user privacy and efficiency. The number of final key bits that Alice knows is close to 1, and Bob’s guessing probability is below 0.15 in our protocol. Moreover, the proposed scheme can be used for any entanglement-based QPQ protocol to remove trust on the devices.

1. Introduction

With the development of telecommunication technology, security and data privacy have attracted wide attention. Users of digital services may not want their information to be leaked to database holders. Private information retrieval (PIR) provides a scheme for this scenario [1,2]. PIR allows user Alice to retrieve an item from database holder Bob without revealing the retrieval address (user privacy). However, in some cases, the database holder may not want to reveal more information about the database than Alice requires (database privacy). Taking this additional security requirement into account is very necessary, especially when the information in the database is valuable and sensitive, such as medical records and bank accounts. This can be achieved by symmetrically private information retrieval (SPIR) [3,4,5].

Since user privacy and database security seem to be in conflict, it is difficult to design information-theoretic secure SPIR schemes [6]. Researchers have studied a weaker version of SPIR, called private query (PQ) [7,8,9,10]. In the PQ protocol, users are allowed to obtain more than one item of the database than SPIR. On the other hand, if the database holder Bob tries to gain Alice’s retrieval address, then Alice can detect that, which is called cheat sensitivity for user privacy. But it is still hard to achieve in the classical domain. Meanwhile, classical schemes might be vulnerable to a quantum adversary [11]. To overcome these problems, quantum private query (QPQ) protocol has been proposed.

In 2008, Giovannetti et al. proposed the first QPQ protocol performed by unitary operations [12], followed by [13,14]. However, all of these protocols are difficult to implement. To make QPQ practical, Jakobi et al. have proposed a new QPQ protocol based on the SARG04 QKD [15]. This type of QPQ protocol is called QKD-based QPQ. Since QKD has been widely studied in both theoretical and experimental research fields [16,17,18,19,20,21,22,23,24], QKD-based QPQ protocol is easier to implement than the original QPQ. Based on different types of QKD protocols, various QKD-based QPQ protocols have been proposed [25,26,27,28,29,30,31]. Furthermore, some techniques have been applied to improve the performance of QPQs. Wei et al. [32] have presented a special “low-shift and addition” technique to establish a generic construction of QKD-based QPQs with ideal database security. Considering that weak coherent pulse sources are usually used in practical implementation, the decoy state method is adopted in the QPQ protocol [33,34].

QKD-based QPQs can be viewed as a cryptographic protocol in which two parties are dishonest [12,13,14,15]. QKD-based QPQs can generally be performed in the following three steps. (1) Oblivious raw key distribution. Alice and Bob first generate an oblivious raw key. (2) Post-processing. In order to reduce Alice’s known bits, Alice and Bob cut the raw key into several substrings with equal length and add them bitwise to obtain the final key. Then Alice knows only one (or a little more than one) bit of the final key. (3) Private query. Alice announces a shift to the final key according to the item she wants to query. Then Bob uses the shifted key to encrypt the database and sends the whole encrypted database to Alice. Finally, Alice can know exactly the bit she wants by decrypting the database, which means that a private query has been performed successfully. The security of all of the above protocols is based on the fact that Bob relies on his devices, i.e., the source which supplies the qubits and the detectors which measure the qubits. To remove trustful assumptions, a device-independent QPQ protocol (DI-QPQ) has been described in [35]. However, it requires the assumption that all detectors at Bob’s end have unit efficiency; that is, he always obtains a conclusive outcome. Recently, Basak et al. have proposed a QPQ protocol for full DI certification using a self-test strategy (FDI-QPQ) [36], followed by [37].

To perform the QPQ protocol with imperfect sources and detectors, we utilize the idea of a local CHSH test proposed by Lim et al. [38]. In the local CHSH test, the sender executes the CHSH test at its terminal as an incentive to verify whether the states used for QKD are maximally entangled. The local CHSH test can provide a certification with imperfect sources. On the other hand, for imperfect detectors, we apply the Navascués–Pironio–Acín (NPA) method arising from quantum non-locality in DI quantum information processing [39]. Inspired by the NPA method, a semi-definite programming (SDP) optimization problem is proposed to analyze the security of QKD [40].

In this paper, by analyzing the security of the DI-QPQ protocol, we find that it cannot achieve full device independent because it requires the assumption that all detectors have unit efficiency. To address this challenge, we propose a QPQ protocol with imperfect sources and detectors (called ISD-QPQ). By adopting the local CHSH test, Bob can certify whether the states are in the desired form or not. We employ the NPA method to construct the SDP optimization problem to solve the predefined threshold probability and Alice’s success guess probability. We use the shift and permutation post-processing method to further improve the efficiency and security of our protocol. Furthermore, we discuss the database security and user privacy of our ISD-QPQ protocol.

The paper is organized as follows. In Section 2, we review the DI-QPQ protocol and analyze the security under imperfect sources and detectors. Next, in Section 3, we detail our IFD-QPQ protocol. In Section 4, by constructing the SDP optimization problem, we prove the correctness, database security and user privacy of IFD-QPQ protocol. The simulation results are shown in Section 5. Finally, Section 6 gives the conclusion.

2. Analysis of DI-QPQ with Imperfect Source and Detectors

2.1. Review of DI-QPQ Protocol

With the idea of a local CHSH-like test, Maitra. A. et al. have proposed the DI-QPQ protocol [35]. This QPQ protocol no longer requires trust in the source as well as the detectors. We first review the DI-QPQ protocol as follows.

(1)

Bob prepares a long sequence of entangled states ${\displaystyle \frac{1}{\sqrt{2}}}({\left|0\right.〉}_B{\left|{\varphi }_0\right.〉}_A+{\left|1\right.〉}_B{\left|{\varphi }_1\right.〉}_A)$, where ${\left|{\varphi }_0\right.〉}_A=cos{\displaystyle \frac{\theta }{2}}\left|0\right.〉+sin{\displaystyle \frac{\theta }{2}}\left|1\right.〉$ and ${\left|{\varphi }_1\right.〉}_A=cos{\displaystyle \frac{\theta }{2}}\left|0\right.〉-sin{\displaystyle \frac{\theta }{2}}\left|1\right.〉$.

(2)

For each prepared entangled state, Bob divides it into two sets. One is $N_{CHSH}$ and the other is $N_{QPQ}$. The set $N_{CHSH}$ contains $\gamma n$ entangled states, whereas $N_{QPQ}$ contains $(1-\gamma )n$ entangled states for $0<\gamma <1$.

(3)

For rounds $i\in \{1,\dots ,\gamma n\}$

• Bob chooses $x_i\in \{0,1\}$ and $y_i\in \{0,1\}$ uniformly at random. If $x_i=0$, he measures the first particle of the entangled state in the $\{\left|0\right.〉,\left|1\right.〉\}$ basis, and if $x_i=1$, he measures it in the $\{\left|+\right.〉,\left|-\right.〉\}$ basis. Similarly, if $y_i=0$, Bob measures the second particle of the entangled state in the $\{\left|{\psi }_1\right.〉,\left|{\psi }_1^{\perp }\right.〉\}$ basis, and if $y_i=1$, he measures it in the $\{\left|{\psi }_2\right.〉,\left|{\psi }_2^{\perp }\right.〉\}$ basis. Here, we consider $\left|{\psi }_1\right.〉=cos{\displaystyle \frac{{\psi }_1}{2}}\left|0\right.〉+sin{\displaystyle \frac{{\psi }_1}{2}}\left|1\right.〉$ and $\left|{\psi }_2\right.〉=cos{\displaystyle \frac{{\psi }_2}{2}}\left|0\right.〉+sin{\displaystyle \frac{{\psi }_2}{2}}\left|1\right.〉$.
• Bob records and encodes the output as $a_i\in \{0,1\}(b_i\in \{0,1\})$ for the first (second) particle. For the first particle in each pair, $a_i=0$ if the measurement result is $\left|0\right.〉$ or $\left|+\right.〉$ and $a_i=1$ if the result is $\left|1\right.〉$ or $\left|-\right.〉$. For the second particle in each pair, $b_i=0$ if the measurement result is $\left|{\psi }_1\right.〉$ or $\left|{\psi }_2\right.〉$ and $b_i=1$ if the result is $\left|{\psi }_1^{\perp }\right.〉$ or $\left|{\psi }_2^{\perp }\right.〉$.
• Define $Y_i=1$, if $a_i\oplus b_i=x_i\wedge y_i$; otherwise, $Y_i=0$.

(4)

If ${\displaystyle \frac{1}{\gamma n}}{\sum }_i{Y}_i<P={\displaystyle \frac{1}{8}}[sin\theta (sin{\psi }_1+sin{\psi }_2)+cos{\psi }_1-cos{\psi }_2]+{\displaystyle \frac{1}{2}}$, Bob aborts the protocol.

(5)

Conditional on the event that the local $N_{CHSH}$ test at Bob’s end has been successful, Bob proceeds to the subset $N_{QPQ}$ and sends the other half of the remaining $(1-\gamma )n$ entangled pairs to Alice.

(6)

Alice performs the private query phase as in [26] or any other entanglement-based QPQ protocol.

2.2. Security of DI-QPQ Protocol with Imperfect Sources and Detectors

We analyze the security of DI-QPQ protocol under imperfect sources in practical. Suppose that the source provides arbitrary entangled states $\alpha {\left|0\right.〉}_B{\left|{\varphi }_0\right.〉}_A+\beta {\left|1\right.〉}_B{\left|{\varphi }_1\right.〉}_A$, where ${\left|\alpha \right|}^2={\displaystyle \frac{1}{2}}+\tau$ and ${\left|\beta \right|}^2={\displaystyle \frac{1}{2}}-\tau$. The joint probability $Pr(a_i\oplus b_i=x_i\wedge y_i)$ can be calculated by

$$\begin{array}{c}\hfill Pr(a_i\oplus b_i=x_i\wedge y_i)={\displaystyle \frac{1}{4}}[Pr\left(00\right|00)+Pr\left(11\right|00)+Pr\left(00\right|01)+Pr\left(11\right|01)\\ \hfill +Pr\left(00\right|10)+Pr(11\left|10\right)+Pr\left(01\right|11)+Pr(10\left|11\right)],\end{array}$$

(1)

where the conditional probability of $(a_i,b_i)$ given $(x_i,y_i)$ can be obtained by

$$\begin{array}{cc}\hfill Pr\left(00\right|00)& =(\overline{\alpha }\langle {\varphi }_0|\langle 0|+\overline{\beta }\langle {\varphi }_1|\langle 1|)(|0\rangle \langle 0|\otimes |{\psi }_1\rangle \langle {\psi }_1|)(\alpha |{\varphi }_0\rangle |0\rangle +\beta |{\varphi }_1\rangle |1\rangle )\hfill \\ \hfill & ={\left|\alpha \right|}^2{(cos{\displaystyle \frac{\theta }{2}}cos{\displaystyle \frac{{\psi }_1}{2}}+sin{\displaystyle \frac{\theta }{2}}sin{\displaystyle \frac{{\psi }_1}{2}})}^2\hfill \\ \hfill & ={\left|\alpha \right|}^2{cos}^2({\displaystyle \frac{\theta -{\psi }_1}{2}}).\hfill \end{array}$$

(2)

Similarly, we have

$$\begin{array}{cc}\hfill & Pr\left(11\right|00)={\left|\beta \right|}^2{sin}^2({\displaystyle \frac{\theta +{\psi }_1}{2}}),\hfill \\ \hfill & Pr\left(00\right|01)={\left|\alpha \right|}^2{cos}^2({\displaystyle \frac{\theta -{\psi }_2}{2}}),\hfill \\ \hfill & Pr\left(11\right|01)={\left|\beta \right|}^2{sin}^2({\displaystyle \frac{\theta +{\psi }_2}{2}}),\hfill \\ \hfill & Pr\left(00\right|10)={\displaystyle \frac{1}{2}}[\alpha cos({\displaystyle \frac{\theta -{\psi }_1}{2}})+\beta sin({\displaystyle \frac{\theta +{\psi }_1}{2}}){]}^2,\hfill \\ \hfill & Pr\left(11\right|10)={\displaystyle \frac{1}{2}}[\alpha sin({\displaystyle \frac{\theta -{\psi }_1}{2}})-\beta cos({\displaystyle \frac{\theta +{\psi }_1}{2}}){]}^2,\hfill \\ \hfill & Pr\left(01\right|11)={\displaystyle \frac{1}{2}}[\alpha sin({\displaystyle \frac{\theta -{\psi }_2}{2}})+\beta cos({\displaystyle \frac{\theta +{\psi }_2}{2}}){]}^2,\hfill \\ \hfill & Pr\left(10\right|11)={\displaystyle \frac{1}{2}}[\alpha cos({\displaystyle \frac{\theta -{\psi }_2}{2}})-\beta sin({\displaystyle \frac{\theta +{\psi }_2}{2}}){]}^2.\hfill \end{array}$$

(3)

According to these conditional probabilities, we can obtain

$$\begin{array}{cc}\hfill Pr(a_i\oplus b_i=x_i\wedge y_i)=& {\displaystyle \frac{1}{8}}(sin\theta (sin{\psi }_1+sin{\psi }_2)+2\tau cos\theta (cos{\psi }_1+cos{\psi }_2)\hfill \\ \hfill & +2\sqrt{{\displaystyle \frac{1}{4}}-{\tau }^2}(cos{\psi }_1-cos{\psi }_2))+{\displaystyle \frac{1}{2}}.\hfill \end{array}$$

(4)

Thus, by calculating the maximum of above equation while traversing the parameter $\tau$, we find that

$$Pr(a_i\oplus b_i=x_i\wedge y_i)<{\displaystyle \frac{1}{8}}[sin\theta (sin{\psi }_1+sin{\psi }_2)+cos{\psi }_1-cos{\psi }_2]+{\displaystyle \frac{1}{2}},$$

(5)

where $\tau \in [0,{\displaystyle \frac{1}{2}}]$. The simulation result is shown in Section 5. That is, in DI-QPQ protocol, the joint probability $Pr(a_i\oplus b_i=x_i\wedge y_i)$ is always less than the threshold parameter P. If Alice and Bob do not share the entangled states of the certain kind, Bob will discover and abort the protocol by performing the local test at his end. Bob can then remove his trust in the source. However, the DI-QPQ protocol requires the assumption that all detectors at Bob’s end have unit efficiency, i.e., he always receives conclusive outcomes. For practical implementation of the protocol, imperfect detectors are generally exploited. Therefore, it is necessary to study the QPQ protocol for imperfect sources and detectors. To solve this problem, we propose a practical QPQ protocol with imperfect sources and detectors, called ISD-QPQ protocol.

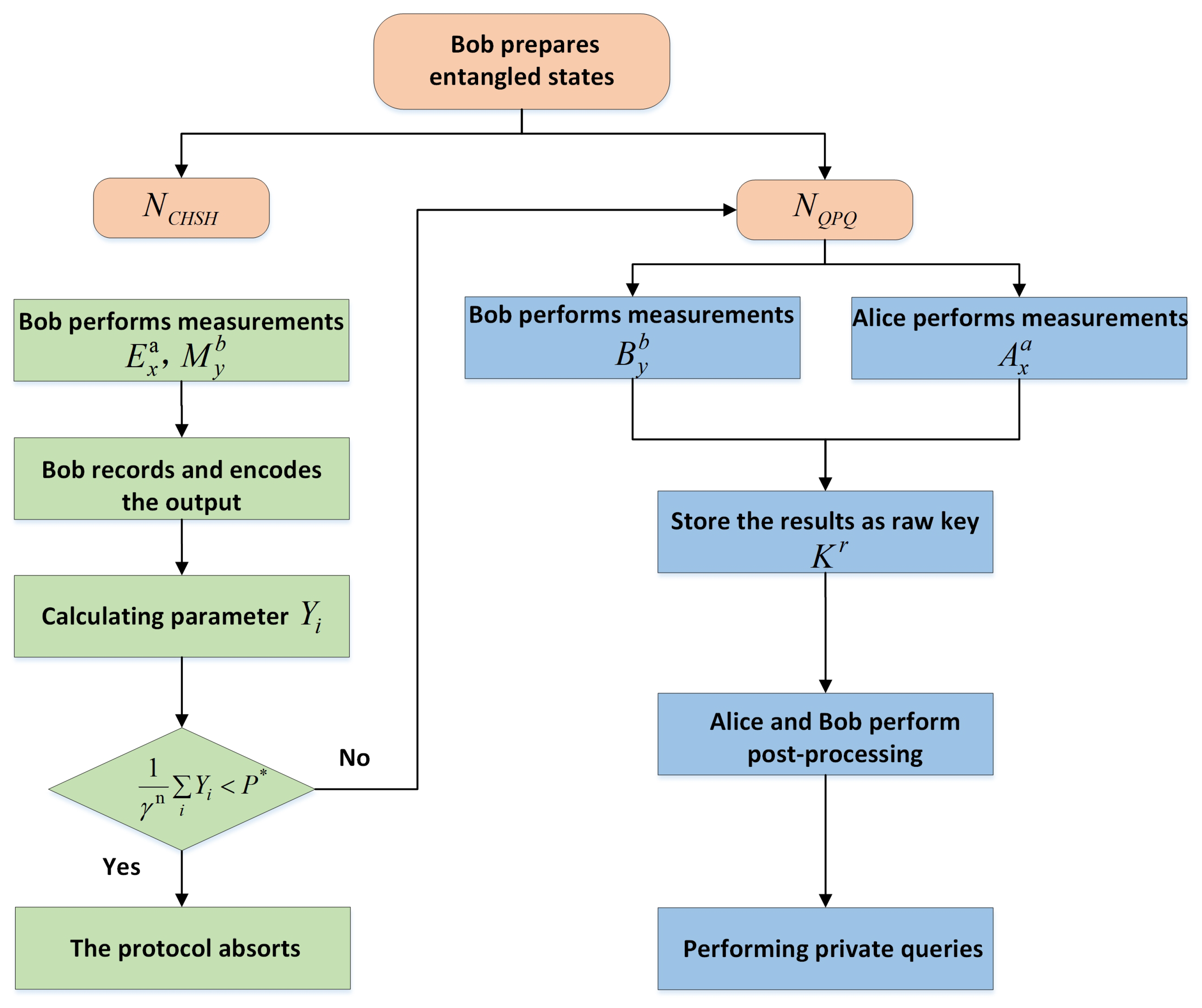
3. Practical Quantum Private Queries with Imperfect Sources and Detectors

Here, we detail our proposed ISD-QPQ protocol as follows.

(1)

The database holder Bob prepares a long sequence of entangled photon pairs in the state

$${|\mathsf{\Phi }\rangle }_{BA}={\displaystyle \frac{1}{\sqrt{2}}}({\left|0\right.〉}_B{\left|{\varphi }_0\right.〉}_A+{\left|1\right.〉}_B{\left|{\varphi }_1\right.〉}_A),$$

(6)

where

$$\begin{array}{c}\hfill {\left|{\varphi }_0\right.〉}_A=cos{\displaystyle \frac{\theta }{2}}\left|0\right.〉+sin{\displaystyle \frac{\theta }{2}}\left|1\right.〉,\\ \hfill {\left|{\varphi }_1\right.〉}_A=cos{\displaystyle \frac{\theta }{2}}\left|0\right.〉-sin{\displaystyle \frac{\theta }{2}}\left|1\right.〉.\end{array}$$

(7)

The parameter $\theta \in (0,{\displaystyle \frac{\pi }{2}})$ can be selected flexibly.

(2)

For each prepared entangled state, Bob divides it into two sets $N_{CHSH}$ and $N_{QPQ}$. The set $N_{CHSH}$ contains $\gamma n$ entangled states, which is used to conduct the CHSH local test, whereas $N_{QPQ}$ contains $(1-\gamma )n$ entangled states for $0<\gamma <1$, which is used to perform private queries.

For round $i\in \{1,\dots ,\gamma n\}$ in $N_{CHSH}$, Bob chooses $x_i\in \{0,1\}$ and $y_i\in \{0,1\}$ uniformly at random. $x_i=0$ denotes Bob measures the first particle of the entangled state in the $\{\left|0\right.〉,\left|1\right.〉\}$ basis. If $x_i=1$, he measures it in the $\{\left|+\right.〉,\left|-\right.〉\}$ basis. If $y_i=0$, Bob measures the second particle of the entangled state in the $\{\left|{\psi }_1\right.〉,\left|{\psi }_1^{\perp }\right.〉\}$ basis, and if $y_i=1$, he measures it in the $\{\left|{\psi }_2\right.〉,\left|{\psi }_2^{\perp }\right.〉\}$ basis. Here, we consider

$$\begin{array}{c}\hfill \left|{\psi }_1\right.〉=cos{\displaystyle \frac{{\psi }_1}{2}}\left|0\right.〉+sin{\displaystyle \frac{{\psi }_1}{2}}\left|1\right.〉,\\ \hfill \left|{\psi }_2\right.〉=cos{\displaystyle \frac{{\psi }_2}{2}}\left|0\right.〉+sin{\displaystyle \frac{{\psi }_2}{2}}\left|1\right.〉.\end{array}$$

(8)

We use positive-operator valued measures (POVMs) to describe Bob’s measurements: Bob randomly performs one of two possible POVMs denoted by $\{E_x^a,M_y^b\}$, where $x\in \{0,1\}$ and $y\in \{0,1\}$ represent the basis choice for the first and the second particles of the entangled state, respectively. Taking signal loss and detection inefficiency into account, each measurement has three possible outcomes $a,b\in \{0,1,\varnothing \}$, where ∅ represents the empty detection event.

(3)

Bob records and encodes the output as $a_i\in \{0,1\}(b_i\in \{0,1\})$ for the first (second) particle. For the first particle in each pair, $a_i=0$ if the measurement result is $\left|0\right.〉$ and $a_i=1$ if the result is $\left|1\right.〉$. For the second particle in each pair, $b_i=0$ if the measurement result is $\left|{\psi }_1\right.〉$ or $\left|{\psi }_2\right.〉$ and $b_i=1$ if the result is $\left|{\psi }_1^{\perp }\right.〉$ or $\left|{\psi }_2^{\perp }\right.〉$.

(4)

Define $Y_i$ for the test round $i\in N_{CHSH}$

$$\begin{array}{cc}\hfill Y_i=& \left\{\begin{array}{c}1\mathrm{if}{a}_i\oplus b_i=x_i\wedge y_i,\hfill \\ 0\mathrm{if}\mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(9)

If ${\displaystyle \frac{1}{\gamma n}}{\sum }_i{Y}_i<P^{*}$, Bob aborts the protocol.

(5)

Conditional on the event that the local $N_{CHSH}$ test at Bob’s end has been successful, Bob proceeds to the subset $N_{QPQ}$ and sends the photon A of the remaining $(1-\gamma )n$ entangled states in each pair to Alice. $\left|{\varphi }_0\right.〉$ and $\left|{\varphi }_1\right.〉$ represent the bits 0 and 1.

(6)

Alice declares which qubits are received successfully. The bits carried by the lost photons are discarded. For each successfully received qubit, Bob measures his corresponding qubits in the $\{{|0\rangle }_B,{|1\rangle }_B\}$ basis. Then, Alice chooses to measures her qubits either in the $\{{|{\varphi }_0\rangle }_A,{|{\varphi }_0^{\perp }\rangle }_A\}$ basis or in the $\{{|{\varphi }_1\rangle }_A,{|{\varphi }_1^{\perp }\rangle }_A\}$ basis randomly. If Alice’s measurement result is $|{\varphi }_0^{\perp }\rangle$, she can obtain that the raw key bit at Bob’s end must be 1. If it is $|{\varphi }_1^{\perp }\rangle$, the raw key bit must be 0. We also use POVMs $\left\{A_x^a\right\}$ and $\left\{B_y^b\right\}$ to describe Alice’s and Bob’s measurements, where $x\in \{0,1\}$ and $y\in \left\{0\right\}$ represent the basis choice, respectively. Taking signal loss and detection inefficiency into account, each measurement has three possible outcomes $a,b\in \{0,1,\varnothing \}$.

(7)

Then, they store the measurement results of remaining signal states as the raw key. They share the raw key $K^r$, in which Bob knows all the bits while Alice only knows part of $K^r$.

(8)

Alice and Bob perform classical post-processing. Assume an N-bit database is concerned, the created string should be of length $k\times N$ (k is a security parameter). Bob first randomly announces a permutation mapping, then Alice announces a shift $s_0$ from $\{0,1,\dots ,kN-1\}$ randomly. After that, they shift the raw key by $s_0$, then apply the permutation mapping on it and cut it into kN-bit substrings. These substrings are added bitwise to obtain the final key $K^f$ in order that Alice knows only roughly one bit in $K^f$. If Alice does not know any bit of $K^f$, the protocol is aborted.

(9)

Suppose Alice knows the j-th bit $K_j^f$ and wants the i-th item $X_i$ in the database, then she declares a shift $s=j-i$. Bob encrypts his database with $K^f$ shifted by s, i.e., $C_n=X_n\oplus K_{n+s}^f$, and sends the encrypted database $C_n$ to Alice. Then, Alice recovers the wanted item by her known bit, i.e., $C_i=X_i\oplus K_j^f$.

For each prepared entangled state, Bob divides it into two sets to perform the CHSH local test steps and the QPQ steps, respectively. Our scheme for testing steps lies on top of the QPQ protocol, which means that Bob performs the local CHSH test before starting the QPQ protocol. Here, we work on the QPQ protocol presented in [26]. It is also feasible to replace the QPQ step of our scheme with any entanglement-based QPQ protocol. Then, our scheme can be used for any entanglement-based QPQ protocol to remove trust in the devices. The simplified ISD-QPQ protocol flowchart as shown below (Figure 1):

4. Security Analysis

Before analyzing the security of our ISD-QPQ protocol, we first enumerate the assumptions required for the security of the protocol as follows:

(1)

Devices are causally independent. This assumption implies that the devices are memoryless.

(2)

The adversary’s attacks are independent and identically distributed.

(3)

All the detectors at Bob’s end have a trusted loss.

In the QPQ protocol, security consists mainly of two parts, database security and user privacy, without considering the attack of the third party. Alice can control the sources and detectors on the Bob side, and she may use the imperfect device with bias to simulate a lossy device. It is necessary to require that the dishonest Alice’s attack strategy is independent of the loss. Dishonest Alice cannot control the sources and measurement devices in Bob’s lab after the devices are installed.

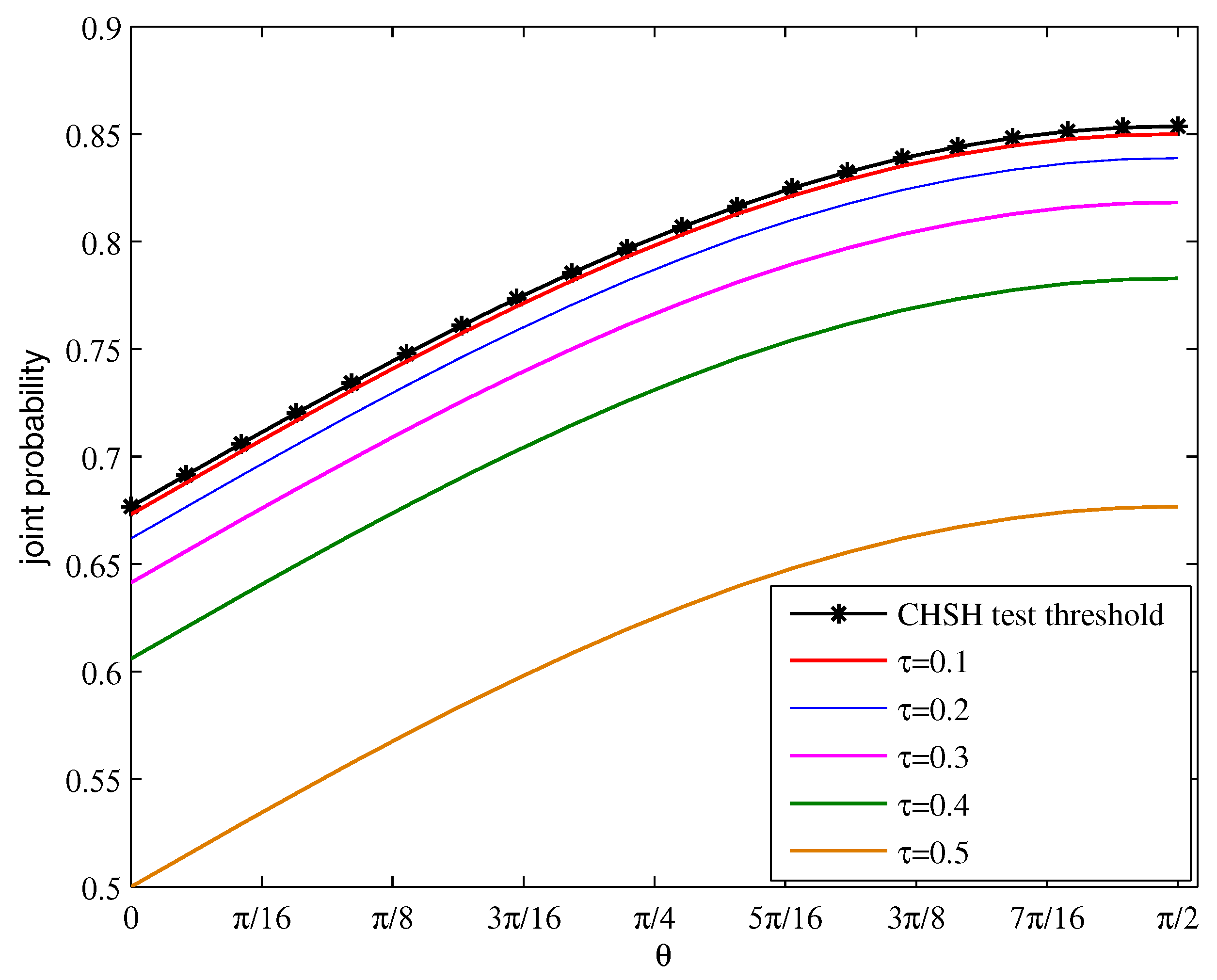
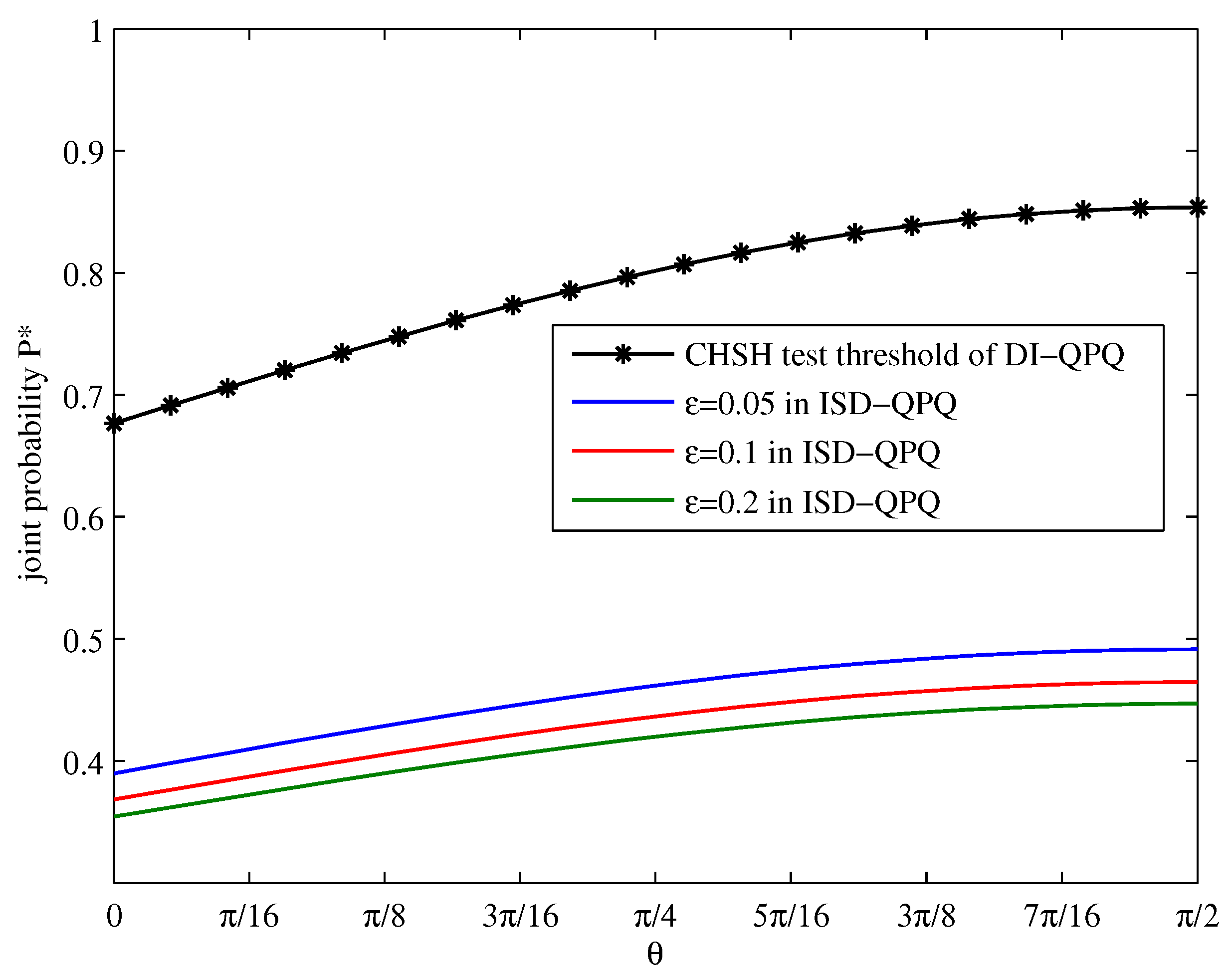
4.1. SDP Optimization Problem for Bounding the Joint Probability

To compute the security of the protocol, we need to give the bound of $P^{*}$. This bound can be used to check whether the entangled states are credible. Here, we employ the SDP optimization method to estimate the $P^{*}$, which converts the initial characterization problem into a hierarchy of semi-definite programs. More specifically, a hierarchy of conditions necessarily satisfied by any distributions representing the probabilities come from local measurements on a shared quantum state was introduced. Each condition in this hierarchy is formulated as a semi-definite program. Each hierarchy forms a convex set that is approximated to the quantum set from outside. By going to higher hierarchies, the approximation becomes tighter. Thus, using this method, we can optimize to bound $P^{*}$ over the various convex sets.

The probability distribution is said to admit a quantum system if for all $a,b,x,y$ there exists a set of measurement operators $\{E_x^a,M_y^b\}$ and a quantum state $\rho$ such that

$$\begin{array}{c}\hfill p(a,b|x,y)=tr(\rho E_x^a\otimes M_y^b).\end{array}$$

(10)

where $\rho$ is shared by two parties, Alice and Bob. ${\left\{E_x^a\right\}}_{a\in A,x\in X},{\left\{M_y^b\right\}}_{b\in B,y\in Y}$ are the measurement operators in Bob’s testing step, where $A,B\in \{0,1,\varnothing \}$ are outcome sets, and $X,Y\in \{0,1\}$ are input sets.

The POVMs follow the following properties: (i) for any $x,y$, $E_x^a{E}_x^{a^{\prime }}=0$ and $M_y^b{M}_y^{b^{\prime }}=0$ for $a\ne a^{\prime },b\ne b^{\prime }$, (ii) ${\mathsf{\Sigma }}_a{E}_x^a=\mathbb{I}$ and ${\mathsf{\Sigma }}_b{M}_y^b=\mathbb{I}$, (iii) ${\left(E_x^a\right)}^2=E_x^a={\left(E_x^a\right)}^{†}$ and ${\left(M_y^b\right)}^2=M_y^b={\left(M_y^b\right)}^{†}$, (iv) $[E_x^a,M_y^b]=0$. Note that with this SDP method, detailed characterization of the quantum signals and measurements, including their dimensions, is no longer required in the analysis.

A series of necessary conditions satisfied by the probabilities of quantum observation can be introduced. Let $\mathsf{S}=\{S_1,\dots ,S_n\}$ be a set of n operators, where each element is a linear combination of products of $E_x^a$ and $M_y^b$. The PSD Gram matrix G associated to the set $\mathsf{S}$ has the definition:

$$G_{i,j}=\mathrm{Tr}\left(S_i^{†}{S}_j\rho \right).$$

(11)

Taking $\mathsf{S}=\{E_x^a,M_y^b,E^{\varnothing }\}$. The important point is that $G_{i,j}$ partially reflects the properties $\left(\mathrm{i}\right)$–$\left(\mathrm{iv}\right)$ satisfied by the operators $E_x^a$ and $M_y^b$. For instance, property (i) and (iii) implies $\mathrm{Tr}\left(S_i^{†}{S}_j\rho \right)=\mathrm{Tr}\left(M_m^c{M}_m^{c^{\prime }}\rho \right)=0$ for $c\ne c^{\prime }$ and $\mathrm{Tr}\left(S_i^{†}{S}_j\rho \right)=\mathrm{Tr}\left(M_m^c{M}_m^c\rho \right)=\mathrm{Tr}\left(M_m^c\rho \right)$ for $c=c^{\prime }$, where $m=x,y$, $c=a,b$; suppose $\mathsf{S}$ contains operators $S_1=M_m^1$, …, and $S_{\left|c\right|}=M_m^{\left|c\right|}$, then property (ii) implies ${\sum }_{i=1}^{\left|c\right|}\mathrm{Tr}\left(S_i\rho \right)=\mathrm{Tr}\left({\sum }_c{M}_m^c\rho \right)=1$. In addition, suppose that $\mathsf{S}$ contains an operator $S_i=E_x^a$ and $S_j=M_y^b{E}_{x^{\prime }}^{a^{\prime }}{M}_{y^{\prime }}^b$, then the property (iv) implies $\mathrm{Tr}\left(S_i^{†}{S}_j\rho \right)=\mathrm{Tr}\left(E_x^a{M}_y^b{E}_{x^{\prime }}^{a^{\prime }}{M}_{y^{\prime }}^b\rho \right)=\mathrm{Tr}\left(E_x^a{E}_{x^{\prime }}^{a^{\prime }}{M}_y^b{M}_{y^{\prime }}^{b^{\prime }}\rho \right)$.

From the definition, the operators of each set $\mathsf{S}$ produce a different Gram matrix G and form different linear constraints. The choice of a particular $\mathsf{S}$ can be organized in a hierarchical structure. More specifically, $\mathsf{S}$ can be defined as

$$\begin{array}{cc}\hfill & {\mathsf{S}}_1=\{E_x^a,M_y^b\}\hfill \\ \hfill & {\mathsf{S}}_2={\mathsf{S}}_1\bigcup \{E_x^a{E}_{x^{\prime }}^{a^{\prime }},E_x^a{M}_y^b,M_y^b{M}_{y^{\prime }}^{b^{\prime }}\}\hfill \\ \hfill & {\mathsf{S}}_3={\mathsf{S}}_2\bigcup \{E_x^a{E}_{x^{\prime }}^{a^{\prime }}{E}_x^a,E_x^a{M}_y^b{E}_x^a,E_x^a{M}_y^b{M}_{y^{\prime }}^{b^{\prime }},E_x^a{E}_x^{a^{\prime }}{M}_y^b,M_y^b{M}_{y^{\prime }}^{b^{\prime }}{M}_y^b,\cdots \}\hfill \\ \hfill & {\mathsf{S}}_4=\cdots \hfill \end{array}$$

(12)

It is evident that ${\mathsf{S}}_1\subseteq {\mathsf{S}}_2\subseteq \cdots$. We define the quantum set by $\mathsf{Q}\left(\lambda \right)$, which is formed by the measurement statistics compatible with the set of prepared quantum signals and Bob’s measurements. Moreover, denote the set of probability distributions defined by the hierarchy of step n as $\mathsf{Q}{\left(\lambda \right)}_n$. Then, we have $\mathsf{Q}\left(\lambda \right)\subseteq \mathsf{Q}{\left(\lambda \right)}_n$. It has been proved in [41] that $\mathsf{Q}{\left(\lambda \right)}_n$ converges to the quantum set, ${lim}_{n\to \infty }{\mathsf{Q}}_n=\mathsf{Q}$. Thus, by going to higher hierarchies, the approximation of $P^{*}$ by the SDP becomes tighter.

We first consider the first hierarchy ($k=1$), where the corresponding set of operators is chosen as in ${\mathsf{S}}_1$. Gram matrix ${\left[G\right]}_1$ is shown in below:

$${\left[G\right]}_1=\left(\begin{array}{cccccc}& I{|\mathsf{\Phi }\rangle }_{BA}& A_0^0{|\mathsf{\Phi }\rangle }_{BA}& E_1^0{|\mathsf{\Phi }\rangle }_{BA}& M_0^0{|\mathsf{\Phi }\rangle }_{BA}& M_1^0{|\mathsf{\Phi }\rangle }_{BA}\\ {\langle \mathsf{\Phi }|}_{BA}I& \lambda & {\langle \mathsf{\Phi }|}_{BA}{E}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_1^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{M}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{M}_1^0{|\mathsf{\Phi }\rangle }_{BA}\\ {\langle \mathsf{\Phi }|}_{BA}{E}_0^0& {\langle \mathsf{\Phi }|}_{BA}{E}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_0^0{E}_1^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_0^0{M}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_0^0{M}_1^0{|\mathsf{\Phi }\rangle }_{BA}\\ \langle {\varphi }_{BA}|E_1^0& {\langle \mathsf{\Phi }|}_{BA}{E}_1^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_0^0{E}_1^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_1^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_1^0{M}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_1^0{M}_1^0{|\mathsf{\Phi }\rangle }_{BA}\\ \langle {\mathsf{\Phi }}_{BA}|M_0^0& {\langle \mathsf{\Phi }|}_{BA}{M}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_0^0{M}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_1^0{M}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{M}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{M}_0^0{M}_1^0{|\mathsf{\Phi }\rangle }_{BA}\\ \langle {\mathsf{\Phi }}_{BA}|M_1^0& {\langle \mathsf{\Phi }|}_{BA}{M}_1^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_0^0{M}_1^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{E}_1^0{M}_1^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{M}_1^0{M}_0^0{|\mathsf{\Phi }\rangle }_{BA}& {\langle \mathsf{\Phi }|}_{BA}{M}_1^0{|\mathsf{\Phi }\rangle }_{BA}\end{array}\right)$$

(13)

$$\begin{array}{c}\hfill P^{*}={\displaystyle \frac{1}{4}}[Pr\left(00\right|00)+Pr\left(11\right|00)+Pr\left(00\right|01)+Pr\left(11\right|01)\\ \hfill +Pr\left(00\right|10)+Pr(11\left|10\right)+Pr\left(01\right|11)+Pr(10\left|11\right)],\end{array}$$

(14)

where the conditional probability of $(a_i,b_i)$ given $(x_i,y_i)$ can be obtained by

$$\begin{array}{cc}\hfill Pr\left(00\right|00)& ={\langle \mathsf{\Phi }|}_{BA}(E_0^0\otimes M_0^0){|\mathsf{\Phi }\rangle }_{BA}.\hfill \end{array}$$

(15)

Similarly, we have

$$\begin{array}{cc}\hfill & Pr\left(11\right|00)={\langle \mathsf{\Phi }|}_{BA}{E}_0^1{M}_0^1{|\mathsf{\Phi }\rangle }_{BA},Pr\left(00\right|01)={\langle \mathsf{\Phi }|}_{BA}{E}_0^0{M}_0^1{|\mathsf{\Phi }\rangle }_{BA},\hfill \\ \hfill & Pr\left(11\right|01)={\langle \mathsf{\Phi }|}_{BA}{E}_1^0{M}_1^1{|\mathsf{\Phi }\rangle }_{BA},Pr\left(00\right|10)={\langle \mathsf{\Phi }|}_{BA}{E}_0^1{M}_0^0{|\mathsf{\Phi }\rangle }_{BA},\hfill \\ \hfill & Pr\left(11\right|10)={\langle \mathsf{\Phi }|}_{BA}{E}_1^1{M}_1^0{|\mathsf{\Phi }\rangle }_{BA},Pr\left(01\right|11)={\langle \mathsf{\Phi }|}_{BA}{E}_0^1{M}_1^1{|\mathsf{\Phi }\rangle }_{BA},\hfill \\ \hfill & Pr\left(10\right|11)={\langle \mathsf{\Phi }|}_{BA}{E}_1^1{M}_0^1{|\mathsf{\Phi }\rangle }_{BA}.\hfill \end{array}$$

(16)

Under the conditions that $p_{\det }$ is fixed to some experimental model, $P^{*}$ is calculated using the SDP method. In particular, the SDP problem for maximizing the probability $P^{*}$ is as follows:

$$\begin{array}{c}\\ \hfill \mathrm{maximize}:& P^{*}\hfill \\ \hfill \mathrm{subject}\mathrm{to}:& \langle \mathsf{\Phi }|\mathsf{\Phi }\rangle =\lambda ,\hfill \\ \hfill & G\ge 0,\hfill \\ \hfill & \mathrm{Tr}\left(P_{k}G\right)=p_k,\hfill \\ \hfill & \mathrm{Tr}\left(T_{k}G\right)=t_k,\hfill \end{array}$$

(17)

where $P_k$’s and $T_k$’s are constant matrices. Note that $P_k$’s are used to extract the terms in G that are associated with the observed distributions $p(a,b|x,y)$; meanwhile, $T_k$’s are used to extract the terms in G that are associated with the linear constraints induced by the quantum operators and states.

Additionally, we require that Bob’s measurements satisfy basis-independent assumption: measurement operators corresponding to detection loss are the same for both measurement settings, i.e., $E_0^{\varnothing }=E_1^{\varnothing }$ and $M_0^{\varnothing }=M_1^{\varnothing }$. This is to ensure that the probability of detecting a signal is independent of Bob’s measurement choice, which is necessary to rule out detection side-channel attacks exploiting the channel loss. Thus, Bob’s three-outcome POVM is equivalent to a two-outcome POVM that determines the key bit, preceded by a basis-independent “filter”.

4.2. Correctness

We analyze the correctness of our proposed ISD-QPQ protocol. When Alice and Bob are honest, Alice can correctly guess only part bits of the entire raw key R at step (8). The success probability of Alice’s guessing a bit in the raw key can be obtained by

$$\begin{array}{cc}\hfill P_{guess}& =Pr(a=0,b=0)+Pr(a=1,b=1)\hfill \\ \hfill & =Pr(a=0|b=0)Pr(b=0)+Pr(a=1|b=1)Pr(b=1).\hfill \end{array}$$

(18)

Assume that all detectors have unit efficiency, that is, they always obtain conclusive outcomes. The success guess probability of Alice will be ${\displaystyle \frac{{sin}^2\theta }{2}}$. Then, we apply the shift and permutation method [27] for classical post-processing. Alice can correctly guess a final key bit with probability ${({\displaystyle \frac{{sin}^2\theta }{2}})}^k$. Considering the imperfect source and detectors, we still adopt the SDP method to maximize the success probability.

With the SDP method, the transmission channel can be seen as an isometric evolution in higher dimension that takes the initial quantum signal state to some pure output signal state $|{\varphi }_z\rangle$, where $z\in \{0,1\}$. The inner product of the output states is preserved after transmission. For each qubit successfully received, Bob measures his corresponding qubits in the $\{{|0\rangle }_B,{|1\rangle }_B\}$ basis. Then, Alice’s qubit randomly collapses to one state in set $\{{|{\varphi }_0\rangle }_A,{|{\varphi }_1\rangle }_A\}$. The POVMs $\left\{A_y^b\right\}$ can be assumed as projective measurements in higher dimensions, where $y\in \{0,1\}$ represents the basis selection. Given signal loss and detection inefficiency, there are three possible outcomes $b\in \{0,1,\varnothing \}$ for each measurement. Then, we say that the probabilities of observing outcomes b given setting y and z admits a quantum system, if there exist a quantum state $|{\varphi }_z\rangle$ and operators $A_y^b$ such that

$$\begin{array}{c}\hfill p\left(b\right|y,z)=\langle {\varphi }_z|A_y^b|{\varphi }_z\rangle .\end{array}$$

(19)

where the operators $\left\{A_y^b\right\}$ follow the properties:

$$\begin{array}{cc}\hfill & \left(\mathrm{i}\right)\mathrm{for}\mathrm{any}y,A_y^b{A}_y^{b^{\prime }}=0,\forall b\ne b^{\prime },\hfill \\ \hfill & \left(\mathrm{i}\mathrm{i}\right){\mathsf{\Sigma }}_b{A}_y^b=\mathbb{I},\hfill \\ & \left(\mathrm{i}\mathrm{i}\mathrm{i}\right){\left(A_y^b\right)}^2=A_y^b={\left(A_y^b\right)}^{†}.\hfill \end{array}$$

Denote $\mathcal{S}=\{S_1,\dots ,S_m\}$ as a finite set of m operators, where each element is a linear combination of products of $\left\{A_y^b\right\}$. We define the $nm\times nm$ block Gram matrix G:

$$\begin{array}{c}\hfill \begin{array}{cc}& G={\mathsf{\Sigma }}_{z,z^{\prime }=1}^n{G}^{z{z}^{\prime }}\otimes |e_z\rangle \langle e_{z^{\prime }}|,\hfill \\ & \mathrm{with},G_{(i,j)}^{z{z}^{\prime }}=\langle {\varphi }_z|S_i^{†}·S_j|{\varphi }_{z^{\prime }}\rangle \hfill \end{array}\end{array}$$

(20)

in which $G_{(i,j)}^{z{z}^{\prime }}$ is defined as the inner product of $\langle {\varphi }_z|S_i^{†}$ and $S_j|{\varphi }_{z^{\prime }}\rangle$, for all $z,z^{\prime }\in \left[n\right]$, $i,j\in \left[m\right]$. $G_{(i,j)}^{z{z}^{\prime }}$ is the $ij$-entry of the matrix $G^{z{z}^{\prime }}$ and ${\left\{|e_z\rangle \right\}}_{z=1}^n$ represents the standard orthonormal basis of ${\mathbb{R}}^n$.

The entries of every sub-block reflect the properties of $\left(\mathrm{i}\right)$–$\left(\mathrm{iii}\right)$. Property (i) implies $\langle {\varphi }_z|A_0^0{A}_0^0|{\varphi }_{z^{\prime }}\rangle =\langle {\varphi }_z|A_0^0|{\varphi }_{z^{\prime }}\rangle$ and $\langle {\varphi }_z|A_0^0{A}^{\varnothing }|{\varphi }_{z^{\prime }}\rangle =0$; property (ii) implies that we can introduce the identity operator $\mathbb{I}$ and remove one of the operators; meanwhile the property (iii) implies $\langle {\varphi }_z|A_y^b{A}_y^{b^{\prime }}|{\varphi }_z\rangle ={\left(\langle {\varphi }_z|A_y^{b^{\prime }}{A}_y^b|{\varphi }_z\rangle \right)}^{†}$. In addition, due to the overlaps of the receive states are known, we have $\langle {\varphi }_z|\mathbb{I}|{\varphi }_{z^{\prime }}\rangle ={\lambda }_{z{z}^{\prime }}$.

Then, we can construct a hierarchical structure $\mathcal{S}$:

$$\begin{array}{c}\hfill \begin{array}{cc}& {\mathcal{S}}_1=\{\mathbb{I},A_y^b\}\hfill \\ & {\mathcal{S}}_2={\mathcal{S}}_1\bigcup \left\{A_y^b{A}_{y^{\prime }}^{b^{\prime }}\right\}\hfill \\ & {\mathcal{S}}_3={\mathcal{S}}_2\bigcup \left\{A_y^b{A}_{y^{\prime }}^{b^{\prime }}{A}_y^b\right\}\hfill \\ & {\mathcal{S}}_4=\cdots \hfill \end{array}\end{array}$$

(21)

After the key establishment phase, suppose that Alice and Bob share N raw key bits: Alice can correctly guess $N{P}_{guess}$ bits of the entire raw key R and only $N{P}_{guess}^k$ bits through classical post-processing. The SDP problem for maximizing the success probability is as follows:

$$\begin{array}{cc}\hfill \mathrm{maximize}:& P_{guess}\hfill \\ \hfill \mathrm{subject}\mathrm{to}:& \langle {\varphi }_z|{\varphi }_{z^{\prime }}\rangle ={\lambda }_{z{z}^{\prime }},\forall z,z^{\prime }\hfill \\ \hfill & G\ge 0,\hfill \\ \hfill & \mathrm{Tr}\left(F_{k}G\right)=f_k,\hfill \\ \hfill & \mathrm{Tr}\left(R_{k}G\right)=r_k,\hfill \\ \hfill & p_{\det }\mathrm{fixed}\mathrm{to}\mathrm{experimental}\mathrm{model}\hfill \end{array}$$

(22)

where $F_k$’s are used to pick up the terms in G which are associated with the observed distributions $p\left(b\right|x,y)$ and $R_k$’s are used to pick up the terms in G which are associated with the linear constraints. This SDP is based on Alice and Bob’s measurements and the SDP in Section 4.1 is used to calculate $P^{*}$ in the CHSH test steps on Bob’s side. So, these two SDP problems are optimal for different sets of states and measurements, respectively.

4.3. Database Security

Database security implies that even a dishonest Alice cannot obtain more items in Bob’s database, that is, Alice only knows one (or a little more) bit of the final key. To get more key bits, an intuitive way for Alice is to adopt the optimal unambiguous state discrimination (USD) measurement strategy [42]. To discriminate between two quantum states, the success probability of USD measurement $P_{USD}$ is bounded by $1-F({\rho }_0,{\rho }_1)$, where $F({\rho }_0,{\rho }_1)$ is the fidelity between the two states to be distinguished. In our ISD-QPQ protocol, dishonest Alice wants to discriminate $|{\varphi }_0\rangle$ and $|{\varphi }_1\rangle$, the success probability $P_{USD}$ is

$$P_{USD}=1-cos\theta ,$$

(23)

where $\theta \in [0,{\displaystyle \frac{\pi }{2}}]$.

ISD-QPQ can resist Alice’s joint USD measurement attack. Since our protocol exploits the shift and permutation method in classical post-processing, Alice cannot ensure the information about which qubits contribute to one final key bit. Even if Alice cheats by performing the measurement in step (10) instead of step (7), the success probability $P_{USD}$ can be reduced to ${(1-cos\theta )}^k$ by post-processing. If malicious Alice performs the joint USD measurement, she can gain $\Delta n$ extra bits. We have the following:

$$\Delta n=N{(1-cos\theta )}^k-N{\left({\displaystyle \frac{{sin}^2\theta }{2}}\right)}^k,$$

(24)

where N is the number of entries in the database. For our protocol, we can choose the optimal k to make the probability that dishonest Alice can know more than the expected number of the final key bits and the protocol does not abort very low.

4.4. User Privacy

User privacy denotes that Bob can deduce the retrieval address with higher probability, in other words, Bob has to obtain the raw key bits which are known to Alice. Bob also has to correctly obtain the right key bit value for Alice, otherwise he may provide a false database item to Alice and can be discovered. This case in the QPQ protocol is called cheat-sensitive. All Bob’s attacks to infer the retrieval address can be discovered by Alice with a nonzero probability in our protocol; see the details in the following.

In the ISD-QPQ protocol, Alice does not report anything about her measurement outcome. Therefore, dishonest Bob has no information about Alice’s measurement basis and outcomes. One possible attack strategy for dishonest Bob is to prepare fake states to receive the corresponding value of Alice’s raw key bits. Since Alice chooses the measurement basis chosen randomly and independently of Bob, he has to guess Alice’s basis randomly. Assume Bob sends a fake state $|X\rangle =cosx|0\rangle +sinx|1\rangle$ to Alice. Alice chooses to measure her qubits with projection measurement. The probability for Alice to obtain the outcomes 0 and 1 are ${sin}^2({\displaystyle \frac{\theta }{2}}+x)$ and ${sin}^2({\displaystyle \frac{\theta }{2}}-x)$, respectively. We derive that when $x={\displaystyle \frac{\pi }{4}}$, Bob can obtain information on the conclusive results of Alice’s bits with an optimal probability. However, Bob would induce some errors by this attack, because he cannot obtain Alice’s key bit with certainty. As a result, Bob may give Alice the wrong answer, and she can discover Bob’s attack with a certain probability.

Performing special measurements is another attack strategy for dishonest Bob. Assume Bob uses other measurement bases instead of von Neumann measurement on his particle. As shown in [26], Bob will improve the conclusive success probability of key bits, but he will certainly miss the value of the key bit. Thus, Bob will run the risk of being discovered if he tries to obtain Alice’s retrieval address. In conclusion, our ISD-QPQ protocol is cheat-sensitive.

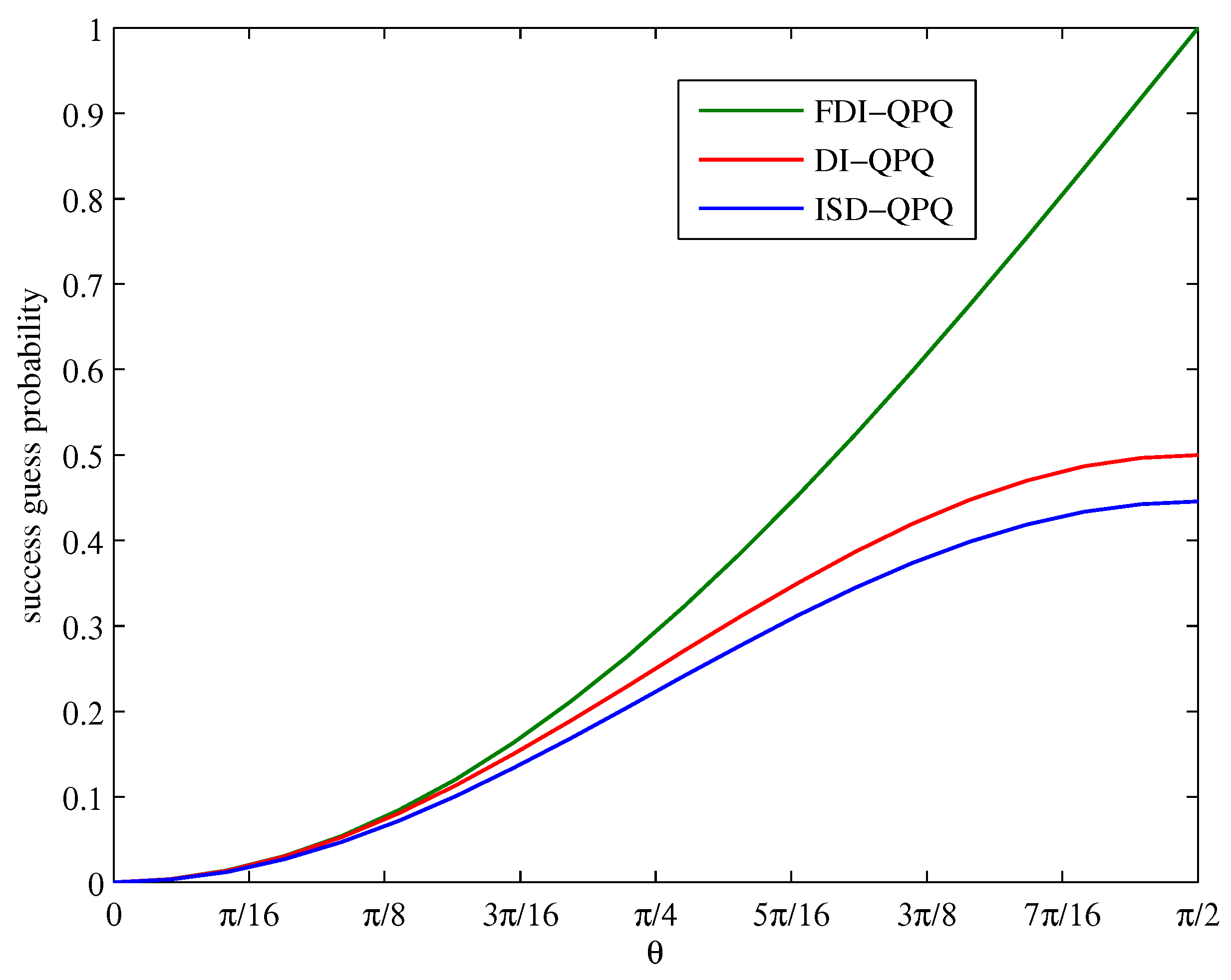
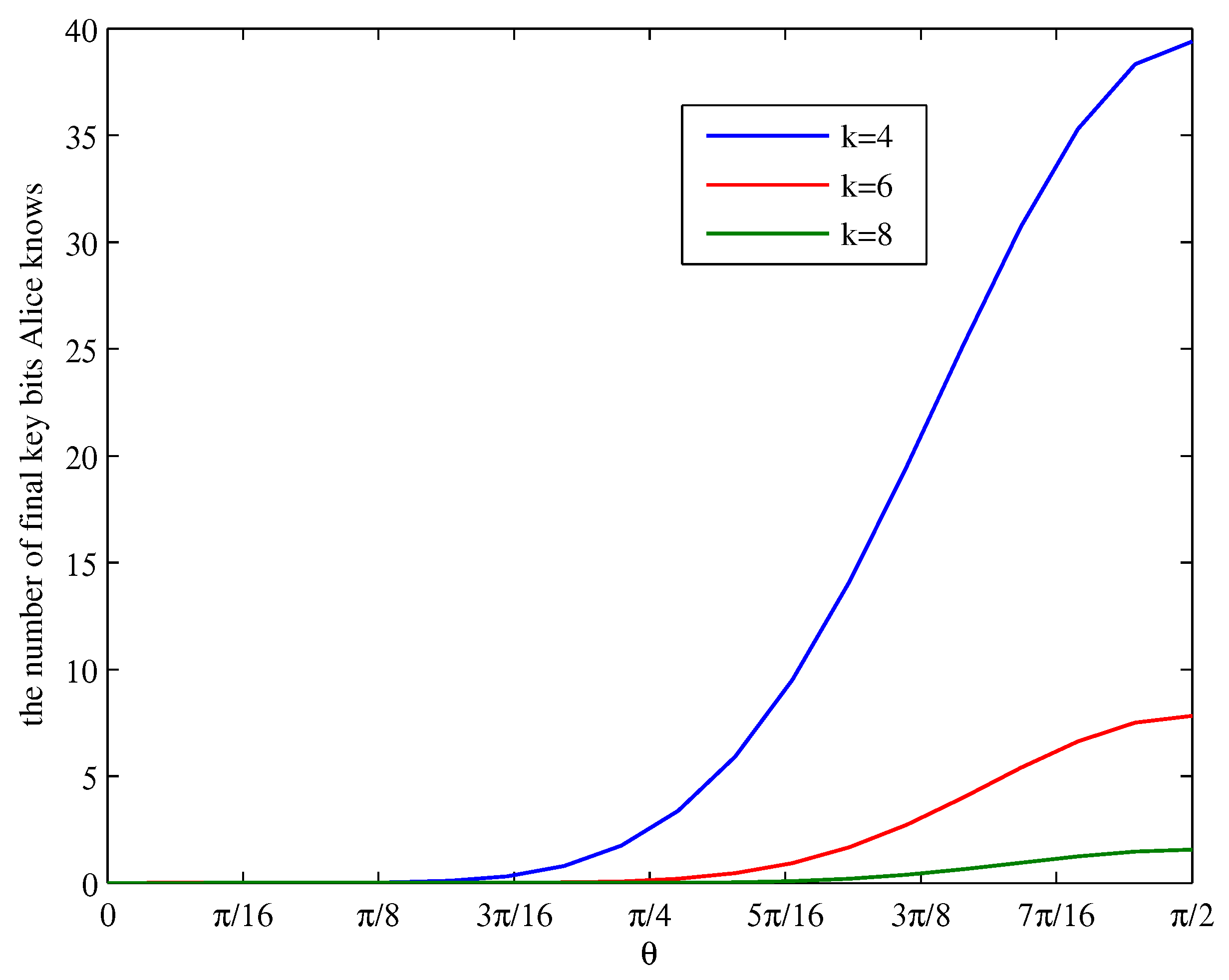
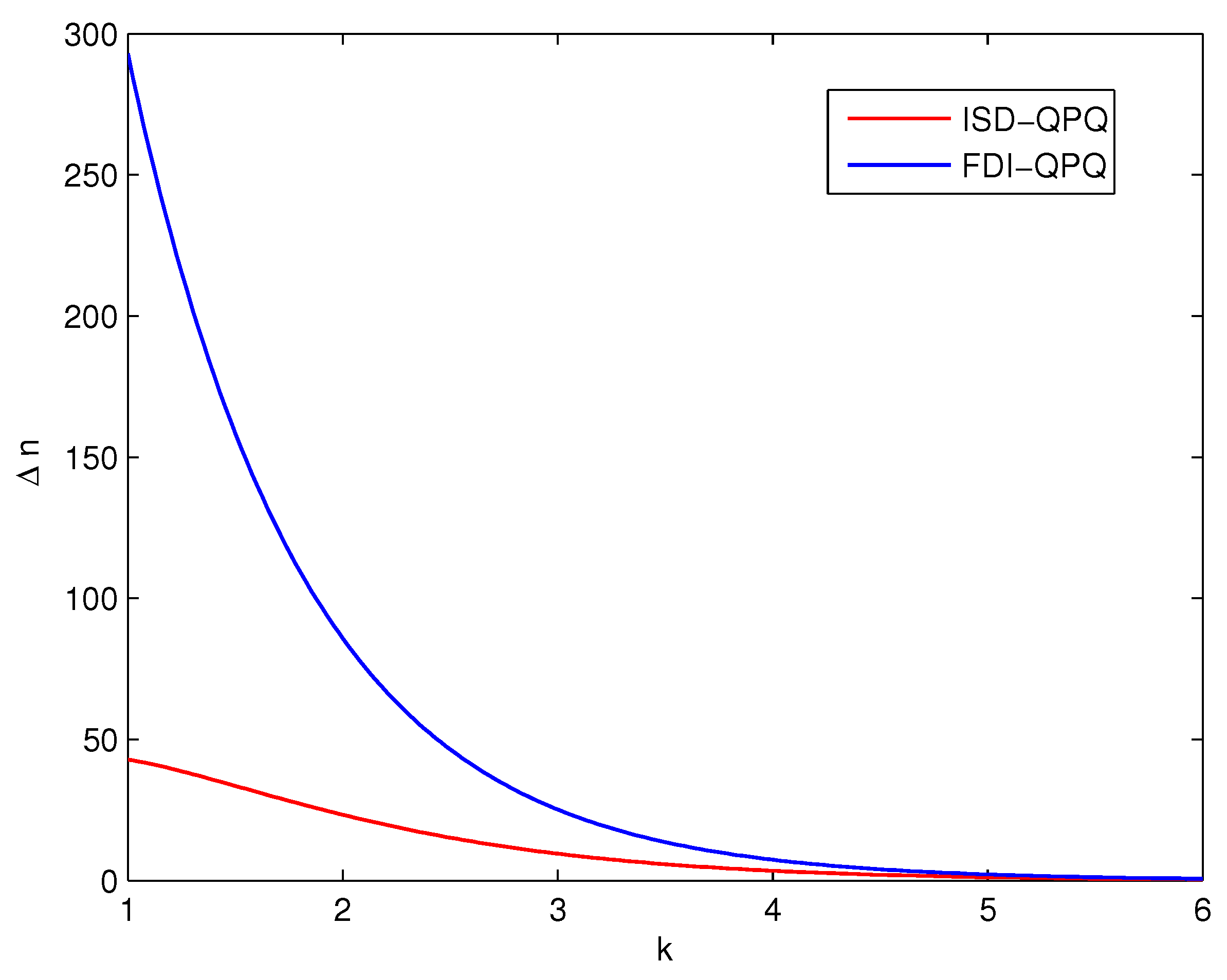
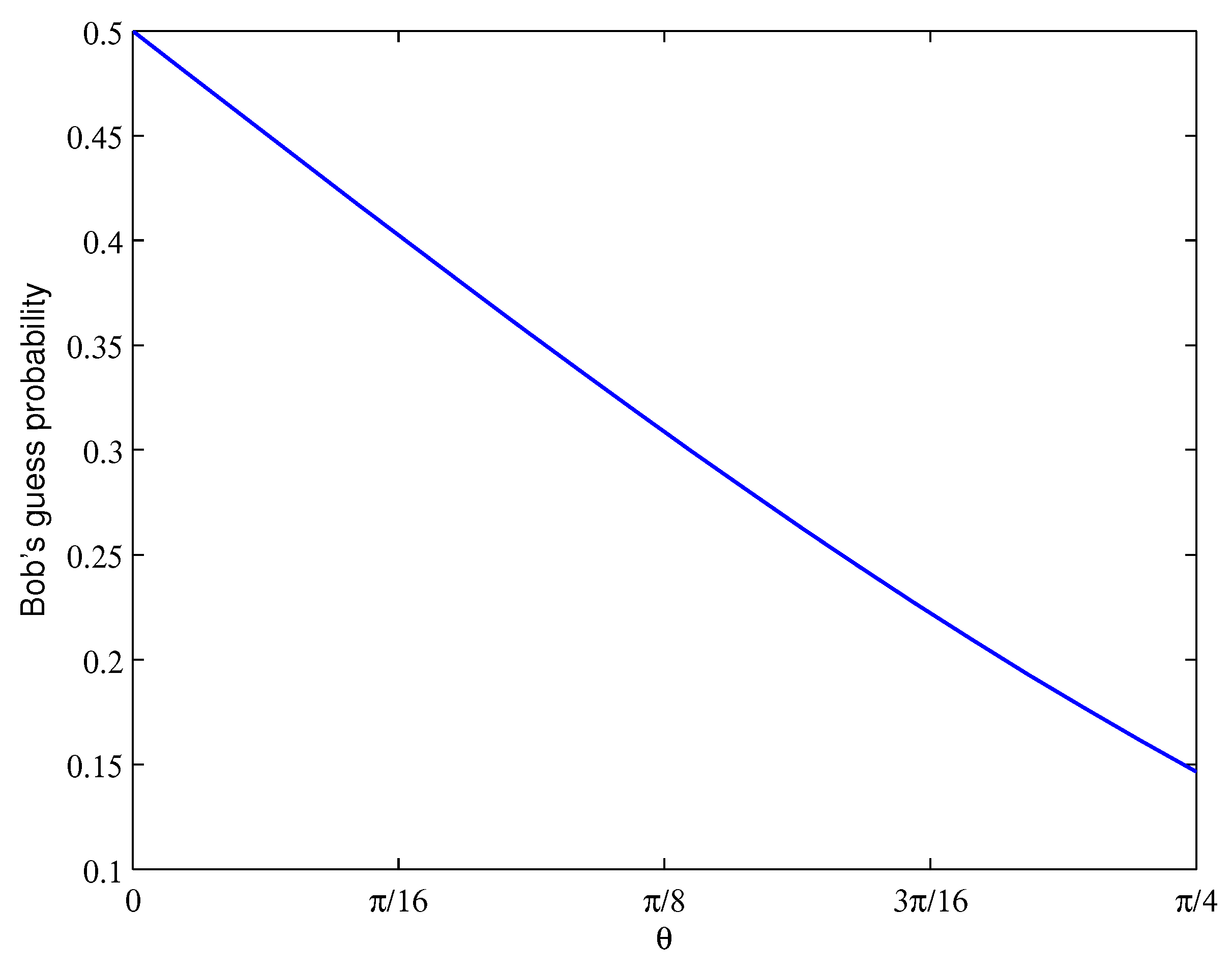
5. Simulation Results

We first simulate the relationship between joint probability $Pr(a_i\oplus b_i=x_i\wedge y_i)$ and choice of $\theta$ with different values of $\tau$, as shown in Figure 2. It shows that the joint probability with imperfect sources is always lower than in the ideal case. Then, we can set the value of the black asterisk curve as the joint probability threshold P in the DI-QPQ protocol. By performing the CHSH local test on Bob’s side, the protocol can be implemented only when the prepared entanglement state is of a specific form. When the entanglement state is the other form, Bob will abort the protocol. Therefore, Bob can remove his trust in sources. The security of DI-QPQ protocol with imperfect sources is proved.

In order to analyze the ISD-QPQ protocol in a realistic detection model, we consider the detection loss rate $ϵ$. We maximize $P^{*}$ over the set of compatible probabilities using the first level of the hierarchy; the results of the numerical optimization are shown in Figure 3. When imperfect detectors are considered, the joint probability $P^{*}$ in the ISD-QPQ protocol is lower than in the previous DI-QPQ protocol. This is expected since imperfect detectors will induce detection loss. In addition, by using the SDP optimization method, we can obtain the CHSH test threshold of our ISD-QPQ protocol with fixed detection loss.

We simulate the success probability of Alice guessing a bit in the raw key using a realistic model, which includes imperfect sources and detectors. As Alice uses two threshold detectors, there are four possible outcomes when she measures a state. By randomly mapping double clicks to 0 or 1, Alice’s measurement realizes a POVM with three outcomes: 0, 1 and inconclusive [45]. Let $P(0,y)$ denote the probability of obtaining the outcomes b. We have the following

$$\begin{array}{cc}\hfill & P(0,y)=C_0\left(y\right)N_1\left(y\right)+{\displaystyle \frac{C_0\left(y\right)C_1\left(y\right)}{2}},\hfill \\ \hfill & P(1,y)=C_1\left(y\right)N_0\left(y\right)+{\displaystyle \frac{C_0\left(y\right)C_1\left(y\right)}{2}},\hfill \\ \hfill & P(\varnothing ,y)=N_0\left(y\right)N_1\left(y\right),\hfill \end{array}$$

(25)

where $y\in \{0,1\}$ represents the basis choice, $C_0$ and $C_1$ ($N_0$ and $N_1$) denote the event of detection $D_0$ and $D_1$ click (do not click), respectively. The notation $b\in \{0,1,\varnothing \}$ represents the outcomes considering the detection loss. The probability of detecting a signal $p_{\det }$ is then given by $p_{det}=P(0,y)+P(1,y)$.

Subsequently, we use the first level of the hierarchy to maximize $P_{guess}$ over the set of compatible probabilities, and the result of the numerical optimization is shown in Figure 4. We compare the success guess probabilities of our ISD-QPQ protocol with the DI-QPQ protocol in [35] and the more recent FDI-QPQ protocol in [31]. It can be clearly seen that our protocol can provide a lower success guess probability than the other two protocols. As a result, the total number of bits consumed is less. By applying the classical post-processing method given in our protocol, Alice knows only roughly one bit in the final key. The results are shown in Figure 5.

In addition, to characterize database security, we simulate the relationship between Alice’s extra bits and the post-processing parameter k when $\theta$ is fixed. The result is shown in Figure 6. We can see that when k increases, the extra bits known for Alice $\Delta n$ decrease. We choose the optimal k to ensure that $\Delta n$ is small enough. The larger k implies that more key bits are consumed. This indicates that the database of our protocol is secure. Compared with the FDI-QPQ protocol in [36], our ISD-QPQ protocol has better performance in terms of database security.

Figure 7 shows the relationship between Bob’s guess probability for Alice’s query item and $\theta$. We can find that Bob’s guess probability gradually tends to 0.15 as $\theta$ tends to ${\displaystyle \frac{\pi }{4}}$. Moreover, Bob’s guess probability is lower in our protocol than in the FDI-QPQ protocol, which is approximately equal to 0.5 [36]. This simulation results indicates that our ISD-QPQ protocol ensures user privacy against dishonest Bob.

We compare our proposed ISD-QPQ protocol with some existing protocols, as shown in

Table 1. The performance comparison of our ISD-QPQ protocol with Yang-QPQ [26], DI-QPQ [35] and FDI-QPQ [36] protocols.

Protocols	Source	Detector	${\mathit{P}}_{\mathit{guess}}$	$\mathbf{\Delta }\mathit{n}$
ISD-QPQ	imperfect	with trust loss	0.227	6
Yang-QPQ	trust	trust	0.145	5
DI-QPQ	imperfect	with unit efficiency	0.253	5
FDI-QPQ	imperfect	without noise	0.286	9

. We choose the optimal k to ensure that $\Delta n\ll N$ is small enough. Set $N=1000$ according to the security analysis above.

Furthermore, the different choice of $\theta$ in our QPQ protocol affects security. From Figure 4 and Figure 5, it can be clearly seen that as $\theta$ tends to ${\displaystyle \frac{\pi }{2}}$, the probability of success guessing and the number of final key bits Alice knows gradually increases. With the increase in $\theta$, the database security will decrease. From Figure 7, we can find that Bob’s guess probability gradually tends to 0.15 as $\theta$ tends to ${\displaystyle \frac{\pi }{4}}$. We derive that when $x={\displaystyle \frac{\pi }{4}}$, Bob can obtain information on the conclusive results of Alice’s bits with an optimal probability. Therefore, the optimal choice of $\theta$ in our QPQ protocol is ${\displaystyle \frac{\pi }{4}}$.

Finally, we discuss how the value of $\gamma$ affects the security and efficiency of our protocol. For each prepared entangled state, Bob divides it into two sets $N_{CHSH}$ and $N_{QPQ}$. The set $N_{CHSH}$ contains $\gamma n$ entangled states, which is used to conduct the CHSH local test, whereas $N_{QPQ}$ contains $(1-\gamma )n$ entangled states for $0<\gamma <1$, which is used to perform private queries. Assuming the size of the database is N and the post-processing parameter k, we have the total number of prepared entangled states $n={\displaystyle \frac{kN}{1-\gamma }}$. As the value of $\gamma$ increases, the efficiency of our protocol will increase. We define the security parameter $t={\displaystyle \frac{\gamma P^{*}kN}{1-\gamma }}$. Taking into account the trade-off between security and efficiency, the optimal value of $\gamma$ can be obtained by $t\ge 0.5N$. For example, assume $N=1000$, $k=3$ and $P^{*}=0.78$, and we can choose $\gamma =0.39$.

6. Conclusions

QKD-based QPQs are the most practical protocols for the SPIR problem. However, most existing protocols assume ideal devices. Considering the practical application of QPQ protocols, we first analyze the security of the DI-QPQ protocol with imperfect sources and detectors, which requires the assumption that all detectors have unit efficiency. To overcome this drawback, we propose our ISD-QPQ protocol with imperfect sources and detectors. Performing the local CHSH test, Bob can check that the states are of the desired form. We prove the security and correctness of the ISD-QPQ protocol. By constructing the SDP optimization problem with the NPA method, we derive the CHSH test threshold and prove the correctness of our protocol. With this SDP method, detailed characterization of the quantum signals and measurements, including their dimensions, is no longer required in the analysis. Furthermore, we use the shift and permutation post-processing method to further improve the security of our protocol.

The simulation results show that the protocol can be implemented only when the prepared entanglement state is of a specific form. Therefore, Bob can remove his trust in sources. When simulating the success guess probability and the number of final key bits Alice knows, we find that our protocol consumes fewer bits than the FDI-QPQ protocol and DI-QPQ protocol, that is, our protocol has higher efficiency. The security of database and user privacy are analyzed. Our ISD-QPQ protocol has higher security than the FDI-QPQ protocol in terms of both database security and user privacy. In addition, we discuss the optimal choice of $\theta$ and $\gamma$.

Furthermore, by replacing the QPQ steps with other entanglement-based QPQ protocol, our scheme can be used for any entanglement-based QPQ protocol to remove trust on devices. However, it remains an open problem to remove the assumption that Bob’s device has a trusted loss value.