Large Language Model-Guided SARSA Algorithm for Dynamic Task Scheduling in Cloud Computing
Abstract
1. Introduction
- Provide a brief introduction of the necessity to perform task scheduling in a cloud environment.
- Employment of the LLM to represent the real-world cloud computing scenario to arrive at better planning and control strategies.
- Illustration of the LLM heuristic value, avoiding the bias in task scheduling policies through significant reshaping of the Q function.
- Proposing a novel LLM-guided SARSA framework along with the supporting algorithm to perform task scheduling.
- Mathematical modeling of an LLM-guided SARSA task scheduler considering the finite cloud scenario and infinite cloud scenario.
- The experimental evaluation of the proposed LLM-guided SARSA task scheduler using the CloudSim express simulator.
2. Related Work
- The task scheduling optimization strategies developed using traditional metaheuristic algorithms consume too many operations, suffer from slow convergence, and often become stuck in local optima.
- Even hybrid forms of the metaheuristics task schedulers consume a large number of training iterations, suffer from slow convergence, and often become stuck in local optima.
- The reinforcement approaches often exhibit high computational complexity and hypersensitivity towards the exploration constant.
- The model-free approaches are data hungry and exhibit poor efficiency since the input data are gathered through trial-and-error mechanisms.
- The machine learning-based task schedulers do not satisfy the real-time response time requirement of IoT devices.
- Swarm optimization techniques end up with a high response time when evaluated over delay-sensitive applications.
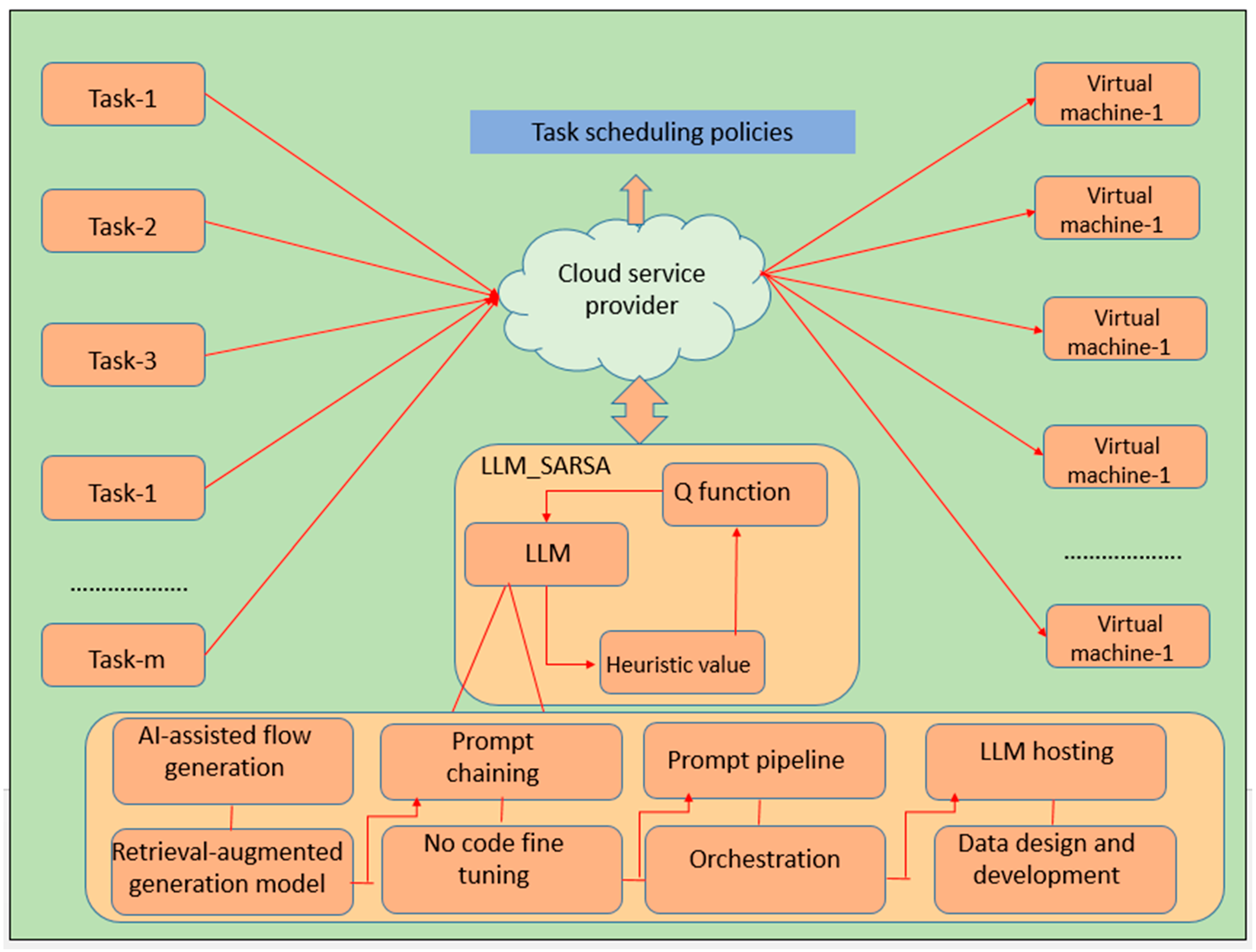
3. System Model
4. Proposed Work
| Algorithm 1: Working of LLM_SARSA task scheduler |
| 1: Start 2: Input: Input the set of task 3: Output: Output task scheduling policies 4: Initialize 5: Initialize LLM heuristic Q buffer 6: For each episode S, perform 7: Training phase of LLM_SARSA 8: For every task in training task set perform 9: Initialize state S, Action A 10: Choose Action A from state S using the policy derived from 11: For each step of episode, perform 12: Take action A, observe reward R, and go to next step 13: Choose action from state using the policy derived from 11: 12: Update , 12: Compute the LLM heuristic value 13: Update the with LLM 14: 15: Employ L2 loss to approximate the value 16: L2( 17: 18: End For of episode until S is terminal 19: End For 20: Testing phase of LLM_SARSA 21: For every task in testing task set perform 22: Initialize state S, Action A 23: Choose Action A from state S using the policy derived from 24: For each step of episode, perform 25: Execute the action from state with updated heuristic value and L2 loss value 26: 27: End For of episode until S is terminal 28: End For 29: End For 30: Output 34: Stop |
5. Mathematical Modeling
5.1. Finite Cloud Scenario
5.2. Infinite Cloud Scenario
6. Results and Discussion
6.1. Makespan Time
6.2. PO2: Degree of Imbalance
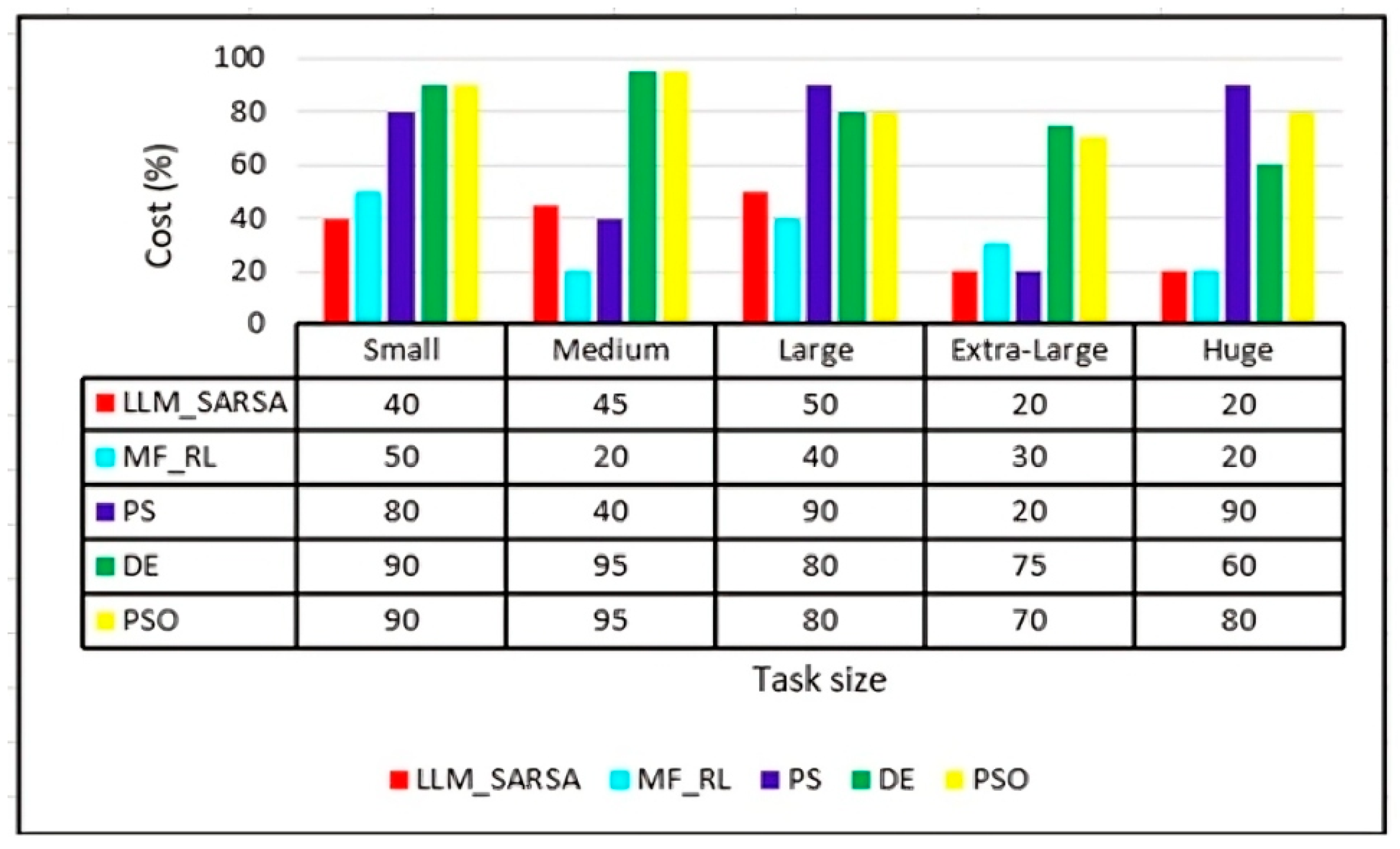
6.3. PO3: Cost
6.4. PO4: Resource Utilization
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gunukula, S. The Future of Cloud Computing: Key Trends and Predictions for the Next Decade. Int. J. Res. Comput. Appl. Inf. Technol. 2024, 7, 528–538. [Google Scholar]
- Wang, Y.; Bao, Q.; Wang, J.; Su, G.; Xu, X. Cloud computing for large-scale resource computation and storage in machine learning. J. Theory Pract. Eng. Sci. 2024, 4, 163–171. [Google Scholar] [CrossRef] [PubMed]
- Soni, P.K.; Dhurwe, H. Challenges and Open Issues in Cloud Computing Services. In Advanced Computing Techniques for Optimization in Cloud; Chapman and Hall/CRC: New York, NK, USA, 2024; pp. 19–37. [Google Scholar]
- Raja, V. Exploring challenges and solutions in cloud computing: A review of data security and privacy concerns. J. Artif. Intell. Gen. Sci. 2024, 4, 121–144. [Google Scholar]
- Pramanik, S. Central Load Balancing Policy Over Virtual Machines on Cloud. In Balancing Automation and Human Interaction in Modern Marketing; IGI Global: Hershey, PA, USA, 2024; pp. 96–126. [Google Scholar]
- Liu, Y.; Meng, Q.; Chen, K.; Shen, Z. Load-aware switch migration for controller load balancing in edge–cloud architectures. Future Gener. Comput. Syst. 2025, 162, 107489. [Google Scholar] [CrossRef]
- Devi, N.; Dalal, S.; Solanki, K.; Dalal, S.; Lilhore, U.K.; Simaiya, S.; Nuristani, N. A systematic literature review for load balancing and task scheduling techniques in cloud computing. Artif. Intell. Rev. 2024, 57, 276. [Google Scholar] [CrossRef]
- Patwari, K.R.; Kumar, R.; Sastry, J.S.V.R.S. A Systematic Review of Optimal Task Scheduling Methods Using Machine Learning in Cloud Computing Environments. In International Conference on Advances in Information Communication Technology & Computing; Springer Nature: Singapore, 2024; pp. 321–333. [Google Scholar]
- Mehta, R.; Sahni, J.; Khanna, K. Task scheduling for improved response time of latency sensitive applications in fog integrated cloud environment. Multimed. Tools Appl. 2023, 82, 32305–32328. [Google Scholar] [CrossRef]
- Jayanetti, A.; Halgamuge, S.; Buyya, R. Multi-agent deep reinforcement learning framework for renewable energy-aware workflow scheduling on distributed cloud data centres. IEEE Trans. Parallel Distrib. Syst. 2024, 35, 604–615. [Google Scholar] [CrossRef]
- Arasan, K.K.; Anandhakumar, P. Energy-efficient task scheduling and resource management in a cloud environment using optimized hybrid technology. Softw. Pract. Exp. 2023, 53, 1572–1593. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, T.; Pan, M.; Zhang, C.; Yu, Y. A-SARSA: A predictive container auto-scaling algorithm based on reinforcement learning. In Proceedings of the 2020 IEEE International Conference on Web Services (ICWS), Beijing, China, 19–23 October 2020; pp. 489–497. [Google Scholar]
- Zhai, Y.; Yang, T.; Xu, K.; Dawei, F.; Yang, C.; Ding, B.; Wang, H. Enhancing decision-making for llm agents via step-level q-value models. arXiv 2024, arXiv:2409.09345. [Google Scholar]
- Wang, B.; Qu, Y.; Jiang, Y.; Shao, J.; Liu, C.; Yang, W.; Ji, X. LLM-empowered state representation for reinforcement learning. arXiv 2024, arXiv:2407.13237. [Google Scholar]
- Zhang, S.; Zheng, S.; Ke, S.; Liu, Z.; Jin, W.; Yang, Y.; Yang, H.; Wang, Z. How Can LLM Guide RL? A Value-Based Approach. arXiv 2024, arXiv:2402.16181. [Google Scholar]
- Prakash, B.; Oates, T.; Mohsenin, T. LLM Augmented Hierarchical Agents. arXiv 2023, arXiv:2311.05596. [Google Scholar]
- Ni, W.; Zhang, Y.; Li, W. Optimal Dynamic Task Scheduling in Heterogeneous Cloud Computing Environment. In Proceedings of the 2024 IEEE International Conference on Industry 4.0, Artificial Intelligence, and Communications Technology (IAICT), BALI, Indonesia, 4–6 July 2024; pp. 40–46. [Google Scholar]
- Sandhu, R.; Faiz, M.; Kaur, H.; Srivastava, A.; Narayan, V. Enhancement in performance of cloud computing task scheduling using optimization strategies. Clust. Comput. 2024, 27, 1–24. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, S.; Fan, W. Task scheduling mechanism based on reinforcement learning in cloud computing. Mathematics 2023, 11, 3364. [Google Scholar] [CrossRef]
- Lipsa, S.; Dash, R.K.; Ivković, N.; Cengiz, K. Task scheduling in cloud computing: A priority-based heuristic approach. IEEE Access 2023, 11, 27111–27126. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Elkhalik, W.A.; Sharawi, M.; Sallam, K.M. Task scheduling approach in cloud computing environment using hybrid differential evolution. Mathematics 2022, 10, 4049. [Google Scholar] [CrossRef]
- Nabi, S.; Ahmad, M.; Ibrahim, M.; Hamam, H. AdPSO: Adaptive PSO-based task scheduling approach for cloud computing. Sensors 2022, 22, 920. [Google Scholar] [CrossRef] [PubMed]
- Habaebi, M.H.; Merrad, Y.; Islam, M.R.; Elsheikh, E.A.; Sliman, F.M.; Mesri, M. Extending CloudSim to simulate sensor networks. Simulation 2023, 99, 3–22. [Google Scholar] [CrossRef]
- Hewage, T.B.; Ilager, S.; Rodriguez, M.A.; Buyya, R. CloudSim express: A novel framework for rapid low code simulation of cloud computing environments. Softw. Pract. Exp. 2024, 54, 483–500. [Google Scholar] [CrossRef]



| Technique | Logic | Makespan Time | Degree of Imbalance | Cost | Resource Utilization |
|---|---|---|---|---|---|
| Reinforcement learning [17,19] | Trial and error | High | High | Very High | Low |
| Optimization strategy [18] | Tabu search | High | Very High | Very High | Medium |
| Metaheuristic strategy [20,21,22] | Popuation-based optimization | Medium | High | Medium | Low |
| and |
| and |
| (35) | |
| and |
| Cluster | Details |
|---|---|
| Cluster 1 | CPU capacity = 0.5, memory capacity = 0.03085, total machines = 6, and average time per task = 1,417, 500 |
| Cluster 2 | CPU capacity = 0.5, memory capacity = 0.06185, total machines = 3, and average time per task = 154, 79 |
| Cluster 3 | CPU capacity = 0.5, memory capacity = 0.1241, total machines = 97, and average time per task = 10,872.95 |
| Cluster 4 | CPU capacity = 0.5, memory capacity = 0.2493, total machines = 10,188, and average time per task = 5276.77 |
| Cluster 5 | CPU capacity = 0.25, memory capacity = 0.2498, total machines = 10,188, and average time per task = 3975.90 |
| Cluster 6 | CPU capacity = 0.5, memory capacity = 0.749, total machines = 2983, and average time per task = 2502.83 |
| Cluster 7 | CPU capacity = 1, memory capacity = 1, total machines = 2218, and average time per task = 2178.14 |
| Cluster 8 | CPU capacity = 0.5, memory capacity = 0.49, total machines = 21,731, and average time per task = 1856.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krishnamurthy, B.; Shiva, S.G. Large Language Model-Guided SARSA Algorithm for Dynamic Task Scheduling in Cloud Computing. Mathematics 2025, 13, 926. https://doi.org/10.3390/math13060926
Krishnamurthy B, Shiva SG. Large Language Model-Guided SARSA Algorithm for Dynamic Task Scheduling in Cloud Computing. Mathematics. 2025; 13(6):926. https://doi.org/10.3390/math13060926
Chicago/Turabian StyleKrishnamurthy, Bhargavi, and Sajjan G. Shiva. 2025. "Large Language Model-Guided SARSA Algorithm for Dynamic Task Scheduling in Cloud Computing" Mathematics 13, no. 6: 926. https://doi.org/10.3390/math13060926
APA StyleKrishnamurthy, B., & Shiva, S. G. (2025). Large Language Model-Guided SARSA Algorithm for Dynamic Task Scheduling in Cloud Computing. Mathematics, 13(6), 926. https://doi.org/10.3390/math13060926






