Formalization of Side-Aware DNA Origami Words and Their Rewriting System, and Equivalent Classes
Abstract
1. Introduction
- We introduce the concept of side-aware DNA origami words, explicitly modeling the directional binding of staples (left or right) to the scaffold. This new concept accommodates the representation of more flexible and biologically realistic DNA origami structures, and is described in Section 3.
- We define the side-aware DNA origami word rewriting system and analyze the properties of its graphical structures, focusing on equivalence classes. Since staples can bind to either side of the scaffold or fail to form stable structures if blocked by staples from the opposite side, the diversity of rewriting patterns increases. We categorize all patterns arising from concatenation and define them as rewriting rules for side-aware DNA origami words. This is described in Section 4.
2. Preliminaries
- for
- for
3. Formalization of Side-Aware DNA Origami Words
- Side-aware DNA origami words, consisting of scaffolds and staples, are represented by graphical structures of width n. These graphical structures contain n columns, and each column has two endpoints: top and bottom. Scaffolds and staples are represented by directed pairs of endpoints. By combining the set of pairs of scaffolds and the set of pairs of staples, we define a graphical structure. Details are described in Section 3.1.
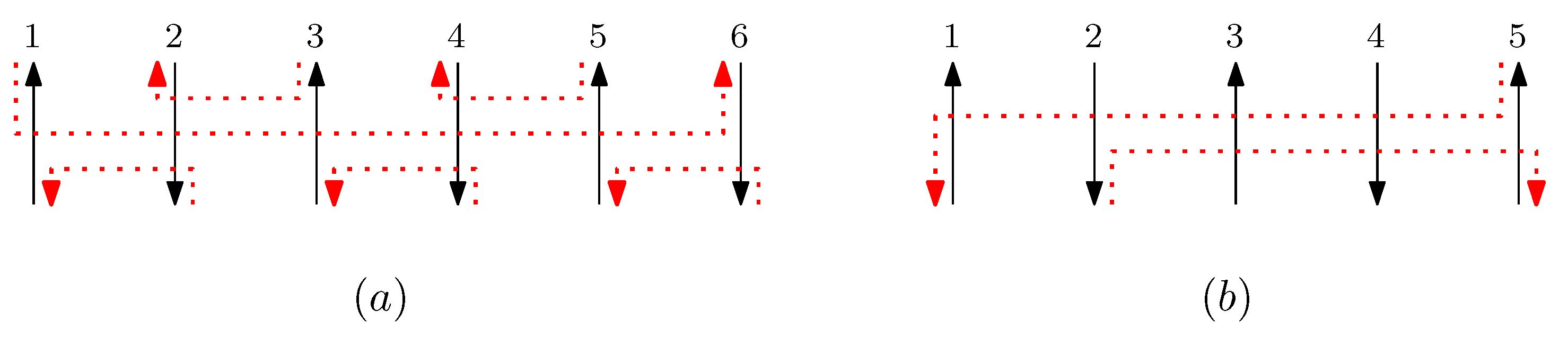
- We define the concatenation of two graphical structures of side-aware DNA origami words. This concatenation is based on the relations of the Jones monoid and its graphical representation, as described in Figure 1. Unlike the classical concatenation of words, the concatenation of graphical structures is performed vertically, aligning their columns. Details are described in Section 3.2.
3.1. Side-Aware DNA Origami Words
- We observe that there are two different types of motifs in the DNA origami structure: there are places where two adjacent scaffolds connect the two columns, and also places where two adjacent staples connect the two columns.
- The scaffolds and staples have directions: adjacent scaffolds are anti-parallel, and a staple is anti-parallel to the connected scaffold.
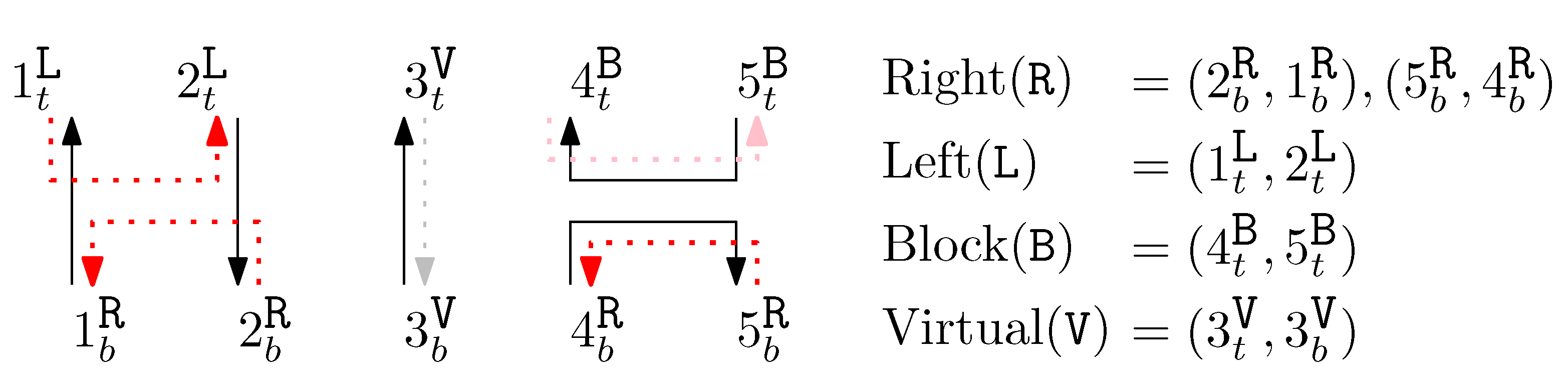
- Each staple end can reside on two different sides of the connected scaffold—left and right.
- Virtual (V): A staple is not present on the given column (we formally regard this “absence” of a staple as one type of staple for the concise definition of concatenation of structures). Other staples can be extended on a virtual staple through concatenation.
- Left (L): Two endpoints of the staple are on the left side of the scaffolds.
- Right (R): Two endpoints of the staple are on the right side of the scaffolds.
- Block (B): A staple is disconnected in-between. Other staples cannot be extended on a block staple through concatenation.
- : The entire context is real, with both and being empty.
- : The context for the scaffold is real, while the context for the staple is virtual.
- : The entire context is virtual.
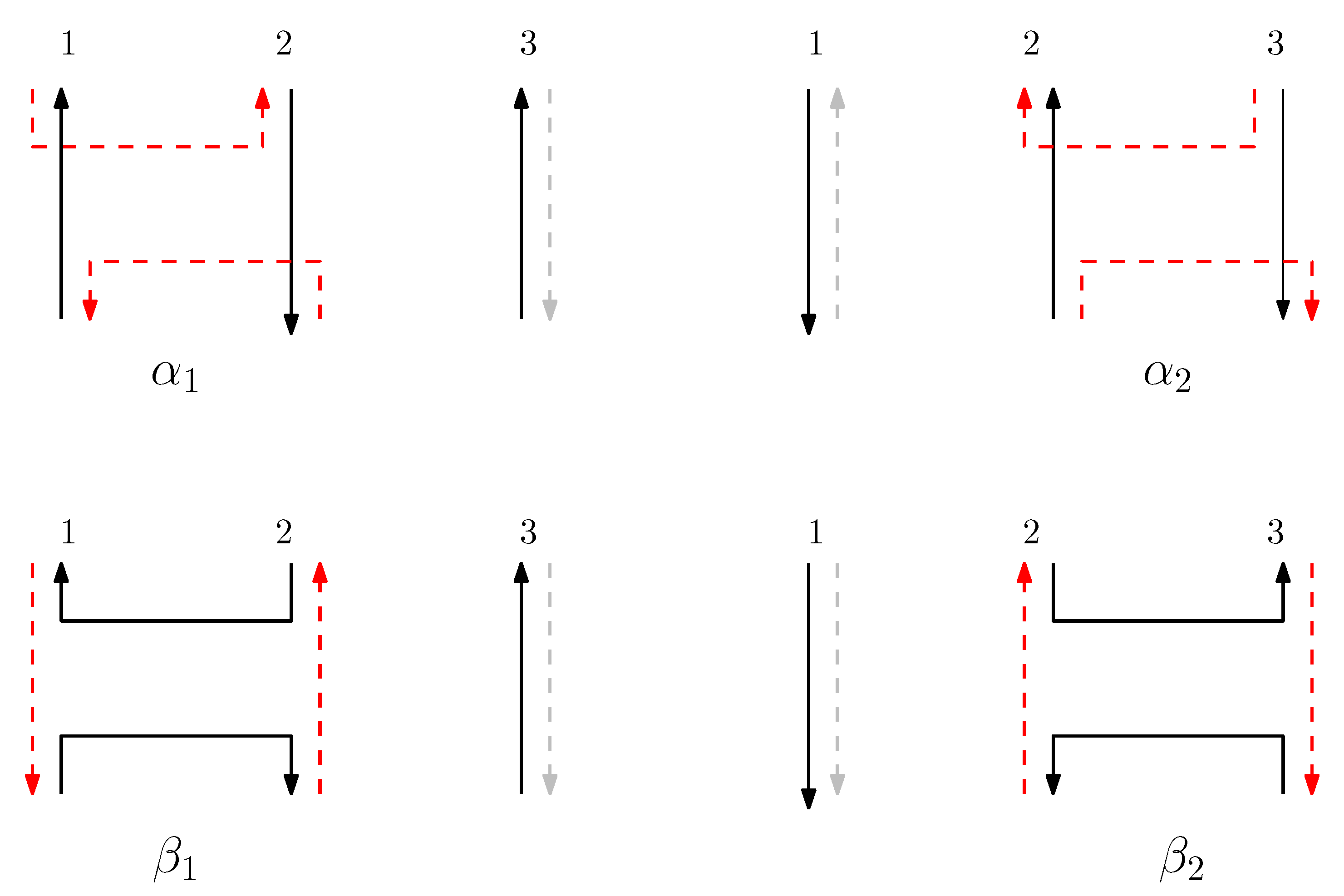
3.2. Concatenation of Side-Aware DNA Origami Words
- (i)
- For all scaffolds in , replace the subscript b by m.
- (ii)
- For all scaffolds in , replace the subscript t by m.
- (iii)
- Given set , for each sequenceof scaffolds where points and have subscripts t or b, add to . Figure 4 shows an example of the set of scaffolds of a graphical structure of a word .
- (i)
- For all staples in , replace the subscript b by m.
- (ii)
- For all staples in , replace the subscript t by m.
- (iii)
- Given set , for each sequenceof staples where s denote positions, s denote staple types and points , and have subscripts t or b, we perform the following:
- (a)
- If (1) or (2) and or (3) and for any , add to .
- (b)
- Otherwise, if for all , add to .
- (c)
- Otherwise, if for any , add to .
- (d)
- Otherwise, add to .
4. Side-Aware DNA Origami Rewriting Systems
4.1. Rewriting Rules
- If under , then under . Namely, if two graphical structures and are the same under , then they should be the same when we ignore sides of staples and connect all staple endpoints at the same position. This implies that for any rule , there exist , and words and such that and .
- If under , then the scaffolds of and are the same under .
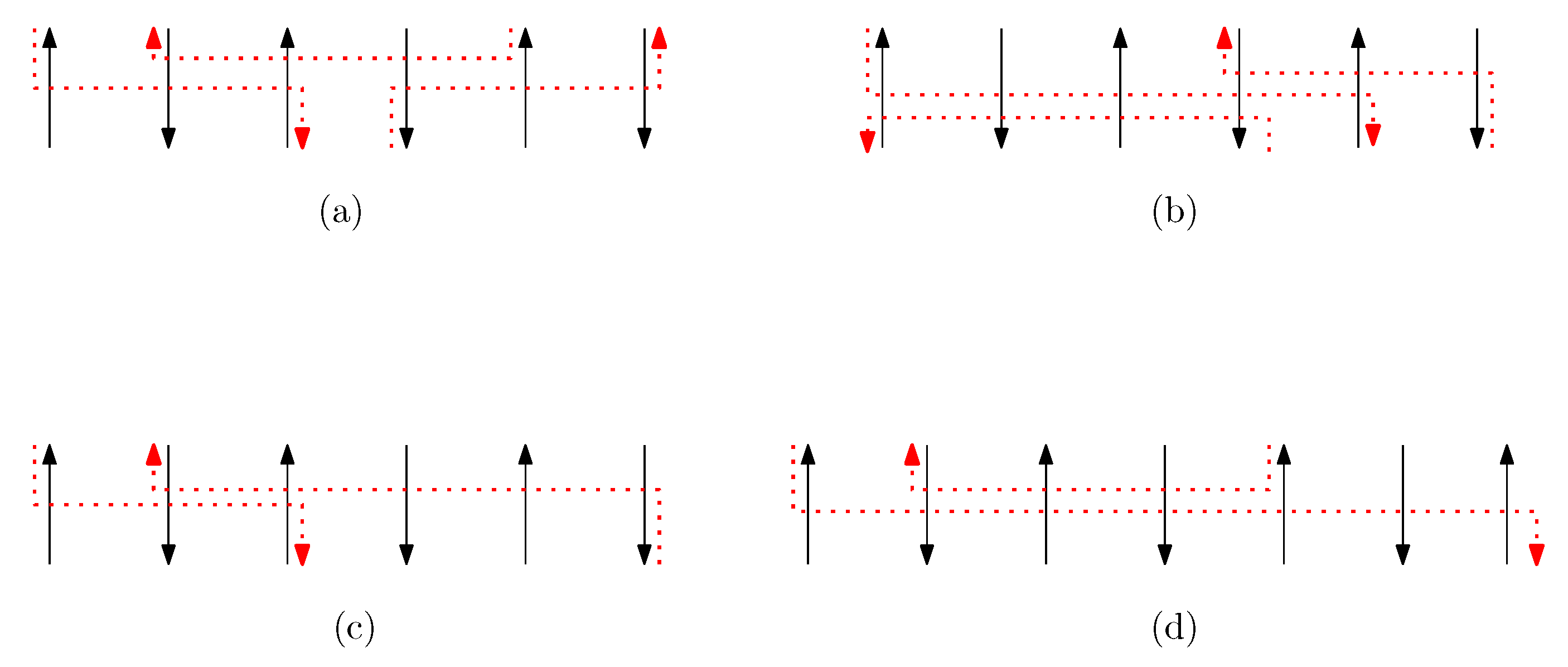
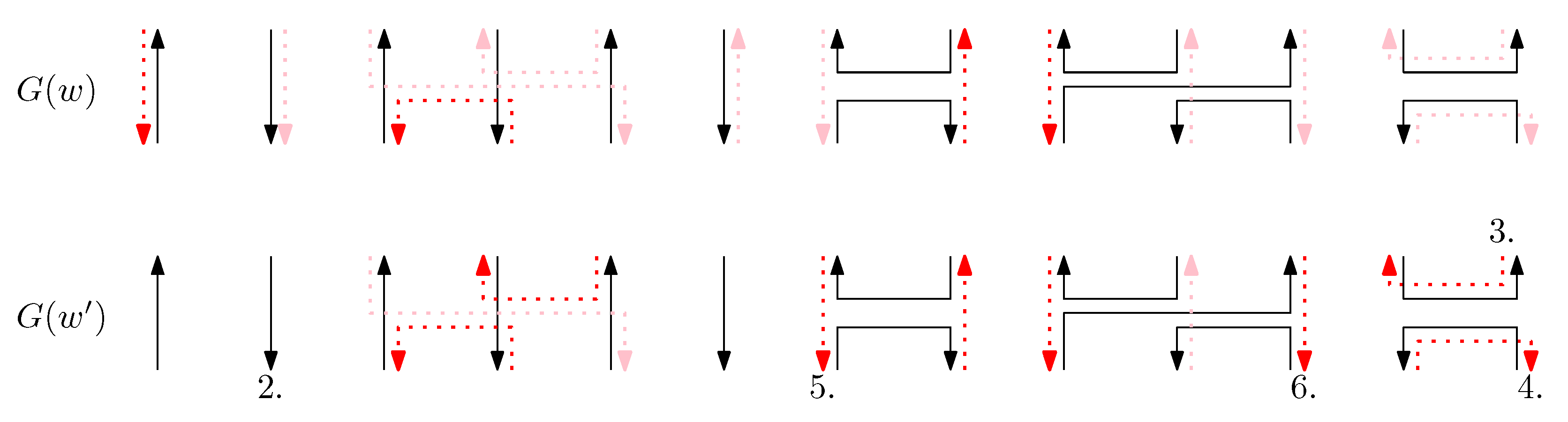
- Staple segments in the generators are categorized into three geometric types: a cap (i.e., ), a cup (i.e., ), and a straight segment (i.e., ()). For convenience, we refer to a cap (cup) between the ith and the st columns as the ith cap (cup), and a straight staple at the ith column as the ith straight staple.
- Cap: We first consider a pair of ith caps for even is. Since the cap segments are at the bottom of the structure, concatenating any prefix does not affect the equivalence of graphical structures. We have six different generators that affect the ith cap segments: through . Figure 6 illustrates an example of and where the only difference is , and changes in the graphical structures from concatenation of these six generators after and . We observe that all generators except make two graphical structures equivalent. For the case, the difference in graphical structures remains the same. Therefore, we establish the override set as for . When i is odd, for , the override set is the same as the even case, which holds for all of the following cases.
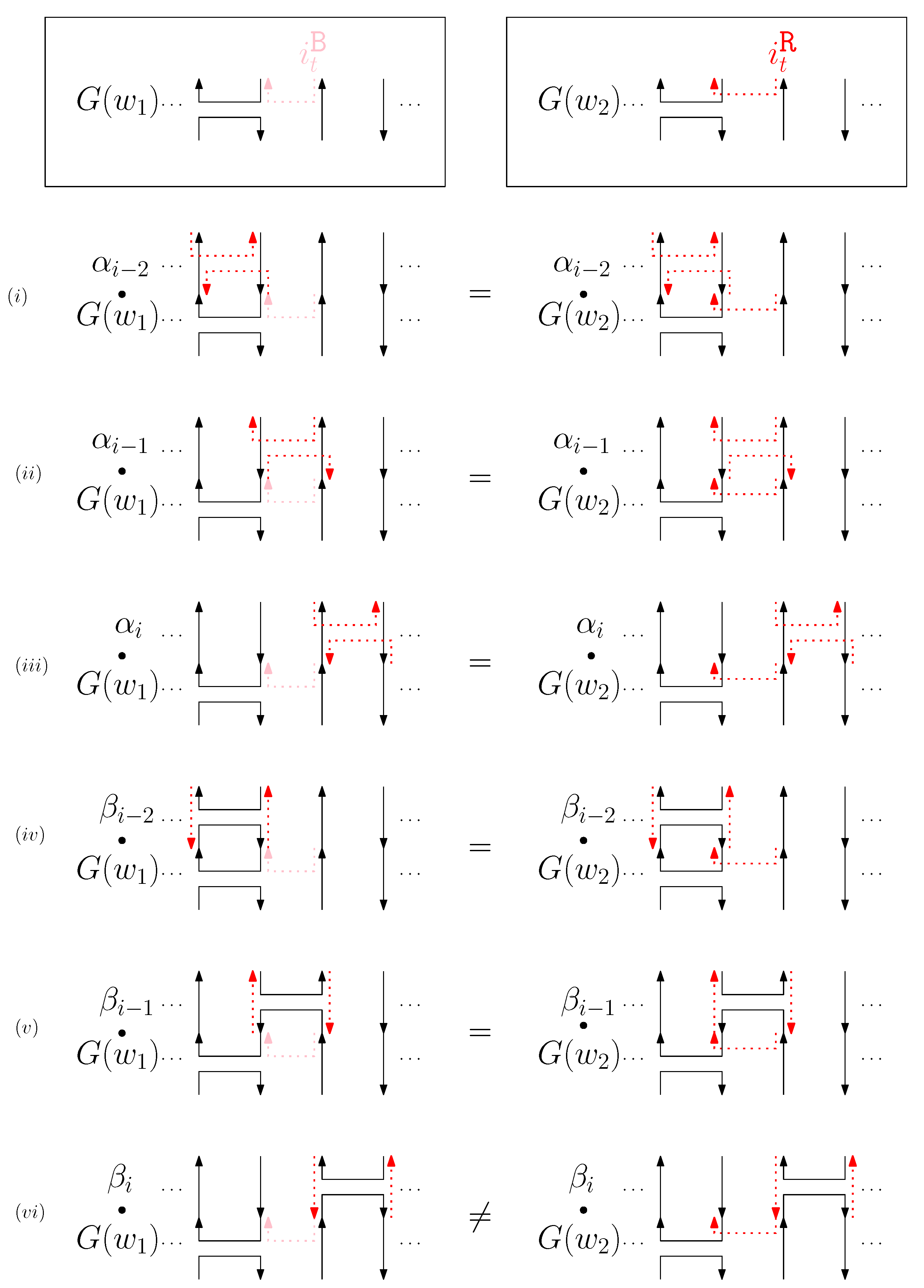
- Cup: We consider a pair of ith cups for odd is. Since the cup segments are at the top of the structure, concatenating any suffix does not affect the equivalence of graphical structures. We have six different generators that affect the ith cap segments: through . Figure 7 illustrates an example of and where the only difference is , and changes in the graphical structures from concatenation of these six generators before and . We observe that all generators except make two graphical structures equivalent. For the case, the difference in graphical structures remains the same. Therefore, we establish the override set as for .
- Straight segment: We have the following cases.
- (a)
- When is right and is block: we consider for odd is. We have four different generators that affect the straight segments: through . Figure 8 illustrates an example of and where the only difference is , and changes in the graphical structures from concatenation of these four generators before and after and . If concatenation of a generator does not make two graphical structures equivalent, it may change the geometric type of the staple segment difference. For example, concatenating before and changes the geometric type of the staple segment difference to the st cap. Thus, for any , holds. We summarize all of the cases as the following override set: for and .
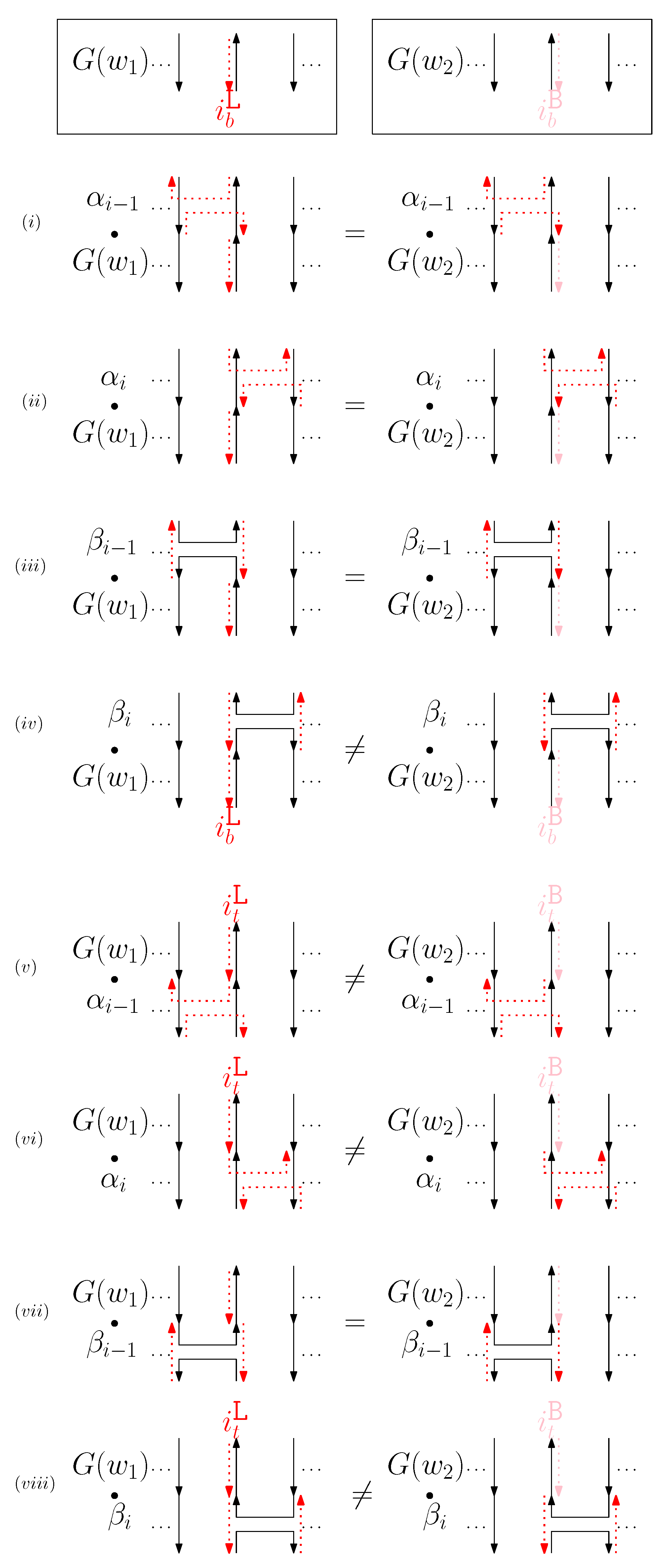
- (b)
- When is left and is block: we consider for odd is in Figure 9. We establish the following override set: for and .
- (c)
- When is virtual and is right: We first consider for odd is in Figure 10. We summarize all of the cases as the following override set: for and .
- (d)
- When is virtual and is left: We consider for odd is in Figure 11. We establish the following override set: for and .
- (e)
- When is virtual and is block: We consider for odd is in Figure 12. We establish the following override set: for and .
- for .
- for .
- for , , , and for .
- for , , , and for .
- for , , , , and for .
- for , ,, , and for .
- for ,, ,, , ,and for .
- : When , the rule also holds under .
- (a)
- When and , we observe that the only difference in graphical structures is the ith cap. Thus, holds for .
- (b)
- When and , we observe that the only difference in graphical structures is the st cup. Thus, holds for .
- (c)
- When , we observe that there are st cup and cap differences. Thus, holds for and .
- : This rule also holds under .
- for : This rule also holds under .
- for
- (a)
- When and , we observe that the only difference in graphical structures is the ith straight virtual/block staples. Thus, holds for .
- (b)
- When and , we observe that the only difference in graphical structures is the nd straight virtual/block staples. Thus, holds for .
- (c)
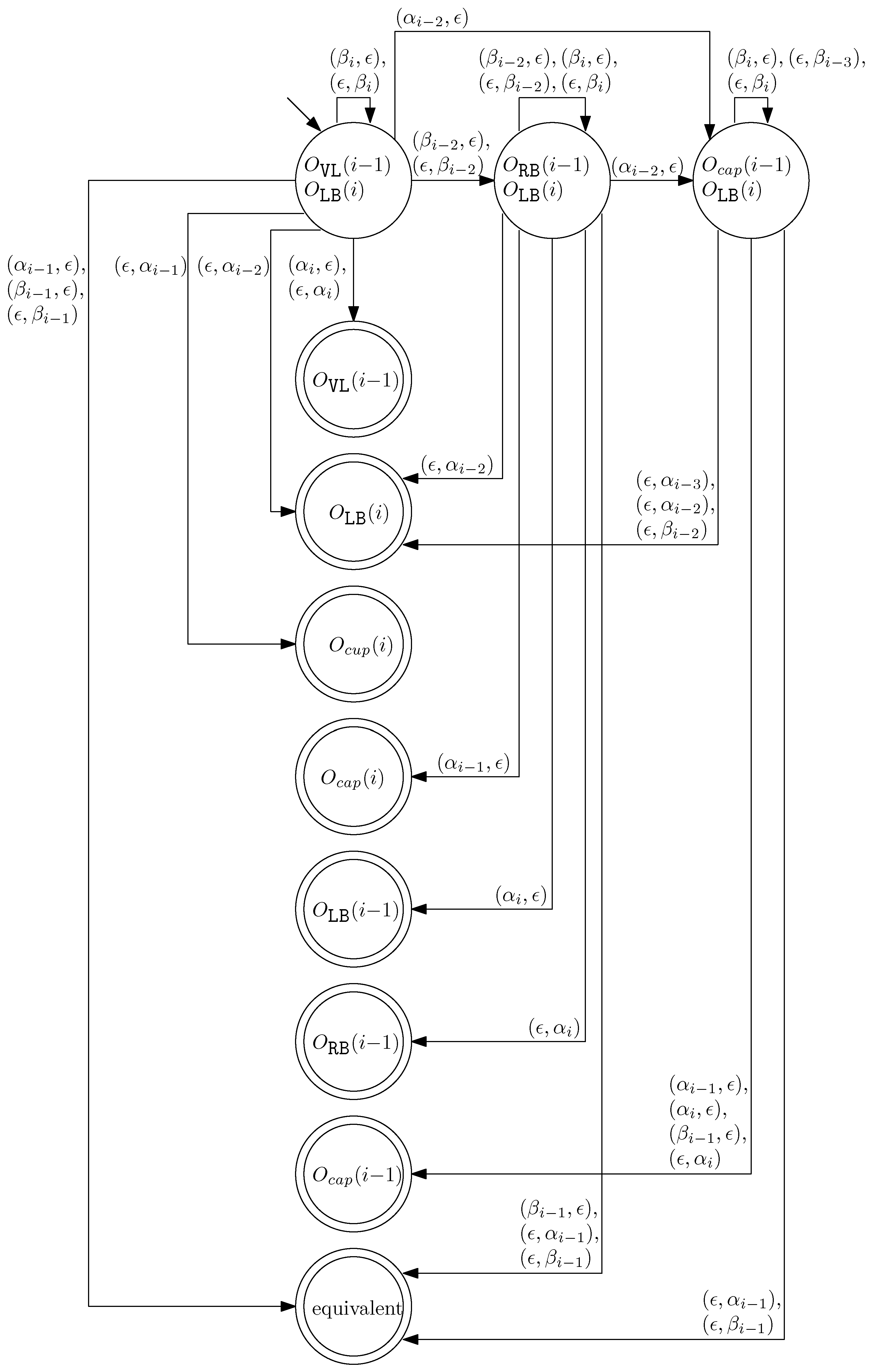
- When and , we observe that the differences in graphical structures are the st straight virtual/block staple and the ith straight left/block staple. Since straight differences on two adjacent columns can become the same by simply applying and , we attach generators that affect the different staple types and observe the changes on the differences. Figure 13 illustrates the transition graph of the changes in the different staple types. Each node denotes the different staple types by override sets for the differences, and each transition has a set of pairs of a prefix and a suffix that changes the different staple types. Nodes with less than or equal to one type difference are double-circled to denote the “final” nodes, since we can directly apply the override set on the node to make two graphical structures equivalent. For and , we start from the node with two override sets and . Then, for example, if we follow transitions and , the resulting node has one override set . From this sequence of transitions, we establish the rewriting rule for , and . In general, we can recursively construct a rewriting rule based on a sequence of transitions that leads to a final node as follows:
- We start with and and the current node with two override sets and .
- For a transition from the current node, append a prefix to and where v does not have any such that the transition exists from the current node.
- For a transition from the current node, append a suffix to and where v does not have any such that the transition exists from the current node.
- Update the current node by following the transition. If the current node is final with the override set O, we establish the rewriting rule for . Otherwise, repeat the process from the current node.
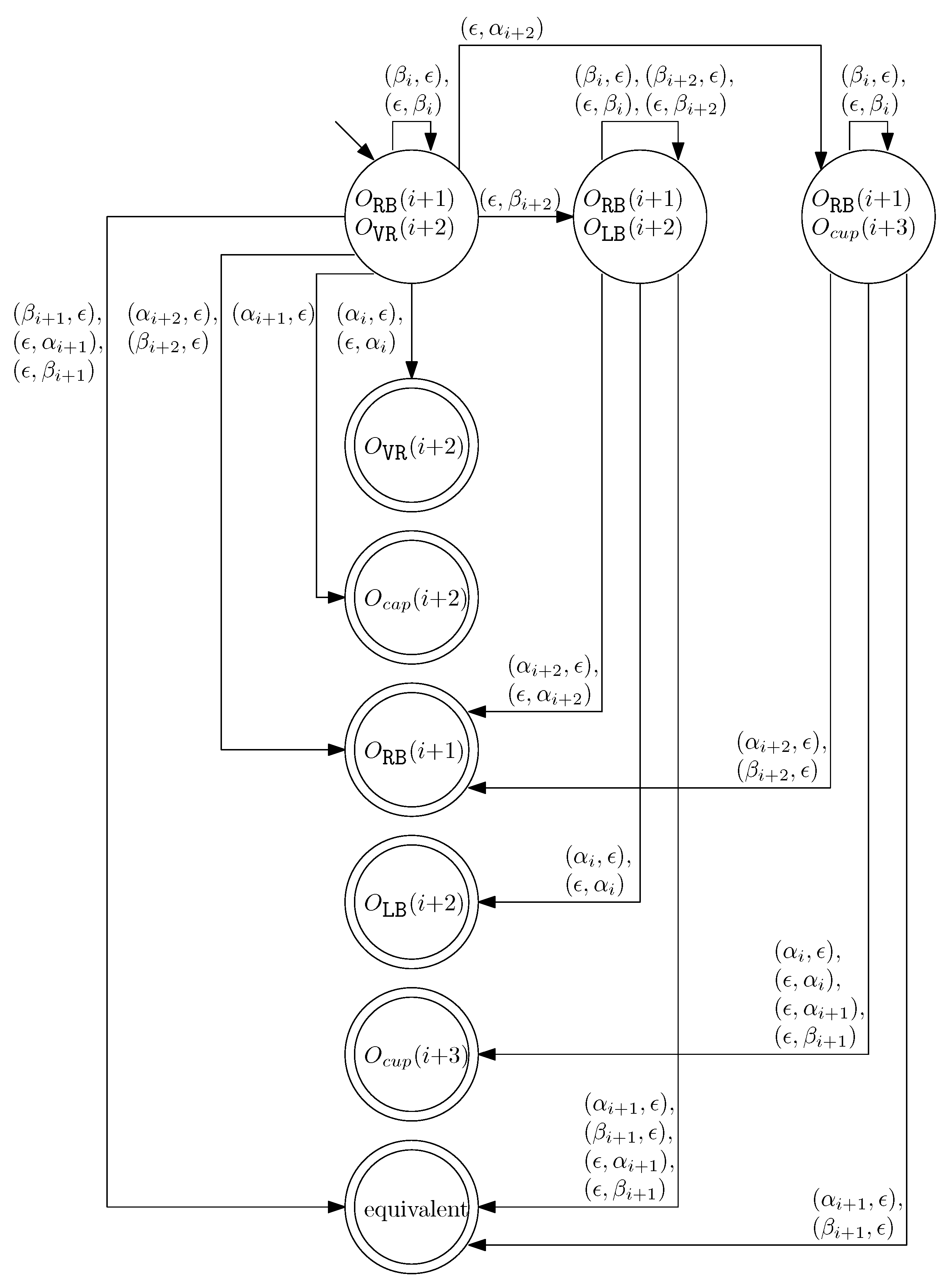
- (d)
- When and , we can similarly construct the transition graph as Figure 14. Based on this transition graph, we can recursively construct a set of rewriting rules.
4.2. Properties of Graphical Structures and Equivalent Classes
- Straight if there exists a straight scaffold on the ith column.
- Crossing if there exists a scaffold from the jth column to the kth column such that or holds.
- Left-sided if the ith column is not crossing and all scaffolds with endpoints on the ith column have the other endpoints on the jth column such that .
- Right-sided if the ith column is not crossing and all scaffolds with endpoints on the ith column have the other endpoints on the jth column such that .
- If a staple is virtual straight, then the staple is on a straight column.
- If a staple is a cup, then the staple is left or block.
- If a staple is a cap, then the staple is right or block.
- If a staple is left straight, then the staple is on a straight or right-sided column.
- If a staple is right straight, then the staple is on a straight or left-sided column.
- If a staple is not a cap/a cup/a straight segment, then the staple is block.
- is isomorphic to .
- A staple is virtual if and only if the staple is straight and on a straight column.
- If a staple is a cup, then the staple is left.
- If a staple is a cap, then the staple is right.
- A staple is left straight if and only if the staple is on a right-sided column.
- A staple is right straight if and only if the staple is on a left-sided column.
- for , .
- for , if and if .
- for , we have .
- for , we have and
- a if a staple segment , where ,
- an if a staple segment , where for ,
- a if a staple segment , where
- an if a staple segment , where for ,
- a if a staple segment , where for .
- (i)
- A bridge of width n is a subset of staple set of the given graphical structure,
- (ii)
- For any staple segments in a bridge of width n, for ,
- (iii)
- For any staple segments in a bridge of width n, , for ,
- (iv)
- A bridge of width n consequently spans n columns,
- (v)
- There is no proper subset of a bridge of width n which is a bridge of width n.
- (i)
- A bridge of width n is a subset of staple set of the given graphical structure,
- (ii)
- For any staple segments in a bridge of width n, for ,
- (iii)
- For any staple segments in a bridge of width n, , for ,
- (iv)
- A bridge of width n consequently spans n columns,
- (v)
- There is no proper subset of a bridge of width n which is a bridge of width n.
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Whitesides, G.M.; Boncheva, M. Beyond Molecules: Self-assembly of mesoscopic and macroscopic components. Proc. Natl. Acad. Sci. USA 2002, 99, 4769–4774. [Google Scholar] [CrossRef] [PubMed]
- Evans, C.G.; Winfree, E. Physical principles for DNA tile self-assembly. Chem. Soc. Rev. 2017, 46, 3808–3829. [Google Scholar] [CrossRef] [PubMed]
- Winfree, E.; Eng, T.; Rozenberg, G. String Tile Models for DNA Computing by Self-Assembly. In Proceedings of the 6th International Workshop on DNA-Based Computers, Leiden, The Netherlands, 13–17 June 2000; pp. 63–88. [Google Scholar]
- Rothemund, P.W.K. Folding DNA to create nanoscale shapes and patterns. Nature 2006, 440, 297–302. [Google Scholar] [CrossRef] [PubMed]
- Garrett, J.; Jonoska, N.; Kim, H.; Saito, M. DNA origami words, graphical structures and their rewriting systems. Nat. Comput. 2021, 20, 217–231. [Google Scholar] [CrossRef]
- Zadegan, R.M.; Norton, M.L. Structural DNA nanotechnology: From design to applications. Int. J. Mol. Sci. 2012, 13, 7149–7162. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Surwade, S.P.; Powell, A.; O’Donnell, C.; Liu, H. Stability of DNA Origami Nanostructure under Diverse Chemical Environments. Chem. Mater. 2014, 26, 5265–5273. [Google Scholar] [CrossRef]
- Voigt, N.V.; Tørring, T.; Rotaru, A.; Jacobsen, M.F.; Ravnsbæk, J.B.; Subramani, R.; Mamdouh, W.; Kjems, J.; Mokhir, A.; Besenbacher, F.; et al. Single-molecule chemical reactions on DNA origami. Nat. Nanotechnol. 2010, 5, 200–203. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Liu, Y.; Rinker, S.; Yan, H. DNA tile based self-assembly: Building complex nanoarchitectures. ChemPhysChem 2006, 7, 1641–1647. [Google Scholar] [CrossRef] [PubMed]
- Douglas, S.M.; Dietz, H.; Liedl, T.; Högberg, B.; Graf, F.; Shih, W.M. Self-assembly of DNA into nanoscale three-dimensional shapes. Nature 2009, 459, 414–418. [Google Scholar] [CrossRef] [PubMed]
- Yin, P.; Hariadi, R.F.; Sahu, S.; Choi, H.M.T.; Park, S.H.; LaBean, T.H.; Reif, J.H. Programming DNA tube circumferences. Science 2008, 321, 824–826. [Google Scholar] [CrossRef]
- SantaLucia, J.; Allawi, H.T.; Seneviratne, P.A. Improved nearest-neighbor parameters for predicting DNA duplex stability. Biochemistry 1996, 35, 3555–3562. [Google Scholar] [CrossRef]
- Wei, B.; Dai, M.; Yin, P. Complex shapes self-assembled from single-stranded DNA tiles. Nature 2012, 485, 623–626. [Google Scholar] [CrossRef] [PubMed]
- Ke, Y.; Ong, L.L.; Shih, W.M.; Yin, P. Three-dimensional structures self-assembled from DNA bricks. Science 2012, 338, 1177–1183. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, A.K.; Huijben, T.A.P.M.; Sison, M.; Di Luca, A.; Chiarelli, G.; Vanni, S.; Brasselet, S.; Mortensen, K.I.; Stefani, F.D.; Pilo-Pais, M.; et al. DNA self-assembly of single molecules with deterministic position and orientation. ACS Nano 2022, 16, 16924–16931. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Lee, J.Y.; Kim, D.-N. Polymorphic design of DNA origami structures through mechanical control of modular components. Nat. Commun. 2017, 8, 2067. [Google Scholar] [CrossRef] [PubMed]
- Ronald, V.B.; Friedrich, O. String-Rewriting Systems; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Louis, H.K. Knots and Physics; World Scientific: Singapore, 2001. [Google Scholar]
- Borisavljević, M.; Došen, K.; Petric, Z. Kauffman Monoids. J. Knot Theory Its Ramif. 2002, 11, 127–143. [Google Scholar] [CrossRef]
- Lau, K.W.; FitzGerald, D.G. Ideal Structure of the Kauffman and Related Monoids. Commun. Algebra 2006, 34, 2617–2629. [Google Scholar] [CrossRef]
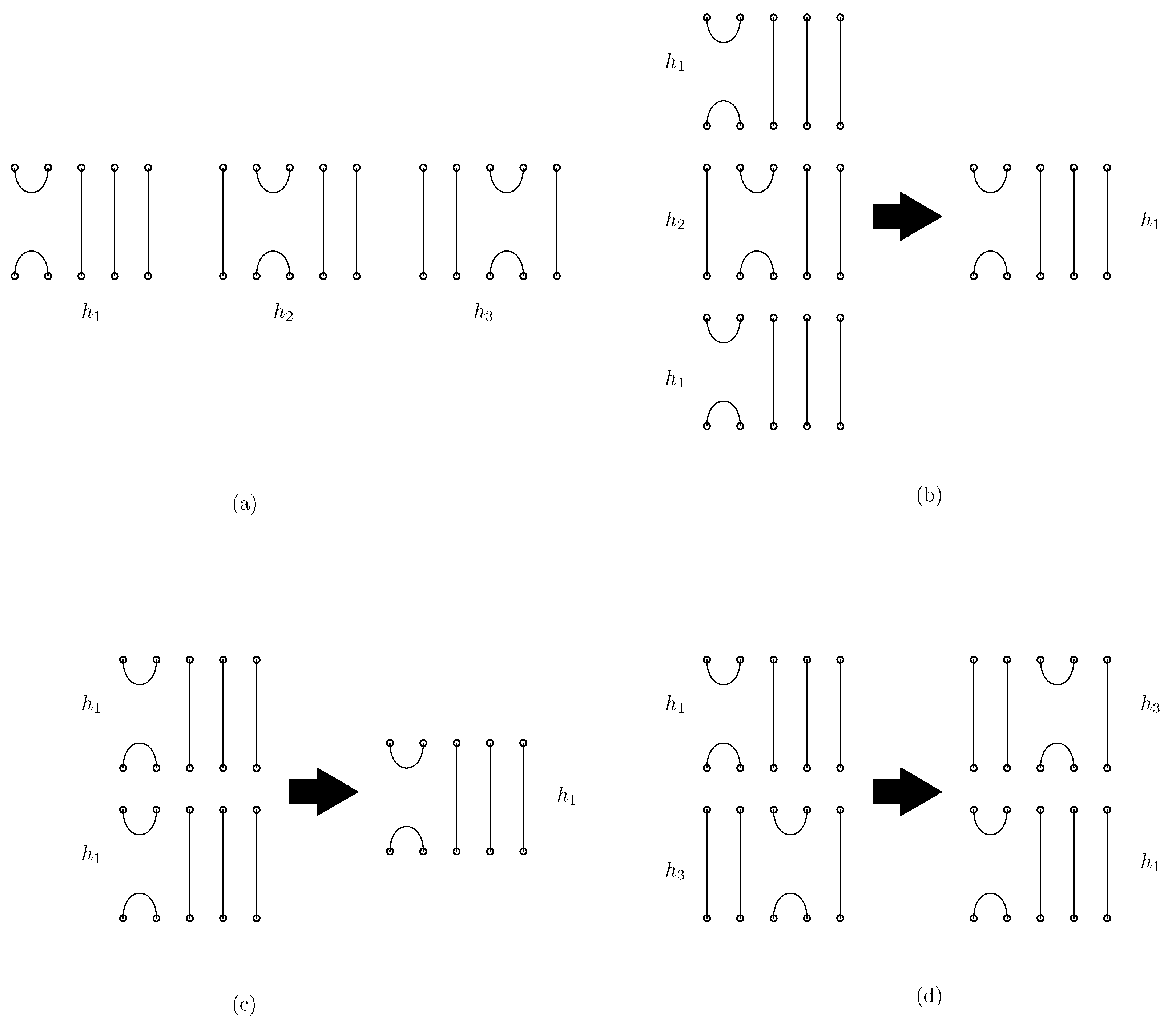
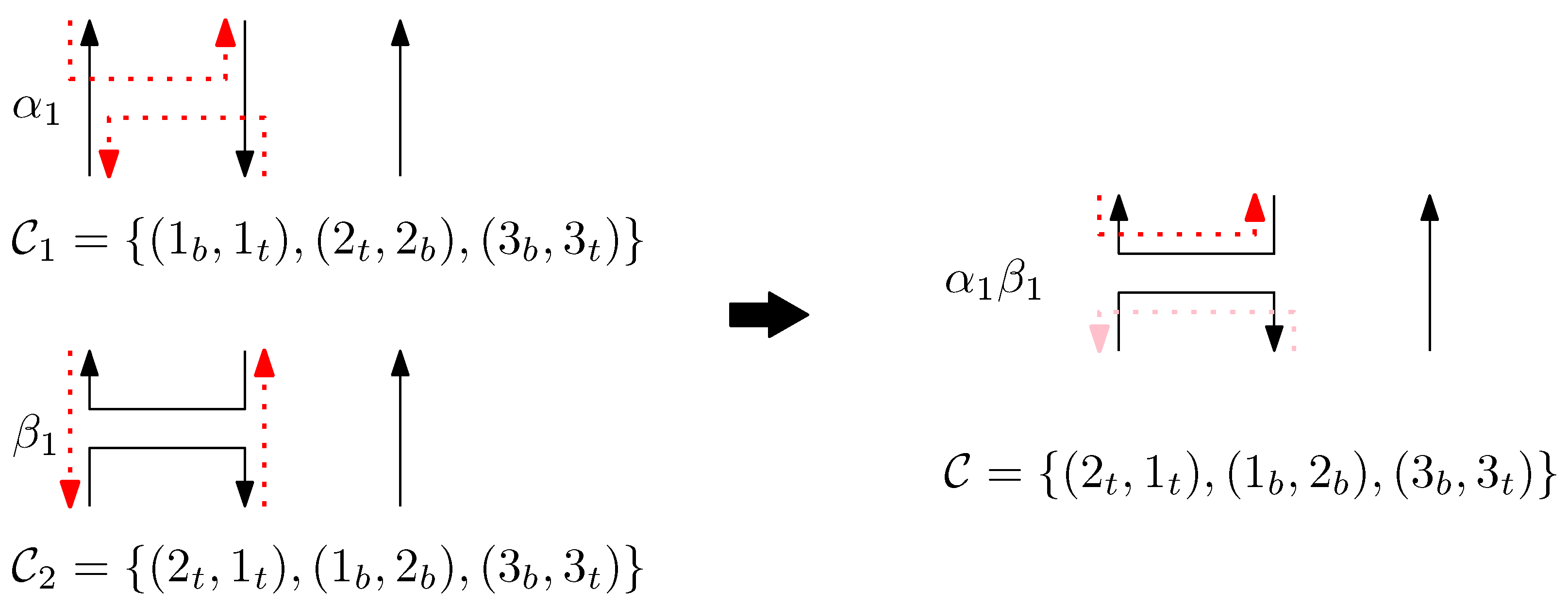
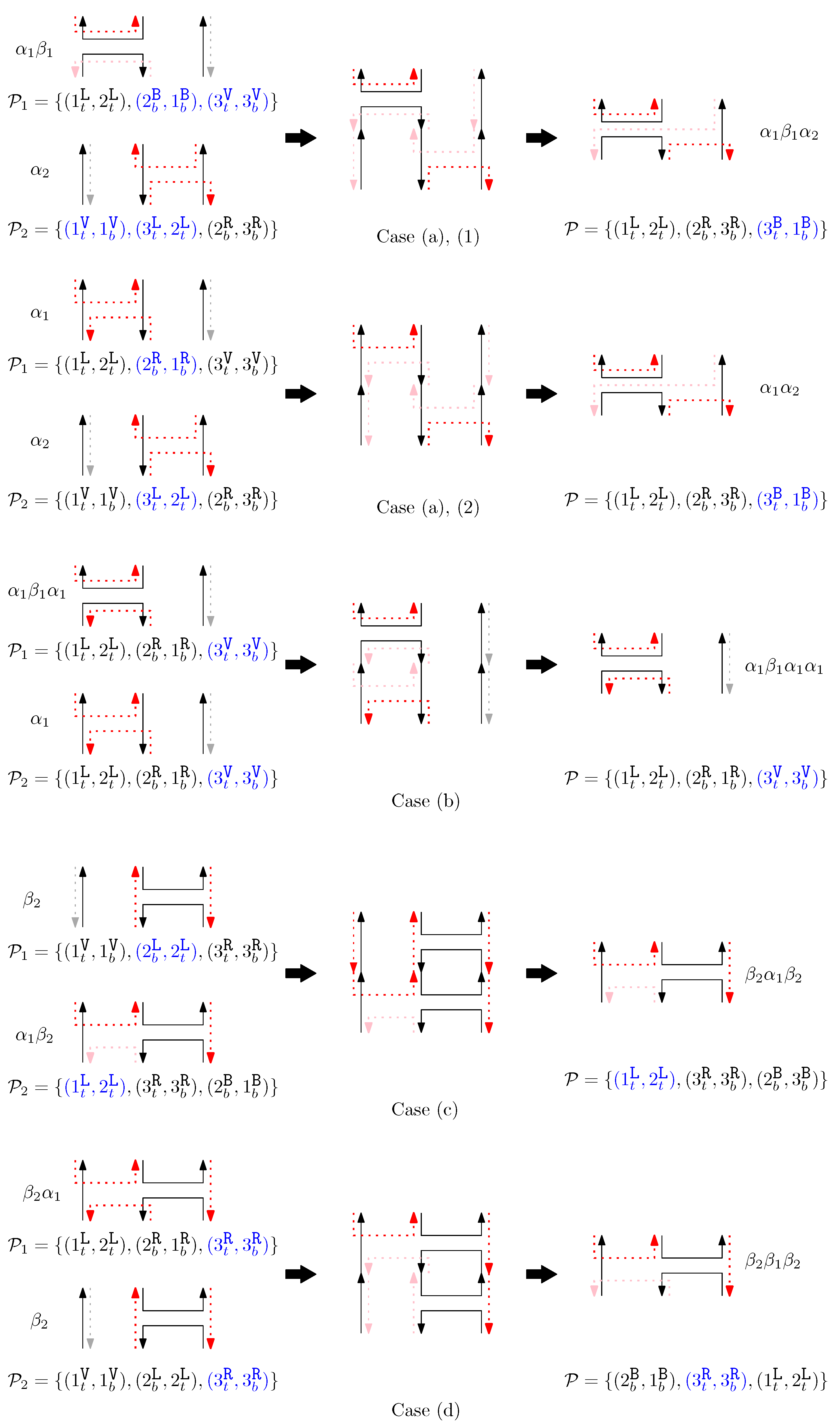
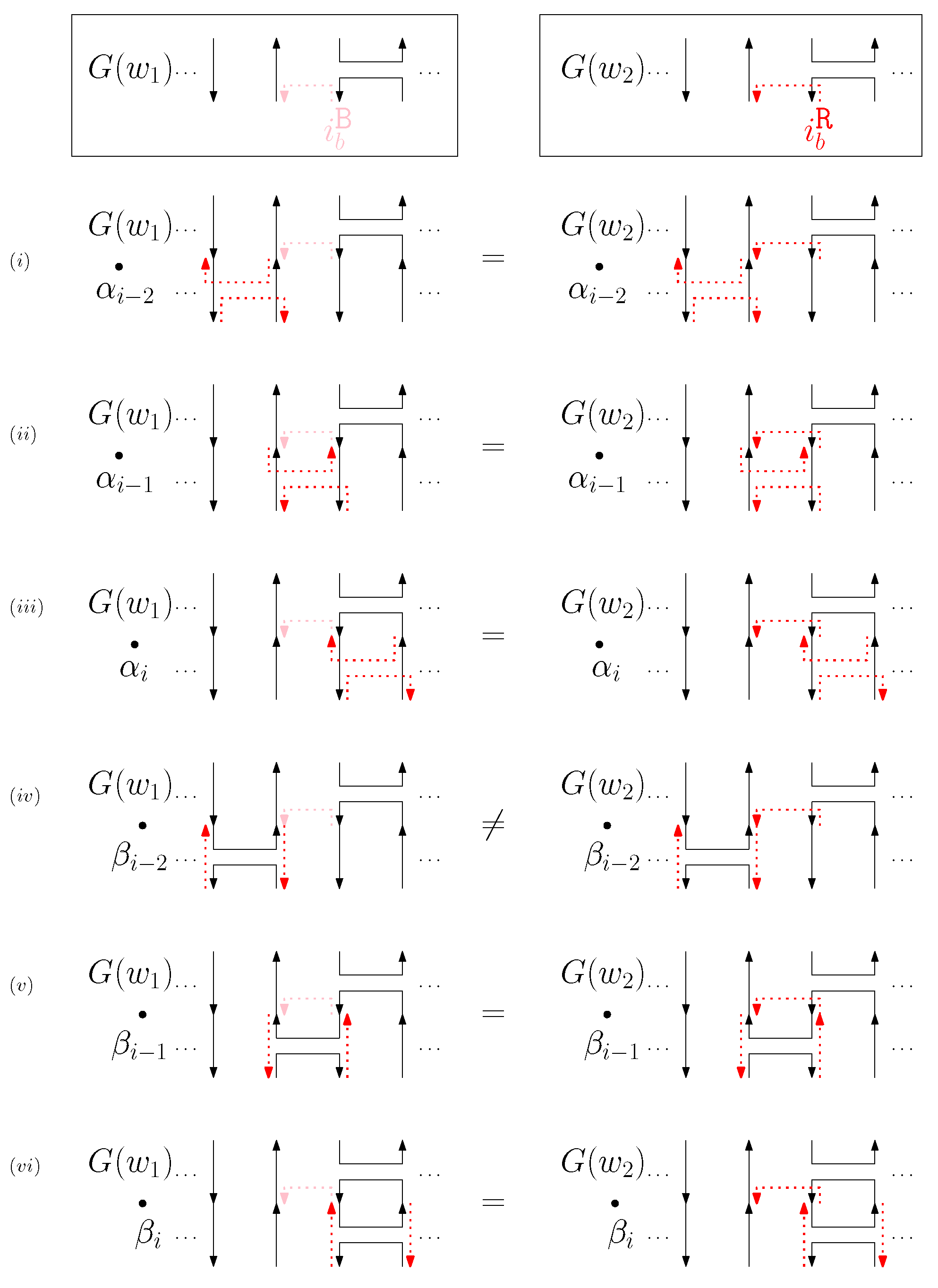
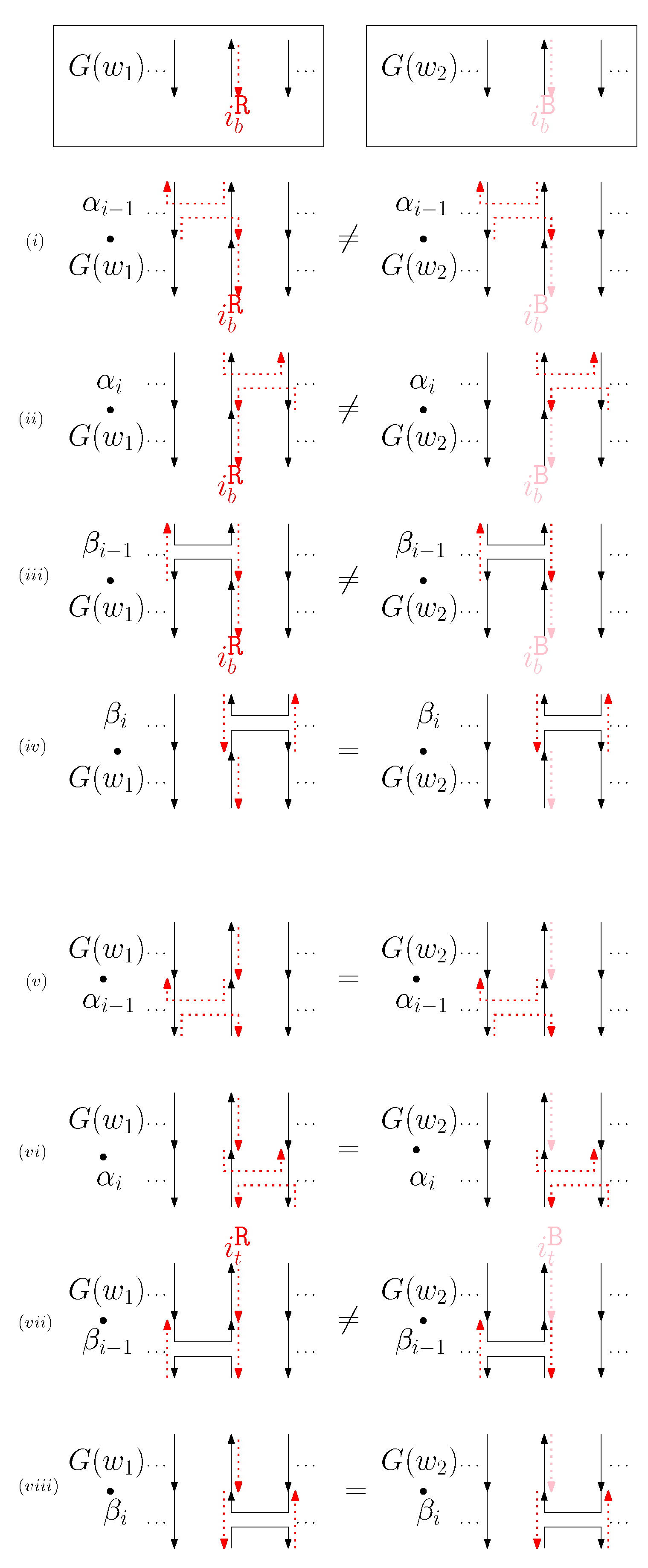
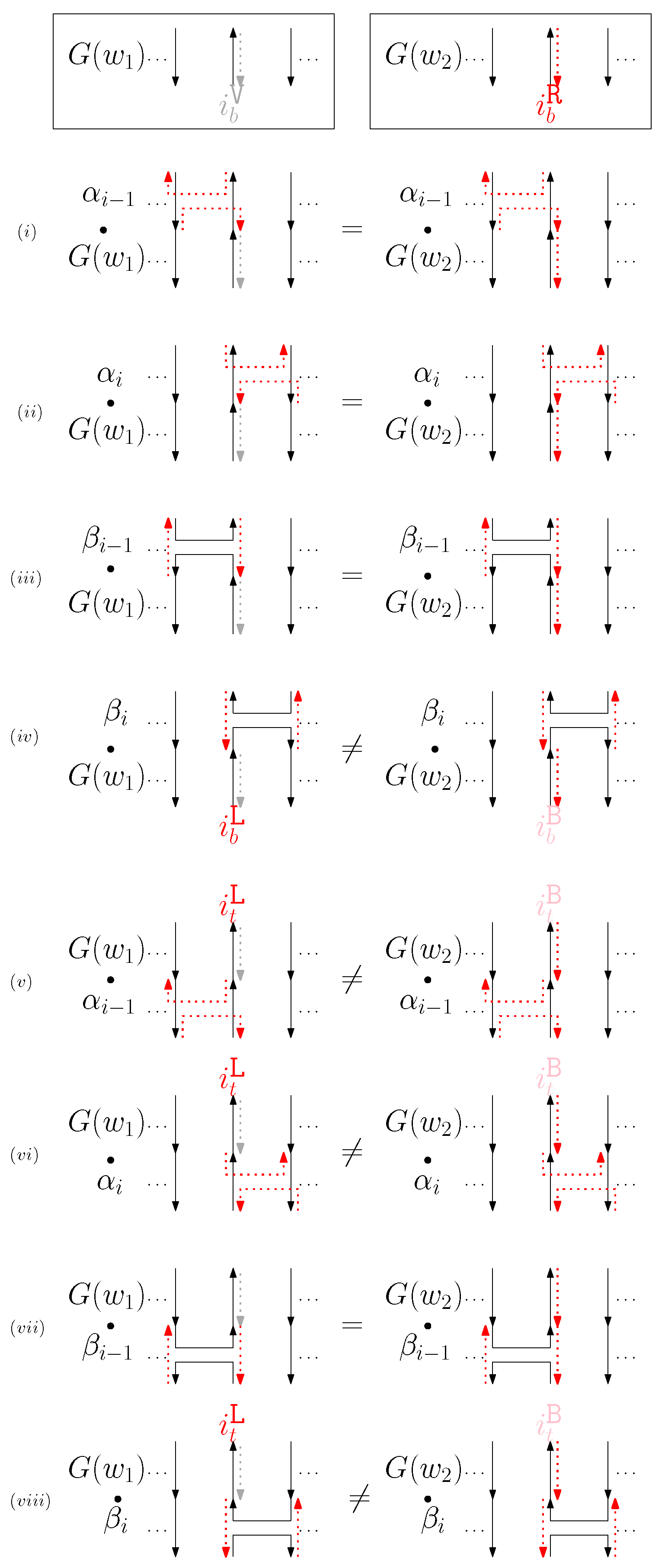
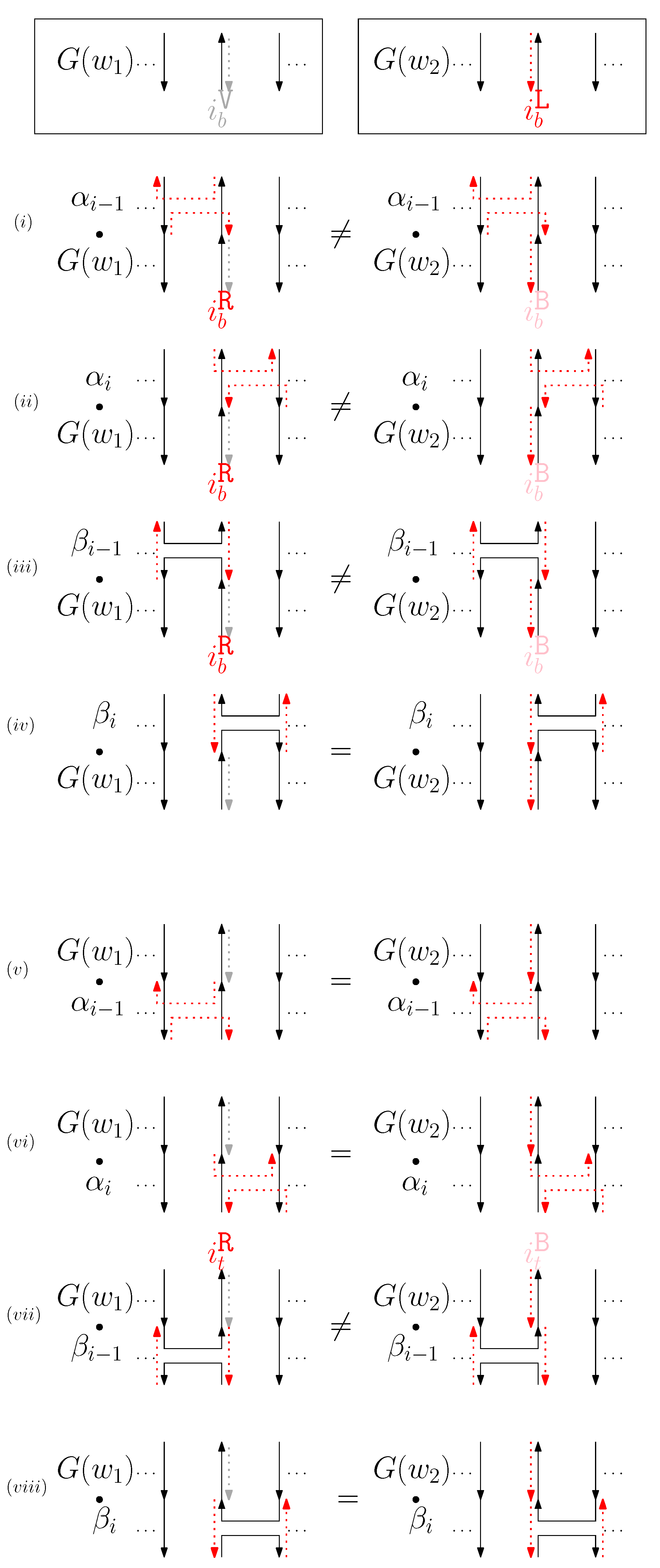
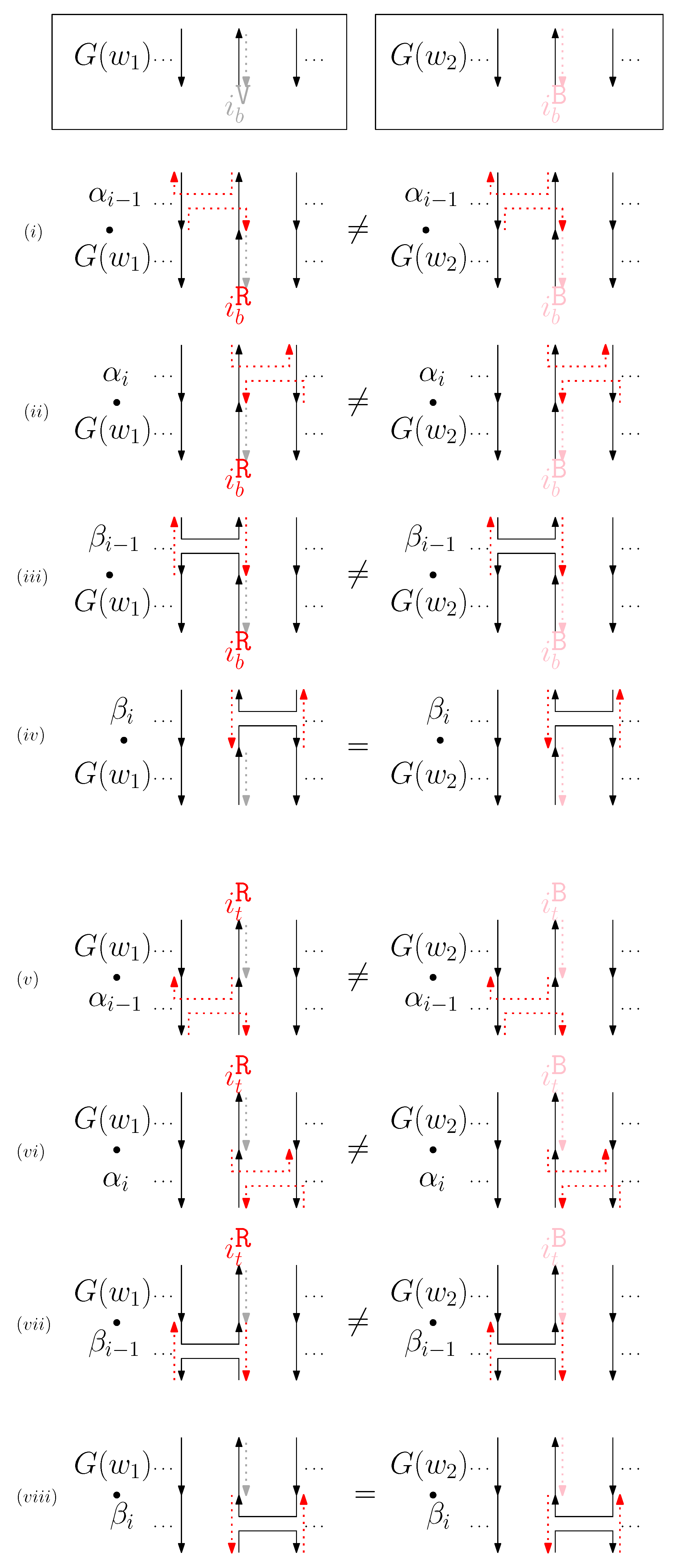
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, D.-J. Formalization of Side-Aware DNA Origami Words and Their Rewriting System, and Equivalent Classes. Mathematics 2025, 13, 895. https://doi.org/10.3390/math13060895
Cho D-J. Formalization of Side-Aware DNA Origami Words and Their Rewriting System, and Equivalent Classes. Mathematics. 2025; 13(6):895. https://doi.org/10.3390/math13060895
Chicago/Turabian StyleCho, Da-Jung. 2025. "Formalization of Side-Aware DNA Origami Words and Their Rewriting System, and Equivalent Classes" Mathematics 13, no. 6: 895. https://doi.org/10.3390/math13060895
APA StyleCho, D.-J. (2025). Formalization of Side-Aware DNA Origami Words and Their Rewriting System, and Equivalent Classes. Mathematics, 13(6), 895. https://doi.org/10.3390/math13060895






