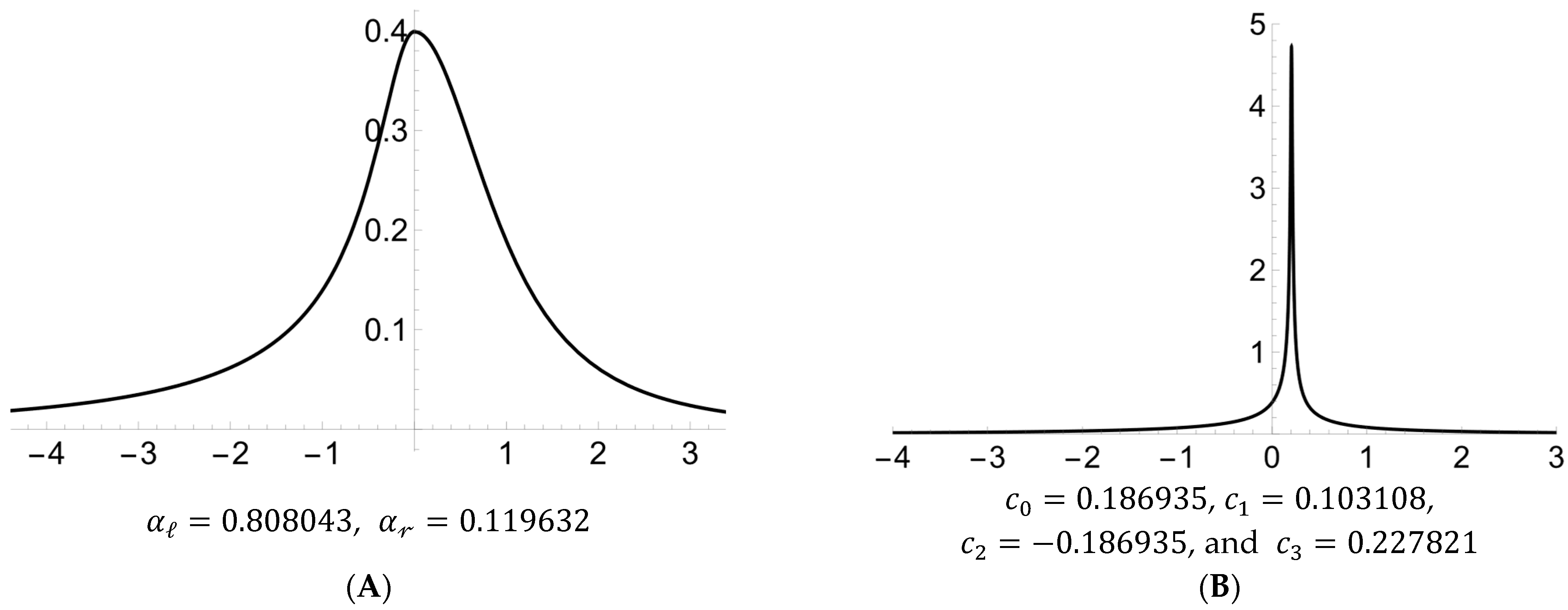1. Introduction
In many practical applications of statistics, the accurate modeling of the distribution of data is crucial for effective analysis and reliable decision making. Although several classical statistical procedures (such as the
t-test, ANOVA, and linear regression) are based on the normality assumption, many real-world data do not exhibit the true characteristics of a normal distribution [
1,
2,
3,
4]. In the field of statistical modeling, the prevalence of non-normal data poses significant challenges for traditional methods in areas such as high-frequency financial trading, economics, public health, psychology, biomedical imaging, and so on. As a result, researchers/practitioners in these fields encounter complex distributional patterns that conventional models struggle to address [
5,
6].
Since the pioneering work of statisticians like R. A. Fisher, Karl Pearson, and William Gosset (pseudonym “Student”), numerous probability distributions have been introduced to model non-normal data. Some of the well-known non-normal distributions are Student’s
t-distribution [
7], Burr distribution [
8], log-normal distribution [
9], Fleishman’s power method distribution [
10], Tukey’s g and h distribution [
11], generalized lambda distribution [
12], skew-normal distribution [
13], and so on. Although each of these distributions is unique and is capable of modeling non-normal data with specific degrees of non-normality, one distribution is not “one size fits all” for modeling all types of non-normal data. Therefore, researchers are continuously developing distributions with unique features to model datasets with specific non-normal characteristics (e.g., heavy-tailed data, highly kurtotic data, bimodal data, and so on).
Among other important distributions, Fleishman’s [
10] third-order power method distribution, together with its extended fifth-order power method [
14] version, has received considerable attention in simulating univariate and multivariate non-normal distributions and in numerous applications (see
Section 2). As a more recent modification to Fleishman’s third-order power method distribution, refs. [
15,
16] introduced two separate families of non-normal distributions via a doubling technique [
17] to simulate non-normal data with a wide range of values of method of moments (MoMs)-based skewness and kurtosis and method of
-moments (Mo
Ms)-based
-skewness and
-kurtosis.
Historically, approaches to modeling non-normal distributions have evolved significantly from basic transformations to more sophisticated methods like the one presented in this paper. Although traditional approaches to handling non-normal data, such as transformation techniques (e.g., log-transformation and Box–Cox transformation) or the use of alternative distributions (e.g., log-normal, skew-normal, and exponential distributions) laid important groundwork, they have their own limitations that may compromise the reliability and accuracy of statistical inferences [
18]. While current modeling techniques struggle with the accurate representation of non-normal data with large values of skewness and kurtosis, our approach utilizing mixed third-order polynomials offers a robust solution, as demonstrated by the simulation results.
A promising approach to addressing the challenge of modeling non-normal distributions involves using a mixture of distributions based on the third-order polynomials of standard normal and logistic variables. These mixture distributions can represent a variety of distributional shapes, accommodating both symmetric and asymmetric features. The use of third-order polynomial terms enables the capture of complex relationships within the data, providing a more nuanced and accurate representation than linear or lower-order polynomial models.
In this paper, we propose two mixtures of polynomial distributions based on piecewise functions of standard normal and logistic variables and explore their applications to approximate and model non-normal distributions. The proposed methodology combines the strengths of both probability distributions: the well-known properties and widespread applicability of normal distribution and the flexibility of the logistic distribution to accommodate skewed and heavy-tailed distributions. By mixing third-order polynomials of normal and logistic variables through piecewise functions, we aim to create a versatile family of distributions that can enhance the precision and adaptability of statistical analysis.
The remainder of this paper is structured as follows. In
Section 2, we review the literature on relevant non-normal distributions and the use of power method polynomials in statistical modeling. In
Section 3, we detail the theoretical foundation of the proposed third-order mix of polynomials based on piecewise functions, including their mathematical derivations and properties. In
Section 4, we present simulation studies and data-fitting examples to demonstrate the application of the proposed distributions when modeling various non-normal data. In
Section 5, we discuss the results in the context of potential applications and implications for future research and provide a summary concluding the key findings.
2. Theoretical Framework
The third-order power method of polynomials originally proposed by Fleishman [
10] can be defined as follows [
4]:
where
with
. The real-valued coefficients
used in Equation (1) can be obtained by solving Equations (2.18)–(2.21) from ([
4], p. 15) for the specified values of the method of moments (MoMs)-based parameters of skewness and kurtosis. It is essential to elaborate on these coefficients and their derivation from foundational works in this field, as they play a critical role in the functionality and effectiveness of the proposed polynomial mixtures. This paper builds on these mathematical foundations by proposing an enhanced approach that incorporates logistic variables into the mix, aiming to address and mitigate some of the known limitations of traditional power method polynomials.
The probability density function
and cumulative distribution function
associated with Equation (1) can be expressed in parametric forms as follows:
where
in Equation (2) is the first derivative of the power method polynomial in Equation (1), which is assumed to be greater than zero for Equation (2) to produce a valid pdf, and
in Equation (3) is the
of
. Following this framework, it is imperative to critically evaluate the recent applications of similar polynomial-based models for modeling non-normal distributions. While these studies have advanced our understanding, they often fall short of addressing the full spectrum of non-normal characteristics observed in real-world data, such as those involving higher moments of distribution. This paper identifies these gaps, particularly focusing on the limitations of current methods to effectively handle data with extreme values of skewness and kurtosis, and proposes a refined approach that seeks to mitigate these issues.
Power method polynomials have been widely used to simulate univariate and multivariate non-normal distributions with specified values of skewness, kurtosis, and Pearson correlation in a variety of contexts [
4]. Some of these contexts include ANOVA [
19,
20,
21], ANCOVA [
22,
23], regression analysis [
24], microarray analysis [
25], multivariate analysis [
26], item response theory [
27], nonparametric statistics [
28], and structural equation modeling [
29].
Most of the applications of power method polynomials involve the MoMs-based procedure, which has its own limitations. One of the limitations associated with MoMs-based power method polynomials is that distributions with large values of skewness and/or kurtosis can peak at the mode and, thus, may not be representative of real-world data [
15,
16]. To demonstrate this limitation,
Figure 1B shows an extremely peaked pdf of a standard normal-based third-order power method distribution with skewness
and kurtosis
.
Another limitation associated with the MoMs-based power method distribution in Equation (1) is that it can produce valid
s for the combinations of skewness (
) and kurtosis (
) (see Figure 2.2 from [
4], p. 20), where
ranges between 0 and 43.2 for standard normal-based power method distributions and between 1.2 and 472.53 for logistic-based PM distributions. Another limitation associated with the MoMs-based power method distribution is that estimates (for example, of skewness, kurtosis, and Pearson correlation) have unfavorable attributes insofar as they can be substantially biased, have high variance, or can be influenced by outliers [
15,
16,
30,
31,
32,
33,
34].
In the context of these limitations, the main objective of this paper is to introduce two families of mixture polynomial (MP) distributions by mixing standard normal- and standard logistic-based third-order polynomials through the method of
-moments (Mo
LMs), specifically, to obviate the problem of (a) the excessive peaking of pdf associated with some power method distributions with substantial departure from normality and (b) bias associated with the MoMs-based estimates of skewness and kurtosis [
15,
16,
35,
36]. Another objective of this study was to extend the range of skewness
and kurtosis
of valid MoMs-based power method distributions that can be used in simulation studies.
3. Methodology
The normal-logistic mixture polynomial (MP) distribution is a piecewise function of standard normal- and logistic-based third-order polynomials, expressed as follows [
15]:
where
,
,
, and
, where the scale parameter,
, of the logistic distribution adjusts the height of its pdf at
to
, which is the height of the standard normal pdf at
.
The pdf of the normal-logistic MP distribution can be defined in parametric form as follows:
where
and
are the pdfs of standard normal and logistic variables
and
, respectively, and
and
are the first derivatives of
and
, respectively.
The logistic-normal MP distribution is a piecewise function of standard logistic- and normal-based third-order polynomials, and is expressed as follows:
where
,
,
and
.
The pdf of the logistic-normal MP distribution can be defined in parametric form as follows:
where
and
are the pdfs of standard logistic and normal variables
and
, respectively, and
and
are the first derivatives of
and
, respectively.
To demonstrate this methodology, the pdf of a normal-logistic MP distribution based on Equations (4) and (5) is presented in panel A of
Figure 1. Specifically, panel A of
Figure 1 is the pdf of a normal-logistic MP distribution with mean
, standard deviation
, skewness
, and kurtosis
with corresponding
-moment-based parameters of
-skewness
and
-kurtosis
. Also presented in panel B of
Figure 1 is the pdf of a standard normal-based third-order power method distribution [
4] that has the same values of skewness and kurtosis as that of the distribution in panel A. An inspection of
Figure 1A,B indicates that the pdf in panel A is more representative of real-world data, whereas the pdf in panel B shows pointed peak at the mode, even though these two pdfs have the same degree of non-normality (i.e., the same values of skewness = −3 and kurtosis = 39). This example illustrates that Fleishman’s (1978) third-order power method distribution, while widely used, can struggle to accurately fit data with extreme values of skewness and kurtosis. In contrast, the proposed MP distributions produce pdfs that provide a better representation of real-world data with the same values of skewness and kurtosis. This implies that the family of MP distributions offers a compelling alternative for modeling data characterized by excessive skewness and kurtosis.
Table 1 indicates that the estimates
and
are much closer to their respective parameters of
L-skewness
and
L-kurtosis
than the MoMs-based estimates
and
of skewness
and kurtosis
. Specifically, the estimates
and
are, on average, 65.62% and 35.21% of their respective parameters (
and
). On the other hand, the estimates
and
are, on average, 96.63% and 98.31% of their respective parameters (
and
). An inspection of
Table 1 also indicates that the standard errors (SEs) associated with estimates
and
are much smaller than those associated with estimates
and
. For each bootstrap estimate in
Table 1, the 95% bootstrap confidence interval (95% C.I.) and standard error (SE) were based on resampling 25,000 statistics using bootstrap functions of the R [
37] package ‘boot’ [
38]. Each statistic was based on a sample size of
.
3.1. L-Moments
For a continuous random variable
from a probability distribution with
and
, the
-th probability-weighted moment (PWM),
, can be expressed as follows [
30]:
-moments, originally proposed by Hosking [
30], are defined as a linear combination of
s. Specifically, the first four
-moments associated with
can be expressed as follows ([
30], p. 107):
where
in Equations (9)–(12) was obtained by evaluating the integral in Equation (8) for
. The coefficients associated with
in Equations (9)–(12) were obtained from ([
31], p. 20).
The first two
-moments,
and
, in Equations (9) and (10) measure the location and scale of distribution and are the arithmetic mean and one-half of the coefficient of the mean difference (or Gini’s index of spread), respectively. The
-moment-based indices of
-skewness
and
-kurtosis
(analogous to skewness and kurtosis) are the ratios defined as
and
, respectively. In general,
-moment ratios are bounded in the interval and
as is the index of
-skewness (
), where a symmetric distribution implies that all
-moment ratios with odd subscripts are zero [
15].
The
-moment-based characterizations of distributions have certain advantages over their conventional moment-based counterparts. For example, in terms of parameter estimation, the Mo
Ms-based estimates of
-skewness,
-kurtosis, and
-correlation are substantially less biased and more precise than the MoMs-based estimates of skewness, kurtosis, and Pearson correlation. Likewise, in terms of distribution fitting, the Mo
Ms-based distributions provide better fits to non-normal data than their MoMs-based counterparts [
15,
16,
32,
33,
34,
35,
39,
40,
41,
42,
43,
44].
According to [
30], if the mean (
) exists, then all other
-moments have finite expectations. To maintain this advantage, it is assumed that the coefficients
and
in Equations (4) and (6) for any distribution are positive (i.e.,
and
) so that its
-th
-moment exists and is finite.
3.2. L-Moments for the Normal-Logistic MP Distributions
The derivation of
-moments associated with the normal-logistic MP distributions can be obtained by first writing Equation (8) as follows:
where
and
have the corresponding pdfs
and
and cdfs
and
where
in the equation for
is the complementary error function [
45] associated with the standard normal distribution.
Evaluating both integrals in Equation (13) for
and 1, it is straightforward to derive
and
, which can be substituted into Equations (9) and (10) to obtain the first two
-moments as follows:
For
and
, the evaluation of the second integral on the right-hand side of Equation (13) is straightforward, but the evaluation of the first integral requires several mathematical manipulations, as shown in [
15]. Specifically, the first three pieces on the right-hand side of Equation (16) were derived by substituting Equations (51) and (52) into
of Equation (12) from [
15]. Note:
in Equation (12) in [
15] was replaced with
in this paper. The first piece on the right-hand side of Equation (17) is based on Equation (17) from [
15].
Hence, substituting
into Equations (11) and (12) and simplifying yields the expressions for
and
, which subsequently yields the expressions for
-skewness
and
-kurtosis
as follows:
The closed-form formulae for
and
, obtained by solving Equations (18) and (19), can be written in simplified forms as follows:
where
and
, and
and
are the estimates of
and
.
3.3. L-Moments for the Logistic-Normal MP Distributions
The derivation of
-moments associated with the logistic-normal MP distributions can be obtained by first writing Equation (8) as follows:
where
and
with pdfs and cdfs given in
Section 3.2.
Evaluating both integrals in Equation (22) for
and 1, it is straightforward to derive
and
, which can be substituted into Equations (9) and (10) to obtain the first two
-moments as follows:
For
and
, the evaluation of the first integral on the right-hand side of Equation (22) is straightforward; however, the evaluation of the second integral requires several mathematical manipulations, as shown in [
15]. Specifically, the last three pieces on the right-hand side of Equation (25) were derived by substituting Equations (53) and (54) into
of Equation (12) from [
15]. Note:
in Equation (12) in [
15] was replaced with
in this paper. In addition, the second expression on the right-hand side of Equation (26) was based on Equation (18) from [
15]. Hence,
and
can be expressed as follows:
Substituting
into Equations (11) and (12) and simplifying yields the expressions for
and
, which subsequently yield the expressions for
-skewness
and
-kurtosis
as follows:
The closed-form formulae for
and
, obtained by solving Equations (27) and (28), can be written in simplified forms as follows:
where
and
, and
and
are the estimates of
and
.
Hence, for the specified values of -skewness and -kurtosis associated with the normal-logistic and logistic-normal MP distributions, the systems of Equations (18), (19), (27) and (28) can be simultaneously solved for the values of and . These solved values of and can be substituted into Equations (14), (15), (23) and (24), respectively, to obtain the corresponding values of -mean and -scale .
Figure 2A,B show Mo
Ms-based boundary graphs of
-skewness
and
-kurtosis
for the two MP distributions to help practitioners choose a specific combination of
and
for simulating data. Specifically,
Figure 2A presents the boundary graph for possible combinations of
-skewness
and
-kurtosis
in Equations (18) and (19), which are associated with normal-logistic MP distributions. The graph in
Figure 2A was drawn by setting
with
for the part on the left side of the vertical axis and by setting
with
for the part on the right side. The minimum value of
in
Figure 2A is shown as
, where
and
. The maximum value of
is shown as
on the left side of the vertical axis and
on the right side, which are associated with the pdfs of symmetric distributions of the forms
[
46] and
, where
. The value of
ranges from
on the left side of the vertical axis to
on the right side. The graph in
Figure 2B, a mirror image of the graph in
Figure 2A, can be used for possible combinations of
and
in Equations (27) and (28) associated with logistic-normal MP distributions.
Similarly, for the specified values of skewness
and kurtosis
associated with the normal-logistic and logistic-normal MP distributions, the systems of Equations (A4), (A5), (A9) and (A10) from
Appendix A and
Appendix B, respectively, can be simultaneously solved for the values of
and
. These solved values of
and
can be substituted into Equations (A2), (A3), (A7) and (A8), respectively, to obtain the corresponding values of the mean
and variance
.
Presented in
Figure A1A of
Appendix C is the boundary graph of possible combinations of skewness
and kurtosis
in Equations (A4) and (A5) associated with the normal-logistic MP distributions. The lower boundary point for the graph in
Figure A1A is
, which is associated with
. The maximum value of
is shown as
on the left side of the vertical axis and
on the right side. The graph in
Figure A1B, a mirror image of the graph in
Figure A1A, can be used for possible combinations of
and
in Equations (A9) and (A10) associated with the logistic-normal MP distributions.
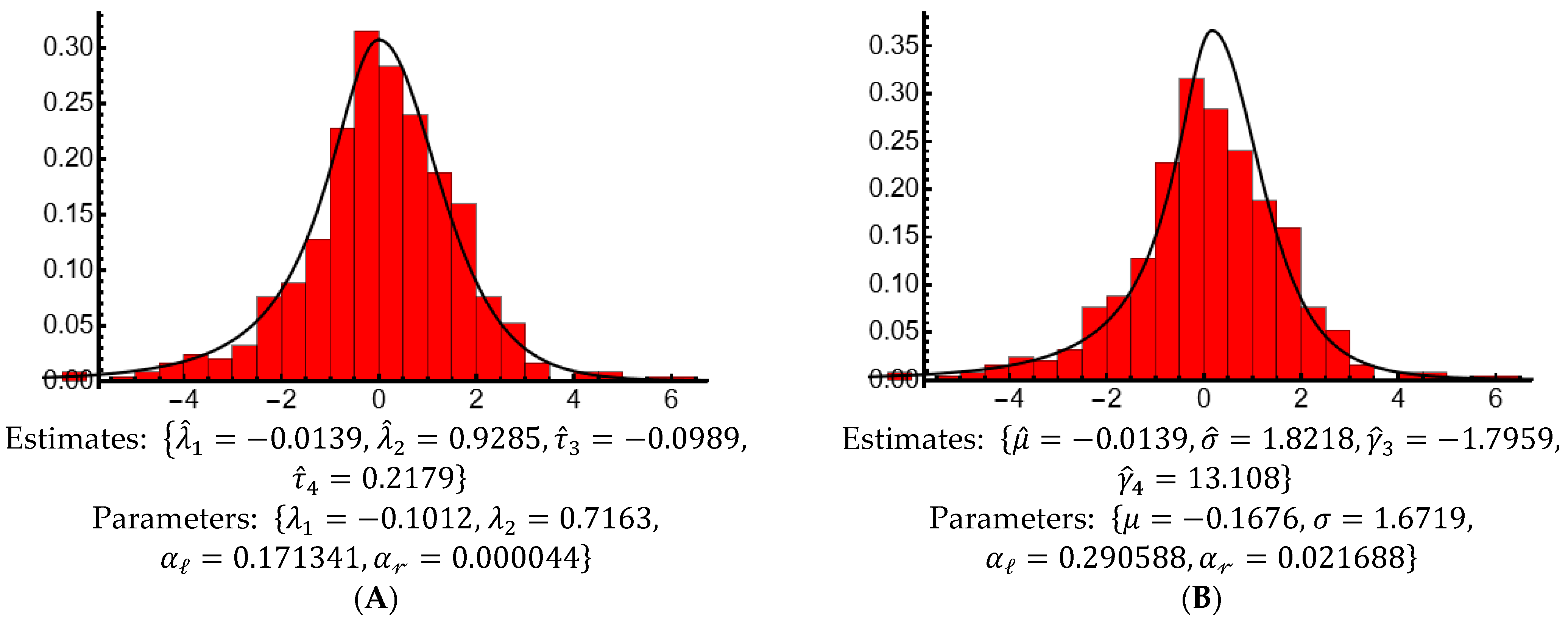
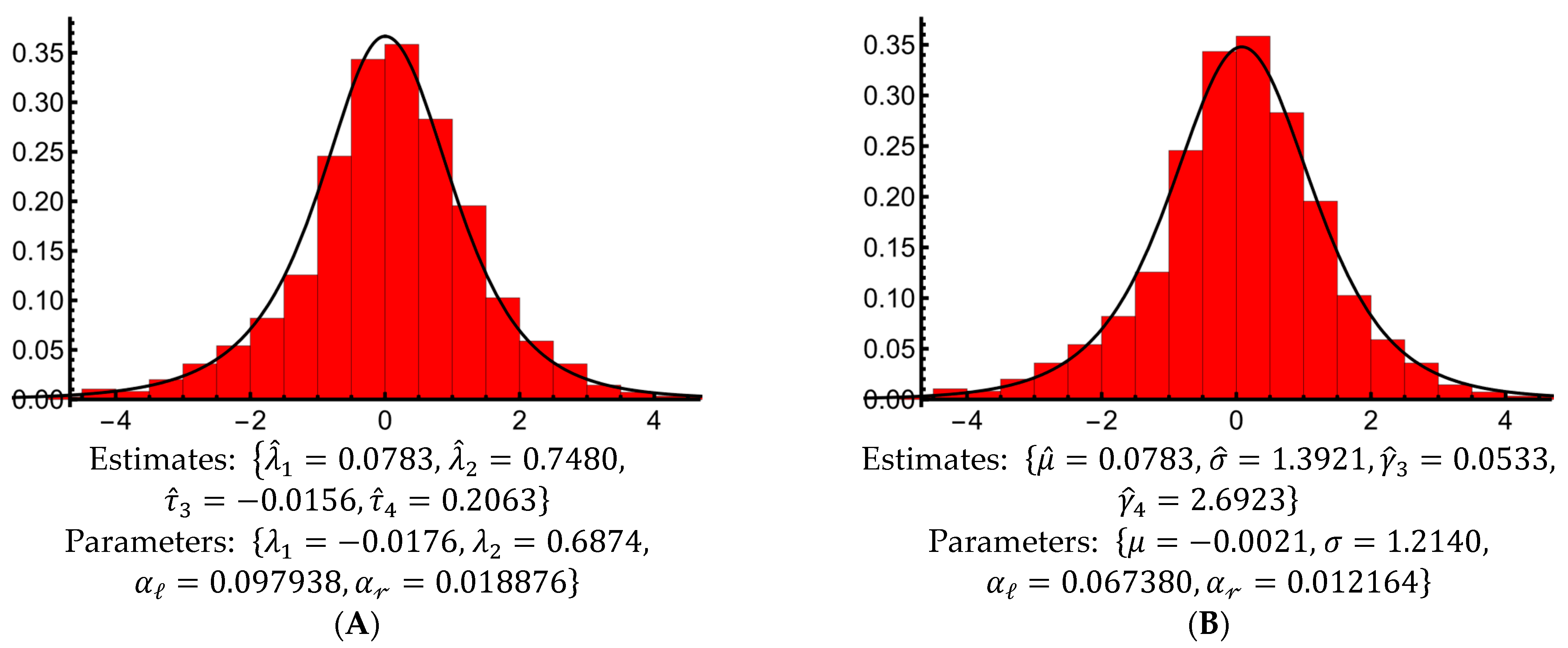
To demonstrate this methodology, the
and
of two normal-logistic (Distributions 1 and 2) and one logistic-normal (Distribution 3) MP distributions are displayed in
Figure 3.
5. Discussion and Conclusions
This paper introduced two families of mixture polynomial (MP) distributions, namely, the normal-logistic and logistic-normal MP distributions, via the method of
-moments (Mo
Ms) and the method of moments (MoMs). The systems of equations for each method (Mo
Ms and MoMs) were derived, and corresponding boundary graphs were plotted (
Figure 2 and
Figure A1 of
Appendix C). Based on
Figure 2A, the lower boundary point for the Mo
Ms-based normal-logistic MP distributions is
, which is associated with
, whereas the upper boundary points corresponding to the negative and positive axes of
are
and
, respectively. Based on
Figure 2B, the lower boundary point for the Mo
Ms-based logistic-normal MP distributions is
, whereas the upper boundary points corresponding to the negative and positive axes of
are
and
, respectively. Furthermore, based on
Figure A1A of
Appendix C, the lower boundary point for MoMs-based normal-logistic MP distributions is
, whereas the upper boundary points corresponding to the negative and positive axes of
are
and
, respectively. Based on
Figure A1B of
Appendix C, the lower boundary point for the MoMs-based logistic-normal MP distributions is
, whereas the upper boundary points corresponding to the negative and positive axes of
are
and
, respectively.
The advantage of the Mo
Ms-based procedure over the MoMs-based procedure can be expressed in the context of parameter estimation and data fitting. The Mo
Ms-based estimates of
-skewness and
-kurtosis are far less biased than the MoMs-based estimates of skewness and kurtosis when samples are drawn from distributions with more severe departures from normality [
15,
16,
30,
31,
32,
35]. The simulation results in
Table 2 and
Table 3 clearly indicate the superiority of the Mo
Ms-based estimates (
and
) of
-skewness
and
-kurtosis
over corresponding MoMs-based estimates (
and
) of skewness
and kurtosis
in terms of much smaller relative biases (RB%) and smaller standard errors (SEs) in the context of normal-logistic and logistic-normal MP distributions in
Figure 3. For example, for a sample of size
, the estimates
and
for Distribution 3 were, on average, 88.69% and 94.85% of their respective parameters, whereas the estimates
and
were, on average, 36.19% and 9.84% of their respective parameters.
Another advantage of Mo
Ms-based estimates over their MoMs-based counterparts can be expressed by comparing their relative standard errors (RSEs), where
(St. Error/Estimate). From
Table 2 and
Table 3, it is evident that the estimates of
and
are more efficient, as their RSEs are considerably smaller than the RSEs associated with the MoMs-based estimates of
and
. For example, in terms of Distribution 2 in
Figure 3, an inspection of
Table 2 and
Table 3 (for
) indicates that the RSE measures of
and
are considerably smaller than the RSE measures of
and
. This comparison of RSEs demonstrates that the Mo
Ms-based estimates of
-skewness and
-kurtosis have higher precision than the MoMs-based estimates of skewness and kurtosis.
Another advantage of this study is that the proposed new family of normal-logistic and logistic-normal MP distributions provides researchers with a much wider selection of non-normal distributions that can be used in simulation studies. For example,
Figure 2A,B show a much wider range of Mo
Ms-based
-skewness
and
-kurtosis
for the proposed normal-logistic and logistic-normal MP distributions than that for traditional power method distributions [
15,
35]. Likewise,
Figure A1A,B of
Appendix C indicate a much wider range of MoMs-based skewness
and kurtosis
for the normal-logistic and logistic-normal MP distributions than that for traditional power method distributions [
4,
10,
15,
16].
In addition, the proposed MP distributions provide much wider selections of
-skewness
and
-kurtosis
and skewness
and kurtosis
compared to the standard normal- and logistic- based double power method distributions [
15] and uniform and triangular- based double power method distributions [
16].
Furthermore, the Mo
Ms-based MP distributions are also superior to MoMs-based distributions in terms of their lower computational cost during parameter estimation. A simple inspection of
Table 2 and
Table 3 indicates that the algorithm for Mo
Ms-based Monte Carlo simulation results for each sample size under the same conditions (e.g., using the loop, number of replications, computation of bootstrap estimates with relevant 95% confidence intervals, and standard errors), takes a relatively shorter execution time than the corresponding MoMs-based algorithm. For example, for
= 1000, the execution time of 83.6 min for the Mo
Ms-based algorithm was substantially lower than the execution time of 290.4 min for the MoMs-based algorithm.
One of the limitations of this study was that we did not consider multivariate aspects of normal-logistic and logistic-normal MP distributions via the multivariate measures of Mo
Ms-based
-skewness,
-kurtosis, and MoMs-based skewness and kurtosis [
50,
51,
52,
53]. In this context, we suggest that the development and evaluation of methodologies for modeling multivariate data through multivariate measures of Mo
Ms-based
-skewness,
-kurtosis, and MoMs-based skewness and kurtosis can be the subjects of future research projects.
In conclusion, the Mo
Ms-based families of normal-logistic and logistic-normal MP distributions are more attractive alternatives than MoMs-based families because of their capability of producing more precise estimates of the parameters and providing better approximations to the empirical distributions of real-world data. Finally, Mathematica [
45] and R [
37] algorithms are available from the first author to implement the Mo
Ms- and MoMs-based procedures.