Research on the Pricing Model of B2B Data Transactions and Its Nature for a Single Industrial Chain
Abstract
1. Introduction
2. Theoretical Analysis
2.1. Definition of B2B Data
2.2. Ownership of B2B Data
2.3. Data Marketization
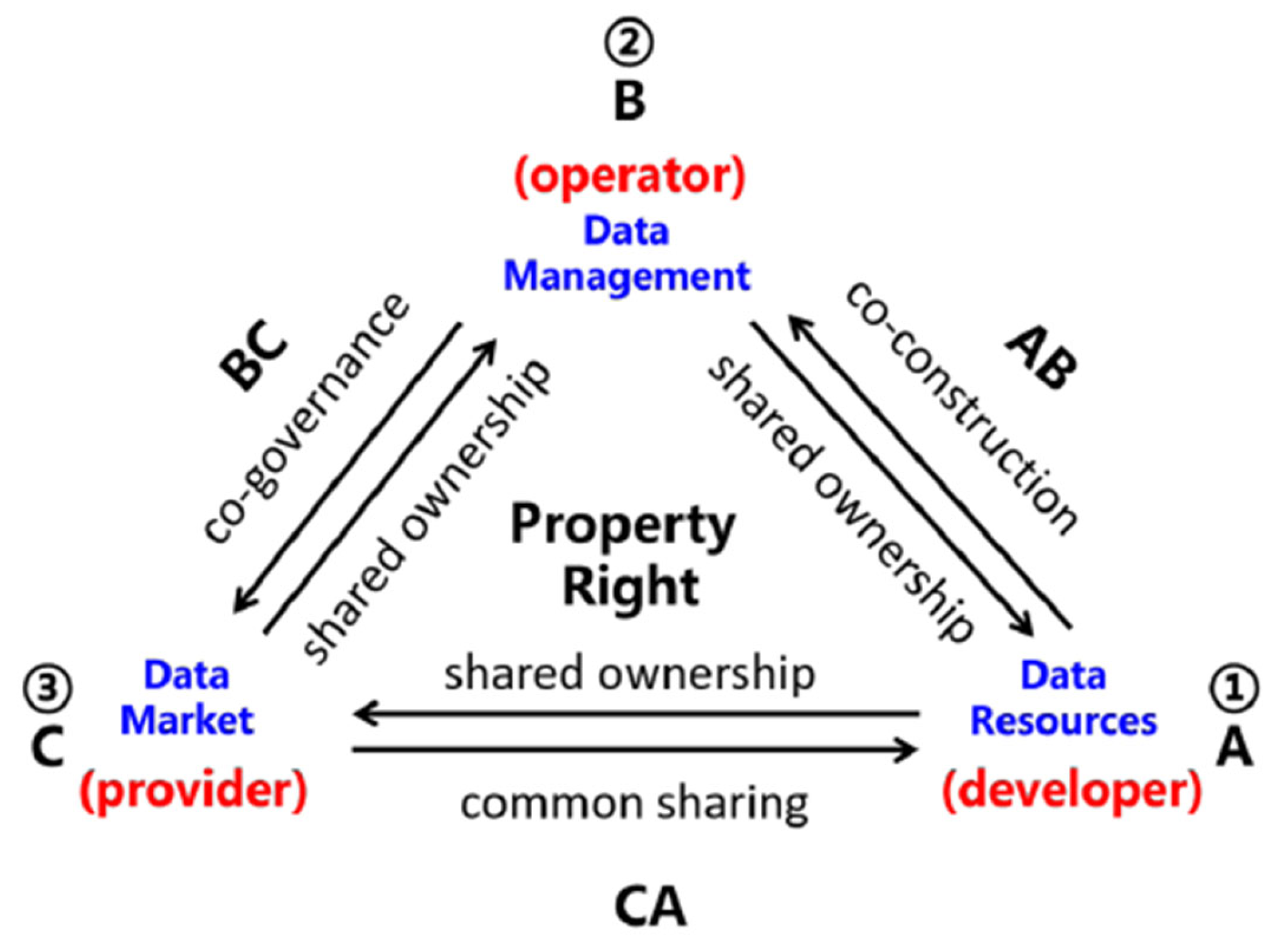
2.4. B2B Data Property Rights Allocation Under the Coordination of the Industrial Chain
2.4.1. B2B Data Participant Ownership Allocation
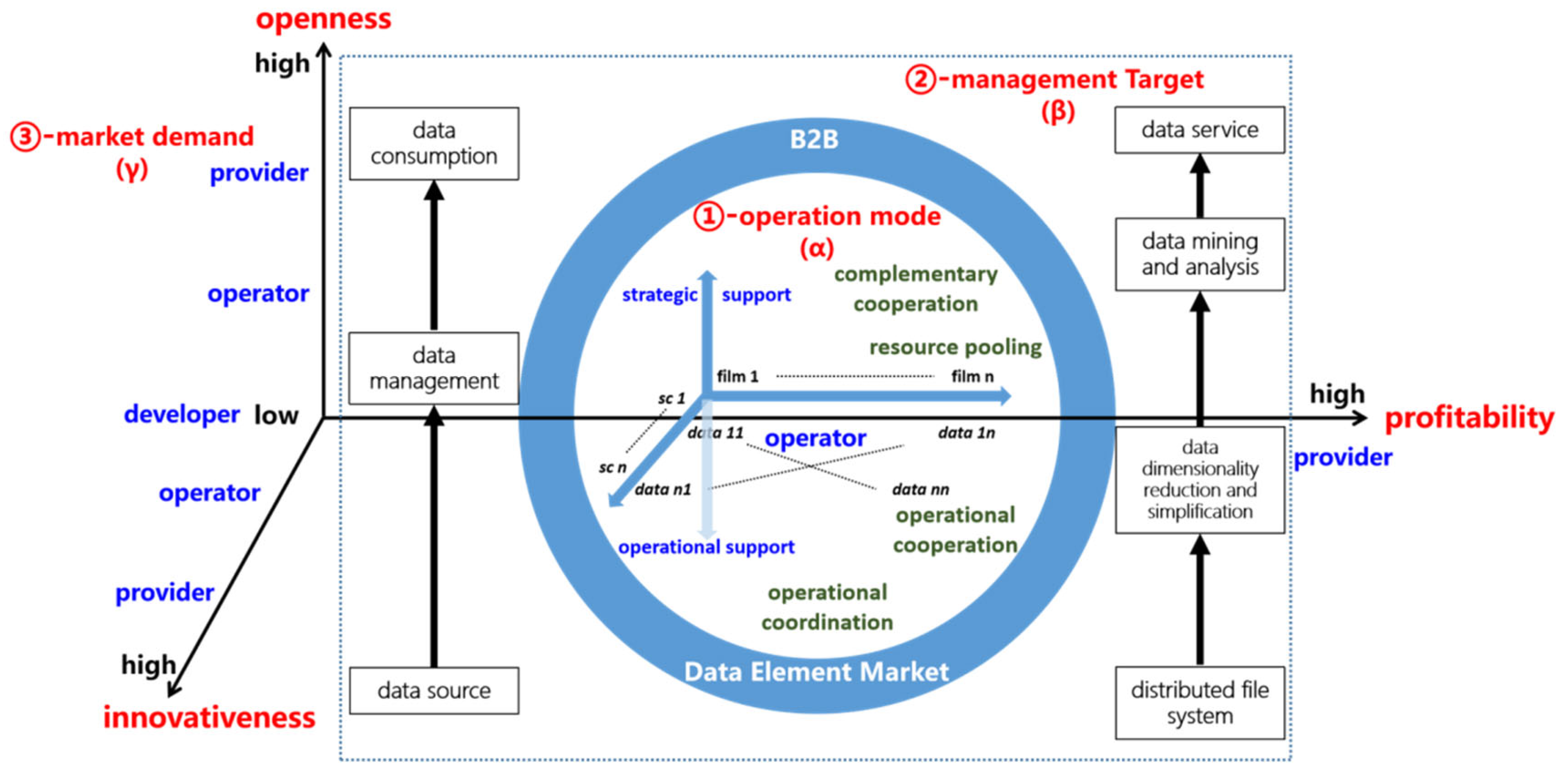
2.4.2. B2B Data Operation Mode and Unified Property Configuration
2.4.3. Ownership Allocation and Relationships
3. Transaction Parameter Description
4. Data Transaction Pricing Model
4.1. Model Description and Assumptions
4.2. Pricing Model Without Incentive Mechanism
4.3. Pricing Model of the Incentive Mechanism for Downstream Industries
4.4. Pricing Model of the Incentive Mechanism for the Upstream Industry
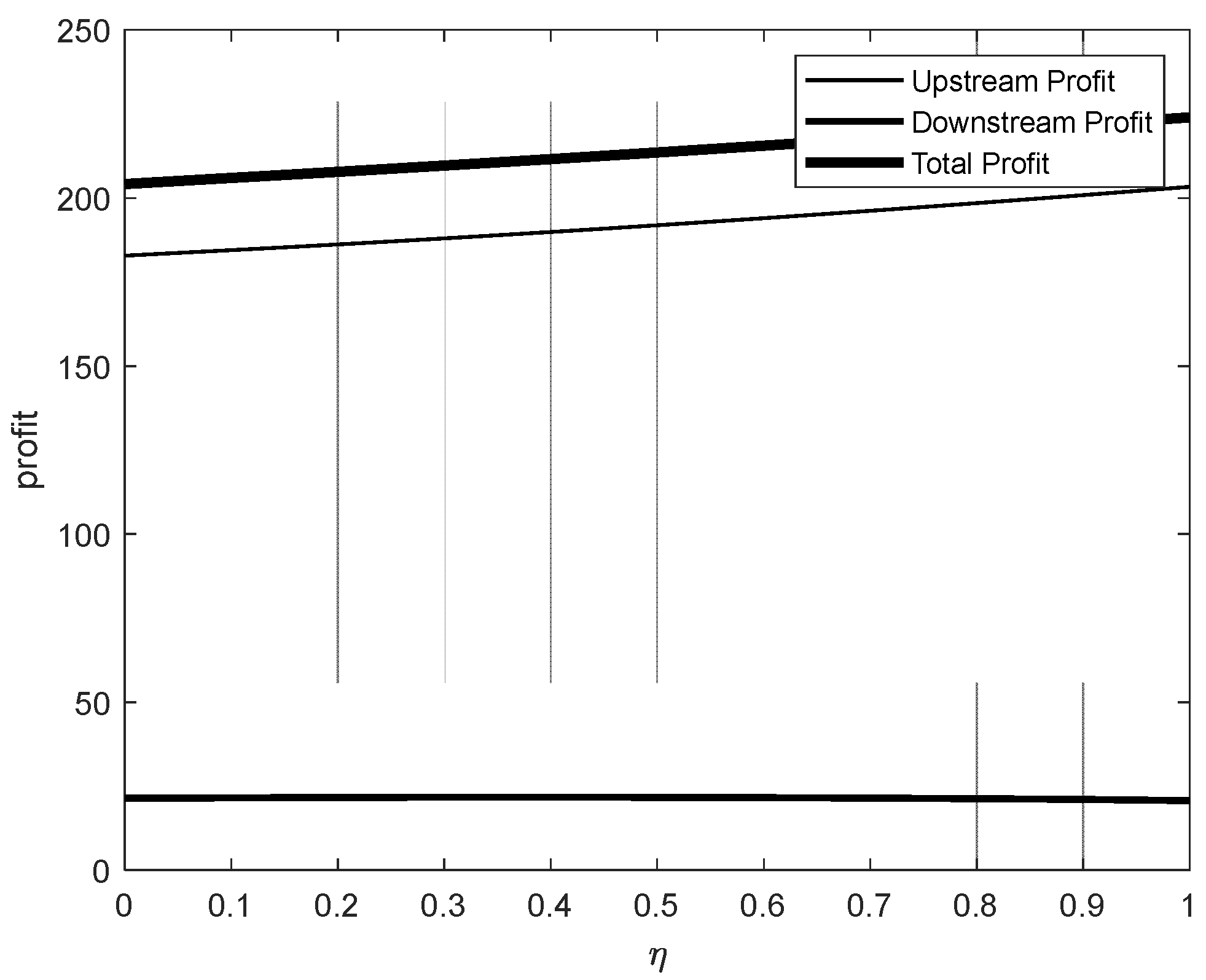
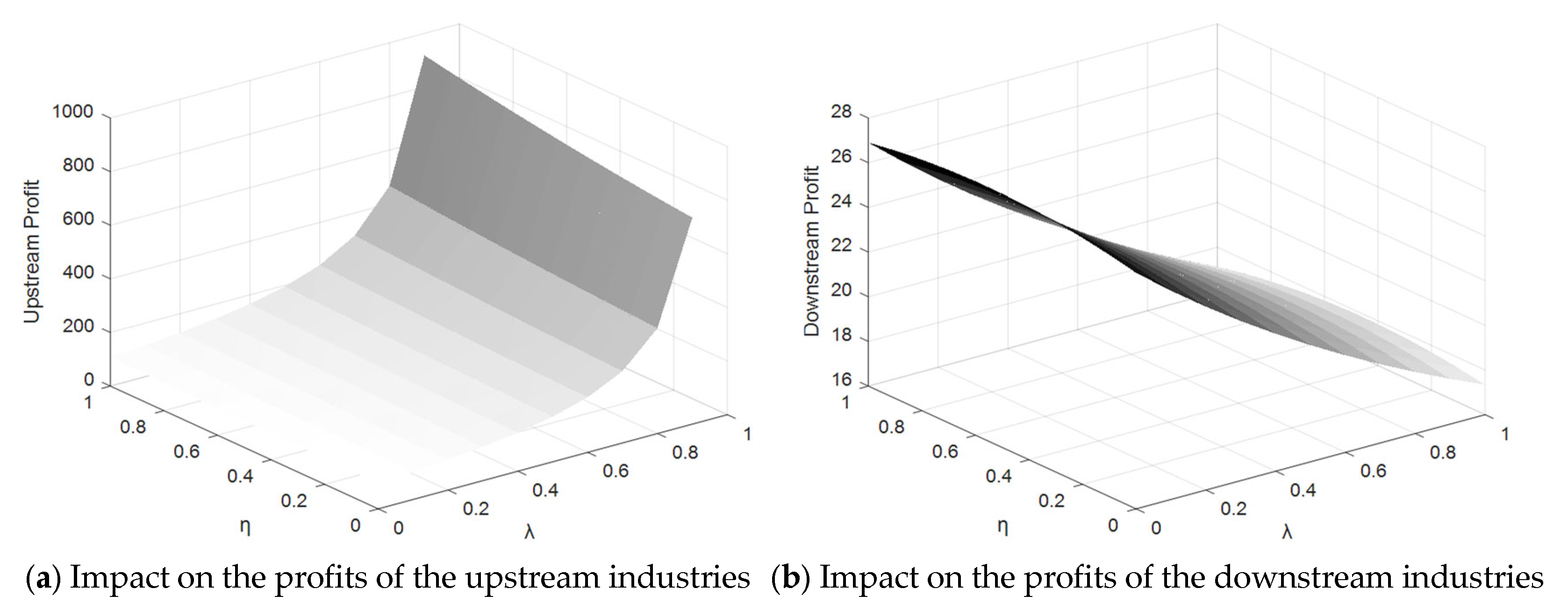
5. Numerical Simulation
6. Parameter Confirmatory Test
- High-Mean Parameters: Parameters such as data encryption protection cost, data encryption protection effort, and data acquisition cost were found to have higher mean values, indicating their significant perceived importance among respondents. These factors play critical roles in market decision making.
- Low-Variance Parameters: The selling price had the lowest standard deviation (0.986), suggesting that respondents have a consistent perception of its importance.
- High-Variance Parameters: Data scarcity showed a higher standard deviation (1.223), reflecting diverse opinions on its significance, likely due to varying situational factors affecting the respondents’ evaluations.
- Concentration of Ratings: Most responses clustered around values of 4 and 5, indicating that the majority of respondents regarded these parameters as highly important in the context of data transactions.
- Data Encryption Protection Efforts and Pricing:
- ◦
- The correlation coefficient between data encryption protection efforts and upstream pricing was 0.437, while that for downstream pricing was 0.419.
- ◦
- This indicates that, as data encryption protection efforts increase, both upstream and downstream prices tend to rise (particularly upstream).
- ◦
- This relationship suggests that enhanced data encryption measures improve data security and market confidence, thereby creating opportunities for higher premiums in data transactions.
- Incentive Mechanism Coefficient and Pricing:
- ◦
- The incentive mechanism coefficient showed moderate positive correlations with upstream pricing (0.456) and downstream pricing (0.468).
- ◦
- This reflects the fact that incentive mechanisms encourage upstream data providers to adopt more active pricing strategies while also increasing the downstream demand side’s willingness to pay, thereby elevating the overall pricing levels in the market.
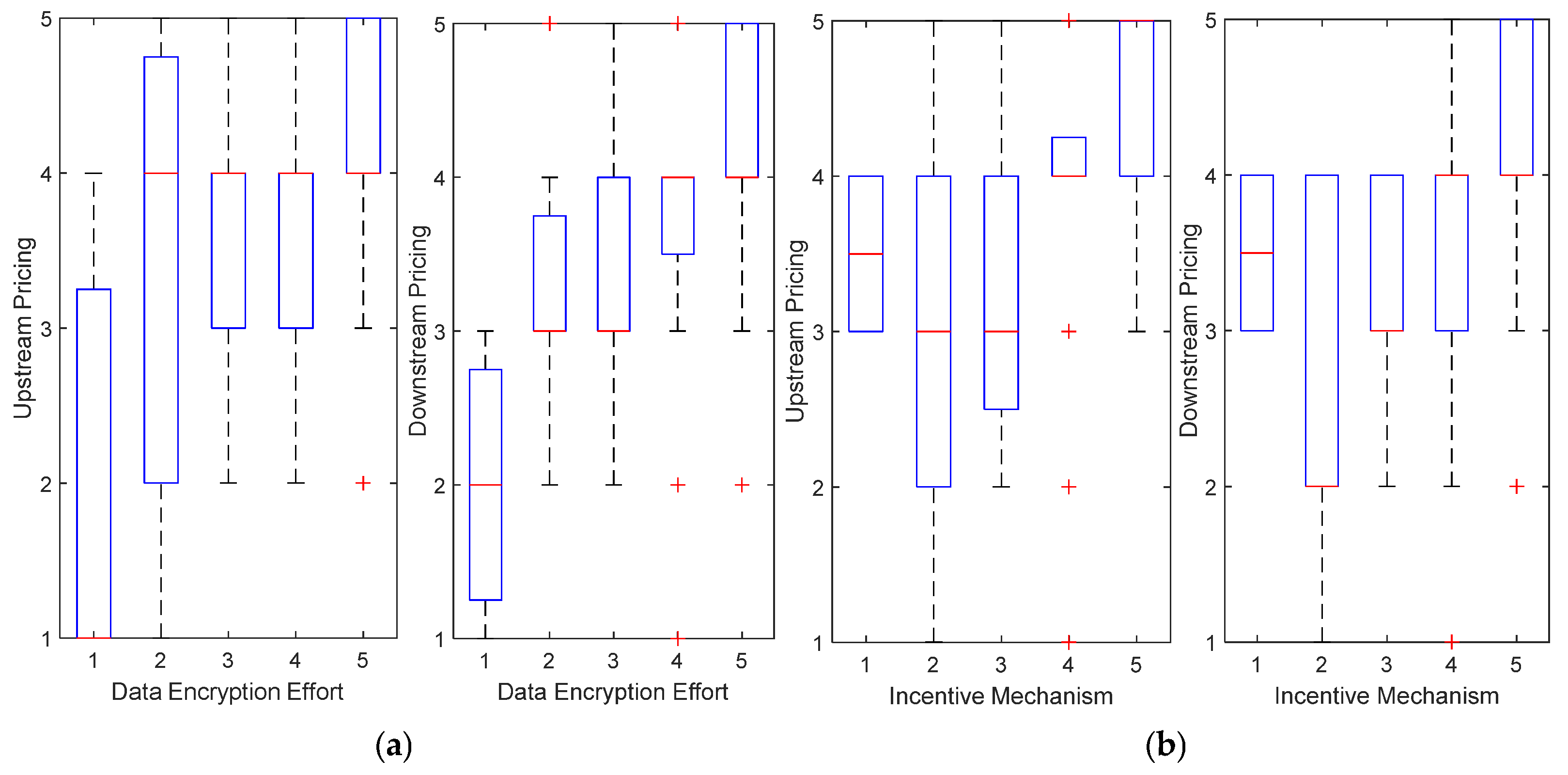
- Data Encryption Protection Efforts (Figure 12a):
- ◦
- The importance of data encryption protection efforts in upstream pricing increased significantly with higher scores.
- ▪
- When the encryption effort score is 1, the median upstream pricing score is 1.
- ▪
- At a score of 5, the median upstream pricing score rises to 4.
- ▪
- This indicates that high levels of encryption protection are crucial for increasing upstream pricing.
- ▪
- For downstream pricing, the scoring trends for encryption efforts were similar but slightly lower overall.
- ▪
- This reflects the respondents’ perception that encryption protection has a less pronounced role in the downstream market when compared with upstream.
- Incentive Mechanism Coefficient (Figure 12b):
- ◦
- The influence of the incentive mechanism coefficient on pricing also increases steadily with higher scores.
- ▪
- As the incentive score increases from 1 to 5, the median upstream pricing score rises from 3.5 to 5.
- ▪
- For downstream pricing, the median score increases from 3.5 to nearly 4.
- ▪
- This suggests that while the incentive mechanism positively affects both upstream and downstream pricing, its impact is more significant for upstream pricing.
7. Conclusions
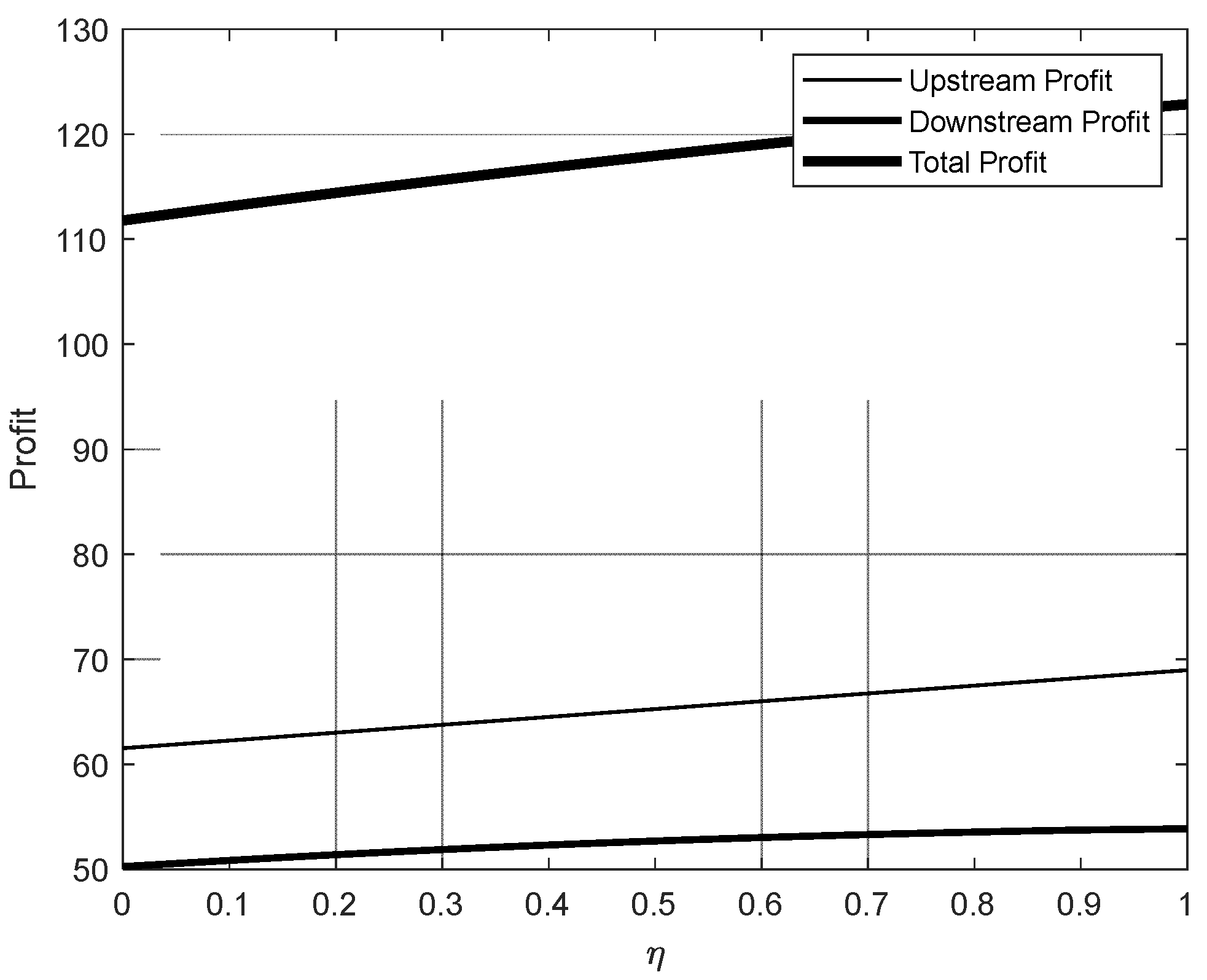
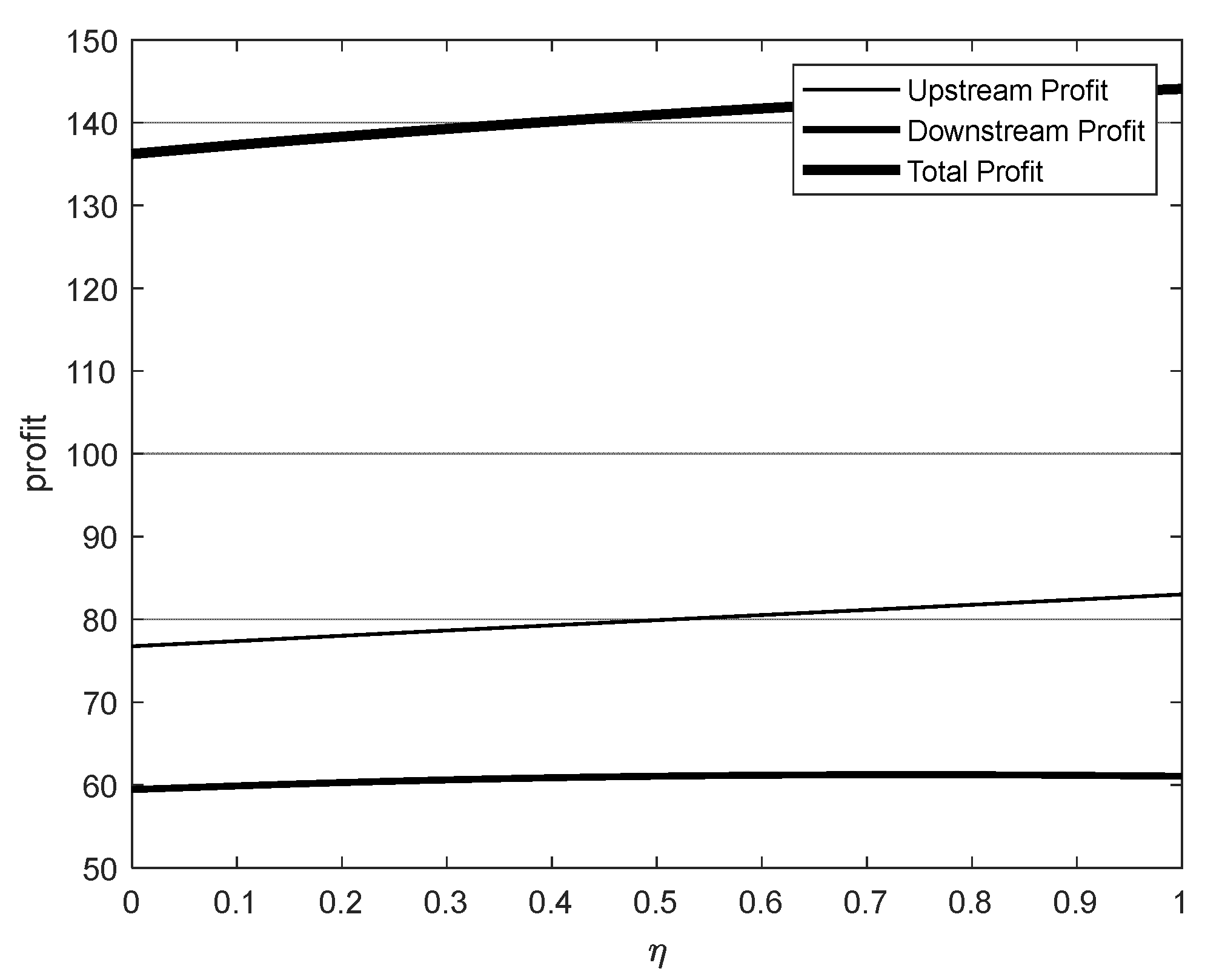
- Impact of Incentive Mechanisms on Pricing Strategies:The introduction of incentive mechanisms significantly influences the pricing strategies of upstream and downstream industries. While incentives applied to both upstream and downstream industries enhance overall profitability, the effects differ based on their position in the industrial chain:
- ◦
- Incentives targeting the downstream industry promote steady and sustainable growth in overall market profits.
- ◦
- Incentives directed at the upstream industry lead to nonlinear amplification of upstream profits but constrain downstream profitability, creating an imbalance in the profit distribution.
- Pricing Behavior Under Different Incentive Scenarios:
- ◦
- When incentives are applied exclusively to the downstream industry, both upstream and downstream enterprises tend to maximize their profits through increased pricing.
- ◦
- In contrast, when only the upstream industry is incentivized, upstream enterprises prefer to raise their prices to capitalize on their strengthened market position. Meanwhile, downstream enterprises often maintain stable pricing to retain their market share and competitiveness, mitigating the impacts of upstream price increases and fluctuations in market demand.
- Effect of Data Encryption Protection:Strengthened data encryption protection significantly enhances the value and security of upstream enterprises’ data, granting them greater market dominance and increased pricing power. However, this creates added capital pressures for downstream enterprises due to the higher costs associated with encryption protection. As a result, downstream enterprises face limited flexibility in adjusting their pricing strategies, further accentuating the disparity in market dynamics between the two segments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, X.; Zhao, M.; Li, T.; Li, S. Data Factor and Enterprise Innovation: The perspective of R & D competition. Econ. Res. 2023, 58, 39–56. [Google Scholar]
- Pei, J. A Survey on Data Pricing: From Economics to Data Science. IEEE Trans. Knowl. Data Eng. 2022, 34, 4586–4608. [Google Scholar]
- Shen, Y.; Guo, B.; Shen, Y.; Duan, X.; Dong, X.; Zhang, H. A Pricing Model for Big Personal Data. Tsinghua Sci. Technol. 2016, 21, 482–490. [Google Scholar]
- Hao, J.; Deng, Z.Y.; Li, J.P. The Evolution of Sata Pricing: From Economics to Computational Intelligence. Heliyon 2023, 9, e20274. [Google Scholar] [PubMed]
- Zhang, M.; Lu, X.; Wu, Y. Data Factor Economics: Characteristics, Right Confirmation, Pricing and Transaction. Economist 2024, 35–44. [Google Scholar]
- Zhang, M.X.; Beltrán, F.; Liu, J.M. A Survey of Data Pricing for Data Marketplaces. IEEE Trans. Big Data 2023, 9, 1038–1056. [Google Scholar]
- Liang, J.; Yuan, C.H. Data Price Determinants Based on a Hedonic Pricing Model. Big Data Res. 2021, 25, 100249. [Google Scholar]
- Surbakti, F.P.S.; Wang, W.; Indulska, M.; Sadiq, S. Factors Influencing Effective Use of Big Data: A research Framework. Inf. Manag. 2020, 57, 103146. [Google Scholar]
- Wang, W.; Zhang, M.J.; Wang, J. Research on Risk Factor Identification in Business Process of Big Data Transaction. Inf. Stud. Theory Appl. 2019, 42, 80–85. [Google Scholar]
- Zhao, X.Y.; Ji, X.F.; Guo, Y.Z. Research on the Model Construction of the Influencing Factors of Data Exchange Platforms under the Innovation Incentive Target--Taking Guiyang Data Exchange Platform as an Example. J. Mod. Inf. 2023, 43, 101–112+124. [Google Scholar]
- Thenmozhi, R.; Shridevi, S.; Mohanty, S.N.; García-Díaz, V.; Gupta, D.; Tiwari, P.; Shorfuzzaman, M. Attribute-Based Adaptive Homomorphic Encryption for Big Data Security. Big Data 2024, 12, 343–356. [Google Scholar] [PubMed]
- Jin, B.; Jiang, D.S.; Xiong, J.B.; Chen, L.; Li, Q. D2D Data Privacy Protection Mechanism Based on Reliability and Homomorphic Encryption. IEEE Access 2018, 6, 51140–51150. [Google Scholar]
- Qiu, H.; Qiu, M.K.; Liu, M.Q.; Ming, Z. Lightweight Selective Encryption for Social Data Protection Based on EBCOT Coding. IEEE Trans. Comput. Soc. Syst. 2020, 7, 205–214. [Google Scholar]
- Xu, Z.; Cao, S.X. Multi-Source Data Privacy Protection Method Based on Homomorphic Encryption and Blockchain. Cmes-Comput. Model. Eng. Sci. 2023, 136, 861–881. [Google Scholar]
- Hu, Q.; Huang, C.; Zhang, G.; Cai, L.; Jiang, T. Towards Accountable and Privacy-preserving Blockchain-based Access Control for Data Sharing. J. Inf. Secur. Appl. 2024, 85, 103866. [Google Scholar]
- Jiang, Y.N.; Zhong, Y.; Ge, X.H. Smart Contract-Based Data Commodity Transactions for Industrial Internet of Things. IEEE Access 2019, 7, 180856–180866. [Google Scholar]
- Ping, H. Network Information Security Data Protection Based on Data Encryption Technology. Wirel. Pers. Commun. 2022, 126, 2719–2729. [Google Scholar]
- Liu, Y.; Yang, C.S.; Liu, Q.; Xu, M.; Zhang, C.; Cheng, L.; Wang, W. PDPHE: Personal Data Protection for Trans-Border Transmission Based on Homomorphic Encryption. Electronics 2024, 13, 1959. [Google Scholar] [CrossRef]
- Zhang, Y.J. Pricing Model of Data Elements Based on Market Mechanism and Transaction Scenario. Soc. Sci. 2023, 72–76+84. [Google Scholar]
- Tian, Y.J.; Ding, Y.R.; Fu, S.J.; Liu, D. Data Boundary and Data Pricing Based on the Shapley Value. IEEE Access 2022, 10, 14288–14300. [Google Scholar]
- Luo, S.Z.; Xing, L.N. Neutrosophic Game Pricing Methods with Risk Aversion for Pricing of Data Products. Expert Syst. 2021, 38, e12697. [Google Scholar]
- Zhao, B.; Zhang, J.Q.; Cao, W.; Li, B.; Zhang, W.; Gao, Y. A dynamic Evaluation Model of Data Price Based on Game Theory. Peer-to-Peer Netw. Appl. 2023, 16, 2073–2088. [Google Scholar]
- Goodhue, D.L.; Quillard, J.A.; Rockart, J.F. Managing the Data Resource: A Contingency Perspective. MIS Q. 1988, 12, 373–392. [Google Scholar]
- Deng, L.L.; Li, C.W. Research on Similarity Calculation Method for Associated Data Resource Set. Inf. Stud. Theory Appl. 2012, 35, 112–116. [Google Scholar]
- Wang, Y.; Cai, S.Q. Towards a Big Data Model for Social Media Platform. J. Manag. 2018, 15, 1064–1071. [Google Scholar]
- Xu, X.C.; Zhang, Z.W.; Hu, Y.R. Research on Deriving Measures of Data Assets in National Accounts. J. Manag. World 2022, 38, 16–30. [Google Scholar]
- Li, J.P. Research on Reconding Data Asset in National Accounts. Stat. Res. 2020, 37, 3–14. [Google Scholar]
- Duan, Z.X.; Wu, Y.Q. Property Right Structure and System Construction of Big Data Resources. E-Government 2017, 23–30. [Google Scholar]
- Zhou, P. The Boundary of Practice and Deconstruction for Right and Interest on Data Transaction. Electron. Intellect. Prop. Rights 2020, 67–77. [Google Scholar]
- Guo, Q.L.; Wang, B.H.; Tian, N.F.; Sun, H.; Wen, B. Data Transactions in Energy Internet: Architecture and Key Technologies. J. Electr. Technol. 2020, 35, 2285–2295. [Google Scholar]
- Zhu, G.L. China’s new Governance Concept in the Process of Comprehensively Deepening Reform. Soc. Sci. China 2017, 27–39. [Google Scholar]
- Fang, J.; Xi, J.P. Thought on Socialism with Chinese Characteristics for a New Era. Comp. Econ. Soc. Syst. 2019, 1–8. [Google Scholar]
- Hu, Y.L.; Gao, C.Y.; Zhang, S.C. Data Resources Sharing Relationship and Modeling Analysis in Big Data Alliance. Inf. Stud. Theory Appl. 2018, 41, 28–33. [Google Scholar]
- Mu, Y.; Wang, W.; Zhao, Y. Research on the Status Quo, Problems and Countermeasures of Asset Management of Data Resources in China. E-Government 2017, 66–74. [Google Scholar]
- Yang, D. The Marketization of Data Elements Reinforces the Government Governance Model. Peoples Forum 2020, 12, 60–62. [Google Scholar]
- Li, T.T.; Li, D.Q.; Wang, M.S. Blockchain-based Fair and Decentralized Data Trading Model. Comput. J. 2022, 65, 2133–2145. [Google Scholar] [CrossRef]
- Koutris, P.; Upadhyaya, P.; Balazinska, M.; Howe, B.; Suciu, D. Query-based Data Oricing. J. ACM 2015, 62, 43. [Google Scholar] [CrossRef]
- Gao, F.P. Data Production Theory--Basic Theory of Data Resource Rights Allocation. SJTU Law Rev. 2019, 5–19. [Google Scholar]
- Li, C.X.; Wen, T.X. Research on the Profit Models of Big Data Transaction in China. J. Intell. 2020, 39, 180–186. [Google Scholar]
- Chen, G.Q.; Ren, M.; Wei, Q.; Guo, X.; Yi, C. Data-Intelligence Empowerment: A New Leap of Information Systems Research. J. Manag. World 2022, 38, 180–196. [Google Scholar]
- Culliton, B.J. Authorship, data ownership examined. Science 1988, 242, 658–659. [Google Scholar] [CrossRef] [PubMed]
- Singh, P.J.; Vipra, J. Economic Rights Over Data: A Framework for Community Data Ownership. Development 2019, 62, 53–57. [Google Scholar]
- McGuire, A.L.; Roberts, J.; Aas, S.; Evans, B.J. Who Owns the Data in a Medical Information Commons? J. Law Med. Ethics 2019, 47, 62–69. [Google Scholar] [PubMed]
- Tang, Q. Study on the Property Right Issues in Big Data Trade. Libr. Inf. 2016, 4, 38–45. [Google Scholar]
- Wen, Y.H. Paradigm Shift, Concept Selection and the Owner of Data Rights Establishment. J. Northeast. Norm. Univ. (Philos. Soc. Sci.) 2019, 69–78. [Google Scholar]
- Hong, Y.X. Realizing the Reform of Market-oriented Allocation of Factors. Economist 2020, 2, 5–14. [Google Scholar]
- Kauremaa, J.; Tanskanen, K. Designing Interorganizational Information Systems for Supply Chain Integration: A Framework. Int. J. Logist. Manag. 2016, 27, 71–94. [Google Scholar]
- Chen, J.; Liu, Y. Operation Management Innovation Enabled by Digitalization and Intellectualization: From Supply Chain to Supply Chain Ecosystem. J. Manag. World 2021, 37, 227–240. [Google Scholar]
- Jiang, J. Cultivate and Develop the Difficult Problems and Legal Response of the Data Element Market. Libr. Inf. 2020, 3, 22–24. [Google Scholar]
- Yan, X.; Li, X. A Study on the Governance Concept of Socialism with Chinese Characteristics. Res. Social. Chin. Charact. 2014, 5, 27–31. [Google Scholar]
- Kang, X. The theoretical characteristics of Xi Jinpings modern national governance view. Stud. Marx. 2016, 10, 59–65. [Google Scholar]
- Hong, I.B. A new framework for interorganizational systems based on the linkage of participants roles. Inf. Manag. 2002, 39, 261–270. [Google Scholar]
- Immonen, A.; Ovaska, E.; Paaso, T. Towards certified open data in digital service ecosystems. Softw. Qual. J. 2018, 26, 1257–1297. [Google Scholar]
- Majchrzak, A.; Markus, M.L.; Wareham, J. Designing for Digital Transformation: Lessons for Information Systems Research from the Study of ICT and Societal Challenges. MIS Q. 2016, 40, 267–277. [Google Scholar]
- Guo, X.L.; Tang, T.T.; Su, Z.H. Pricing Strategies Considering Logistics Service Efforts on the Online Freight Platform. Chin. J. Manag. Sci. 2022. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, N.; Hu, B.; Zhao, Y.; Guo, H. Research on Cold Chain Pricing Model of Fresh Products Based on Freshness and Fairness Concern Behavior. Front. Sci. Technol. Eng. Manag. 2024. Available online: https://kns.cnki.net/kcms/detail/34.1013.N.20240717.1636.002.html (accessed on 1 March 2025).
- Gordon, L.A.; Loeb, M.P. The Economics of Information Security Investment. ACM Trans. Inf. Syst. Secur. 2002, 5, 438–457. [Google Scholar]
- Biswas, S.; Junk, K.; Palamidessi, C. An Incentive Mechanism for Trading Personal Data in Data Markets. In Theoretical Aspects of Computing—ICTAC 2021; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]





| Symbol | Meaning |
|---|---|
| Represents the level of effort in data encryption protection , where . It quantifies the intensity of participants’ input in protection measures. | |
| Denotes the degree of data discount , where , which is used to measure the price loss of data during the transaction process. | |
| Represents the data acquisition cost, reflecting the expenses incurred by data providers for data collection, processing, and transmission. | |
| Indicates potential market demand, measuring the market’s purchase intention and the scale of demand for the data. | |
| Refers to the data encryption protection cost coefficient, describing how sensitive the encryption cost is to changes in the level of protection effort. | |
| The data provider decides the selling price. | |
| The data demanders decide the selling price. | |
| Quantifies the market’s sensitivity to data price fluctuations, indicating how demand responds to price changes. | |
| Represents the scarcity of data, reflecting its availability and exclusivity in the market. | |
| Denotes the transaction proportion of sensitive data , where . It quantifies the share of sensitive data in overall market transactions. | |
| Represents the incentive mechanism coefficient , where , to describe the degree of influence that the incentive mechanism has on the behavior of market participants. |
| Parameter | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Numeric value | 0.3 | 0.3 | 3 | 150 | 5 | 7 | 3 | 0.3 | 0.3 |
| Symbol | Mean | Standard Error | Mode | Minimum Value | Maximum Value |
|---|---|---|---|---|---|
| 3.862 | 1.064 | 4 | 1 | 5 | |
| 3.702 | 1.096 | 4 | 1 | 5 | |
| 3.766 | 1.072 | 4 | 1 | 5 | |
| 3.606 | 1.128 | 4 | 1 | 5 | |
| 3.926 | 1.029 | 4 | 1 | 5 | |
| 3.809 | 1.148 | 4 | 1 | 5 | |
| 3.957 | 1.126 | 5 | 1 | 5 | |
| 3.809 | 1.029 | 4 | 1 | 5 | |
| 3.681 | 0.986 | 4 | 1 | 5 | |
| 3.745 | 1.154 | 4 | 1 | 5 | |
| 3.798 | 1.223 | 5 | 1 | 5 |
| 1 | 0.474 | 0.442 | 0.471 | 0.363 | 0.437 | 0.419 | 0.514 | 0.491 | 0.527 | 0.396 | |
| 0.474 | 1 | 0.419 | 0.497 | 0.308 | 0.369 | 0.408 | 0.409 | 0.378 | 0.295 | 0.376 | |
| 0.442 | 0.419 | 1 | 0.534 | 0.554 | 0.504 | 0.432 | 0.491 | 0.483 | 0.514 | 0.501 | |
| 0.471 | 0.497 | 0.534 | 1 | 0.410 | 0.560 | 0.449 | 0.515 | 0.501 | 0.535 | 0.426 | |
| 0.363 | 0.308 | 0.554 | 0.410 | 1 | 0.410 | 0.424 | 0.455 | 0.228 | 0.356 | 0.419 | |
| 0.437 | 0.369 | 0.504 | 0.560 | 0.410 | 1 | 0.501 | 0.447 | 0.387 | 0.502 | 0.456 | |
| 0.419 | 0.408 | 0.432 | 0.449 | 0.424 | 0.501 | 1 | 0.542 | 0.338 | 0.568 | 0.468 | |
| 0.514 | 0.409 | 0.491 | 0.515 | 0.455 | 0.447 | 0.542 | 1 | 0.504 | 0.543 | 0.490 | |
| 0.491 | 0.378 | 0.483 | 0.501 | 0.228 | 0.387 | 0.338 | 0.504 | 1 | 0.444 | 0.620 | |
| 0.527 | 0.295 | 0.514 | 0.535 | 0.356 | 0.502 | 0.568 | 0.543 | 0.444 | 1 | 0.508 | |
| 0.396 | 0.376 | 0.501 | 0.426 | 0.419 | 0.456 | 0.468 | 0.490 | 0.620 | 0.508 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, W.; Yu, H.; Wang, M.C. Research on the Pricing Model of B2B Data Transactions and Its Nature for a Single Industrial Chain. Mathematics 2025, 13, 1002. https://doi.org/10.3390/math13061002
Zhuang W, Yu H, Wang MC. Research on the Pricing Model of B2B Data Transactions and Its Nature for a Single Industrial Chain. Mathematics. 2025; 13(6):1002. https://doi.org/10.3390/math13061002
Chicago/Turabian StyleZhuang, Weiqing, Hanyu Yu, and Morgan C. Wang. 2025. "Research on the Pricing Model of B2B Data Transactions and Its Nature for a Single Industrial Chain" Mathematics 13, no. 6: 1002. https://doi.org/10.3390/math13061002
APA StyleZhuang, W., Yu, H., & Wang, M. C. (2025). Research on the Pricing Model of B2B Data Transactions and Its Nature for a Single Industrial Chain. Mathematics, 13(6), 1002. https://doi.org/10.3390/math13061002





