Center of Trapezoid Graph: Application in Selecting Center Location to Set up a Private Hospital
Abstract
1. Introduction
1.1. Some Definitions
1.2. Review of the Related Works
1.3. Result
1.4. Structure of Article
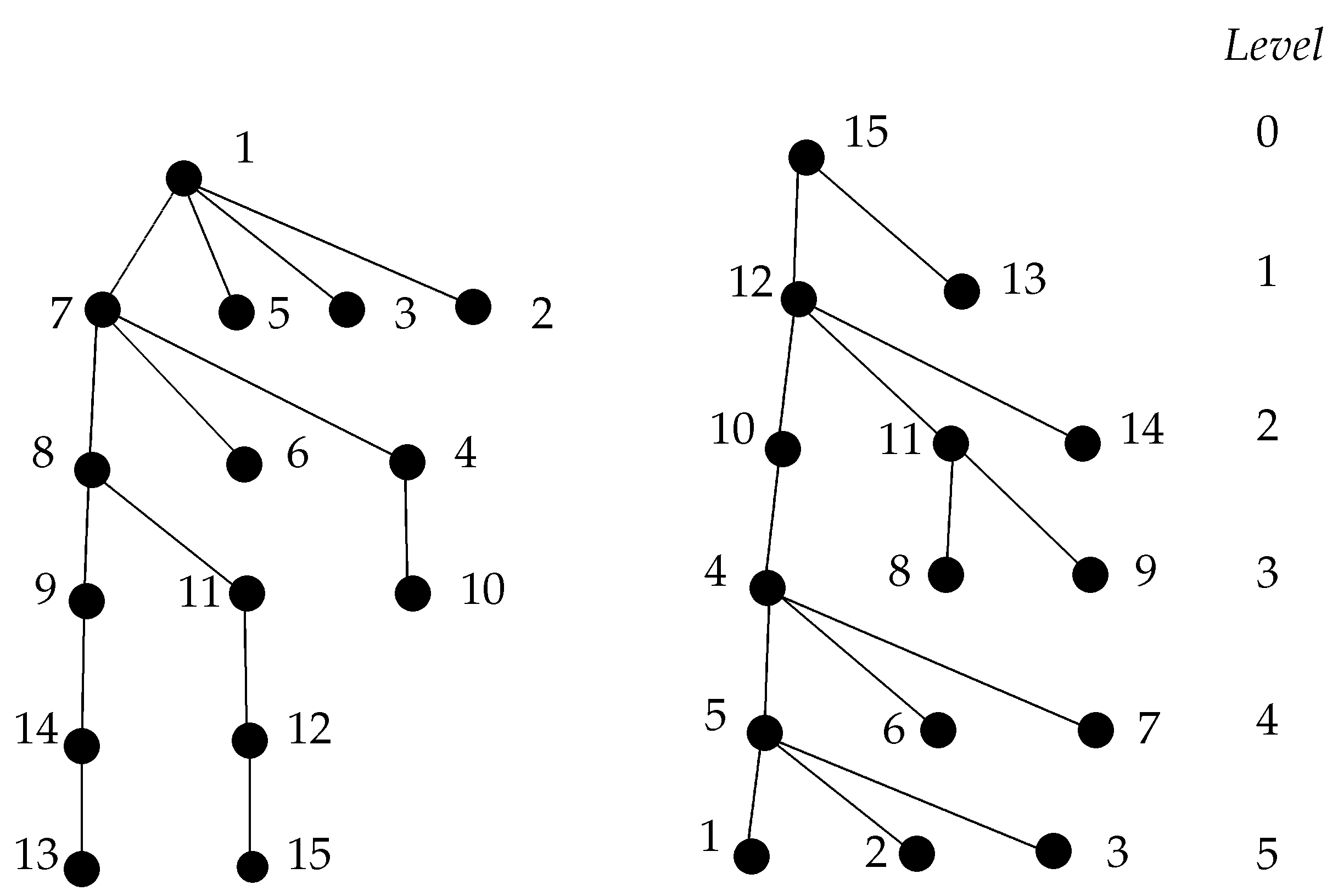
2. Formation of BFS Tree Based on BFS
Detection of the Main Path and Alternative-Path on Trees
- or
- or
- (1)
- Vertex n is located at the last level of the tree .
- (2)
- Vertex n is situated at the level of the tree .
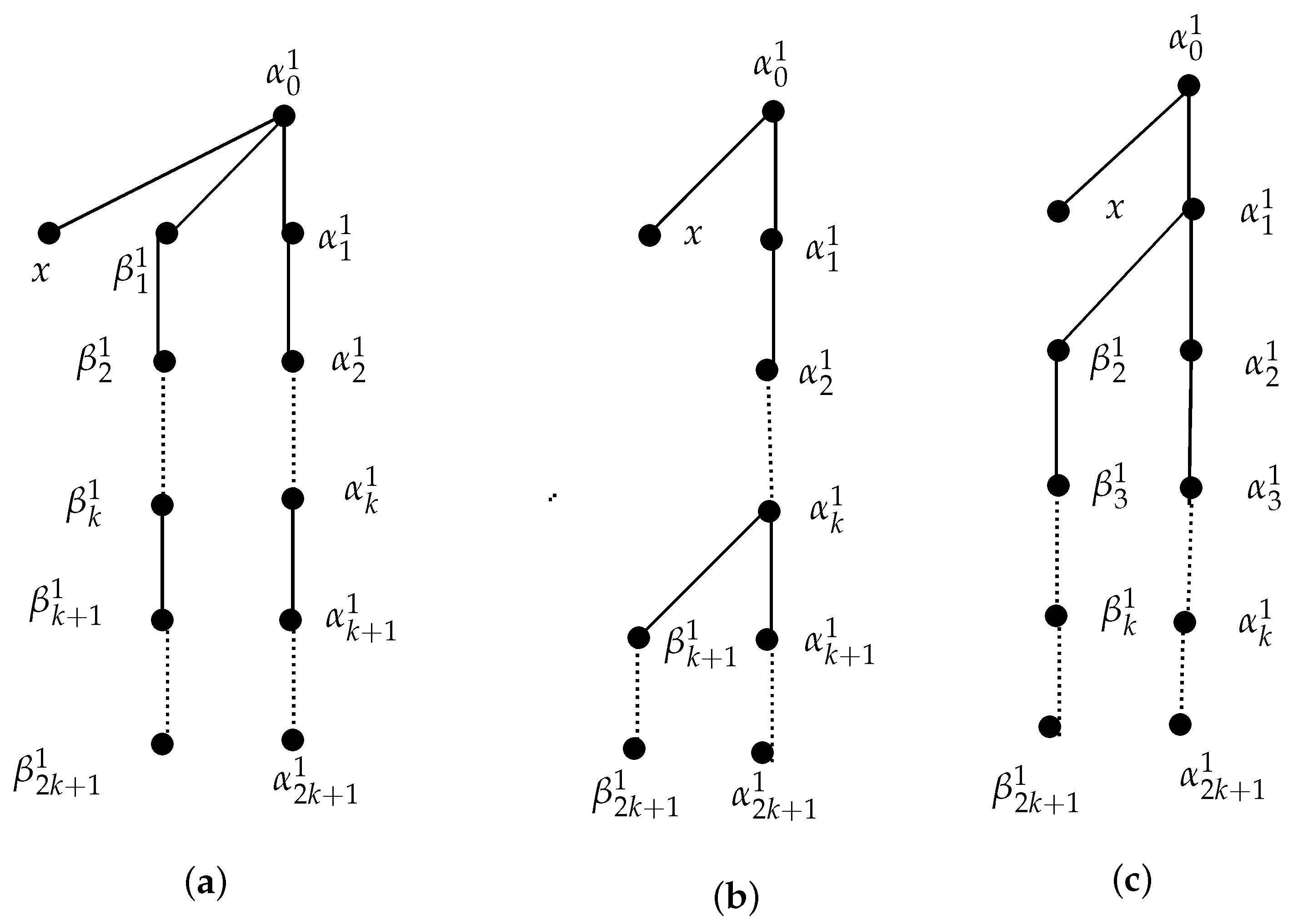
3. Some Results Related to , and Center of Trapezoid Graphs
- Case 1:
- In that case, if the distinct part of the alternative path () starts from or a higher level of (see Figure 5b, here, is the common part of both the alternative path and the main path), then (along the main path), , (as ); (along the main path), and (along the alternative path). So, , ∀ and . Therefore, and is a central vertex of the trapezoid graph G. Similarly, some other leaf nodes at level of may be central node of G. So, the center of G lies in .
- Case 2:
- If both and exist (see Figure 5a, here, the alternative path and the main path are distinct, except the root), then and , and for , ∀.
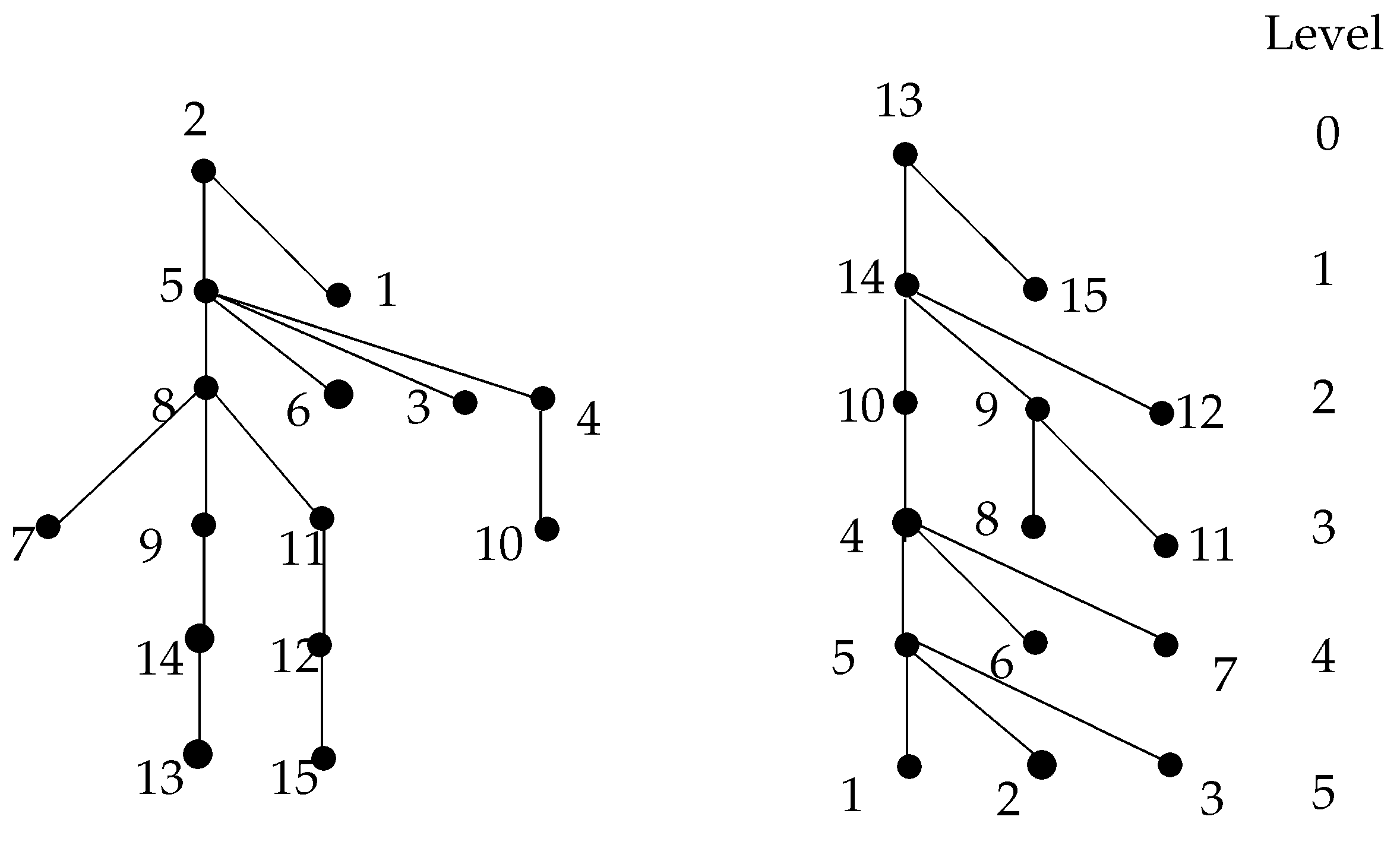
4. Computation of Central Vertices and Radius
- where is the top-right vertex of the trapezoid belonging to the set and
- where is the bottom-right vertex of the trapezoid belonging to the set .
- max{ where is the top-left vertex of the trapezoid belongs to the set B} and
- max{ where is the bottom-left vertex of the trapezoid belongs to the set B}.
4.1. Algorithm and Its Complexity
| Algorithm 1: Algorithm DIA-RAD-CEN-TRA. |
Input: Trapezoid representation of a trapezoid graph G, for . Output: , and central vertices of G. Step 1: Make 4 BFS trees , , and . Step 2: Obtain the heights and of , , and , respectively. Step 3: Mark the main paths and alternative-paths of , , and . Step 4: Find the sets for . Step 5: If and there exist at least two nodes such that and , for all and , for all then (by Lemma 4) Else (Lemma 4). End if Step 6: If one of and is even, say and then and set (Lemma 6). Else if one of and is even, say and then or and set (Lemma 7). Else if one of and are odd, say and , then and set (Lemma 8). Else if one of and are odd, say and , then or and set (by Lemma 9). Step 7: Arrange the vertices of P in ascending order, say . Step 8: Step 8.1: Find set A where the members of A are the common adjacent trapezoid of and except the trapezoid(s) corresponding to the internal nodes at level 1 of and . Step 8.2: Find min{ where is the top-right vertex of the trapezoid belonging to the set A}. Step 8.3: Find min{ where is the bottom-right vertex of the trapezoid belonging to the set A}. Step 8.4: Find another set B where the members of B are the common adjacent trapezoid of and except the trapezoid(s) corresponding to the internal nodes at level 1 of and . Step 8.5: Find max{ where is the top-left vertex of the trapezoid belonging to the set B}. Step 8.6: Find max{ where is the bottom-left vertex of the trapezoid belonging to the set B}. Step 9: Compute the set corresponding to , , , . Step 10: If S is a non-empty set, then we construct the BFS trees and with and t, if they exist, as roots, respectively. Else go to Step 11 End if Step 11: Compute the distance of the vertices of P from (if they exist) and find the maximum value for each row using Table 3. Step 13: Find where min{ and find corresponding to s (in Table 3), where . Step 14: Set . End if End DIA-RAD-CEN-TRA. |
4.2. Explanatory Example
5. Real Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BFS tree whose root is z. | |
| ’s height. | |
| Level of the node u on BFS tree. | |
| The parent node of u. | |
| Node located on the main path of at ith level. | |
| Node situated on the alternative path of at level i. | |
| The node set of situated at level i. | |
| . | |
| The shortest distance between two nodes and . | |
| Eccentricity of . | |
| The diameter of G. | |
| The radius of G. | |
| Center of G. | |
| The set of nodes adjacent to y, and y itself. | |
| a | Index of the trapezoid with the minimum bottom-left corner point position. |
| b | Index of the trapezoid with the minimum bottom-right corner point position. |
| The distance between the vertices x and . | |
| The eccentricity of the node . |
References
- Dagan, I.; Golumbic, M.C.; Pinter, R.Y. Trapezoid graphs and their coloring. Discret. Appl. Math. 1988, 21, 35–46. [Google Scholar] [CrossRef]
- Ma, T.; Spinrad, J.P. An O(n2) algorithm for 2-chain problem on certain classes of perfect graphs. In Proceedings of the 2nd ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, USA, 28–30 January 1991. [Google Scholar]
- Corneil, D.G.; Kamula, P.A. Extension of permutation and interval graphs. Congr. Numer. 1987, 58, 267–276. [Google Scholar]
- Golumbic, M.C. Algorithmic Graph Theory and Perfect Graphs; Elsevier B.V.: Amsterdam, The Netherlands, 2004; Volume 57. [Google Scholar]
- Liang, Y.D. Domination in trapezoid graphs. Inf. Process. Lett. 1994, 52, 309–315. [Google Scholar] [CrossRef]
- Pramanik, T.; Mondal, S.; Pal, M. The Diameter of an Interval Graph is Twice of its Radius. World Acad. Sci. Technol. Int. J. Math. Comput. Phys. Electr. Comput. Eng. 2011, 5, 1412–1417. [Google Scholar]
- Abbound, A.; Grandoni, F.; Williams, V.V. Subcubic Equivalences Between Graph Centrality Problems, APSP and diameter. In Proceedings of the 26th Annual ACM-SIAM Symposium on Discrete Algorithms, San Diego, CA, USA, 4–6 January 2015; pp. 1681–1697. [Google Scholar]
- Stummer, C.; Doerner, K.; Focke, A.; Heidenberger, K. Determining location and size of medical departments in a hospital network: A multiobjective decision support approach. Health Care Manag. Sci. 2004, 7, 63–71. [Google Scholar] [CrossRef]
- Wu, C.R.; Lin, C.T.; Chen, H.C. Optimal selection of location for Taiwanese hospitals to ensure a competitive advantage by using the analytic hierarchy process and sensitivity analysis. Build. Environ. 2007, 42, 1431–1444. [Google Scholar] [CrossRef]
- Syam, S.S. A multiple server location-allocation model for service system design. Comput. Oper. Res. 2008, 5, 2248–2265. [Google Scholar] [CrossRef]
- Vahidnia, M.H.; Alesheikh, A.A.; Alimohammadi, A. Hospital site selection using fuzzy AHP and its derivatives. J. Environ. Manag. 2009, 90, 3048–3056. [Google Scholar] [CrossRef] [PubMed]
- Shariff, S.S.R.; Moin, N.H.; Omar, M. Location allocation modeling for healthcare facility planning in Malaysia. Comput. Ind. Eng. 2012, 62, 1000–1010. [Google Scholar] [CrossRef]
- Kim, D.G.; Kim, Y.D. A Lagrangian heuristic algorithm for a public healthcare facility location problem. Ann. Oper. Res. 2013, 206, 221–240. [Google Scholar] [CrossRef]
- Shariff, S.S.R.; Moin, N.H.; Omar, M. Planning of public healthcare facility using a location allocation modelling: A case study. In Proceedings of the Statistics and Operational Research International Conference (SORIC 2013), Sarawak, Malaysia, 3–5 December 2013; AIP Publishing LLC: Melville, NY, USA, 2014; Volume 296, pp. 282–296. [Google Scholar] [CrossRef]
- Beheshtifar, S.; Alimoahmmadi, A. A multiobjective optimization approach for location-allocation of clinics. Int. Trans. Oper. Res. 2015, 22, 313–328. [Google Scholar] [CrossRef]
- Elkady, S.K.; Abdelsalam, H.M. A simulation-based optimization approach for healthcare facility location allocation decision. In Proceedings of the Science and Information Conference 2015, London, UK, 28–30 July 2015; pp. 500–505. [Google Scholar]
- Maric, M.; Stanimirovic, Z.; Bozovic, S. Hybrid metaheuristic method for determining locations for long-term health care facilities. Ann. Oper. Res. 2015, 227, 3–23. [Google Scholar] [CrossRef]
- Elkady, S.K.; Abdelsalam, H.M. A modified multi-objective particle swarm optimisation algorithm for healthcare facility planning. Int. J. Bus. Syst. Res. 2016, 10, 1–22. [Google Scholar] [CrossRef]
- Ouyang, R.; Faiz, T.I.; Noor-E-Alam, M. An ILP model for healthcare facility location problem with long term demand. In Proceedings of the 2016 International Conference on Industrial Engineering and Operations Management, Kuala Lumpur, Malaysia, 8–10 March 2016; IEOM Society International: Detroit, MI, USA, 2014; pp. 840–847. [Google Scholar]
- Ye, H.; Kim, H. Locating healthcare facilities using a network-based covering location problem. GeoJournal 2016, 81, 875–890. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, K.; Liu, S.; Huang, B. A multi-objective optimization approach for health-care facility location-allocation problems in highly developed cities such as Hong Kong. Comput. Environ. Urban Syst. 2016, 59, 220–230. [Google Scholar] [CrossRef]
- Behzad, M.; Chartrand, G. Introduction to the Theory of Graphs; Allyn and Bacon: Boston, MA, USA, 1971. [Google Scholar]
- Cheopoi, V. Centers of Triangulated Graphs. Mat. Zametki 1988, 43, 143–151. [Google Scholar] [CrossRef]
- Takes, F.W.; Kosters, W.A. Determining the Diameter of Small World Networks. In proceedings of the In Proceedings of the 20th ACM Conference on Information and Knoledge Management (CIKM 2011), Glasgow, UK, 24–28 October 2011; pp. 1191–1196. [Google Scholar] [CrossRef]
- Farley, A.; Proskurowski, A. Computation of the Center and Diameter of Outerplanar Graphs. Discret. Appl. Math. 1980, 2, 185–191. [Google Scholar] [CrossRef]
- Goldman, A.J. Minimax Location of a Facility in a Network. Transp. Sci. 1972, 6, 407–418. [Google Scholar] [CrossRef]
- Pal, M.; Bhattacharjee, G.P. Optimal Sequential and Parallel Algorithms for Computing the Diameter and the Center of Interval Graph. Int. J. Comput. Math. 1995, 59, 1–13. [Google Scholar] [CrossRef]
- Chepoi, V.D.; Dragan, F. A Linear-time Algorithm for Finding a Central Vertex of a Chordal Graph. Lect. Notes Comput. Sci. 1994, 855, 159–170. [Google Scholar] [CrossRef]
- Lan, Y.F.; Wanga, Y.L.; Suzuki, H. A Linear-time Algorithm for Solving the Center Problem on Weighted Cactus Graphs. Inf. Process. Lett. 1999, 71, 205–212. [Google Scholar] [CrossRef]
- Olariu, S. A Simple Linear Time Algorithm for Computing the Center of an Interval Graph. Int. J. Comput. Math. 1990, 34, 121–128. [Google Scholar] [CrossRef]
- Olariu, S.; Schwing, J.L.; Zhang, J. Optimal Parallel Algorithms for Problems Modelled by a Family of Intervals. IEEE Trans. Parallels Distrib. Syst. 1992, 3, 364–374. [Google Scholar] [CrossRef]
- Saha, A. Computation of Average Distance, Radius and Center of a Circular-Arc Graph in Parallel. J. Phys. Sci. 2006, 10, 178–187. [Google Scholar]
- Borassi, M.; Cresccnzi, P.; Habib, M.; Kosters, W.A.; Marino, A.; Takes, F.W. Fast Diameter and Radius BFS- based Computation in(weakly connected) Real-World Graphs: With an application to the six degrees of separation games. Theory Comput. Sci. 2015, 586, 59–80. [Google Scholar] [CrossRef]
- Abbound, A.; Wang, J.; Williams, V.V. Approximation and Fixed Parameter Sub Quadratic Algorithms for Radius and Diameter in Sparse Graphs. In Proceedings of the 27th Annual ACM-SIAM Symposium on Discrete Algorithms, Arlington, VA, USA, 10–12 January 2016; pp. 377–391. [Google Scholar]
- Laskar, R.; Shier, D. On powers and centers of chordal graphs. Discret. Appl. Math. 1983, 6, 139–147. [Google Scholar] [CrossRef]
- Mahesh, C.P. Distance in Graph Theory and its Application. Int. J. Adv. Eng. Technol. 2011, 3, 147–150. [Google Scholar]
- Nandi, S.; Mondal, S.; Barman, S.C. Computation of diameter, radius and center of permutation graphs. Discret. Math. Algorithms Appl. 2021, 14, 2250039. [Google Scholar] [CrossRef]
- Prisner, E. Radius versus diameter in cocomparability and intersection graphs. Discret. Math. 1997, 163, 109–117. [Google Scholar] [CrossRef]
- Tarjan, R.E. Depth-First Search and Linear Graph Algorithms. SIAM J. Comput. 1972, 1, 146–160. [Google Scholar] [CrossRef]
- Chen, C.C.Y.; Das, S.K. Breadth-First Traversal of Trees and Integer Sorting in Parallel. Inf. Process. Lett. 1992, 41, 39–49. [Google Scholar] [CrossRef]
- Olariu, S. An Optimal Greedy Heuristic to Color Interval Graphs. Inf. Process. Lett. 1991, 37, 21–25. [Google Scholar] [CrossRef]
- Barman, S.; Mondal, S.; Pal, M. An Efficient Algorithm to find Next-to-Shortest Path on Permutation Graphs. J. Appl. Math. Comput. 2009, 31, 369–384. [Google Scholar] [CrossRef]
- Mondal, S.; Pal, M.; Pal, T.K. An optimal algorithm for solving all-pairs shortest paths on trapezoid graphs. Int. J. Comput. Eng. Sci. 2002, 3, 103–116. [Google Scholar] [CrossRef]
- Barman, S.; Mondal, S.; Pal, M. A Linear Time Algorithm to Construct a Tree 4-Spanner on Trapezoid Graphs. Int. J. Comput. Math. 2010, 87, 743–755. [Google Scholar] [CrossRef]
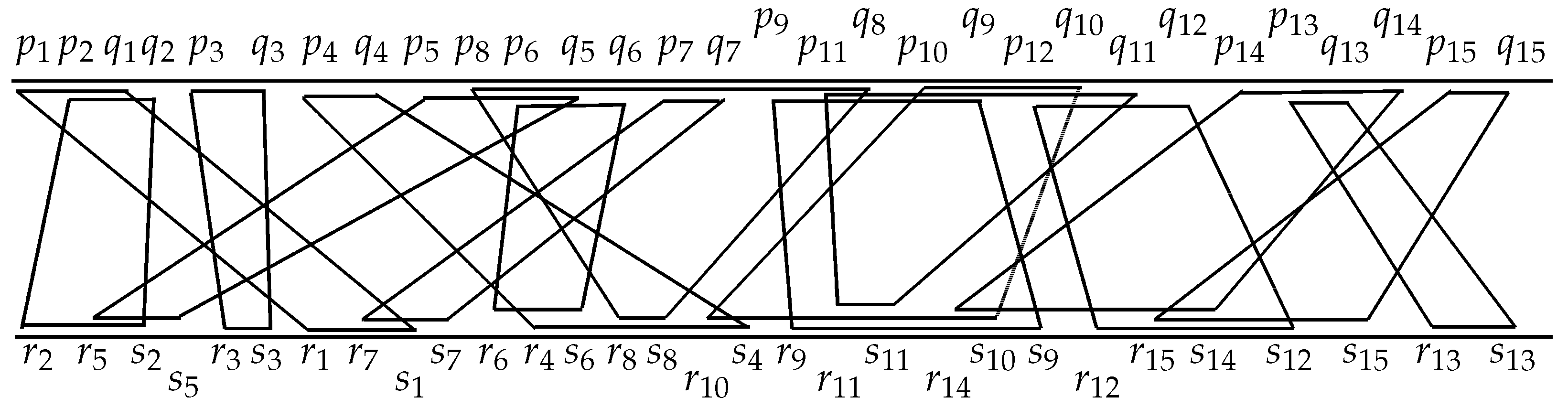


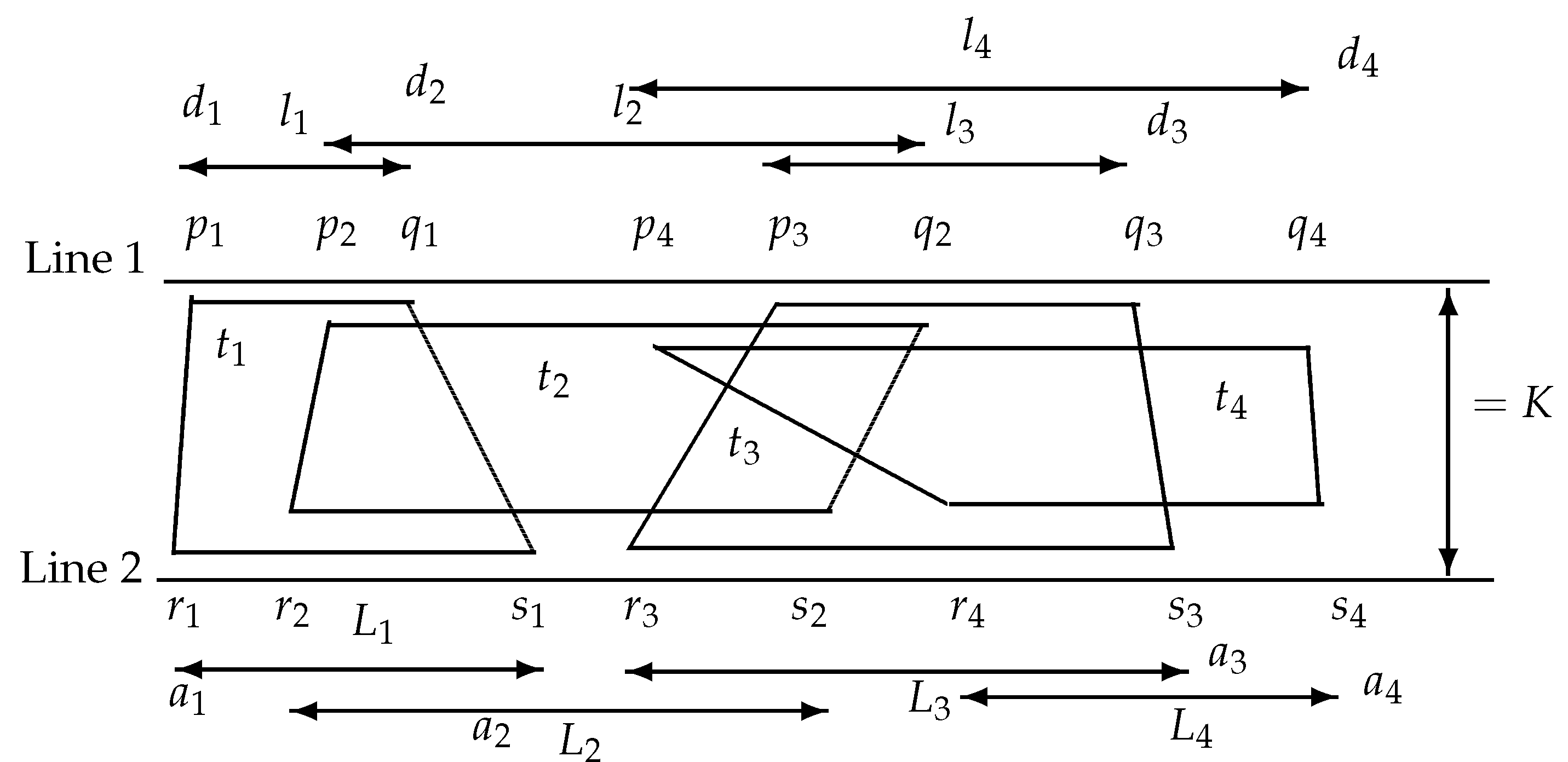
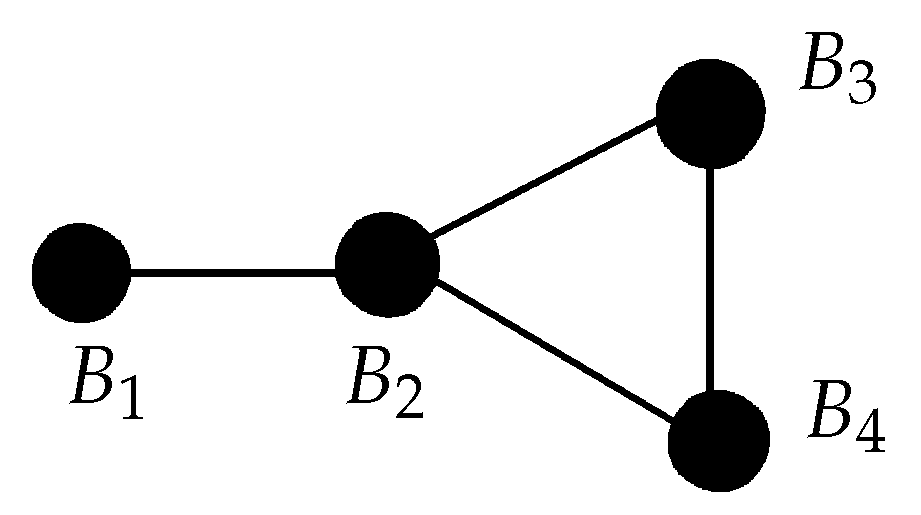
| (say) | |||||
| (say) | |||||
| … | … | … | … | … | … |
| (say) |
| (say) | |||||
| (say) | |||||
| … | … | … | … | … | … |
| (say) |
| (say) | |||
| (say) | |||
| … | … | … | … |
| (say) |
| 4 | = 2 | ||
| 6 | = 2 | ||
| 8 | = 2 | ||
| 9 | = 3 | ||
| 10 | = 3 | ||
| 11 | = 3 |
| 4 | = 3 | ||
| 6 | = 4 | ||
| 8 | = 3 | ||
| 9 | = 3 | ||
| 10 | = 2 | ||
| 11 | = 3 |
| 4 | 2 | 3 | = 3 |
| 6 | 2 | 4 | = 4 |
| 8 | 2 | 3 | = 3 |
| 9 | 3 | 3 | = 3 |
| 10 | 3 | 2 | = 3 |
| 11 | 3 | 3 | = 3 |
| Name of Blocks | Hospital’s Position | Latitude | Longitude | Length of NH/SH | Average Local Route Distance | Free Range of Ambulance |
|---|---|---|---|---|---|---|
| K | ||||||
| K | ||||||
| K | ||||||
| K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nandi, S.; Mondal, S.; Samanta, S.; Barman, S.C.; Mrsic, L.; Kalampakas, A. Center of Trapezoid Graph: Application in Selecting Center Location to Set up a Private Hospital. Mathematics 2025, 13, 885. https://doi.org/10.3390/math13050885
Nandi S, Mondal S, Samanta S, Barman SC, Mrsic L, Kalampakas A. Center of Trapezoid Graph: Application in Selecting Center Location to Set up a Private Hospital. Mathematics. 2025; 13(5):885. https://doi.org/10.3390/math13050885
Chicago/Turabian StyleNandi, Shaoli, Sukumar Mondal, Sovan Samanta, Sambhu Charan Barman, Leo Mrsic, and Antonios Kalampakas. 2025. "Center of Trapezoid Graph: Application in Selecting Center Location to Set up a Private Hospital" Mathematics 13, no. 5: 885. https://doi.org/10.3390/math13050885
APA StyleNandi, S., Mondal, S., Samanta, S., Barman, S. C., Mrsic, L., & Kalampakas, A. (2025). Center of Trapezoid Graph: Application in Selecting Center Location to Set up a Private Hospital. Mathematics, 13(5), 885. https://doi.org/10.3390/math13050885









