The Waxing and Waning of Fear Influence the Control of Vector-Borne Diseases
Abstract
1. Introduction
2. Methods
3. Results
3.1. Analytical Solutions
3.2. Numerical Simulations
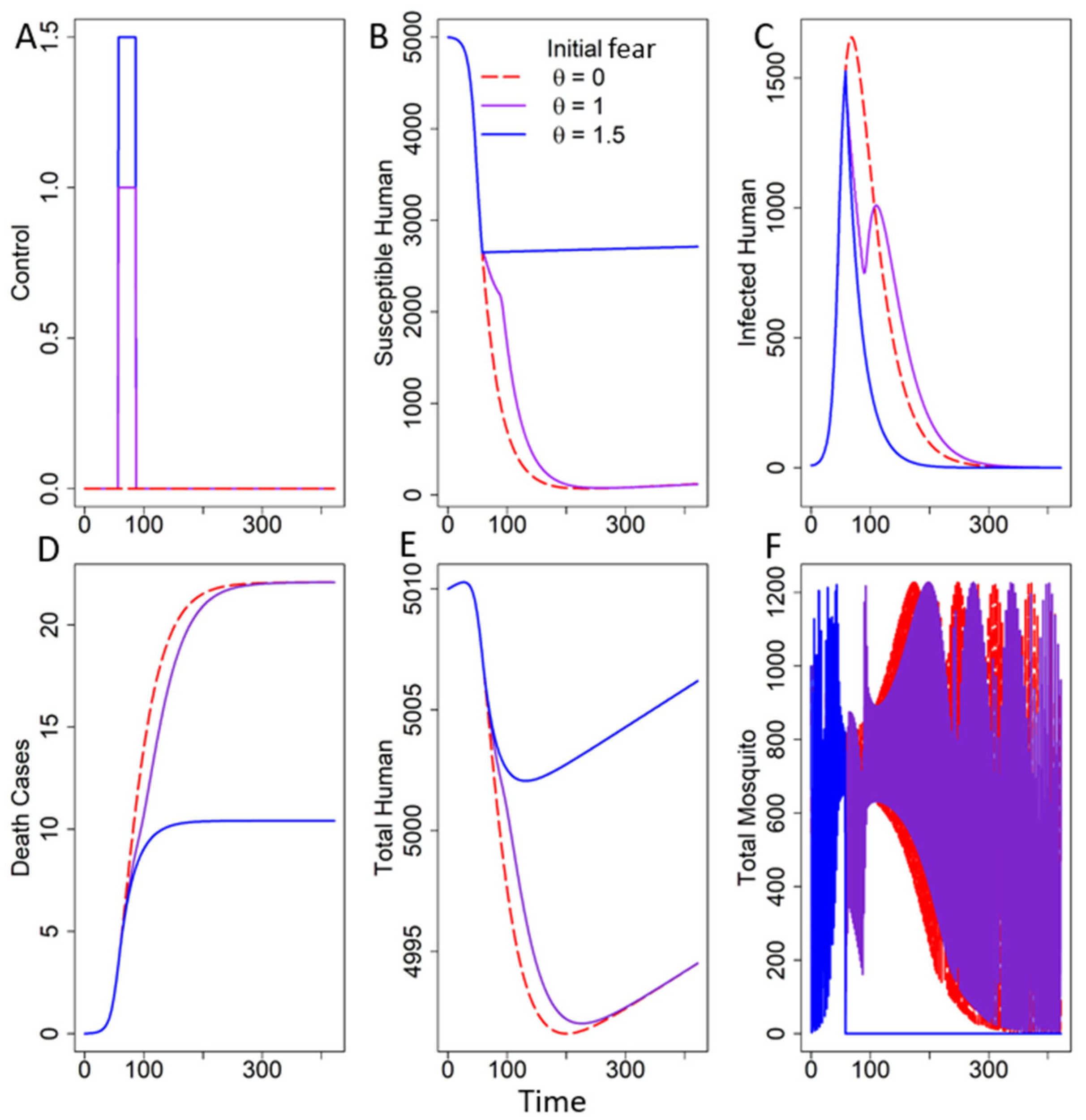
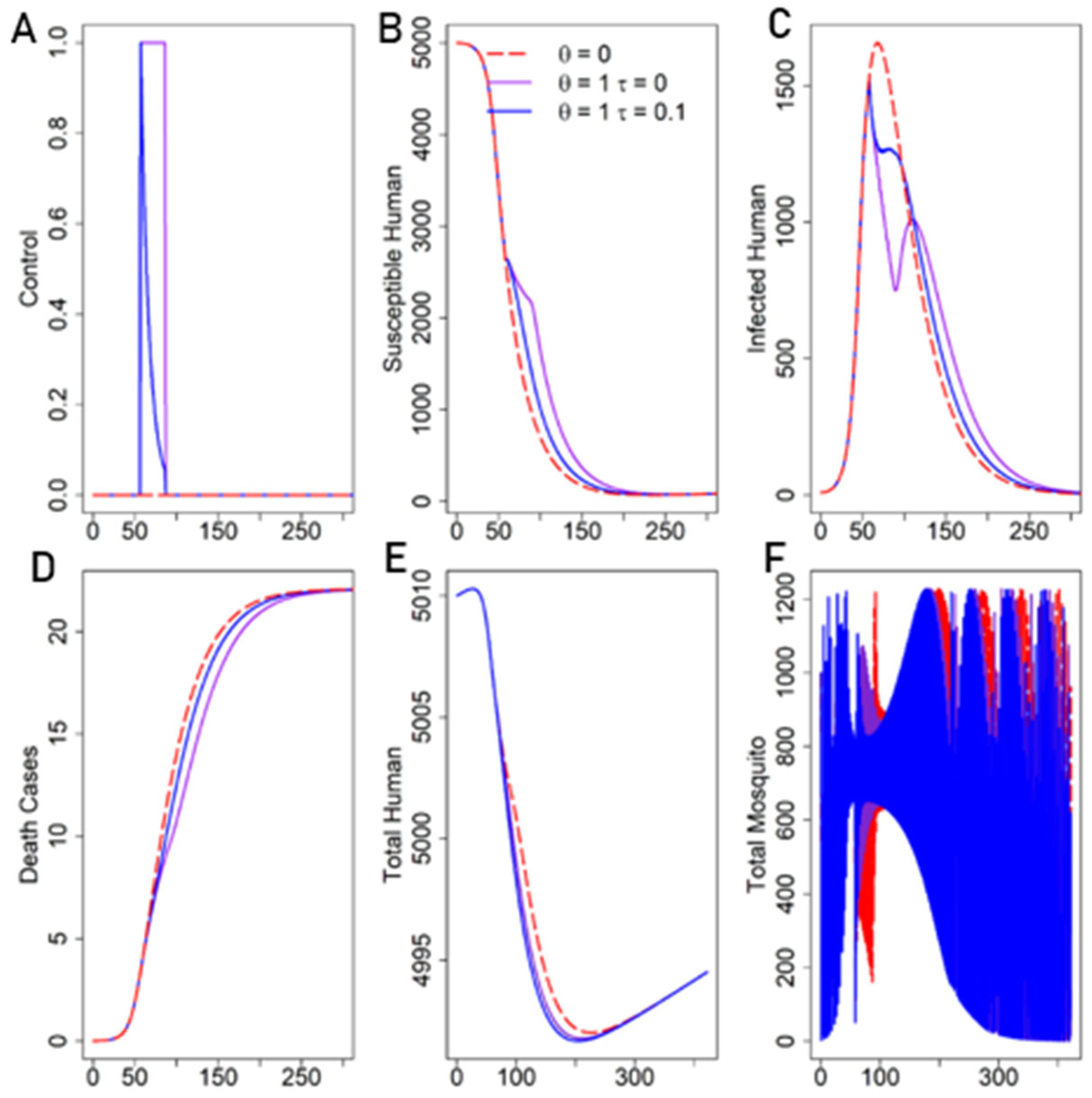
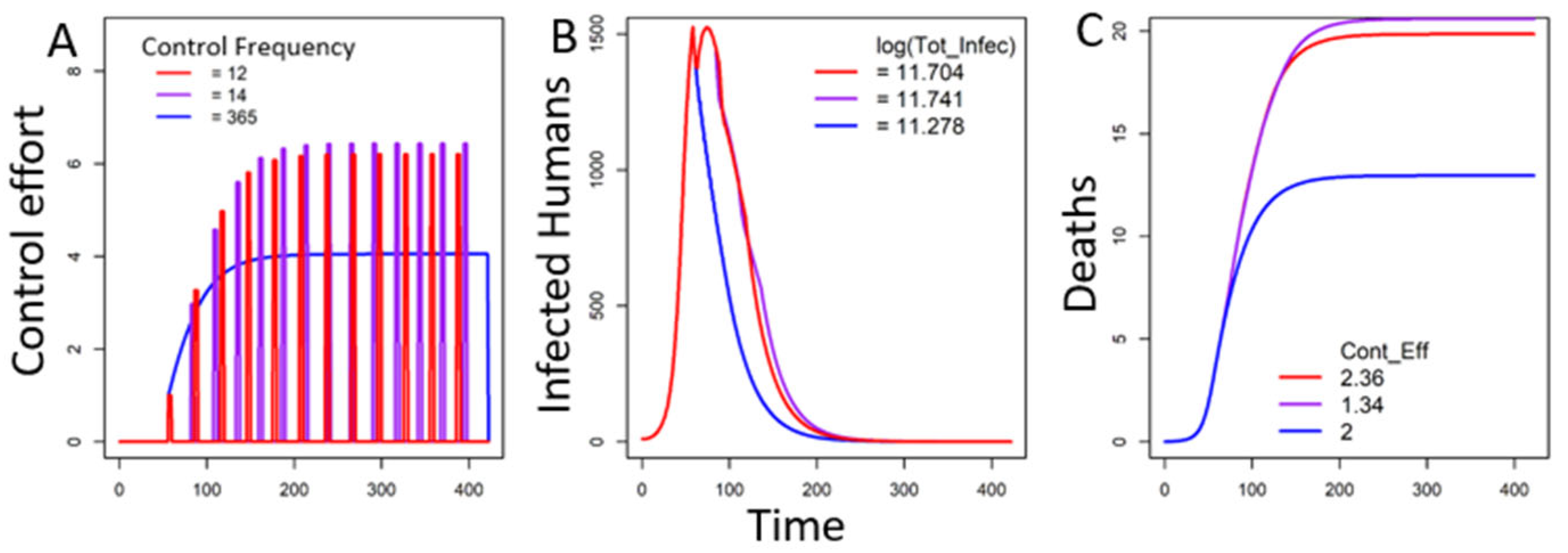
3.2.1. Fear Under One Trigger
In the Absence of Decay of Fear
In the Presence of Decay of Fear
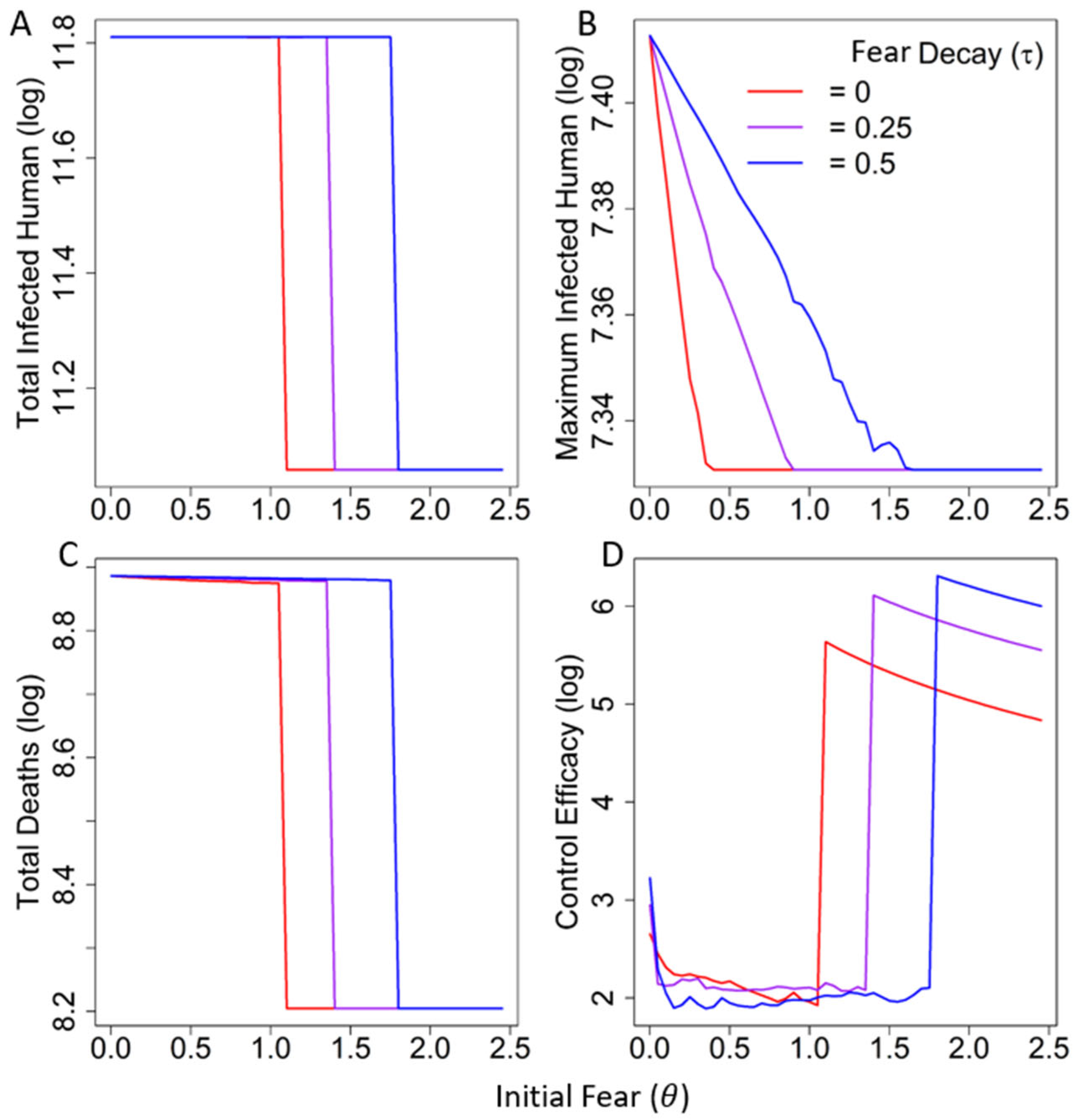
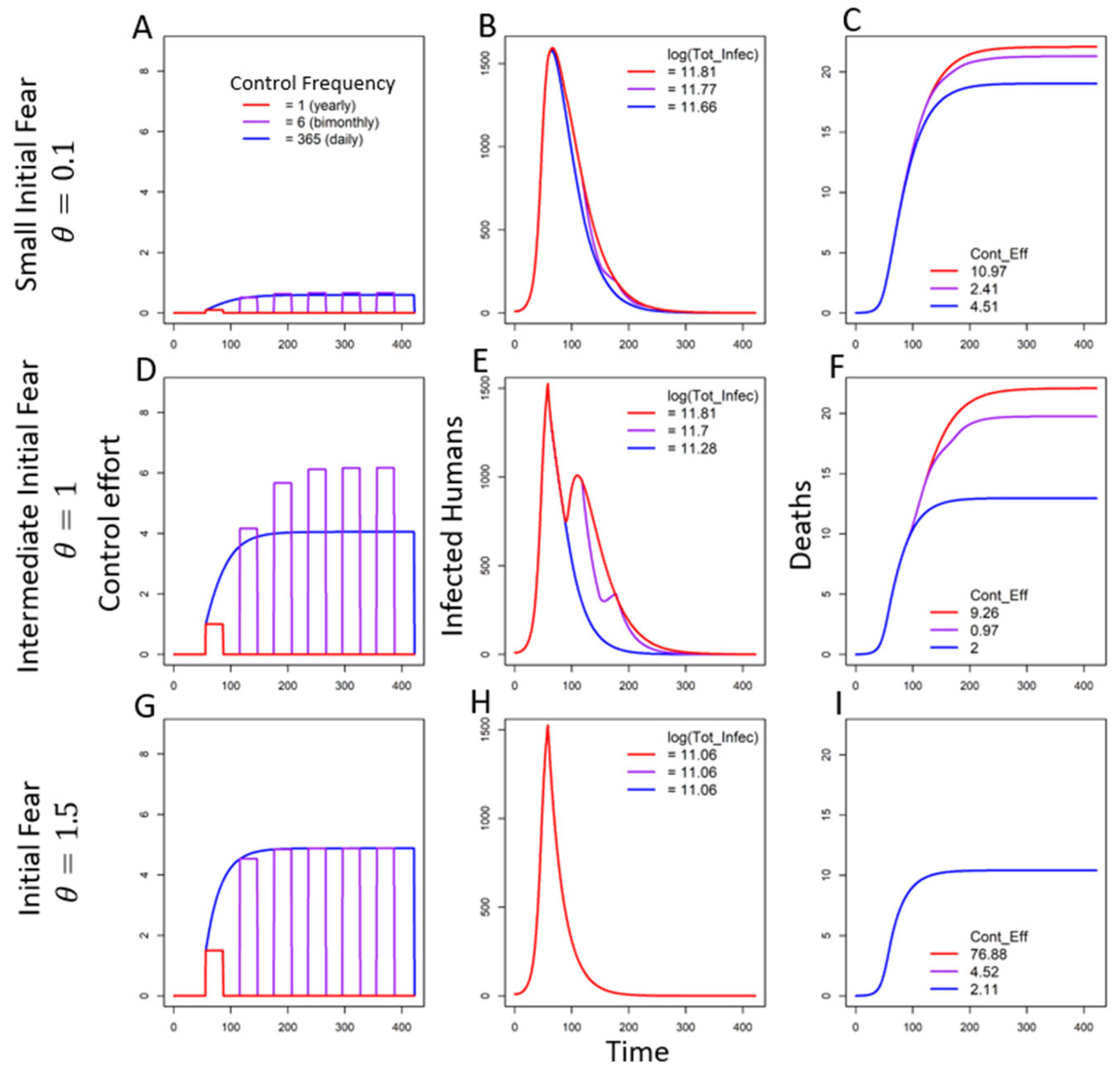
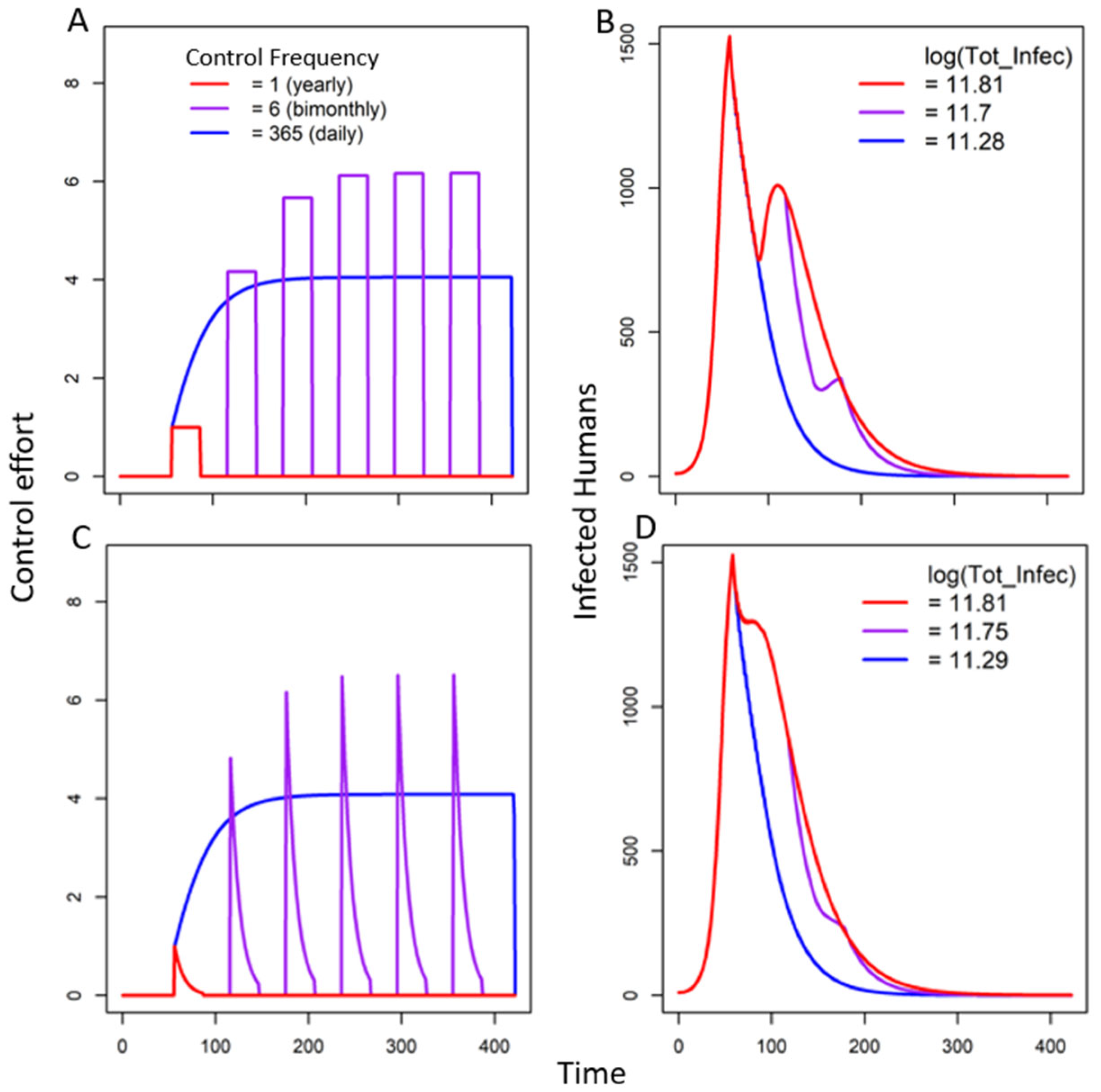
3.2.2. Seasonal Fear Under Multiple Triggers
In the Absence of Decay of Fear
In the Presence of Decay of Fear
4. Discussion
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VBD | Vector-Borne Disease |
| CD | Control Duration (days for one control period) |
References
- Althouse, B.M.; Scarpino, S.V.; Meyers, L.A.; Ayers, J.W.; Bargsten, M.; Baumbach, J.; Brownstein, J.S.; Castro, L.; Clapham, H.; Cummings, D.A. Enhancing disease surveillance with novel data streams: Challenges and opportunities. EPJ Data Sci. 2015, 4, 17. [Google Scholar] [CrossRef] [PubMed]
- Sabin, N.S.; Calliope, A.S.; Simpson, S.V.; Arima, H.; Ito, H.; Nishimura, T.; Yamamoto, T. Implications of human activities for (re) emerging infectious diseases, including COVID-19. J. Physiol. Anthropol. 2020, 39, 29. [Google Scholar] [CrossRef] [PubMed]
- Stockmaier, S.; Stroeymeyt, N.; Shattuck, E.C.; Hawley, D.M.; Meyers, L.A.; Bolnick, D.I. Infectious diseases and social distancing in nature. Science 2021, 371, eabc8881. [Google Scholar] [CrossRef]
- Cheng, V.C.-C.; Wong, S.-C.; Chuang, V.W.-M.; So, S.Y.-C.; Chen, J.H.-K.; Sridhar, S.; To, K.K.-W.; Chan, J.F.-W.; Hung, I.F.-N.; Ho, P.-L. The role of community-wide wearing of face mask for control of coronavirus disease 2019 (COVID-19) epidemic due to SARS-CoV-2. J. Infect. 2020, 81, 107–114. [Google Scholar] [CrossRef]
- Manfredi, P.; D’Onofrio, A. Modeling the Interplay Between Human Behavior and the Spread of Infectious Diseases; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Almaghrabi, M.K. Public awareness, attitudes, and adherence to COVID-19 quarantine and isolation in Saudi Arabia. Int. J. Gen. Med. 2021, 14, 4395–4403. [Google Scholar] [CrossRef] [PubMed]
- Elgendy, M.O.; Abd Elmawla, M.N.; Abdel Hamied, A.M.; El Gendy, S.O.; Abdelrahim, M.E. COVID-19 patients and contacted person awareness about home quarantine instructions. Int. J. Clin. Pract. 2021, 75, e13810. [Google Scholar] [CrossRef]
- Masadeh, M.M.; Alzoubi, K.H.; Al-Azzam, S.I.; Al-Agedi, H.S.; Abu Rashid, B.E.; Mukattash, T.L. Public awareness regarding children vaccination in Jordan. Hum. Vaccines Immunother. 2014, 10, 1762–1766. [Google Scholar] [CrossRef]
- Capasso, V.; Serio, G. A generalization of the Kermack-McKendrick deterministic epidemic model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Jiao, J.; Suarez, G.P.; Fefferman, N.H. How public reaction to disease information across scales and the impacts of vector control methods influence disease prevalence and control efficacy. PLoS Comput. Biol. 2021, 17, e1008762. [Google Scholar] [CrossRef]
- d’Onofrio, A.; Manfredi, P. The interplay between voluntary vaccination and reduction of risky behavior: A general behavior-implicit SIR model for vaccine preventable infections. In Current Trends in Dynamical Systems in Biology and Natural Sciences; Springer: Cham, Switzerland, 2020; pp. 185–203. [Google Scholar]
- Chen, Y.; Bi, K.; Zhao, S.; Ben-Arieh, D.; Wu, C.-H.J. Modeling individual fear factor with optimal control in a disease-dynamic system. Chaos Solitons Fractals 2017, 104, 531–545. [Google Scholar] [CrossRef]
- Pappas, G.; Kiriaze, I.J.; Giannakis, P.; Falagas, M.E. Psychosocial consequences of infectious diseases. Clin. Microbiol. Infect. 2009, 15, 743–747. [Google Scholar] [CrossRef] [PubMed]
- Epstein, J.M.; Parker, J.; Cummings, D.; Hammond, R.A. Coupled contagion dynamics of fear and disease: Mathematical and computational explorations. PLoS ONE 2008, 3, e3955. [Google Scholar] [CrossRef]
- Maji, C. Impact of Media-Induced Fear on the Control of COVID-19 Outbreak: A Mathematical Study. Int. J. Differ. Equ. 2021, 1, 2129490. [Google Scholar] [CrossRef]
- Funk, S.; Salathé, M.; Jansen, V.A. Modelling the influence of human behaviour on the spread of infectious diseases: A review. J. R. Soc. Interface 2010, 7, 1247–1256. [Google Scholar] [CrossRef]
- Manwar, M.H.G.; Khan, R.A.H. A Review on Vector Borne Diseases and Controlling Challenges. J. Algebr. Stat. 2022, 13, 398–409. [Google Scholar]
- Chala, B.; Hamde, F. Emerging and re-emerging vector-borne infectious diseases and the challenges for control: A review. Front. Public Health 2021, 9, 715759. [Google Scholar] [CrossRef]
- Guastello, S.J.; Koopmans, M.; Pincus, D. Chaos and Complexity in Psychology: The Theory of Nonlinear Dynamical Systems; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Hohm, I.; Wormley, A.S.; Schaller, M.; Varnum, M.E. Homo temporus: Seasonal cycles as a fundamental source of variation in human psychology. Perspect. Psychol. Sci. 2024, 19, 151–172. [Google Scholar] [CrossRef]
- Magnusson, A.; Boivin, D. Seasonal affective disorder: An overview. Chronobiol. Int. 2003, 20, 189–207. [Google Scholar] [CrossRef]
- Han, L.; Wang, K.; Du, Z.; Cheng, Y.; Simons, J.S.; Rosenthal, N.E. Seasonal variations in mood and behavior among Chinese medical students. Am. J. Psychiatry 2000, 157, 133–135. [Google Scholar] [CrossRef]
- Siegel, M. False Alarm: The Truth About the Epidemic of Fear; Turner Publishing Company: Paducah, KY, USA, 2008. [Google Scholar]
- Kindt, M. The surprising subtleties of changing fear memory: A challenge for translational science. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 20170033. [Google Scholar] [CrossRef]
- Palmer, M.S.; Gaynor, K.M.; Abraham, J.O.; Pringle, R.M. The role of humans in dynamic landscapes of fear. Trends Ecol. Evol. 2023, 38, 217–218. [Google Scholar] [CrossRef] [PubMed]
- Cuervo-Parra, J.A.; Cortés, T.R.; Ramirez-Lepe, M. Mosquito-borne diseases, pesticides used for mosquito control, and development of resistance to insecticides. In Insecticides Resistance; InTechOpen: Rijeka, Croatia, 2016; Volume 2, pp. 111–134. [Google Scholar]
- Kaur, A.; Tyson, R.; Moyles, I. The impact of fear and behaviour response to established and novel diseases. arXiv 2024, arXiv:2406.15595. [Google Scholar]
- Yang, E.; Kim, J.; Pennington-Gray, L. Social media information and peer-to-peer accommodation during an infectious disease outbreak. J. Destin. Mark. Manag. 2021, 19, 100538. [Google Scholar] [CrossRef]
- Lerouge, R.; Lema, M.D.; Arnaboldi, M. The role played by government communication on the level of public fear in social media: An investigation into the Covid-19 crisis in Italy. Gov. Inf. Q. 2023, 40, 101798. [Google Scholar] [CrossRef]
- Dillard, J.P.; Li, R.; Yang, C. Fear of Zika: Information seeking as cause and consequence. Health Commun. 2021, 36, 1785–1795. [Google Scholar] [CrossRef]
- Steimer, T. The biology of fear-and anxiety-related behaviors. Dialogues Clin. Neurosci. 2002, 4, 231–249. [Google Scholar] [CrossRef] [PubMed]
- Ash, T.; Bento, A.M.; Kaffine, D.; Rao, A.; Bento, A.I. Disease-economy trade-offs under alternative epidemic control strategies. Nat. Commun. 2022, 13, 3319. [Google Scholar] [CrossRef]
- Oleś, K.; Gudowska-Nowak, E.; Kleczkowski, A. Understanding disease control: Influence of epidemiological and economic factors. PLoS ONE 2012, 7, e36026. [Google Scholar] [CrossRef]
- Hindes, J.; Bianco, S.; Schwartz, I.B. Optimal periodic closure for minimizing risk in emerging disease outbreaks. PLoS ONE 2021, 16, e0244706. [Google Scholar] [CrossRef]
- Suarez, G.P.; Udiani, O.; Allan, B.F.; Price, C.; Ryan, S.J.; Lofgren, E.; Coman, A.; Stone, C.M.; Gallos, L.K.; Fefferman, N.H. A generic arboviral model framework for exploring trade-offs between vector control and environmental concerns. J. Theor. Biol. 2020, 490, 110161. [Google Scholar] [CrossRef]
- Ross, R. Some quantitative studies in epidemiology. Nature 1911, 87, 466–467. [Google Scholar] [CrossRef]
- Macdonald, G. The analysis of infection rates in diseases in which super infection occurs. Trop. Dis. Bull. 1950, 47, 907–915. [Google Scholar] [PubMed]
- Gao, D.; Lou, Y.; He, D.; Porco, T.C.; Kuang, Y.; Chowell, G.; Ruan, S. Prevention and control of Zika as a mosquito-borne and sexually transmitted disease: A mathematical modeling analysis. Sci. Rep. 2016, 6, 28070. [Google Scholar] [CrossRef]
- Agency, C.I. The World Factbook 2009; Central Intelligence Agency: McLean, VA, USA, 2009. [Google Scholar]
- Stone, C.M.; Schwab, S.R.; Fonseca, D.M.; Fefferman, N.H. Human movement, cooperation and the effectiveness of coordinated vector control strategies. J. R. Soc. Interface 2017, 14, 20170336. [Google Scholar] [CrossRef] [PubMed]
- Ellington, S.R.; Devine, O.; Bertolli, J.; Quiñones, A.M.; Shapiro-Mendoza, C.K.; Perez-Padilla, J.; Rivera-Garcia, B.; Simeone, R.M.; Jamieson, D.J.; Valencia-Prado, M. Estimating the number of pregnant women infected with Zika virus and expected infants with microcephaly following the Zika virus outbreak in Puerto Rico, 2016. JAMA Pediatr. 2016, 170, 940–945. [Google Scholar] [CrossRef]
- Cortez, M.H.; Abrams, P.A. Hydra effects in stable communities and their implications for system dynamics. Ecology 2016, 97, 1135–1145. [Google Scholar] [CrossRef]
- Abrams, P.A. When does greater mortality increase population size? The long history and diverse mechanisms underlying the hydra effect. Ecol. Lett. 2009, 12, 462–474. [Google Scholar] [CrossRef]
- Jiao, J.; Pilyugin, S.S.; Osenberg, C.W. Random movement of predators can eliminate trophic cascades in marine protected areas. Ecosphere 2016, 7, e01421. [Google Scholar] [CrossRef]
- Galor, O. Discrete Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Ossimitz, G.; Mrotzek, M. The basics of system dynamics: Discrete vs. continuous modelling of time. In Proceedings of the 26th International Conference of the System Dynamics Society, Athens, Greece, 20–24 July 2008. [Google Scholar]
- Person, B.; Sy, F.; Holton, K.; Govert, B.; Liang, A.; Team, S.C.O.; Garza, B.; Gould, D.; Hickson, M.; McDonald, M. Fear and stigma: The epidemic within the SARS outbreak. Emerg. Infect. Dis. 2004, 10, 358. [Google Scholar] [CrossRef] [PubMed]
- Napolioni, V.; Murray, D.R.; Comings, D.E.; Peters, W.R.; Gade-Andavolu, R.; MacMurray, J. Interaction between infectious diseases and personality traits: ACP1* C as a potential mediator. Infect. Genet. Evol. 2014, 26, 267–273. [Google Scholar] [CrossRef]
- Schaller, M.; Murray, D.R. Pathogens, personality, and culture: Disease prevalence predicts worldwide variability in sociosexuality, extraversion, and openness to experience. J. Personal. Soc. Psychol. 2008, 95, 212. [Google Scholar] [CrossRef]
- Roosa, K.; Fefferman, N.H. A general modeling framework for exploring the impact of individual concern and personal protection on vector-borne disease dynamics. Parasites Vectors 2022, 15, 361. [Google Scholar] [CrossRef] [PubMed]
- Manrubia, S.; Zanette, D.H. Individual risk-aversion responses tune epidemics to critical transmissibility (R= 1). R. Soc. Open Sci. 2022, 9, 211667. [Google Scholar] [CrossRef]
- Wang, B. How to change American attitudes towards the epidemic. Int. J. Front. Sociol. 2020, 2, 139–142. [Google Scholar]
- Chakrabarty, D. Community, State and the Body: Epidemics and popular culture in colonial India 1. In Medical Marginality in South Asia; Routledge: Milton Park, UK, 2013; pp. 36–58. [Google Scholar]
- Buckee, C.; Noor, A.; Sattenspiel, L. Thinking clearly about social aspects of infectious disease transmission. Nature 2021, 595, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Chew, Q.H.; Wei, K.C.; Vasoo, S.; Chua, H.C.; Sim, K. Narrative synthesis of psychological and coping responses towards emerging infectious disease outbreaks in the general population: Practical considerations for the COVID-19 pandemic. Singap. Med. J. 2020, 61, 350. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, J.M.; Tybur, J.M.; Blackwell, A.D. What role does pathogen-avoidance psychology play in pandemics? Trends Cogn. Sci. 2021, 25, 177–186. [Google Scholar] [CrossRef]
- Weston, D.; Ip, A.; Amlôt, R. Examining the application of behaviour change theories in the context of infectious disease outbreaks and emergency response: A review of reviews. BMC Public Health 2020, 20, 1483. [Google Scholar] [CrossRef]
- Bedson, J.; Skrip, L.A.; Pedi, D.; Abramowitz, S.; Carter, S.; Jalloh, M.F.; Funk, S.; Gobat, N.; Giles-Vernick, T.; Chowell, G. A review and agenda for integrated disease models including social and behavioural factors. Nat. Hum. Behav. 2021, 5, 834–846. [Google Scholar] [CrossRef]
- Murray, D.R.; Prokosch, M.L.; Airington, Z. PsychoBehavioroimmunology: Connecting the behavioral immune system to its physiological foundations. Front. Psychol. 2019, 10, 200. [Google Scholar] [CrossRef]
- Schaller, M.; Park, J.H. The behavioral immune system (and why it matters). Curr. Dir. Psychol. Sci. 2011, 20, 99–103. [Google Scholar] [CrossRef]
- Abramowitz, S.A.; Hipgrave, D.B.; Witchard, A.; Heymann, D.L. Lessons from the West Africa Ebola epidemic: A systematic review of epidemiological and social and behavioral science research priorities. J. Infect. Dis. 2018, 218, 1730–1738. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Operational Guide for Engaging Communities in Contact Tracing, 28 May 2021; World Health Organization: Geneva, Switzerland, 2021. [Google Scholar]
- Zelner, J.; Masters, N.B.; Naraharisetti, R.; Mojola, S.A.; Chowkwanyun, M.; Malosh, R. There are no equal opportunity infectors: Epidemiological modelers must rethink our approach to inequality in infection risk. PLoS Comput. Biol. 2022, 18, e1009795. [Google Scholar] [CrossRef] [PubMed]
| Variables | Description | Initial Values |
|---|---|---|
| Total human population size | ||
| Susceptible humans | 5000 | |
| Infected humans | 10 | |
| Recovered humans | 0 | |
| Death cases in humans | 0 | |
| Susceptible mosquitoes | 1000 | |
| Infected mosquitoes | 0 | |
| Control on mosquito | 0 |
| Parameters | Description | Value | Reference |
|---|---|---|---|
| Transmission rate in humans | [10,38] | ||
| Transmission rate in mosquitoes | [10,38] | ||
| Natural mortality in humans | [39] | ||
| Natural mortality in mosquitoes | 1/13 | [40] | |
| Birth rate in humans | [41] | ||
| Recovery rate in humans | 0.037 | [38] | |
| Composite rate | 190/3,474,182 | [41] | |
| Egg laying rate for mosquitoes | 5 | ||
| Initial fear | 1 or very | ||
| Fear decay | 0.1 or vary | ||
| Critical deaths that trigger the control | 3 | ||
| CD | Days for one control period | 30 or vary | |
| Carrying capacity of mosquito | 3500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, J. The Waxing and Waning of Fear Influence the Control of Vector-Borne Diseases. Mathematics 2025, 13, 879. https://doi.org/10.3390/math13050879
Jiao J. The Waxing and Waning of Fear Influence the Control of Vector-Borne Diseases. Mathematics. 2025; 13(5):879. https://doi.org/10.3390/math13050879
Chicago/Turabian StyleJiao, Jing. 2025. "The Waxing and Waning of Fear Influence the Control of Vector-Borne Diseases" Mathematics 13, no. 5: 879. https://doi.org/10.3390/math13050879
APA StyleJiao, J. (2025). The Waxing and Waning of Fear Influence the Control of Vector-Borne Diseases. Mathematics, 13(5), 879. https://doi.org/10.3390/math13050879






