Jacobi–Jordan Conformal Algebras: Basics, Constructions and Related Structures
Abstract
1. Introduction
2. Jacobi–Jordan Conformal Algebras and Their Modules
2.1. Definitions and Basic Results
- (i)
- For every , there exists such that for all ;
- (ii)
- ;
- (iii)
- .
- (1)
- ,
- (2)
- ,
- (3)
- .
2.2. -Operators on Jacobi–Jordan Conformal Algebras
2.3. Symplectic Jacobi–Jordan Conformal Algebras
3. Quadratic Jacobi–Jordan Conformal Algebras and Mock-Gel’fand–Dorfman Bialgebras
3.1. Mock-Gel’fand–Dorfman Bialgebras
3.2. Quadratic Jacobi–Jordan Conformal Algebras and Their Characterization
4. The -Split Extending Structures Problem
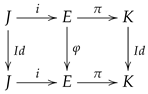
4.1. Unified Products of Jacobi–Jordan Conformal Algebras
- 1.
- Let . Then, the mapis bijective, where is the equivalence class of with respect to ≡.
- 2.
- Let . Then, the mapis bijective, where is the equivalence class of with respect to ≈.
4.2. Applications to Special Cases of Unified Products
4.2.1. Twisted Products of Jacobi–Jordan Conformal Algebras
4.2.2. Crossed Products of Jacobi–Jordan Conformal Algebras
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zusmanovich, P. Special and exceptional mock-Lie algebras. Linear Algebra Appl. 2017, 518, 79–96. [Google Scholar] [CrossRef]
- Zhevlakov, K.A. Solvability and nilpotence of Jordan rings. Algebra Logika 1966, 5, 37–58. (In Russian) [Google Scholar]
- Baklouti, A.; Benayadi, S. Pseudo-Euclidean Jordan Algebras. Comm. Algebra 2015, 43, 2094–2123. [Google Scholar] [CrossRef]
- Baklouti, A.; Benayadi, S. Symplectic Jacobi-Jordan algebras. Linear Multilinear Algebra 2021, 69, 1557–1578. [Google Scholar] [CrossRef]
- Baklouti, A.; Benayadi, S.; Makhlouf, A.; Mansour, S. Jacobi–Jordan-admissible algebras and pre-Jacobi–Jordan algebras. J. Algebra Its Appl. 2025, 24, 2550142. [Google Scholar] [CrossRef]
- Baklouti, A.; Benayadi, S.; Makhlouf, A.; Mansour, S. Cohomology and deformations of Jacobi–Jordan algebras. arXiv 2021, arXiv:2109.12364. [Google Scholar]
- Benali, K.; Chtioui, T.; Hajjaji, A.; Mabrouk, S. Bialgebras, the Yang-Baxter equation and Manin triples for mock-Lie algebras. Acta Comment. Univ. Tartu. Math. 2023, 27. [Google Scholar] [CrossRef]
- Burde, D.; Fialowski, A. Jacobi-Jordan Algebras. Linear Algebra Appl. 2014, 459, 586–594. [Google Scholar] [CrossRef]
- Camacho, L.M.; Kaygorodov, I.; Lopatkin, V.; Salim, M.A. The variety of dual mock-Lie algebras. Comm. in Math. 2020, 28, 161–178. [Google Scholar] [CrossRef]
- Getzler, E.; Kapranov, M. Cyclic operads and cyclic homology. In Geometry, Topology and Physics for Raoul Bott; Yau, S.-T., Ed.; International Press: Vienna, Austria, 1995; pp. 167–201. [Google Scholar]
- Okubo, S.; Kamiya, N. Jordan-Lie super algebra and Jordan-Lie triple system. J. Algebra 1997, 198, 388–411. [Google Scholar] [CrossRef]
- Walcher, S. On algebras of rank three. Comm. Algebra 1999, 27, 3401–3438. [Google Scholar] [CrossRef]
- Wörz-Busekros, A. Bernstein Algebras. Arch. Math. 1987, 48, 388–398. [Google Scholar] [CrossRef]
- Zhevlakov, K.A.; Slinko, A.M.; Shestakov, I.P.; Shirshov, A.I. Rings That Are Nearly Associative; Nauka: Moscow, Russia, 1978. (In Russian). Academic Press: Cambridge, MA, USA, 1982; (English translation). [Google Scholar]
- Belavin, A.A.; Polyakov, A.M.; Zamolodchikov, A.B. Infinite conformal symmetry in two-dimensional quantum field theory. Nucl. Phys. 1984, 241, 333–380. [Google Scholar] [CrossRef]
- Borcherds, R.E. Vertex algebras, Kac-Moody algebras, and the Monster. Proc. Natl. Acad. Sci. USA 1986, 83, 3068–3071. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, I.B.; Lepowsky, J.; Meurman, A. Vertex Operator Algebras and the Monster, Pure and Applied Mathematics; Academic Press: New York, NY, USA, 1998; Volume 134. [Google Scholar]
- Kac, V.G. Vertex Algebras for Beginners, 2nd ed.; University Lecture Series; AMS: Providence, RI, USA, 1996; Volume 10. [Google Scholar]
- D’Andrea, A.; Kac, V. Structure theory of finite conformal algebras. Sel. Math. New Ser. 1998, 4, 377–418. [Google Scholar] [CrossRef]
- Bakalov, B.; D’Andrea, A.; Kac, V.G. Theory of finite pseudoalgebras. Adv. Math. 2001, 162, 1–140. [Google Scholar] [CrossRef]
- Cheng, S.-J.; Kac, V.G. Conformal modules. Asian J. Math. 1997, 1, 181–193, Erratum in Asian J. Math. 1998, 2, 153–156. [Google Scholar] [CrossRef]
- Bakalov, B.; Kac, V.G.; Voronov, A. Cohomology of conformal algebras. Commun. Math. Phys. 1999, 200, 561–598. [Google Scholar] [CrossRef]
- Dolguntseva, I.A. The Hochschild cohomology for associative conformal algebras. Algebra Log. 2007, 46, 373–384. [Google Scholar] [CrossRef]
- Kolesnikov, P.S.; Kozlov, R.A. On the Hochschild cohomologies of associative conformal algebras with a finite faithful representation. Commun. Math. Phys. 2019, 369, 351–370. [Google Scholar] [CrossRef]
- Beilinson, A.A.; Drinfeld, V.G. Chiral algebras. In American Mathematical Society Colloquium Publications; AMS: Providence, RI, USA, 2004; Volume 51. [Google Scholar]
- Boyallian, C.; Kac, V.G.; Liberati, J.I. On the classification of subalgebras of CendN and gcN. J. Algebra 2003, 260, 32–63. [Google Scholar] [CrossRef]
- Boyallian, C.; Kac, V.G.; Liberati, J.I. Finite growth representations of infinite Lie conformal algebras. J. Math. Phys. 2003, 44, 754–770. [Google Scholar] [CrossRef]
- De Sole, A.; Kac, V.G. Subalgebras of gcN and Jacobi polynomials. Canad. Math. Bull. 2002, 45, 567–605. [Google Scholar] [CrossRef]
- Kac, V.G. Formal distribution algebras and conformal algebras. In Proceedings of the XIIth International Congress in Mathematical Physics (ICMP’97), Brisbane, Australia, 13–19 July 1997; International Press: Cambridge, MA, USA, 1999; pp. 80–97. [Google Scholar]
- Retakh, A. Associative conformal algebras of linear growth. J. Algebra 2001, 237, 769–788. [Google Scholar] [CrossRef]
- Retakh, A. On associative conformal algebras of linear growth II. J. Algebra 2006, 304, 543–556. [Google Scholar] [CrossRef]
- Zelmanov, E.I. On the structure of conformal algebras. In Combinatorial and Computational Algebra; Li, W.W., Shum, K.P., Tong, T., Eds.; Contemporary Mathematics, Volume 264; American Mathematical Society: Providence, RI, USA, 2000. [Google Scholar]
- Zelmanov, E.I. Idempotents in conformal algebras. In Proceedings of the Third International Algebra Conference, Tainan, Taiwan, 16 June–1 July 2002; Fong, Y., Shiao, L.-S., Zelmanov, E., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; pp. 257–266. [Google Scholar]
- Kolesnikov, P.S. Associative conformal algebras with finite faithful representation. Adv. Math. 2006, 202, 602–637. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Bai, C.M. On antisymmetric infinitesimal conformal bialgebras. J. Algebra 2021, 586, 325–356. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Bai, C.M. Conformal classical Yang-Baxter equation, S-equation and O-operators. Lett. Math. Phys. 2020, 110, 885–909. [Google Scholar] [CrossRef]
- Hong, Y.Y. Extending structures and classifying complements for left-symmetric algebras. arXiv 2015, arXiv:1511.08571. [Google Scholar] [CrossRef]
- Agore, A.L.; Militaru, G. Extending structures II: The quantum version. J. Algebra 2011, 336, 321–341. [Google Scholar] [CrossRef]
- Agore, A.L.; Militaru, G. Extending structures I: The level of groups. Algebr. Represent Theory 2014, 17, 831–848. [Google Scholar] [CrossRef]
- Agore, A.L.; Militaru, G. Extending structures for Lie algebras. Monatsh. Math. 2014, 174, 169–193. [Google Scholar] [CrossRef]
- Agore, A.L.; Militaru, G. On a type of commutative algebras. Linear Algebra Appl. 2015, 485, 222–249. [Google Scholar] [CrossRef]
- Agore, A.L.; Militaru, G. Extending Structures. Fundamentals and Applications; Monographs and Research Notes in Mathematics; Taylor and Francis Group: Abingdon, UK, 2019; 224p. [Google Scholar]
- Hong, Y.Y. Extending structures for associative conformal algebras. Linear Multilinear Algebra 2019, 67, 196–212. [Google Scholar] [CrossRef]
- Hong, Y.Y. Extending structures for Lie conformal algebras. Algebr. Represent. Theory 2017, 20, 209–230. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chtioui, T.; Mabrouk, S.; Makhlouf, A. Jacobi–Jordan Conformal Algebras: Basics, Constructions and Related Structures. Mathematics 2025, 13, 843. https://doi.org/10.3390/math13050843
Chtioui T, Mabrouk S, Makhlouf A. Jacobi–Jordan Conformal Algebras: Basics, Constructions and Related Structures. Mathematics. 2025; 13(5):843. https://doi.org/10.3390/math13050843
Chicago/Turabian StyleChtioui, Taoufik, Sami Mabrouk, and Abdenacer Makhlouf. 2025. "Jacobi–Jordan Conformal Algebras: Basics, Constructions and Related Structures" Mathematics 13, no. 5: 843. https://doi.org/10.3390/math13050843
APA StyleChtioui, T., Mabrouk, S., & Makhlouf, A. (2025). Jacobi–Jordan Conformal Algebras: Basics, Constructions and Related Structures. Mathematics, 13(5), 843. https://doi.org/10.3390/math13050843






