Enhancing Unmanned Aerial Vehicle Object Detection via Tensor Decompositions and Positive–Negative Momentum Optimizers
Abstract
1. Introduction
1.1. Motivation
1.2. Our Contribution
2. State of the Art
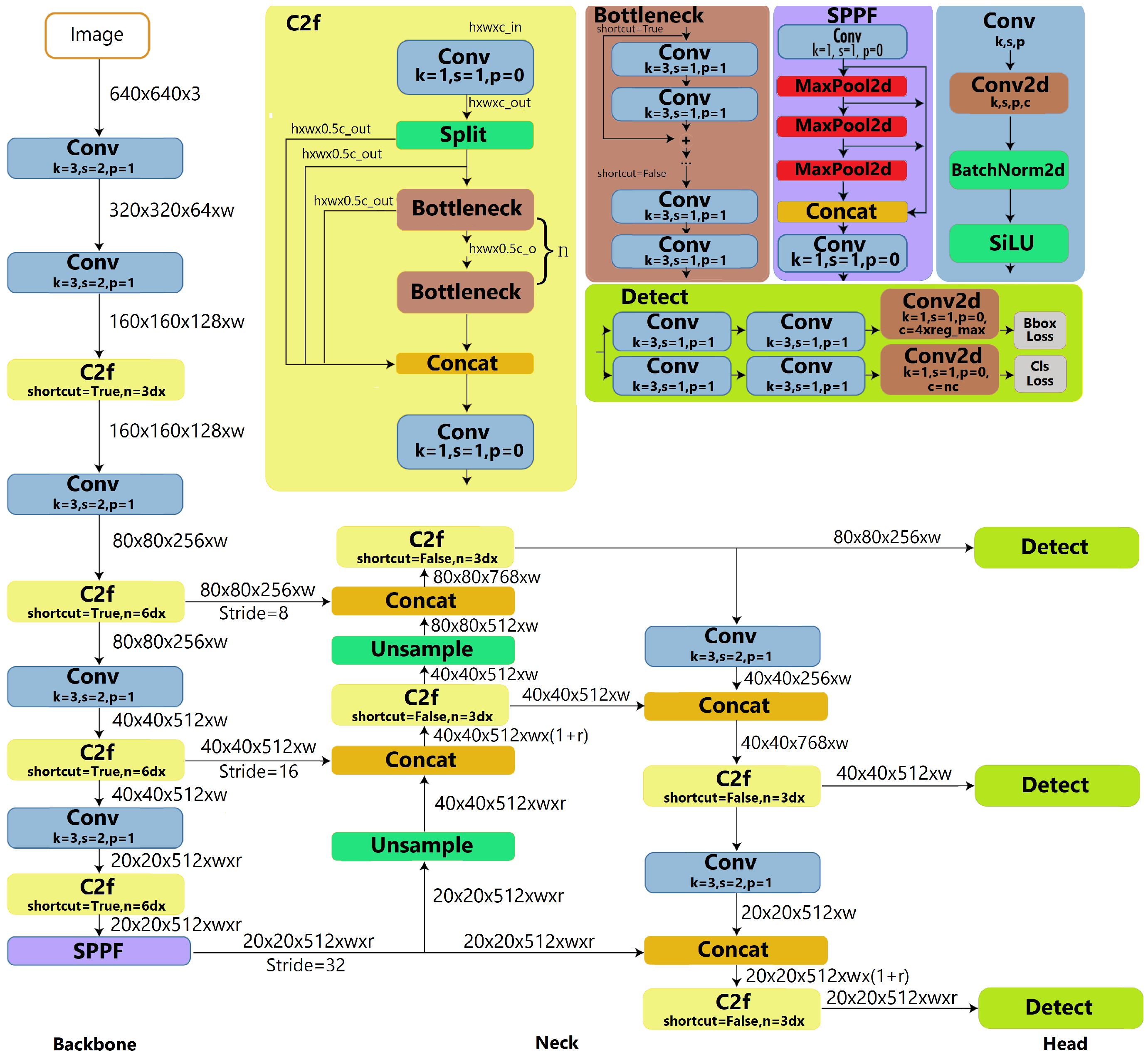
2.1. Yolov8 Architecture
2.2. Tensor Decompositions
2.3. Optimization Algorithms
3. Proposed Yolov8-CP-Astrid and Yolov8-Tucker-2 Neural Networks
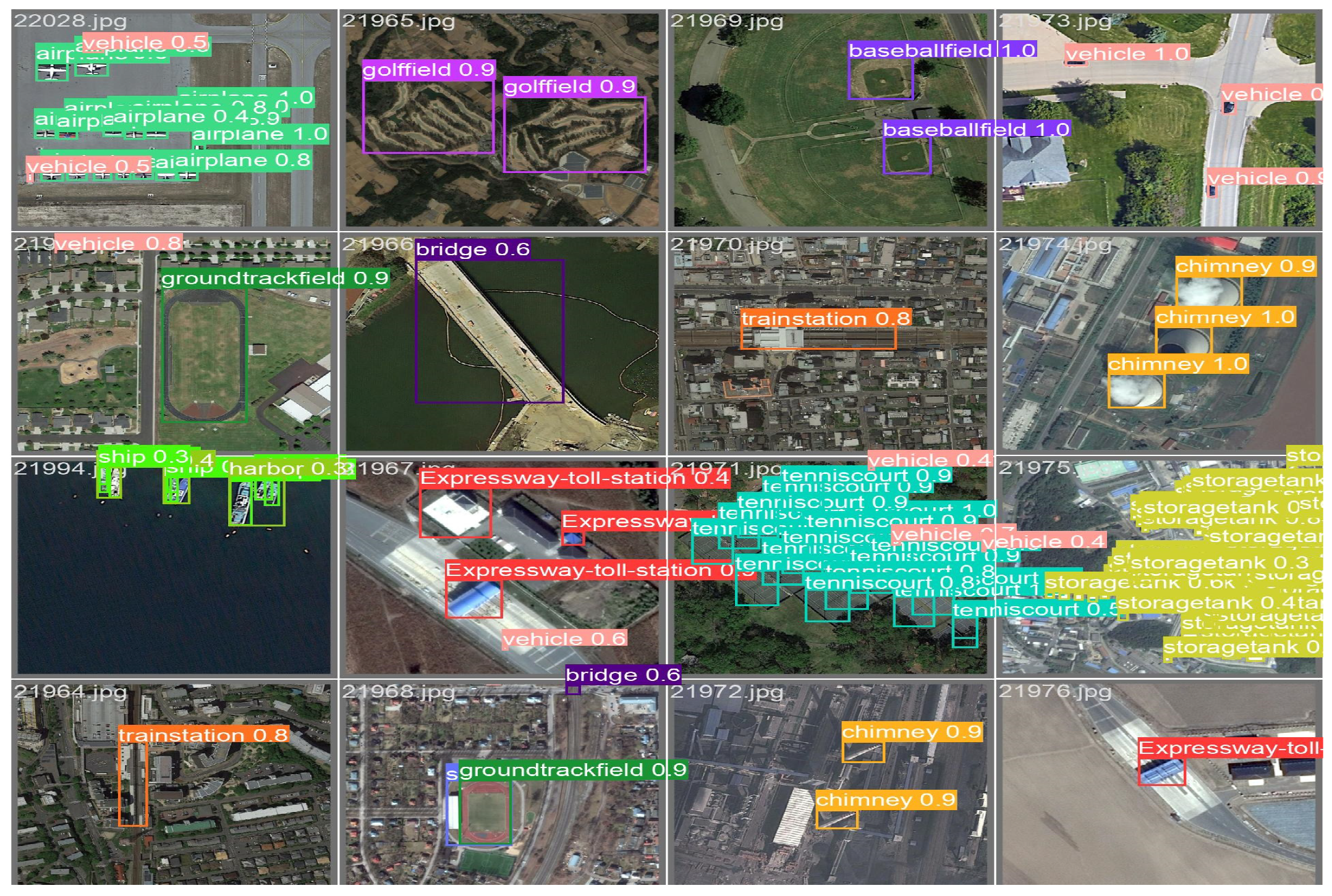
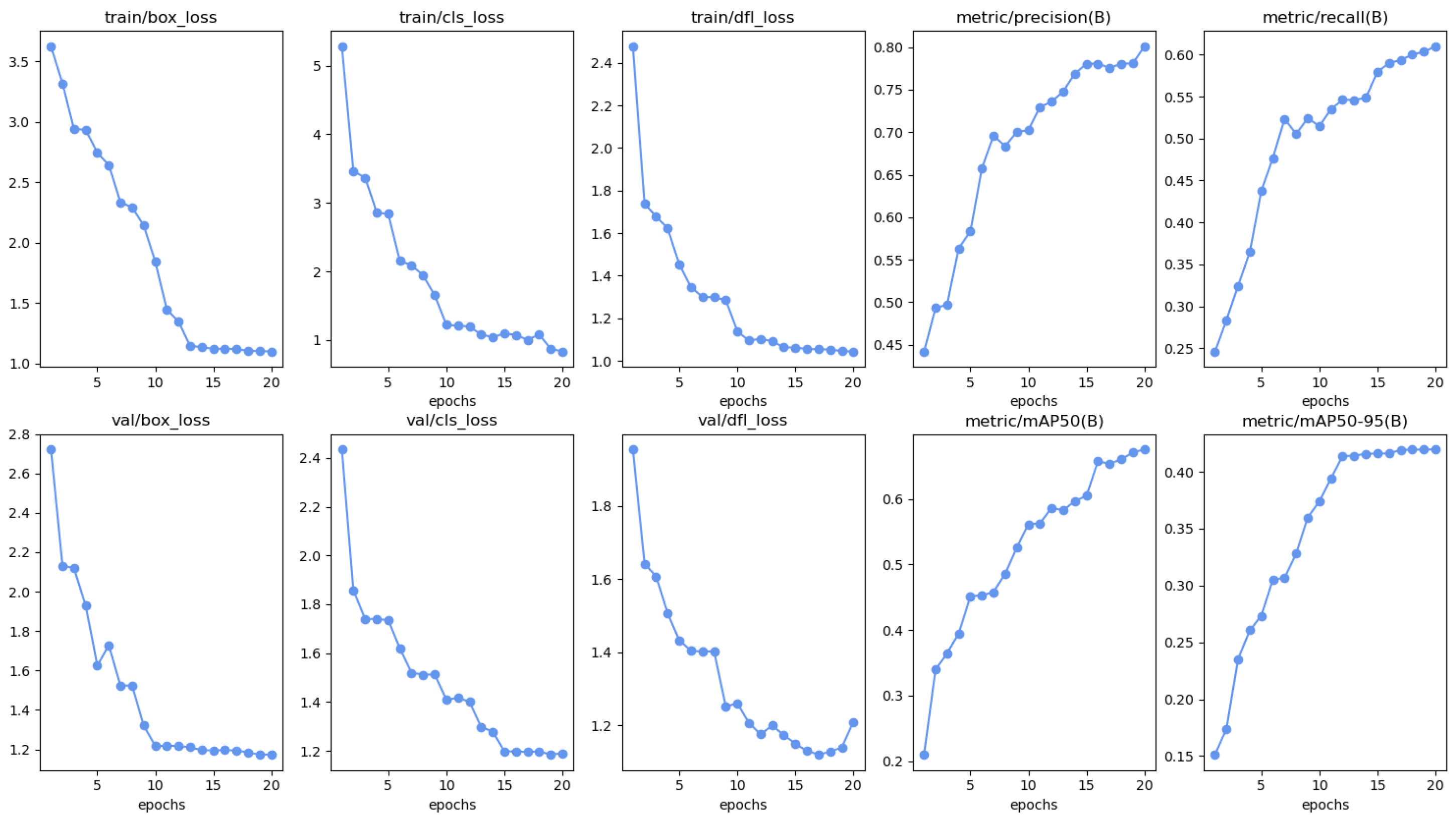
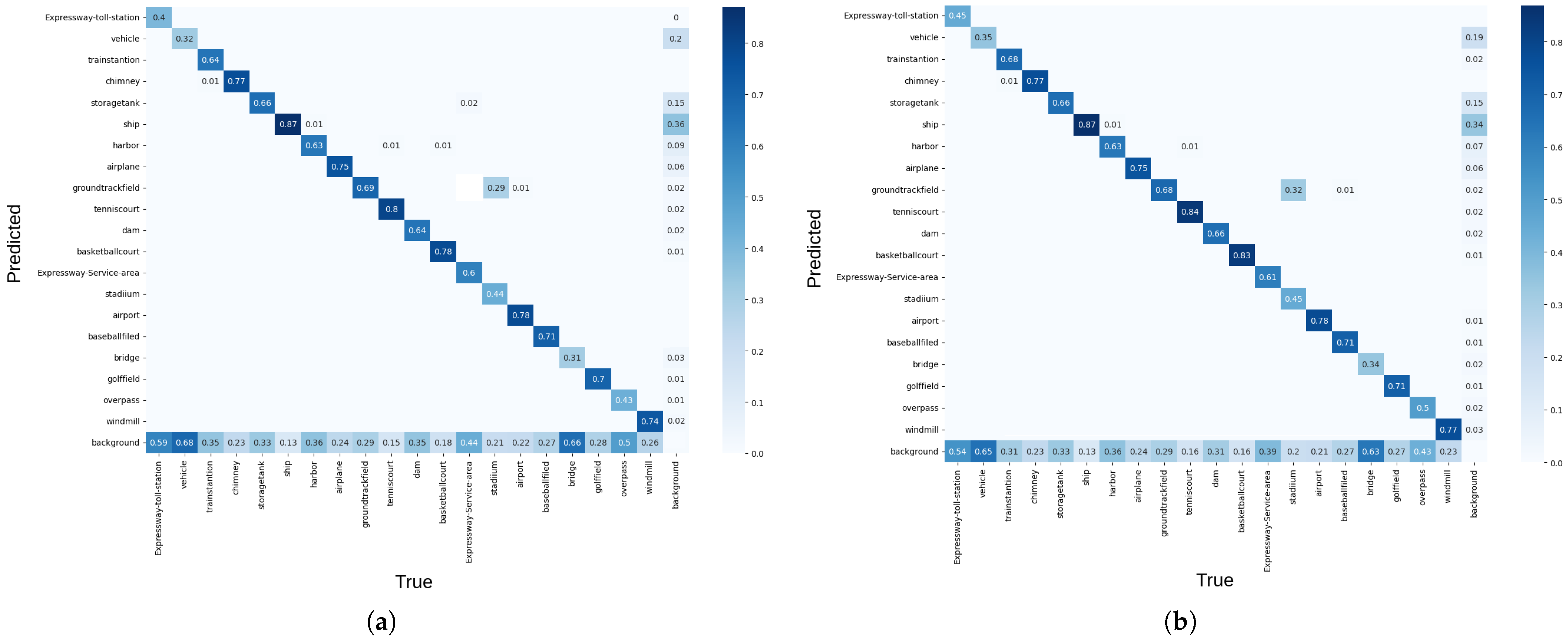
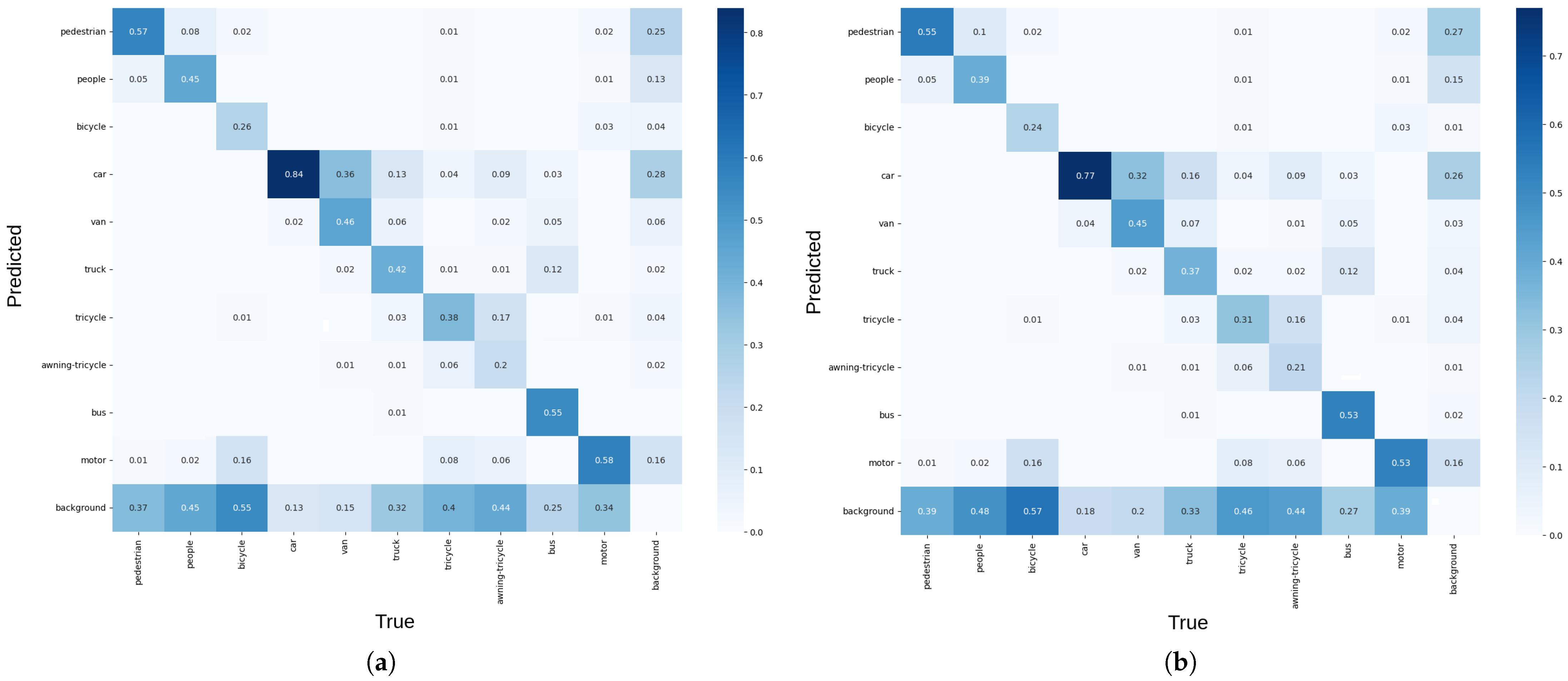
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tzeng, Y.C.; Chen, K.S.; Kao, W.-L.; Fung, A.K. A dynamic learning neural network for remote sensing applications. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1096–1102. [Google Scholar] [CrossRef]
- Xia, N.; Cheng, L.; Li, M. Mapping Urban Areas Using a Combination of Remote Sensing and Geolocation Data. Remote Sens. 2019, 11, 1470. [Google Scholar] [CrossRef]
- Li, A.S.; Chirayath, V.; Segal-Rozenhaimer, M.; Torres-Pérez, J.L.; van den Bergh, J. NASA NeMO-Net’s Convolutional Neural Network: Mapping Marine Habitats with Spectrally Heterogeneous Remote Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5115–5133. [Google Scholar] [CrossRef]
- Wu, C.; Lou, Y.; Wang, L.; Li, J.; Li, X.; Chen, G. SPP-CNN: An Efficient Framework for Network Robustness Prediction. IEEE Trans. Circuits Syst. I 2023, 70, 4067–4079. [Google Scholar] [CrossRef]
- Adla, D.; Reddy, G.V.R.; Nayak, P.; Karuna, G. A full-resolution convolutional network with a dynamic graph cut algorithm for skin cancer classification and detection. Healthc. Anal. 2023, 3, 100154. [Google Scholar] [CrossRef]
- Li, Y.; Fan, Q.; Huang, H.; Han, Z.; Gu, Q. A Modified YOLOv8 Detection Network for UAV Aerial Image Recognition. Drones 2023, 7, 304. [Google Scholar] [CrossRef]
- Bagherzadeh, S.A.; Asadi, D. Detection of the ice assertion on aircraft using empirical mode decomposition enhanced by multi-objective optimization. Mech. Syst. Signal Process. 2017, 88, 9–24. [Google Scholar] [CrossRef]
- Gawlikowski, J.; Tassi, C.R.N.; Ali, M.; Lee, J.; Humt, M.; Feng, J.; Kruspe, A.; Triebel, R.; Jung, P.; Roscher, R.; et al. A survey of uncertainty in deep neural networks. Artif. Intell. Rev. 2023, 56, 1513–1589. [Google Scholar] [CrossRef]
- Marinó, G.C.; Petrini, A.; Malchiodi, D.; Frasca, D. Deep neural networks compression: A comparative survey and choice recommendations. Neurocomputing 2023, 520, 152–170. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, M.; Shi, J.Q. A Survey on Deep Neural Network Pruning: Taxonomy, Comparison, Analysis, and Recommendations. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 10558–10578. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, D.; Wang, L. Convolution Accelerator Designs Using Fast Algorithms. Algorithms 2019, 12, 112. [Google Scholar] [CrossRef]
- Ozaki, K.; Ogita, T.; Oishi, S.I.; Rump, S.M. Error-free transformations of matrix multiplication by using fast routines of matrix multiplication and its applications. Numer. Algorithms 2012, 59, 95–118. [Google Scholar] [CrossRef]
- Wu, Q.; Jiang, Z.; Hong, K.; Liu, H.; Yang, L.T.; Ding, J. Tensor-Based Recurrent Neural Network and Multi-Modal Prediction with Its Applications in Traffic Network Management. IEEE Trans. Netw. Serv. Manag. 2021, 18, 780–792. [Google Scholar] [CrossRef]
- Giraud, M.; Itier, V.; Boyer, R.; Zniyed, Y.; de Almeida, A.L. Tucker Decomposition Based on a Tensor Train of Coupled and Constrained CP Cores. IEEE Signal Process. Lett. 2023, 30, 758–762. [Google Scholar] [CrossRef]
- Abdulkadirov, R.; Lyakhov, P.; Bergerman, M.; Reznikov, D. Satellite image recognition using ensemble neural networks and difference gradient positive-negative momentum. Chaos Solitons Fractals 2024, 179, 114432. [Google Scholar] [CrossRef]
- Lyakhov, P.A.; Lyakhova, U.A.; Abdulkadirov, R.I. Non-convex optimization with using positive-negative moment estimation and its application for skin cancer recognition with a neural network. Comput. Opt. 2024, 48, 260–271. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, Q.; Li, X.; Liu, J. A Survey on Tensor Techniques and Applications in Machine Learning. IEEE Access 2019, 7, 162950–162990. [Google Scholar] [CrossRef]
- Boizard, M.; Boyer, R.; Favier, G.; Cohen, J.E.; Comon, P. Performance estimation for tensor CP decomposition with structured factors. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 3482–3486. [Google Scholar]
- Jang, J.-G.; Kang, U. D-Tucker: Fast and Memory-Efficient Tucker Decomposition for Dense Tensors. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 1850–1853. [Google Scholar]
- Gabor, M.; Zdunek, R. Compressing convolutional neural networks with hierarchical Tucker-2 decomposition. Appl. Soft Comput. 2023, 132, 109856. [Google Scholar] [CrossRef]
- Oseledets, I.V. Tensor-train decomposition. SIAM J. Sci. Comput. 2011, 33, 2295–2317. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Singh, N.; Data, D.; George, J.; Diggavi, S. SQuARM-SGD: Communication-Efficient Momentum SGD for Decentralized Optimization. IEEE J. Sel. Areas Inf. Theory 2021, 2, 954–969. [Google Scholar] [CrossRef]
- Astrid, M.; Lee, S.-I.; Seo, B.-S. Rank selection of CP-decomposed convolutional layers with variational Bayesian matrix factorization. In Proceedings of the 2018 20th International Conference on Advanced Communication Technology (ICACT), Chuncheon, Republic of Korea, 11–14 February 2018; pp. 347–350. [Google Scholar]
- Han, Y.; Lin, Q.H.; Kuang, L.D.; Gong, X.F.; Cong, F.; Wang, Y.P.; Calhoun, V.D. Low-Rank Tucker-2 Model for Multi-Subject fMRI Data Decomposition with Spatial Sparsity Constraint. IEEE Trans. Med. Imaging 2022, 41, 667–679. [Google Scholar] [CrossRef] [PubMed]
- Phan, A.-H.; Sobolev, K.; Sozykin, K.; Ermilov, D.; Gusak, J.; Tichavskỳ, P.; Glukhov, V.; Oseledets, I.; Cichocki, A. Stable low-rank tensor decomposition for compression of convolutional neural network. Lect. Notes Comput. Sci. 2020, 12374, 522–539. [Google Scholar]
- Lebedev, V.; Ganin, Y.; Rakhuba, M.; Oseledets, I.; Lempitsky, V. Speeding up convolutional neural networks using fine-tuned cp-decomposition. arXiv 2024, arXiv:1412.6553. [Google Scholar]
- Kossaifi, J.; Panagakis, Y.; Anandkumar, A.; Pantic, M. TensorLy: Tensor Learning in Python. J. Mach. Learn. Res. 2019, 20, 1–6. [Google Scholar]
- Wang, H.; Jiang, H.; Sun, J.; Zhang, S.; Chen, C.; Hua, X.S.; Luo, X. DIOR: Learning to Hash with Label Noise via Dual Partition and Contrastive Learning. IEEE Trans. Knowl. Data Eng. 2024, 36, 1502–1517. [Google Scholar] [CrossRef]
- Sharifuzzaman, S.A.S.M.; Tanveer, J.; Chen, Y.; Chan, J.H.; Kim, H.S.; Kallu, K.D.; Ahmed, S. Bayes R-CNN: An Uncertainty-Aware Bayesian Approach to Object Detection in Remote Sensing Imagery for Enhanced Scene Interpretation. Remote Sens. 2024, 16, 2405. [Google Scholar] [CrossRef]
- Sagar, A.S.; Chen, Y.; Xie, Y.; Kim, H.S. MSA R-CNN: A comprehensive approach to remote sensing object detection and scene understanding. Expert Syst. Appl. 2024, 241, 122788. [Google Scholar] [CrossRef]
- Ye, Y.; Ren, X.; Zhu, B.; Tang, T.; Tan, X.; Gui, Y.; Yao, Q. An Adaptive Attention Fusion Mechanism Convolutional Network for Object Detection in Remote Sensing Images. Remote Sens. 2022, 14, 516. [Google Scholar] [CrossRef]
- Zhan, W.; Sun, C.; Wang, M.; She, J.; Zhang, Y.; Zhang, Z.; Sun, Y. An improved Yolov5 real-time detection method for small objects captured by UAV. Soft Comput. 2022, 26, 361–373. [Google Scholar] [CrossRef]
- Alhawsawi, A.N.; Khan, S.D.; Rehman, F.U. Enhanced YOLOv8-Based Model with Context Enrichment Module for Crowd Counting in Complex Drone Imagery. Remote Sens. 2024, 16, 4175. [Google Scholar] [CrossRef]
- Li, H.; Huang, Y.; Zhang, Z. An Improved Faster R-CNN for Same Object Retrieval. IEEE Access 2017, 5, 13665–13676. [Google Scholar] [CrossRef]
- Chen, S.; Miao, Z.; Chen, H.; Mukherjee, M.; Zhang, Y. Point-attention Net: A graph attention convolution network for point cloudsegmentation. Appl. Intell. 2023, 53, 11344–11356. [Google Scholar] [CrossRef]
- Yang, C.; Kong, X.; Cao, Z.; Peng, Z. Cirrus Detection Based on Tensor Multi-Mode Expansion Sum Nuclear Norm in Infrared Imagery. IEEE Access 2020, 8, 149963–149983. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, J.; Long, Y.; Shang, Z.; An, Z. Infrared Patch-Tensor Model with Weighted Tensor Nuclear Norm for Small Target Detection in a Single Frame. IEEE Access 2018, 6, 76140–76152. [Google Scholar] [CrossRef]
- Zhong, Z.; Wei, F.; Lin, Z.; Zhang, C. ADA-Tucker: Compressing deep neural networks via adaptive dimension adjustment tucker decomposition. Neural Netw. 2019, 110, 104–115. [Google Scholar] [CrossRef] [PubMed]
- Denton, E.L.; Zaremba, W.; Bruna, J.; Cun, Y.L.; Fergus, R. Exploiting linear structure within convolutional networks for efficient evaluation. In Proceedings of the NIPS’14: Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1269–1277. [Google Scholar]
- Shin, Y.; Darbon, J.; Karniadakis, G.E. Accelerating gradient descent and Adam via fractional gradients. Neural Netw. 2023, 161, 185–201. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, F. An Elementary Introduction to Information Geometry. Entropy 2020, 22, 1100. [Google Scholar] [CrossRef]
- Abdulkadirov, R.; Lyakhov, P.; Nagornov, N. Survey of Optimization Algorithms in Modern Neural Networks. Mathematics 2023, 11, 2466. [Google Scholar] [CrossRef]
- Hussain, K.; Mohd Salleh, M.N.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar]
- Teodoro, G.S.; Machado, J.A.T.; De Oliveira, E.C. A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 2019, 388, 195–208. [Google Scholar] [CrossRef]
- Mohapatra, R.; Saha, S.; Coello, C.A.C.; Bhattacharya, A.; Dhavala, S.S.; Saha, S. AdaSwarm: Augmenting Gradient-Based Optimizers in Deep Learning with Swarm Intelligence. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 6, 329–340. [Google Scholar] [CrossRef]
- Martens, J. New insights and perspectives on the natural gradient method. J. Mach. Learn. Res. 2020, 21, 5776–5851. [Google Scholar]
- Azizan, N.; Lale, S.; Hassibi, B. Stochastic Mirror Descent on Overparameterized Nonlinear Models. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7717–7727. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.Y.; Broughton, M.; Mohseni, M.; Babbush, R.; Boixo, S.; Neven, H.; McClean, J.R. Power of data in quantum machine learning. Nat. Commun. 2021, 12, 2631. [Google Scholar] [CrossRef]

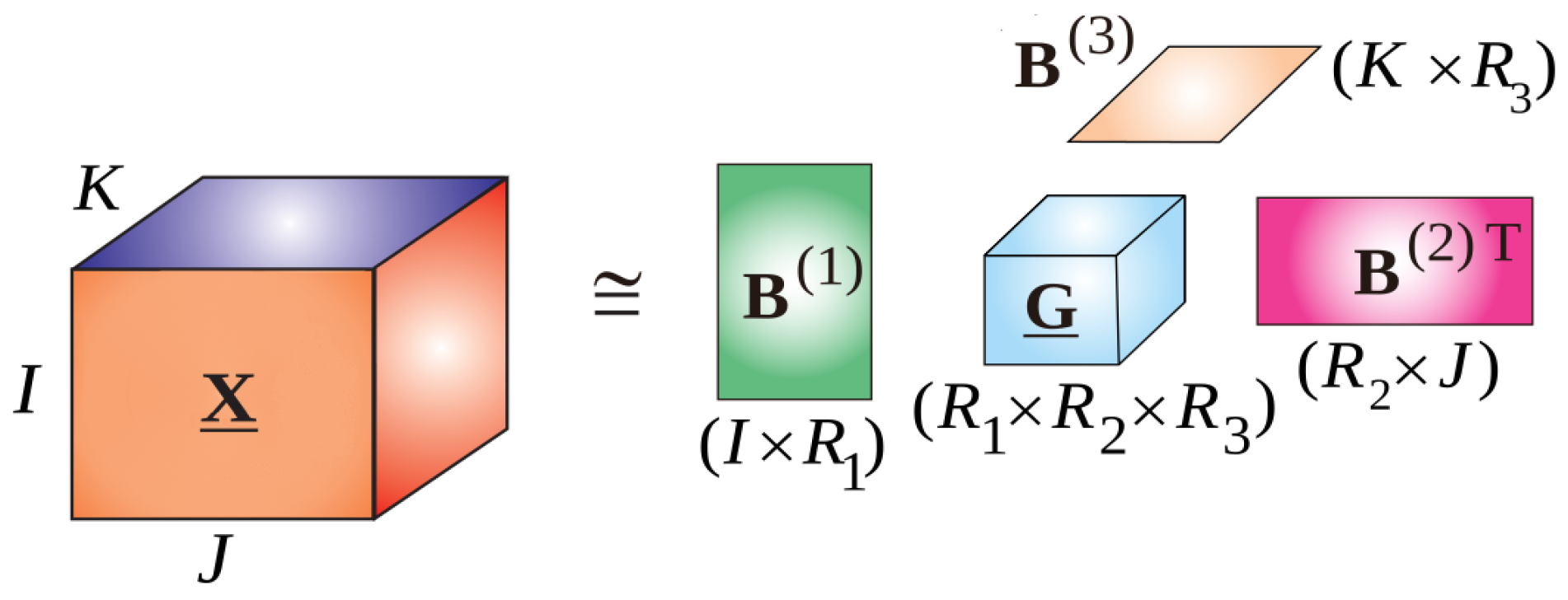










| Decomposition | Computational Complexity | References |
|---|---|---|
| Full Tensor Format | - | |
| Canonical Polyadic | [18] | |
| Tucker | [19] | |
| Hierarchical Tucker | [20] | |
| Tensor Train | [21] |
| Layer Factorization | Computational Complexity | References |
|---|---|---|
| Full convolution | - | |
| CP-Astrid | [24] | |
| CP-Lebedev | [26] | |
| Tucker-2 | [25] | |
| Tucker-2-CP | [27] |
| Neural Network | Optimizer | Box Loss | Cls Loss | Dfl Loss | P (%) | R (%) | Time (s) | FPS |
|---|---|---|---|---|---|---|---|---|
| Yolov8n | SGD | 1.34 | 0.721 | 1.167 | 81.945 | 59.774 | 24,119.94 | 69.98 |
| Adam | 1.131 | 0.743 | 1.033 | 82.045 | 60.653 | 24,177.19 | 70.14 | |
| DiffGrad | 0.978 | 0.611 | 0.992 | 84.586 | 62.109 | 24,273.14 | 71.32 | |
| Yogi | 0.984 | 0.640 | 0.986 | 84.416 | 61.025 | 24,192.47 | 71.65 | |
| DiffPNM | 0.894 | 0.428 | 0.930 | 86.305 | 63.841 | 24301.57 | 72.57 | |
| YogiPNM | 0.917 | 0.455 | 0.914 | 86.26 | 63.517 | 24,283.95 | 72.32 | |
| PNMBelief | 0.934 | 0.520 | 0.946 | 86.111 | 63.299 | 24,503.03 | 72.14 | |
| Proposed | SGD | 2.893 | 1.523 | 1.922 | 73.108 | 55.489 | 11,464.56 | 61.64 |
| Adam | 2.344 | 1.128 | 1.455 | 79.463 | 58.041 | 11,523.63 | 62.46 | |
| DiffGrad | 1.455 | 1.161 | 1.385 | 81.402 | 59.144 | 11,554.03 | 62.88 | |
| Yogi | 1.573 | 1.294 | 1.422 | 81.318 | 59.097 | 11,537.84 | 62.72 | |
| Yolov8n-CP-Astrid | DiffPNM | 1.254 | 0.946 | 1.188 | 81.593 | 59.704 | 11540.17 | 63.32 |
| YogiPNM | 1.017 | 1.005 | 1.225 | 82.050 | 60.109 | 11,501.01 | 63.58 | |
| PNMBelief | 1.308 | 1.120 | 1.427 | 81.356 | 59.110 | 11,576.46 | 63.19 | |
| Proposed | SGD | 2.485 | 1.382 | 1.603 | 74.581 | 58.853 | 13,442.75 | 64.27 |
| Adam | 2.144 | 1.176 | 1.367 | 81.833 | 59.647 | 13,849.85 | 65.11 | |
| DiffGrad | 1.346 | 0.870 | 1.184 | 82.113 | 60.309 | 13,884.55 | 65.73 | |
| Yogi | 1.372 | 0.845 | 1.150 | 82.124 | 60.428 | 138,762.30 | 65.79 | |
| Yolov8n-Tucker-2 | DiffPNM | 1.099 | 0.814 | 1.040 | 82.885 | 60.881 | 14,510.85 | 66.12 |
| YogiPNM | 1.142 | 0.895 | 0.998 | 82.843 | 60.811 | 14,399.25 | 65.92 | |
| PNMBelief | 1.224 | 1.104 | 1.209 | 82.045 | 60.292 | 14,737.85 | 65.84 |
| Neural Network | Optimizer | Box Loss | Cls Loss | Dfl Loss | P (%) | R (%) | Time (s) | FPS |
|---|---|---|---|---|---|---|---|---|
| Yolov8n | SGD | 1.433 | 0.964 | 1.309 | 77.753 | 28.192 | 9433.42 | 63.19 |
| Adam | 1.295 | 0.922 | 1.214 | 78.603 | 29.348 | 9511.09 | 65.39 | |
| DiffGrad | 1.243 | 0.912 | 1.224 | 79.053 | 29.614 | 9589.48 | 66.42 | |
| Yogi | 1.250 | 0.918 | 1.217 | 78.044 | 29.582 | 9514.60 | 65.70 | |
| DiffPNM | 1.084 | 0.844 | 1.159 | 79.372 | 30.198 | 9610.80 | 68.23 | |
| YogiPNM | 1.126 | 0.884 | 1.190 | 79.344 | 30.084 | 9583.48 | 68.14 | |
| PNMBelief | 1.224 | 0.901 | 1.231 | 79.162 | 29.842 | 9587.94 | 67.64 | |
| Proposed | SGD | 2.593 | 1.782 | 1.997 | 71.249 | 24.814 | 5806.05 | 55.14 |
| Adam | 2.665 | 1.857 | 2.045 | 71.040 | 24.576 | 5842.63 | 56.05 | |
| DiffGrad | 2.375 | 1.686 | 1.863 | 71.704 | 25.430 | 5865.94 | 56.47 | |
| Yogi | 2.349 | 1.634 | 1.799 | 71.859 | 25.900 | 5851.10 | 56.55 | |
| Yolov8n-CP-Astrid | DiffPNM | 2.074 | 1.576 | 1.704 | 72.571 | 26.463 | 5894.03 | 57.74 |
| YogiPNM | 2.099 | 1.621 | 1.750 | 72.493 | 26.395 | 5884.74 | 57.10 | |
| PNMBelief | 2.154 | 1.690 | 1.803 | 72.111 | 26.245 | 5896.48 | 56.83 | |
| Proposed | SGD | 2.328 | 1.652 | 1.740 | 73.746 | 26.704 | 6078.64 | 57.78 |
| Adam | 2.362 | 1.670 | 1.748 | 73.583 | 26.585 | 6104.55 | 58.84 | |
| DiffGrad | 2.075 | 1.582 | 1.689 | 73.815 | 27.020 | 6154.81 | 59.53 | |
| Yogi | 2.136 | 1.648 | 1.703 | 73.784 | 26.913 | 6131.66 | 59.42 | |
| Yolov8n-Tucker-2 | DiffPNM | 1.928 | 1.594 | 1.644 | 74.306 | 27.822 | 6224.34 | 60.75 |
| YogiPNM | 1.894 | 1.570 | 1.625 | 74.788 | 27.914 | 6166.30 | 60.32 | |
| PNMBelief | 1.983 | 1.609 | 1.651 | 74.156 | 27.417 | 6189.94 | 60.30 |
| Neural Network | Key Idea | Year |
|---|---|---|
| R-CNN [35] | Region-based object segmentation | 2017 |
| AttentionNet [36] | Quantized weak directions, | 2017 |
| ensemble of iterative predictions | ||
| TMESNN [37] | Tensor multi-mode | 2018 |
| expansion sum nuclear norm | ||
| Yolov8 [6] | Backbone, neck, and head blocks | 2023 |
| IPTM [38] | Infrared patch-tensor model | 2024 |
| with Tensor multi-mode | ||
| expansion sum nuclear norm | ||
| Proposed Yolov8-CP-Astrid | CP-Astrid decomposition of | 2024 |
| backbone, neck, and head blocks | ||
| Proposed Yolov8-Tucker-2 | Tucker-2 decomposition of | 2024 |
| backbone, neck, and head blocks |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulkadirov, R.; Lyakhov, P.; Butusov, D.; Nagornov, N.; Reznikov, D.; Bobrov, A.; Kalita, D. Enhancing Unmanned Aerial Vehicle Object Detection via Tensor Decompositions and Positive–Negative Momentum Optimizers. Mathematics 2025, 13, 828. https://doi.org/10.3390/math13050828
Abdulkadirov R, Lyakhov P, Butusov D, Nagornov N, Reznikov D, Bobrov A, Kalita D. Enhancing Unmanned Aerial Vehicle Object Detection via Tensor Decompositions and Positive–Negative Momentum Optimizers. Mathematics. 2025; 13(5):828. https://doi.org/10.3390/math13050828
Chicago/Turabian StyleAbdulkadirov, Ruslan, Pavel Lyakhov, Denis Butusov, Nikolay Nagornov, Dmitry Reznikov, Anatoly Bobrov, and Diana Kalita. 2025. "Enhancing Unmanned Aerial Vehicle Object Detection via Tensor Decompositions and Positive–Negative Momentum Optimizers" Mathematics 13, no. 5: 828. https://doi.org/10.3390/math13050828
APA StyleAbdulkadirov, R., Lyakhov, P., Butusov, D., Nagornov, N., Reznikov, D., Bobrov, A., & Kalita, D. (2025). Enhancing Unmanned Aerial Vehicle Object Detection via Tensor Decompositions and Positive–Negative Momentum Optimizers. Mathematics, 13(5), 828. https://doi.org/10.3390/math13050828










