Abstract
The widespread use of mobile devices has led to the continuous collection of vast amounts of user-generated data, supporting data-driven decisions across a variety of fields. However, the growing volume of these data raises significant privacy concerns, especially when they include personal information vulnerable to misuse. Differential privacy (DP) has emerged as a prominent solution to these concerns, enabling the collection of user-generated data for data-driven decision-making while protecting user privacy. Despite their strengths, existing DP-based data collection frameworks are often faced with a trade-off between the utility of the data and the computational overhead. To address these challenges, we propose the differentially private fractional coverage model (DPFCM), a DP-based framework that adaptively balances data utility and computational overhead according to the requirements of data-driven decisions. DPFCM introduces two parameters, α and β, which control the fractions of collected data elements and user data, respectively, to ensure both data diversity and representative user coverage. In addition, we propose two probability-based methods for effectively determining the minimum data each user should provide to satisfy the DPFCM requirements. Experimental results on real-world datasets validate the effectiveness of DPFCM, demonstrating its high data utility and computational efficiency, especially for applications requiring real-time decision-making.
MSC:
68P27
1. Introduction
The widespread use of mobile devices has led to the continuous generation and collection of a vast amount of diverse data. When such user-generated data are collected, they can be used to make data-driven decisions across a wide range of applications. These data enable improved decision-making processes, allowing systems to respond to real-time information and improve services in a variety of areas, including transportation, healthcare, retail, and urban planning [1,2,3,4]. For example, in transportation, real-time data from users allow digital map applications to monitor traffic patterns and suggest alternative routes [5]. In healthcare, wearable devices collect data on users’ physical activity, heart rate, and other health metrics [6]. Healthcare providers then use this information to remotely monitor patients and make personalized recommendations. This approach promotes preventive care, ultimately leading to better patient outcomes and a more responsive healthcare system.
As the collection of data from users has become more prevalent, concerns about data privacy have increased. Including sensitive information in these datasets increases the risk of privacy breaches, as unauthorized access or misuse can have serious consequences for individuals [7,8]. In response to these challenges, significant efforts have been made to protect user privacy through various techniques. Among these, differential privacy (DP) [9] has emerged as a leading standard. DP adds controlled noise to real datasets, allowing analysts to derive insights without exposing individual data points, thereby protecting personal information.
There are two primary frameworks for collecting sensitive data from users using DP: local differential privacy (LDP) [10,11] and distributed differential privacy (DDP) [12,13]. Both frameworks are designed to operate in environments with untrusted servers, adding noise to the data locally, before they are transmitted to a central server. This approach protects individual privacy by ensuring that the raw data are never directly exposed. LDP has the advantage of relatively low computational overhead; however, the added noise can result in significant data distortion, which can reduce the utility of the collected data. In contrast, DDP provides greater data utility but requires significantly more computational resources, largely due to the use of complex cryptographic techniques.
The utility requirements of collected data vary significantly based on the specific objectives and operational needs of each application. Some applications require highly accurate, comprehensive datasets for accurate analysis and reliable results. For these applications, data completeness is critical to delivering results that satisfy strict performance criteria. In contrast, other applications are more flexible in their data needs, capable of extracting meaningful insights even from partial or incomplete datasets. For these applications, identifying general patterns or trends in real-time is often more important than perfect accuracy, allowing them to perform effectively even with incomplete data.
This variability in utility requirements plays a crucial role in the design of data collection and privacy mechanisms. Applications that do not require exhaustive datasets can benefit from approaches that emphasize efficiency over complete data collection. Motivated by this need, we propose a novel DP-based data collection framework that exploits the adequacy of partial data collection for certain applications, particularly those that require efficiency for real-time decision-making. In particular, the contribution of this paper can be summarized as follows:
- We introduce the differentially private fractional coverage model (DPFCM), which is designed to meet the needs of applications that can operate effectively with partial data collection. DPFCM specifies two parameters, and , which are determined by the specific purpose of the application. -DPFCM aims to collect at least a fraction of the total data elements, with the requirement that for each of these collected elements, data are also collected from at least a fraction of the users. This method guarantees that both the breadth of data elements and the depth of user representation are maintained, supporting robust data utility even when only partial data are collected.
- We propose two different probability-based approaches that effectively determine the minimum number of data elements the server should collect from each user to satisfy the requirements of an -DPFCM. These approaches establish precise lower bounds on data collection, ensuring that the utility requirements of the model are satisfied while optimizing for efficiency.
- Finally, we validate the effectiveness of our proposed framework through experiments on real-world datasets, demonstrating that DPFCM achieves high data utility with reduced data collection requirements. Our results show that DPFCM maintains high data utility and computational efficiency, confirming its practical value in real-world applications.
The rest of this paper is structured as follows: Section 2 reviews the related work, and Section 3 presents the necessary background information. Section 4 formally defines the problem addressed in this paper and discusses existing approaches. Section 5 details the proposed -DPFCM framework. Section 6 evaluates the proposed approach through experiments conducted on real-world datasets and Section 7 presents the conclusions of the paper.
2. Related Work
DP has been widely used to protect sensitive data in various data collection scenarios. One of the most representative models is LDP, in which each user independently perturbs his or her data prior to transmission. Depending on the type of sensitive data being collected, existing LDP mechanisms can be broadly divided into two groups: methods designed for categorical data and those tailored for numerical data. For categorical data, the randomized response technique is often used to ensure privacy while allowing accurate frequency estimation. RAPPOR [10] was developed to collect user data, such as the default home page of their browser, in Google Chrome while maintaining privacy. The frequency estimation scheme proposed by Bassily and Smith [14] builds on randomized response techniques, optimizing communication efficiency by encoding user responses into a compact bit representation before transmission. Optimal local hashing [11] further improves frequency estimation under LDP by using a hash-based encoding scheme. For numerical data, various perturbation mechanisms, including Laplace, Gaussian, and staircase noise, are commonly used. Among them, the staircase mechanism [15] is recognized as an optimal noise-adding method, achieving lower expected error than the Laplace mechanism in specific scenarios. Although LDP ensures privacy by adding noise at the user level, it often results in significant utility loss due to the high noise required to meet privacy guarantees.
DDP-based data collection is primarily categorized into two main approaches. The first category integrates DP with secure aggregation to enable privacy-preserving data collection in distributed environments [12,13]. Early works in this category focused on secure data collection in distributed systems. For instance, Lyu et al. [16] applied DP with secure aggregation to collect smart grid data in a fog computing architecture. More recently, this approach has received considerable attention in federated learning, where DP is used to protect local model updates prior to aggregation [17]. Truex et al. [18] leveraged homomorphic encryption alongside DP to securely collect local learning parameters from participating users in federated learning. Much of the research in this area has been dedicated to improving scalability and computational efficiency for large-scale learning [19,20]. Bell et al. [20] introduced an efficient secure aggregation method for federated learning, where the overhead scales logarithmically with the number of participating users. We note that the proposed framework in this paper is general enough to incorporate such advanced secure aggregation techniques.
The second main approach to DDP-based data collection utilizes the shuffle model [13,21], where an additional untrusted server, known as the shuffler, is introduced between users and the data collector. Users independently randomize their data before sending it to the shuffler, which then aggregates and randomly reorders the data before forwarding it to the data collector. The shuffle model has been widely explored, leading to various enhancements in aggregation and privacy amplification techniques [22,23,24]. However, a major limitation is its reliance on an untrusted shuffler, which introduces deployment challenges and potential vulnerabilities. In many real-world applications, the availability and trustworthiness of a shuffler cannot be guaranteed, making the model impractical for certain data collection scenarios.
Geo-indistinguishability (Geo-Ind) extends DP with a distance-based privacy metric [25,26,27,28]. The most commonly used mechanisms in Geo-Ind for data collection are the planar Laplace mechanism and the perturbation function-based mechanism. The Laplace mechanism perturbs a user’s true location by adding noise from a 2D Laplace distribution before sending it to the server [25]. In contrast, the perturbation function-based mechanism pre-calculates an obfuscation function on the server and distributes it to users, who then apply the received function to perturb their data before uploading it to the server [29,30,31,32]. Unlike DP, which enforces a consistent privacy guarantee regardless of data values, Geo-Ind allows privacy loss to increase with distance, making it vulnerable to attacks that exploit spatial correlations. Consequently, this approach is unsuitable for direct application to our problem, where strong and consistent privacy protection is required over all data points.
3. Preliminary
DP is a mathematical framework that provides probabilistic privacy protection even against attackers with arbitrary background knowledge [9]. It guarantees that an attacker cannot confidently identify an individual’s inclusion in a dataset. Formally, an algorithm satisfies -DP if, for any two neighboring datasets and differing by one record, and for any output O of , the following probability condition holds:
Here, the privacy budget, , controls the privacy strength.
The Gaussian mechanism is commonly used to achieve -DP. For a given function f, the Gaussian mechanism produces a differentially private output by adding random noise drawn from a Gaussian distribution with mean 0 and variance [9].
The standard deviation is calculated as , where (global sensitivity) is the maximum change in the output of the function f when a single record in the dataset is modified.
Local Differential Privacy (LDP) In traditional DP settings, a trusted server collects original data from individuals, applies noise to the aggregated data, and shares the data in a privacy-preserving manner. However, real-world scenarios do not always allow for such a trusted server. LDP addresses this limitation by allowing each data owner to independently apply noise to their data before sharing it with an untrusted server [10,11]. Formally, a randomized algorithm satisfies (, )-LDP if, for any two data values and , and any output O of , the following condition holds:
The above equation ensures that the aggregator cannot confidently determine whether the output of was generated from or , and thus guarantees the privacy of the individual’s input. This property prevents the inference of sensitive information by ensuring that any two inputs, and , produce outputs that are statistically indistinguishable within the bounds defined by the privacy parameters.
Distribute Differential Privacy (DDP) Like LDP, DDP enables privacy in data collection without relying on a trusted central server. In DDP, each user i adds independent noise to their data , resulting in locally randomized data . Here, represents noise drawn from a Gaussian distribution with mean 0 and variance , where n is the total number of users. When all n users’ contributions are aggregated by the untrusted server, the result is the following:
where represents the combined noise. Thus, DP is satisfied for the aggregated result, , rather than for each individual user’s data. By adding noise collaboratively across all users, the model ensures that the aggregated result satisfies -DP for the entire dataset while minimizing the noise that each individual must add. However, since individual data do not satisfy DP, computationally intensive cryptographic techniques are necessary to ensure that individual contributions remain protected during the aggregation process.
4. Problem Definition and Baseline Approaches
4.1. Problem Definition
In this section, we formally define the problem addressed in this paper. Let us assume that a set of users is defined as . Let be the set of all possible data elements. Each user has a set of data elements, represented by , where denotes the value associated with data element for user . In many real-world applications, the number of data elements m is large, and thus is often zero, resulting in a sparse representation of . For example, in location-based services, each might represent a unique point of interest (PoI), and might indicate the frequency of visits by user to that PoI. In this case, since there are many PoIs and most users visit only a small number of them, the data are very sparse.
In this paper, we assume that for each , the value corresponds to sensitive data that could reveal user preferences. Therefore, it is necessary to protect this information when sharing it with external parties. The goal of the service provider (i.e., the central server) is to collect the values from all users in U. However, since represents sensitive information, it is necessary to apply DP to protect the sensitive information of individual users. Specifically, for each data element , the service provider aims to compute the aggregate sum across all users, while ensuring that each user’s privacy is preserved.
4.2. Baseline Approaches
Algorithm 1 represents the baseline approach using LDP to the problem addressed in this paper. This pseudocode corresponds to the procedure for the t-th participating user, which is applied identically to all other users. Algorithm 1 ensures privacy by perturbing each user’s non-zero data values before reporting them to the central server. We assume that reporting only non-zero data does not significantly reveal sensitive information, as the sparsity of real-world datasets often limits the risk of identification from missing values alone. Each user initializes an empty list, , and iterates through all data elements, adding Gaussian noise, , to non-zero values (line 2–6). The noisy values are stored in , which is then sent to the server.
| Algorithm 1 Baseline Approach Based on LDP (Each Participating User Processing) |
|
In Algorithm 1, each user independently perturbs their data to satisfy (,)-DP locally. However, since the goal of this work is to compute the sum of all users’ data for each element, adding noise locally at the user level leads to excessive noise in the aggregated result. For example, consider a data element where h users have non-zero values. The aggregated result at the server would contain noise , which increases with the number of contributing users h. Instead, adding the noise directly to the aggregated sum would only require , significantly improving the utility of the result while still satisfying (,)-DP.
Algorithm 2 presents a DDP-based baseline approach to the problem addressed in this paper. In this approach, each participating user iterates through all data elements, adding noise from a Gaussian distribution, , where n is the total number of participating users (line 3). The noisy values are then encrypted using a threshold-based homomorphic encryption scheme (line 4). These encrypted noisy values are appended to , which is then sent to the server for decryption and aggregation.
| Algorithm 2 Baseline Approach Based on DDP (Each Participating User Processing) |
|
Although in Algorithm 2, the noise added by each user does not satisfy -DP for individual local data, the aggregated noise across all users ensures that the final aggregated result satisfies (,)-DP [12,13]. For instance, for the k-th data element, the aggregated value across all users is computed as , which satisfies the (,)-DP for the aggregated data. As a result, compared to the LDP-based solution, the DDP-based approach achieves better data utility in the aggregated results. However, in Algorithm 2, since -DP is not satisfied for each user’s individual local data, it is essential to ensure that the server can only access the aggregated results and cannot access individual user data. This requires cryptographic techniques such as homomorphic encryption [17,18] and multi-party aggregation [19,20], which allow the server to process only the aggregated results while preventing access to individual user contributions. However, these techniques are widely recognized for their computational overheads, which can significantly increase overall system complexity.
5. Proposed Approach
Although the DDP-based approach presents a promising solution by reducing noise relative to the LDP-based approach, it is not directly applicable to the problem addressed in this paper. In particular, two key challenges prevent the straightforward application of DDP to our problem:
- Impracticality of Applying DDP to All Data. The DDP-based baseline approach in Algorithm 2 is highly inefficient because it requires cryptographic techniques to be applied to all m data elements across n users. In real-world scenarios, where m (the number of data elements) is extremely large, the computational overhead of cryptographic techniques becomes prohibitive, especially when n is also large. The complexity of these techniques scales with both the number of users and the size of the dataset [17,20]. As a result, applying DDP to all data elements in scenarios with a large number of users is highly inefficient due to the significant computational cost.
- Non-Zero Data Variability. An alternative solution is to apply DDP only to data elements with non-zero values, similar to the LDP-based approach in Algorithm 1. In this approach, each user i perturbs its data by adding independent noise , where h represents the total number of users contributing to the aggregation for a specific data element. However, this solution is not feasible for sparse datasets, as each user typically has a different set of non-zero data elements. Since h depends on the number of users contributing non-zero values for a given data element , the server cannot determine h for each element without knowing the users’ individual non-zero data. Consequently, the noise variance cannot be accurately calibrated, resulting in the failure to satisfy (,)-DP globally.
These challenges highlight the limitations of directly applying DDP to our problem, and the need for an alternative approach. In this section, we propose the -DPFCM framework, which builds on DDP to balance data utility and efficiency while adapting to the specific requirements of the application.
5.1. Definition of -DPFCM
In this subsection, we formally define the proposed -DPFCM.
Definition 1
(-DPFCM). A data collection process satisfies -DPFCM if it satisfies the following two conditions for the given set of users and data elements :
where is the set of collected data elements, and , and
where is the set of users contributing to data element , and .
The -DPFCM framework introduces two key parameters, and , which control the breadth and depth of data collection, respectively. specifies the minimum fraction of the total data elements that must be collected to ensure sufficient diversity in the dataset. For example, if and the total number of items is , at least 900 items must be included in the collection process. On the other hand, determines the minimum fraction of users who must contribute data for each collected element, ensuring reliable user representation. For instance, if and the total number of users , at least 300 users must provide data for each selected element.
Figure 1 shows an example of -DPFCM applied to a scenario with five users and 10 data elements. This example satisfies the -DPFCM requirements because the set consists of data elements for which at least four users contribute their data to the server, thereby meeting the specified thresholds for both and . We note that by adjusting and , the framework can balance the trade-off between the diversity of data elements and the robustness of user contributions, supporting efficient and utility-driven data collection in real-world applications.
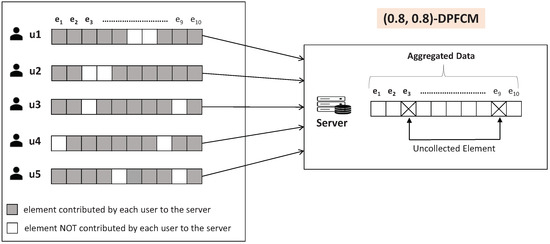
Figure 1.
An example of -DPFCM with 5 users and 10 data elements.
5.2. Overview of -DPFCM Framework
Figure 2 shows an overview of the proposed -DPFCM framework, which consists of three phases.
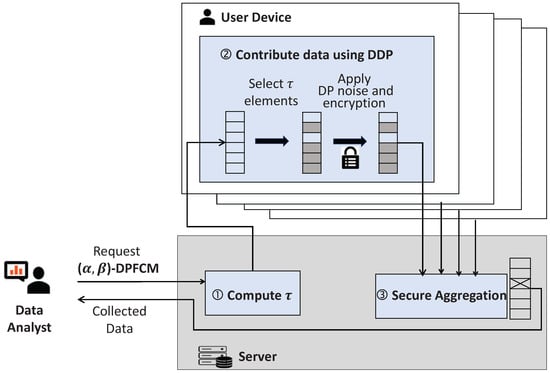
Figure 2.
An overview of the proposed -DPFCM framework.
- Computing minimum user contributions: The data collection server calculates the minimum number of data elements, , that each user must contribute to the server to satisfy the requirements of the -DPFCM framework, and then distributes it to all users (Section 5.3).
- Contributing data using DDP: Each user employs a DDP-based mechanism to report at least data elements to the server (Section 5.4).
- Secure aggregation: The server aggregates encrypted contributions for each data element, verifies that the threshold is satisfied, and securely decrypts the noisy values for qualifying elements (Section 5.5).
In the next subsections, we will present the detailed descriptions of each step in the proposed -DPFCM framework.
5.3. Computing Minimum User Contributions for -DPFCM
The requirement of the -DPFCM cannot be satisfied if each user sends only its non-zero data elements to the server, as in the LDP-based approach described in Algorithm 1. To address this, it is necessary to determine the minimum number of data elements that each user must contribute to the central server in order to satisfy the requirement of the -DPFCM. In this subsection, we propose two different probability-based approaches.
5.3.1. Binomial Model-Based Approach
To determine the minimum number of data elements each user must send to satisfy -DPFCM, we represent the selection process using a binomial distribution. Let us assume that each user randomly selects data elements from a total of m available data elements. The probability that any specific data element is selected by a user is given by .
We then model the number of users selecting a specific data element as a random variable X. Since each user’s selection is independent of others, X follows a binomial distribution,
where n is the total number of users and is the probability of a user selecting . This distribution effectively captures the likelihood of a specific data element being selected by a given number of users.
The probability that the number of users selecting is greater than or equal to the threshold specified in Equation (6) is represented as . Moreover, according to the condition in Equation (5), at least a fraction of the total data elements must be collected. This implies that can be interpreted as the confidence level required to satisfy . This condition can be expressed using the cumulative distribution function (CDF) of the binomial distribution:
Finally, we compute the cumulative probability using the CDF of the binomial distribution as follows:
We need to compute the minimum value of that satisfies the above equation, which provides a probabilistic guarantee that at least data elements are selected, each with contributions from at least users.
5.3.2. Chernoff Bound-Based Approach
The next approach for computing the minimum to satisfy -DPFCM is to use the Chernoff bound. The Chernoff bound provides an exponential bound on the tail probabilities of a random variable and is particularly useful for bounding the sum of independent random variables. For a random variable X with expectation , the lower bound of the Chernoff bound is defined as follows:
This bound provides an exponential decay rate for the probability that X is less than . By applying this Chernoff lower bound, we can determine the minimum threshold such that the probability of X being greater than or equal to is at least .
As in the case of Section 5.3.1, let us assume that each user randomly selects data elements from a total of m available data elements. Thus, the probability that any specific data element is selected is . We model the number of users selecting a specific data element as a random variable X. The expected value of X, denoted as , is computed as follows:
To satisfy the -DPFCM requirements, we need to ensure that the probability of X being greater than or equal to is at least . This requirement can be rewritten as follows:
To apply the Chernoff bound in this context, we define such that . Substituting this into the Chernoff bound in Equation (10), we obtain
By rearranging the terms, the inequality becomes
By taking the natural logarithm on both sides, we derive
By substituting and , the inequality becomes
To further simplify, we multiply both sides of the equation by :
We need to compute the minimum value of that satisfies the above inequality, thereby ensuring that the -DPFCM requirements are satisfied.
The choice between the binomial model-based approach and the Chernoff bound-based approach determines how the minimum required user contribution is calculated. The binomial approach tends to produce a lower , optimizing efficiency by reducing computational overhead. However, this efficiency comes with a trade-off. That is, there is a small probability that the -DPFCM condition may not be fully satisfied. In contrast, the Chernoff approach slightly overestimates , which guarantees that the -DPFCM condition is always satisfied, but leads to a higher computational cost due to the increased number of reported data elements. The experimental results in Section 6 confirm this trade-off, demonstrating that while the binomial model-based approach minimizes computational overhead, the Chernoff bound-based approach is preferable when strict satisfaction of -DPFCM is the priority.
5.3.3. Algorithm for Computing Minimum User Contribution
Since deriving a closed-form solution for Equations (9) and (17) is not feasible, we use an iterative method to compute the minimum efficiently. Algorithm 3 provides the pseudocode for this iterative approach. The algorithm begins by initializing to the smallest possible value, . The algorithm iteratively increments by one and checks whether the specified condition (Binomial or Chernoff) is satisfied based on the chosen method. The BinomialCondition procedure checks whether the condition specified in Equation (9) is satisfied (lines 16–19), while the ChernoffCondition procedure checks whether the Chernoff bound-based inequality in Equation (17) holds (lines 20–24). The algorithm continues until a valid is found.
| Algorithm 3 Pseudocode for Computing Minimum |
|
By restricting each user to uploading data elements, as determined by Algorithm 3, we effectively address the two key challenges previously identified: the impracticality of applying DDP to all data and non-zero data variability. To address the impracticality of applying DDP to all data, the proposed framework allows each user to upload only a subset of data elements, significantly reducing computational overhead. By selecting and reporting only a subset of data elements rather than the entire dataset, the computational overhead is significantly reduced, enabling scalability for large datasets. For non-zero data variability, the proposed framework ensures that each user sends at least data elements to the server. The value of is determined using either the proposed binomial model-based approach or the Chernoff bounds-based approach. By ensuring that each user contributes data elements, the -DPFCM condition is satisfied, enabling DDP-based data collection regardless of variations in non-zero data across users.
5.4. Contributing Data Using DDP
After calculating the minimum , the server distributes this value to all participating users. Each user is then required to select at least of data elements from their available dataset. These selected data elements are then sent back to the server. Algorithm 4 provides the pseudocode for the user-side processing of the proposed -DPFCM algorithm. This algorithm is based on the principles of DDP, but introduces a novel approach to reduce the computational overhead associated with DDP-based schemes. Unlike existing DDP methods, which require users to report all data elements to the server for our problem, the proposed algorithm allows each user to report only a subset of data elements, specified by . By limiting the number of reported elements to , the algorithm significantly reduces the computational overhead associated with DDP.
| Algorithm 4 Pseudocode for the User-Side Processing of -DPFCM |
|
The algorithm begins by initializing an empty list, , and then iterates over all data elements, adding Gaussian noise with variance to non-zero values (line 4). The noisy values are encrypted using a homomorphic encryption scheme with a given threshold, such as that given in [33] (line 5). The noisy and encrypted values are appended to . If the size of is less than the required threshold , the user randomly selects additional indices whose corresponding data element value is zero, applies the same noise addition and encryption steps, and appends the results to (lines 8–12). Finally, the encrypted list is sent to the server for aggregation.
5.5. Secure Aggregation of User Contributions
After receiving the encrypted data from users, the server aggregates the contributions for each data element, checks whether the number of contributions meets the threshold , and securely decrypts the noisy aggregated values for elements that qualify. Algorithm 5 provides the pseudocode for the server-side processing of the proposed -DPFCM algorithm. Upon receiving from n users, the server first aggregates the data for each data element (line 1). Let assume that represents the aggregated results for all data elements, where denotes the set of users who uploaded to the server.
The server then uses the homomorphic properties of the encryption scheme to securely aggregate these encrypted values. If the number of users who submitted encrypted noisy values for a specific data element k satisfies the condition , the server computes the encrypted aggregated noisy value by multiplying the encrypted values provided by all contributing users in , leveraging the additive homomorphic property of the encryption scheme (line 5). Next, the server initiates the threshold decryption process (line 6–10). It randomly selects a subset of users, , such that , to collaboratively decrypt the aggregated value. The server queries each user in with . Each user computes a partial decryption of the encrypted value using their share of the private key and sends the result back to the server. The server then combines the partial decryptions to compute the final aggregated noisy value, . Finally, the server stores the result in the result set, , and repeats the process for all data elements that satisfy the condition .
| Algorithm 5 Pseudocode for the Sever-Side Processing of -DPFCM |
|
5.6. Analysis of Effect of and on
In the -DPFCM framework, the parameters and play a critical role in determining the minimum number of data elements, , that each user must contribute. The value of has a direct impact on the overall efficiency of the framework, affecting both user-side processing, as described in Algorithm 4, and server-side processing, as described in Algorithm 5. A higher value of increases the utility of the collected dataset. However, this comes at the cost of higher computational requirements. On the other hand, a smaller reduces the computational overhead, improving the scalability and efficiency of the system. However, it may compromise the utility of the collected data. Thus, in this subsection, we analyze the effect of and on based on the previously proposed binomial model-based and Chernoff bound-based approaches.
5.6.1. Effect of on
The parameter specifies the fraction of data elements that must meet the contribution threshold of at least users. A higher implies stricter requirements as a larger proportion of data elements must satisfy this condition.
- Binomial Model-Based Approach: Using the condition from Equation (9), an increase in decreases , tightening the inequality. To satisfy this tighter condition, the cumulative probability must decrease. This requires an increase in , as increasing increases the probability that more users will select each data element, thus shifting the probability mass of the binomial towards higher values of X.
- Chernoff Bound-Based Approach: From Equation (17), an increase in results in a larger on the right-hand side. To maintain the inequality, must be increased to ensure that the left-hand side remains greater than or equal to the right-hand side. Specifically, a larger compensates by increasing both the quadratic term and the overall product with .
In summary, for both approaches, as increases, must also increase to satisfy the stricter condition that a larger proportion of data elements meet the required contribution threshold.
5.6.2. Effect of on
The parameter represents the fraction of users, , that must contribute to each data element for it to qualify. A higher increases the required number of contributions for each data element.
- Binomial Model-Based Approach: From Equation (9), the inequality involves a summation up to . Increasing raises this upper limit, requiring the binomial probability mass to shift toward higher values of X. To achieve this, must increase, as a higher ensures that more users contribute to each data element, thereby meeting the increased threshold.
- Chernoff Bound-Based Approach: From Equation (17), an increase in raises the term , which reduces the factor on the left-hand side. To restore balance, must be increased to ensure that the left side satisfies the inequality.
Therefore, for both approaches, as increases, must also increase to satisfy the stricter condition requiring more user contributions for each data element.
5.6.3. Discussion on Selecting Appropriate Values for and
In the -DPFCM framework, the parameters and significantly influence the minimum value of , which determines the number of data elements that each user must contribute. If either or increases, must also increase to satisfy the stricter requirements imposed by these parameters. Higher values of demand that a larger proportion of data elements meet the contribution threshold, while higher values of require more users to contribute to each data element. As a result, increasing and increases the utility of the collected dataset by collecting more comprehensive and representative data.
However, this improvement in utility comes at a cost. An increased value of directly results in higher computational overhead due to the DDP mechanism. Users must process and transmit more data elements, and the server must handle more contributions, increasing the complexity of secure aggregation and decryption. Therefore, the balance between utility and efficiency becomes critical.
The proposed approach allows for dynamic adjustment of the efficiency–utility trade-offs for data collection by carefully selecting the values of and based on the intended data analysis objectives and available computational resources. For applications that prioritize high utility, larger values of and can be chosen to ensure a more comprehensive and representative dataset. On the other hand, for scenarios where efficiency and scalability are critical due to resource constraints, smaller values of and can be chosen to minimize the computational overhead, thereby optimizing the use of available resources.
6. Experiments
In this section, we evaluate the proposed scheme using real datasets. We first describe the experimental setup and then present a discussion of the results.
6.1. Experimental Setup
Datasets: In this study, we evaluate the performance of the proposed method using real-world data to demonstrate its practical applicability. The T-Drive dataset [34], which consists of GPS-based driving records of 10,357 taxis operating in Beijing, was used for our experiments. To generate a PoI dataset from the T-Drive data, we employed the following process: First, the entire geographic region was divided into 10,000 equally sized zones, and the location of each taxi was mapped to its corresponding zone. Second, in order to focus on areas of significant activity, the 1000 most frequently visited zones were identified and considered as PoIs. The number of visits to each zone was used as the value associated with the PoI. Finally, to simulate different dataset sizes, we randomly selected two subsets of taxis from the 10,357 available taxis, consisting of 1000 and 3000 taxis, respectively. In this setup, each taxi was considered as a user, the PoIs were treated as a set of data elements (E), and the frequency of each taxi’s visits to a PoI was used as the value () associated with the data element .
Baseline: For the proposed -DPFCM framework, we implemented two different methods: the binomial model-based approach () and the Chernoff bound-based approach (). To evaluate the effectiveness of our framework, we conducted a comparative evaluation against the LDP-based method using the staircase mechanism [15] (), which introduces less noise into the original data compared to the Gaussian and Laplace mechanisms, as well as the DDP-based approach () from [18].
Evaluation Metrics: In our experiments, we used mean absolute error (MAE) and Jensen–Shannon divergence (JSD) as evaluation metrics for comparative analysis. MAE is defined as follows:
Here, represents the true aggregated frequency value for the data element , computed as the sum of all individual contributions over n users, expressed as . On the other hand, denotes the noisy aggregated frequency value computed using the DP mechanism.
Furthermore, JSD is defined as follows:
Here, represents the Kullback–Leibler divergence, P denotes the true probability distribution of the aggregated frequency values derived by normalizing across all data elements, and corresponds to the noisy probability distribution obtained by normalizing the DP private noisy aggregated values .
6.2. Evaluation of Computation Methods in -DPFCM Framework
Before presenting the experimental results on the utility of the collected data, we first evaluate the effectiveness of the proposed binomial model-based and Chernoff bound-based approaches for computing . Figure 3 shows the differences in computed using the Chernoff bound-based approach and the binomial model-based approach under varying values of and . As shown in the figure, the values computed using the Chernoff bound-based approach are consistently higher than those derived from the binomial model-based approach. This is because the Chernoff bound provides a conservative estimate by bounding the tail probabilities with an exponential decay term, providing a stronger guarantee that the desired confidence level is met. The squared deviation factor, , in the Chernoff inequality amplifies deviations, leading to an overestimation of . In contrast, the binomial model-based approach directly computes the exact probabilities using the CDF of the binomial distribution. This results in accurate values that are sufficient to meet the requirements without unnecessary overestimation.
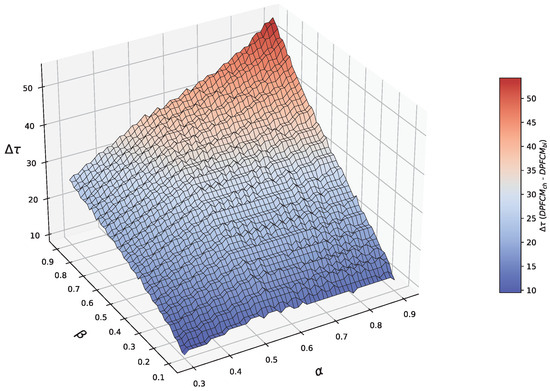
Figure 3.
Difference in between the Chernoff bound-based approach and the binomial model-based approach.
Table 1 shows the failure rate of -DPFCM requirements for the binomial model-based () and the Chernoff bound-based () approaches. The failure rate is defined as the proportion of experiments in which the -DPFCM requirement was not satisfied:
In this experiment, the total number of experiments conducted is 200. The failure rate provides a measure of the effectiveness of each approach in satisfying the -DPFCM requirement under varying values of and .

Table 1.
Failure rate of -DPFCM requirements for binomial model-based and Chernoff bound-based approaches.
As shown in Table 1, the approach has zero failure rates for lower values. However, it tends to increase the failure rate as and increase. On the contrary, the approach consistently achieves a zero failure rate across all parameter settings, indicating that it satisfies the -DPFCM requirement in all experiments, regardless of the values of and .
The experimental results in this subsection regarding the computation of highlight distinct trade-offs between the two approaches, as explained in Section 5.3. The binomial model-based approach () utilizes tighter values, making it highly effective in reducing the computational overhead of using DDP, as fewer data elements need to be processed by both users and the server. However, this efficiency comes at the cost of occasional failure to satisfy the -DPFCM requirement. In contrast, the approach based on the Chernoff bound () uses slightly overestimated values, which results in a slightly higher computational overhead. However, this ensures that the -DPFCM requirement is always satisfied. Thus, it is desirable to use for applications where efficiency and scalability are critical, even with occasional failures in meeting data collection requirements. On the other hand, is better suited for applications where satisfying data collection requirements is paramount and sufficient computing resources are available.
Figure 4 presents a comparison of the number of data elements sent by each user to the server in the DDP-based approaches (i.e., the proposed and methods, and DDP). The experiments were conducted with two different user sizes (1000 and 3000). As shown in the figure, compared to DDP where users must send all data elements to the server, the proposed approaches require users to send only selected data elements. This results in a significant reduction in the number of data elements sent to the server, thereby significantly reducing the overhead associated with cryptographic operations in the DDP-based approach. This reduction highlights the efficiency of the proposed framework, particularly in scenarios where minimizing computational overhead is critical.
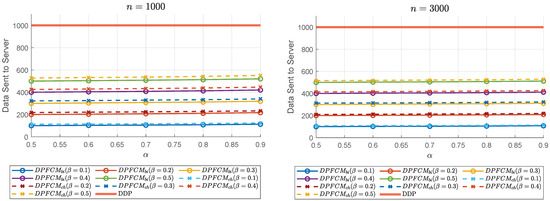
Figure 4.
Comparison of data elements sent by each user to server.
Scalability and Computational Considerations
As demonstrated in the experimental results, -DPFCM effectively reduces the number of transmitted data elements compared to DDP-based approaches, enhancing scalability for large-scale applications. However, since secure aggregation is employed to protect user data during collection, it introduces additional computational costs, which increase with the number of participating users.
Recent advances in secure aggregation techniques, particularly in federated learning, have introduced efficient cryptographic protocols that significantly reduce communication complexity and computational overhead while maintaining strong privacy guarantees. Protocols such as those proposed in [19,20] utilize optimized masking techniques and dropout-resistant aggregation mechanisms, ensuring that secure aggregation remains scalable even as the number of users increases. With these protocols, -DPFCM remains computationally viable for large-scale applications. In addition, reducing the number of transmitted data elements further mitigates the cryptographic overhead introduced by secure aggregation.
6.3. Evaluation Results on Data Utility
In this subsection, we present the evaluation results for the data utility of the collected data. Figure 5 and Figure 6 illustrate the impact of the privacy budget, , on MAE and JSD, respectively. The experiments were conducted using two different values of , specifically 0.6 and 0.9, while varying from 0.1 to 0.5. The number of users was fixed at 1000, while was varied from 0.25 to 1.0. Note that in Figure 5 and Figure 6, some results for are presented with text annotations on the bars, as the results differ significantly from those of the other approaches.
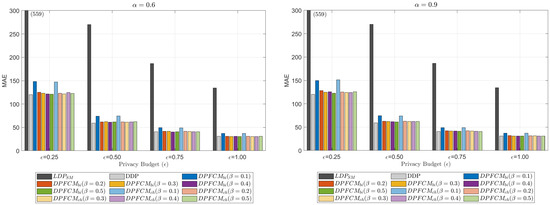
Figure 5.
Impact of and on MAE.
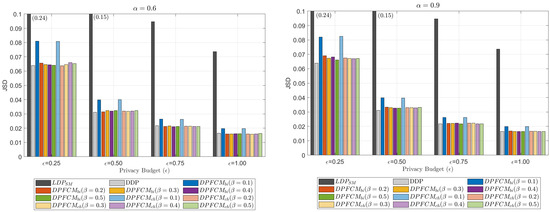
Figure 6.
Impact of and on JSD.
As the privacy budget decreases, both MAE and JSD increase consistently across all evaluated methods. This behavior reflects the inherent trade-off in DP-based approaches: achieving stronger privacy guarantees (lower ) necessitates adding more noise to the data, which consequently reduces the utility of the aggregated results. This trade-off is a fundamental characteristic of DP, where greater privacy protection comes at the expense of accuracy in data analysis. Among the evaluated methods, shows the worst performance in terms of both MAE and JSD. This is mainly due to the significant noise added at the local level for each user’s data, which significantly distorts the aggregated results. The localized noise addition of , while enhancing privacy, leads to excessive obfuscation that severely impacts data utility. Given that is a more optimized approach compared to the Gaussian and Laplace mechanisms, these results highlight the fundamental limitations of LDP-based methods in data collection. As a result, LDP-based methods are unsuitable for scenarios requiring high data utility, particularly in applications where precise statistical analysis or accurate pattern recognition is essential.
The proposed -DPFCM framework, including and , significantly outperforms the method in both MAE and JSD metrics. Furthermore, the results achieved by the proposed framework are comparable to those of DDP-based approaches, which are characterized by significantly higher computational overhead. This increased overhead in DDP is due to the requirement that each user sends all DP-noised data elements to the server, which then processes the encrypted data for decryption. As shown in the experimental results in Figure 4, the proposed -DPFCM framework significantly reduces the computational burden by requiring users to send only selected data elements, while still maintaining utility comparable to DDP-based methods.
Figure 5 and Figure 6 also illustrate the impact of on the data utility of the collected data. As increases, both MAE and JSD show a decreasing trend. This is because a higher ensures that more users contribute to each data element, thereby improving the accuracy in the aggregated results. In particular, there is a significant decrease in both MAE and JSD when is increased from 0.1 to 0.2. Beyond this point, the improvements in MAE and JSD become marginal. This observation confirms that, even with a small value of , which significantly reduces the number of data elements transmitted to the server compared to DDP, the proposed -DPFCM framework achieves performance comparable to that of DDP.
The experimental results in this subsection verify that the proposed -DPFCM framework significantly outperforms in terms of data utility, while achieving results comparable to DDP. Furthermore, it significantly reduces the number of data elements transmitted to the server, making -DPFCM an effective solution for applications that prioritize both utility and efficiency.
7. Conclusions and Future Work
In this paper, we addressed the challenge of balancing data utility and computational efficiency in privacy-preserving data collection frameworks. Motivated by the variability in data utility requirements across applications, we proposed the -DPFCM framework, which provides a flexible solution for applications that can effectively operate with partial data collection. DPFCM introduces two key parameters, and , which allow the framework to control the breadth of data elements collected and the depth of user representation, respectively. To satisfy the -DPFCM requirements, we developed two probability-based methods—binomial model-based and Chernoff bound-based approaches—that determine the minimum data contribution required from each user.
The experimental results validate the practicality and effectiveness of DPFCM. Using real-world datasets, we verified that the proposed framework achieves comparable data utility to DDP, which is known for its high computational cost. At the same time, DPFCM significantly reduces computational overhead by requiring users to contribute only a fraction of their data. This efficiency is particularly valuable for applications requiring real-time decision-making, where responsiveness is critical.
While this work focuses primarily on the efficiency-utility trade-offs in privacy-preserving data collection, an important aspect for future research is the impact of high-frequency collisions on aggregate results. In scenarios where multiple users report the same data elements, such collisions can affect the statistical properties of the collected dataset. Investigating mitigation strategies for such effects will be an important direction for future research.
Author Contributions
Conceptualization, J.K.; Methodology, J.K.; Software, J.K.; Validation, J.K.; Formal analysis, J.K.; Investigation, J.K.; Writing—original draft, J.K.; Writing—review & editing, S.-H.C.; Visualization, J.K.; Project administration, S.-H.C.; Funding acquisition, J.K. and S.-H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF-2023R1A2C1004919) and Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. 2021-0-00884, Development of Integrated Platform for Untact Collaborative Solution and Blockchain Based Digital Work).
Data Availability Statement
The original data presented in the study are openly available in Kaggle at https://www.microsoft.com/en-us/research/publication/t-drive-trajectory-data-sample/ (accessed on 1 August 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rong, C.; Ding, J.; Li, Y. An interdisciplinary survey on origin-destination flows modeling: Theory and techniques. ACM Comput. Surv. 2024, 57, 1–49. [Google Scholar] [CrossRef]
- Behara, K.N.S.; Bhaskar, A.; Chung, E. A DBSCAN-based framework to mine travel patterns from origin-destination matrices: Proof-of-concept on proxy static OD from Brisbane. Transp. Res. Part Emerg. Technol. 2021, 131, 103370. [Google Scholar] [CrossRef]
- Jia, J.S.; Lu, X.; Yuan, Y.; Xu, G.; Jia, J.; Christakis, N.A. Population flow drives spatio-temporal distribution of COVID-19 in China. Nature 2020, 582, 389–394. [Google Scholar] [CrossRef]
- Chen, R.; Li, L.; Ma, Y.; Gong, Y.; Guo, Y.; Ohtsuki, T.; Pan, M. Constructing mobile crowdsourced COVID-19 vulnerability map with geo-indistinguishability. IEEE Internet Things J. 2022, 9, 17403–17416. [Google Scholar] [CrossRef]
- Yu, Z.; Ma, H.; Guo, B.; Yangi, Z. Crowdsensing 2.0. Commun. ACM 2021, 64, 76–80. [Google Scholar] [CrossRef]
- Kim, J.W.; Lim, J.H.; Moon, S.M.; Jang, B. Collecting health lifelog data from smartwatch users in a privacy-preserving manner. IEEE Trans. Consum. Electron. 2019, 65, 369–378. [Google Scholar] [CrossRef]
- Saura, J.R.; Ribeiro-Soriano, D.; Palacios-Marques, D. From user-generated data to data-driven innovation: A research agenda to understand user privacy in digital markets. Int. J. Inf. Manag. 2021, 60, 102331. [Google Scholar] [CrossRef]
- Jiang, H.; Li, J.; Zhao, P.; Zeng, F.; Xiao, Z.; Iyengar, A. Location privacy-preserving mechanisms in location-based services: A comprehensive survey. Acm Comput. Surv. 2021, 54, 1–36. [Google Scholar] [CrossRef]
- Dwork, C. Differential privacy. In Proceedings of the International Colloquium on Automata, Languages, and Programming, Venice, Italy, 12–15 July 2006; pp. 1–12. [Google Scholar]
- Erlingsson, U.; Pihur, V.; Korolova, A. RAPPOR: Randomized aggregatable privacy-preserving ordinal response. In Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; pp. 1054–1067. [Google Scholar]
- Wang, T.; Blocki, J.; Li, N.; Jha, S. Locally differentially private protocols for frequency estimation. In Proceedings of the USENIX Conference on Security Symposium, Berkeley, CA, USA, 14–16 August 2017. [Google Scholar]
- Goryczka, S.; Xiong, L. A comprehensive comparison of multiparty secure additions with differential privacy. IEEE Trans. Dependable Secur. Comput. 2015, 14, 463–477. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Jia, J.; Wu, Y.; Hu, C.; Dong, C.; Liu, Z.; Chen, X.; Peng, Y.; Wang, S. Distributed differential privacy via shuffling versus aggregation: A curious study. IEEE Trans. Inf. Forensics Secur. 2024, 19, 2501–2516. [Google Scholar] [CrossRef]
- Bassily, R.; Smith, A. Local, private, efficient protocols for succinct histograms. In Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing, Portland, OR, USA, 14–17 June 2015. [Google Scholar]
- Geng, Q.; Kairouz, P.; Oh, S.; Viswanath, P. The staircase mechanism in differential privacy. IEEE J. Sel. Top. Signal Process. 2015, 9, 1176–1184. [Google Scholar] [CrossRef]
- Lyu, L.; Nandakumar, K.; Rubinstein, B.; Jin, J.; Bedo, J.; Palaniswami, M. PPFA: Privacy preserving fog-enabled aggregation in smart grid. IEEE Trans. Ind. Inform. 2018, 14, 3733–3744. [Google Scholar] [CrossRef]
- Xie, Q.; Jiang, S.; Jiang, L.; Huang, Y.; Zhao, Z.; Khan, S. Efficiency optimization techniques in privacy-preserving federated learning with homomorphic encryption: A brief survey. IEEE Internet Things J. 2024, 11, 24569–24580. [Google Scholar] [CrossRef]
- Truex, S.; Baracaldo, N.; Anwar, A.; Steinke, T.; Ludwig, H.; Zhang, R.; Zhou, Y. A hybrid approach to privacy-preserving federated learning. In Proceedings of the the ACM Workshop on Artificial Intelligence and Security, London, UK, 15 November 2019. [Google Scholar]
- Kadhe, S.; Rajaraman, N.; Koyluoglu, O.O.; Ramchandran, K. FastSecAgg: Scalable secure aggregation for privacy-preserving federated learning. arXiv 2020, arXiv:2009.11248. [Google Scholar]
- Bell, J.H.; Bonawitz, K.A.; Gascon, A.; Lepoint, T.; Raykova, M. Secure single-server aggregation with (poly)logarithmic overhead. In Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, Virtual, 9–16 November 2020; pp. 1253–1269. [Google Scholar]
- Balle, B.; Bell, J.; Gascon, A.; Nissim, K. The privacy blanket of the shuffle model. In Proceedings of the International Cryptology Conference, Santa Barbara, CA, USA, 12–18 August 2019; pp. 638–667. [Google Scholar]
- Scott, M.; Cormode, G.; Maple, C. Aggregation and transformation of vector-valued messages in the shuffle model of differential privacy. IEEE Trans. Inf. Forensics Secur. 2022, 17, 612–627. [Google Scholar] [CrossRef]
- Chen, E.; Cao, Y.; Ge, Y. A generalized shuffle framework for privacy amplification: Strengthening privacy guarantees and enhancing utility. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 26–27 February 2024; pp. 11267–11275. [Google Scholar]
- Li, K.; Zhang, H.; Liue, Z. A range query scheme for spatial data with shuffled differential privacy. Mathematics 2024, 12, 1934. [Google Scholar] [CrossRef]
- Andres, M.E.; Bordenabe, N.E.; Chatzikokolakis, K.; Palamidessi, C. Geo-indistinguishability: Differential privacy for location-based systems. In Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, Berlin, Germany, 4–8 November 2013; pp. 901–914. [Google Scholar]
- Kim, J.W.; Edemacu, K.; Jang, B. Privacy-preserving mechanisms for location privacy in mobile crowdsensing: A survey. J. Netw. Comput. Appl. 2023, 200, 103315. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, D.; Du, J.T.; Chen, J. Geo-Ellipse-Indistinguishability: Community-aware location privacy protection for directional distribution. IEEE Trans. Knowl. Data Eng. 2023, 35, 6957–6967. [Google Scholar] [CrossRef]
- Fathalizadeh, A.; Moghtadaiee, V.; Alishahi, M. Indoor geo-indistinguishability: Adopting differential privacy for indoor location data protection. IEEE Trans. Emerg. Top. Comput. 2023, 12, 293–306. [Google Scholar] [CrossRef]
- Jin, W.; Xiao, M.; Guo, L.; Yang, L.; Li, M. ULPT: A user-centric location privacy trading framework for mobile crowd sensing. IEEE Trans. Mob. Comput. 2022, 21, 3789–3806. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, X.; Guo, L.; Li, M. Incentivizing crowdsensing-based noise monitoring with differentially-private locations. IEEE Trans. Mob. Comput. 2021, 20, 519–532. [Google Scholar] [CrossRef]
- Zhang, P.; Cheng, X.; Su, S.; Wang, N. Area coverage-based worker recruitment under geo-indistinguishability. Comput. Netw. 2022, 217, 109340. [Google Scholar] [CrossRef]
- Song, S.; Kim, J.W. Adapting geo-indistinguishability for privacy-preserving collection of medical microdata. Electronics 2023, 12, 2793. [Google Scholar] [CrossRef]
- Tian, H.; Zhang, F.; Shao, Y.; Li, B. Secure linear aggregation using decentralized threshold additive homomorphic encryption for federated learning. arXiv 2021, arXiv:2111.10753. [Google Scholar]
- T-Drive Trajectory Data Sample. 2018. Available online: https://www.microsoft.com/en-us/research/publication/t-drive-trajectory-data-sample (accessed on 1 August 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).