Proportional Log Survival Model for Discrete Time-to-Event Data
Abstract
1. Introduction
2. Proportional Log Survival Model for Discrete Time-to-Event-Data
2.1. Model Formulation
2.2. Parameter Estimation
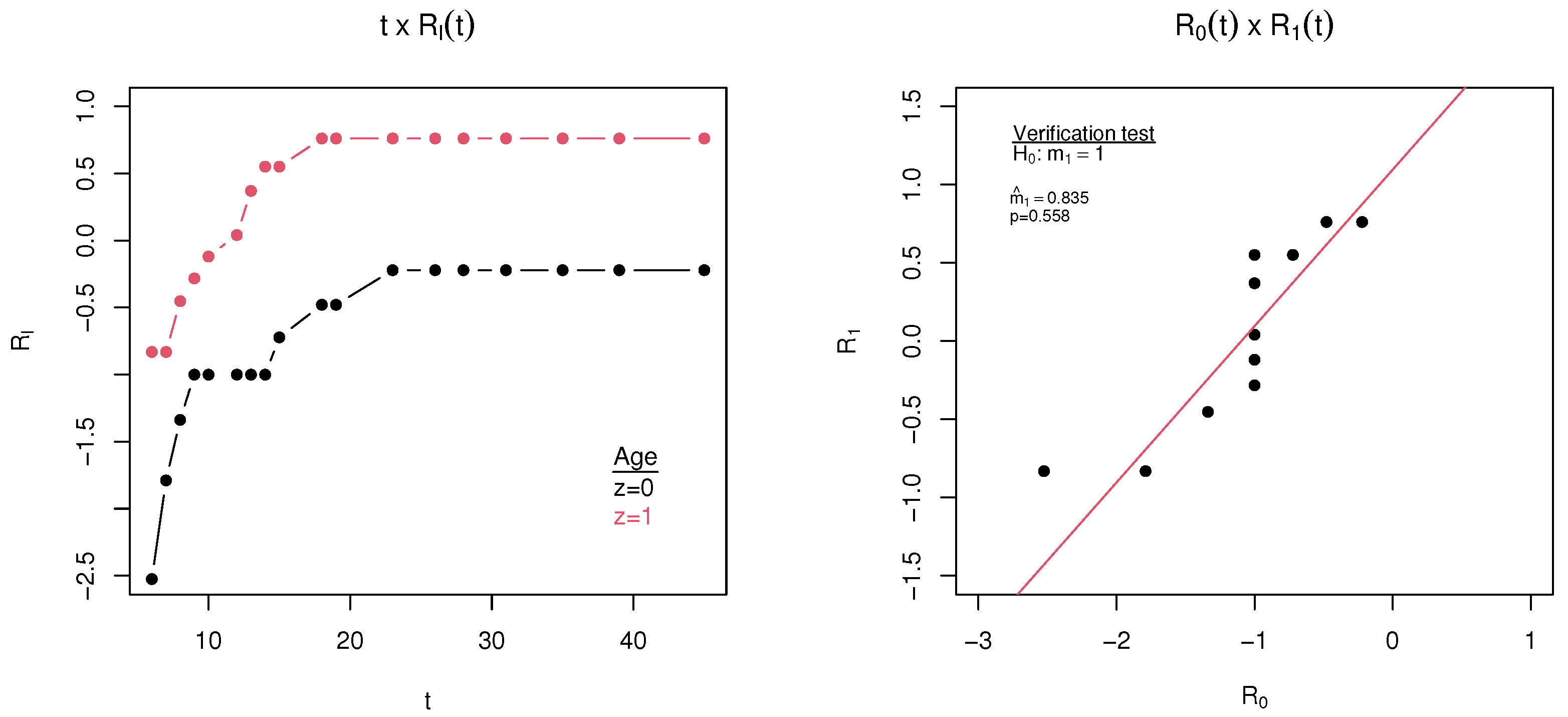
2.3. Verification of the Proportional Log Survival Assumption
2.4. Discrete Weibull Proportional Log Survival Model (PLSM-DW)
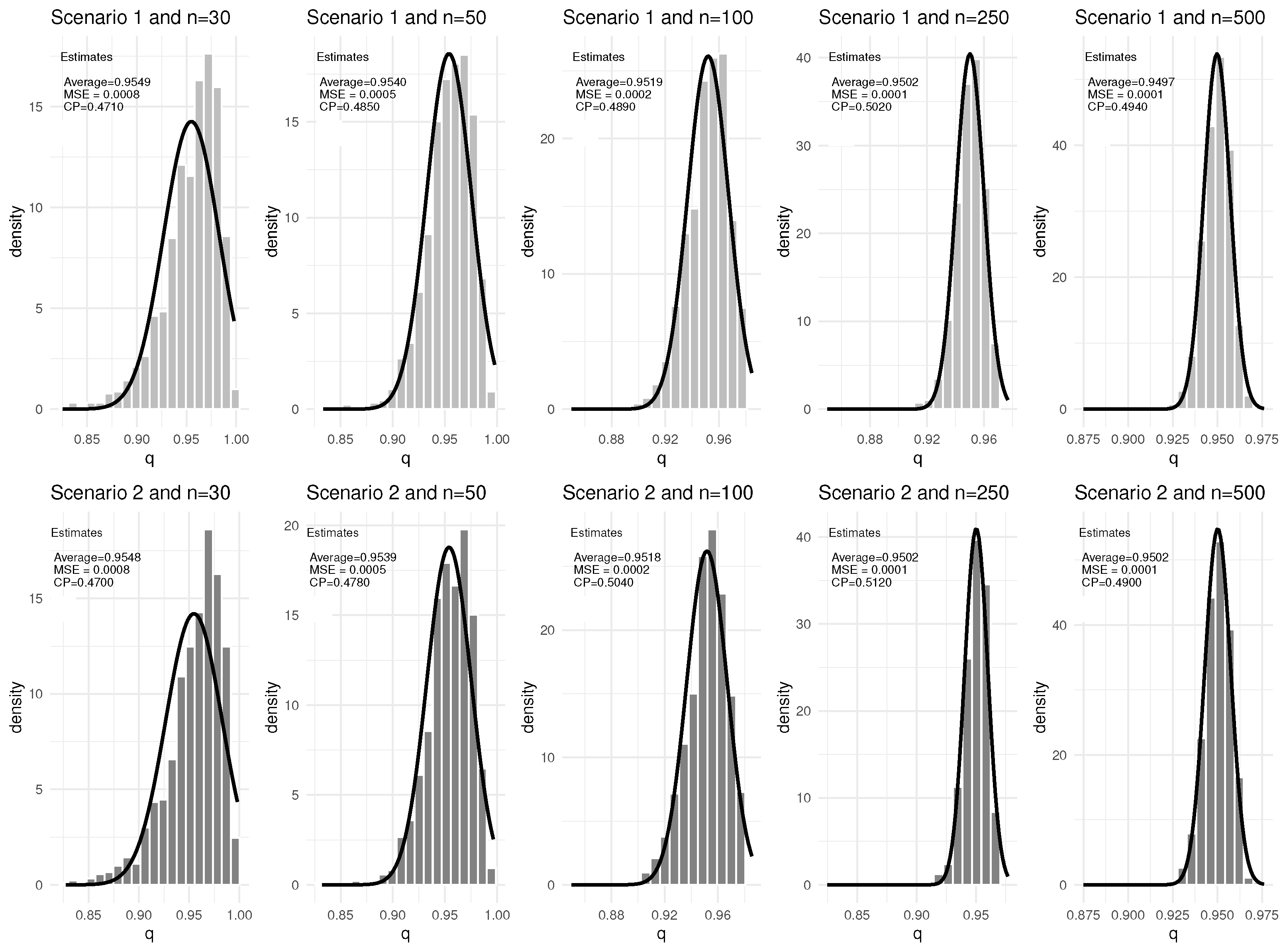
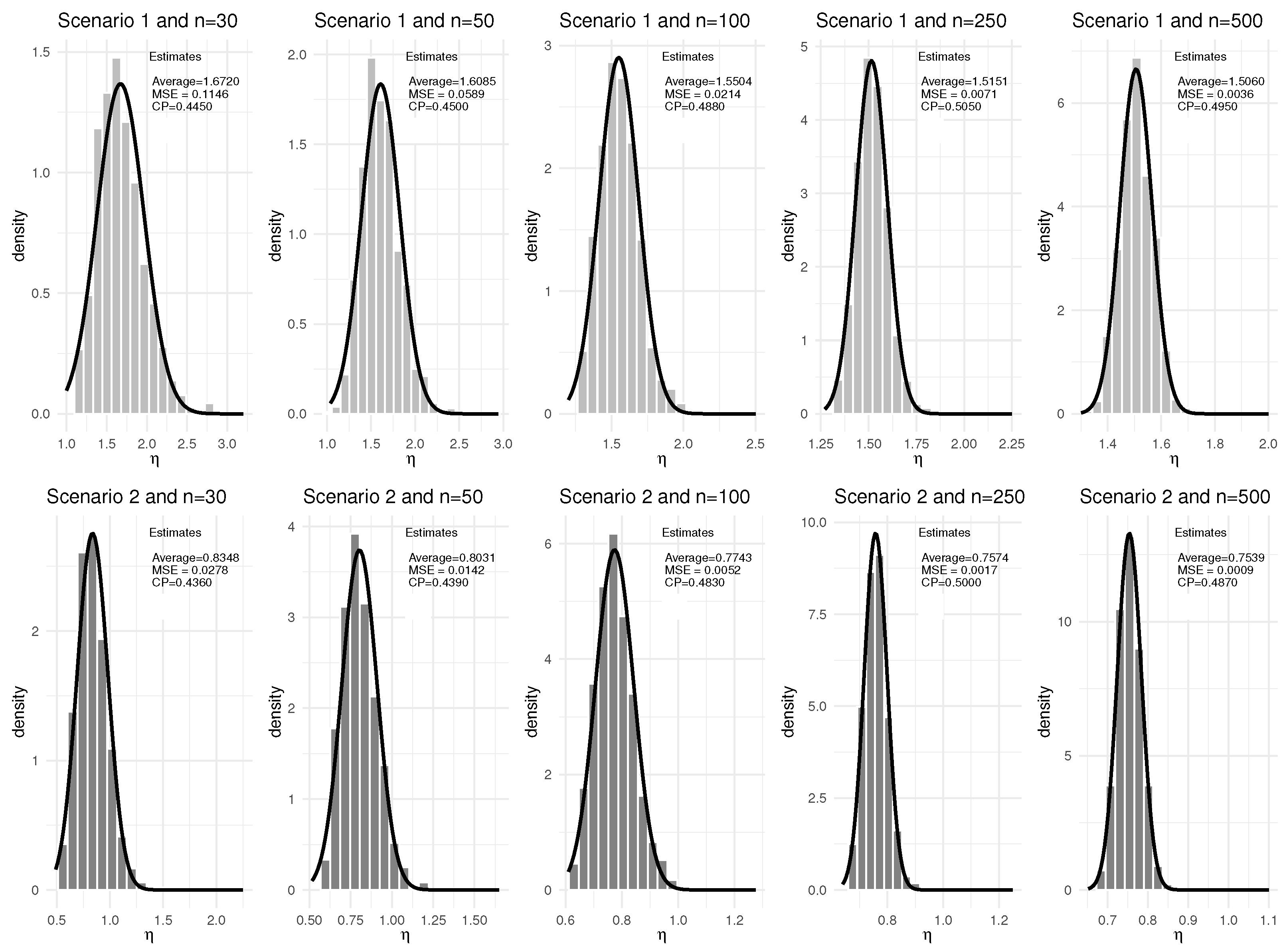
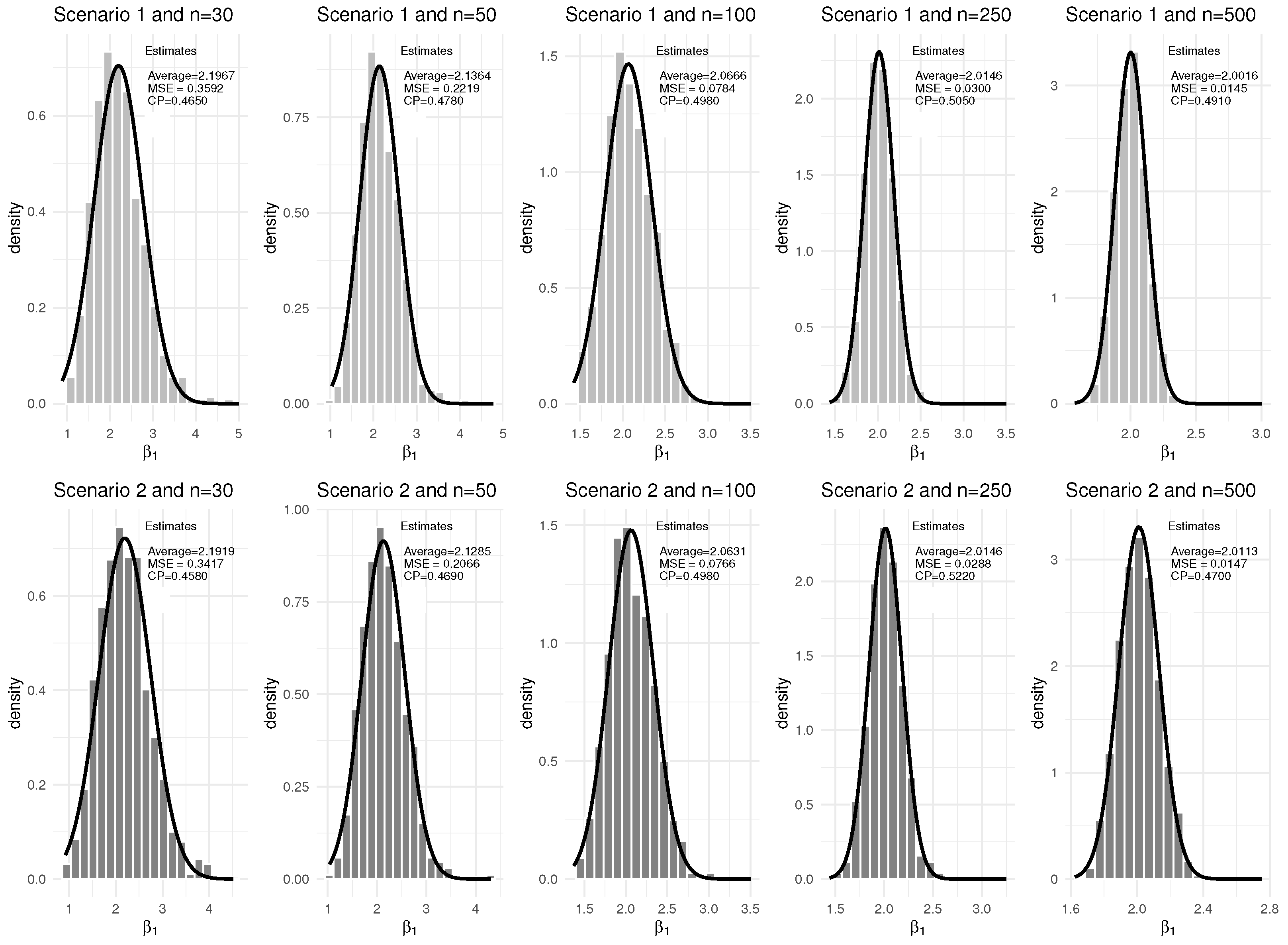
3. Simulation Study
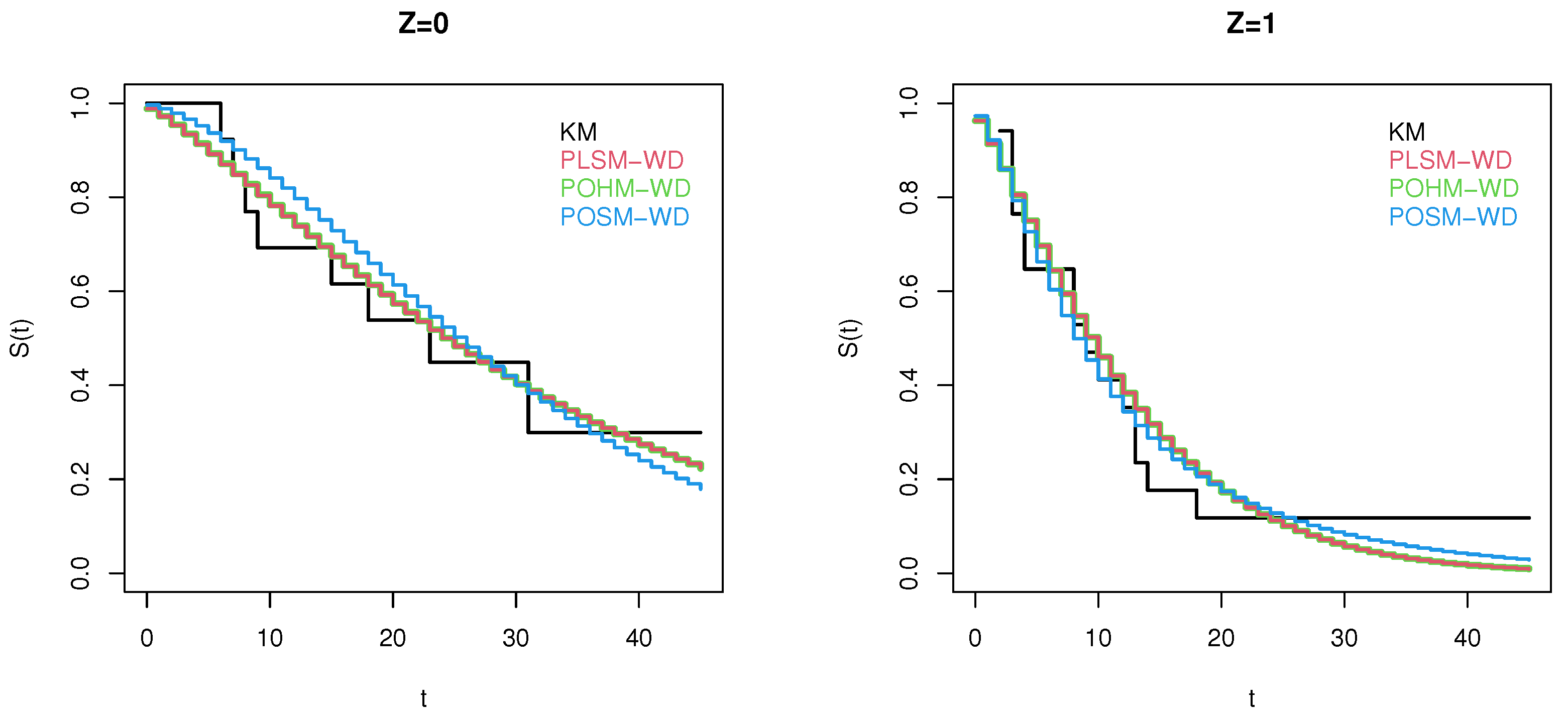
4. Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AML | acute myeloid leukemia |
| CI | confidence interval |
| CP | coverage probability |
| DW | discrete Weibull |
| KM | Kaplan–Meier |
| MSE | Mean squared error |
| PH | proportional hazard |
| PLSM | proportional log survival model |
| PLSM-DW | discrete Weibull proportional log survival model |
| POHM | Proportional odds hazard model |
| POHM-DW | discrete Weibull proportional odds hazard model |
| POSM-DW | discrete Weibull proportional odds survival model |
References
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. B (Methodol.) 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Caroni, C. Regression models for lifetime data: An overview. Stats 2022, 5, 1294–1304. [Google Scholar] [CrossRef]
- Gupta, R.C.; Gupta, R.D. Proportional reversed hazard rate model and its applications. J. Stat. Plan. Inf. 2007, 137, 3525–3536. [Google Scholar] [CrossRef]
- Bennett, S. Analysis of survival data by the proportional odds model. Stat. Med. 1983, 2, 273–277. [Google Scholar] [CrossRef] [PubMed]
- Oakes, D.; Dasu, T. Inference for the proportional mean residual life model. Inst. Math. Stat. Lect. Notes 2003, 43, 105–116. [Google Scholar]
- Shrahili, M.; Albabtain, A.A.; Kayid, M.; Kaabi, Z. Stochastic aspects of proportional vitalities model. Mathematics 2020, 8, 1823. [Google Scholar] [CrossRef]
- Asadi, M.; Berred, A. Properties and estimation of the mean past lifetime. Statistics 2012, 46, 405–417. [Google Scholar] [CrossRef]
- Bandos, H. Regression on Median Residual Life Function for Censored Survival Data. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2007. [Google Scholar]
- Vieira, M.G.; Cardial, M.R.P.; Matsushita, R.; Nakano, E.Y. Proportional odds hazard model for discrete time-to-event data. Axioms 2023, 12, 1102. [Google Scholar] [CrossRef]
- Cardial, M.R.P.; Cobre, J.; Nakano, E.Y. A discrete Weibull proportional odds survival model. J. Appl. Stat. 2025, 52, 429–447. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, T.; Osaki, S. The discrete Weibull distribution. IEEE Trans. Reliab. 1975, 24, 300–301. [Google Scholar] [CrossRef]
- Lee, E.T.; Wang, J. Statistical Methods for Survival Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Tutz, G.; Schmid, M. Modeling Discrete Time-to-Event Data; Springer: New York, NY, USA, 2016. [Google Scholar]
- Lehmann, E.L.; Casella, G. Theory of Point Estimation; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Para, B.A.; Jan, T.R. Discrete version of log-logistic distribution and its applications in genetics. Int. J. Mod. Math. Sci. 2016, 14, 407–422. [Google Scholar]
- Cardial, M.R.P.; Fachini-Gomes, J.B.; Nakano, E.Y. Exponentiated discrete Weibull distribution for censored data. Braz. J. Biom. 2020, 38, 35–56. [Google Scholar]
- Krishna, H.; Pundir, P.S. Discrete Burr and discrete Pareto distributions. Stat. Methodol. 2009, 6, 177–188. [Google Scholar] [CrossRef]
- Chakraborty, S. Generating discrete analogues of continuous probability distributions—A survey of methods and constructions. J. Stat. Distrib. Appl. 2015, 2, 1–30. [Google Scholar] [CrossRef]
- Jayakumar, K.; Babu, M.G. Discrete Weibull geometric distribution and its properties. Commun.-Stat.-Theory Methods 2018, 47, 1767–1783. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 20 January 2025).
- Brunello, G.H.V.; Nakano, E.Y. A Bayesian Measure of Model Accuracy. Entropy 2024, 26, 510. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, E.L.; Meier, P. Nonparametric estimation from incomplete observations. J. Am. Stat. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Nakano, E.Y.; Carrasco, C.G. Uma avaliação do uso de um modelo contínuo na análise de dados discretos de sobrevivência. Trends Comput. Appl. Math. 2006, 7, 91–100. [Google Scholar] [CrossRef][Green Version]

| Scenario | q | Baseline Hazard | |||
|---|---|---|---|---|---|
| 1.50 | 0.95 | 2.0 | 1.0 | Increasing | |
| 0.75 | 0.95 | 2.0 | 1.0 | Decreasing |
| n | Scen. | Cens. Perc. | q | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Average | MSE | CP | Average | MSE | CP | Average | MSE | CP | Average | MSE | CP | |||
| 30 | 0% | 0.9549 | 0.0008 | 0.4710 | 1.6720 | 0.1146 | 0.4450 | 2.1967 | 0.3592 | 0.4650 | 1.1116 | 0.1102 | 0.4660 | |
| 0.9548 | 0.0008 | 0.4700 | 0.8348 | 0.0278 | 0.4360 | 2.1919 | 0.3417 | 0.4580 | 1.1096 | 0.1044 | 0.4670 | |||
| 10% | 0.9531 | 0.0009 | 0.4910 | 1.6805 | 0.1316 | 0.4550 | 2.1873 | 0.4327 | 0.4580 | 1.1102 | 0.1385 | 0.4740 | ||
| 0.9548 | 0.0008 | 0.4800 | 0.8468 | 0.0345 | 0.4420 | 2.2406 | 0.4215 | 0.4700 | 1.0937 | 0.0984 | 0.4550 | |||
| 30% | 0.9525 | 0.0013 | 0.4690 | 1.7631 | 0.2399 | 0.4190 | 2.1337 | 0.4754 | 0.4740 | 1.0854 | 0.1533 | 0.4580 | ||
| 0.9530 | 0.0010 | 0.4550 | 0.8463 | 0.0430 | 0.4250 | 2.2026 | 0.4496 | 0.4650 | 1.1266 | 0.2111 | 0.4820 | |||
| 50 | 0% | 0.9540 | 0.0005 | 0.4850 | 1.6085 | 0.0589 | 0.4500 | 2.1364 | 0.2219 | 0.4780 | 1.0789 | 0.0629 | 0.4550 | |
| 0.9539 | 0.0005 | 0.4780 | 0.8031 | 0.0142 | 0.4390 | 2.1285 | 0.2066 | 0.4690 | 1.0781 | 0.0617 | 0.4520 | |||
| 10% | 0.9534 | 0.0006 | 0.4740 | 1.6253 | 0.0784 | 0.4350 | 2.1543 | 0.2522 | 0.4440 | 1.0635 | 0.0630 | 0.4980 | ||
| 0.9536 | 0.0005 | 0.4800 | 0.8104 | 0.0150 | 0.4500 | 2.1180 | 0.1898 | 0.4830 | 1.0263 | 0.0552 | 0.5060 | |||
| 30% | 0.9538 | 0.0007 | 0.4550 | 1.6511 | 0.1005 | 0.4150 | 2.1014 | 0.2798 | 0.4490 | 1.0477 | 0.0717 | 0.4460 | ||
| 0.9542 | 0.0006 | 0.4580 | 0.7920 | 0.0208 | 0.4950 | 2.1823 | 0.2808 | 0.4690 | 1.0798 | 0.0818 | 0.4850 | |||
| 100 | 0% | 0.9519 | 0.0002 | 0.4890 | 1.5504 | 0.0214 | 0.4880 | 2.0666 | 0.0784 | 0.4980 | 1.0357 | 0.0252 | 0.5000 | |
| 0.9518 | 0.0002 | 0.5040 | 0.7743 | 0.0052 | 0.4830 | 2.0631 | 0.0766 | 0.4980 | 1.0345 | 0.0246 | 0.4970 | |||
| 10% | 0.9505 | 0.0003 | 0.5000 | 1.5460 | 0.0244 | 0.4680 | 2.0348 | 0.0942 | 0.4510 | 1.0247 | 0.0236 | 0.4770 | ||
| 0.9507 | 0.0003 | 0.4930 | 0.7824 | 0.0064 | 0.4690 | 2.0296 | 0.0852 | 0.4960 | 1.0186 | 0.0215 | 0.4930 | |||
| 30% | 0.9530 | 0.0003 | 0.4910 | 1.5711 | 0.0382 | 0.4860 | 2.0271 | 0.1182 | 0.4730 | 1.0045 | 0.0269 | 0.4390 | ||
| 0.9510 | 0.0003 | 0.4870 | 0.7722 | 0.0080 | 0.4880 | 2.0587 | 0.0970 | 0.4940 | 1.0336 | 0.0290 | 0.4890 | |||
| 250 | 0% | 0.9502 | 0.0001 | 0.5020 | 1.5151 | 0.0071 | 0.5050 | 2.0146 | 0.0300 | 0.5050 | 1.0068 | 0.0068 | 0.5310 | |
| 0.9502 | 0.0001 | 0.5120 | 0.7574 | 0.0017 | 0.5000 | 2.0146 | 0.0288 | 0.5220 | 1.0068 | 0.0066 | 0.5370 | |||
| 10% | 0.9508 | 0.0001 | 0.5080 | 1.5228 | 0.0086 | 0.4980 | 2.0112 | 0.0301 | 0.5200 | 1.0039 | 0.0088 | 0.4720 | ||
| 0.9499 | 0.0001 | 0.5070 | 0.7636 | 0.0022 | 0.4740 | 1.9993 | 0.0319 | 0.4740 | 1.0013 | 0.0074 | 0.4940 | |||
| 30% | 0.9518 | 0.0001 | 0.5010 | 1.5273 | 0.0120 | 0.4920 | 1.9853 | 0.0386 | 0.4860 | 0.9897 | 0.0114 | 0.4510 | ||
| 0.9513 | 0.0001 | 0.5090 | 0.7513 | 0.0029 | 0.4890 | 2.0446 | 0.0387 | 0.4920 | 1.0233 | 0.0102 | 0.4830 | |||
| 500 | 0% | 0.9497 | 0.0001 | 0.4940 | 1.5060 | 0.0036 | 0.4950 | 2.0016 | 0.0145 | 0.4910 | 1.0039 | 0.0034 | 0.4880 | |
| 0.9502 | 0.0001 | 0.4900 | 0.7539 | 0.0009 | 0.4870 | 2.0113 | 0.0147 | 0.4700 | 1.0050 | 0.0036 | 0.5030 | |||
| 10% | 0.9510 | 0.0001 | 0.4950 | 1.5124 | 0.0041 | 0.4960 | 2.0046 | 0.0152 | 0.5160 | 1.0006 | 0.0041 | 0.5160 | ||
| 0.9505 | 0.0001 | 0.5070 | 0.7592 | 0.0011 | 0.4950 | 2.0096 | 0.0143 | 0.5080 | 1.0033 | 0.0040 | 0.4830 | |||
| 30% | 0.9523 | 0.0001 | 0.4840 | 1.5185 | 0.0059 | 0.5140 | 1.9775 | 0.0198 | 0.4810 | 0.9830 | 0.0057 | 0.4580 | ||
| 0.9509 | 0.0001 | 0.5140 | 0.7483 | 0.0014 | 0.5040 | 2.0185 | 0.0179 | 0.5030 | 1.0148 | 0.0047 | 0.5160 | |||
| Survival Time | z | Survival Time | z |
|---|---|---|---|
| 18 | 0 | 8 | 1 |
| 9 | 0 | 2 | 1 |
| 28+ | 0 | 26+ | 1 |
| 31 | 0 | 10 | 1 |
| 39+ | 0 | 4 | 1 |
| 19+ | 0 | 3 | 1 |
| 45+ | 0 | 4 | 1 |
| 6 | 0 | 18 | 1 |
| 8 | 0 | 8 | 1 |
| 15 | 0 | 3 | 1 |
| 23 | 0 | 14 | 1 |
| 28+ | 0 | 3 | 1 |
| 7 | 0 | 13 | 1 |
| 12 | 1 | 13 | 1 |
| 9 | 1 | 35+ | 1 |
| Variable | Parameters | Estimate | Standard Error | CI (95%) | p-Value |
|---|---|---|---|---|---|
| Age a | q | 0.9881 | 0.0084 | [0.9528; 0.9971] | - |
| 1.2611 | 0.1962 | [0.8545; 1.8611] | - | ||
| 1.1484 | 0.4383 | [0.2894; 2.0074] | 0.0088 |
| Covariate Level | |||
|---|---|---|---|
| 0.11122 | 0.11297 | 0.16937 | |
| 0.14214 | 0.14049 | 0.11118 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franque, T.C.E.; Cardial, M.R.P.; Nakano, E.Y. Proportional Log Survival Model for Discrete Time-to-Event Data. Mathematics 2025, 13, 800. https://doi.org/10.3390/math13050800
Franque TCE, Cardial MRP, Nakano EY. Proportional Log Survival Model for Discrete Time-to-Event Data. Mathematics. 2025; 13(5):800. https://doi.org/10.3390/math13050800
Chicago/Turabian StyleFranque, Tiago Chandiona Ernesto, Marcílio Ramos Pereira Cardial, and Eduardo Yoshio Nakano. 2025. "Proportional Log Survival Model for Discrete Time-to-Event Data" Mathematics 13, no. 5: 800. https://doi.org/10.3390/math13050800
APA StyleFranque, T. C. E., Cardial, M. R. P., & Nakano, E. Y. (2025). Proportional Log Survival Model for Discrete Time-to-Event Data. Mathematics, 13(5), 800. https://doi.org/10.3390/math13050800








