A Non-Self-Referential Characterization of the Gram–Schmidt Process via Computational Induction
Abstract
1. Introduction
- ;
- ;
- ;⋮
- ;
- ;⋮
- .
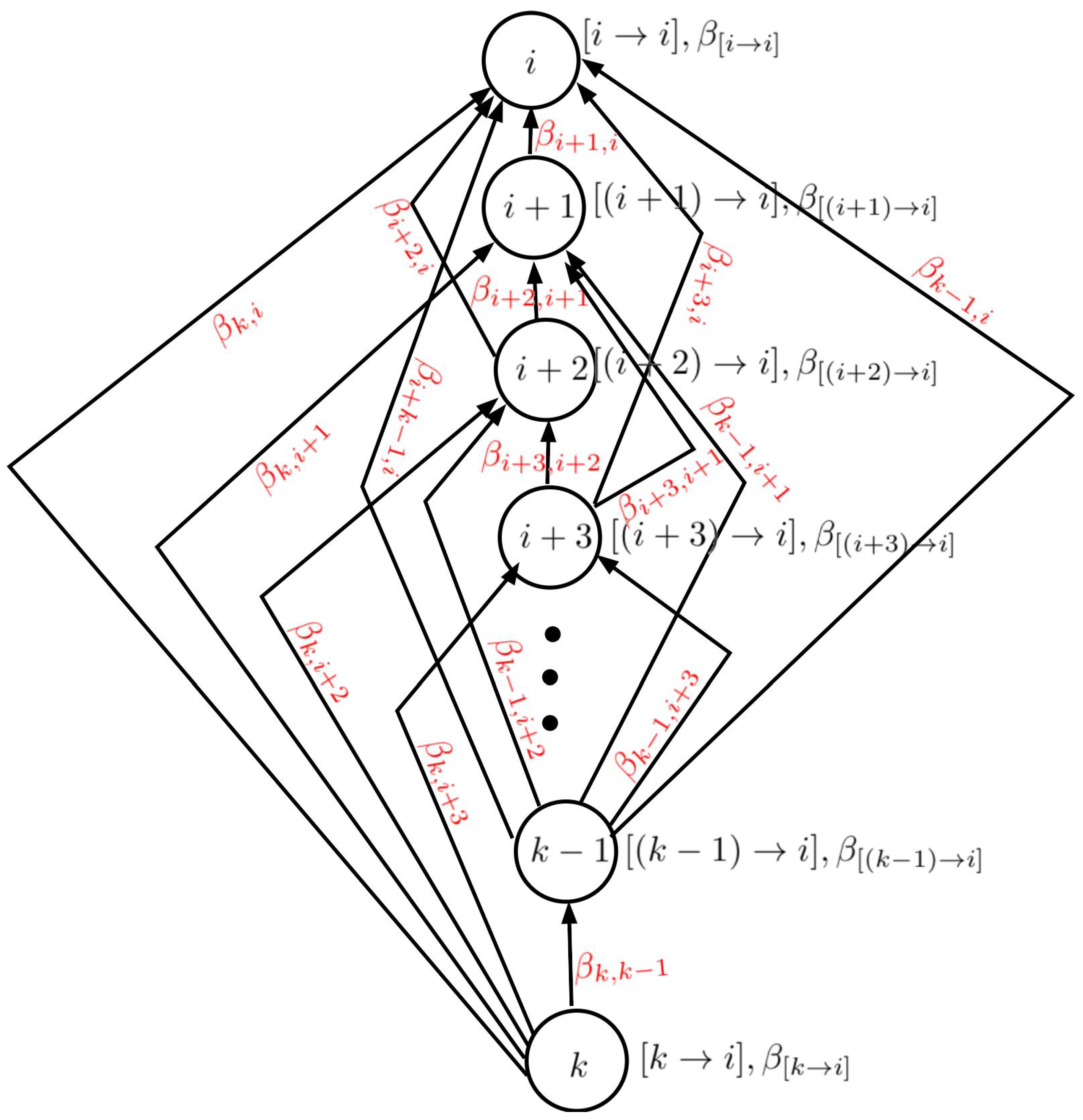
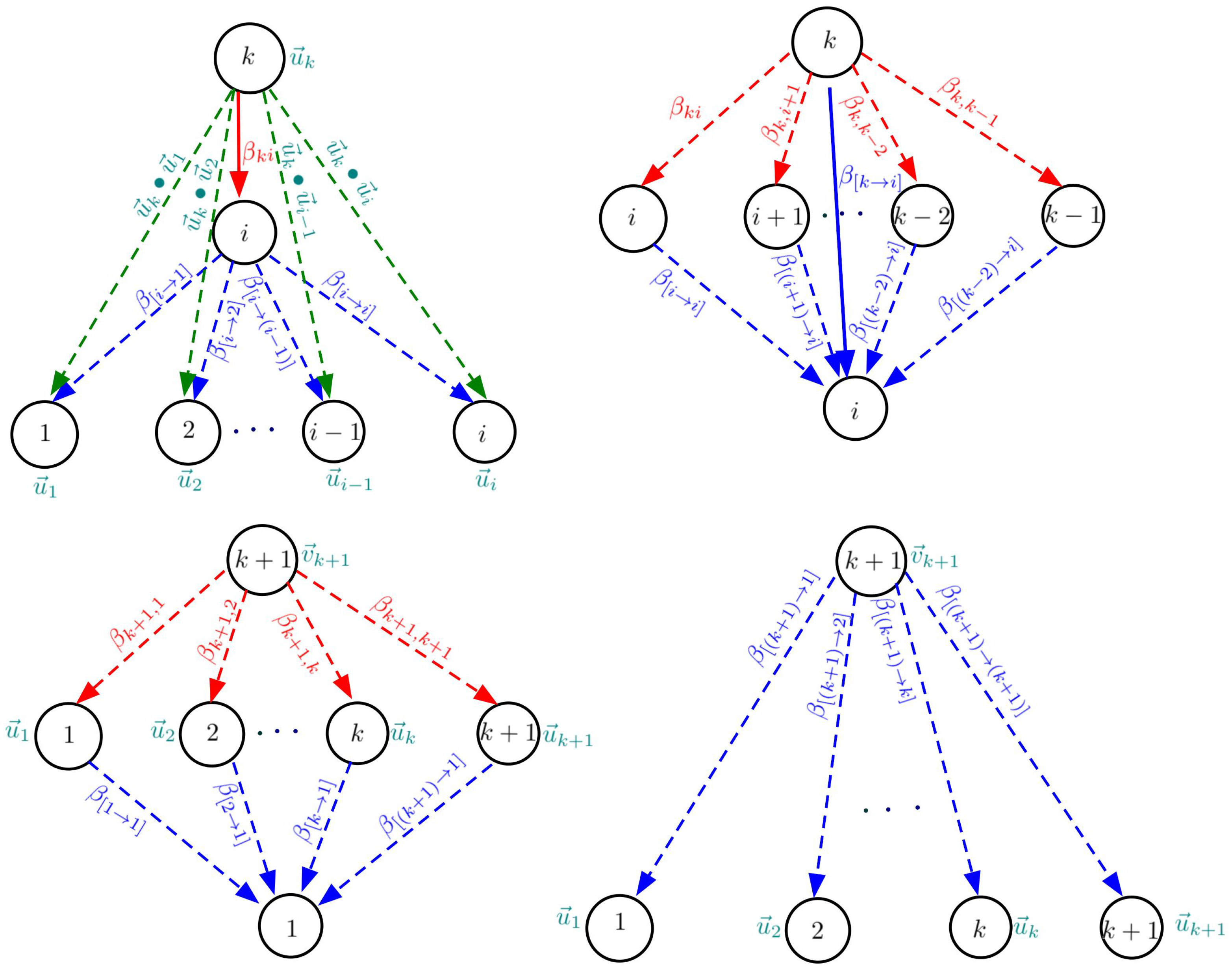
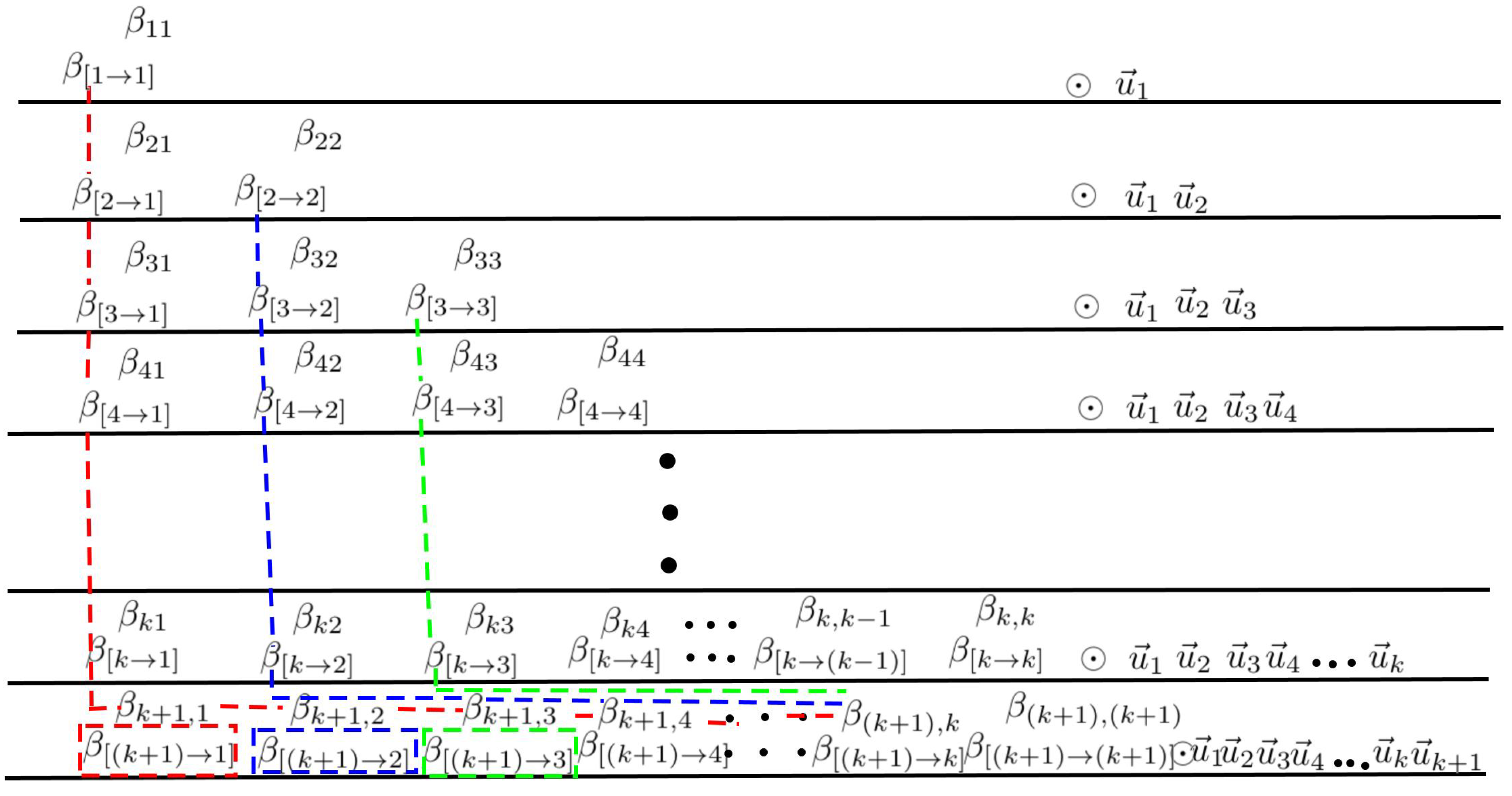
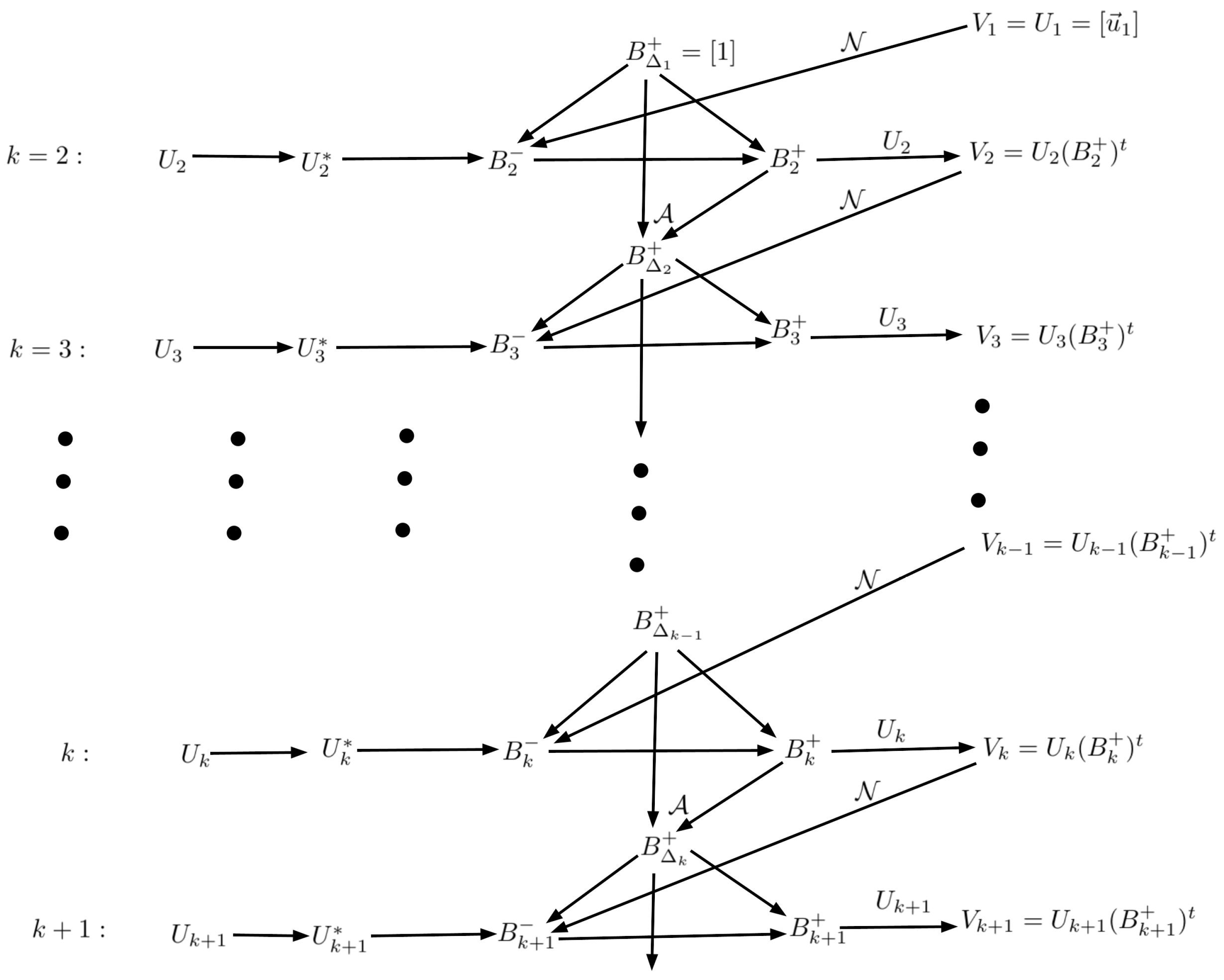
2. Theories and Methods
- ;
- ;
- ;
- 1.
- ; ; ;; ;
- 2.
- ; ;;; ;
- 3.
- ; ; ;;
- 4.
- ; ; ; .
3. Application One
- ;
- ;
- ;
- .

4. Application Two
- Collect time-series data (from Year 2013 to Year 2023) for 202 countries (see Numbered 202 countries.pdf in https://github.com/raymingchen/Gram-Schimdt-Process/blob/ae4e4e7d98059e4dc1cd08b3591b884d4acdc13a/Numbered%20202%20countries.pdf (accessed on 10 February 2025)) from Data Bank. The source data are further processed to fit our purpose and saved as data.csv (https://github.com/raymingchen/Gram-Schimdt-Process/blob/920de0ef528c06058cf0178b2b1718d99862c254/data.csv (accessed on 10 February 2025)). There are six indicators to be studied:
- () Control of Corruption: Estimate;
- () Government Effectiveness: Estimate;
- () Political Stability and Absence of Violence/Terrorism: Estimate;
- () Regulatory Quality: Estimate;
- () Rule of Law: Estimate;
- () Voice and Accountability: Estimate.
For the source data, the meaning of the indicators and how they are collected/computed in the database, please refer to Worldwide Governance Indicators, in particular its Metadata, or https://databank.worldbank.org/source/worldwide-governance-indicators?l=en# (accessed on 10 February 2025). We could use the set of column vectors to denote the set of all the time-series data collected, where each column vector is a 6-by-1 column vector (matrix) recording the values of for country j at Year t. - Single out 6 representative countries as benchmarks: China (), France (), Germany (), India (), Russia Federatioin (), USA ()-the exact content could refer to 6 representative.pdf (https://github.com/raymingchen/Gram-Schimdt-Process/blob/920de0ef528c06058cf0178b2b1718d99862c254/6%20representatives.pdf (accessed on 10 February 2025)); let column vectors denote the values of at Year t; and a 6-by-6 matrix ; for example, is the matrix form of the following tabulated data of Table 1.
- For each Year t, define a 202-by-6 matrix where T denotes the transpose. For example (round to 2 decimal places),and implement the matrix multiplication (regarded as a set of projections from the vectors in onto the vectors in ) to form a 202-by-6 matrix that records the projection values of all the 202 countries onto the 6 representatives at Year t. We partially demonstrate (round to 2 decimal places) the 202-by-6 matrix, where each row vector represents the projection of vector on the representative vectors . For the full matrix, one could refer to the file named Y_2013ontoU2013.pdf (https://github.com/raymingchen/Gram-Schimdt-Process/blob/3443a9e08ab603e7754d959acfd1189f1e30e248/Y_2013ontoU2013.pdf (accessed on 10 February 2025)). We also skip all the other presentations of ;
- For each year t, find the set of orthogonal vectors of the 6 representatives to yield the maximally-independent vectors (or hidden features) in terms of 6 representatives via the non-self referential representation presented in this article. The implementation of this conversion could refer to Non-self-referential GSP.R in https://github.com/raymingchen/Gram-Schimdt-Process/blob/3d28a5349bf514770c23a5df8950f8fc674aa9d7/Non_self_referential%20GSP.R (accessed on 10 February 2025). For the whole results from to , please refer to https://github.com/raymingchen/Gram-Schimdt-Process/blob/e6f2c27c9ab16a17e0370d1e1c7bd0382f49aeef/Vk_2013to2023.pdf (accessed on 10 February 2025). For example (round to 2 decimal places),;
- Since (by Lemma 2), we compute , indeed we could recursively compute these values directly from evaluating each via our method (this is implemented by the file named code and data for application Two_19.R in https://github.com/raymingchen/Gram-Schimdt-Process/blob/5c8327b7782a16fcd06092814b9192a1fdf8182e/code%20and%20data%20for%20application%20Two_19.R (accessed on 10 February 2025)). For example (round to 2 decimal places and read as row vectors),where each is the projection of the vector onto . For a complete computed result of , please refer to the file Vk_2013to2023.pdf in https://github.com/raymingchen/Gram-Schimdt-Process/blob/8edd29d1b755559b5755a491422f534dd30dd8fa/Vk_2013to2023.pdf (accessed on 10 February 2025)
- For each year t, compute the set of cosine values . For a partial demonstration (round to 2 decimal places), where reflects the similarity of governance systems between country j and the other 6 orthogonal features.
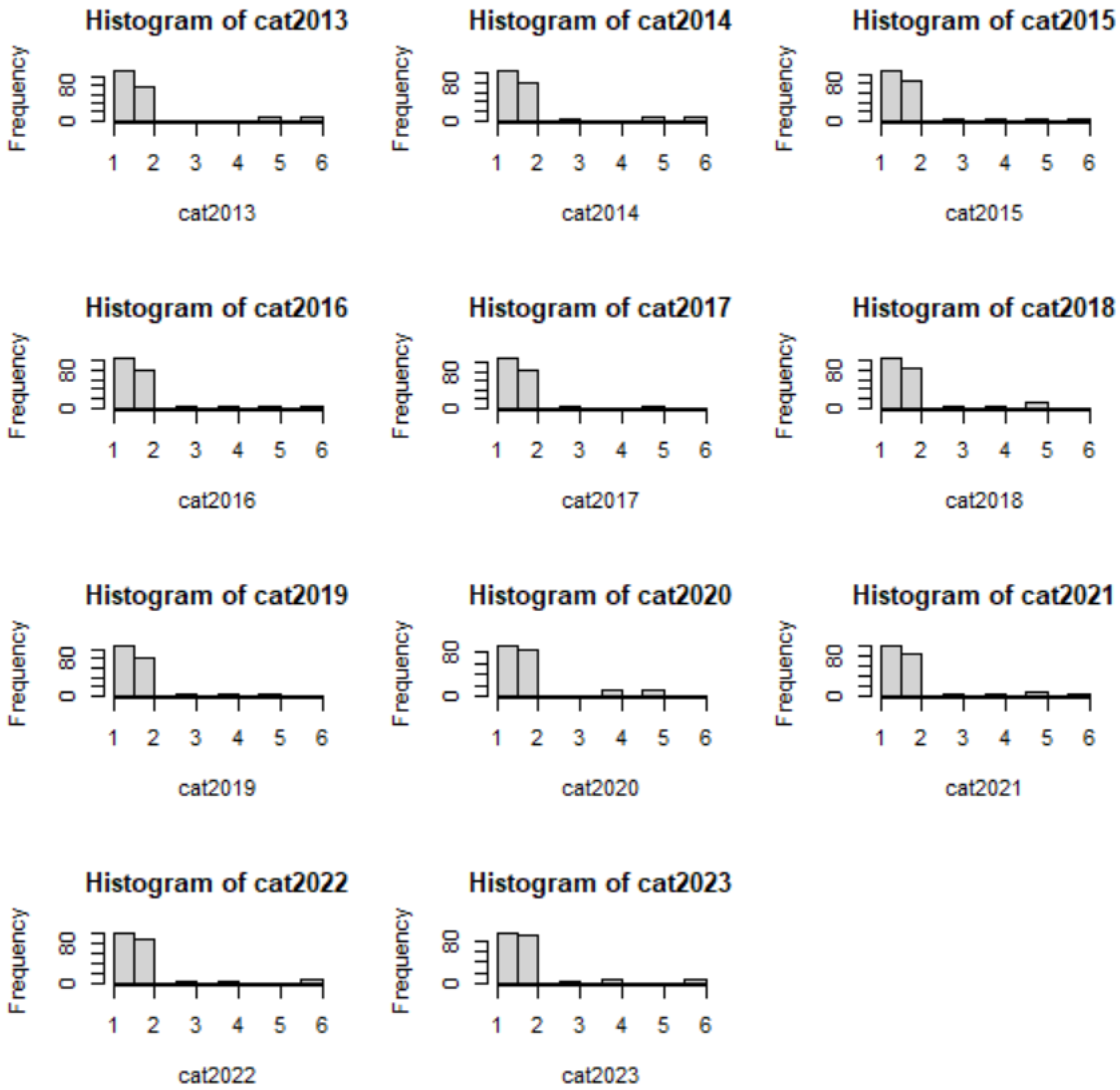
- Assign the categories (from 1 to 6) for each country by its maximal cosine value among all the 6 features. For each year t, find the positions (among columns) that yield the maximal values of , row by row—let us name the categorization at year t by . For example, in the previous case, . The detailed categorization for all is presented in the Appendix A Listing A1. The categorization regarding the 6 representative countries is in particular singled out in Table 2. As for the statistics of the categorization distribution for the other countries, they are revealed in Figure 6.
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Categorization of the 202 Countries Year by Year: 2013–2023
| Listing A1. The categories assigned to the 202 countries from Year 2013 (cat2013) to 2023 (cat2023). In total, there were six categories—1, 2, 3, 4, 5, and 6—for the 202 countries (in which square brackets are used to identify the order of these countries). |
| > cat2013: [1] 1 1 1 2 1 2 1 1 2 2 2 1 2 2 1 2 1 2 1 1 1 1 1 2 5 2 5 1 1 2 1 1 2 2 [35] 1 1 2 1 1 1 1 1 2 1 2 1 2 2 2 1 2 1 1 1 1 1 1 2 1 1 1 2 2 2 1 1 2 2 [69] 5 2 2 2 1 1 1 1 1 1 2 2 2 1 1 1 1 2 2 2 5 2 2 2 1 1 6 1 2 1 1 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 6 1 2 5 6 1 1 5 1 1 1 2 6 1 2 2 1 1 1 5 [137] 2 2 1 6 5 1 1 1 1 2 2 2 2 2 1 1 2 1 1 1 1 2 1 2 2 2 1 1 2 1 2 1 2 2 [171] 2 1 1 2 2 1 2 1 1 1 1 1 1 5 1 2 1 6 1 1 2 2 2 2 1 6 1 1 1 1 1 1. > cat2014: [1] 1 3 1 2 1 2 1 1 2 2 2 1 2 2 1 2 1 2 1 1 2 1 1 2 5 2 2 1 1 2 1 1 2 2 [35] 1 1 2 1 5 1 1 1 2 1 2 1 2 2 2 1 2 1 1 1 5 1 1 2 1 1 1 2 2 2 1 1 2 2 [69] 6 2 2 2 1 1 1 1 1 1 2 2 2 1 1 1 1 2 2 2 5 2 2 2 1 1 6 1 2 1 1 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 6 1 2 1 6 1 1 2 1 1 1 2 1 1 2 2 1 1 1 2 [137] 2 2 1 6 2 1 1 5 1 2 2 2 2 2 1 2 2 1 1 6 3 2 1 2 2 2 1 1 2 1 2 1 3 2 [171] 2 1 1 2 2 1 2 1 1 1 1 1 6 5 1 2 1 6 1 1 2 2 2 2 1 6 1 1 1 1 1 1. > cat2015: [1] 1 3 1 2 1 2 1 1 2 2 2 1 2 2 1 2 1 2 1 1 2 1 1 2 1 2 2 1 1 2 1 1 2 2 [35] 1 1 2 1 2 1 1 1 2 1 2 1 2 2 2 1 2 1 1 1 1 1 1 2 1 1 1 2 2 2 1 1 2 2 [69] 6 2 2 2 1 1 1 1 1 1 2 2 2 1 1 1 1 2 2 2 4 2 2 2 1 1 5 1 2 1 1 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 5 1 2 1 5 1 1 2 1 1 1 2 1 1 2 2 1 1 1 2 [137] 2 2 1 2 2 1 1 3 1 2 2 2 2 2 1 2 2 1 1 5 3 2 1 2 2 2 1 1 2 1 2 1 2 2 [171] 2 1 1 2 2 1 2 1 1 1 1 1 6 4 1 2 1 6 1 1 2 2 2 2 1 6 1 1 1 1 1 1. > cat2016: [1] 1 3 1 2 1 2 1 1 2 2 2 1 2 2 1 2 1 2 1 1 2 1 1 2 1 2 2 1 1 2 1 1 2 2 [35] 1 1 2 1 4 1 1 1 2 1 2 1 2 2 2 1 2 1 1 1 1 1 1 2 1 1 5 2 2 2 1 1 2 2 [69] 6 2 2 2 1 1 1 1 1 1 2 2 2 1 1 1 1 2 2 2 4 2 2 2 1 1 5 1 2 1 1 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 5 1 2 1 5 1 4 2 1 1 1 2 1 1 2 2 1 1 1 3 [137] 2 2 1 2 3 1 1 3 1 2 2 2 2 2 1 2 2 1 1 5 4 2 1 2 2 2 1 1 2 1 2 1 2 2 [171] 2 1 1 2 2 1 2 1 1 1 1 1 6 4 1 1 1 6 1 1 2 2 2 2 1 6 1 1 1 1 1 1. > cat2017: [1] 1 3 1 2 1 2 1 1 2 2 2 1 2 2 1 2 1 2 1 1 2 1 1 2 1 2 2 1 1 2 1 1 2 2 [35] 1 1 2 1 4 1 1 1 2 1 2 1 2 2 2 1 2 1 1 1 1 1 1 2 1 1 2 2 2 2 1 1 2 2 [69] 5 2 2 2 1 1 1 1 1 1 2 2 2 1 1 1 1 2 2 2 2 2 2 2 1 1 5 1 2 1 1 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 5 1 2 1 1 1 1 2 1 1 1 2 1 1 2 2 1 1 1 2 [137] 2 2 1 2 2 1 1 3 1 2 2 2 2 2 1 2 2 1 1 1 1 2 1 2 2 2 1 1 2 1 2 1 2 2 [171] 2 1 1 2 2 1 2 1 1 1 1 1 5 5 1 1 1 5 1 1 2 2 2 2 1 6 1 1 1 1 1 1. > cat2018: [1] 1 5 1 2 1 2 5 3 2 2 2 1 2 2 1 2 1 2 1 1 2 1 1 2 1 2 2 1 1 2 1 1 2 2 [35] 1 1 2 1 4 1 1 1 2 1 2 1 2 2 2 1 2 1 1 1 1 1 1 2 1 1 2 2 2 2 1 1 2 2 [69] 5 2 2 3 1 1 1 1 1 1 2 2 2 1 1 1 1 2 2 2 2 2 2 2 1 1 5 1 2 1 1 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 5 1 2 1 5 1 5 2 1 1 1 2 2 1 2 2 1 1 1 2 [137] 2 2 1 2 5 1 1 3 1 2 2 2 2 2 1 2 2 1 1 4 1 2 1 2 2 2 1 1 5 1 2 1 2 2 [171] 2 1 1 2 2 1 2 1 1 1 1 1 5 5 1 1 1 6 1 1 2 2 2 2 1 5 1 1 1 1 1 1. > cat2019: [1] 1 5 1 2 1 2 1 2 2 2 2 1 2 2 1 2 1 2 1 1 2 1 1 2 1 2 2 1 1 2 1 1 2 2 [35] 1 1 2 1 2 1 1 1 2 1 2 1 2 2 2 1 2 1 1 1 1 1 1 2 1 1 2 2 2 2 1 1 2 2 [69] 4 2 2 3 1 1 1 1 1 1 2 2 2 1 1 1 1 2 2 2 2 2 2 1 1 1 3 1 2 1 1 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 3 1 2 1 3 1 5 2 1 1 1 2 3 1 2 2 1 1 1 2 [137] 2 2 1 2 2 1 1 2 1 2 2 2 2 2 1 1 2 1 1 1 1 2 1 2 2 2 1 1 5 1 2 1 2 2 [171] 2 1 1 2 2 1 2 1 1 1 1 1 6 4 1 1 1 3 1 1 2 2 2 2 1 4 1 1 1 1 1 1. > cat2020: [1] 1 5 1 2 1 2 4 2 2 2 2 1 2 2 1 2 1 2 4 1 2 1 1 2 4 2 2 1 1 2 1 1 2 2 [35] 1 1 2 1 5 1 1 1 2 1 2 1 2 2 2 1 2 5 1 1 5 1 1 2 1 1 2 2 2 2 1 1 2 2 [69] 4 2 2 2 1 1 1 1 1 1 2 2 2 1 5 1 1 2 2 2 2 2 2 2 1 1 2 1 2 1 2 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 4 1 2 1 4 5 5 2 1 1 1 2 2 1 2 2 1 1 1 2 [137] 2 2 1 2 2 1 5 2 1 2 2 2 2 2 1 1 2 1 1 4 5 2 1 2 2 2 4 1 5 1 2 1 2 2 [171] 2 1 1 2 2 1 2 1 1 1 4 1 6 4 4 1 1 3 1 1 2 2 2 2 1 4 1 1 1 1 1 1. > cat2021: [1] 1 5 1 2 1 2 1 2 2 2 2 1 2 2 1 2 1 2 1 1 1 1 1 2 4 2 2 1 1 2 1 1 2 2 [35] 1 1 2 1 5 1 1 1 2 1 2 1 2 2 2 1 2 5 1 1 1 1 1 2 1 1 2 2 2 2 1 1 2 2 [69] 4 2 2 2 1 1 1 1 1 1 2 2 2 1 2 1 1 2 2 2 2 2 2 2 1 1 3 1 2 1 2 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 1 1 2 1 1 5 4 2 1 1 1 2 2 1 2 2 1 1 1 2 [137] 2 2 1 2 2 1 1 5 1 2 2 2 2 2 1 2 2 1 2 1 5 2 1 2 2 2 1 1 4 1 2 1 2 2 [171] 2 1 1 2 2 1 2 1 1 1 1 1 6 5 1 1 1 3 1 1 2 2 2 2 1 6 1 1 1 1 1 1. > cat2022: [1] 1 2 1 2 1 2 1 4 2 2 2 1 2 2 1 2 1 2 1 1 2 1 1 2 1 2 2 1 1 2 1 1 2 2 [35] 1 1 2 1 6 1 1 1 2 1 2 1 2 2 2 1 2 6 1 1 1 1 1 2 1 1 2 2 2 2 1 1 2 2 [69] 1 2 2 2 1 1 1 1 1 1 2 2 2 1 2 1 1 2 2 2 2 2 2 2 1 1 3 1 2 1 2 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 3 1 2 1 1 6 1 2 1 1 1 2 2 1 2 2 1 1 1 2 [137] 2 2 1 2 6 1 1 6 6 2 2 2 2 2 1 2 2 1 2 1 6 2 1 2 2 2 1 1 4 1 2 1 2 2 [171] 2 1 1 2 2 1 2 1 1 2 1 1 4 4 1 1 1 2 1 1 2 2 2 2 1 3 1 1 1 1 1 1. > cat2023: [1] 1 2 1 2 1 2 1 5 2 2 2 1 2 2 1 2 1 2 4 1 2 1 1 2 4 2 2 1 1 2 1 1 2 2 [35] 1 1 2 1 6 1 1 1 2 1 2 1 2 2 2 1 2 2 1 1 1 1 1 2 1 1 2 2 2 2 1 1 2 2 [69] 4 2 2 2 1 1 1 1 1 1 2 2 2 1 2 1 1 2 2 2 2 2 2 2 1 1 3 1 2 1 2 1 1 2 [103] 1 1 1 1 2 2 2 2 1 1 2 1 1 2 4 1 2 1 3 6 4 2 1 1 1 2 2 1 2 2 1 1 1 2 [137] 2 2 1 2 6 1 6 6 6 2 2 2 2 2 1 2 2 1 2 1 6 2 1 2 2 2 1 1 4 1 2 1 2 2 [171] 2 1 1 2 2 1 2 1 1 6 1 1 4 4 1 1 1 2 1 1 2 2 2 2 1 3 1 1 1 1 1 1. |
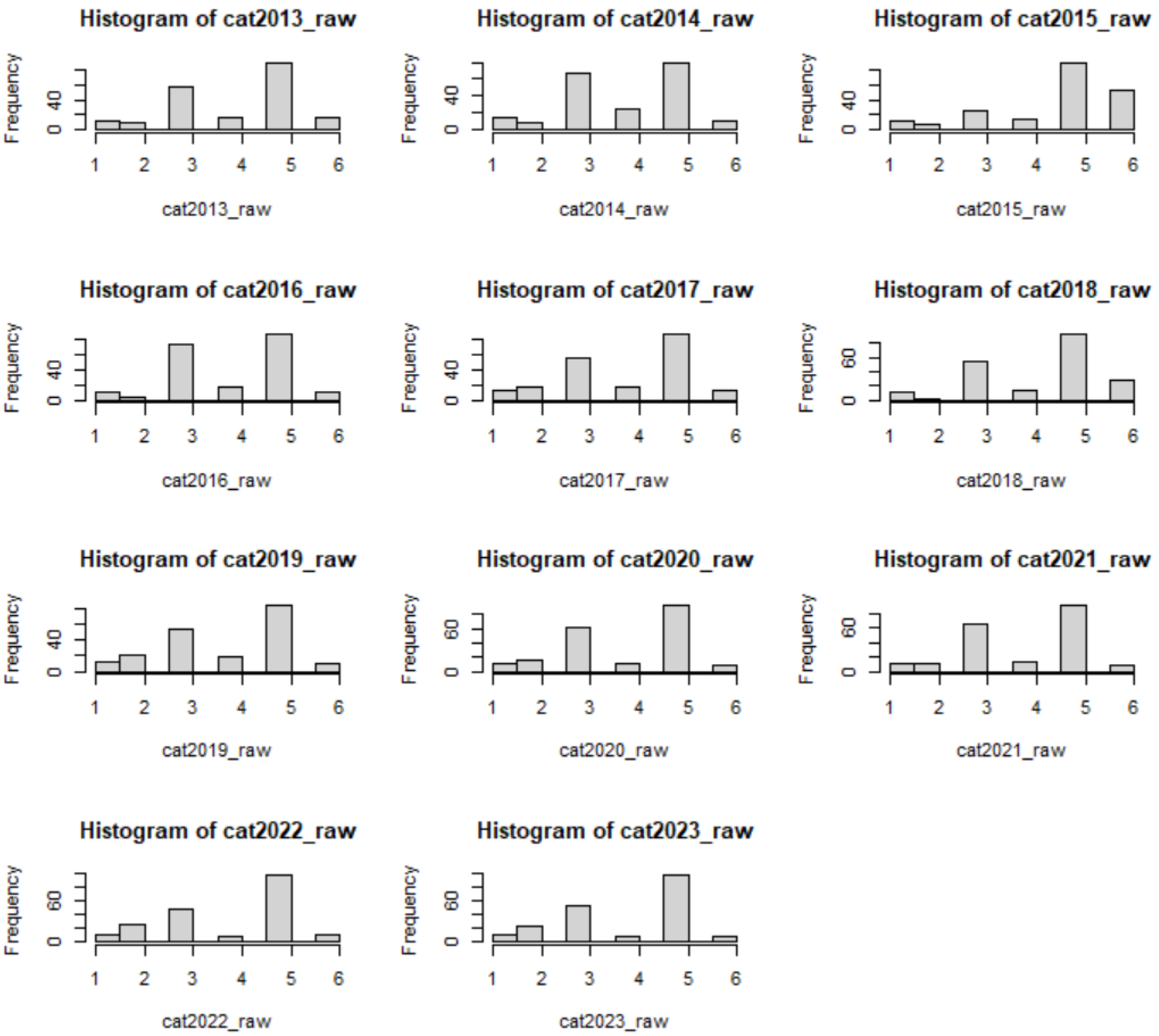
Appendix B. Raw Categorization of 202 Countries Year by Year: 2013–2023
| > cat2013_raw |
| [1] 5 5 5 3 5 3 5 5 3 3 3 5 3 1 5 3 1 3 4 5 3 5 5 3 4 6 3 5 5 3 5 5 3 3 |
| [35] 5 5 3 1 4 5 5 5 3 5 6 1 2 6 3 5 3 5 5 5 5 5 5 3 1 5 1 3 2 2 5 5 2 3 |
| [69] 3 2 3 3 5 5 5 5 5 5 6 3 3 4 5 5 5 3 2 3 2 3 3 1 5 5 3 5 6 5 1 5 5 6 |
| [103] 5 5 5 5 3 3 3 6 5 5 6 5 4 3 4 5 6 4 3 5 5 6 5 5 5 3 4 5 3 3 5 5 5 5 |
| [137] 3 1 5 3 4 5 5 4 4 3 6 3 6 6 5 1 3 5 1 5 4 3 5 6 3 3 5 5 2 5 2 5 3 3 |
| [171] 3 5 4 3 3 5 6 5 5 4 5 5 3 2 4 4 5 3 5 5 6 3 6 3 5 3 5 1 5 5 5 5 |
| > cat2014_raw |
| [1] 5 5 5 6 5 3 4 5 3 3 3 5 3 1 5 3 1 3 4 4 3 5 5 3 4 3 3 5 5 2 5 5 3 3 |
| [35] 5 5 3 1 4 5 5 5 3 5 3 1 3 3 3 5 3 5 5 5 5 5 5 3 1 5 1 3 2 3 5 5 2 3 |
| [69] 4 2 3 3 5 5 5 5 5 5 3 3 3 4 4 5 5 3 2 3 4 6 3 1 1 4 4 5 6 5 1 5 1 3 |
| [103] 5 4 5 5 3 3 3 3 5 5 6 5 4 3 4 5 3 5 3 5 5 3 5 5 5 3 4 5 3 3 5 4 5 3 |
| [137] 3 3 5 4 3 5 5 4 4 3 3 3 6 3 5 1 3 4 1 4 3 6 5 6 3 3 4 5 2 5 2 1 3 3 |
| [171] 3 5 4 3 3 5 3 5 5 5 5 5 3 2 4 5 5 3 5 4 6 6 6 3 5 3 5 1 5 5 5 5 |
| > cat2015_raw |
| [1] 5 5 5 6 5 6 4 5 3 3 6 5 6 1 5 6 5 3 4 5 6 5 5 6 4 6 3 5 5 6 5 5 6 6 |
| [35] 5 5 3 1 4 5 5 5 3 5 6 1 3 6 3 5 6 5 5 5 5 5 5 3 1 5 3 3 2 3 5 5 2 3 |
| [69] 4 2 6 3 5 5 5 5 5 5 6 6 6 4 4 5 5 3 2 3 4 6 6 1 5 5 6 5 2 5 1 5 5 3 |
| [103] 5 5 5 5 6 6 6 6 5 5 6 5 5 6 6 5 6 5 6 5 5 3 5 5 5 6 6 5 3 6 5 5 5 5 |
| [137] 6 1 5 6 3 5 5 5 4 6 6 6 6 3 5 1 6 5 1 4 6 6 5 6 6 6 5 5 2 5 2 1 3 6 |
| [171] 6 5 4 3 6 5 6 5 5 1 5 5 4 6 4 4 5 6 5 5 6 3 6 3 5 4 5 1 5 5 5 5 |
| > cat2016_raw |
| [1] 5 5 5 3 5 3 4 5 3 3 3 5 3 1 5 3 5 3 4 5 3 5 5 3 4 3 3 4 5 3 5 5 3 3 |
| [35] 5 5 3 1 4 5 5 5 3 5 3 1 3 3 3 5 3 5 5 5 5 5 5 3 5 5 3 3 2 6 5 5 2 3 |
| [69] 4 2 3 3 5 5 5 4 5 5 6 3 3 4 4 5 5 3 2 3 3 3 3 1 5 4 3 5 6 5 1 5 5 6 |
| [103] 5 5 5 5 3 3 3 3 5 5 6 5 5 3 3 5 3 5 3 5 3 3 5 5 5 3 3 5 3 3 5 5 5 5 |
| [137] 3 1 5 3 6 5 5 4 4 3 3 6 3 6 5 1 3 5 1 4 4 3 5 3 3 3 5 5 2 5 6 5 3 3 |
| [171] 3 5 4 3 3 5 3 5 5 1 5 5 3 3 4 5 5 3 5 4 3 3 6 3 5 3 5 1 5 5 5 5 |
| > cat2017_raw |
| [1] 5 5 5 3 5 3 4 5 3 3 3 5 3 1 5 3 5 3 5 5 3 5 5 3 4 6 3 4 5 3 5 5 3 3 |
| [35] 5 5 3 1 4 5 5 5 3 5 3 1 3 3 3 5 3 5 5 5 5 5 5 3 1 5 3 3 2 2 5 5 6 3 |
| [69] 4 2 3 3 5 5 5 4 5 5 6 3 3 4 4 5 5 3 6 3 2 3 2 1 1 5 2 5 6 5 1 5 5 6 |
| [103] 5 5 5 5 3 3 3 6 5 5 6 5 4 3 2 5 3 5 2 5 5 6 5 5 5 2 3 5 3 3 5 5 5 5 |
| [137] 3 1 5 2 3 5 5 4 4 3 3 3 1 2 5 1 2 5 1 4 5 3 5 6 3 2 4 5 4 5 2 5 3 3 |
| [171] 3 5 4 3 3 5 3 5 5 1 5 5 2 4 4 5 5 2 5 4 6 3 6 3 5 2 5 1 5 5 5 5 |
| > cat2018_raw |
| [1] 5 5 5 6 5 3 4 5 3 3 3 5 3 1 5 3 5 3 5 5 3 5 5 3 4 6 6 4 5 3 5 5 3 6 |
| [35] 5 5 3 1 4 5 5 5 3 5 6 1 3 6 3 5 3 5 5 5 5 5 5 3 5 5 3 3 2 6 5 5 6 3 |
| [69] 4 3 3 3 5 5 5 5 5 5 6 6 3 4 4 5 5 3 2 3 6 6 3 1 1 5 3 5 6 5 1 5 5 6 |
| [103] 5 5 5 5 3 6 3 6 5 5 6 5 5 3 3 5 6 5 3 5 5 6 5 5 5 3 3 5 3 3 5 5 5 5 |
| [137] 3 1 5 3 6 5 5 5 4 3 3 6 6 6 5 1 3 5 1 4 5 3 5 6 3 3 5 5 4 5 6 5 3 3 |
| [171] 3 5 5 3 3 5 6 5 5 1 5 5 3 4 4 5 5 3 5 4 6 3 6 3 5 3 5 1 5 5 5 5 |
| > cat2019_raw |
| [1] 5 5 5 3 5 3 4 4 3 3 3 5 3 1 5 3 1 3 5 5 3 5 5 3 4 6 2 4 5 3 5 5 3 3 |
| [35] 5 5 2 1 4 5 5 5 3 5 2 1 2 2 3 5 3 5 5 5 5 5 5 3 5 5 3 3 2 2 5 5 6 3 |
| [69] 4 2 3 3 5 5 5 4 5 5 6 2 3 4 4 5 5 3 6 2 2 3 3 1 1 5 3 5 6 5 1 5 5 2 |
| [103] 5 5 5 5 3 2 3 3 5 5 6 5 4 2 3 5 2 4 3 5 5 2 5 5 5 3 3 5 3 3 5 5 5 5 |
| [137] 3 1 5 3 2 5 5 4 4 3 3 2 6 2 5 1 3 5 1 4 5 3 5 3 2 3 5 5 4 5 2 5 3 3 |
| [171] 3 5 4 3 3 5 2 5 5 1 5 5 3 4 4 5 5 3 5 4 6 3 6 3 5 3 5 1 5 5 5 5 |
| > cat2020_raw |
| [1] 5 5 5 3 5 3 4 4 3 3 2 5 3 1 5 3 5 3 5 5 3 5 5 3 4 3 3 4 5 3 5 5 3 3 |
| [35] 5 5 3 1 4 5 5 5 3 5 3 5 2 2 3 5 3 5 5 5 5 5 5 3 5 5 3 3 2 2 5 5 6 3 |
| [69] 3 2 3 3 5 5 5 5 5 5 6 3 3 4 4 5 5 3 6 3 2 3 3 1 1 5 3 5 2 5 1 5 5 2 |
| [103] 5 5 5 5 3 3 3 3 5 5 6 5 5 2 3 5 2 5 3 5 5 6 5 5 5 3 3 5 3 3 5 5 5 5 |
| [137] 3 1 5 3 2 5 5 4 5 3 3 3 6 3 5 1 3 5 1 4 5 3 5 3 3 2 5 5 4 5 2 5 3 3 |
| [171] 3 5 5 3 3 5 2 5 5 1 5 5 2 4 4 5 5 3 5 5 6 3 6 3 5 3 5 1 5 5 5 5 |
| > cat2021_raw |
| [1] 5 5 5 3 5 3 5 4 3 3 2 5 3 1 5 3 5 3 5 5 3 5 5 3 4 3 3 4 5 3 5 5 3 3 |
| [35] 5 5 3 1 4 5 5 5 3 5 3 5 2 3 3 5 3 5 5 5 5 5 5 3 5 5 3 3 2 2 5 5 6 3 |
| [69] 4 2 3 3 5 5 5 5 5 5 6 3 3 4 4 5 5 3 6 3 2 3 3 1 5 5 3 5 2 5 1 5 5 3 |
| [103] 5 5 5 5 3 3 3 6 5 5 6 1 5 3 3 5 3 5 3 5 5 6 5 5 5 3 3 5 3 3 5 5 5 4 |
| [137] 3 1 5 3 4 5 5 5 4 3 3 3 6 3 5 1 3 5 1 4 5 3 5 3 3 2 5 5 4 5 2 5 3 3 |
| [171] 3 5 5 3 3 5 2 5 5 1 5 5 3 2 4 5 5 3 5 4 6 3 6 3 5 3 5 1 5 5 5 5 |
| > cat2022_raw |
| [1] 5 4 5 3 5 3 5 5 3 3 2 5 3 1 5 3 5 3 5 5 3 5 5 3 5 3 3 5 5 3 5 5 2 2 |
| [35] 5 5 3 1 4 5 5 5 3 5 2 5 2 2 3 5 3 4 5 5 5 5 5 3 5 5 3 3 2 2 5 5 6 3 |
| [69] 4 2 3 3 5 5 5 5 5 5 6 2 3 4 4 5 5 2 6 3 2 2 3 1 1 5 3 5 2 5 1 5 5 2 |
| [103] 5 5 5 5 3 2 2 6 5 5 6 5 5 2 3 5 2 5 3 5 5 6 5 5 5 3 3 5 3 3 5 5 5 6 |
| [137] 2 1 5 3 5 5 5 5 5 3 2 3 6 3 5 1 3 5 1 5 4 3 5 3 2 2 5 5 4 5 2 5 3 3 |
| [171] 3 5 5 3 2 5 2 5 5 1 5 5 3 2 5 5 5 3 5 5 6 3 6 3 5 3 5 1 5 5 5 5 |
| > cat2023_raw |
| [1] 5 4 5 3 5 3 5 4 3 3 2 5 3 1 5 3 5 3 5 5 3 5 5 3 5 3 3 5 5 3 5 5 3 2 |
| [35] 5 5 2 1 5 5 5 5 3 5 2 5 2 2 2 5 3 4 5 5 5 5 5 3 5 5 3 3 2 2 5 5 6 3 |
| [69] 4 3 3 3 5 5 5 5 5 5 6 3 3 4 4 5 5 2 6 3 2 2 3 1 1 5 3 5 2 5 1 5 5 3 |
| [103] 5 5 5 5 3 2 2 6 5 5 6 5 5 3 3 5 3 5 3 4 5 2 5 5 5 3 3 5 2 3 5 5 5 2 |
| [137] 3 1 5 3 5 5 5 5 4 3 2 3 6 3 5 1 3 5 1 5 5 3 5 6 3 2 5 5 4 5 2 5 3 3 |
| [171] 3 5 5 3 2 5 2 5 5 1 5 5 3 2 5 5 5 3 5 5 6 3 6 3 5 3 5 1 5 5 5 5 |
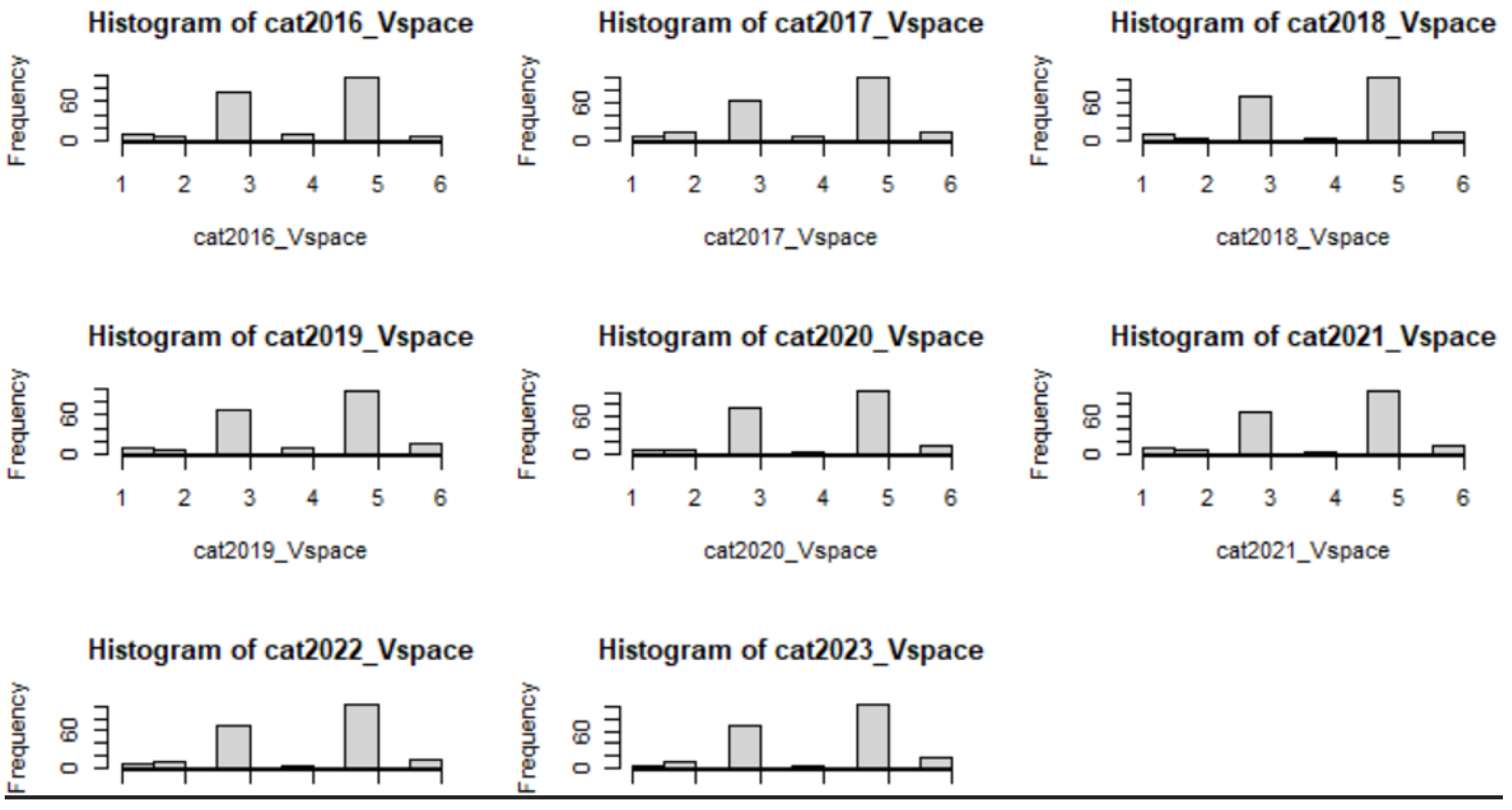
Appendix C. V-Space Categorization of 202 Countries Year by Year: 2013–2023
| > cat2013_Vspace; |
| [1] 5 5 5 3 5 3 5 1 3 3 3 5 3 1 5 3 5 3 4 5 3 |
| [22] 5 5 3 2 3 3 5 5 3 5 5 3 3 5 5 6 1 4 5 5 5 |
| [43] 3 5 3 1 6 3 3 5 3 5 5 5 5 5 5 3 1 5 5 3 2 |
| [64] 2 5 5 2 3 2 2 3 3 5 5 5 5 5 5 6 3 3 4 5 5 |
| [85] 5 3 2 3 3 3 3 1 5 5 4 5 2 5 1 5 5 3 5 5 5 |
| [106] 5 3 3 3 6 5 5 6 5 5 3 4 5 3 4 3 5 5 3 5 5 |
| [127] 5 3 4 5 3 3 5 5 5 5 3 6 5 3 2 5 5 5 4 3 3 |
| [148] 2 3 2 5 1 3 5 1 5 4 3 5 6 3 3 5 5 2 5 2 5 |
| [169] 3 3 3 5 4 3 3 5 3 5 5 5 5 5 5 2 4 4 5 4 5 |
| [190] 5 6 6 6 3 5 3 5 1 5 5 5 5 |
| > cat2014_Vspace; |
| [1] 5 5 5 3 5 3 5 5 3 3 3 5 3 1 5 3 5 3 4 5 3 |
| [22] 5 5 3 4 6 3 5 5 3 5 5 3 3 5 5 3 1 4 5 5 5 |
| [43] 3 5 3 5 3 3 3 5 3 5 5 5 5 5 5 3 5 5 5 3 2 |
| [64] 3 5 5 2 3 4 2 3 3 5 5 5 5 5 5 6 3 3 4 4 5 |
| [85] 5 3 2 3 2 6 3 1 5 5 3 5 2 5 1 5 5 3 5 4 5 |
| [106] 5 3 3 3 6 5 5 6 5 5 3 4 5 3 5 3 5 5 3 5 5 |
| [127] 5 3 4 5 3 3 5 5 5 3 3 6 5 3 2 5 5 4 4 3 3 |
| [148] 3 6 2 5 1 3 5 1 4 3 6 5 6 3 3 5 5 2 5 2 1 |
| [169] 3 3 3 5 4 3 3 5 6 5 5 1 5 5 3 2 4 1 5 3 5 |
| [190] 5 6 6 6 3 5 3 5 5 5 5 5 5 |
| > cat2015_Vspace; |
| [1] 5 5 5 6 5 3 5 5 3 3 3 5 3 1 5 3 5 3 5 5 6 |
| [22] 5 5 6 4 6 2 5 5 3 5 5 6 6 5 5 3 1 4 5 5 5 |
| [43] 3 5 3 5 3 3 6 5 3 5 5 5 5 5 5 3 5 5 5 6 2 |
| [64] 3 5 5 2 3 4 2 3 3 5 5 5 5 5 5 6 3 3 4 5 5 |
| [85] 5 6 2 3 2 6 3 1 5 5 3 5 2 5 1 5 5 3 5 5 5 |
| [106] 5 6 3 6 6 5 5 6 5 5 3 3 5 6 5 3 5 5 3 5 5 |
| [127] 5 3 3 5 3 6 5 5 5 5 3 6 5 3 3 5 5 5 4 3 3 |
| [148] 3 6 3 5 1 3 5 1 5 3 6 5 6 3 3 5 5 2 5 2 5 |
| [169] 3 3 3 5 5 3 6 5 6 5 5 1 5 5 5 3 4 1 5 3 5 |
| [190] 5 6 6 6 3 5 4 5 1 5 5 5 5 |
| > cat2016_Vspace; |
| [1] 5 5 5 3 5 3 4 5 3 3 3 5 3 1 5 3 5 3 5 5 3 |
| [22] 5 5 3 4 3 3 5 5 3 5 5 3 3 5 5 3 1 4 5 5 5 |
| [43] 3 5 3 5 3 3 3 5 3 5 5 5 5 5 5 3 5 5 3 3 2 |
| [64] 3 5 5 2 3 4 2 3 3 5 5 5 5 5 5 6 3 3 4 5 5 |
| [85] 5 3 2 3 3 3 3 1 5 5 3 5 6 5 5 5 5 3 5 5 5 |
| [106] 5 3 3 3 3 5 5 6 5 5 3 3 5 3 5 3 5 5 3 5 5 |
| [127] 5 3 3 5 3 3 5 5 5 5 3 3 5 3 3 5 5 5 4 3 3 |
| [148] 3 3 3 5 1 3 5 1 5 5 3 5 3 3 3 5 5 2 5 3 5 |
| [169] 3 3 3 5 5 3 3 5 3 5 5 1 5 5 3 3 4 1 5 3 5 |
| [190] 5 6 6 6 3 5 4 5 1 5 5 5 5 |
| > cat2017_Vspace; |
| [1] 5 5 5 3 5 3 4 5 3 3 3 5 3 1 5 3 5 2 5 5 3 |
| [22] 5 5 3 4 6 3 5 5 3 5 5 3 3 5 5 3 1 5 5 5 5 |
| [43] 3 5 3 5 3 3 3 5 3 5 5 5 5 5 5 3 5 5 3 3 2 |
| [64] 2 5 5 6 3 4 2 3 3 5 5 5 5 5 5 6 3 3 4 5 5 |
| [85] 5 3 6 2 2 3 3 1 5 5 3 5 6 5 5 5 5 3 5 5 5 |
| [106] 5 3 3 3 6 5 5 6 5 5 3 3 5 3 5 3 5 5 6 5 5 |
| [127] 5 3 3 5 3 3 5 5 5 5 3 6 5 3 2 5 5 5 5 3 3 |
| [148] 3 6 2 5 1 3 5 1 4 5 3 5 6 3 3 5 5 2 5 2 5 |
| [169] 3 3 3 5 5 3 3 5 3 5 5 1 5 5 3 2 4 5 5 3 5 |
| [190] 5 6 3 6 3 5 3 5 5 5 5 5 5 |
| > cat2018_Vspace; |
| [1] 5 5 5 3 5 3 4 5 3 3 3 5 3 1 5 3 5 3 5 5 3 |
| [22] 5 5 3 5 6 3 5 5 3 5 5 3 6 5 5 3 1 5 5 5 5 |
| [43] 3 5 3 5 3 3 3 5 3 5 5 5 5 5 5 3 5 5 6 3 2 |
| [64] 3 5 5 2 3 4 3 3 3 5 5 5 5 5 5 6 3 3 4 5 5 |
| [85] 5 3 2 3 3 3 3 1 5 5 3 5 6 5 1 5 5 6 5 5 5 |
| [106] 5 3 3 3 6 5 5 6 5 5 3 3 5 3 5 3 5 5 6 5 5 |
| [127] 5 3 3 5 3 3 5 5 5 1 3 6 5 3 3 5 5 5 5 3 3 |
| [148] 3 6 3 5 1 3 5 1 5 5 3 5 6 3 3 5 5 2 5 3 5 |
| [169] 3 3 3 5 5 3 3 5 3 5 5 1 5 5 3 3 5 5 5 3 5 |
| [190] 5 6 3 6 3 5 3 5 5 5 5 5 5 |
| > cat2019_Vspace; |
| [1] 5 5 5 3 5 3 4 4 3 3 3 5 3 1 5 3 5 3 5 5 3 |
| [22] 5 5 3 4 6 3 5 5 3 5 5 3 3 5 5 2 1 4 5 5 5 |
| [43] 3 5 3 5 3 3 3 5 3 5 5 5 5 5 5 3 5 5 6 3 2 |
| [64] 2 5 5 6 3 4 3 3 3 5 5 5 5 5 5 6 3 3 4 5 5 |
| [85] 5 3 6 3 3 3 3 1 1 5 3 5 6 5 1 5 5 2 5 5 5 |
| [106] 5 3 3 3 6 5 5 6 5 5 3 3 5 3 5 3 5 5 6 5 5 |
| [127] 5 3 3 5 3 3 5 5 5 5 3 6 5 3 3 5 5 4 5 3 3 |
| [148] 3 6 3 5 1 3 5 1 5 5 3 5 6 3 3 5 5 2 5 3 5 |
| [169] 3 3 3 5 5 3 3 5 3 5 5 1 5 5 3 4 4 5 5 3 5 |
| [190] 5 6 3 6 3 5 5 5 5 5 5 5 5 |
| > cat2020_Vspace; |
| [1] 5 5 5 3 5 3 5 4 3 3 3 5 3 1 5 3 5 3 5 5 3 |
| [22] 5 5 3 5 6 3 5 5 3 5 5 3 3 5 5 3 1 5 5 5 5 |
| [43] 3 5 3 5 2 3 3 5 3 5 5 5 5 5 5 3 5 5 3 3 2 |
| [64] 2 5 5 6 3 3 3 3 3 5 5 5 5 5 5 6 3 3 4 4 5 |
| [85] 5 3 6 3 3 3 3 1 5 5 3 5 2 5 1 5 5 3 5 5 5 |
| [106] 5 3 3 3 6 5 5 6 5 5 3 3 5 3 5 3 5 5 3 5 5 |
| [127] 5 3 3 5 3 3 5 5 5 5 3 6 5 3 3 5 5 5 5 3 3 |
| [148] 3 6 3 5 1 3 5 1 5 5 3 5 6 3 3 5 5 3 5 3 5 |
| [169] 3 3 3 5 5 3 3 5 2 5 5 1 5 5 3 3 5 5 5 3 5 |
| [190] 5 6 3 6 3 5 3 5 5 5 5 5 5 |
| > cat2021_Vspace; |
| [1] 5 5 5 3 5 3 5 4 3 3 3 5 3 1 5 3 5 3 5 5 3 |
| [22] 5 5 3 5 6 3 5 5 3 5 5 3 3 5 5 3 1 4 5 5 5 |
| [43] 3 5 3 5 3 3 2 5 3 5 5 5 5 5 5 3 5 5 6 2 2 |
| [64] 2 5 5 6 3 5 3 3 3 5 5 5 5 5 5 6 3 3 4 4 5 |
| [85] 5 3 6 3 3 3 3 1 5 5 3 5 2 5 1 5 5 3 5 5 5 |
| [106] 5 3 3 3 6 5 5 6 5 5 3 3 5 3 5 3 5 5 3 5 5 |
| [127] 5 3 3 5 3 3 5 5 5 5 3 1 5 3 3 5 5 5 5 3 3 |
| [148] 3 6 3 5 1 3 5 1 5 5 3 5 6 3 3 5 5 3 5 3 5 |
| [169] 3 3 3 5 5 3 2 5 2 5 5 1 5 5 3 3 5 5 5 3 5 |
| [190] 5 6 3 6 3 5 3 5 5 5 5 5 5 |
| > cat2022_Vspace; |
| [1] 5 5 5 3 5 3 5 5 3 3 2 5 3 6 5 3 5 3 5 5 3 |
| [22] 5 5 3 5 6 3 5 5 3 5 5 3 3 5 5 3 1 5 5 5 5 |
| [43] 3 5 3 5 3 3 2 5 3 5 5 5 5 5 5 3 5 5 6 3 2 |
| [64] 2 5 5 6 3 5 3 3 3 5 5 5 5 5 5 6 3 3 4 4 5 |
| [85] 5 3 6 3 3 2 3 1 1 5 3 5 2 5 6 5 5 3 5 5 5 |
| [106] 5 3 3 3 6 5 5 6 5 5 3 3 5 3 5 3 5 5 3 5 5 |
| [127] 5 3 3 5 3 3 5 5 5 3 3 1 5 3 5 5 5 5 5 3 3 |
| [148] 3 6 3 5 6 3 5 4 5 5 3 5 6 3 3 5 5 5 5 3 5 |
| [169] 3 3 3 5 5 3 3 5 2 5 5 1 5 5 3 3 5 5 5 3 5 |
| [190] 5 6 2 6 3 5 3 5 1 5 5 5 5 |
| > cat2023_Vspace; |
| [1] 5 3 5 3 5 3 5 5 3 3 3 5 3 6 5 3 5 3 5 5 3 |
| [22] 5 5 3 5 6 3 5 5 3 5 5 3 3 5 5 3 1 5 5 5 5 |
| [43] 3 5 3 5 3 3 2 5 3 3 5 5 5 5 5 3 5 5 3 2 2 |
| [64] 2 5 5 6 3 5 3 3 3 5 5 5 5 5 5 6 3 3 4 4 5 |
| [85] 5 3 6 3 3 2 3 4 5 5 3 5 2 5 6 5 5 3 5 5 5 |
| [106] 5 3 3 3 6 5 5 6 5 5 3 3 5 3 5 3 5 5 3 5 5 |
| [127] 5 3 3 5 2 3 5 5 5 3 3 6 5 3 5 5 5 5 5 3 3 |
| [148] 3 6 3 5 6 3 5 6 5 5 3 5 6 3 3 5 5 5 5 3 5 |
| [169] 3 3 3 5 5 3 2 5 2 5 5 1 5 5 3 5 5 5 5 3 5 |
| [190] 5 6 3 6 3 5 3 5 5 5 5 5 5 |
References
- Deng, Y. On p-adic Gram–Schmidt Orthogonalization Process. Front. Math. 2024. [Google Scholar] [CrossRef]
- Huang, X.; Caron, M.; Hindson, D. A recursive Gram-Schmidt orthonormalization procedure and its application to communications. In Proceedings of the 2001 IEEE Third Workshop on Signal Processing Advances in Wireless Communications (SPAWC’01), Taiwan, China, 20–23 March 2001; Workshop Proceedings (Cat. No.01EX471). pp. 340–343. [Google Scholar]
- Balabanov, O.; Grigori, L. Randomized Gram-Schmidt process with application to GMRES. Siam J. Sci. Comput. 2022, 44, A1450–A1474. [Google Scholar] [CrossRef]
- Ford, W. Numerical Linear Algebra with Applications: Using MATLAB and Octave; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Morrison, D.D. Remarks on the Unitary Triangularization of a Nonsymmetric Matrix. J. ACM 1960, 7, 185–186. [Google Scholar] [CrossRef]
- Skogholt, J.; Lil, K.H.; Næs, T.; Smilde, A.K.; Indahl, U.G. Selection of principal variables through a modified Gram–Schmidt process with and without supervision. J. Chemom. 2023, 37, e3510. [Google Scholar] [CrossRef]
- Robinson, P.J.; Saranraj, A. Intuitionistic Fuzzy Gram-Schmidt Orthogonalized Artificial Neural Network for Solving MAGDM Problems. Indian J. Sci. Technol. 2024, 17, 2529–2537. [Google Scholar] [CrossRef]
- Dax, A. A modified Gram–Schmidt algorithm with iterative orthogonalization and column pivoting. Linear Algebra Its Appl. 2000, 310, 25–42. [Google Scholar] [CrossRef]
- Trefethen, L.N.; Bau, D. Numerical Linear Algebra; SIAM: New Delhi, India, 1997. [Google Scholar]
- Bremner, M.R. Lattice Basis Reduction: An Introduction to the LLL Algorithm and Its Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Available online: http://www.noahsd.com/mini_lattices/02__GS_and_LLL.pdf (accessed on 10 February 2025).
- Giraud, L.; Langou, J.; Rozložník, M.; Eshof, J.V.D. Rounding error analysis of the classical Gram–Schmidt orthogonalization process. Numer. Math. 2005, 101, 87–100. [Google Scholar] [CrossRef]
- Giraud, L.; Langou, J.; Rozloznik, M. The loss of orthogonality in the Gram–Schmidt orthogonalization process. Comput. Math. Appl. 2005, 50, 1069–1075. [Google Scholar] [CrossRef]
- Imakura, A.; Yamamoto, Y. Efficient implementations of the modified Gram–Schmidt orthogonalization with a non-standard inner product. Jpn. J. Indust. Appl. Math. 2019, 36, 619–641. [Google Scholar] [CrossRef]
- Sreedharan, V.P. A note on the modified gram-schmidt process. Int. J. Comput. Math. 1988, 24, 277–290. [Google Scholar] [CrossRef]
| Indicators | ||||||
|---|---|---|---|---|---|---|
| 1.3 | 1.8 | −0.52 | 1.31 | |||
| 1.48 | 1.51 | 1.52 | ||||
| 0.45 | 0.93 | 0.64 | ||||
| 1.15 | 1.54 | 1.26 | ||||
| 1.4 | 1.64 | 1.55 | ||||
| 1.22 | 1.41 | 0.43 | 1.10 |
| Year | China | France | Germany | India | Russia | USA |
|---|---|---|---|---|---|---|
| 2013 | 1 | 2 | 2 | 1 | 1 | 2 |
| 2014 | 1 | 2 | 2 | 1 | 1 | 2 |
| 2015 | 1 | 2 | 2 | 1 | 1 | 2 |
| 2016 | 1 | 2 | 2 | 1 | 1 | 2 |
| 2017 | 1 | 2 | 2 | 1 | 1 | 2 |
| 2018 | 1 | 2 | 2 | 1 | 1 | 2 |
| 2019 | 1 | 2 | 2 | 1 | 1 | 2 |
| 2020 | 1 | 2 | 2 | 1 | 1 | 2 |
| 2021 | 1 | 2 | 2 | 1 | 1 | 2 |
| 2022 | 1 | 2 | 2 | 1 | 1 | 2 |
| 2023 | 1 | 2 | 2 | 1 | 1 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.-M. A Non-Self-Referential Characterization of the Gram–Schmidt Process via Computational Induction. Mathematics 2025, 13, 768. https://doi.org/10.3390/math13050768
Chen R-M. A Non-Self-Referential Characterization of the Gram–Schmidt Process via Computational Induction. Mathematics. 2025; 13(5):768. https://doi.org/10.3390/math13050768
Chicago/Turabian StyleChen, Ray-Ming. 2025. "A Non-Self-Referential Characterization of the Gram–Schmidt Process via Computational Induction" Mathematics 13, no. 5: 768. https://doi.org/10.3390/math13050768
APA StyleChen, R.-M. (2025). A Non-Self-Referential Characterization of the Gram–Schmidt Process via Computational Induction. Mathematics, 13(5), 768. https://doi.org/10.3390/math13050768








