Stability-Optimized Graph Convolutional Network: A Novel Propagation Rule with Constraints Derived from ODEs
Abstract
1. Introduction
1.1. Related Work
1.2. Our Approach
- We developed a time-varying differential equation model for graph convolution propagation, establishing mathematical criteria for the Precision Weight Parameter Mechanism through stability mapping analysis.
- We formulated stability domain constraints for the weight matrix through Jacobian spectral analysis and proposed a Dynamic Step-size Adjustment Mechanism based on forward Euler discretization, applying stability mapping during gradient descent.
- We designed stable propagation rules integrating dual protection mechanisms with self-loop factors, optimizing feature stability and independence through quantitative metrics.
2. Preliminaries
2.1. Continuous Dynamics Model
2.1.1. Stability Analysis of Equilibrium State
2.1.2. Stability Guarantee of the Forward Euler Discretization Scheme
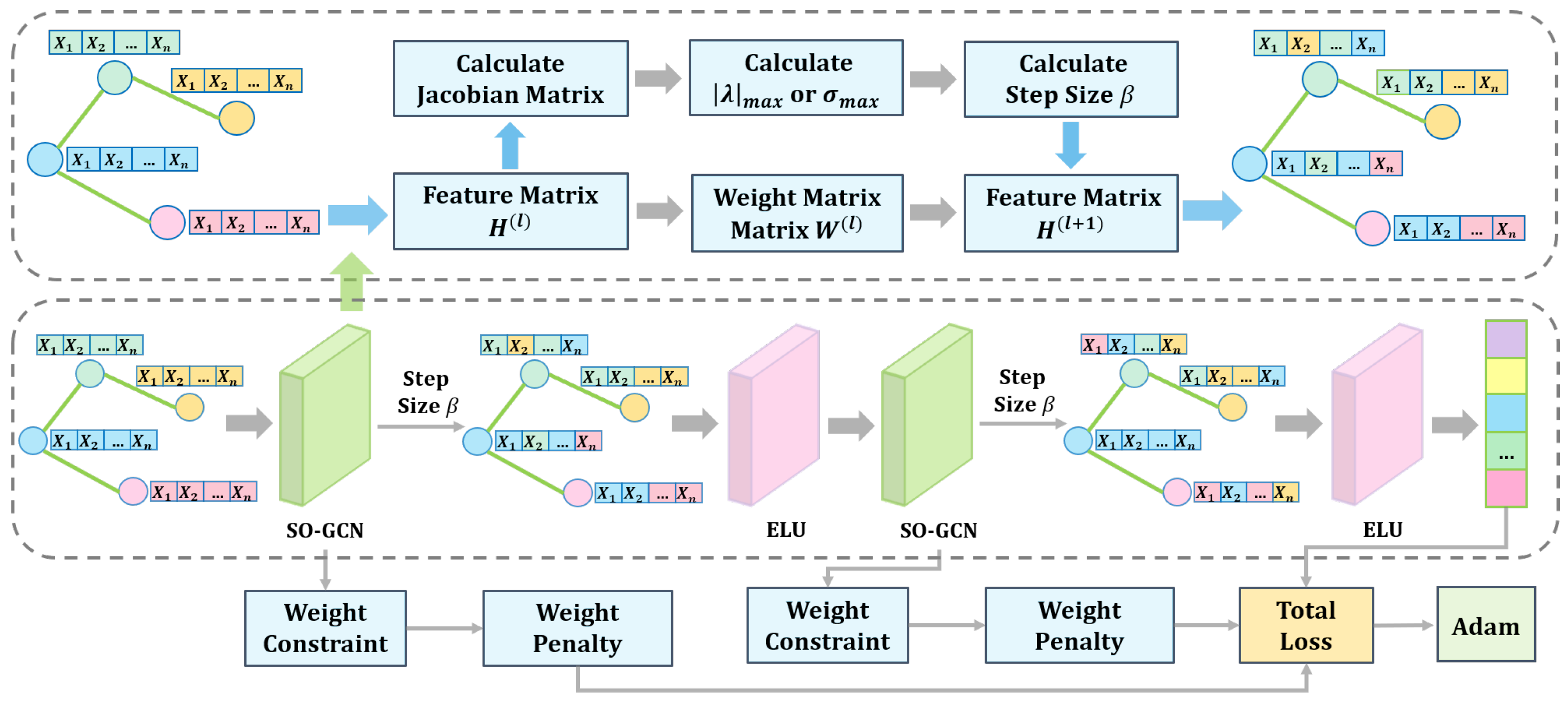
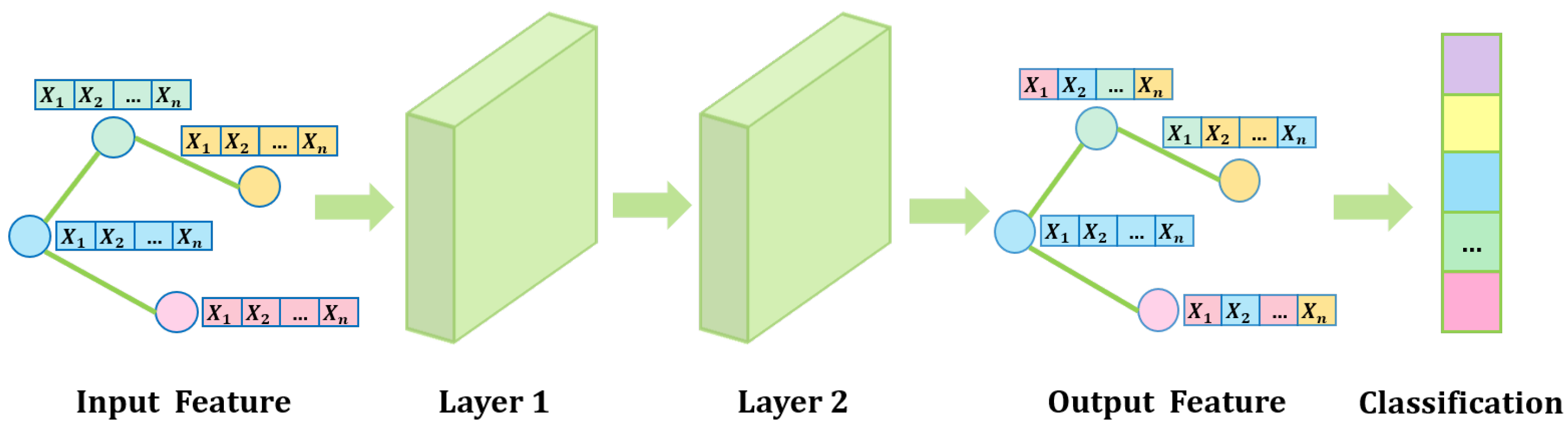
3. Stability-Optimized Graph Convolutional Network
3.1. Network Overview
- Precision Weight Parameter Mechanism (PW Mechanism): constrains the Frobenius norm of the weight matrix through stability analysis of differential equations;
- Dynamic Step-size Adjustment Mechanism (DS Mechanism): adaptively controls the propagation step size based on the instantaneous Jacobian matrix;
- Stable propagation rule: combines the PW Mechanism and DS Mechanism to optimize both numerical stability and model expressiveness.
3.2. Stability-Optimized Propagation Rule
3.2.1. Precision Weight Parameter Mechanism
| Algorithm 1: Precision Weight Parameter Mechanism |
|
3.2.2. Dynamic Step-Size Adjustment Mechanism
| Algorithm 2: Dynamic Step-size Adjustment Mechanism |
|
4. Experiments
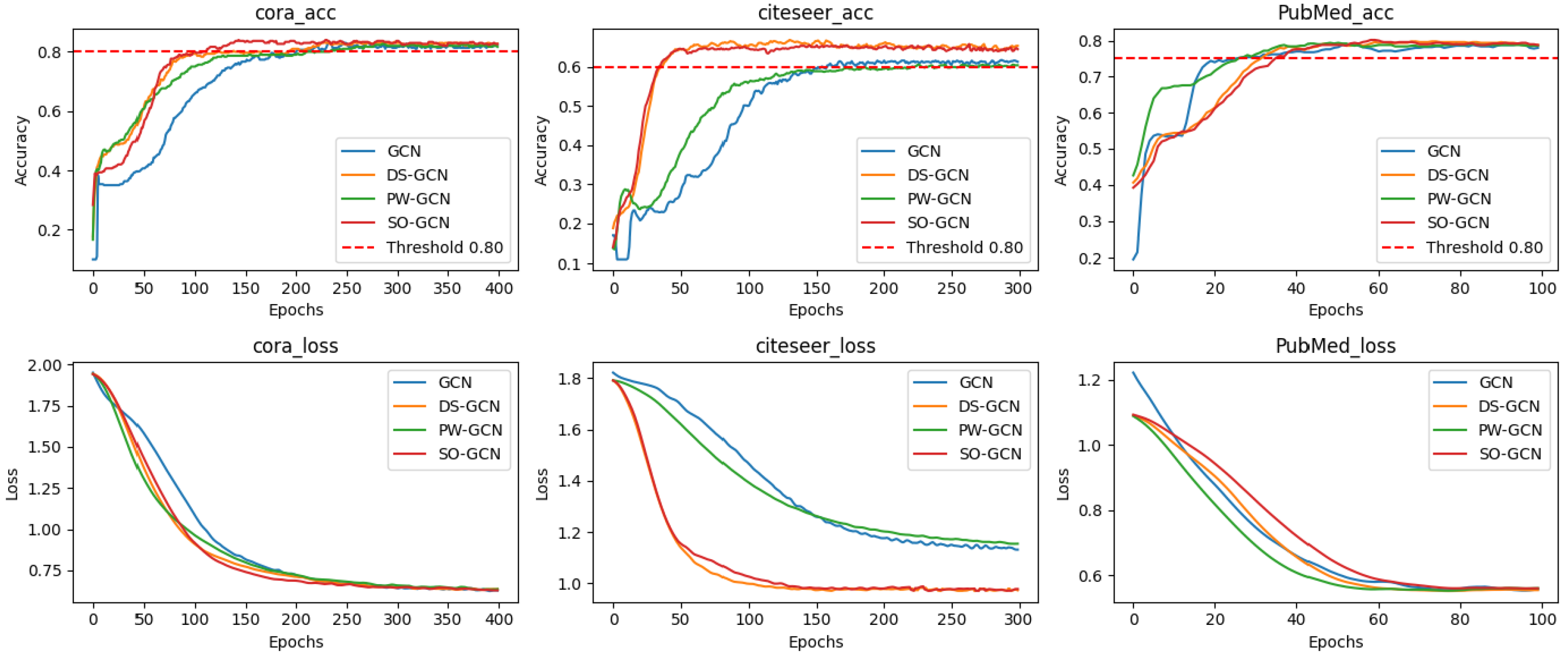
4.1. Experiment Results and Analysis
4.2. Depth Analysis and Feature Preservation
4.3. Computational Complexity Analysis
5. Conclusions
- In heterophilic graph settings such as social network anomaly detection, the Dynamic Step-size Adjustment Mechanism dynamically suppresses noise propagation through spectral characteristic perception;
- On knowledge graphs with sparse features but complex structures, such as biomedical networks, the Precision Weight Parameter Mechanism optimizes information propagation efficiency through Frobenius norm constraints;
- In industrial-grade graph computing systems (e.g., multi-hop inference in recommendation systems), the synergistic effect of dual stabilization mechanisms ensures numerical stability during higher-order propagation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix A.1. Existence of Theorem 1
Appendix A.2. Uniqueness of Theorem 1
Appendix B. Proof of Theorem 2
Appendix C. Proof of Theorem 3
References
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with localized spectral filtering. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3844–3852. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1024–1034. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- Fout, A.; Byrd, J.; Shariat, B.; Ben-Hur, A. Protein interface prediction using graph convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6533–6542. [Google Scholar]
- Li, X.; Chen, S.; Hu, X.; Yang, J. Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift. arXiv 2018, arXiv:1801.05134. [Google Scholar]
- Oono, K.; Suzuki, T. Graph Neural Networks Exponentially Lose Expressive Power for Node Classification. arXiv 2019, arXiv:1905.10947. Available online: https://api.semanticscholar.org/CorpusID:209994765 (accessed on 27 May 2019).
- Wang, X.; Zhang, M. How Powerful are Spectral Graph Neural Networks. In Proceedings of the 39th International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 23341–23362. [Google Scholar]
- Chien, E.; Peng, J.; Li, P.; Milenkovic, O. Adaptive Universal Generalized PageRank Graph Neural Network. arXiv 2020, arXiv:2001.06922. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Xu, B.; Shen, H.; Cao, Q.; Cen, K.; Cheng, X. Graph convolutional networks using heat kernel for semi-supervised learning. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 1928–1934. [Google Scholar]
- Li, Q.; Han, Z.; Wu, X.-M. Deeper insights into graph convolutional networks for semi-supervised learning. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 3538–3545. [Google Scholar]
- Pei, H.; Wei, B.; Chang, K.C.-C.; Lei, Y.; Yang, B. Geom-GCN: Geometric Graph Convolutional Networks. arXiv 2020, arXiv:2002.05287. [Google Scholar]
- Chen, D.; Liao, R. Stability and Generalization of Graph Neural Networks via Spectral Dynamics. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 11289–11302. [Google Scholar]
- Rusch, T.K.; Bronstein, M.; Mishra, S. Gradient Gating for Deep Multi-Rate Learning on Graphs. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2022; pp. 22136–22149. [Google Scholar]
- Topping, J.; Giovanni, F.D.; Chamberlain, B.P.; Dong, X.; Bronstein, M.M. Understanding Over-Squashing and Bottlenecks on Graphs via Curvature. In Proceedings of the 10th International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Dong, Y.; Ding, K.; Jalaeian, B.; Ji, S.; Li, J. AdaGNN: Graph Neural Networks with Adaptive Frequency Response Filter. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Virtual Event, Australia, 1–5 November 2021. [Google Scholar]
- Yang, Z.; Cohen, W.; Salakhutdinov, R. Revisiting semi-supervised learning with graph embeddings. In Proceedings of the International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Lim, D.; Robinson, J.; Zhao, L.; Smidt, T.; Sra, S.; Maron, H.; Jegelka, S. Sign and basis invariant networks for spectral graph representation learning. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual, 1 May 2023. [Google Scholar]
- Metz, L.; Maheswaranathan, N.; Freeman, C.D.; Poole, B.; Sohl-Dickstein, J.N. Tasks, stability, architecture, and compute: Training more effective learned optimizers, and using them to train themselves. arXiv 2009, arXiv:2009.11243. [Google Scholar]
- Haber, E.; Lensink, K.; Treister, E.; Ruthotto, L. IMEXnet: A Forward Stable Deep Neural Network. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 2525–2534. [Google Scholar]
- Haber, E.; Ruthotto, L. Stable architectures for deep neural networks. Inverse Probl. 2018, 34, 014004. [Google Scholar] [CrossRef]
- Haber, E.; Ruthotto, L.; Holtham, E. Learning across scales—A multiscale method for convolution neural networks. arXiv 2017, arXiv:1703.02009. [Google Scholar] [CrossRef]
- Brouwer, L.E.J. Über Abbildung von Mannigfaltigkeiten. Math. Ann. 1911, 71, 97–115. [Google Scholar] [CrossRef]
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
| Dataset | Nodes | Edges | Classes | Features | Homophily Level |
|---|---|---|---|---|---|
| Cora | 2708 | 5429 | 7 | 1433 | 0.81 |
| CiteSeer | 3327 | 4732 | 6 | 3703 | 0.74 |
| PubMed | 19,717 | 44,338 | 3 | 500 | 0.80 |
| Chameleon | 2277 | 36,101 | 3 | 2325 | 0.18 |
| Texas | 183 | 309 | 5 | 1703 | 0.11 |
| Squirrel | 5201 | 217,073 | 3 | 2089 | 0.018 |
| Method | Cora | CiteSeer | PubMed | Texas | Chameleon | Squirrel | Avg |
|---|---|---|---|---|---|---|---|
| GCN | 83.60 | 50.23 | 75.70 | 44.74 | 46.55 | 68.08 | 61.48 |
| PW-GCN | 84.50 | 50.53 | 77.53 | 50.36 | 46.20 | 67.13 | 62.71 |
| DS-GCN | 84.20 | 58.07 | 76.07 | 51.30 | 52.25 | 70.18 | 65.34 |
| SO-GCN | 84.70 | 60.90 | 78.40 | 56.8 | 57.77 | 71.07 | 68.01 |
| Method | Cora | CiteSeer | PubMed | Texas | Chameleon | Squirrel |
|---|---|---|---|---|---|---|
| MLP | 57.00 | 53.35 | 72.90 | 67.18 | 51.44 | 38.56 |
| ChebNet | 73.60 | 53.85 | 69.00 | 73.78 | 55.77 | 39.75 |
| GIN | 64.20 | 44.80 | 73.30 | 59.46 | 68.64 | 42.75 |
| GraphSAGE | 78.00 | 52.19 | 76.00 | 56.76 | 65.67 | 53.20 |
| GCN | 83.60 | 50.23 | 75.70 | 44.74 | 46.55 | 68.08 |
| GAT | 84.10 | 48.57 | 77.70 | 46.85 | 57.31 | 43.65 |
| SO-GCN | 84.70 | 60.90 | 78.40 | 56.83 | 57.77 | 71.07 |
| Dataset | Model | 2 Layers | 3 Layers | 4 Layers | 5 Layers | 6 Layers | 7 Layers |
|---|---|---|---|---|---|---|---|
| Cora | GCN | 0.836 | 0.750 | 0.707 | 0.472 | 0.431 | 0.413 |
| SO-GCN | 0.847 | 0.791 | 0.738 | 0.574 | 0.568 | 0.557 | |
| CiteSeer | GCN | 0.502 | 0.413 | 0.302 | 0.273 | 0.277 | 0.274 |
| SO-GCN | 0.609 | 0.519 | 0.460 | 0.381 | 0.374 | 0.369 | |
| PubMed | GCN | 0.757 | 0.749 | 0.758 | 0.532 | 0.479 | 0.458 |
| SO-GCN | 0.784 | 0.761 | 0.759 | 0.684 | 0.607 | 0.554 |
| Dataset | Layers | Model | HSIC (Layers 1–2) | HSIC (Input–Layer 1) |
|---|---|---|---|---|
| Cora | 2 | GCN | 0.18 ± 0.02 | 0.40 ± 0.03 |
| SO-GCN | 0.10 ± 0.01 | 0.38 ± 0.02 | ||
| 4 | GCN | 0.25 ± 0.03 | 0.32 ± 0.04 | |
| SO-GCN | 0.15 ± 0.02 | 0.35 ± 0.03 | ||
| 7 | GCN | 0.29 ± 0.04 | 0.28 ± 0.05 | |
| SO-GCN | 0.18 ± 0.03 | 0.33 ± 0.04 | ||
| CiteSeer | 2 | GCN | 0.22 ± 0.03 | 0.35 ± 0.04 |
| SO-GCN | 0.12 ± 0.02 | 0.34 ± 0.03 | ||
| 4 | GCN | 0.31 ± 0.04 | 0.25 ± 0.05 | |
| SO-GCN | 0.20 ± 0.03 | 0.30 ± 0.04 | ||
| 7 | GCN | 0.36 ± 0.05 | 0.21 ± 0.06 | |
| SO-GCN | 0.25 ± 0.04 | 0.28 ± 0.05 | ||
| PubMed | 2 | GCN | 0.15 ± 0.02 | 0.45 ± 0.03 |
| SO-GCN | 0.08 ± 0.01 | 0.43 ± 0.02 | ||
| 4 | GCN | 0.20 ± 0.03 | 0.38 ± 0.04 | |
| SO-GCN | 0.12 ± 0.02 | 0.40 ± 0.03 | ||
| 7 | GCN | 0.26 ± 0.04 | 0.30 ± 0.05 | |
| SO-GCN | 0.20 ± 0.03 | 0.40 ± 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Zhu, H.; Han, S. Stability-Optimized Graph Convolutional Network: A Novel Propagation Rule with Constraints Derived from ODEs. Mathematics 2025, 13, 761. https://doi.org/10.3390/math13050761
Chen L, Zhu H, Han S. Stability-Optimized Graph Convolutional Network: A Novel Propagation Rule with Constraints Derived from ODEs. Mathematics. 2025; 13(5):761. https://doi.org/10.3390/math13050761
Chicago/Turabian StyleChen, Liping, Hongji Zhu, and Shuguang Han. 2025. "Stability-Optimized Graph Convolutional Network: A Novel Propagation Rule with Constraints Derived from ODEs" Mathematics 13, no. 5: 761. https://doi.org/10.3390/math13050761
APA StyleChen, L., Zhu, H., & Han, S. (2025). Stability-Optimized Graph Convolutional Network: A Novel Propagation Rule with Constraints Derived from ODEs. Mathematics, 13(5), 761. https://doi.org/10.3390/math13050761






