Theoretical Study on the Failure of Rocks with Preexisting Cracks Considering the Extension of the Crack Tip Plastic Zone
Abstract
1. Introduction
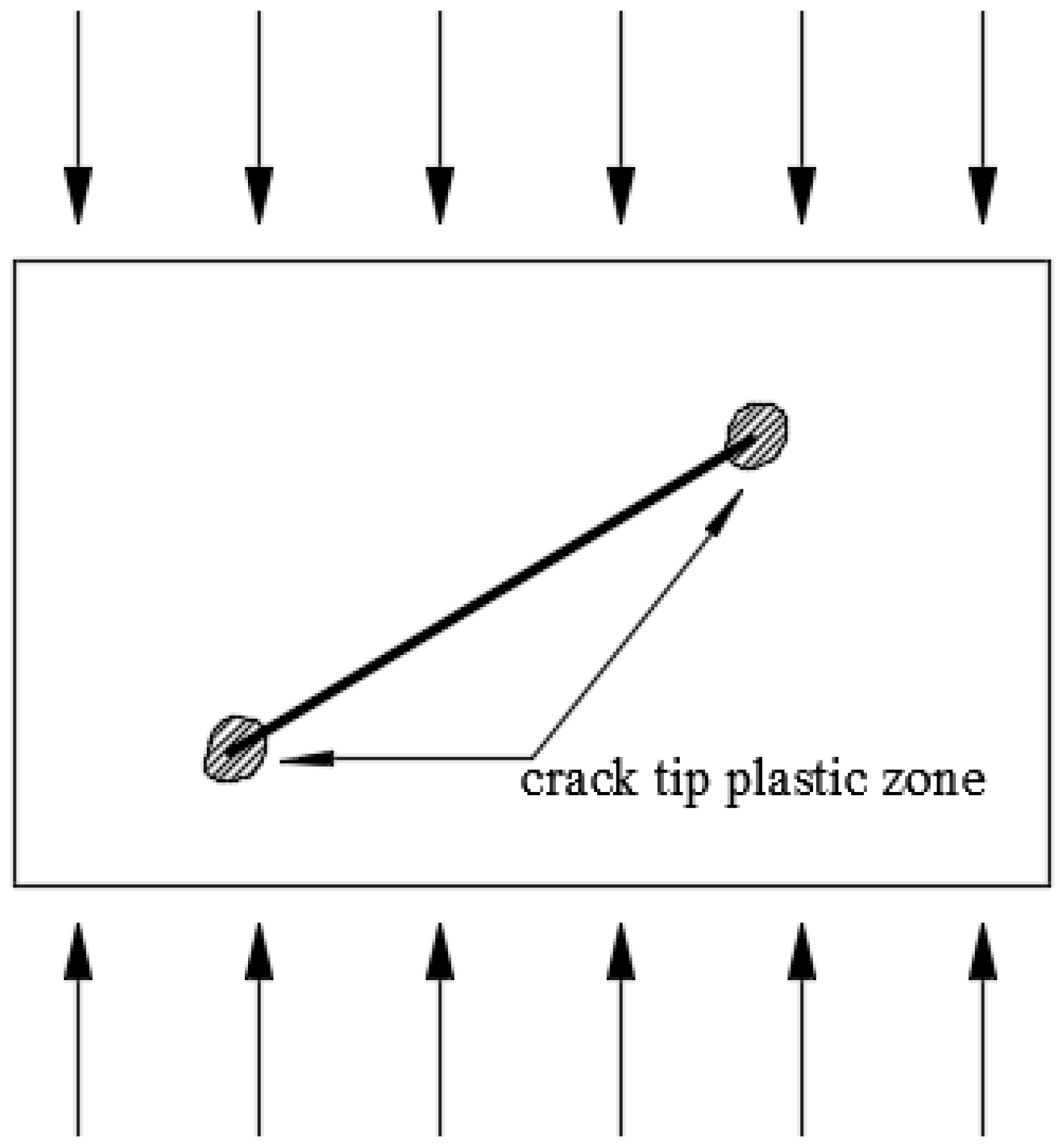
2. Crack Tip Plastic Zone of Rocks
3. Extension of Crack Tip Plastic Zone Influenced by Crack Spacing
3.1. Study on Equal-Length Cracks
3.2. Study on Unequal-Length Cracks
4. Verification Studies
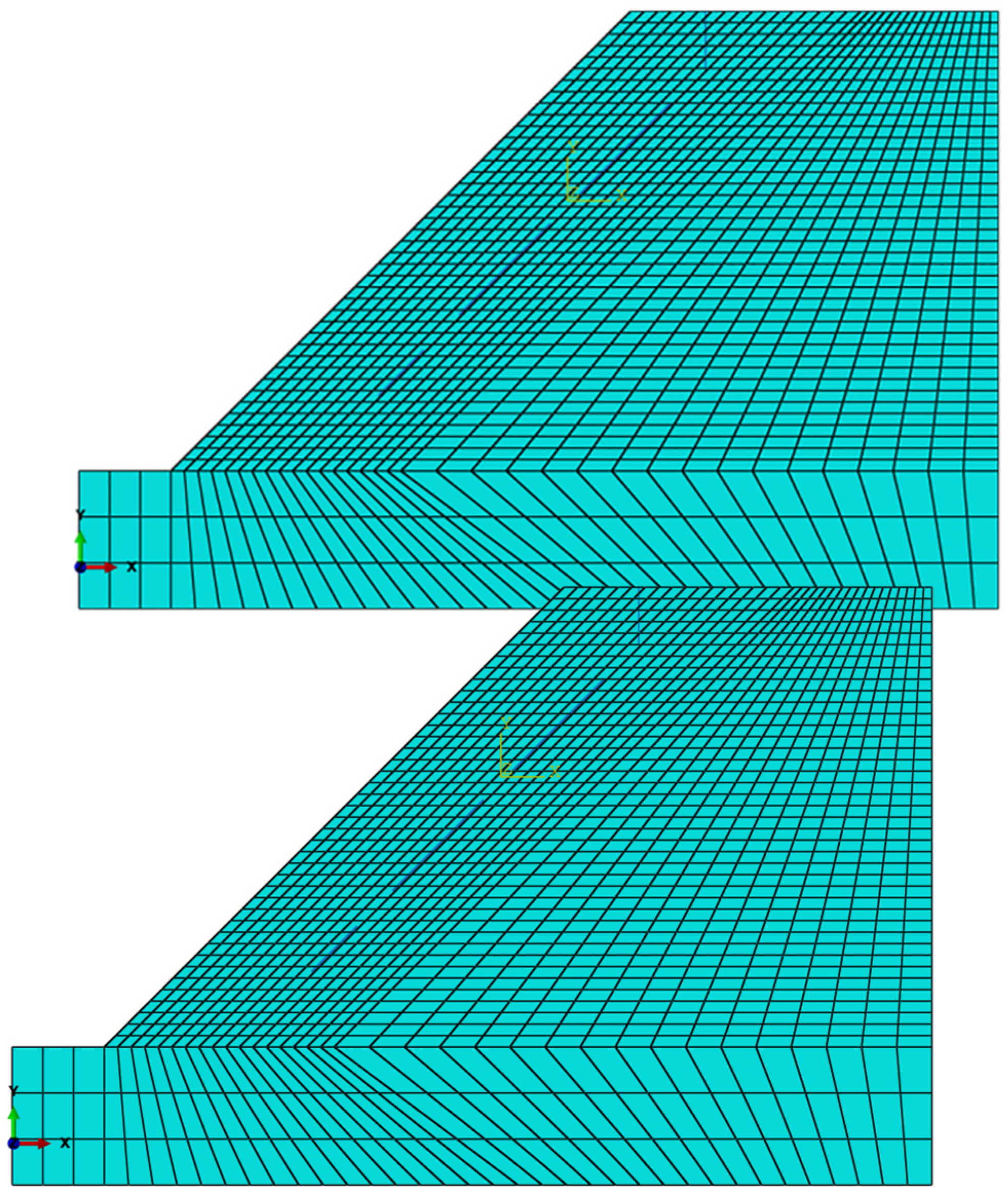
4.1. Numerical Study
4.2. Experimental Study
5. Conclusions
- (1)
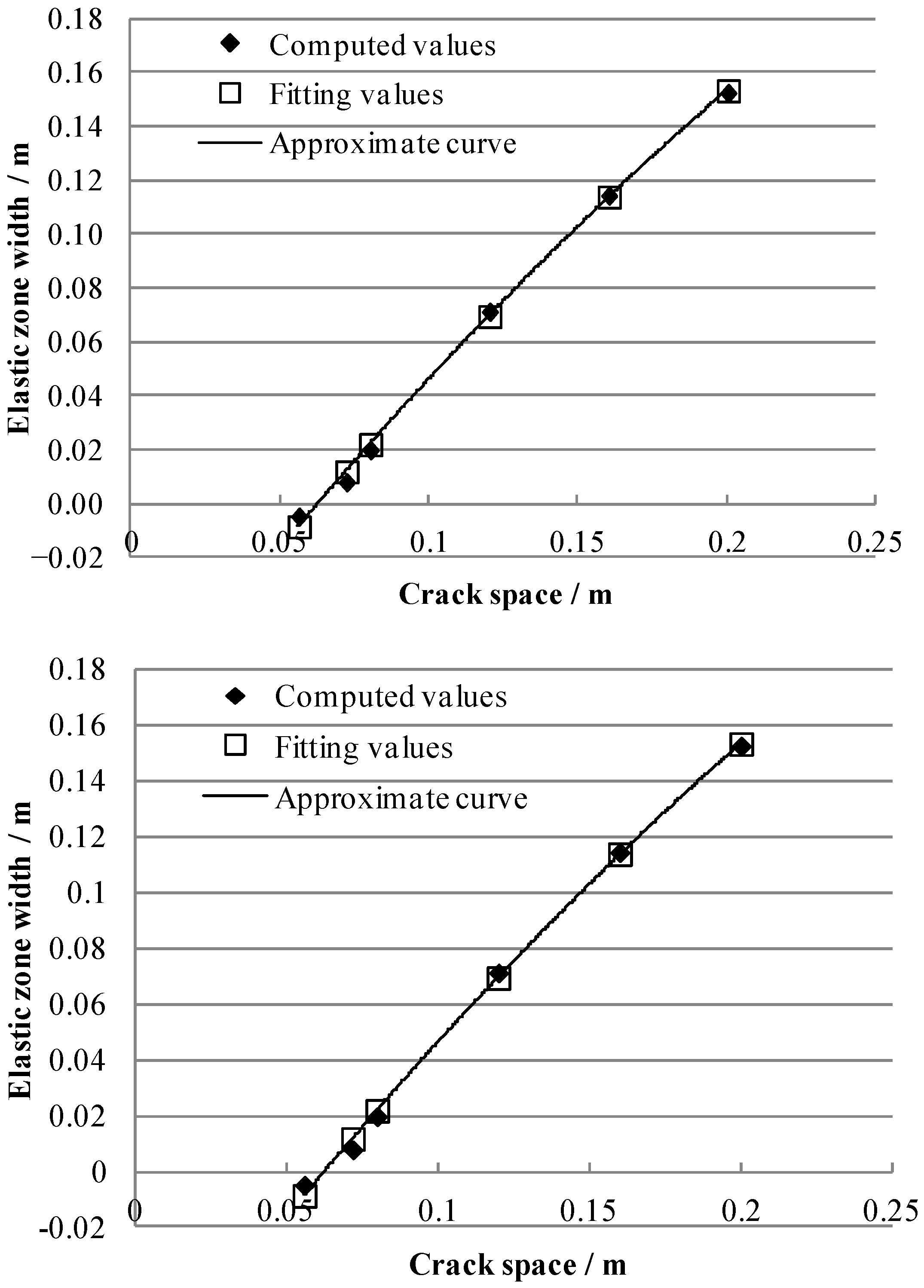
- For two cracks of equal length, as the crack spacing decreases, the plastic zones at the two crack tips develop very quickly, and the cracks extend quickly. Moreover, one quadratic polynomial function can be used to describe the relationship between the elastic zone width between two cracks and the crack spacing.
- (2)
- For two cracks of equal length, the threshold value of crack spacing can be represented by the ratio of crack spacing to crack length of 0.2. Therefore, the ratio of crack spacing to crack length of 0.2 can be taken as the basic condition to determine the crack penetration; that is, if this ratio is equal to or less than 0.2, the two cracks can be considered one combined crack if the requirement for computing accuracy is not very strict.
- (3)
- For two cracks of unequal length, as the crack spacing decreases, the plastic zones at the crack tips develop very quickly, and the cracks extend quickly. Moreover, one linear function can be used to describe the relationship between the elastic zone width between two cracks and the crack spacing.
- (4)
- For two cracks of unequal length, the threshold value of crack spacing can be represented by the ratio of crack spacing to secondary crack length of 0.3. Therefore, the ratio of crack spacing to secondary crack length of 0.3 can be taken as the basic condition to determine the crack penetration; that is, if this ratio is equal to or less than 0.3, the two cracks can be considered one combined crack if the requirement for computing accuracy is not very strict.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gross, D.; Seelig, T. Fracture Mechanics; Springer: Heidelberg/Berlin, Germany, 2011. [Google Scholar]
- Rossmanith, H. Rock Fracture Mechanics; Springer: Heidelberg/Berlin, Germany, 1983. [Google Scholar]
- Cao, P.; Liu, T.Y.; Pu, C.Z.; Lin, H. Crack propagation and coalescence of brittle rock-like specimens with pre-existing cracks in compression. Eng. Geol. 2015, 187, 113–121. [Google Scholar] [CrossRef]
- Huang, D.; Gu, D.M.; Yang, C.; Huang, R.Q.; Fu, G.Y. Investigation on Mechanical Behaviors of Sandstone with Two Preexisting Flaws under Triaxial Compression. Rock Mech. Rock Eng. 2016, 49, 375–399. [Google Scholar] [CrossRef]
- Luo, Y.; Ren, L.; Xie, L.Z.; Ai, T.; He, B. Fracture Behavior Investigation of a Typical Sandstone Under Mixed-Mode I/II Loading Using the Notched Deep Beam Bending Method. Rock Mech. Rock Eng. 2017, 50, 1987–2005. [Google Scholar] [CrossRef]
- Zhao, C.; Zhou, Y.M.; Zhao, C.F.; Bao, C. Cracking Processes and Coalescence Modes in Rock-Like Specimens with Two Parallel Pre-existing Cracks. Rock Mech. Rock Eng. 2018, 51, 3377–3393. [Google Scholar] [CrossRef]
- Sivakumar, G.; Maji, V.B. A Study on Crack Initiation and Propagation in Rock with Pre-existing Flaw under Uniaxial Compression. Indian Geotech. J. 2018, 48, 626–639. [Google Scholar] [CrossRef]
- Wang, H.Y. Poro-elasto-plastic modeling of complex hydraulic fracture propagation: Simultaneous multi-fracturing and producing well interference. Acta Mech. 2016, 227, 507–525. [Google Scholar] [CrossRef]
- Wu, Z.J.; Wong, L.N.Y. Elastic–plastic cracking analysis for brittle–ductile rocks using manifold method. Int. J. Fract. 2013, 180, 71–91. [Google Scholar] [CrossRef]
- Fakhimi, A.; Wan, F. Discrete element modeling of the process zone shape in mode I fracture at peak load and in post-peak regime. Int. J. Rock Mech. Min. Sci. 2016, 85, 119–128. [Google Scholar] [CrossRef]
- Funatsu, T.; Shimizu, N.; Kuruppu, M.; Matsui, K. Evaluation of Mode I Fracture Toughness Assisted by the Numerical Determination of K-Resistance. Rock Mech. Rock Eng. 2015, 48, 143–157. [Google Scholar] [CrossRef]
- Tarokh, A.; Makhnenko, R.Y.; Fakhimi, A.; Labuz, J.F. Scaling of the fracture process zone in rock. Int. J. Fract. 2017, 204, 191–204. [Google Scholar] [CrossRef]
- Wei, M.D.; Dai, F.; Xu, N.W.; Zhao, T.; Xia, K.W. Experimental and numerical study on the fracture process zone and fracture toughness determination for ISRM-suggested semi-circular bend rock specimen. Eng. Fract. Mech. 2016, 154, 43–56. [Google Scholar] [CrossRef]
- Wei, M.D.; Dai, F.; Xu, N.W.; Zhao, T. Stress intensity factors and fracture process zones of ISRM-suggested chevron notched specimens for mode I fracture toughness testing of rocks. Eng. Fract. Mech. 2016, 168, 174–189. [Google Scholar] [CrossRef]
- Galouei, M.; Fakhimi, A. Size effect, material ductility and shape of fracture process zone in quasi-brittle materials. Comput. Geotech. 2015, 65, 126–135. [Google Scholar] [CrossRef]
- Wu, Z.J.; Ma, L.L.; Fan, L.F. Investigation of the characteristics of rock fracture process zone using coupled FEM/DEM method. Eng. Fract. Mech. 2018, 200, 355–374. [Google Scholar] [CrossRef]
- Wu, H.J.; Wang, Z.C.; Wang, C. The Mechanism Study of Cracks Propagation of Different Floor Strata Combinations Under Mining. Geotech. Geol. Eng. 2018, 36, 3743–3749. [Google Scholar] [CrossRef]
- Papanastasiou, P.; Durban, D. The Influence of Crack-Face Normal and Shear Stress Loading on Hydraulic Fracture-Tip Singular Plastic Fields. Rock Mech. Rock Eng. 2018, 51, 3191–3203. [Google Scholar] [CrossRef]
- Papanastasiou, P.; Atkinson, C. Representation of crack-tip plasticity in pressure sensitive geomaterials. Int. J. Fract. 2000, 102, 271–286. [Google Scholar] [CrossRef]
- Ai, T.; Wu, C.H.; Zhang, R.; Xiang, Z.Y.; Yuan, Y.Y.; Wang, S.Y. On the Plastic Zone around a Crack Tip in a Rock Specimen. In Proceedings of the 2nd International Conference on Electronic & Mechanical Engineering and Information Technology, Shenyang, China, 7 September 2012; Atlantis Press: Paris, France; pp. 683–686. [Google Scholar]
- Brooks, Z.; Ulm, F.J.; Einstein, H.H. Environmental scanning electron microscopy (ESEM) and nanoindentation investigation of the crack tip process zone in marble. Acta Geotech. 2013, 8, 223–245. [Google Scholar] [CrossRef]
- Erarslan, N. Microstructural investigation of subcritical crack propagation and Fracture Process Zone (FPZ) by the reduction of rock fracture toughness under cyclic loading. Eng. Geol. 2016, 208, 181–190. [Google Scholar] [CrossRef]
- Dutler, N.; Nejati, M.; Valley, B.; Amann, F.; Molinari, G. On the link between fracture toughness, tensile strength, and fracture process zone in anisotropic rocks. Eng. Fract. Mech. 2018, 201, 56–79. [Google Scholar] [CrossRef]
- Zietlow, W.K.; Labuz, J.F. Measurement of the intrinsic process zone in rock using acoustic emission. Int. J. Rock Mech. Min. Sci. 1998, 35, 291–299. [Google Scholar] [CrossRef]
- Vavroa, L.; Součeka, K.; Kytýřb, D.; Fílab, T.; Keršnerc, Z.; Vavroa, M. Visualization of the Evolution of the Fracture Process Zone in Sandstone by Transmission Computed Radiography. Procedia Eng. 2017, 191, 689–696. [Google Scholar] [CrossRef]
- Ghamgosar, M.; Erarslan, N.; Williams, D.J. Experimental Investigation of Fracture Process Zone in Rocks Damaged Under Cyclic Loadings. Exp. Mech. 2017, 57, 97–113. [Google Scholar] [CrossRef]
- Maji, V.B.; Sivakumar, G. Crack Initiation-Propagation and Failure Modes in Rocks. In Geotechnics for Natural and Engineered Sustainable Technologies, Developments in Geotechnical Engineering; Krishna, A.M., Ed.; Springer: Singapore, 2018; pp. 317–328. [Google Scholar]
- Teruo, N. Constitutive Modeling of Geomaterials: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Zheng, Y.R.; Kong, L. Geotechnical Plastic Mechanics; China Architecture & Building Press: Beijing, China, 2019. [Google Scholar]
- Zhang, Q.Q.; Song, H.P.; Gao, C.F. The intrinsic relationship of the thermal stress intensity factor and the temperature difference at the crack surface. J. Therm. Stress. 2024, 47, 897–908. [Google Scholar] [CrossRef]
- Song, H.P.; Xie, K.K.; Gao, C.F. Temperature, thermal flux and thermal stress distribution around an elliptic cavity with temperature-dependent material properties. Int. J. Solids Struct. 2021, 216, 136–144. [Google Scholar]
- Gao, W.; Yuan, S.; Ge, S.S.; Zhao, Z.H.; Han, Y. Theoretical study on the stress intensity factor at the crack tip of a water-bearing rock. Appl. Math. Model. 2025, 142, 115976. [Google Scholar] [CrossRef]
- Kachanov, M. Elastic solids with many cracks: A simple method of analysis. Int. J. Solids Struct. 1987, 23, 23–43. [Google Scholar] [CrossRef]
- Xi, J.Y.; Chen, Z.H.; Zhang, W. Fracture Mechanics Analysis of Unequal Cracks Interaction under Uniaxial Tension. Chin. J. Rock Mech. Eng. 2014, 33 (Suppl. S2), 3625–3630. [Google Scholar]
- Jaeger, J.C.; Cook, N.G.W.; Zimmerman, R.W. Fundamentals of Rock Mechanics; Blackwell Publishing: Malden, MA, USA, 2017. [Google Scholar]
- Gao, W.; Xiao, T.; Wang, X.; Wang, C. Theoretical study on extension of crack tip plastic zone by remote simple tensile considering crack interaction. Eur. J. Mech. A-Solid. 2019, 77, 103814. [Google Scholar] [CrossRef]
- Belytschko, T.; Moes, N.; Usui, S.; Parimik, C. Arbitrary discontinuities in finite elements. Int. J. Numer. Meth. Eng. 2001, 50, 993–1013. [Google Scholar] [CrossRef]
- Stolarska, M.; Chopp, D.L.; Moes, N.; Belyschko, T. Modeling crack growth by level sets in the extended finite element method. Int. J. Numer. Meth. Eng. 2001, 51, 943–960. [Google Scholar] [CrossRef]
- Dawson, E.M.; Roth, W.H.; Drescher, A. Slope stability analysis by strength reduction. Géotechnique 1999, 49, 835–840. [Google Scholar] [CrossRef]
- Xi, J.Y. Interaction and Propagation Research of the Cracks with Unequal Length in Cement Brittle Materials. Ph.D. Thesis, China University of Mining & Technology (Beijing), Beijing, China, 2015. [Google Scholar]





| d/a | rB/m | /m | /2d/% |
|---|---|---|---|
| 0.16 | 0.0789 | −0.0048 | 6.46 |
| 0.18 | 0.0746 | 0.0079 | 9.61 |
| 0.2 | 0.0711 | 0.0198 | 21.81 |
| 0.3 | 0.0593 | 0.0712 | 54.56 |
| 0.4 | 0.0523 | 0.1143 | 68.60 |
| 0.5 | 0.0476 | 0.1524 | 76.20 |
| d/a2 | rB/m | rC/m | /m |
|---|---|---|---|
| 0.22 | 0.1155 | 0.0865 | −0.0260 |
| 0.24 | 0.1124 | 0.0830 | −0.0034 |
| 0.26 | 0.1097 | 0.0799 | 0.0184 |
| 0.3 | 0.1052 | 0.0749 | 0.0599 |
| 0.4 | 0.0977 | 0.0662 | 0.1561 |
| 0.5 | 0.0930 | 0.0606 | 0.2463 |
| Parameter | Young’s Modulus/GPa | Poisson’s Ratio | Internal Frictional Angle/Degree | Adhesion/MPa | Tensile Strength/MPa | Unit Weight/kN/m3 |
|---|---|---|---|---|---|---|
| Value | 12.2 | 0.28 | 30 | 1.2 | 4 | 24.1 |
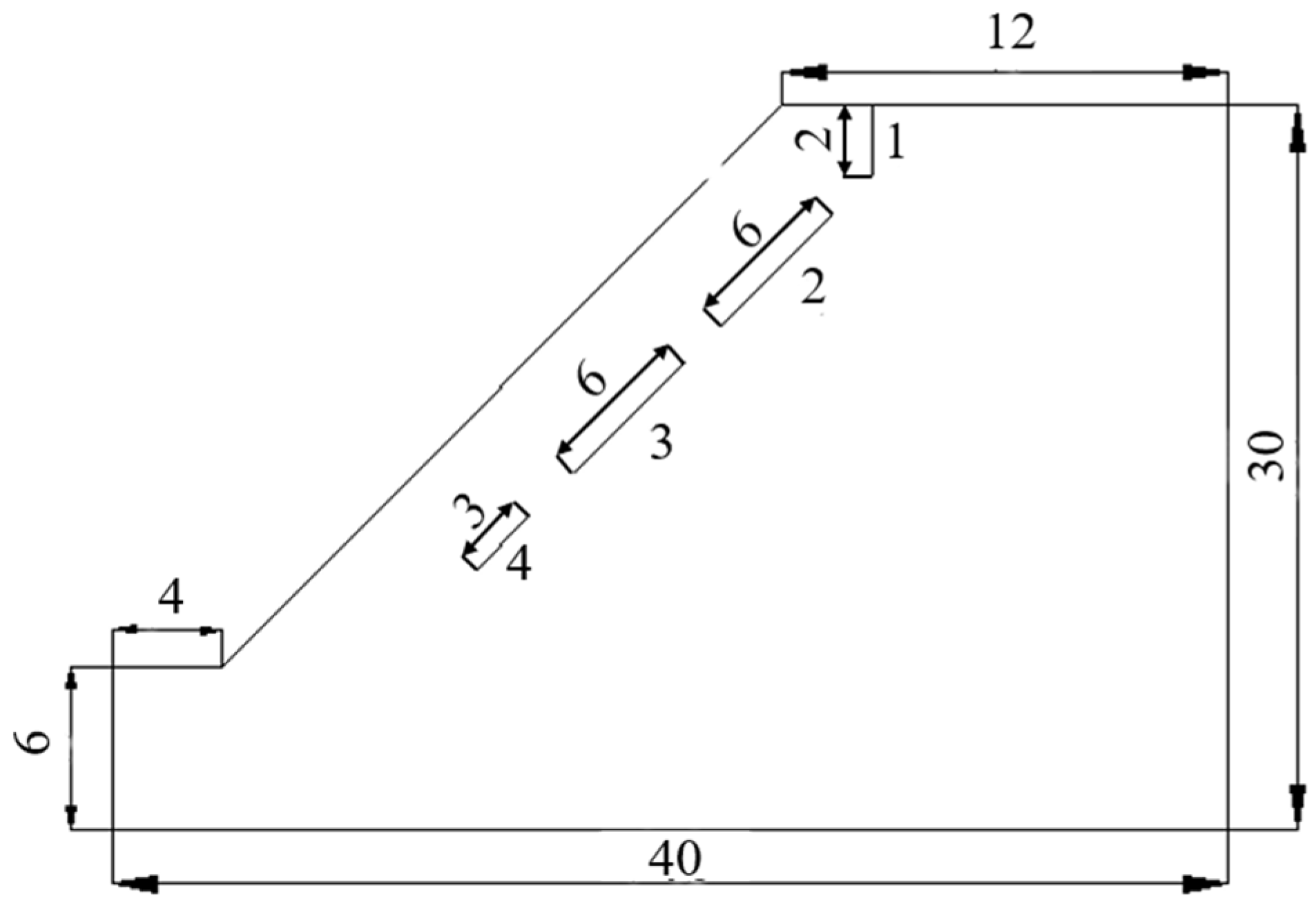
| Number | Dip Angle/Degree | Length/m | Distance/m |
|---|---|---|---|
| 1 | 90 | 2 | 0 |
| 2 | 45 | 6 | 2.4 |
| 3 | 45 | 6 | 2 |
| 4 | 45 | 3 | 2.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Gao, W.; Chen, X.; Wang, X. Theoretical Study on the Failure of Rocks with Preexisting Cracks Considering the Extension of the Crack Tip Plastic Zone. Mathematics 2025, 13, 718. https://doi.org/10.3390/math13050718
Zheng X, Gao W, Chen X, Wang X. Theoretical Study on the Failure of Rocks with Preexisting Cracks Considering the Extension of the Crack Tip Plastic Zone. Mathematics. 2025; 13(5):718. https://doi.org/10.3390/math13050718
Chicago/Turabian StyleZheng, Xuegui, Wei Gao, Xin Chen, and Xu Wang. 2025. "Theoretical Study on the Failure of Rocks with Preexisting Cracks Considering the Extension of the Crack Tip Plastic Zone" Mathematics 13, no. 5: 718. https://doi.org/10.3390/math13050718
APA StyleZheng, X., Gao, W., Chen, X., & Wang, X. (2025). Theoretical Study on the Failure of Rocks with Preexisting Cracks Considering the Extension of the Crack Tip Plastic Zone. Mathematics, 13(5), 718. https://doi.org/10.3390/math13050718









