A Self-Normalized Online Monitoring Method Based on the Characteristic Function
Abstract
1. Introduction
2. Self-Normalized Monitoring Method
3. Asymptotic Properties
- Step 1
- Connect the training samples by their time index numbers to form a ring.
- Step 2
- Draw a series of random blocks for from the ring formed by the training sample, where . Merge these blocks sequentially and select the first observations as the pseudo-sample, denoted as .
- Step 3
- Treat the first m bootstrap observations as training sample and compute the bootstrap statistic:
- Step 4
- Repeat step 2 and 3 for a total of B times to get B bootstrap statistics. Sort these statistics in ascending order as . Then, the critical value is estimated as
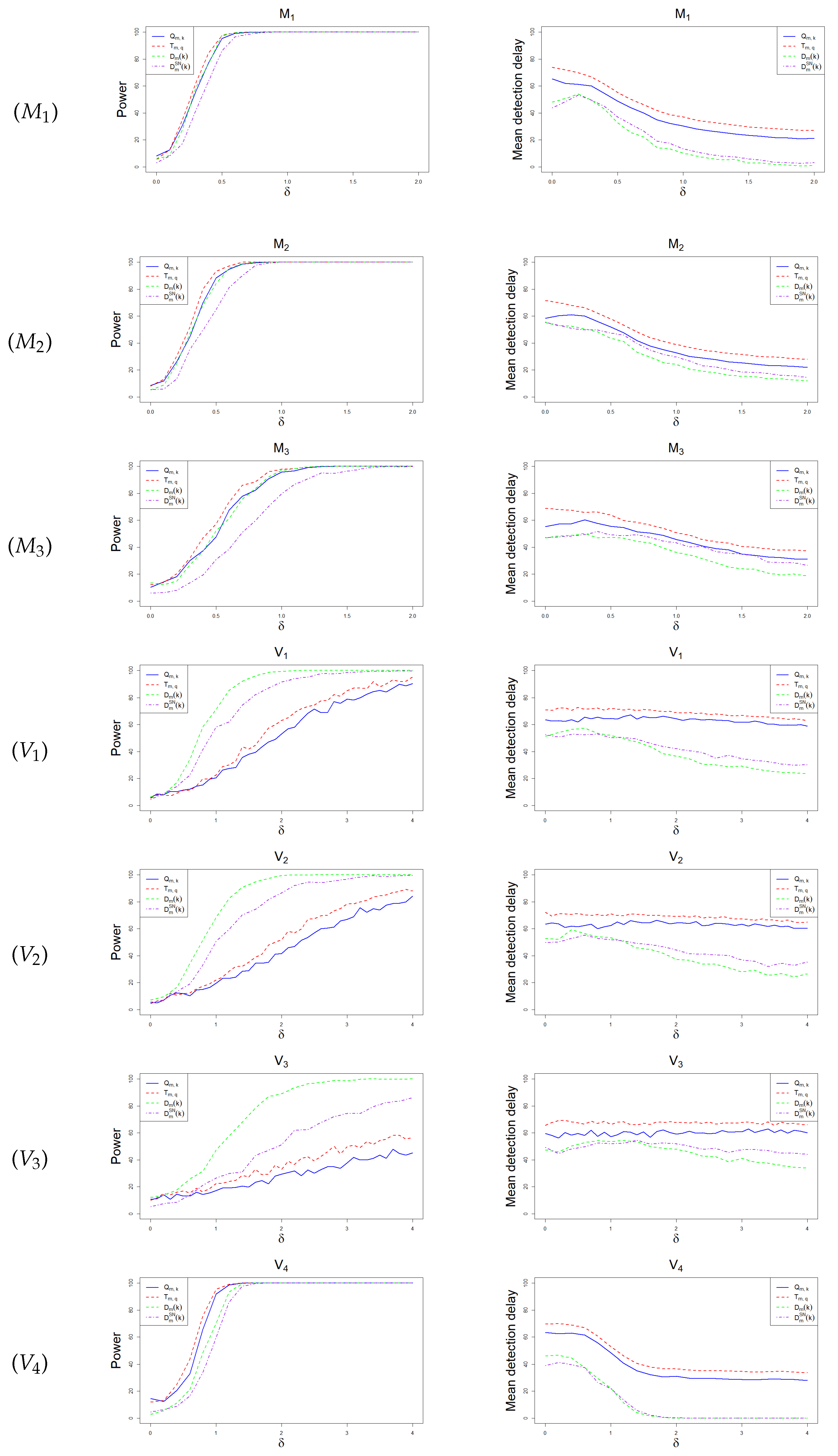
4. Numerical Simulation
4.1. Under the Null Hypothesis
- ()
- , where
- ()
- , where .
- ()
- BEKK-GARCH(1,1) modelwhere
4.2. Under the Alternative Hypothesis
- (M1)
- , where .
- (M2)
- , where .
- (M3)
- As in except that .
- (V1)
- , and , .
- (V2)
- , where and is the same as in .
- (V3)
- As in except that .
- (V4)
- Let denote the BEKK-GARCH (1,1) model as in model and assume its variance changes in such a way that and ,
5. Data Example
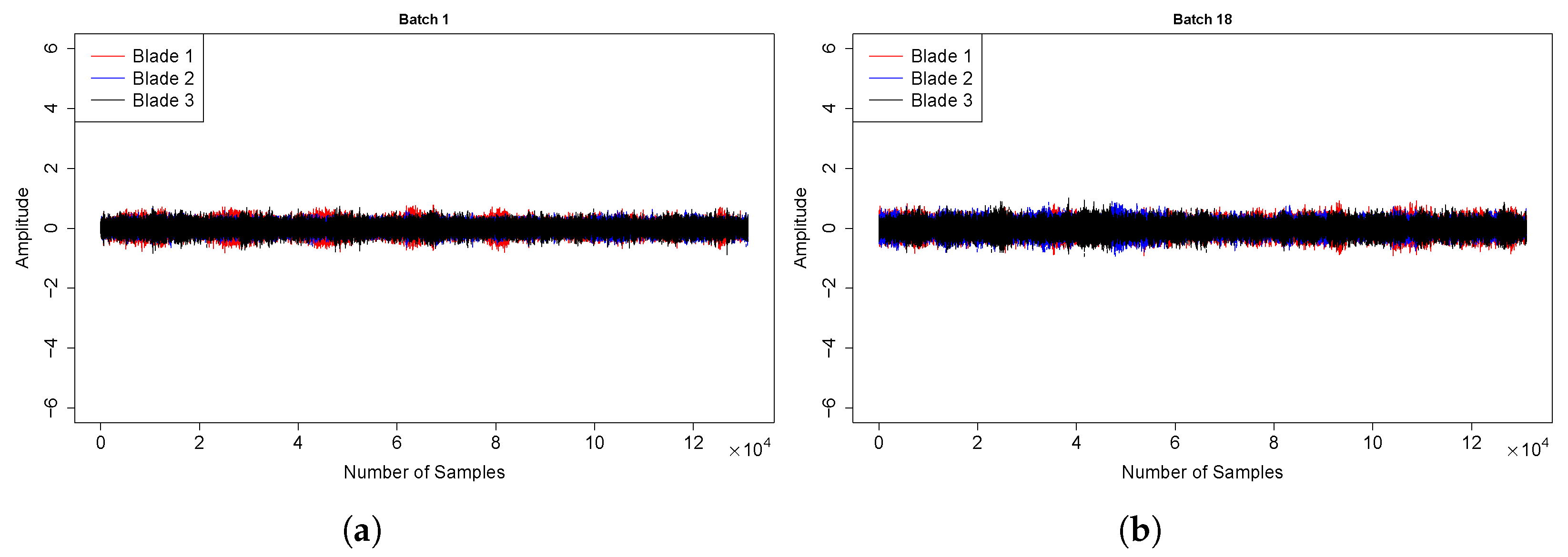
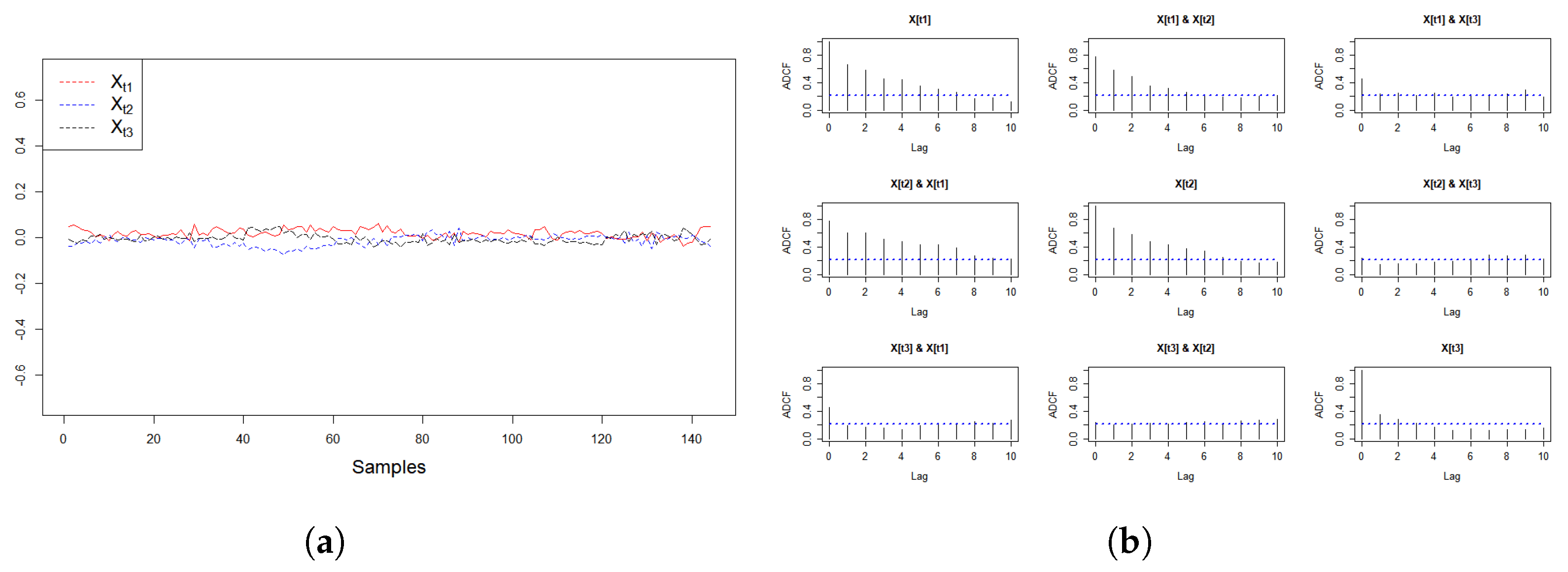
5.1. Wind Turbine #1
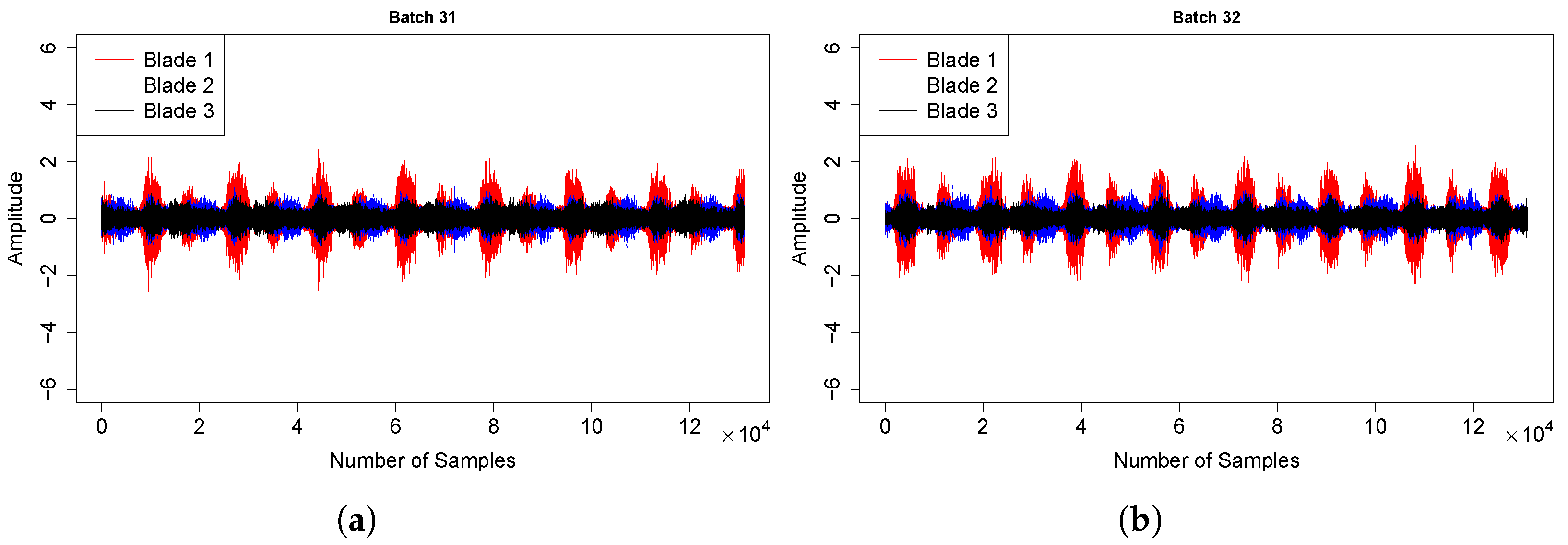
5.2. Wind Turbine #5
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Page, E.S. A test for a change in a parameter occurring at an unknown point. Biometrika 1955, 42, 523–527. [Google Scholar] [CrossRef]
- Csörgö, M.; Horváth, L. Limit Theorems in Change-Point Analysis; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Aue, A.; Horváth, L. Structural breaks in time series. J. Time Ser. Anal. 2013, 34, 1–16. [Google Scholar] [CrossRef]
- Chu, C.S.J.; Stinchcombe, M.; White, H. Monitoring structural change. Econom. J. Econom. Soc. 1996, 64, 1045–1065. [Google Scholar] [CrossRef]
- Aue, A.; Kirch, C. The state of cumulative sum sequential changepoint testing 70 years after Page. Biometrika 2024, 111, 367–391. [Google Scholar] [CrossRef]
- Horváth, L.; Hušková, M.; Kokoszka, P.; Steinebach, J. Monitoring changes in linear models. J. Stat. Plan. Inference 2004, 126, 225–251. [Google Scholar] [CrossRef]
- Aue, A.; Horváth, L.; Kokoszka, P.; Steinebach, J. Monitoring shifts in mean: Asymptotic normality of stopping times. Test 2008, 17, 515–530. [Google Scholar] [CrossRef][Green Version]
- Horváth, L.; Kokoszka, P.; Zhang, A. Monitoring constancy of variance in conditionally heteroskedastic time series. Econom. Theory 2006, 22, 373–402. [Google Scholar] [CrossRef]
- Berkes, I.; Gombay, E.; Horváth, L.; Kokoszka, P. Sequential change-point detection in GARCH (p, q) models. Econom. Theory 2004, 20, 1140–1167. [Google Scholar] [CrossRef]
- Na, O.; Lee, Y.; Lee, S. Monitoring parameter change in time series models. Stat. Methods Appl. 2011, 20, 171–199. [Google Scholar] [CrossRef]
- Kirch, C.; Kamgaing, J.T. On the use of estimating functions in monitoring time series for change points. J. Stat. Plan. Inference 2015, 161, 25–49. [Google Scholar] [CrossRef]
- Gösmann, J.; Stoehr, C.; Heiny, J.; Dette, H. Sequential change point detection in high dimensional time series. Electron. J. Stat. 2022, 16, 3608–3671. [Google Scholar] [CrossRef]
- Sundararajan, R.R.; Pourahmadi, M. Nonparametric change point detection in multivariate piecewise stationary time series. J. Nonparametr. Stat. 2018, 30, 926–956. [Google Scholar] [CrossRef]
- Pein, F.; Sieling, H.; Munk, A. Heterogeneous change point inference. J. R. Stat. Soc. Ser. B Stat. Methodol. 2017, 79, 1207–1227. [Google Scholar] [CrossRef]
- Guo, L.; Modarres, R. Two multivariate online change detection models. J. Appl. Stat. 2022, 49, 427–448. [Google Scholar] [CrossRef] [PubMed]
- Hušková, M.; Hlávka, Z. Nonparametric sequential monitoring. Seq. Anal. 2012, 31, 278–296. [Google Scholar]
- Hlávka, Z.; Hušková, M.; Meintanis, S.G. Change-point methods for multivariate time-series: Paired vectorial observations. Stat. Pap. 2020, 61, 1351–1383. [Google Scholar] [CrossRef]
- Kojadinovic, I.; Verdier, G. Nonparametric sequential change-point detection for multivariate time series based on empirical distribution functions. Electron. J. Stat. 2021, 15, 773–829. [Google Scholar] [CrossRef]
- Hong, Y.; Wang, X.; Wang, S. Testing strict stationarity with applications to macroeconomic time series. Int. Econ. Rev. 2017, 58, 1227–1277. [Google Scholar] [CrossRef]
- Lee, S.; Meintanis, S.G.; Pretorius, C. Monitoring procedures for strict stationarity based on the multivariate characteristic function. J. Multivar. Anal. 2022, 189, 104892. [Google Scholar] [CrossRef]
- Horváth, L.; Kokoszka, P.; Wang, S. Monitoring for a change point in a sequence of distributions. Ann. Stat. 2021, 49, 2271–2291. [Google Scholar] [CrossRef]
- Holmes, M.; Kojadinovic, I.; Verhoijsen, A. Multi-purpose open-end monitoring procedures for multivariate observations based on the empirical distribution function. J. Time Ser. Anal. 2024, 45, 27–56. [Google Scholar] [CrossRef]
- Shao, X.; Zhang, X. Testing for change points in time series. J. Am. Stat. Assoc. 2010, 105, 1228–1240. [Google Scholar] [CrossRef]
- Hoga, Y. Monitoring multivariate time series. J. Multivar. Anal. 2017, 155, 105–121. [Google Scholar] [CrossRef]
- Dette, H.; Gösmann, J. A likelihood ratio approach to sequential change point detection for a general class of parameters. J. Am. Stat. Assoc. 2020, 115, 1361–1377. [Google Scholar] [CrossRef]
- Chan, N.H.; Ng, W.L.; Yau, C.Y. A self-normalized approach to sequential change-point detection for time series. Stat. Sin. 2021, 31, 491–517. [Google Scholar]
- Fan, Y.; de Micheaux, P.L.; Penev, S.; Salopek, D. Multivariate nonparametric test of independence. J. Multivar. Anal. 2017, 153, 189–210. [Google Scholar] [CrossRef]
- Kirch, C.; Stoehr, C. Sequential change point tests based on U-statistics. Scand. J. Stat. 2022, 49, 1184–1214. [Google Scholar] [CrossRef]
- Weber, S.M. Change-Point Procedures for Multivariate Dependent Data. Ph.D. Thesis, Karlsruher Institut für Technologie (KIT), Karlsruhe, Germany, 2017. [Google Scholar]
- Kirch, C.; Weber, S. Modified sequential change point procedures based on estimating functions. Electron. J. Stat. 2018, 12, 1579–1613. [Google Scholar] [CrossRef]
- Politis, D.N.; Romano, J.P. The stationary bootstrap. J. Am. Stat. Assoc. 1994, 89, 1303–1313. [Google Scholar] [CrossRef]
- Politis, D.N.; White, H. Automatic Block-Length Selection for the Dependent Bootstrap. Econom. Rev. 2004, 23, 53–70. [Google Scholar] [CrossRef]
- Jentsch, C.; Rao, S.S. A test for second order stationarity of a multivariate time series. J. Econom. 2015, 185, 124–161. [Google Scholar] [CrossRef]
- Giacomini, R.; Politis, D.N.; White, H. A warp-speed method for conducting Monte Carlo experiments involving bootstrap estimators. Econom. Theory 2013, 29, 567–589. [Google Scholar] [CrossRef]
- Kojadinovic, I. npcp: Some Nonparametric CUSUM Tests for Change-Point Detection in Possibly Multivariate Observations; R Package Version 0.2-6; 2024. Available online: https://CRAN.R-project.org/package=npcp (accessed on 5 December 2024).
- James, N.A.; Zhang, W.; Matteson, D.S. ecp: An R Package for Nonparametric Multiple Change Point Analysis of Multivariate Data; R Package Version 3.1.6; 2019. Available online: https://CRAN.R-project.org/package=ecp (accessed on 5 December 2024).
- Zhou, Z. Measuring nonlinear dependence in time-series, a distance correlation approach. J. Time Ser. Anal. 2012, 33, 438–457. [Google Scholar] [CrossRef]
- Billingsley, P. Convergence of Probability Measures; John Wiley & Sons: Hoboken, NJ, USA, 1968. [Google Scholar]
- Hlávka, Z.; Hušková, M.; Kirch, C.; Meintanis, S.G. Fourier–type tests involving martingale difference processes. Econom. Rev. 2017, 36, 468–492. [Google Scholar] [CrossRef]
- Ibragimov, I.A.; Hasminskii, R.Z. Statistical Estimation: Asymptotic Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Yokoyama, R. Moment bounds for stationary mixing sequences. Z. Wahrscheinlichkeitstheorie Verwandte Geb. 1980, 52, 45–57. [Google Scholar] [CrossRef]

| m | L | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 1 | 5.7 | 7.2 | 10.5 | 11.5 | 22.4 | 4.8 | 6.7 | 7.5 | 17.0 | 7.2 | 9.7 | 9.7 | |
| 2 | 5.2 | 8.2 | 11.6 | 14.0 | 23.8 | 6.0 | 5.4 | 5.4 | 14.2 | 6.4 | 12.2 | 8.6 | ||
| 3 | 5.4 | 8.7 | 9.8 | 13.4 | 24.4 | 5.7 | 3.5 | 7.7 | 16.0 | 6.2 | 11.8 | 10.1 | ||
| 200 | 1 | 6.5 | 6.6 | 8.6 | 11.2 | 14.9 | 6.5 | 4.9 | 7.0 | 12.6 | 6.0 | 10.6 | 9.7 | |
| 2 | 4.7 | 6.7 | 8.3 | 11.4 | 17.8 | 5.8 | 4.9 | 5.4 | 12.0 | 5.8 | 9.5 | 7.9 | ||
| 3 | 5.2 | 7.0 | 7.9 | 10.4 | 20.2 | 5.8 | 5.1 | 6.2 | 12.2 | 5.5 | 8.5 | 8.5 | ||
| 100 | 1 | 5.1 | 8.0 | 10.7 | 12.8 | 23.6 | 4.5 | 4.8 | 3.5 | 10.9 | 7.3 | 12.3 | 9.7 | |
| 2 | 5.8 | 7.0 | 9.8 | 12.8 | 24.3 | 3.2 | 3.9 | 3.5 | 12.2 | 7.0 | 9.4 | 8.9 | ||
| 3 | 5.3 | 7.6 | 10.5 | 13.2 | 26.7 | 6.2 | 4.4 | 6.2 | 14.7 | 6.8 | 11.0 | 12.2 | ||
| 200 | 1 | 4.7 | 7.5 | 8.0 | 11.8 | 16.9 | 5.2 | 4.6 | 4.8 | 9.5 | 5.5 | 9.6 | 9.1 | |
| 2 | 5.3 | 6.4 | 8.9 | 11.1 | 17.3 | 4.3 | 4.0 | 3.7 | 10.2 | 5.9 | 8.6 | 7.8 | ||
| 3 | 5.0 | 7.1 | 8.2 | 12.0 | 18.8 | 4.5 | 4.6 | 5.9 | 12.6 | 5.3 | 9.2 | 8.7 | ||
| 100 | 1 | 5.8 | 7.2 | 11.4 | 13.9 | 31.5 | 3.9 | 5.9 | 9.6 | 14.5 | 7.0 | 13.3 | 4.2 | |
| 2 | 5.7 | 8.8 | 12.2 | 16.0 | 29.3 | 5.1 | 6.2 | 8.4 | 12.6 | 6.2 | 10.9 | 3.4 | ||
| 3 | 4.9 | 6.3 | 9.4 | 10.7 | 34.0 | 3.7 | 5.6 | 9.7 | 14.2 | 5.2 | 11.5 | 3.7 | ||
| 200 | 1 | 4.6 | 7.3 | 9.5 | 12.1 | 23.3 | 3.7 | 4.8 | 7.2 | 9.7 | 6.6 | 10.4 | 4.9 | |
| 2 | 4.0 | 7.2 | 8.7 | 10.1 | 19.6 | 4.1 | 5.5 | 9.9 | 8.5 | 6.8 | 11.2 | 5.7 | ||
| 3 | 5.2 | 7.5 | 9.2 | 10.0 | 23.5 | 4.4 | 4.7 | 9.0 | 8.5 | 7.5 | 9.8 | 4.8 | ||
| 100 | 1 | 5.0 | 4.0 | 5.6 | 6.6 | 4.0 | 3.7 | 4.4 | 3.6 | 3.4 | 4.7 | 6.3 | 4.2 | |
| 2 | 4.5 | 5.1 | 4.9 | 5.7 | 5.4 | 3.6 | 4.1 | 4.4 | 4.6 | 4.6 | 6.5 | 3.8 | ||
| 3 | 5.9 | 5.6 | 4.3 | 4.1 | 4.3 | 2.9 | 3.1 | 3.9 | 3.7 | 4.0 | 6.2 | 4.5 | ||
| 200 | 1 | 4.8 | 3.8 | 5.0 | 3.9 | 5.2 | 4.1 | 3.1 | 4.8 | 5.8 | 4.9 | 4.1 | 5.2 | |
| 2 | 4.3 | 5.3 | 4.3 | 5.2 | 5.4 | 2.5 | 5.3 | 4.5 | 3.1 | 4.4 | 5.2 | 5.5 | ||
| 3 | 5.1 | 4.0 | 5.1 | 4.6 | 3.5 | 3.9 | 3.9 | 4.1 | 3.2 | 5.8 | 5.6 | 5.4 |
| m | L | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 100 | 1 | 90.2 | 82.5 | 63.7 | 36.4 | 30.5 | 20.4 | 62.8 | |
| 2 | 91.5 | 89.3 | 73.1 | 40.6 | 36.3 | 21.6 | 65.6 | ||
| 3 | 94.6 | 91.8 | 74.8 | 49.2 | 42.8 | 30.2 | 66.3 | ||
| 200 | 1 | 94.5 | 94.2 | 77.9 | 53.8 | 52.3 | 29.6 | 79.7 | |
| 2 | 97.4 | 96.6 | 81.4 | 59.3 | 57.4 | 35.5 | 84.2 | ||
| 3 | 96.9 | 97.1 | 86.7 | 68.4 | 60.0 | 41.3 | 87.1 | ||
| 100 | 1 | 99.0 | 98.6 | 84.3 | 45.3 | 33.1 | 26.5 | 82.5 | |
| 2 | 100.0 | 99.9 | 95.4 | 64.0 | 53.3 | 33.0 | 91.8 | ||
| 3 | 100.0 | 100.0 | 98.2 | 82.4 | 74.6 | 46.1 | 97.6 | ||
| 200 | 1 | 100.0 | 99.9 | 95.5 | 75.3 | 67.6 | 36.4 | 95.3 | |
| 2 | 100.0 | 100.0 | 99.4 | 93.3 | 88.3 | 52.5 | 99.2 | ||
| 3 | 100.0 | 100.0 | 99.9 | 97.1 | 95.5 | 73.9 | 99.7 | ||
| 100 | 1 | 91.1 | 87.7 | 70.9 | 75.3 | 70.3 | 63.4 | 56.7 | |
| 2 | 91.0 | 91.8 | 80.4 | 80.9 | 76.1 | 64.2 | 43.3 | ||
| 3 | 94.6 | 93.5 | 79.6 | 79.6 | 78.5 | 69.7 | 45.4 | ||
| 200 | 1 | 95.7 | 95.2 | 83.0 | 89.0 | 87.3 | 74.8 | 63.6 | |
| 2 | 98.9 | 97.1 | 89.0 | 90.7 | 89.3 | 80.2 | 57.6 | ||
| 3 | 99.1 | 98.5 | 89.7 | 93.0 | 90.6 | 80.5 | 53.7 | ||
| 100 | 1 | 84.1 | 82.5 | 52.1 | 62.4 | 48.8 | 37.2 | 45.2 | |
| 2 | 82.6 | 83.3 | 59.1 | 69.9 | 65.7 | 39.1 | 43.7 | ||
| 3 | 87.4 | 88.0 | 66.6 | 72.1 | 69.8 | 43.8 | 39.8 | ||
| 200 | 1 | 95.1 | 90.8 | 71.3 | 78.8 | 76.8 | 59.3 | 47.0 | |
| 2 | 97.5 | 94.7 | 75.8 | 85.0 | 82.0 | 61.8 | 48.0 | ||
| 3 | 96.5 | 94.5 | 82.9 | 86.3 | 80.7 | 66.8 | 44.9 |
| Wind Turbine #1 | L | p Value | |
|---|---|---|---|
| 1 | NA | 0.098 | |
| 2 | NA | 0.076 | |
| 3 | 509 | 0.037 | |
| 4 | 519 | 0.026 | |
| 5 | 658 | 0.039 | |
| 1 | NA | 0.468 | |
| 2 | NA | 0.454 | |
| 3 | NA | 0.377 | |
| 4 | NA | 0.355 | |
| 5 | NA | 0.389 |
| Wind Turbine #5 | L | p Value | |
|---|---|---|---|
| 1 | 225 | <0.001 | |
| 2 | 229 | <0.001 | |
| 3 | 230 | <0.001 | |
| 1 | 246 | 0.006 | |
| 2 | 249 | 0.013 | |
| 3 | 253 | 0.021 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yang, B. A Self-Normalized Online Monitoring Method Based on the Characteristic Function. Mathematics 2025, 13, 710. https://doi.org/10.3390/math13050710
Wang Y, Yang B. A Self-Normalized Online Monitoring Method Based on the Characteristic Function. Mathematics. 2025; 13(5):710. https://doi.org/10.3390/math13050710
Chicago/Turabian StyleWang, Yang, and Baoying Yang. 2025. "A Self-Normalized Online Monitoring Method Based on the Characteristic Function" Mathematics 13, no. 5: 710. https://doi.org/10.3390/math13050710
APA StyleWang, Y., & Yang, B. (2025). A Self-Normalized Online Monitoring Method Based on the Characteristic Function. Mathematics, 13(5), 710. https://doi.org/10.3390/math13050710






