Identifying Higher-Order Moment Risk Contagion Between the US Dollar Exchange Rate and China’s Major Asset Classes
Abstract
1. Introduction
2. Methodology
2.1. Capital Asset Pricing Model Specification and Co-Higher-Moment Factors
2.2. Contagion Effect Test Based on Co-Higher-Order Moments
2.2.1. Risk Spillover Test Based on Correlation
2.2.2. Risk Spillover Test Based on Co-Skewness
2.2.3. Risk Spillover Test Based on Co-Kurtosis
2.2.4. Risk Spillover Test Based on Co-Volatility
3. Data Selection
4. Empirical Research
4.1. Data Preprocessing
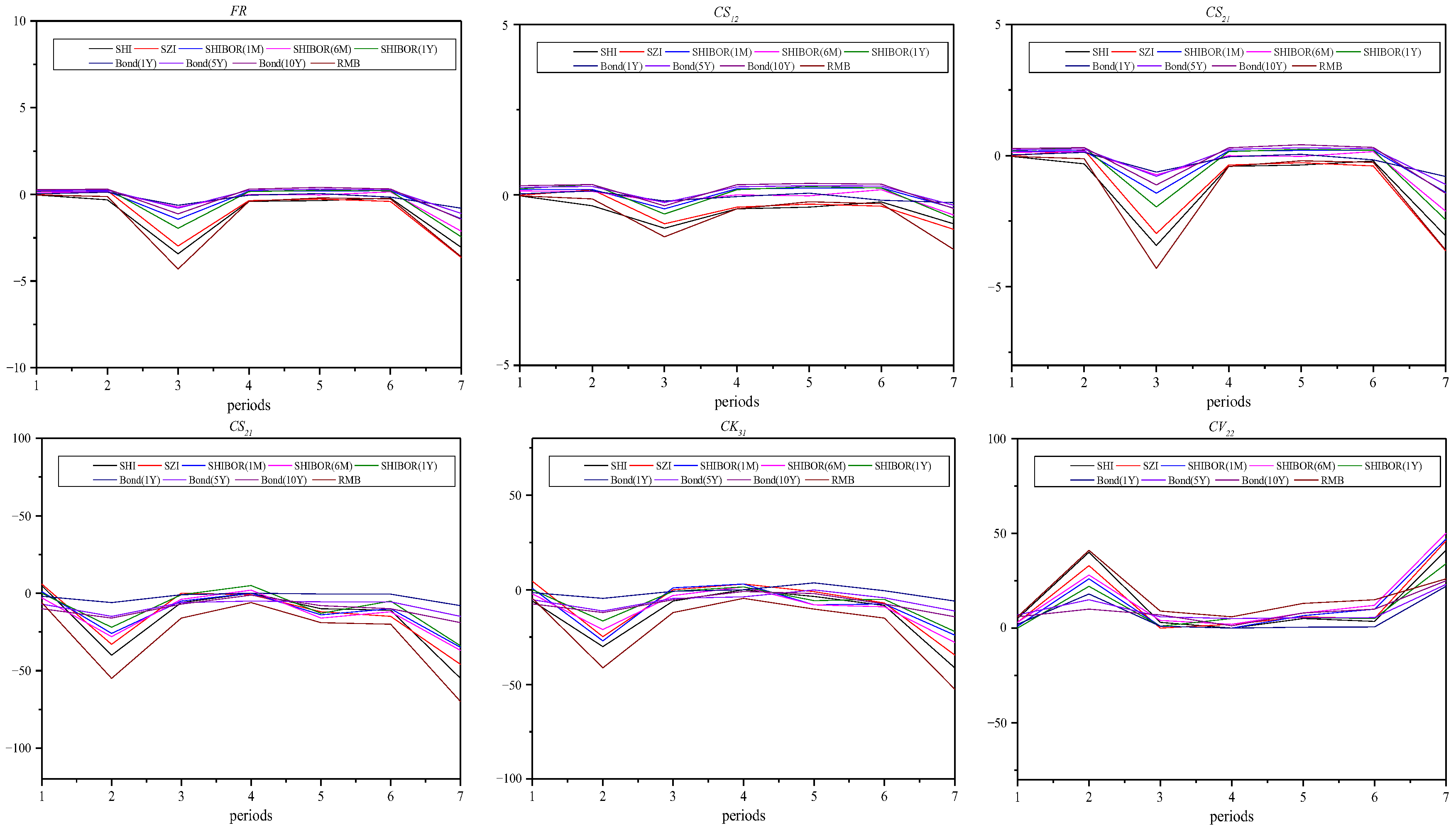
4.2. Dynamics of Various Moment Risk Linkages
4.3. Contagion Test Based on Various Co-Higher-Moment Factors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmad, W.; Sehgal, S.; Bhanumurthy, N.R. Eurozone crisis and BRIICKS stock markets: Contagion or market interdependence? Econ. Model 2013, 33, 209–225. [Google Scholar] [CrossRef]
- Bello, J.; Guo, J.; Newaz, M.K. Financial contagion effects of major crises in African stock markets. Int. Rev. Financ. Anal. 2022, 82, 102128. [Google Scholar] [CrossRef]
- Luo, T.; Zhang, L.X.; Sun, H.P.; Bai, J.C. Enhancing exchange rate volatility prediction accuracy: Assessing the influence of different indices on the USD/CNY exchange rate. Financ. Res. Lett. 2023, 58, 104483. [Google Scholar] [CrossRef]
- You, K.F.; Sarantis, N. A twelve-area model for the equilibrium Chinese Yuan/US dollar nominal exchange rate. J. Int. Financ. Mark. Inst. Money 2012, 22, 151–170. [Google Scholar] [CrossRef]
- Chancharat, S.; Sinlapates, P. Dependences and dynamic spillovers across the crude oil and stock markets throughout the COVID-19 pandemic and Russia-Ukraine conflict: Evidence from the ASEAN+6. Financ. Res. Lett. 2023, 57, 104249. [Google Scholar] [CrossRef]
- Wang, Y.; You, X.; Zhang, Y.; Yang, H. Does the risk spillover in global financial markets intensify during major public health emergencies? Evidence from the COVID-19 crisis. Pac.-Basin Financ. J. 2024, 83, 102272. [Google Scholar] [CrossRef]
- Zhang, W.; He, X.; Hamori, S. The impact of the COVID-19 pandemic and Russia-Ukraine war on multiscale spillovers in green finance markets: Evidence from lower and higher order moments. Int. Rev. Financ. Anal. 2023, 89, 102735. [Google Scholar] [CrossRef]
- Ahelegbey, D.F.; Giudici, P.; Hashem, S.Q. Network VAR models to measure financial contagion. N. Am. J. Econ. Financ. 2021, 55, 101318. [Google Scholar] [CrossRef]
- Akhtaruzzaman, M.; Boubaker, S.; Sensoy, A. Financial contagion during COVID-19 crisis. Financ. Res. Lett. 2021, 38, 101604. [Google Scholar] [CrossRef] [PubMed]
- Arfaoui, N.; Yousaf, I. Impact of covid-19 on volatility spillovers across international markets: Evidence from VAR asymmetric Bekk-Garch model. Ann. Financ. Econ. 2022, 17, 2250004. [Google Scholar] [CrossRef]
- Abduraimova, K. Contagion and tail risk in complex financial networks. J. Bank. Financ. 2022, 143, 106560. [Google Scholar] [CrossRef]
- Aboura, S.; Chevallier, J. Tail risk and the return-volatility relation. Res. Int. Bus. Financ. 2018, 46, 16–29. [Google Scholar] [CrossRef]
- Abuzayed, B.; Al-Fayoumi, N. Risk spillover from crude oil prices to GCC stock market returns: New evidence during the COVID-19 outbreak. N. Am. J. Econ. Financ. 2021, 58, 101476. [Google Scholar] [CrossRef]
- Forbes, K.J.; Rigobon, R. No Contagion, Only Interdependence: Measuring Stock Market Comovements. J. Financ. 2002, 57, 2223–2261. [Google Scholar] [CrossRef]
- Luchtenberg, K.F.; Vu, Q.V. The 2008 financial crisis: Stock market contagion and its determinants. Res. Int. Bus. Financ. 2015, 33, 178–203. [Google Scholar] [CrossRef]
- Wang, B.; Xiao, Y. Risk spillovers from China’s and the US stock markets during high-volatility periods: Evidence from East Asianstock markets. Int. Rev. Financ. Anal. 2023, 86, 102538. [Google Scholar] [CrossRef]
- Kilic, E. Contagion effects of U.S. Dollar and Chinese Yuan in forward and spot foreign exchange markets. Econ. Model. 2017, 62, 51–67. [Google Scholar] [CrossRef]
- Naresh, G.; Vasudevan, G.; Mahalakshmi, S.; Thiyagarajan, S. Spillover effect of US dollar on the stock indices of BRICS. Res. Int. Bus. Financ. 2018, 44, 359–368. [Google Scholar] [CrossRef]
- Fry, R.; Martin, V.L.; Tang, C. A new class of tests of contagion with applications. J. Bus. Econ. Stat. 2010, 28, 423–437. [Google Scholar] [CrossRef]
- Fry-Mckibbin, R.; Hsiao, C.Y.L. External Dependence Tests for Contagion; ACT: Bengaluru, India; Centre for Applied Macroeconomic Analysis: Canberra, Australia, 2015. [Google Scholar]
- Lye, J.N.; Martin, V.L. Robust estimation, nonnormalities, and generalized exponential distributions. J. Am. Stat. Assoc. 1993, 88, 261–267. [Google Scholar] [CrossRef]
- Fry-Mckibbin, R.; Martin, V.L.; Tang, C. Financial contagion and asset pricing. J. Bank. Financ. 2014, 47, 296–308. [Google Scholar] [CrossRef]
- Wen, X.Q.; Cheng, H. Which is the safe haven for emerging stock markets, gold or the US dollar? Emerg. Mark. Rev. 2018, 35, 69–90. [Google Scholar] [CrossRef]
- Druck, P.; Magud, N.E.; Mariscal, R. Collateral damage: Dollar strength and emerging markets’ growth. N. Am. J. Econ. Financ. 2018, 43, 97–117. [Google Scholar] [CrossRef]
- Kunkler, M. The Chinese renminbi’s co-movement with the US dollar: Addressing the numéraire issue. Financ. Res. Lett. 2021, 40, 101741. [Google Scholar] [CrossRef]
- Black, F. Capital market equilibrium with restricted borrowing. J. Bus. 1972, 45, 444–455. [Google Scholar] [CrossRef]
- Lintner, J. The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Rev. Econ. Stat. 1965, 47, 13–37. [Google Scholar] [CrossRef]
- Sharpe, W.F. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Financ. 1964, 19, 425–442. [Google Scholar]
- Martellini, L.; Ziemann, V. Improved estimates of higher-order comoments and implications for portfolio selection. Rev. Financ. Stud. 2010, 23, 1467–1502. [Google Scholar] [CrossRef]
- Hwang, S.; Satchel, S.E. Modelling emerging market risk premia using higher moments. Int. J. Financ. Econ. 1999, 4, 271–296. [Google Scholar] [CrossRef]
- Jiang, Z.; Krishnamurthy, A.; Lustig, H. Foreign Safe Asset Demand and the Dollar Exchange Rate. J. Financ. 2021, 76, 1049–1089. [Google Scholar] [CrossRef]
- Farooque, O.A.; Baghdadi, G.; Trinh, H.H.; Khandaker, S. Stock liquidity during COVID-19 crisis: A cross-country analysis of developed and emerging economies, and economic policy uncertainty. Emerg. Mark. Rev. 2023, 55, 101025. [Google Scholar] [CrossRef]
- Yarovaya, L.; Brzeszczyński, J.; Lau CK, M. Intra- and inter-regional return and volatility spillovers across emerging and developed markets: Evidence from stock indices and stock index futures. Int. Rev. Financ. Anal. 2016, 43, 96–114. [Google Scholar] [CrossRef]
- Boubaker, S.; Jouini, J.; Lahiani, A. Financial contagion between the US and selected developed and emerging countries: The case of the subprime crisis. Q. Rev. Econ. Financ. 2016, 61, 14–28. [Google Scholar] [CrossRef]
| Market Regime | Starting Date | Ending Date | USD Operating Trend |
|---|---|---|---|
| Regime 1 (Subsample 1) | 1 January 2010 | 26 July 2011 | Depreciation |
| Regime 2 (Subsample 2) | 27 July 2011 | 17 May 2014 | Consolidation |
| Regime 3 (Subsample 3) | 18 May 2014 | 22 May 2015 | Appreciation |
| Regime 4 (Subsample 4) | 23 May 2015 | 31 March 2017 | Consolidation |
| Regime 5 (Subsample 5) | 1 April 2017 | 11 March 2018 | Depreciation |
| Regime 6 (Subsample 6) | 12 March 2018 | 7 May 2021 | Consolidation |
| Regime 7 (Subsample 7) | 8 May 2021 | 30 June 2023 | Appreciation |
| Mean | Std. Dev | Skewness | Kurtosis | Jarque-Bera Test | ADF Test | Q(10) | |
|---|---|---|---|---|---|---|---|
| Full sample | 0.011 | 1.3254 | 0.652 *** | 3.978 *** | 1252.141 *** | −36.841 *** | 658.548 *** |
| Subsample 1 | −0.142 | 2.312 | −0.854 *** | 4.958 *** | 101.325 *** | −25.584 *** | 4.051 ** |
| Subsample 2 | 0.011 | 1.251 | 0.125 | 1.958 *** | 79.854 *** | −19.865 *** | 1.987 |
| Subsample 3 | 0.212 | 2.521 | 1.212 *** | 5.958 *** | 50.854 | −9.655 *** | 8.954 *** |
| Subsample 4 | 0.021 | 1.351 | 0.235 | 2.548 *** | 12.846 *** | −7.837 *** | 1.987 * |
| Subsample 5 | −1.685 | 3.645 | 0.856 *** | 4.185 *** | 20.845 *** | −6.846 *** | 3.145 *** |
| Subsample 6 | 0.023 | 0.978 | 1.521 | 2.314 *** | 60.545 *** | −6.667 *** | 2.084 |
| Subsample 7 | 0.545 | 2.207 | 0.438 *** | 6.854 *** | 87.854 *** | −13.854 *** | 16.847 *** |
| SHI | SZI | SHIBOR (1M) | SHIBOR (6M) | SHIBOR (1Y) | Bond (1Y) | Bond (5Y) | Bond (10Y) | RMB | ||
|---|---|---|---|---|---|---|---|---|---|---|
| FR | S1 vs. S2 | 0.247 | 0.337 | 0.26 | 0.302 | 0.332 | 0.324 | 0.424 | 0.496 | 2.304 ** |
| S2 vs. S3 | 0.952 | 0.522 | 0.646 | 0.808 | 0.922 | 0.265 | 0.347 | 5.405 *** | 6.521 *** | |
| S3 vs. S4 | 1.231 * | 0.325 | 0.389 | 0.471 | 0.529 | 0.115 | 0.151 | 0.176 | 3.032 ** | |
| S4 vs. S5 | 0.854 | 0.748 | 0.133 | 0.135 | 0.137 | 0.521 | 0.683 | 1.797 ** | 5.789 *** | |
| S5 vs. S6 | 0.668 | 0.647 | 0.25 | 0.289 | 0.316 | 0.328 | 0.430 | 2.502 ** | 5.965 *** | |
| S6 vs. S7 | 2.128 * | 0.987 * | 0.477 | 0.586 | 0.664 | 0.268 | 0.351 | 3.410 ** | 7.125 *** | |
| CS12 | S1 vs. S2 | 0.951 | 0.498 | 0.292 | 0.382 | 0.446 | 0.135 | 0.177 | 0.207 | 0.302 |
| S2 vs. S3 | 0.745 | 0.389 | 0.239 | 0.312 | 0.412 | 0.521 | 0.683 | 0.797 | 2.058 ** | |
| S3 vs. S4 | 0.733 | 1.133 | 0.104 | 0.136 | 0.158 | 0.264 | 0.346 | 0.404 | 1.978 * | |
| S4 vs. S5 | 0.695 | 1.195 | 0.469 | 0.615 | 1.617 | 0.008 | 0.010 | 0.012 | 3.521 ** | |
| S5 vs. S6 | 0.515 | 0.798 | 0.295 | 0.387 | 2.252 | 0.125 | 0.164 | 0.191 | 2.846 ** | |
| S6 vs. S7 | 2.158 ** | 1.158 ** | 0.241 | 0.316 | 0.307 | 0.352 | 0.461 | 0.539 | 1.854 * | |
| CS21 | S1 vs. S2 | 3.698 ** | 4.058 ** | 0.104 | 0.137 | 0.159 | 0.120 | 0.157 | 0.184 | 1.096 |
| S2 vs. S3 | 6.945 *** | 7.845 *** | 0.229 | 0.300 | 0.349 | 0.365 | 0.478 | 0.558 | 2.546 ** | |
| S3 vs. S4 | 4.041 | 3.941 ** | 1.394 * | 0.516 | 0.603 | 0.652 | 0.854 | 0.998 | 1.118 * | |
| S4 vs. S5 | 1.124 | 0.324 | 0.411 | 0.539 | 0.629 | 0.485 | 0.635 | 0.742 | 3.749 ** | |
| S5 vs. S6 | 6.987 *** | 7.187 *** | 0.255 | 0.335 | 0.391 | 0.398 | 0.521 | 0.609 | 2.595 ** | |
| S6 vs. S7 | 9.845 *** | 10.045 *** | 0.104 | 0.137 | 0.159 | 0.274 | 0.359 | 0.419 | 14.896 *** | |
| CK13 | S1 vs. S2 | 3.945 ** | 5.155 ** | 0.171 | 1.207 * | 0.234 | 0.105 | 0.138 | 0.161 | 6.545 ** |
| S2 vs. S3 | 8.454 *** | 7.694 *** | 0.415 | 0.528 | 0.608 | 0.231 | 0.303 | 9.353 *** | 52.654 | |
| S3 vs. S4 | 2.152 ** | 3.152 ** | 0.702 | 0.904 | 1.048 | 0.398 | 0.521 | 0.609 | 1.565 | |
| S4 vs. S5 | 7.954 *** | 6.874 *** | 0.535 | 0.685 | 0.792 | 0.415 | 0.544 | 0.635 | 3.945 ** | |
| S5 vs. S6 | 6.978 *** | 7.978 *** | 0.448 | 0.998 * | 0.659 | 0.258 | 0.338 | 0.395 | 4.854 ** | |
| S6 vs. S7 | 10.251 *** | 8.921 *** | 0.324 | 0.409 | 0.469 | 0.162 | 0.212 | 2.248 * | 16.854 *** | |
| CK31 | S1 vs. S2 | 2.125 ** | 1.865 ** | 0.326 | 0.393 | 0.442 | 0.215 | 0.282 | 0.329 | 6.845 ** |
| S2 vs. S3 | 7.958 *** | 6.668 *** | 0.475 | 0.588 | 0.668 | 0.364 | 0.477 | 0.557 | 11.985 *** | |
| S3 vs. S4 | 0.568 | 0.389 | 0.526 | 0.655 | 0.746 | 0.415 | 0.544 | 0.635 | 1.201 | |
| S4 vs. S5 | 0.415 | 2.265 ** | 0.496 | 0.615 | 0.713 | 0.385 | 0.504 | 0.589 | 3.684 ** | |
| S5 vs. S6 | 1.689 ** | 3.607 ** | 0.375 | 0.457 | 0.515 | 0.264 | 0.346 | 0.404 | 4.854 ** | |
| S6 vs. S7 | 1.895 ** | 3.812 ** | 1.296 *** | 1.663 *** | 1.924 *** | 1.185 * | 1.552 * | 1.813 | 22.985 *** | |
| CV22 | S1 vs. S2 | 5.451 ** | 4.951 ** | 0.312 | 0.441 | 0.532 | 0.415 | 0.544 | 0.635 | 5.978 ** |
| S2 vs. S3 | 4.125 ** | 3.795 ** | 0.262 | 0.375 | 0.455 | 0.365 | 0.478 | 0.558 | 12.845 *** | |
| S3 vs. S4 | 0.648 | 0.568 | 0.195 | 0.287 | 0.353 | 0.298 | 0.390 | 0.456 | 9.856 ** | |
| S4 vs. S5 | 2.125 ** | 3.145 ** | 0.209 | 0.306 | 0.374 | 0.312 | 0.409 | 0.477 | 10.854 *** | |
| S5 vs. S6 | 0.514 | 0.778 | 0.178 | 0.265 | 0.327 | 0.281 | 0.368 | 0.430 | 9.989 *** | |
| S6 vs. S7 | 0.498 | 0.877 | 0.354 | 0.685 | 0.261 | 0.952 * | 1.332 * | 0.364 | 38.654 *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Z.; Zhang, C.; Li, J. Identifying Higher-Order Moment Risk Contagion Between the US Dollar Exchange Rate and China’s Major Asset Classes. Mathematics 2025, 13, 707. https://doi.org/10.3390/math13050707
Zou Z, Zhang C, Li J. Identifying Higher-Order Moment Risk Contagion Between the US Dollar Exchange Rate and China’s Major Asset Classes. Mathematics. 2025; 13(5):707. https://doi.org/10.3390/math13050707
Chicago/Turabian StyleZou, Zongfeng, Chao Zhang, and Judong Li. 2025. "Identifying Higher-Order Moment Risk Contagion Between the US Dollar Exchange Rate and China’s Major Asset Classes" Mathematics 13, no. 5: 707. https://doi.org/10.3390/math13050707
APA StyleZou, Z., Zhang, C., & Li, J. (2025). Identifying Higher-Order Moment Risk Contagion Between the US Dollar Exchange Rate and China’s Major Asset Classes. Mathematics, 13(5), 707. https://doi.org/10.3390/math13050707






